A Multi-Objective Crossover Parallel Combinatorial Optimization (MCPCO) Model for Site Selection of Catalyst Elements in Urban Micro-Renewal

Abstract

The site selection of catalyst elements plays a crucial role in urban micro-renewal. Existing site selection models are incapable of configuring multiple types of elements in parallel and exhibit limited capacity in translating urban spatial structures and balancing conflicting stakeholder interests, failing to meet the comprehensive and complex requirements inherent in catalyst element site selection problems. Drawing on the perspectives of urban planning, operations research, and computer science, this study proposes a Multi-objective Ccrossover Parallel Combinatorial Optimization (MCPCO) model for the site selection of catalyst elements, along with a corresponding optimization method. This model uses concise and universal model architecture to map complex and specific real-world problems, optimizing the simultaneous configuration of multiple types of catalyst elements under multiple and conflicting objectives. An empirical study, using the renewal of the Liuhe Confucian Temple historical area in Nanjing as a case study, demonstrates that the model effectively maps and solves the site selection problem of catalyst elements in urban micro-renewal, providing a useful reference for similar problems especially characterized by parallel site selection of multiple types of elements.

1. Introduction

The growing urban population and deteriorating natural environment have made sustainable development a critical issue in contemporary urban construction [1]. Currently, a considerable number of cities worldwide have entered a phase of stock-based development [2]. Against this backdrop, micro-renewal (organic renewal) characterized by “small-scale, incremental” interventions has gained widespread attention [3]. Urban micro-renewal emphasizes preserving historical urban fabric and place identity to the greatest extent possible. Through strategies such as community-led renewal [4], “plug-in” renewal [5,6], and urban acupuncture [7], it integrates local resource-based industries into community development and residents’ daily lives, thereby achieving sustainable regional vitality [8,9]. A key step in this process involves identifying suitable priority renewal nodes that are crucial for enhancing the efficiency and effectiveness of urban renewal [10,11].

In urban micro-renewal, priority renewal nodes are often referred to as “catalyst elements” [12,13]. The term “catalyst” originally describes substances in chemical reactions that accelerate the reaction process without consuming themselves. In the field of urban planning and design, Attoe and Logan first proposed the urban catalyst theory in 1986 [13], being the earliest to use “catalyst elements” to describe priority renewal nodes in urban renewal that produce ripple effects. This theory advocates revitalizing existing urban elements by introducing new elements rather than completely altering urban spatial patterns, analogizing the interaction mechanism between new and existing elements to catalytic effects. With the advancement of urban renewal practices worldwide, the introduction and design of catalyst elements have become crucial strategies in urban renewal and have been widely applied in project implementations [14,15].

In existing studies related to urban micro-renewal, catalyst elements manifest in diverse physical forms. Sternberg posits that large-scale public buildings such as stadiums and museums can serve as catalyst elements to support the development of surrounding areas. Planners should comprehensively determine the layout design of catalyst elements by considering factors including pedestrian accessibility, entrance/exit points, and crowd flow patterns [16]. Yin et al. focused on green space catalyst elements, establishing an evaluation index system from physical, social, and economic dimensions to assess their catalytic effects [17]. Wang et al. developed a micro-renewal plan for Pingjiang Historic District in Suzhou, China, by introducing five types of point-based catalyst elements: contextual stitching catalysts, industrial activation catalysts, community revitalization catalysts, ecological restoration catalysts, and transportation optimization catalysts [18]. Huang et al., examining the old urban area of Haikou, China, identified four types of point-based catalyst elements: historic buildings, public spaces, transportation nodes, and industrial insertions. They further connected some point-based catalysts to form three types of linear catalyst elements—residential, commercial, and cultural—creating an integrated catalyst system to restructure spatial configurations [19]. Taylor et al. utilized waterfront spaces as catalyst elements in urban renewal projects, achieving significant positive outcomes [20].

Based on urban catalyst theory and extensive urban micro-renewal practices, catalyst elements are typically classified into various types according to differences in their physical carriers’ functional attributes (cultural, commercial, landscape, etc.), morphological characteristics (point-based, line-based, area-based, etc.), and scale (small, medium, large, etc. [21]).To promote comprehensive development of urban districts through micro-renewal, it is inevitable to introduce multiple types of catalyst elements into urban districts. Some studies focus on the introduction of a single type of catalyst element, which usually only constitutes partial intervention in a complete micro-renewal plan for an urban district.

After completing the typological planning of catalyst elements, the subsequent challenge lies in addressing their spatial allocation. In the design of a micro-renewal plan for an urban district, determining the geographical placement of introduced catalyst elements (typically comprising multiple types)—specifically establishing the geospatial location of each catalyst element’s physical carrier—is herein referred to as the “catalyst element site selection problem”.

The site selection of catalyst elements presents a high degree of complexity, encompassing both conditional complexity and structural complexity. Conditional complexity arises from the intricate urban environments and conflicting stakeholder interests inherent in micro-regeneration projects. Structural complexity arises from the need to coordinate multiple types of catalyst elements with interdependent relationships. By contrast, different types of catalyst elements can all guide area development within certain parameters; each type produces unique catalytic effects unattainable by other types. Consequently, during site selection, these elements both constrain one another through their shared characteristics and synergize through their distinctive characteristics. This intricate interconnection necessitates that all types of catalyst elements must be sited simultaneously and concurrently (hereafter defined as “parallel” site selection). Alternative approaches—such as batch site selection (introducing different types sequentially) or phased site selection (first identifying locations then determining catalyst types)—represent isolated, partial logic that fails to address this inherent complexity.

Current approaches to addressing the site selection problem for catalyst elements primarily rely on designers’ experiential judgment. However, the inherent complexity of the issue inevitably leads to scientific and precision deficiencies in such empirical decision-making, making the adoption of technical methods to determine or assist in determining the location of catalyst elements highly necessary. In the broader context of site selection for urban elements, technical methodologies have seen notable development and application. Wang et al. observed that theoretical approaches to facility site selection increasingly emphasize the application of complex algorithms to better approximate real-world conditions, with methods such as container modeling, shortest-path analysis, and gravity models being employed for location evaluation [22]. Sun et al. focused on the accessibility of service facilities within 15-min living circles, conducting comprehensive spatial assessments of six facility types using urban data including areas of interest (AOIs) and road networks [23]. Feng et al. integrated point-of-interest (POI) data with machine learning algorithms to train a site selection model for elderly care facilities, achieving a predictive accuracy rate of 87.54% [24]. Zhou et al. addressed the multi-objective optimization problem of urban airline terminal site selection through genetic algorithms [25]. Wang et al. proposed a computational derivation method for catalyst element placement, specifically solving the site selection problem for four types of catalyst elements—commercial, activity, landscape, and transportation—in historic district renewal [26].

Current research specifically targeting technical methods for site selection of catalyst elements remains limited, with existing computational models demonstrating low capability in mapping real-world problems and offering restricted functionality. For instance, Wang et al. [26] derived multiple coordinates within an urban district based on a series of self-defined rules (without considering whether these locations could actually be redeveloped) and then subjectively determined the functional attributes for each coordinate. This approach essentially treats the four types of catalyst elements as a single type, where the typological differences between catalyst elements do not actually influence the site selection outcomes. It represents a typical example of the “phased site selection” logic mentioned previously.

However, the site selection problem of catalyst elements can fundamentally be characterized as a multi-type site selection problem for urban elements with interrelationships. Regarding its essential formulation, existing technical methods have achieved considerable results in comprehensive evaluation [16,17], yet lack optimization-related research. Current research on the optimization of urban element site selection suffers from a fundamental limitation: it can only address single-type elements, failing to achieve parallel configuration of multiple element types. Moreover, most studies focus primarily on the application of optimization algorithms, paying insufficient attention to the model’s capacity to reflect complex real-world problems. In summary, research on technical methods for site selection of catalyst elements remains in its nascent stage. Developing mathematical (optimization) models that can effectively map the site selection of catalyst elements problem represents a critical research focus moving forward.

2. Research Framework

2.1. Establishment of Research Objectives

Based on the current research status and methodological limitations regarding the site selection problem of catalyst elements, this study aims to propose an optimization model that can first meet the functional requirements for modeling posed by the fundamental characteristics of the site selection problem for catalyst elements, thereby achieving optimal solutions. Secondly, in terms of model performance, it should be able to map the highly complex catalyst element site selection problems with as simple a model architecture as possible, while also mapping the highly specific catalyst element site selection problems with as general a model architecture as possible. Additionally, the model should be extendable to urban problems that share similar or simplified structures with catalyst element site selection problems.

Building upon extensive theoretical and practical research in urban micro-regeneration, this study summarizes the fundamental characteristics of catalyst element site selection problems from a mathematical modeling perspective, including but not limited to the following:

1.

Within the context of urban micro-regeneration, the core concept of catalyst element site selection involves guiding incremental urban development through minimal interventions in existing elements. If we consider all nodal, physical urban components (buildings, building clusters, plazas, landscapes, etc., hereafter referred to as “urban physical spatial nodes”) within a given urban area as a complete set, then the objects selected for catalytic transformation constitute only a minimal subset of this complete set;

2.

The implanted catalyst elements are typically multi-typed, with each type possessing attributes that include at least function, morphology, and scale;

3.

The total quantity of catalytic elements, constituted by their number and scale, is constrained by two factors: (1) investment costs preventing excessive deployment, and (2) the micro-regeneration principle advocating restrained intervention. This quantity is ultimately set as a fixed value through comprehensive evaluation of project budget, planning scheme, and supply–demand dynamics;

4.

For any given type of catalyst element, its theoretically optional nodes (existing urban physical spatial nodes that could potentially be transformed into this type of catalyst element) are generally those nodes that match the physical characteristics of that catalyst type. For instance, for a building-based catalyst element, the theoretically optional node set should consist primarily or exclusively of existing buildings, achievable through renovation or limited reconstruction, rather than non-building elements like plazas or green spaces;

5.

For any given type of catalyst element, its suitable optional nodes (existing urban physical spatial nodes appropriate for transformation into this catalyst type, hereafter called “optional nodes”) represent a subset of the theoretically optional nodes. These suitable optional nodes are typically identified through field surveys or specific technical methods [26];

6.

A single urban physical spatial node may simultaneously qualify as a suitable optional node for multiple types of catalyst elements. For example, a historic building could be transformed into either a small exhibition space or a commercial establishment; a vacant lot could become either a small plaza or a green landscape;

7.

Different types of catalyst elements, as well as different physical carriers of the same catalyst type, are interrelated rather than isolated, exhibiting at least two types of relationships: mutual constraints and synergistic effects.

Based on the fundamental characteristics of catalyst element site selection problems, the optimization model for addressing such problems should meet the following requirements (including but not limited to):

• The model should allow catalyst elements to be classified into multiple types according to multidimensional criteria (function, morphology, scale, etc.);
• The model should enable simultaneous site selection of multiple types of catalyst elements while accounting for their interrelationships;
• The model should permit each type of catalyst element to be sited within its respective set of suitable optional nodes;
• The model should allow a single urban physical spatial node to serve simultaneously as a suitable optional node for multiple types of catalyst elements;
• The model should accommodate arbitrary comprehensive evaluation methods for assessing any given catalyst element site selection scheme, ultimately achieving optimization of the site selection solution.

2.2. Development of Research Contents

Based on the aforementioned research objectives, this study proposes an optimization model that integrates urban planning, operations research, and computer science to address the characteristics and requirements of catalyst element site selection: the Multi-objective Crossover Parallel Combinatorial Optimization (MCPCO) model. Due to the limitations of conventional optimization algorithms, this research develops a targeted optimization algorithm specifically adapted for this model.

To fulfill Requirement 5, the model is fundamentally designed as a multi-objective optimization model.

To fulfill Requirement 3, this study introduces a “parallel” architecture. First, to enable quantitative selection of catalyst elements from a finite set of urban physical spatial nodes, the model is discretized from a multi-objective optimization model into a multi-objective combinatorial optimization model. However, conventional combinatorial optimization models typically only address the combinatorial selection of a single type of element within its optional set. Therefore, this study first defines an architecture capable of coupling arbitrarily similar basic combinatorial problems in parallel and independently, thereby allowing the model to accommodate multiple types of catalyst elements, with each type performing combinatorial selection within its corresponding suitable optional nodes set. The combinatorial problem after introducing this architecture can essentially be regarded as multiple parallel basic combinatorial problems; hence, this study names it the “parallel” architecture. The introduction of this parallel architecture enables the model to perform parallel selection of multiple types of catalyst elements, thereby eliminating crude or even erroneous site selection logics such as batch site selection or phased site selection.

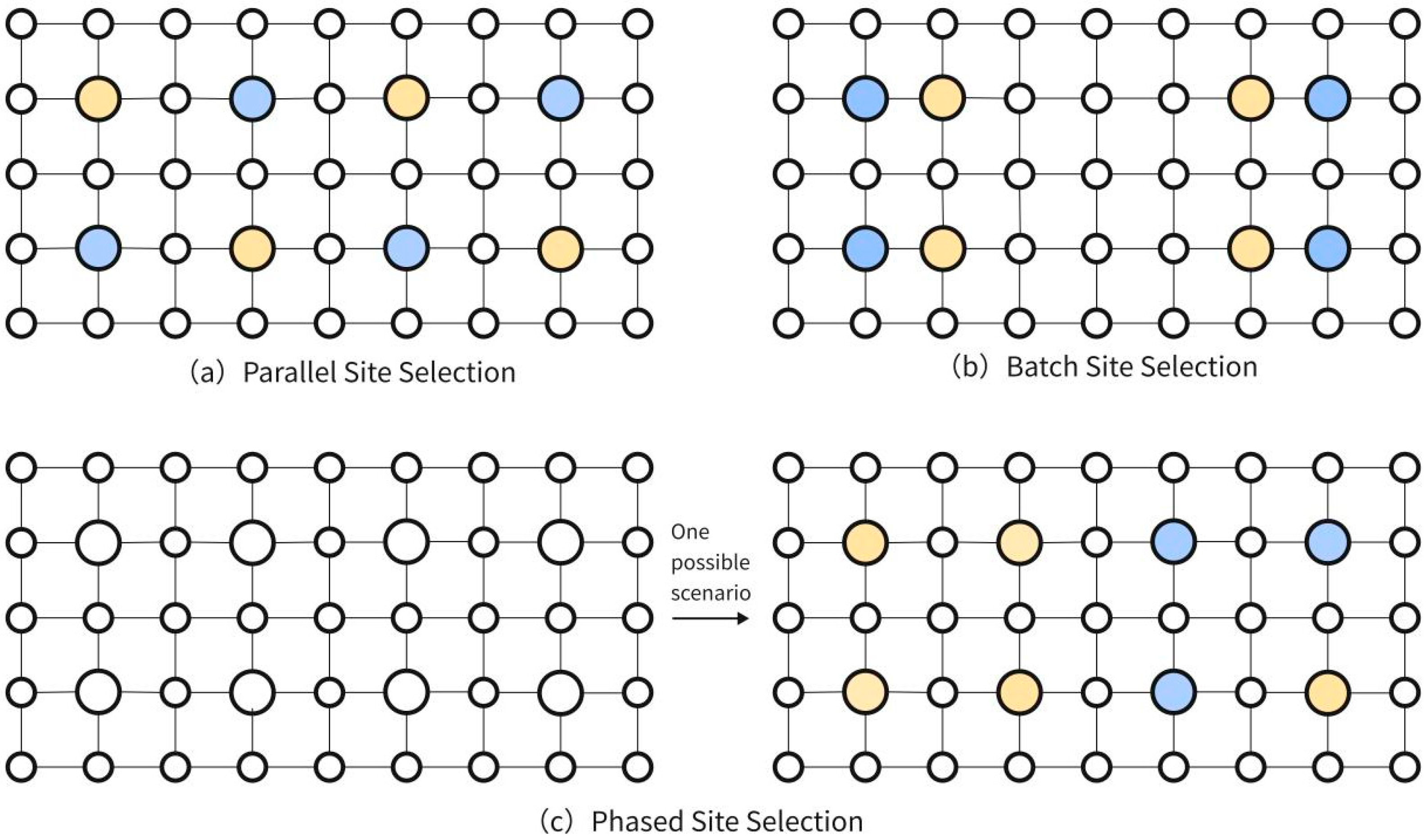
Taking the simplified urban spatial structure shown in Figure 1 as an example, four Type A catalytic elements (yellow) and four Type B catalytic elements (blue) were allocated in the area with layout fairness as the sole evaluation criterion. If the parallel site selection logic (1-a) is adopted, a site selection solution can be obtained where all catalyst elements occupy positions fairly and each type of catalyst element is also distributed equitably. If the batch site selection logic (1-b) is employed, the first batch of catalyst elements (Type A) preferentially occupy the most optimal fair positions, while the subsequent batch (Type B), due to the preemption of the best locations, can only be placed near these optimal positions. This site selection logic leads to inequality between different types of catalyst elements, inevitably resulting in a certain degree of inefficient clustering in the layout outcome. If the phased site selection logic (1-c) is applied—first determining the eight fairest positions by ignoring the internal differences among catalytic elements and then assigning the type of each element based on subjective judgment or other methods—this approach fails to reflect the interrelationships between different catalyst elements and their impact on the layout, while also introducing a degree of subjectivity into the results.

To fulfill Requirement 4, this study introduces a “crossover” architecture as a subsidiary structure to the “parallel” architecture, which allows partial intersections among multiple parallel basic combinatorial problems. When an urban node can simultaneously serve as a suitable optional node for multiple types of catalyst elements, i.e., it has multifunctional capacity, this study refers to such candidate locations as “versatile optional nodes.” If versatile optional nodes are defined in the catalyst element site selection problem, the optional sets for some types of catalyst elements will exhibit intersections. In this case, the model is said to possess a “crossover” architecture, and the framework is extended to the “Multi-objective Crossover Parallel Combinatorial Optimization Model.”

To address Requirement 1, the model assigns catalyst elements attributes along two dimensions—function and scale—while handling morphological differences through optimization objectives. For catalyst elements differing only in function and scale, they can be represented by points at their geometric centers. When morphological differences exist, since lines and areas can be treated as collections of points, line-based and area-based catalyst elements essentially constitute aggregated sets of point-based elements. By configuring appropriate optimization objectives, point-based catalyst elements can be clustered to form line-based or area-based elements. Therefore, the proposed model intentionally does not incorporate morphological definitions for catalyst elements, ensuring all elements can be abstracted as points without fundamental scale differences. The introduction of line-based and area-based catalyst elements in the study district is instead achieved through optimization objective settings (see Section 4 for case examples). This design affords the model a high degree of conciseness.

To achieve Requirement 2, the interrelationships among catalyst elements are incorporated through optimization objectives. The synergistic relationships between different types of catalyst elements are reflected by optimization objectives that do not distinguish between element types, enabling all catalyst elements to coordinate their placement based on shared goals, such as “layout equity for all catalyst elements”. Conversely, conflicting relationships between different types of catalyst elements are addressed through type-specific optimization objectives, allowing each type to prioritize its own placement preferences, such as “independent layout equity for public-space-type catalyst elements.”

In summary, the Multi-objective Crossover Parallel Combinatorial Optimization (MCPCO) model not only satisfies all requirements imposed by the fundamental characteristics of catalyst element site selection problems, but also achieves the mapping of highly complex and specific problems through a maximally simple and general model architecture. It represents a highly compatible, precise, efficient, and scalable solution for addressing catalyst element site selection in urban micro-renewal. To accommodate certain distinctive features of catalyst element site selection problems, the model necessarily incorporates “parallel” and “crossover” architectures, while other characteristics are addressed through conventional optimization model frameworks. It should be noted that these “parallel” and “crossover” architectures were specifically proposed in this study to deconstruct the complexity inherent in urban problems. From an operations research perspective, site selection problems featuring this “crossover-parallel” architecture could be considered a special type of Generalized Assignment Problem (GAP) with nonlinear optimization objectives [27,28]. However, maintaining our urban planning disciplinary standpoint, this study deliberately avoids adopting the “assignment” terminology commonly used in operations research.

This study focuses on the catalyst element site selection problem in urban micro-regeneration and proposes the “Multi-objective Crossover Parallel Combinatorial Optimization (MCPCO) Model” to address such challenges. Specifically, the research first qualitatively determines the targeted optimization model architecture in Section 2 based on the fundamental characteristics of catalyst element site selection problems. Section 3 then quantitatively elaborates on the model composition and its comprehensive application methodology for catalyst element site selection, along with proposing corresponding optimization solution approaches. Section 4 implements the model in the micro-renewal project of Liuhe Confucian Temple Historic District in Nanjing, China, and adaptively modifies the genetic algorithm as an example to develop an improved genetic algorithm for achieving optimal solutions in this case. The results demonstrate that the catalyst element site selection method based on the MCPCO model can objectively, comprehensively, and precisely determine the layout configuration of catalyst elements, enhance the quality of urban micro-renewal design schemes, amplify the beneficial impacts of catalytic effects, and ultimately provide methodological evidence for sustainable urban development.

3. Methodology: The MCPCO Model

The MCPCO model represents a specialized type of optimization model with unique architectural features. From an operations research perspective, this model extends conventional combinatorial optimization models through two key innovations: (1) the incorporation of a “parallel” architecture enables the parallel coupling of fundamental combinatorial problems, thereby permitting classified site selection of catalyst elements; (2) the introduction of a “crossover” architecture allows for controlled interactions between these parallel-coupled combinatorial problems, enhancing the model’s adaptability by enabling any urban node to be simultaneously designated as a suitable optional node for different types of catalyst elements. These distinctive architectural characteristics render conventional optimization algorithms inefficient or ineffective for this model, necessitating the development of specialized solution methodologies as presented in this study.

The framework of the Multi-objective Crossover Parallel Combinatorial Optimization Model will be elaborated through five components, each addressing an essential core problem in catalyst element site selection optimization:

• Urban spatial data translation component: transforms urban spatial structures into specific data structures;
• Crossover parallel combinatorial structure construction component: determines the structure of feasible solutions and feasible regions based on the formulation of catalyst element site selection problems;
• Multi-objective formulation component: addresses the setting and joint processing methods for optimization objectives in catalyst element site selection;
• Optimization algorithm configuration component: proposes targeted solution methods for the MCPCO model;
• Catalyst Validation component: conducts pass/fail validation of optimized solutions based on specified evaluation metrics;

The complete framework of the MCPCO model for catalyst element site selection problems is illustrated in Figure 2.

3.1. Urban Spatial Data Translation

The data translation of urban spatial information serves as the prerequisite for constructing the MCPCO model. Its primary objective is to transform concrete urban spaces within a defined area into abstract data structures, thereby preparing the necessary data for subsequent optimization computations. For urban spatial data translation, coordinate models, graph theory models, or mesh models are typically employed.

The coordinate model records the two-dimensional coordinates of each urban node, using straight-line distances to approximate road-network distances (shortest path along roads), resulting in relatively low model complexity. The graph theory model can precisely describe the structural relationships between roads, buildings, and open spaces in urban environments, calculating the exact road-network distance between any two urban nodes. However, this model has relatively higher complexity and is more suitable for small-to-medium-scale urban districts. The mesh model employs an orthogonal grid system to map urban space, but suffers from two main limitations: ambiguous representation of urban objects by grid cells, and difficulty in controlling grid precision. Consequently, it is only applicable to large-scale urban districts with less stringent layout requirements.

Figure 3 demonstrates these three approaches using a section of Nanjing’s Liuhe Confucian Temple District as an example, showing how each model extracts the spatial structure of this area differently.

When adopting graph-theoretic models to extract urban spatial structures as graph representations, this study formalizes the following fundamental abstraction principles: (1) Urban physical spatial nodes are extracted as points, with their positions defined at their geometric centers. (2) Straight roads are extracted as line segments, and road intersections as points. Curved roads are decomposed into multiple straight segments or, when spatial structure permits, approximated by a single straight segment. However, the distance between its endpoints must be manually assigned based on the original curved road’s total length. (3) Entry path structures (topological structures describing connectivity between physical nodes and roads) are created by adding points where roads enter physical spatial nodes.

The choice of model for digitizing urban districts should be determined by the problem characteristics and computational requirements. For instance, when representing potential locations for catalyst element transformation, both coordinate models and graph theory models use points for specific and precise representation, while mesh models employ square grids to map urban areas. The area represented by each grid depends on the model’s precision, which may result in either a single physical urban node being represented by multiple grids or multiple nodes being represented by a single grid, leading to ambiguous and coarse representation. For calculating distances between any two urban nodes, graph theory models provide accurate road-network distances, whereas coordinate and mesh models only offer approximate straight-line distances. Since urban micro-renewal problems typically involve diverse computational needs, it is common practice to simultaneously construct multiple digitization models to obtain various structural data formats for different computational processes.

3.2. Crossover Parallel Combinatorial Structure Construction

The catalyst elements are classified based on their functional and scale differences to construct a parallel combinatorial structure. Each type of catalyst element is distinguished from others by its functional and scale attributes, such as large-scale cultural catalyst elements, medium-scale commercial catalyst elements, small-scale plaza catalyst elements, or medium-scale cultural–commercial–mixed catalyst elements. It should be noted that in practical applications, the classification criteria for catalyst elements can be either complexified or simplified according to problem requirements. While functional and scale attributes represent common, referential classification bases, one of the model’s core concepts is to reflect any differences in input elements (that do not cause order-of-magnitude changes in scale) through categorization.

Once the classification method is established, the following must be determined for each type of catalyst element: (1) the locations of optional nodes and (2) the required quantity. The locations of optional nodes are identified through field surveys or technical methods, while the required quantity is determined based on practical constraints such as investment costs and supply–demand relationships. The site selection problem for a single type of catalyst element constitutes an independent combinatorial optimization problem. When considering all types collectively, it forms a parallel combinatorial optimization problem. If certain urban physical spatial nodes can simultaneously serve as optional nodes for multiple types of catalyst elements (i.e., “versatile optional nodes”), the parallel combinatorial structures are no longer entirely independent but instead exhibit partial crossover. This extends the parallel combinatorial optimization problem into a crossover parallel combinatorial optimization problem, consequently increasing its complexity.

If the number of introduced catalyst element types is n, with the required quantity for each type being R_i (1≤ i ≤ n, i ∈ Z), and the set of optional nodes for each type of catalyst element denoted as S_i (1 ≤ i ≤ n, i ∈ Z), then any feasible solution can be represented by a set X, expressed as

$$\begin{array}{c}X={\displaystyle \bigcup _{\mathrm{i}=1}^{\mathrm{n}}}\{{\mathrm{A}}_{\mathrm{i}1},{\mathrm{A}}_{\mathrm{i}2},···,{\mathrm{A}}_{\mathrm{i}{\mathrm{R}}_{\mathrm{i}}}\},{\mathrm{A}}_{\mathrm{i}\mathrm{j}}\in {\mathrm{S}}_{\mathrm{i}}\end{array}$$

(1)

If there exist α and β such that ${\mathrm{S}}_{\mathsf{\alpha }}\cap {\mathrm{S}}_{\mathsf{\beta }}\ne \mathrm{\varnothing }$, then the model architecture is extended from a parallel combinatorial architecture to a crossover parallel combinatorial architecture. An element is called a k-ary optional node if it simultaneously belongs to k of the sets S_i (1≤ i ≤ n, i ∈ Z). If in a given problem every element is at most an m-ary optional node, then the problem is called an m-type crossover parallel combinatorial optimization problem.

3.3. Multi-Objective Formulation

The catalyst element site selection problem often involves complex and conflicting renewal objectives. Common objectives include, but are not limited to, layout equity, redevelopment urgency, economic benefits, etc., while specific problems may additionally generate their unique optimization objectives. The determination of optimization objectives should be based on both the commonalities and specificities of the problem, focusing on its primary contradictions. After identifying the optimization objectives, each objective needs to be quantified and normalized, enabling unique representation through data scaled between 0 and 1. For objectives with unclear upper and lower bounds, stochastic methods can be employed to approximately determine their value ranges prior to data normalization.

Upon completing the specification and quantification of all optimization objectives, this study recommends transforming the multi-objective optimization into a single-objective optimization through the linear weighting method, which aggregates all objective function values via weighted summation. Weight determination should incorporate both objective importance (employing expert evaluation, Analytic Hierarchy Process (AHP), etc.) and data variability (using Coefficient of Variation Method (CVM) or Entropy Weight Method (EWM)). The linear weighting method offers computational simplicity and efficiency, making it particularly suitable for the schematic design phase of urban renewal projects. Maintaining the multi-objective structure to solve the Pareto frontier solution set would incur substantial computational overhead and heightened solving complexity. Moreover, the ultimate selection from the Pareto frontier still necessitates designers’ subjective evaluation of relative objective importance and is therefore temporarily not considered in this study.

In summary, if the catalyst element site selection problem has k optimization objectives (all to be minimized, where smaller values indicate better solutions), with corresponding weights w_i (1 ≤ i ≤ k, i ∈ Z), and each objective is determined by function fi (1 ≤ i ≤ k, i ∈ Z), and value ranges [D_i1,D_i2] (1 ≤ i ≤ k, i ∈ Z), then for a given feasible solution X, the comprehensive evaluation function F(X) is

$$\begin{array}{c}F(X)={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{k}}}{\mathrm{w}}_{\mathrm{i}}{\displaystyle \frac{{\mathrm{f}}_{\mathrm{i}}\left(\mathrm{X}\right)-{\mathrm{D}}_{\mathrm{i}1}}{{\mathrm{D}}_{\mathrm{i}2}-{\mathrm{D}}_{\mathrm{i}1}}}\end{array}$$

(2)

3.4. Optimization Algorithm Configuration

The MCPCO model possesses a unique architecture that precludes the direct application of existing optimization algorithms. This study develops scenario-specific solution approaches, deriving novel optimization techniques grounded in mathematics and computer science for components where conventional algorithms prove unsuitable or ineffective. The systematic methodology for the optimization algorithm configuration ultimately established is as stated below:

For a standalone combinatorial optimization problem, if the complexity is relatively low, an exhaustive search (brute-force) method can be directly employed. However, combinatorial optimization problems are prone to combinatorial explosion, and their complexity is typically high. In such cases, Monte Carlo algorithms or heuristic optimization algorithms are commonly adopted. Although solutions obtained via Monte Carlo algorithms may lack optimality guarantees, this approach offers advantages of simple principles and strong problem adaptability, making it suitable for rapid solving of urban design problems. In contrast, heuristic optimization algorithms yield higher-quality solutions but involve more complex principles and implementation difficulties. Furthermore, emerging combinatorial problem-solving approaches, particularly machine learning-based methods [29,30], can be considered. This study maintains that for critical catalyst element site selection with high complexity, heuristic optimization algorithms should be prioritized to obtain the highest possible solution quality—provided sufficient time, computational resources, and technical conditions are available.

Non-crossover parallel combinatorial optimization problems represent simple couplings of multiple independent combinatorial optimization problems. From a mathematical perspective, the feasible solution space size (number of feasible solutions) of non-crossover parallel combinatorial optimization problems can be calculated using the fundamental counting principle; from a computer science perspective, directly concatenating the solution algorithms of independent combinatorial optimization problems can meet basic solving requirements, though certain processing during concatenation can improve solution quality and algorithm convergence speed. The complexity of non-crossover parallel combinatorial optimization problems can be reflected through feasible solution space size—if the parallel combinatorial optimization problem consists of k independent subproblems, each taking the form of selecting m_i (1 ≤ i ≤ k, i ∈ Z) elements from n_i (1 ≤ i ≤ k, i ∈ Z) elements, then the feasible solution space size R is given by

$$\begin{array}{c}R={\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{k}}}{\complement }_{{\mathrm{n}}_{\mathrm{i}}}^{{\mathrm{m}}_{\mathrm{i}}}\end{array}$$

(3)

If the model is extended to a crossover parallel combinatorial optimization model, the structural complexity of the model will increase significantly. On the one hand, the scale of the feasible region will become difficult to evaluate, as mathematical methods cannot provide a direct counting approach for parallel combinatorial problems with a crossover architecture. On the other hand, crossover parallel combinatorial optimization (CPCO) problems belong to NP-hard problems, and currently, there is no widely recognized and reliable optimization algorithm capable of directly solving them with high quality, nor does any programming language platform provide built-in functions specifically designed for such models. The core challenge lies in the fact that, due to the existence of versatile optional nodes, the number of elements selected from each optional set is not fixed. Given these difficulties, this study proposes the following solution theory for CPCO problems.

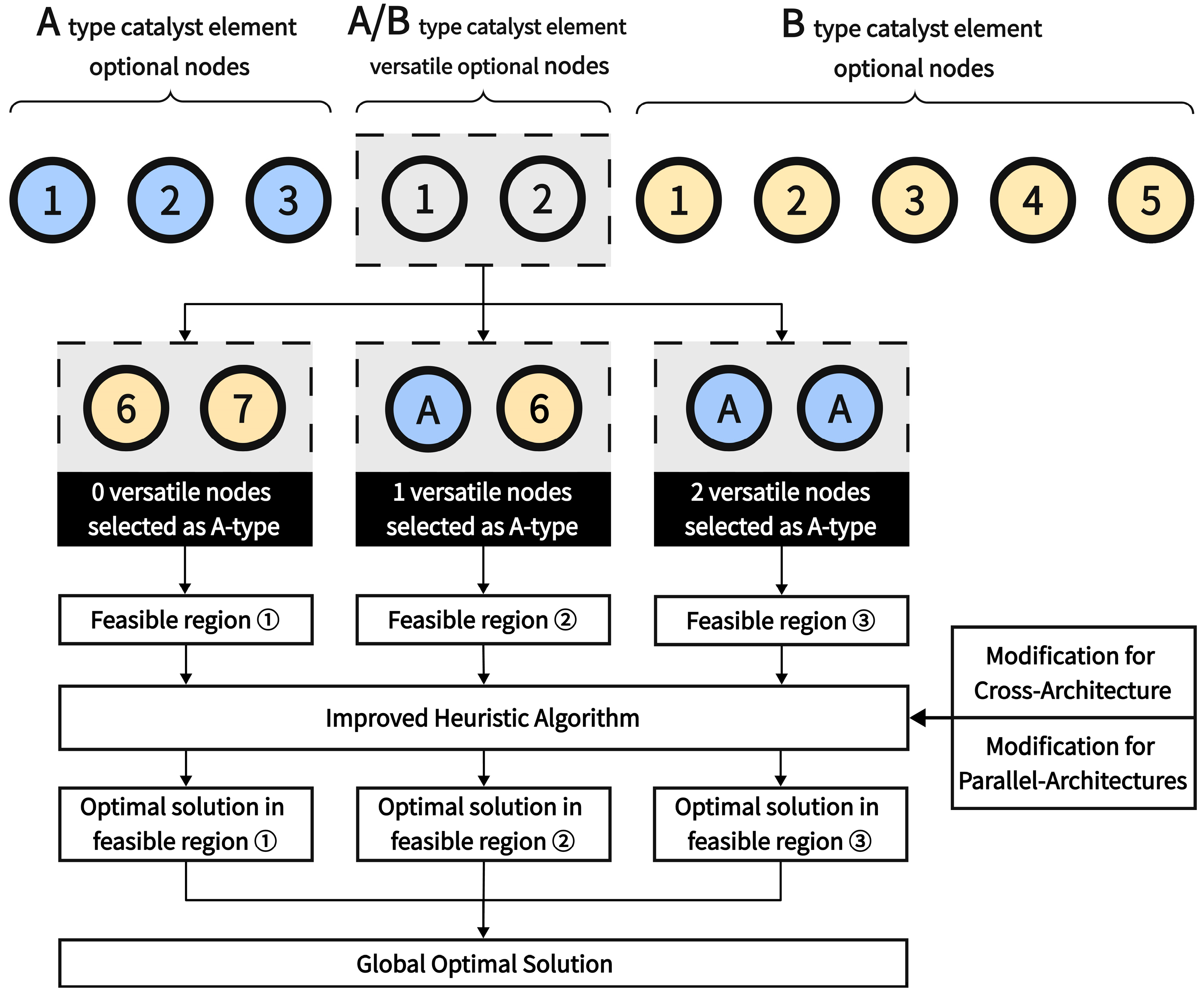
From a mathematical perspective, to calculate the number of feasible solutions for crossover parallel combinatorial problems, it is inevitable to conduct categorical analysis regarding the attribution of polyhedral optional points. If a batch (assuming k) of versatile optional nodes simultaneously serve as optional nodes for n types of catalyst elements, then after individually specifying which type of catalyst element each versatile optional node is converted into, the problem degenerates into a non-crossover parallel combinatorial problem. However, the number of classification scenarios is enormous (the number of classification scenarios is an exponential function of k). Without proof, this study asserts that specifying how many of the k versatile optional nodes are converted into n-1 types of catalyst elements constitutes the classification method with the fewest scenarios, where each scenario degenerates into a non-crossover parallel combinatorial problem essentially (The number of classification scenarios is a power function of k). In particular (as is often the case in catalytic element site selection problems), if k versatile optional nodes simultaneously serve as optional points for two types (A and B) of catalyst elements, with demand quantities a and b (k ≤ min{a,b}) for types A and B, respectively, and the numbers of non-versatile optional nodes convertible into types A and B catalytic elements are m and n (a ≤ m, b ≤ n), respectively, then the number of classification scenarios is k + 1. For the (i + 1)-th (0 ≤ i ≤ k, i ∈ Z) category, where i versatile optional nodes are designated to be converted into type A catalytic elements, the number of feasible solutions Ri + 1 contained in this category is

$$\begin{array}{c}{\mathrm{R}}_{\mathrm{i}+1}={\complement }_{\mathrm{k}}^{\mathrm{i}}{\complement }_{\mathrm{m}}^{\mathrm{a}-\mathrm{i}}{\complement }_{\mathrm{n}+\mathrm{k}-\mathrm{i}}^{\mathrm{b}}\end{array}$$

(4)

From a computer science perspective, to traverse all feasible solutions, one must conduct batch traversal according to the aforementioned mathematical classification logic. However, practical catalytic element site selection problems often suffer from combinatorial explosion, where the feasible solution space becomes too large for exhaustive traversal. In such cases, Monte Carlo algorithms or heuristic algorithms may be considered. The Monte Carlo algorithm can circumvent the structural complexity of the problem by requiring only a random feasible solution generation function, though the quality of obtained solutions tends to be low. To acquire high-quality solutions, heuristic optimization algorithms must be employed. Since existing heuristic algorithms can only directly support general combinatorial optimization problems, this study proposes a two-aspect modification of heuristic optimization algorithms to make them compatible with the unique problem structure of CPCO problems.

From a computer science perspective, the first aspect involves crossover architecture-specific modification, including categorical treatment of the feasible domain and representation method processing for feasible solutions. The feasible domain is classified to ensure that the problem within each sub-feasible domain is non-crossing parallel combinatorial, while the representation of feasible solutions is processed to establish a one-to-one correspondence between any feasible solution and a data sequence meeting heuristic algorithm requirements. After partitioning the feasible domain into multiple sub-domains, the optimization algorithm is applied to each sub-domain to obtain local optimal solutions, which are then compared to determine the global optimal solution. The second aspect focuses on parallel architecture-specific modification to enable synchronous optimization of parallel combinatorial problems, with additional consideration given to setting hyperparameters by weight when applying the algorithm to branch combinatorial problems. In Section 3.4 of this paper, these two modification approaches are implemented in a genetic algorithm, resulting in an improved genetic algorithm specifically designed for CPCO problems, while other heuristic optimization algorithms can be similarly modified following analogous logic.

Under normal circumstances, the suitable transformation directions for an urban physical space node do not exceed two types, making it convenient and precise to apply the aforementioned grouping approach for solutions; however, for more complex scenarios where the catalyst element site selection problem constitutes an m-type (m ≥ 3) CPCO problem, establishing the grouping solution logic becomes considerably more challenging, in which case conventional heuristic algorithms may be employed for forced solutions. For instance, when utilizing genetic algorithms, one could forcibly repair genes after crossover operations to ensure algorithmic continuity, albeit at the cost of severely compromising the generational correlation between offspring and parent solutions.

Building upon this theory, Figure 4 illustrates, through a special yet generally representative scenario, the procedural steps for employing heuristic algorithms to solve the global optimal solution of a two-type CPCO problem.

In summary, the selection of an MCPCO solving algorithm should be based on multiple factors, including the problem formulation, computational complexity, and the required solution quality. This study summarizes the solution methods with relatively high comprehensive performance across various scenarios, as presented in

Table 1. Solution methods for the MCPCO model.

Scenarios	Solution Methods
A standalone combinatorial optimization problem	Heuristic optimization algorithms
A non-crossover parallel combinatorial optimization problem	Heuristic optimization algorithms with simple preprocessing
A 2-type CPCO problem	Improved heuristic optimization algorithms with group-based solving strategy
An n(n≥3)-type CPCO problem	Monte Carlo algorithm /Heuristic optimization algorithms (high-quality solutions cannot be guaranteed)

.

3.5. Catalyst Verification Module

Optimization alone can only ensure the efficient utilization of resources, but potential risks remain, such as insufficient catalyst elements failing to initiate chain reactions or excessive catalyst elements leading to inefficient solutions. Therefore, a validation module is incorporated at the terminal end of the model to mitigate fundamental flaws caused by improper input settings. This study refers to this module as the “Catalyst Validation” module.

There is currently no unified standard for catalyst validation, nor is it easy to establish one, as differences in geographical conditions, cognitive perspectives, and economic factors all influence the rationality assessment of catalyst element site selection schemes. This study maintains that optimized schemes should undergo validation whenever possible. However, if a specific micro-renewal project cannot determine a scientifically sound catalyst validation method, this step may be temporarily omitted. As a reference, this study proposes that a basic catalyst validation module consists of validation indicators and validation rules. The validation indicators are used to assess specific characteristics of the catalyst element site selection scheme, such as the average distance between catalyst elements, the maximum distance between catalyst elements, and the predicted probability of catalyst reaction occurrence. The validation rules are used to define the threshold criteria for each validation indicator. The formulation of these rules relies on quantitative evaluation of the catalytic effects generated by the catalyst elements, for which existing studies [17,31,32] can provide relevant references.

The catalytic validation module is encapsulated as a validation function G(a vector-valued function). For any given site selection scheme X, it returns a validation vector G(X). If the acceptance domain for the validation vector is Ω, then the passing criterion for any catalyst element site selection scheme is expressed as

$$\begin{array}{c}G(X)\in \Omega \end{array}$$

(5)

3.6. Model Summary

In summary, the urban catalyst element site selection problem is formulated as a multi-objective crossover parallel combinatorial optimization (MCPCO) model with the following framework:

$$\begin{gathered} \mathrm{m}\mathrm{i}\mathrm{n} \mathrm{F}(\mathrm{X})=\sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{w}}_{\mathrm{i}}{\displaystyle \frac{{\mathrm{f}}_{\mathrm{i}}\left(\mathrm{X}\right)-{\mathrm{D}}_{\mathrm{i}1}}{{\mathrm{D}}_{\mathrm{i}2}-{\mathrm{D}}_{\mathrm{i}1}}} \\ \begin{array}{c}s.t.\left\{\begin{array}{c}\mathrm{X}={\displaystyle \bigcup _{\mathrm{i}=1}^{\mathrm{n}}}\{{\mathrm{A}}_{\mathrm{i}1},{\mathrm{A}}_{\mathrm{i}2},···,{\mathrm{A}}_{\mathrm{i}{\mathrm{R}}_{\mathrm{i}}}\},{\mathrm{A}}_{\mathrm{i}\mathrm{j}}\in {\mathrm{S}}_{\mathrm{i}}\\ |X|={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\mathrm{Q}}_{\mathrm{i}}\end{array}\right.\end{array} \\ \mathrm{X}\mathrm{’}={\mathrm{X}}_{0\hspace{1em}}\mathrm{i}\mathrm{f} \mathrm{G}\left({\mathrm{X}}_0\right)\in \Omega \end{gathered}$$

(6)

Here, k denotes the number of optimization objectives for the catalyst element site selection scheme, w_i (1 ≤ i ≤ k, i ∈ Z) represents the weight assigned to the i-th optimization objective, f_i (1 ≤ i ≤ k, i ∈ Z) is the evaluation function for the i-th optimization objective with its value range defined as [D_i1,D_i2] (1 ≤ i ≤ k, i ∈ Z), and X signifies a feasible catalyst element site selection scheme; n indicates the number of catalyst element types specified by the problem, R_i (1 ≤ i ≤ n, i ∈ Z) denotes the required quantity for the i-th type of catalyst element, S_i(1 ≤ i ≤ n, i ∈ Z) constitutes the set of optional nodes for the i-th type of catalyst element; X₀ represents the globally optimal solution obtained from the MCPCO model, G stands for the catalyst validation function, X’ indicates the final catalyst element site selection scheme that passes validation, Ω represents the acceptable domain for the validation vector.

3.7. The Application of the Model

Although the MCPCO model is designed for catalyst element site selection, it possesses broad applicability. The model is suitable for modeling and optimizing complex urban element site selection problems of any form and scale with fixed input quantities, particularly excelling in handling the simultaneous configuration of multiple types of elements. Furthermore, the model can be extended to generalized assignment problems that share a similar structure.

When using the MCPCO model to address the site selection of one or multiple types of urban elements, it should be fully integrated with political, economic, cultural, and other multifaceted factors to ensure the model aligns as closely as possible with real-world conditions. On one hand, the impact of complex urban environments on site selection can be incorporated into the model in the form of constraints or penalty functions, ensuring the model adheres to realistic restrictions. On the other hand, the diverse interests of urban residents, project contractors, and governments can be included as optimization objectives, achieving a balance of interests through optimization. Thorough investigation and analysis of the urban context, along with the integration and weighting of multiple stakeholders’ interests, are essential prerequisites for scientifically solving urban element site selection problems using the MCPCO model.

The optimal solution derived from the model can serve as a core reference for urban renewal plans; however, it is generally not implemented directly as the final scheme. This is because no model, regardless of its sophistication, can fully capture all nuances of real-world complexity. This study recommends that after obtaining the optimal solution, further refinements should be made by incorporating aspects not considered in the model, and extensive feedback from stakeholders should be solicited to ultimately develop a scientifically sound and comprehensive renewal plan.

4. Case Study

The Liuhe Confucian Temple Historic District is located in the central area of Liuhe District, Nanjing, China, and is one of the 28 officially designated historic preservation zones in Nanjing (as shown in Figure 5). This district retains significant historical value and experiences high pedestrian flow both within and around its perimeter, making large-scale demolition and reconstruction activities unsuitable. Instead, a gradual micro-renewal approach has been proposed to revitalize the area and promote its development.

Based on comprehensive surveys of the district’s historical context and current conditions, the plan calls for introducing three types of catalyst elements: historical catalysts, commercial catalysts, and public-space catalysts. These elements will be strategically implemented to create a systematic micro-renewal scheme that generates widespread impact through targeted interventions.

Among these, commercial catalyst elements refer to cultural tourism-oriented commercial facilities with public benefits—such as boutique hotels, cultural creative spaces, and time-honored restaurants—that serve as anchor tenants to drive district-wide commercial development. Public-space catalyst elements denote small-scale public activity areas located at street corners or within residential blocks. Historical catalyst elements comprise historically significant adaptive reuse projects, including memorial halls and exhibition spaces converted from heritage-protected buildings.

This micro-renewal scheme incorporating all three catalyst types represents the core (though not exhaustive) component of a comprehensive renewal plan, demonstrating the application methodology of the MCPCO model in actual projects.

4.1. Data Translation for Liuhe Confucian Temple District

The Liuhe Confucian Temple District in Nanjing covers a total area of 146,254 square meters. At this scale, approximating road-network distances with straight-line measurements would introduce significant errors. Therefore, the spatial structure was first translated using a graph theory model, with Floyd’s algorithm employed to calculate road-network distances between any two nodes, supporting subsequent distance-related computations.

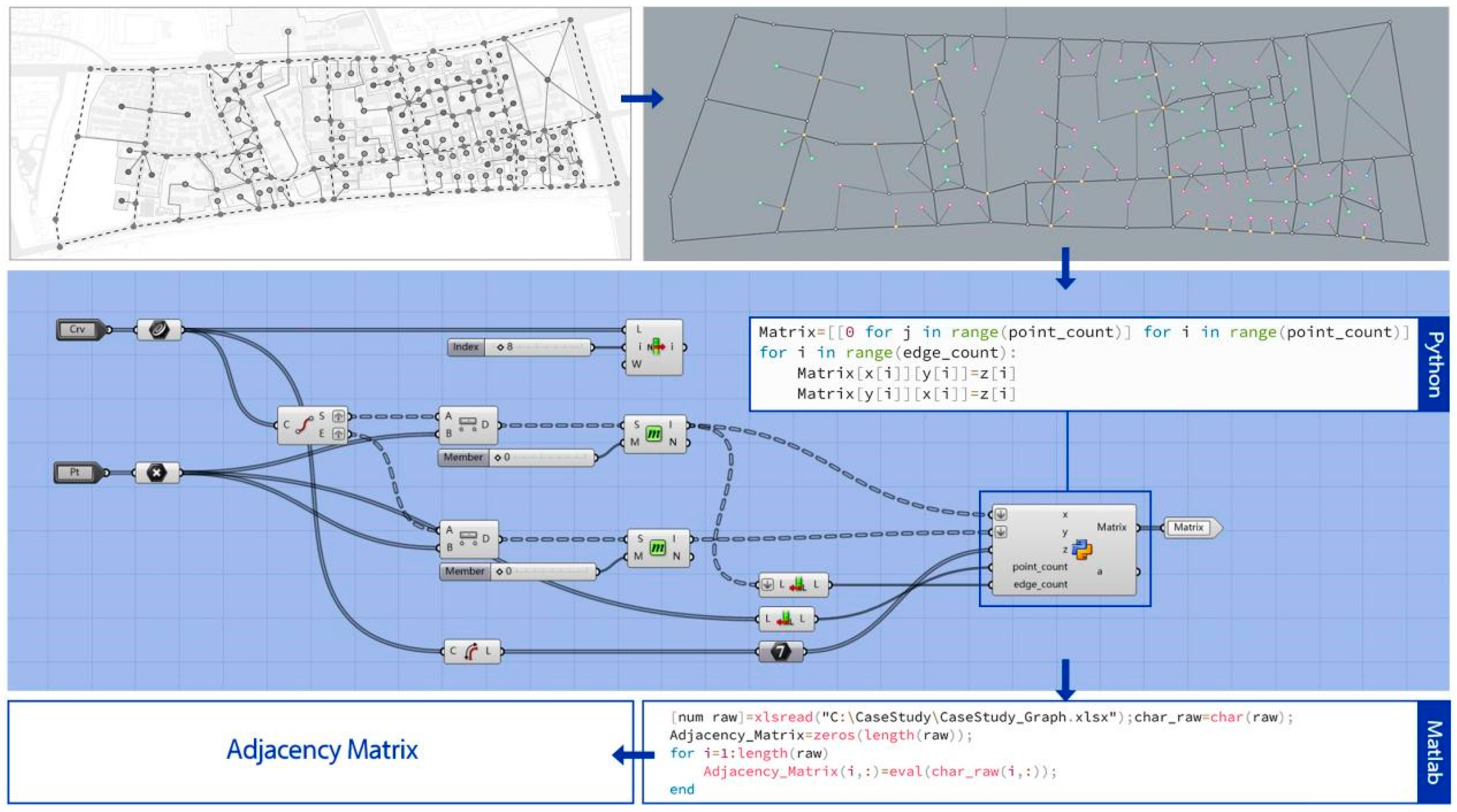
To extract the spatial structure of this district based on graph theory, this study proposes a Rhino-Grasshopper-Matlab workflow, where the process of abstracting Liuhe Confucian Temple’s spatial configuration into a graph structure (Figure 6) involves the following: acquiring the master plan of the target urban area (Figure 6a), extracting the road network (Figure 6b), delineating each physical spatial node’s boundaries based on property rights and other information (Figure 6c), collecting entry path structure data through field surveys, and ultimately representing the urban district’s spatial structure as a point–line topological graph (Figure 6d).

The graph structure is correspondingly modeled in Rhino (where each node is automatically numbered), followed by using Grasshopper to import point and line sets and generate lists recording adjacency matrix information (since Grasshopper lacks native matrix data structures), with this process encapsulated into a reusable component. Finally, Matlab converts the list data into adjacency matrices (Figure 7).

4.2. Construction of Crossover Parallel Combinatorial Structure for the Case Study

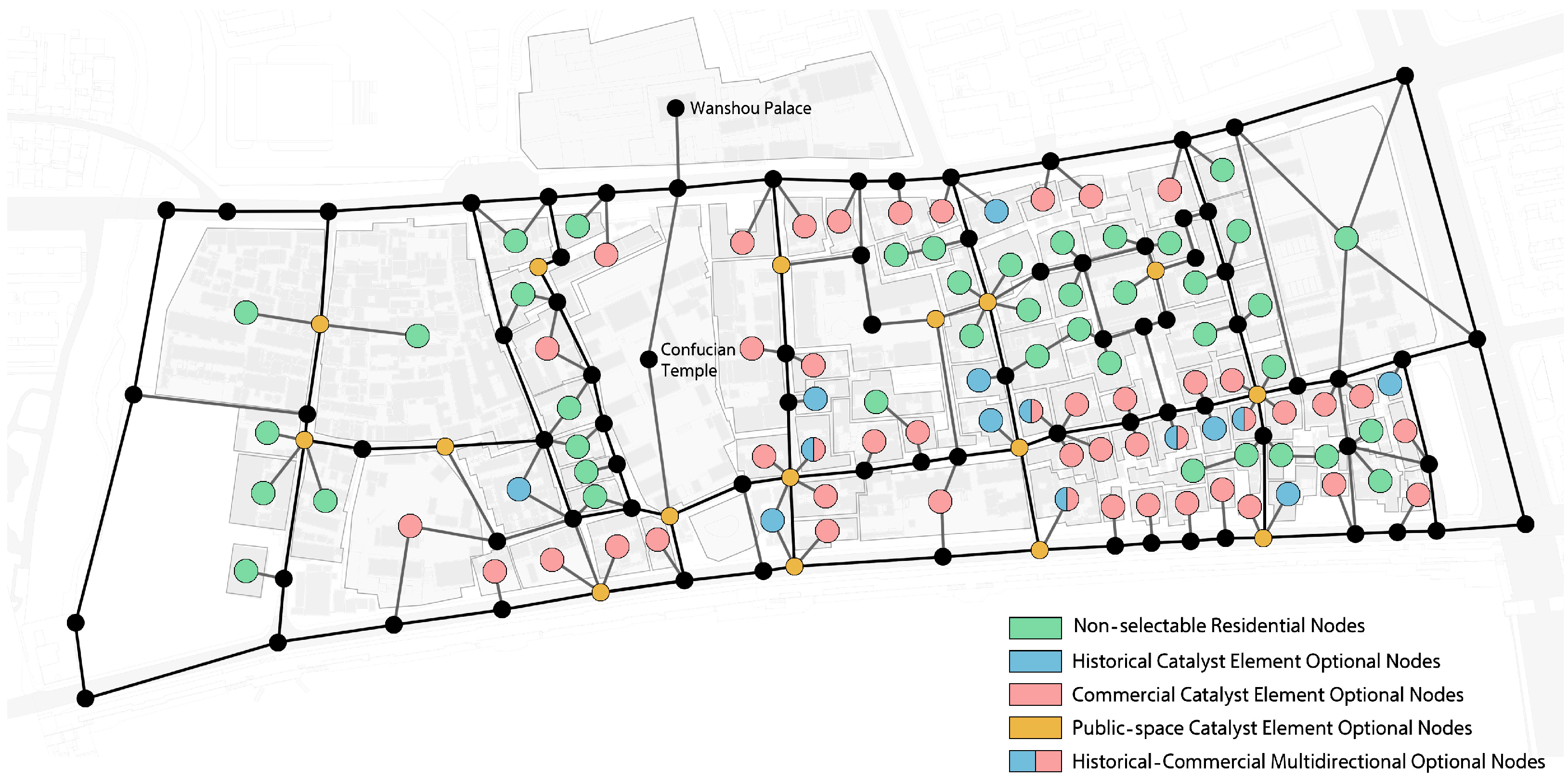
Based on the comprehensive analysis of the current conditions in Liuhe Confucian Temple District, this study identified nine optional nodes for historical catalyst elements, 41 for commercial catalyst elements, 16 for public-space catalyst elements, and five versatile optional nodes that qualify as both historical and commercial catalyst elements. Through demand assessment and budget analysis, it was determined that the micro-renewal plan would implement four historical catalyst elements, 12 commercial catalyst elements, and six public-space catalyst elements as primary intervention targets. The spatial distribution of optional nodes for each catalyst element type is illustrated in Figure 8.

It should be noted that versatile optional nodes can ultimately only be transformed into one type of catalyst element; in this case, the 2-ary nodes for both historical and commercial catalysts may be developed as either historical catalyst elements or commercial catalyst elements, or remain unmodified. If a catalyst node is deemed capable of simultaneously serving commercial functions and historical preservation purposes within this modeling framework, a new catalyst element type should be established: “historical-commercial composite catalyst elements,” though this consideration is temporarily excluded in the current case study.

4.3. Multi-Objective Formulation for the Case Study

The renewal project of Liuhe Confucian Temple District faces intricate urban environments and conflicting stakeholder interests, necessitating a multidimensional value system to comprehensively evaluate the quality of catalyst element site selection schemes. This value system encompasses eight optimization objectives: (1) comprehensive layout equity for all catalyst element types, calculated as the average distance from all unmodified nodes to their nearest catalyst element; (2) independent layout equity for public-space catalyst elements, measured by the resident population-weighted average distance from all nodes to their nearest public-space catalyst element (with population data obtained through door-to-door surveys in this case); (3) degree of renewal difficulty, assessed based on property rights of selected nodes; (4) renewal urgency, evaluated according to structural deterioration of targeted buildings; (5) historical value of historical catalyst elements, determined by heritage significance of nodes selected for historical catalyst elements; (6) average distance from historical catalyst elements to Liuhe Confucian Temple; (7) quantity of commercial catalyst elements along main commercial streets (Xianfu Street, as shown in Figure 2), designed to promote line-based catalyst formation from point-based commercial elements; and (8) average distance from commercial catalyst elements to Liuhe Confucian Temple.

This case employs the linear weighting method to integrate multiple optimization objectives, with weight determination considering both objective importance and variability through a dual approach: expert scoring method (ESM) for subjective weights and coefficient of variation method (CVM) for objective weights, where the final adopted weights are the averages of both sets. For the coefficient of variation-based weights, 1 million feasible solutions were randomly generated to record the values of all eight objectives, from which weights were derived according to the coefficient of variation formula. The randomly generated data also served as parameters for normalizing each objective. The calculated weights for all optimization objectives are presented in

Table 2. The calculated weights for all optimization objectives.

Optimization Objectives	ESM Weights	ESM Weights	Average Weights
comprehensive layout equity for all catalyst element types	0.2832	0.0818	0.1825
independent layout equity for public-space catalyst elements	0.2065	0.1423	0.1744
degree of renewal difficulty	0.0735	0.0735	0.0735
renewal urgency	0.0854	0.0517	0.0686
historical value of historical catalyst elements	0.0727	0.1573	0.1150
average distance from historical catalyst elements to Liuhe Confucian Temple	0.0821	0.1143	0.0982
quantity of commercial catalyst elements along main commercial streets	0.1431	0.2982	0.2207
average distance from commercial catalyst elements to Liuhe Confucian Temple	0.0535	0.0809	0.0672

.

4.4. Enhanced Genetic Algorithm Design and Optimization

In this case, the feasible solution space has a magnitude of 1017, and the computation of objective function values for any given feasible solution also carries considerable complexity, resulting in high overall problem complexity. To match both the problem’s complexity and the unique characteristics of the crossover parallel combinatorial structure, this study adopts a combined approach of partitioned solving and genetic algorithms based on the solution theory outlined in Section 3.4. By partitioning the feasible domain into five sub-feasible domains according to i (0 ≤ i ≤ 4), versatile optional nodes are developed as historical catalyst elements, and the CPCO problem in any given sub-domain reduces to a non-crossover parallel combinatorial optimization problem.

Each partitioned subproblem is mathematically tractable. Taking the scenario where two versatile optional nodes are selected as historical catalyst elements as an example: first, two elements are chosen from the five versatile optional nodes (yielding ${\complement }_5^2$ scenarios), then two (by subtracting two from four) elements are selected from the original nine historical optional nodes (yielding ${\complement }_9^2$ scenarios). The remaining three unselected versatile optional nodes are merged into the commercial optional nodes set, expanding it to 44 elements (41 original + 3 merged), from which 12 commercial catalyst elements are selected (yielding ${\complement }_{44}^{12}$ scenarios). Finally, six public-space catalyst elements are chosen from the 16 optional nodes (yielding ${\complement }_{16}^6$ scenarios). Thus, fixing two versatile optional nodes as historical catalyst elements generates ${\mathrm{C}}_5^2{\mathrm{C}}_9^2{\mathrm{C}}_{44}^{12}{\mathrm{C}}_{16}^6$ feasible solutions.

Table 3. All partitioning criteria and their corresponding feasible solution quantities.

Grouping	Partitioning Criteria	Feasible Solution Quantities	Order of Magnitude
Group 1	0 versatile optional nodes selected as historical catalyst elements	${\mathrm{C}}_5^0{\mathrm{C}}_9^4{\mathrm{C}}_{46}^{12}{\mathrm{C}}_{16}^6$	${10}^{16}$
Group 2	1 versatile optional node selected as historical catalyst elements	${\mathrm{C}}_5^1{\mathrm{C}}_9^3{\mathrm{C}}_{45}^{12}{\mathrm{C}}_{16}^6$	${10}^{16}$
Group 3	2 versatile optional nodes selected as historical catalyst elements	${\mathrm{C}}_5^2{\mathrm{C}}_9^2{\mathrm{C}}_{44}^{12}{\mathrm{C}}_{16}^6$	${10}^{16}$
Group 4	3 versatile optional nodes selected as historical catalyst elements	${\mathrm{C}}_5^3{\mathrm{C}}_9^1{\mathrm{C}}_{43}^{12}{\mathrm{C}}_{16}^6$	${10}^{16}$
Group 5	4 versatile optional nodes selected as historical catalyst elements	${\mathrm{C}}_5^4{\mathrm{C}}_9^0{\mathrm{C}}_{42}^{12}{\mathrm{C}}_{16}^6$	${10}^{14}$

details all partitioning criteria and their corresponding feasible solution quantities.

Moreover, each partitioned subproblem is computationally codifiable. This study employs genetic algorithm-based optimization, which necessitates bijective mapping between feasible solutions and binary strings. As demonstrated in Figure 9, the binary encoding scheme for group 3 where two versatile optional nodes are selected as historical catalyst elements exemplifies this correspondence principle.

Based on the binary encoding method, every feasible solution across the 71 catalyst element optional nodes can be bijectively mapped to a 74-bit binary string. This encoding partitions into four segments of 5-bit, 9-bit, 44-bit, and 16-bit lengths, with each segment maintaining fixed counts of 1s and 0s. Specifically, a 41-bit segment recording commercial catalyst element selections is followed by a three-bit segment indicating whether the three versatile optional nodes (not selected as historical catalyst elements) are chosen as commercial ones. These three bits constitute a “chained binary encoding”—a novel designation in this study for context-dependent bits whose interpretation relies on preceding segment outputs. This chained encoding serves as a core mechanism for handling crossover architecture in the proposed genetic algorithm.

In summary, the original problem comprising three crossover parallel combinatorial subproblems is decomposed into subgroups, each containing four independent parallel combinatorial subproblems. Accordingly, the classical genetic algorithm crossover and mutation operators are adapted into segmented crossover and segmented mutation operators.

During segmented crossover operations, while each binary segment of parent individuals contains the prescribed number of 1s, the two offspring generated through conventional crossover may violate this requirement in their respective segments. To address this, two approaches can be considered: either defining a specialized crossover operator that inherently preserves the count of 1s, or employing random crossover followed by individual repair. For simplicity, this study adopts the approach of random crossover with repair: First, a 74-bit crossover mask (equal to parent length) is randomly generated to determine gene exchange positions. After crossover, for any segment exceeding its required count of 1s by k, k randomly selected 1s are deleted; conversely, for segments deficient by k 1s, k 1s are randomly added. This segmented crossover operator is illustrated in Figure 10.

The segmented mutation in this case differs from conventional genetic algorithms that use fixed mutation rates, instead adopting weighted mutation rates. This study proposes that mutation rates for each binary segment should vary according to the total combinatorial possibilities of each segment. However, considering that the combinatorial number ${\mathrm{C}}_{\mathrm{n}}^{\mathrm{m}}$ is overly sensitive to the values of n and m, a weighting function using logarithmic correction is designed. If a binary string is divided into k segments with segment lengths n_i (1 ≤ i ≤ k) and required counts of 1s m_i (1 ≤ i ≤ k), given an average mutation rate ξ (0 < kξ < 1), the mutation rate ξ_i for the i-th binary segment is

$$\begin{array}{c}{\mathsf{\xi }}_{\mathrm{i}}={\displaystyle \frac{\mathrm{l}\mathrm{n}{\complement }_{{\mathrm{n}}_{\mathrm{i}}}^{{\mathrm{m}}_{\mathrm{i}}}}{\sum _{\mathrm{j}=1}^{\mathrm{k}}\mathrm{l}\mathrm{n}{ \complement }_{{\mathrm{n}}_{\mathrm{j}}}^{{\mathrm{m}}_{\mathrm{j}}}}}k\xi \end{array}$$

(7)

In this case study with ξ = 0.1, the segment-specific mutation rates are 0.024, 0.037, 0.246, and 0.093 for the four binary segments, respectively, whereas direct combinatorial weighting would yield extreme values of 0.000, 0.000, 0.400, and 0.000.

In summary, building upon existing genetic algorithm theory, this study first proposes a novel binary encoding structure to map any feasible solution for combinatorial optimization problems with crossover parallel architectures, and subsequently develops corresponding crossover and mutation operators tailored to the characteristics of such problems. These algorithmic refinements preserve the fundamental principles of genetic algorithms while enabling effective solutions to the proposed CPCO problems.

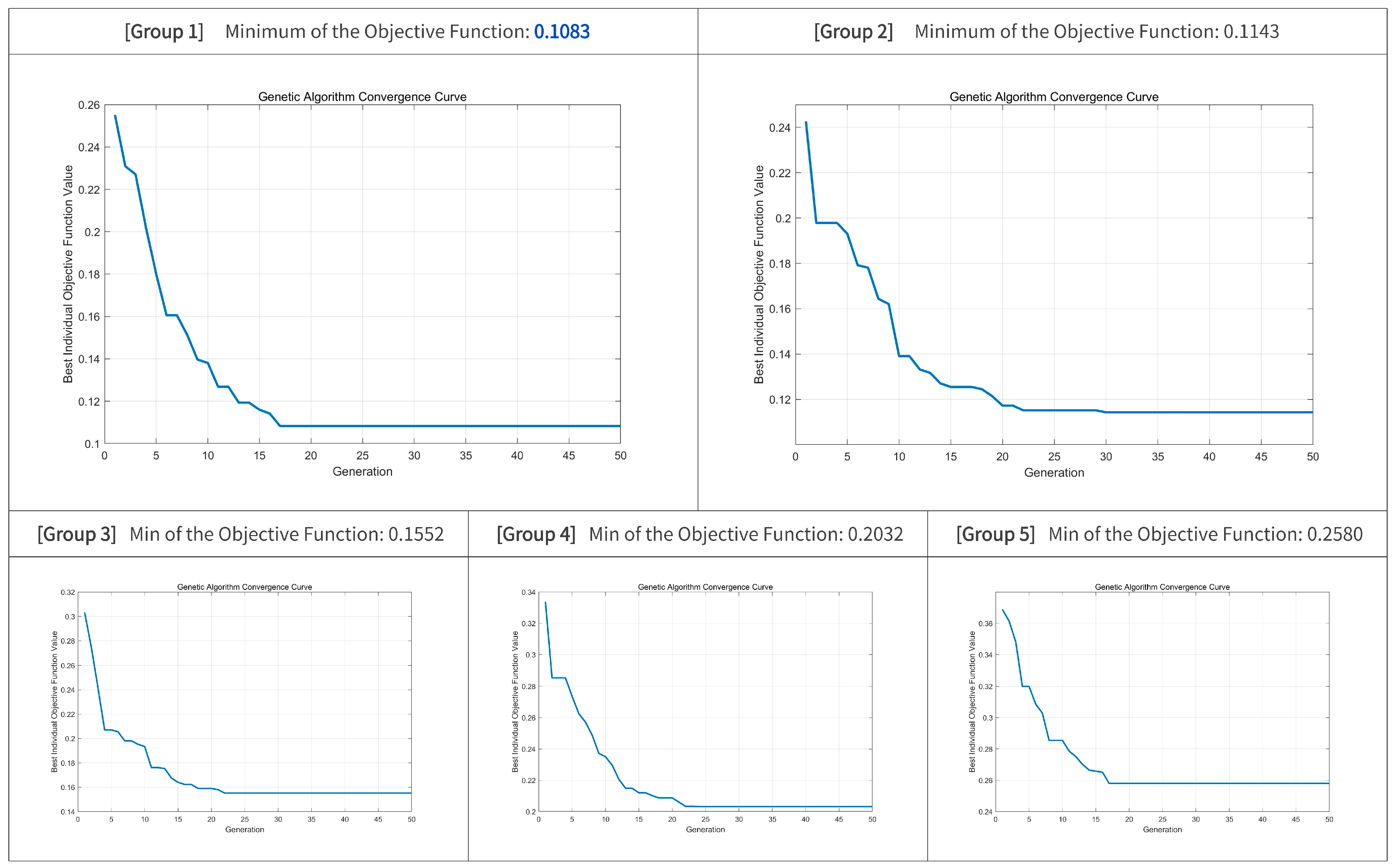
Based on the improved genetic algorithm, local optimal solutions were obtained for the sub-feasible domains under five groups. The corresponding convergence curves and derived local optima for each group are illustrated in Figure 11.

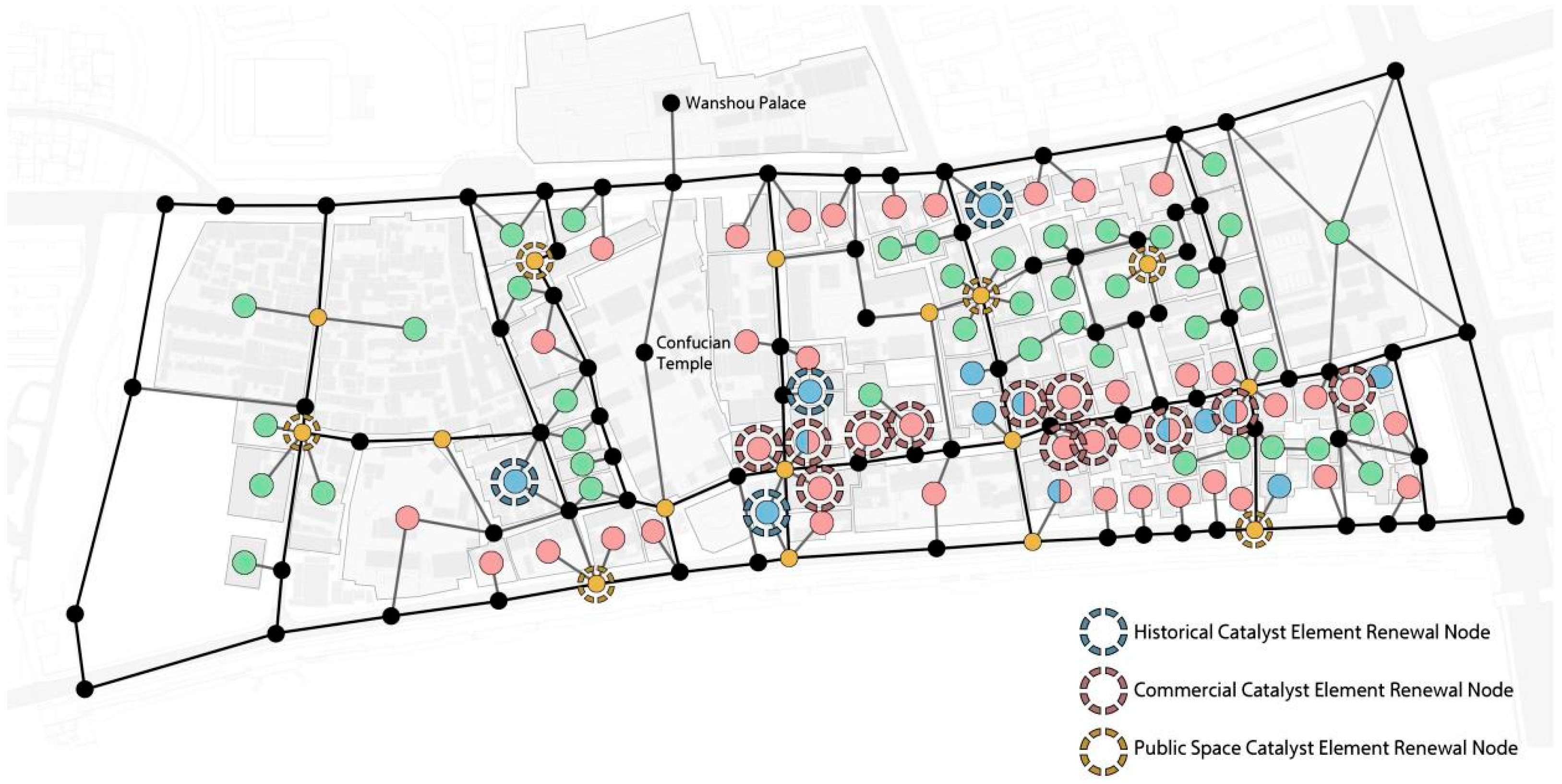
The locally optimal solution obtained for Group 1 simultaneously represents the global optimum, with Figure 12 illustrating the corresponding practical micro-renewal catalyst element site selection scheme derived from this optimal solution.

Finally, this case employs a customized, simplified catalytic validation approach, specifically (1) establishing the validation indicator “maximum distance between adjacent catalyst elements” with an empirically determined threshold of ≤100 m based on field research and professional judgment, and (2) calculating through coordinate modeling that the actual maximum distance between adjacent catalyst elements is 85.6 m, thereby passing validation.

The catalyst site selection scheme derived from the MCPCO model in this case represents the optimal solution under objectives jointly determined by both the design team and project clients. As anticipated, it demonstrates characteristic features including but not limited to (1) uniform distribution across all catalyst types, (2) independent uniform distribution of individual catalyst types, and (3) linear alignment of point-based commercial catalyst elements along the main street. Ultimately, the solution successfully passed the catalyst validation module while receiving unanimous approval from project clients.

5. Discussion and Conclusion

5.1. Discussion

The Multi-objective Crossover Parallel Combinatorial Optimization (MCPCO) model serves as a powerful quantitative tool for addressing catalyst element site selection in urban micro-renewal. On one hand, traditional site selection models in urban planning (e.g., P-Median, Gravity P-Median, Location Set Covering, etc.) are unable to achieve parallel site selection for multiple types of elements under multi-objective conditions. On the other hand, traditional optimization models in operations research fail to effectively map the unique structural characteristics of catalyst element site selection problems. Therefore, this study proposes the MCPCO model to specifically address catalyst element site selection and demonstrates its applicability to any form of multi-type element parallel site selection problem.

This study prioritizes the simplicity and generality of the model, which also introduces certain limitations. First, the model primarily addresses the common structural characteristics of catalyst element site selection problems and may not adapt to a minority of exceptional scenarios (e.g., dynamically adjustable input quantities). Second, while the MCPCO model is proposed for generalized catalyst site selection problems and maintains a degree of abstraction, Section 3 discusses a series of potential implementation challenges, and Section 4 provides a concrete application case. Nevertheless, practitioners may still encounter scenario-specific details not covered by this study.

Furthermore, mathematical models inherently suffer from limitations such as high specificity with limited generalizability, as well as technical complexity that hinders practical implementation. Although this study has thoroughly addressed these issues through model simplification and functional encapsulation to reduce usability barriers, applying the model directly to real-world urban problems may still entail certain complexities and challenges.

Therefore, the next research phase will prioritize enhancing the usability of the MCPCO model. This will be achieved through two approaches: (1) Systematic encapsulation of the model and improved algorithms on programming platforms (e.g., MATLAB, Python) to enable urban designers to utilize the model with only basic programming proficiency; (2) Integration of the model into mainstream GIS software (e.g., ArcGIS) for direct application via interface operations. Notably, the programming-based approach offers greater flexibility for customized applications.

5.2. Conclusions

Targeting the catalyst element site selection problem in urban micro-renewal, this study proposes an optimization model with specialized architecture: the Multi-objective Crossover Parallel Combinatorial Optimization (MCPCO) model, designed to meet the multifaceted requirements imposed by the problem’s characteristics. The catalyst element site selection problem requires the simultaneous combinatorial optimization of multiple interrelated element types, which exceeds the capability of traditional optimization models. To address this, our study innovatively introduces a “crossover-parallel” architecture in the MCPCO model, enabling holistic parallel and partially crossover-based combinatorial optimization of multi-type elements. Furthermore, this model exhibits high integration capability and generalizability, which are primarily manifested in (1) mapping highly complex catalyst element site selection problems through an exceptionally simple model architecture, and (2) accommodating highly specific site selection requirements via a maximally general framework. Since the model’s specialized architecture invalidates existing optimization algorithms, this study also proposes a systematic optimization methodology.

The model’s implementation framework comprises five sequential components: urban spatial data translation, crossover parallel combinatorial structure construction, multi-objective formulation, optimization algorithm configuration, and catalyst validation. This study applies the model to the catalyst element site selection problem in the Liuhe Confucian Temple Historic District of Nanjing, China, serving as a demonstrative implementation of all five model components. Specifically, following the algorithmic configuration methodology, we develop an improved genetic algorithm featuring (1) a fixed-length binary mapping method for feasible solutions based on “chained binary bits”, and (2) specialized crossover and mutation operators designed for encoded solutions. The proposed algorithm ultimately achieves a high-quality solution for the MCPCO model.

The MCPCO model proposed in this study, while specifically developed for catalyst element site selection problems, demonstrates generalizability to various urban design problems characterized by simultaneous multi-type element placement. Furthermore, this research holds certain implications for both fundamental development and practical applications in operations research.