Modeling the Short- and Long-Term Impacts of Climate Change on Wheat Production in Egypt Using Autoregressive Distributed Lag Approach
Abstract
1. Introduction
2. Methodology
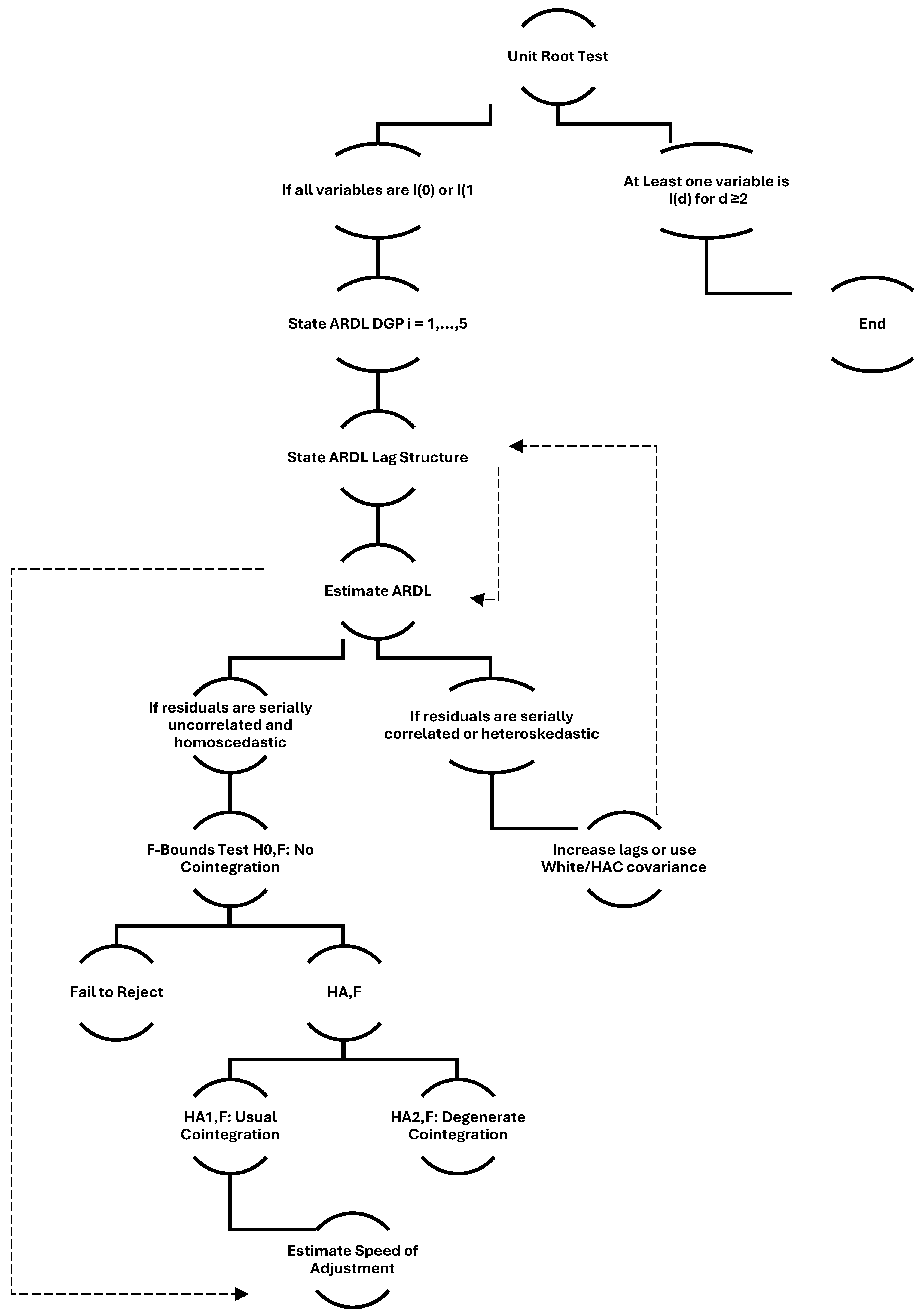
2.1. Testing the Time Series Stationarity
2.2. Autoregressive Distributed Lag (ARDL) Model
3. Results and Discussion
3.1. Unit Root Test Results
3.2. Specifying ARDL Data Generating Process
3.3. Lag Order and Bound Test for Cointegration
3.4. ARDL Model Estimations, Both Long- and Short-Term
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. World Food and Agriculture Statistical Yearbook 2023; FAO: Rome, Italy, 2023. [Google Scholar]
- USDA. Grain: World Markets and Trade. United States Department of Agriculture Foreign Agricultural Service, USA. 2024. Available online: https://www.fas.usda.gov/sites/default/files/2025-05/2024-Jan-Grain.pdf (accessed on 15 April 2025).
- Mostafa, S.M.; Wahed, O.; El-Nashar, W.Y.; El-Marsafawy, S.M.; Abd-Elhamid, H.F. Impact of climate change on water resources and crop yield in the Middle Egypt region. AQUA—Water Infrastruct. Ecosyst. Soc. 2021, 70, 1066–1084. [Google Scholar] [CrossRef]
- The World Bank Group. Climate Risk Profile: Egypt; The World Bank Group: Washington, DC, USA, 2024; p. 28. [Google Scholar]
- Abd El Maksoud, T.D. The impact of climate change-related factors on food production in Egypt. Int. J. Mod. Agric. Environ. 2022, 2, 15–25. [Google Scholar] [CrossRef]
- Chandio, A.A.; Gokmenoglu, K.K.; Ahmad, F. Addressing the long-and short-run effects of climate change on major food crops production in Turkey. Environ. Sci. Pollut. Res. 2021, 28, 51657–51673. [Google Scholar] [CrossRef] [PubMed]
- You, L.; Rosegrant, M.W.; Wood, S.; Sun, D. Impact of growing season temperature on wheat productivity in China. Agric. For. Meteorol. 2009, 149, 1009–1014. [Google Scholar] [CrossRef]
- Verma, L.; Singh, A.K.; Singh, S.; Tiwari, D.; Zaidi, S.T.; Yadav, R.K.; Mishra, S.R.; Singh, A.K. Temperature Stress Its Impact on Yield of Various Wheat Varieties at Different Growth Stages. Natl. Acad. Sci. Lett. 2024, 47, 219–225. [Google Scholar] [CrossRef]
- Tao, F.L.; Zhang, Z.Z. Climate change, wheat productivity and water use in the North China Plain: A new super-ensemble-based probabilistic projection. Agric. For. Meteorol. 2013, 170, 146–165. [Google Scholar] [CrossRef]
- Oliver, R.J.; Finch, J.W.; Taylor, G. Second generation bioenergy crops and climate change: A review of the effects of elevated atmospheric CO2 and drought on water use and the implications for yield. GCB Bioenergy Bioprod. A Sustain. Bioecon. 2009, 1, 97–114. [Google Scholar] [CrossRef]
- Kheir, A.M.S.; El Baroudy, A.; Aiad, M.A.; Zoghdan, M.G.; Abd El-Aziz, M.A.; Ali, M.G.M.; Fullen, M.A. Impacts of rising temperature, carbon dioxide concentration, and sea level on wheat production in North Nile delta. Sci. Total Environ. 2019, 651, 3161–3173. [Google Scholar] [CrossRef]
- Asfew, M.; Bedemo, A. Impact of climate change on cereal crops production in Ethiopia. Adv. Agric. 2022, 2022, 2208694. [Google Scholar] [CrossRef]
- Chandio, A.A.; Jiang, Y.; Fatima, T.; Ahmad, F.; Ahmad, M.; Li, J. Assessing the impacts of climate change on cereal production in Bangladesh: Evidence from ARDL modeling approach. Int. J. Clim. Change Strateg. Manag. 2022, 14, 125–147. [Google Scholar] [CrossRef]
- Chandio, A.A.; Jiang, Y.; Rauf, A.; Ahmad, F.; Amin, W.; Shehzad, K. Assessment of formal credit and climate change impact on agricultural production in Pakistan: A time series ARDL modeling approach. Sustainability 2020, 12, 5241. [Google Scholar] [CrossRef]
- Onyeneke, R.U.; Ejike, R.D.; Osuji, E.E.; Chidiebere-Mark, N.M. Does climate change affect crops differently? New evidence from Nigeria. Environ. Dev. Sustain. 2024, 26, 393–419. [Google Scholar] [CrossRef]
- Ozdemir, D. The impact of climate change on agricultural productivity in Asian countries: A heterogeneous panel data approach. Environ. Sci. Pollut. Res. 2022, 29, 8205–8217. [Google Scholar] [CrossRef]
- Tagwi, A. The impacts of climate change, carbon dioxide emissions (CO2) and renewable energy consumption on agricultural economic growth in South Africa: ARDL approach. Sustainability 2022, 14, 16468. [Google Scholar] [CrossRef]
- Warsame, A.A.; Sheik-Ali, I.A.; Ali, A.O.; Sarkodie, S.A. Climate change and crop production nexus in Somalia: An empirical evidence from ARDL technique. Environ. Sci. Pollut. Res. 2021, 28, 19838–19850. [Google Scholar] [CrossRef]
- Gamal, R.; Abou-Hadid, A.F.; Omar, M.E.D.; Elbana, M. Does climate change affect wheat productivity and water demand in arid regions? Case study of Egypt. J. Agric. Food Res. 2024, 16, 101181. [Google Scholar] [CrossRef]
- Swelam, A.; Farag, A.; Ramasamy, S.; Ghandour, A. Effect of Climate Variability on Water Footprint of Some Grain Crops under Different Agro-Climatic Regions of Egypt. Atmosphere 2022, 13, 1180. [Google Scholar] [CrossRef]
- Makar, R.S.; Shahin, S.A.; El-Nazer, M.; Wheida, A.; Abd El-Hady, M. Evaluating the Impacts of Climate Change on Irrigation Water Requirements. Sustainability 2022, 14, 14833. [Google Scholar] [CrossRef]
- Roushdi, M. Investigation the implications of climate change on crop water requirements in Western Nile Delta, Egypt. Water Sci. 2024, 38, 77–91. [Google Scholar] [CrossRef]
- Gamal, G.; Samak, M.; Shahba, M. The possible impacts of different global warming levels on major crops in Egypt. Atmosphere 2021, 12, 1589. [Google Scholar] [CrossRef]
- Ali, S. An Economic Study of The Impact of Climate Change on The Productivity of Wheat Crop in Egypt. J. Adv. Agric. Res. 2023, 28, 380–394. [Google Scholar] [CrossRef]
- Abdelaal, E.; Elsherbini, M. An economic study for climate change impact on wheat production in the northern west coast region of Egypt. Arab Univ. J. Agric. Sci. 2021, 29, 183–196. [Google Scholar] [CrossRef]
- FAO. FAOSTAT; FAO: Rome, Italy, 2024. [Google Scholar]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ryan, O.; Haslbeck, J.; Waldorp, L. Non-stationarity in time-series analysis: Modeling stochastic and deterministic trends. Multivar. Behav. Res. 2025, 60, 556–588. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econom. J. Econom. Soc. 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis; Department of Applied Economics, University of Cambridge: Cambridge, UK, 1995; Volume 9514. [Google Scholar]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxf. Bull. Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Popp, S. A Nonlinear Unit Root Test in the Presence of an Unknown Break; Ruhr Economic Papers, No. 45; Rheinisch-Westfälisches Institut für Wirtschaftsforschung (RWI): Essen, Germany, 2008; ISBN 978-3-86788-046-6. [Google Scholar] [CrossRef]
- Sephton, P.S. Finite sample lag adjusted critical values of the ADF-GLS test. Comput. Econ. 2022, 59, 177–183. [Google Scholar] [CrossRef]
- Pesaran, H.H.; Shin, Y. Generalized impulse response analysis in linear multivariate models. Econ. Lett. 1998, 58, 17–29. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Impact of Climate Change on the Agricultural Sector in Egypt. In Conventional Water Resources and Agriculture in Egypt; Negm, A.M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 213–227. [Google Scholar]
- Wang, X.; Zhang, J.; Zhao, Y.; Liu, X.; Gao, H.; Cheng, M.; Zhang, G.; Chen, Y. Evaluation of farmland soil health and optimization of evaluation system under different green manure applications in a semi-arid irrigation area. Land Degrad. Dev. 2024, 35, 1913–1926. [Google Scholar] [CrossRef]
- Ali, M.G.; Ibrahim, M.M.; El Baroudy, A.; Fullen, M.; Omar, E.S.; Ding, Z.; Kheir, A.M. Climate change impact and adaptation on wheat yield, water use and water use efficiency at North Nile Delta. Front. Earth Sci. 2020, 14, 522–536. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for testing the constancy of regression relationships over time. J. R. Stat. Soc. Ser. B Stat. Methodol. 1975, 37, 149–163. [Google Scholar] [CrossRef]


| Abb. | Description | Unit | Source |
|---|---|---|---|
| WP | Wheat production | Tons | [21] |
| Ha | Wheat harvested area | Hectare | [21] |
| Fert. | Fertilizer consumption | Kilogram/hectare | [21] |
| Tract | Number of tractors | number | [21] |
| CO2 | Carbon dioxide emissions | Metric tons/capita | [21] |
| WTEMP. | Mean winter temperature | °C | [21] |
| SPTEMP | Mean spring temperature | °C | [21] |
| Rf | Rainfall | mm | [21] |
| Variables | ADF Test | PP Test | Integration Order | ||
|---|---|---|---|---|---|
| Level | Level | ||||
| Constant | Constant and Trend | Constant | Constant and Trend | ||
| Production | −0.558 | −2.140 | −0.477 | −2.146 | |
| Area | −0.373 | −2.607 | −0.264 | −2.567 | |
| Fertilizers | −2.218 | −1.414 | −2.097 | −1.347 | |
| Tractors | −2.016 | −0.225 | −1.807 | −0.476 | |
| CO2 | −1.152 | −1.523 | −1.186 | −2.023 | |
| Winter temperature | −4.812 ** | −5.832 *** | −6.817 *** | −7.963 *** | I(0) |
| Spring temperature | −3.901 * | −8.707 *** | −6.492 *** | −8.707 *** | I(0) |
| Rainfall | −4.694 ** | −5.925 *** | −7.525 *** | −7.673 *** | I(0) |
| Variables | First difference | First difference | |||
| Constant | Constant and Trend | Constant | Constant and Trend | ||
| Production | −10.113 *** | −10.030 *** | −9.899 *** | −9.790 *** | I(1) |
| Area | −8.490 *** | −8.497 *** | −8.488 *** | −8.497 *** | I(1) |
| Fertilizers | −5.040 *** | −8.585 *** | −8.237 *** | −8.584 *** | I(1) |
| Tractors | −5.991 *** | −6.327 *** | −6.030 *** | −6.327 *** | I(1) |
| CO2 | −8.928 *** | −8.965 *** | −8.917 *** | −8.950 *** | I(1) |
| Winter temperature | −5.250 *** | −5.247 *** | −33.824 *** | −34.674 *** | |
| Spring temperature | −5.033 *** | −5.045 *** | −51.329*** | −54.420 *** | |
| Rainfall | −11.436 *** | −11.335 *** | −15.164*** | −18.030 *** | |
| Cointegration Bound Test | Value | K |
|---|---|---|
| F-statistics | 7.301 | 7 |
| Significance | At I(0) | At I(1) |
| At 10% | 2.044 | 3.104 |
| At 5% | 2.373 | 3.540 |
| At 1% | 3.129 | 4.507 |
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| Long-term estimation | ||||
| Ln area | 1.078 | 0.480 | 2.248 | 0.037 |
| Ln fertilizers | 0.749 | 0.542 | 1.381 | 0.183 |
| Ln tractors | 1.493 | 0.493 | 3.029 | 0.007 |
| Ln CO2 | −1.762 | 0.592 | −2.974 | 0.008 |
| Ln WTEMP | 6.886 | 2.594 | 2.654 | 0.016 |
| Ln SPTEMP | 3.563 | 2.396 | 1.487 | 0.153 |
| Ln RAIN | 0.253 | 0.159 | 1.590 | 0.128 |
| C | −42.309 | 14.091 | −3.003 | 0.007 |
| Short-term estimation | ||||
| D(Ln area) | 1.075 | 0.068 | 15.716 | 0.000 |
| D(Ln fertilizers) | 0.049 | 0.053 | 0.917 | 0.371 |
| D(Ln tractors) | 0.007 | 0.096 | 0.073 | 0.942 |
| D(Ln CO2) | −0.072 | 0.054 | −1.331 | 0.199 |
| D(Ln WTEMP) | −0.096 | 0.099 | −0.967 | 0.346 |
| D(Ln SPTEMP) | −0.520 | 0.132 | −3.927 | 0.001 |
| D(Ln RAIN) | −0.054 | 0.018 | −3.066 | 0.006 |
| CointEq(−1) | −0.288 | 0.030 | −9.663 | 0.000 |
| Diagnostic Test | Value (Probability) |
|---|---|
| R2 | 0.998 |
| Adjusted R2 | 0.997 |
| F-statistic | 808.417 (0.000) |
| Ramsey RESET | 1.817 (0.193) |
| Durbin–Watson | 2.034 |
| Breusch–Godfrey Serial Correlation | 1.063 (0.316) |
| Heteroskedasticity Test: ARCH | 0.189 (0.890) |
| CUSUM | Stable |
| CUSUM square | Stable |
| Null Hypothesis | F-Statistic | Prob. | Null Hypothesis | F-Statistic | Prob. |
|---|---|---|---|---|---|
| AREA ⟶ PRODUCTION | 4.25 ** | 0.04 | CO2 ⟶ FERTILIZERS | 0.00 | 0.97 |
| PRODUCTION ⟶ AREA | 10.21 *** | 0.00 | FERTILIZERS ⟶ CO2 | 2.41 | 0.13 |
| FERTILIZERS ⟶ PRODUCTION | 3.83 | 0.06 | WTEMP ⟶ FERTILIZERS | 0.31 | 0.58 |
| PRODUCTION ⟶ FERTILIZERS | 0.01 | 0.93 | FERTILIZERS ⟶ WTEMP | 5.43 ** | 0.02 |
| TRACT ⟶ PRODUCTION | 6.91 *** | 0.01 | SPTEMP ⟶ FERTILIZERS | 0.03 | 0.87 |
| PRODUCTION ⟶ TRACT | 1.52 | 0.22 | FERTILIZERS ⟶ SPTEMP | 11.68 *** | 0.00 |
| CO2 ⟶ PRODUCTION | 2.80 | 0.10 | RAIN ⟶ FERTILIZERS | 0.51 | 0.48 |
| PRODUCTION ⟶ CO2 | 1.88 | 0.18 | FERTILIZERS ⟶ RAIN | 1.56 | 0.22 |
| WTEMP ⟶ PRODUCTION | 1.23 | 0.27 | CO2 ⟶ TRACT | 0.11 | 0.74 |
| PRODUCTION ⟶ WTEMP | 11.78 *** | 0.00 | TRACT ⟶ CO2 | 7.34 *** | 0.01 |
| SPTEMP ⟶ PRODUCTION | 0.08 | 0.78 | WTEMP ⟶ TRACT | 4.00 ** | 0.05 |
| PRODUCTION ⟶ SPTEMP | 19.76 *** | 0.00 | TRACT ⟶ WTEMP | 9.25 *** | 0.00 |
| RAIN ⟶ PRODUCTION | 2.22 | 0.14 | SPTEMP ⟶ TRACT | 1.26 | 0.27 |
| PRODUCTION ⟶ RAIN | 4.04 ** | 0.05 | TRACT ⟶ SPTEMP | 14.41 *** | 0.00 |
| FERTILIZERS ⟶ AREA | 3.71 | 0.06 | RAIN ⟶ TRACT | 1.05 | 0.31 |
| AREA ⟶ FERTILIZERS | 0.04 | 0.84 | TRACT ⟶ RAIN | 2.63 | 0.11 |
| TRACT ⟶ AREA | 6.12 ** | 0.02 | W_TEMP ⟶ CO2 | 0.06 | 0.81 |
| AREA ⟶ TRACT | 1.96 | 0.17 | CO2 ⟶ WTEMP | 11.67 *** | 0.00 |
| CO2 ⟶ AREA | 5.22 ** | 0.03 | SPTEMP ⟶ CO2 | 0.42 | 0.52 |
| AREA ⟶ CO2 | 0.81 | 0.37 | CO2 ⟶ SPTEMP | 18.92 *** | 0.00 |
| W_TEMP ⟶ AREA | 0.13 | 0.72 | RAIN ⟶ CO2 | 0.14 | 0.71 |
| AREA ⟶ WTEMP | 13.69 *** | 0.00 | CO2 ⟶ RAIN | 2.93 | 0.09 |
| SPTEMP ⟶ AREA | 0.02 | 0.89 | SPTEMP ⟶ WTEMP. | 2.00 | 0.16 |
| AREA ⟶ SP_TEMP | 18.36 *** | 0.00 | WTEMP ⟶ SPTEMP | 0.38 | 0.54 |
| RAIN ⟶ AREA | 0.72 | 0.40 | RAIN ⟶ WTEMP | 15.43 *** | 0.00 |
| AREA ⟶ RAIN | 5.98 ** | 0.02 | WTEMP ⟶ RAIN | 1.16 | 0.28 |
| TRACT ⟶ FERTILIZERS | 1.54 | 0.22 | RAIN ⟶ SPTEMP | 3.73 | 0.06 |
| FERTILIZERS ⟶ TRACT | 2.59 | 0.11 | SPTEMP ⟶ RAIN | 2.37 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alboghdady, M.; Abbas, S.; Alashry, M.K.; Hu, Y.; El-Hendawy, S. Modeling the Short- and Long-Term Impacts of Climate Change on Wheat Production in Egypt Using Autoregressive Distributed Lag Approach. Land 2025, 14, 1962. https://doi.org/10.3390/land14101962
Alboghdady M, Abbas S, Alashry MK, Hu Y, El-Hendawy S. Modeling the Short- and Long-Term Impacts of Climate Change on Wheat Production in Egypt Using Autoregressive Distributed Lag Approach. Land. 2025; 14(10):1962. https://doi.org/10.3390/land14101962
Chicago/Turabian StyleAlboghdady, Mohamed, Salwa Abbas, Mohamed Khairy Alashry, Yuncai Hu, and Salah El-Hendawy. 2025. "Modeling the Short- and Long-Term Impacts of Climate Change on Wheat Production in Egypt Using Autoregressive Distributed Lag Approach" Land 14, no. 10: 1962. https://doi.org/10.3390/land14101962
APA StyleAlboghdady, M., Abbas, S., Alashry, M. K., Hu, Y., & El-Hendawy, S. (2025). Modeling the Short- and Long-Term Impacts of Climate Change on Wheat Production in Egypt Using Autoregressive Distributed Lag Approach. Land, 14(10), 1962. https://doi.org/10.3390/land14101962









