Machine Learning-Based Assessment of Watershed Morphometry in Makran
Abstract
1. Introduction
2. Materials and Methods
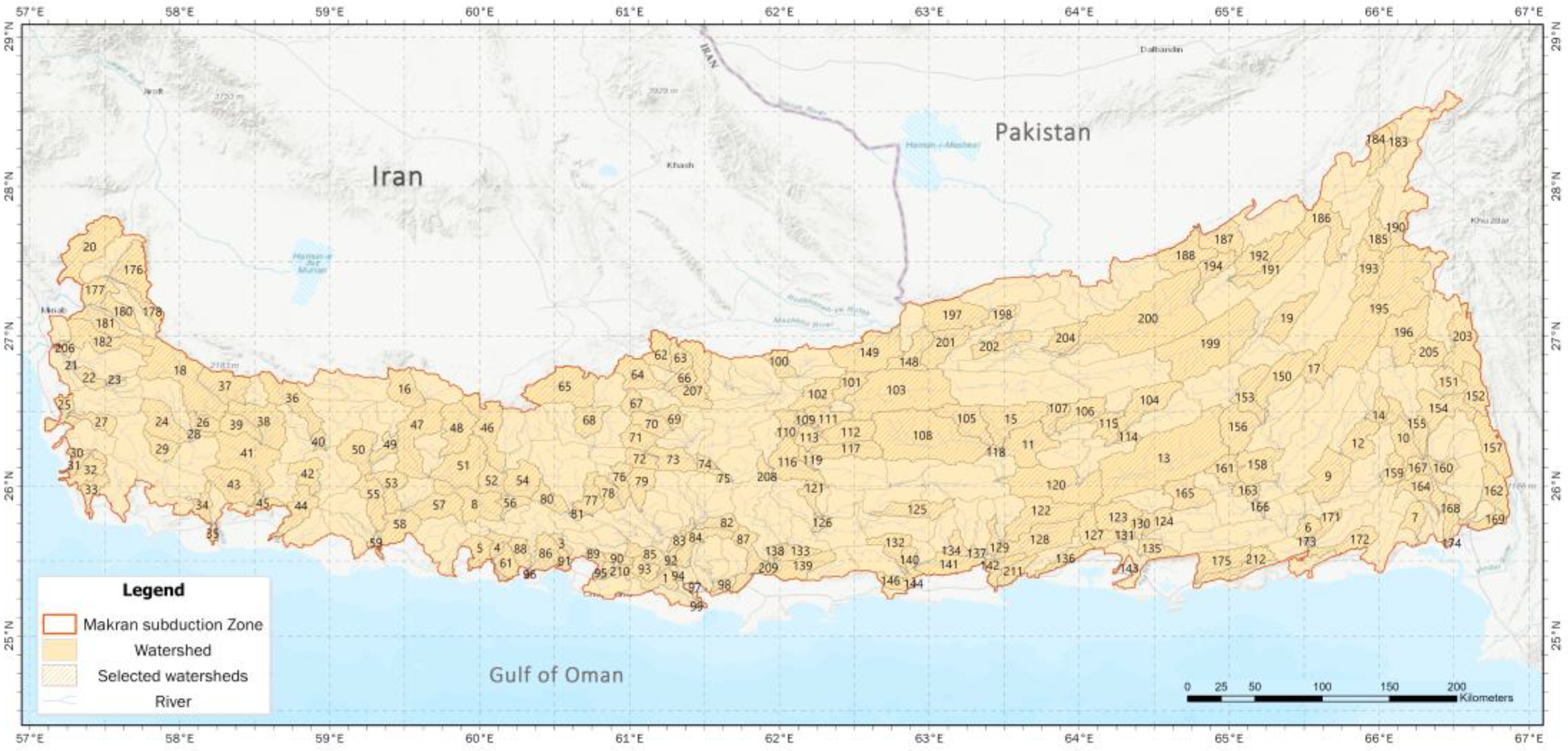
2.1. Study Area
2.2. Extracting the Geomorphic Parameters
2.3. Calculating Criterion Weights by FAHP
2.4. Description and Application of the Criterion
2.4.1. Hypsometric Integral (Hi)
2.4.2. Basin Shape (Bs)
2.4.3. Circularity Basin (Cb)
2.4.4. Elongation Ratio (Er)
2.4.5. Ruggedness Number (Rn)
2.4.6. River Sinuosity (Rs)
2.4.7. Compactness Coefficient (Cc)
2.4.8. Form Factor (Ff)
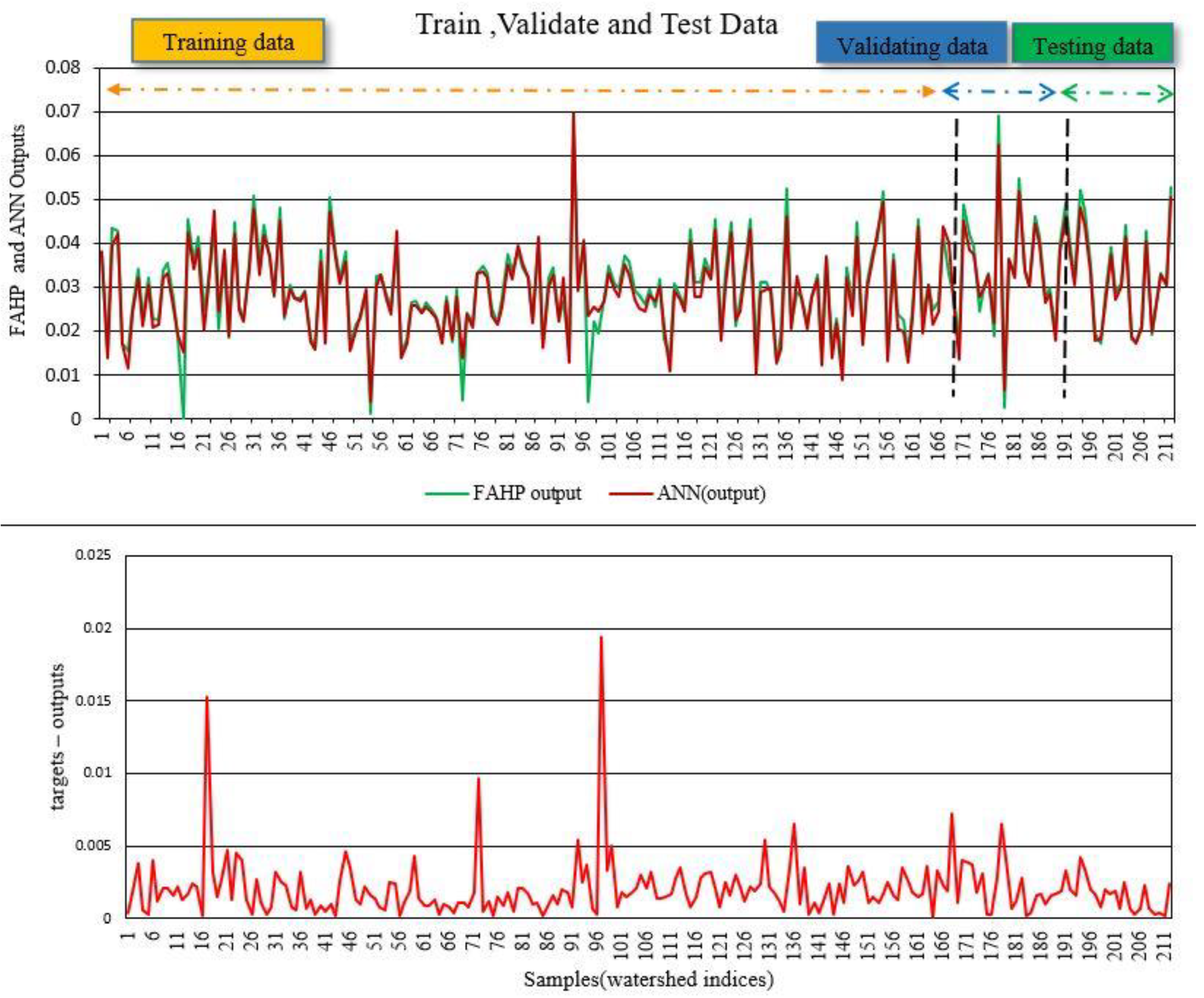
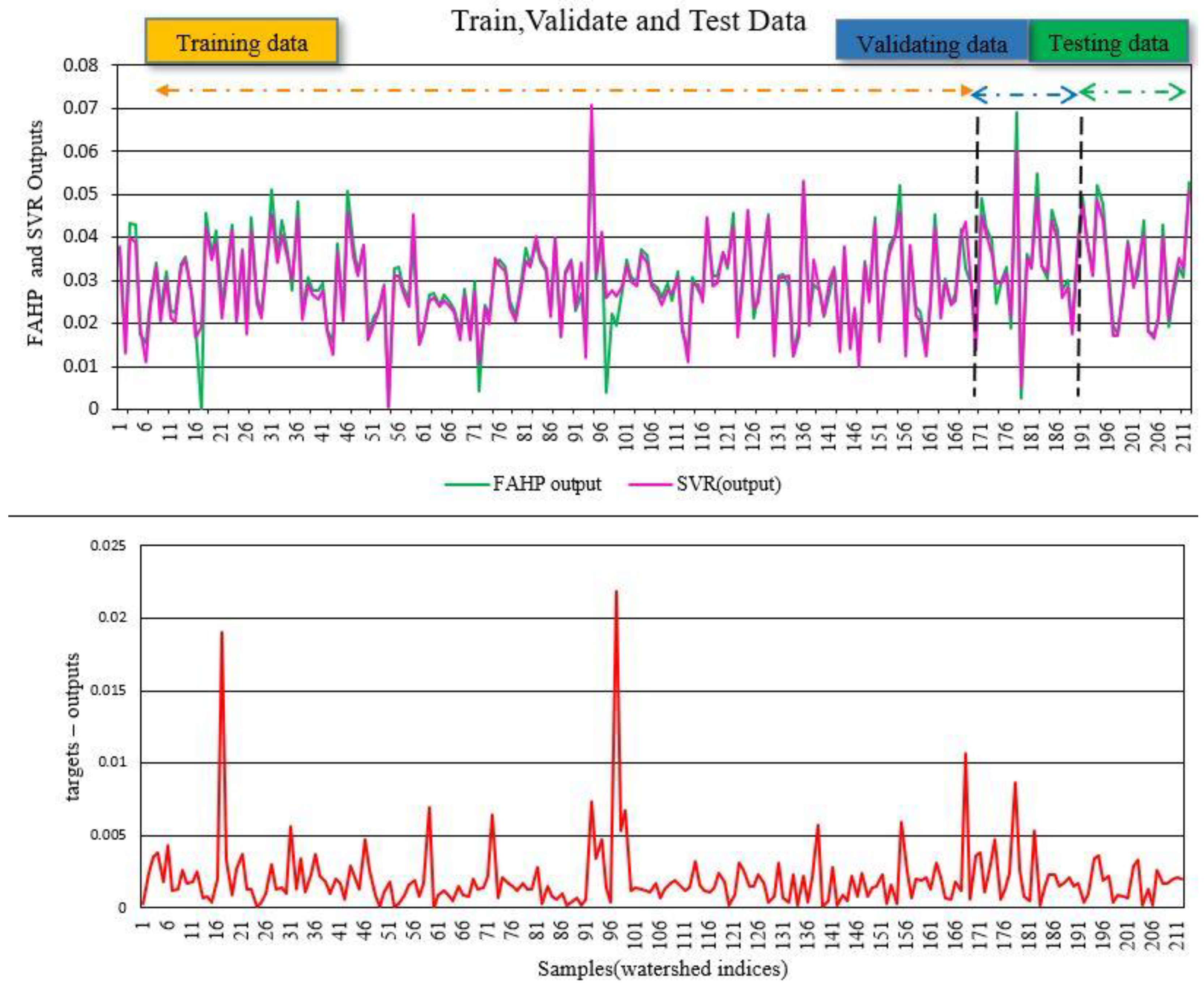
2.5. Machine Learning Algorithms
2.5.1. Artificial Neural Networks (ANNs)
- Data processing occurs in the units known as neurons. The neurons (or artificial neurons) present a model of brain neurons.
- The exchange of data is facilitated through communication between neurons.
- There is a weight for communicative ways between neurons.
- Every neuron utilizes a nonlinear function to process its inputs (weighted data), producing a specific output [82].
2.5.2. Support Vector Regression (SVR)
2.5.3. Multivariate Linear Regression (MLR)
2.6. Integrating the FAHP and ML Algorithms
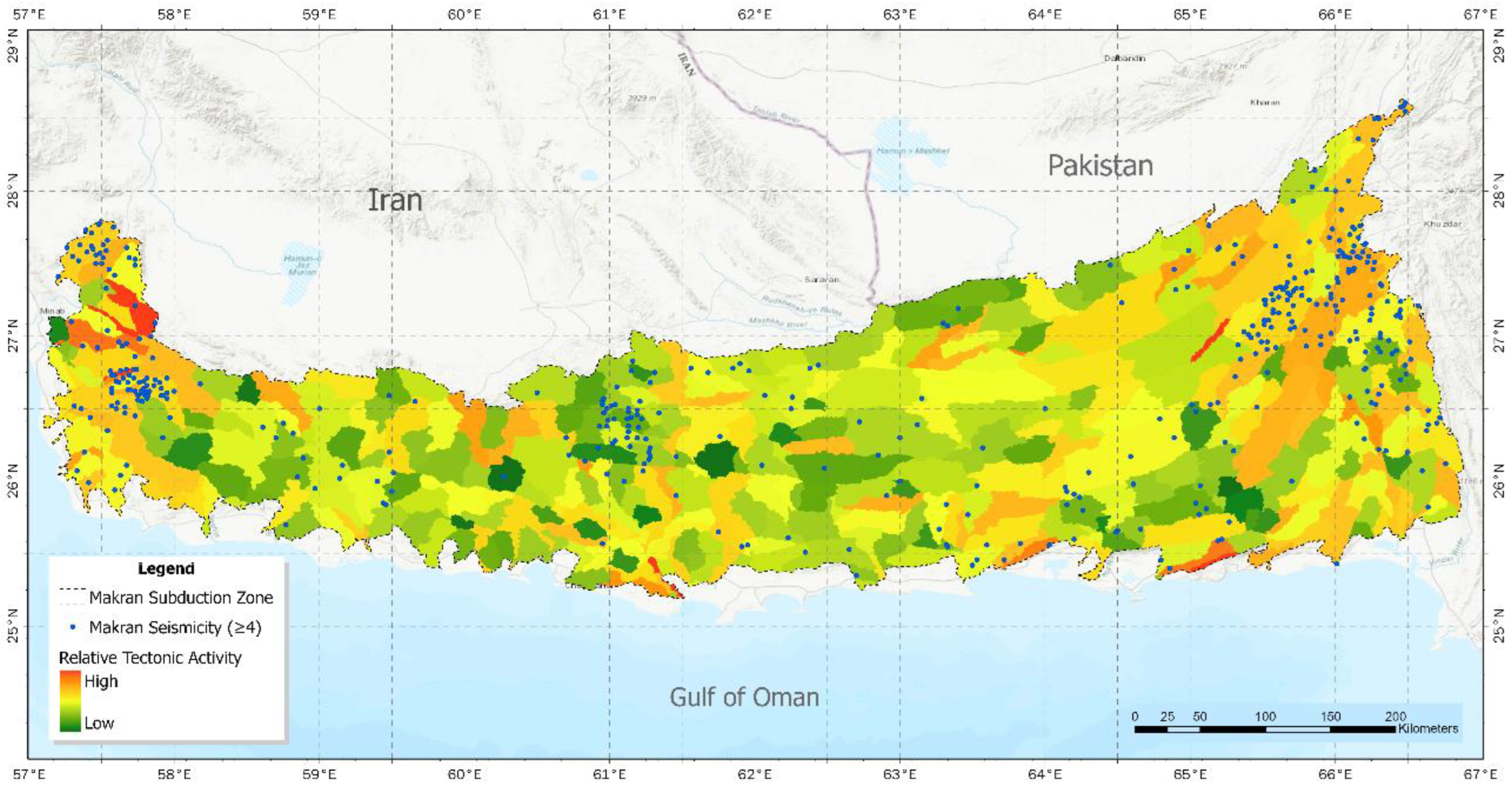
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Christophe, O.; Olaniyi Ti, D. Applications of Geographical Information Systems (GIS) for Spatial Decision Support in Eco-Tourism Development. Environ. Res. J. 2010, 4, 187–194. [Google Scholar] [CrossRef]
- Segura, F.S.; Pardo-Pascual, J.E.; Rosselló, V.M.; Fornós, J.J.; Gelabert, B. Morphometric Indices as Indicators of Tectonic, Fluvial and Karst Processes in Calcareous Drainage Basins, South Menorca Island, Spain. Earth Surf. Process. Landf. 2007, 32, 1928–1946. [Google Scholar] [CrossRef]
- Juez, C.; Garijo, N.; Hassan, M.A.; Nadal-Romero, E. Intraseasonal-to-Interannual Analysis of Discharge and Suspended Sediment Concentration Time-Series of the Upper Changjiang (Yangtze River). Water Resour. Res. 2021, 57, e2020WR029457. [Google Scholar] [CrossRef]
- Mesa, L.M. Morphometric Analysis of a Subtropical Andean Basin (Tucumán, Argentina). Environ. Geol. 2006, 50, 1235–1242. [Google Scholar] [CrossRef]
- Kermani, A.F.; Derakhshani, R.; Bafti, S.S. Data on Morphotectonic Indices of Dashtekhak District, Iran. Data Brief. 2017, 14, 782–788. [Google Scholar] [CrossRef]
- Rahbar, R.; Bafti, S.S.; Derakhshani, R. Investigation of the Tectonic Activity of Bazargan Mountain in Iran. Sustain. Dev. Mt. Territ. 2017, 9, 380–386. [Google Scholar] [CrossRef]
- Aher, P.D.; Adinarayana, J.; Gorantiwar, S.D. Quantification of Morphometric Characterization and Prioritization for Management Planning in Semi-Arid Tropics of India: A Remote Sensing and GIS Approach. J. Hydrol. 2014, 511, 850–860. [Google Scholar] [CrossRef]
- Salvany, J.M. Tilting Neotectonics of the Guadiamar Drainage Basin, SW Spain. Earth Surf. Process. Landf. 2004, 29, 145–160. [Google Scholar] [CrossRef]
- Javed, A.; Khanday, M.Y.; Rais, S. Watershed Prioritization Using Morphometric and Land Use/Land Cover Parameters: A Remote Sensing and GIS Based Approach. J. Geol. Soc. India 2011, 78, 63–75. [Google Scholar] [CrossRef]
- Rashidi, A.; Abbassi, M.-R.; Nilfouroushan, F.; Shafiei, S.; Derakhshani, R.; Nemati, M. Morphotectonic and Earthquake Data Analysis of Interactional Faults in Sabzevaran Area, SE Iran. J. Struct. Geol. 2020, 139, 104147. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. Geol. Soc. Am. Bull 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) Analysis of Erosional Topography. Geol. Soc. Am. Bull 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland. In USGS Professional Paper; US Government Printing Office: Washington, DA, USA, 1957; Volume 294. [Google Scholar]
- Ribolini, A.; Spagnolo, M. Drainage Network Geometry versus Tectonics in the Argentera Massif (French-Italian Alps). Geomorphology 2008, 93, 253–266. [Google Scholar] [CrossRef]
- Bemis, S.P.; Micklethwaite, S.; Turner, D.; James, M.R.; Akciz, S.T.; Thiele, S.; Bangash, H.A. Ground-Based and UAV-Based Photogrammetry: A Multi-Scale, High-Resolution Mapping Tool for Structural Geology and Paleoseismology. J. Struct. Geol. 2014, 69, 163–178. [Google Scholar] [CrossRef]
- Ozdemir, H.; Bird, D. Evaluation of Morphometric Parameters of Drainage Networks Derived from Topographic Maps and DEM in Point of Floods. Environ. Geol. 2009, 56, 1405–1415. [Google Scholar] [CrossRef]
- Chorowicz, J.; Dhont, D.; Gündogdu, N. Neotectonics in the Eastern North Anatolian Fault Region (Turkey) Advocates Crustal Extension: Mapping from SAR ERS Imagery and Digital Elevation Model. J. Struct. Geol. 1999, 21, 511–532. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep Learning-Based Landslide Susceptibility Mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef]
- Ghosh, M.; Gope, D. Hydro-Morphometric Characterization and Prioritization of Sub-Watersheds for Land and Water Resource Management Using Fuzzy Analytical Hierarchical Process (FAHP): A Case Study of Upper Rihand Watershed of Chhattisgarh State, India. Appl. Water Sci. 2021, 11, 17. [Google Scholar] [CrossRef]
- Kumar, R.; Dwivedi, S.B.; Gaur, S. A Comparative Study of Machine Learning and Fuzzy-AHP Technique to Groundwater Potential Mapping in the Data-Scarce Region. Comput. Geosci. 2021, 155, 104855. [Google Scholar] [CrossRef]
- Zaresefat, M.; Ahrari, M.; Reza Shoaei, G.; Etemadifar, M.; Aghamolaie, I.; Derakhshani, R. Identification of Suitable Site-Specific Recharge Areas Using Fuzzy Analytic Hierarchy Process (FAHP) Technique: A Case Study of Iranshahr Basin (Iran). Air Soil Water Res. 2022, 15, 11786221211063849. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R.; Nikpeyman, V.; GhasemiNejad, A.; Raoof, A. Using Artificial Intelligence to Identify Suitable Artificial Groundwater Recharge Areas for the Iranshahr Basin. Water 2023, 15, 1182. [Google Scholar] [CrossRef]
- Önüt, S.; Efendigil, T.; Soner Kara, S. A Combined Fuzzy MCDM Approach for Selecting Shopping Center Site: An Example from Istanbul, Turkey. Expert. Syst. Appl. 2010, 37, 1973–1980. [Google Scholar] [CrossRef]
- Bui, D.T.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land Subsidence Susceptibility Mapping in South Korea Using Machine Learning Algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of Evidence and Artificial Neural Networks for Potential Groundwater Spring Mapping: An Application to the Mt. Modino Area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R. A Comparative Assessment between Three Machine Learning Models and Their Performance Comparison by Bivariate and Multivariate Statistical Methods in Groundwater Potential Mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Bui, D.T. Landslide Susceptibility Evaluation and Management Using Different Machine Learning Methods in the Gallicash River Watershed, Iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef]
- Sarangi, A.; Madramootoo, C.A.; Enright, P.; Prasher, S.O.; Patel, R.M. Performance Evaluation of ANN and Geomorphology-Based Models for Runoff and Sediment Yield Prediction for a Canadian Watershed. Curr. Sci. 2005, 89, 2022–2033. [Google Scholar]
- El Hamdouni, R.; Irigaray, C.; Fernández, T.; Chacón, J.; Keller, E.A. Assessment of Relative Active Tectonics, Southwest Border of the Sierra Nevada (Southern Spain). Geomorphology 2008, 96, 150–173. [Google Scholar] [CrossRef]
- Dykstra, J.D.; Birnie, R.W. Reconnaissance Geologic Mapping in Chagai Hills, Baluchistan, Pakistan, by Computer Processing of Landsat Data. Am. Assoc. Pet. Geol. Bull. 1979, 63, 1490–1503. [Google Scholar] [CrossRef]
- Kamali, Z.; Nazari, H.; Rashidi, A.; Heyhat, M.R.; Khatib, M.M.; Derakhshani, R. Seismotectonics, Geomorphology and Paleoseismology of the Doroud Fault, a Source of Seismic Hazard in Zagros. Appl. Sci. 2023, 13, 3747. [Google Scholar] [CrossRef]
- Derakhshani, R.; Farhoudi, G. Existence of the Oman Line in the Empty Quarter of Saudi Arabia and Its Continuation in the Red Sea. J. Appl. Sci. 2005, 5, 745–752. [Google Scholar] [CrossRef]
- Ghanbarian, M.A.; Derakhshani, R. The Folds and Faults Kinematic Association in Zagros. Sci. Rep. 2022, 12, 8350. [Google Scholar] [CrossRef]
- Regard, V.; Hatzfeld, D.; Molinaro, M.; Aubourg, C.; Bayer, R.; Bellier, O.; Yamini-Fard, F.; Peyret, M.; Abbassi, M. The Transition between Makran Subduction and the Zagros Collision: Recent Advances in Its Structure and Active Deformation. Geol. Soc. Lond. Spec. Publ. 2010, 330, 43–64. [Google Scholar] [CrossRef]
- Lawrence, R.D.; Khan, S.H.; Nakata, T. Chaman Fault, Pakistan-Afghanistan. Ann. Tecton. 1992, 6, 196–223. [Google Scholar]
- Mokhtari, M.; Abdollahie Fard, I.; Hessami, K. Structural Elements of the Makran Region, Oman Sea and Their Potential Relevance to Tsunamigenisis. Nat. Hazards 2008, 47, 185–199. [Google Scholar] [CrossRef]
- Kopp, C.; Fruehn, J.; Flueh, E.R.; Reichert, C.; Kukowski, N.; Bialas, J.; Klaeschen, D. Structure of the Makran Subduction Zone from Wide-Angle and Reflection Seismic Data. Tectonophysics 2000, 329, 171–191. [Google Scholar] [CrossRef]
- Byrne, D.E.; Sykes, L.R.; Davis, D.M. Great Thrust Earthquakes and Aseismic Slip along the Plate Boundary of the Makran Subduction Zone. J. Geophys. Res. Solid Earth 1992, 97, 449–478. [Google Scholar] [CrossRef]
- DeMets, C.; Gordon, R.G.; Argus, D.F.; Stein, S. Current Plate Motions. Geophys. J. Int. 1990, 101, 425–478. [Google Scholar] [CrossRef]
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abbassi, M.R.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ashtiani, A.; Bayer, R. Present-Day Crustal Deformation and Plate Kinematics in the Middle East Constrained by GPS Measurements in Iran and Northern Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef]
- Wong, I.G. Low Potential for Large Intraslab Earthquakes in the Central Cascadia Subduction Zone. Bull. Seismol. Soc. Am. 2005, 95, 1880–1902. [Google Scholar] [CrossRef]
- Cruz, G.; Wyss, M. Large Earthquakes, Mean Sea Level, and Tsunamis along the Pacific Coast of Mexico and Central America. Bull. Seismol. Soc. Am. 1983, 73, 553–570. [Google Scholar] [CrossRef]
- Gahalaut, V.K.; Catherine, J.K. Rupture Characteristics of 28 March 2005 Sumatra Earthquake from GPS Measurements and Its Implication for Tsunami Generation. Earth Planet. Sci. Lett. 2006, 249, 39–46. [Google Scholar] [CrossRef]
- Bevis, M.; Taylor, F.W.; Schutz, B.E.; Recy, J.; Isacks, B.L.; Helu, S.; Singh, R.; Kendrick, E.; Stowell, J.; Taylor, B.; et al. Geodetic Observations of Very Rapid Convergence and Back-Arc Extension at the Tonga Arc. Nature 1995, 374, 249–251. [Google Scholar] [CrossRef]
- Kawasaki, I.; Asai, Y.; Tamura, Y. Space-Time Distribution of Interplate Moment Release Including Slow Earthquakes and the Seismo-Geodetic Coupling in the Sanriku-Oki Region along the Japan Trench. Tectonophysics 2001, 330, 267–283. [Google Scholar] [CrossRef]
- Zarifi, Z. Unusual Subduction Zones: Case Studies in Colombia and Iran. Ph.D. Thesis, The University of Bergen, Bergen, Norway, 2006. [Google Scholar]
- Grando, G.; McClay, K. Morphotectonics Domains and Structural Styles in the Makran Accretionary Prism, Offshore Iran. Sediment. Geol. 2007, 196, 157–179. [Google Scholar] [CrossRef]
- Snead, R.E. Recent Morphological Changes along the Coast of West Pakistan. Ann. Assoc. Am. Geogr. 1967, 57, 550–565. [Google Scholar] [CrossRef]
- Wiedicke, M.; Neben, S.; Spiess, V. Mud Volcanoes at the Front of the Makran Accretionary Complex, Pakistan. Mar. Geol. 2001, 172, 57–73. [Google Scholar] [CrossRef]
- JAXA ALOS Global Digital Surface Model “ALOS World 3D—30 m” (AW3D30). 2023. Available online: https://www.eorc.jaxa.jp/ALOS/en/dataset/aw3d30/aw3d30_e.htm (accessed on 23 March 2023).
- Florinsky, I.V.; Skrypitsyna, T.N.; Luschikova, O.S. Comparative Accuracy of the AW3D30 DSM, ASTER GDEM, and SRTM1 DEM: A Case Study on the Zaoksky Testing Ground, Central European Russia. Remote Sens. Lett. 2018, 9, 706–714. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.; Ke, L.; Jiang, L.; Pan, Y.; Ma, R. Global Open-Access DEM Performances in Earth’s Most Rugged Region High Mountain Asia: A Multi-Level Assessment. Geomorphology 2019, 338, 16–26. [Google Scholar] [CrossRef]
- D’Apuzzo, L.; Marcarelli, G.; Squillante, M. Analysis of Qualitative and Quantitative Rankings in Multicriteria Decision Making. New Econ. Windows 2009, 7, 157–170. [Google Scholar] [CrossRef]
- Darko, A.; Chan, A.P.C.; Ameyaw, E.E.; Owusu, E.K.; Pärn, E.; Edwards, D.J. Review of Application of Analytic Hierarchy Process (AHP) in Construction. Int. J. Constr. Manag. 2019, 19, 436–452. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, D. Facility Layout Planning with SHELL and Fuzzy AHP Method Based on Human Reliability for Operating Theatre. J. Healthc. Eng. 2019, 2019, 8563528. [Google Scholar] [CrossRef] [PubMed]
- Musumba, G.W.; Wario, R.D. Towards Fuzzy Analytical Hierarchy Process Model for Performance Evaluation of Healthcare Sector Services. In Information and Communication Technology for Development for Africa; Mekuria, F., Nigussie, E., Tegegne, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 93–118. [Google Scholar]
- Pourebrahim, S.; Hadipour, M.; Mokhtar, M.B.; Taghavi, S. Application of VIKOR and Fuzzy AHP for Conservation Priority Assessment in Coastal Areas: Case of Khuzestan District, Iran. Ocean Coast. Manag. 2014, 98, 20–26. [Google Scholar] [CrossRef]
- Akbar, M.A.; Alsanad, A.; Mahmood, S.; Alothaim, A. Prioritization-Based Taxonomy of Global Software Development Challenges: A FAHP Based Analysis. IEEE Access 2021, 9, 37961–37974. [Google Scholar] [CrossRef]
- Atıcı, U.; Adem, A.; Şenol, M.B.; Dağdeviren, M. A Comprehensive Decision Framework with Interval Valued Type-2 Fuzzy AHP for Evaluating All Critical Success Factors of e-Learning Platforms. Educ. Inf. Technol. 2022, 27, 5989–6014. [Google Scholar] [CrossRef]
- Xie, J.; Liu, B.; He, L.; Zhong, W.; Zhao, H.; Yang, X.; Mai, T. Quantitative Evaluation of the Adaptability of the Shield Machine Based on the Analytic Hierarchy Process (AHP) and Fuzzy Analytic Hierarchy Process (FAHP). Adv. Civ. Eng. 2022, 2022, 3268150. [Google Scholar] [CrossRef]
- Mohebbi Tafreshi, G.; Nakhaei, M.; Lak, R. Land Subsidence Risk Assessment Using GIS Fuzzy Logic Spatial Modeling in Varamin Aquifer, Iran. GeoJournal 2019, 86, 1203–1223. [Google Scholar] [CrossRef]
- Bahrani, S.; Ebadi, T.; Ehsani, H.; Yousefi, H.; Maknoon, R. Modeling Landfill Site Selection by Multi-Criteria Decision Making and Fuzzy Functions in GIS, Case Study: Shabestar, Iran. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Hierarchical Analysis of Behavior in Competition: Prediction in Chess. Behav. Sci. 1980, 25, 180–191. [Google Scholar] [CrossRef]
- Argyriou, A. A Methodology for the Rapid Identification of Neotectonic Features Using Geographical Information Systems and Remote Sensing. A Case Study from Western Crete: Greece. Ph.D. Thesis, University of Portsmouth, Portsmouth, UK, 2012. [Google Scholar]
- Pérez-Peña, J.V.; Azor, A.; Azañón, J.M.; Keller, E.A. Active Tectonics in the Sierra Nevada (Betic Cordillera, SE Spain): Insights from Geomorphic Indexes and Drainage Pattern Analysis. Geomorphology 2010, 119, 74–87. [Google Scholar] [CrossRef]
- Walcott, R.C.; Summerfield, M.A. Scale Dependence of Hypsometric Integrals: An Analysis of Southeast African Basins. Geomorphology 2008, 96, 174–186. [Google Scholar] [CrossRef]
- Dehbozorgi, M.; Pourkermani, M.; Arian, M.; Matkan, A.A.; Motamedi, H.; Hosseiniasl, A. Quantitative Analysis of Relative Tectonic Activity in the Sarvestan Area, Central Zagros, Iran. Geomorphology 2010, 121, 329–341. [Google Scholar] [CrossRef]
- Chen, Y.C.; Cheng, K.Y.; Huang, W.S.; Sung, Q.C.; Tsai, H. The Relationship between Basin Hypsometric Integral Scale Dependence and Rock Uplift Rate in a Range Front Area: A Case Study from the Coastal Range, Taiwan. J. Geol. 2019, 127, 223–239. [Google Scholar] [CrossRef]
- Liao, Y.; Zheng, M.; Li, D.; Wu, X.; Liang, C.; Nie, X.; Huang, B.; Xie, Z.; Yuan, Z.; Tang, C. Relationship of Benggang Number, Area, and Hypsometric Integral Values at Different Landform Developmental Stages. Land Degrad. Dev. 2020, 31, 2319–2328. [Google Scholar] [CrossRef]
- Pande, C.; Moharir, K.; Pande, R. Assessment of Morphometric and Hypsometric Study for Watershed Development Using Spatial Technology—A Case Study of Wardha River Basin in Maharashtra, India. Int. J. River Basin Manag. 2018, 19, 43–53. [Google Scholar] [CrossRef]
- Keller, E.A.; Pinter, N. Active Tectonics, Earthquakes, Uplift, and Landscape, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Cheng, W.; Wang, N.; Zhao, M.; Zhao, S. Relative Tectonics and Debris Flow Hazards in the Beijing Mountain Area from DEM-Derived Geomorphic Indices and Drainage Analysis. Geomorphology 2016, 257, 134–142. [Google Scholar] [CrossRef]
- Bahrami, S.; Capolongo, D.; Mofrad, M.R. Morphometry of Drainage Basins and Stream Networks as an Indicator of Active Fold Growth (Gorm Anticline, Fars Province, Iran). Geomorphology 2020, 355, 107086. [Google Scholar] [CrossRef]
- Faghih, A.; Samani, B.; Kusky, T.; Khabazi, S.; Roshanak, R. Geomorphologic Assessment of Relative Tectonic Activity in the Maharlou Lake Basin, Zagros Mountains of Iran. Geol. J. 2012, 47, 30–40. [Google Scholar] [CrossRef]
- Potter, P.E. A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee. J. Geol. 1957, 65, 112–113. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative Geomorphology of Drainage Basins and Channel Networks, Part II. In Handbook of Applied Hydrology; McGraw-Hill: New York, NY, USA, 1964; pp. 4–39. [Google Scholar]
- Sreedevi, P.D.; Subrahmanyam, K.; Ahmed, S. The Significance of Morphometric Analysis for Obtaining Groundwater Potential Zones in a Structurally Controlled Terrain. Environ. Geol. 2005, 47, 412–420. [Google Scholar] [CrossRef]
- Sreedevi, P.D.; Owais, S.; Khan, H.H.; Ahmed, S. Morphometric Analysis of a Watershed of South India Using SRTM Data and GIS. J. Geol. Soc. India 2009, 73, 543–552. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative Analysis of Watershed Geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, P.; Rai, P.K. Correction to: Morphotectonic Analysis of Sheer Khadd River Basin Using Geo-Spatial Tools. Spat. Inf. Res. 2018, 26, 405–414. [Google Scholar] [CrossRef]
- Bendjoudi, H.; Hubert, P. The Gravelius Compactness Coefficient: Critical Analysis of a Shape Index for Drainage Basins. Hydrol. Sci. J. 2002, 47, 921–930. [Google Scholar] [CrossRef]
- Jalaee, M.S.; Shakibaei, A.; Ghaseminejad, A.; Jalaee, S.A.; Derakhshani, R. A Novel Computational Intelligence Approach for Coal Consumption Forecasting in Iran. Sustainability 2021, 13, 7612. [Google Scholar] [CrossRef]
- Jalaee, S.A.; Shakibaei, A.; Akbarifard, H.; Horry, H.R.; GhasemiNejad, A.; Nazari Robati, F.; Amani zarin, N.; Derakhshani, R. A Novel Hybrid Method Based on Cuckoo Optimization Algorithm and Artificial Neural Network to Forecast World’s Carbon Dioxide Emission. MethodsX 2021, 8, 101310. [Google Scholar] [CrossRef]
- Shokri, S.; Sadeghi, M.T.; Marvast, M.A.; Narasimhan, S. Improvement of the Prediction Performance of a Soft Sensor Model Based on Support Vector Regression for Production of Ultra-Low Sulfur Diesel. Pet. Sci. 2015, 12, 177–188. [Google Scholar] [CrossRef]
- Kazem, A.; Sharifi, E.; Hussain, F.K.; Saberi, M.; Hussain, O.K. Support Vector Regression with Chaos-Based Firefly Algorithm for Stock Market Price Forecasting. Appl. Soft Comput. J. 2013, 13, 947–958. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A Review on Linear Regression Comprehensive in Machine Learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Lacasta, A.; Juez, C.; Murillo, J.; García-Navarro, P. An Efficient Solution for Hazardous Geophysical Flows Simulation Using GPUs. Comput. Geosci. 2015, 78, 63–72. [Google Scholar] [CrossRef]
- Huang, C.; Sun, Y.; An, Y.; Shi, C.; Feng, C.; Liu, Q.; Yang, X.; Wang, X. Three-Dimensional Simulations of Large-Scale Long Run-out Landslides with a GPU-Accelerated Elasto-Plastic SPH Model. Eng. Anal. Bound. Elem. 2022, 145, 132–148. [Google Scholar] [CrossRef]



| Intensity of Importance | Interpretation |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance |
| 5 | Essential |
| 7 | Extreme importance |
| 9 | Extreme importance |
| 2, 4, 6, 8 | Intermediate values between adjacent scale values |
| Linear and Areal Aspects | Hi | Bs | Cb | Er | Rn | Rs | Cc | Ff | Score |
|---|---|---|---|---|---|---|---|---|---|
| Hypsometric integral (Hi) | 0.5 | 0.5 | 2 | 0.5 | 0.5 | 2 | 2 | 0.136 | |
| Basin shape (Bs) | 2 | 2 | 2 | 2 | 2 | 2 | 0.037 | ||
| Circularity basin (Cb) | 0.33 | 0.5 | 2 | 2 | 0.5 | 0.123 | |||
| Elongation ratio (Er) | 2 | 2 | 2 | 2 | 0.084 | ||||
| Ruggedness number (Rn) | 2 | 3 | 2 | 0.078 | |||||
| River sinuosity (Rs) | 0.5 | 0.5 | 0.297 | ||||||
| CoefficientCompactness (Cc) | 0.5 | 0.050 | |||||||
| Form factor (Ff) | 0.197 | ||||||||
| CI | 0.03 | ||||||||
| Methods | MSE | MAE | R2 |
|---|---|---|---|
| ANN | 4.14 × 10−6 | 0.00151 | 0.974 |
| SVR | 8.12 × 10−6 | 0.00194 | 0.947 |
| MLR | 5.06 × 10−6 | 0.00161 | 0.967 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derakhshani, R.; Zaresefat, M.; Nikpeyman, V.; GhasemiNejad, A.; Shafieibafti, S.; Rashidi, A.; Nemati, M.; Raoof, A. Machine Learning-Based Assessment of Watershed Morphometry in Makran. Land 2023, 12, 776. https://doi.org/10.3390/land12040776
Derakhshani R, Zaresefat M, Nikpeyman V, GhasemiNejad A, Shafieibafti S, Rashidi A, Nemati M, Raoof A. Machine Learning-Based Assessment of Watershed Morphometry in Makran. Land. 2023; 12(4):776. https://doi.org/10.3390/land12040776
Chicago/Turabian StyleDerakhshani, Reza, Mojtaba Zaresefat, Vahid Nikpeyman, Amin GhasemiNejad, Shahram Shafieibafti, Ahmad Rashidi, Majid Nemati, and Amir Raoof. 2023. "Machine Learning-Based Assessment of Watershed Morphometry in Makran" Land 12, no. 4: 776. https://doi.org/10.3390/land12040776
APA StyleDerakhshani, R., Zaresefat, M., Nikpeyman, V., GhasemiNejad, A., Shafieibafti, S., Rashidi, A., Nemati, M., & Raoof, A. (2023). Machine Learning-Based Assessment of Watershed Morphometry in Makran. Land, 12(4), 776. https://doi.org/10.3390/land12040776








