Sensitivity Analysis in Mean Annual Sediment Yield Modeling with Respect to Rainfall Probability Distribution Functions
Abstract
1. Introduction
2. Materials and Methods
2.1. Applied Methodology
2.2. Rainfall Probability Distribution Functions
2.2.1. Gumbel Type I (Small Sample Size)
2.2.2. Gumbel Type I (Large Sample Size)
2.2.3. Log-Pearson Type III
2.2.4. SQRT-Exponential Type Distribution of the Maximum
2.3. Probabilistic Combination Model
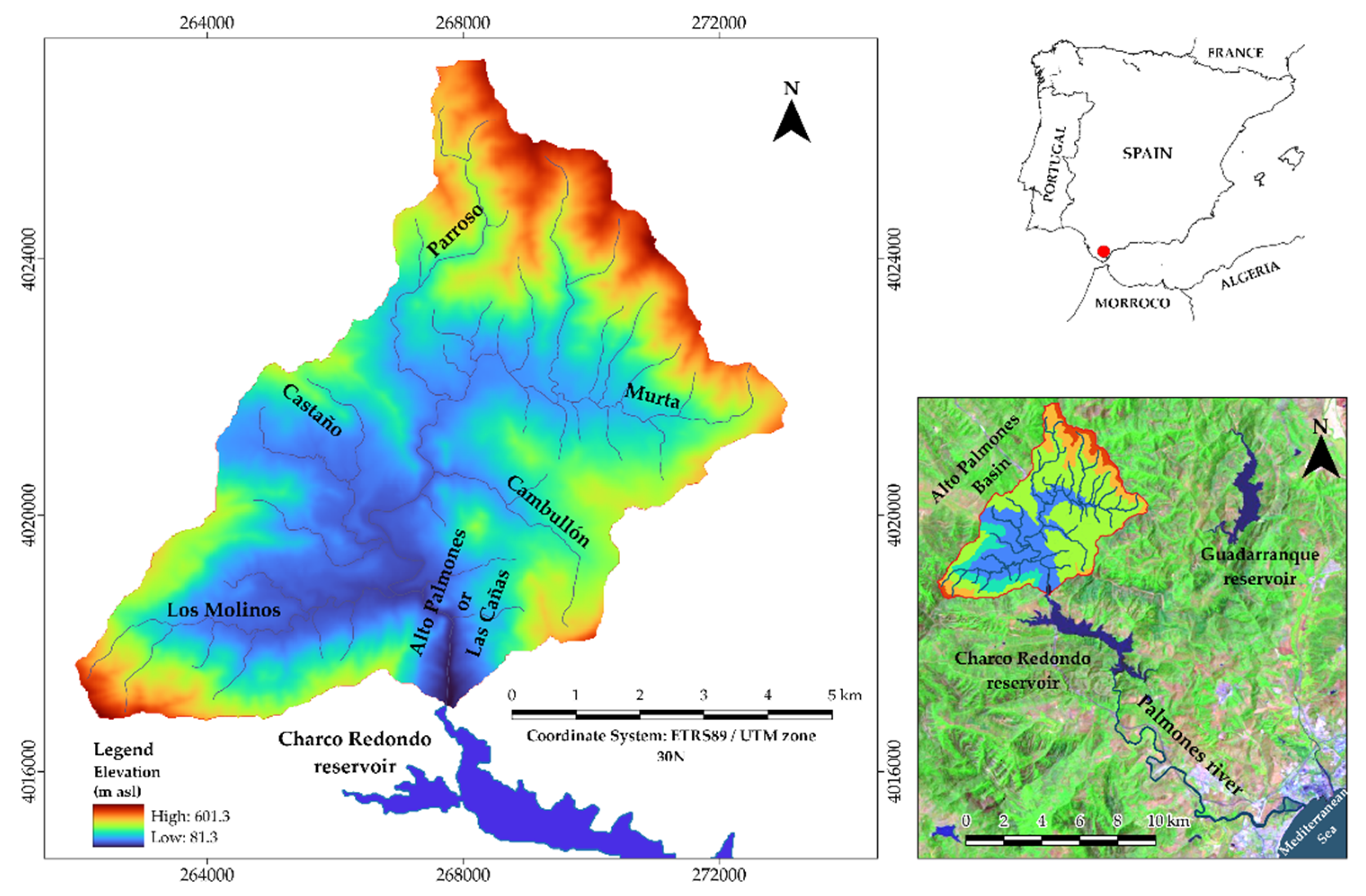
2.4. Study Area
2.4.1. Location
2.4.2. Climatology and Rainfall Dataset
2.4.3. Geology, Soils, Forest Cover and MUSLE Parameters
- Algibe sands, which include soils with a sandy-loam texture on the “Algibe” lithological units present in the basin. They are taxonomically described as Eutric Cambisols, Chromic Luvisols and Lithosols with Dystric Cambisols and Rankers. They belong to the USDA Inceptisol Order. Their presence in the areas of greater relief of the basin is clear.
- Clays of the Campo de Gibraltar include clayey soils, with the texture, composition and development characteristics of the corresponding lithological units of the Campo de Gibraltar. They are taxonomically described as Chromic Vertisols and Vertic Cambisols with Calcic Cambisols, Calcareous Regosols and Pellic Vertisols. They belong to the Vertisol Order of the USDA. They are very clearly present in the areas of the basin with lower slopes.
- 1.
- The K factor (erodibility) for each unit of soil is computed using the four parameters included in Table 3. The weighing according to the area of each unit of soil for each sub-basin allows us to obtain the representative value of the K factor for the sub-basins. The values displayed in Table 2 and Table 3 are obtained by textural sampling of the soils [24]. The use of vectorial information from thematical maps of soils and lithological units [40,41] is useful to delimitate the corresponding units and their division by sub-basins.
- 2.
- The LS factor (slope length and steepness) is calculated in various phases. For the purposes of study, a digital elevation model (DEM) is available. The model has a resolution of 5 m. It was obtained by automatic stereo-correlation from the 2013 photogrammetric flight of the Spanish Aerial Orthophotography National Plan. It was created with a resolution of 50 cm/pixel [40]. The phases of the process comprise the following:
- a.
- A slope map is obtained with QGIS [42].
- b.
- Using the algorithm `r.watershed’ provided by GRASS [42] for QGIS, the LS factor is obtained in a distributed manner by the development of a geo-process with this algorithm.
- c.
- Using the raster calculator from QGIS, the average values of the LS for the sub-basins are obtained.
- 3.
- The C factor (crop/vegetation) is calculated in different steps, which are as follows:
- a.
- The use of a vectorial environmental database for soil uses [40]. It allows us to obtain a previous coverage map. The information used for the previous map is vectorial and is from 2018.
- b.
- The use of orthophotos to corroborate the previous information, including orthophotos from the region of Andalusia, with a resolution of 0.5 m. These orthophotos were generated by the Spanish National Geographic Institute in 2016.
- c.
- The use of fieldwork and a general inventory categorized by vegetation layers to determine the parcels [24].
- d.
- 4.
- The P factor (conservation practice) was assigned a value of 1 due to the fact that there are no crops in any of the parcels. There is just one agricultural parcel in sub-basin 6. This crop is not relevant, since it is dedicated to cultivating fodder in a forest context. Due to the physical characteristics and the administrative environmental protection, that restricting viable or permitted land uses [38], it is not currently used for agriculture purposes (nor is such use likely in the future).
2.4.4. Basin Lag Time and Curve Number
3. Results and Discussion
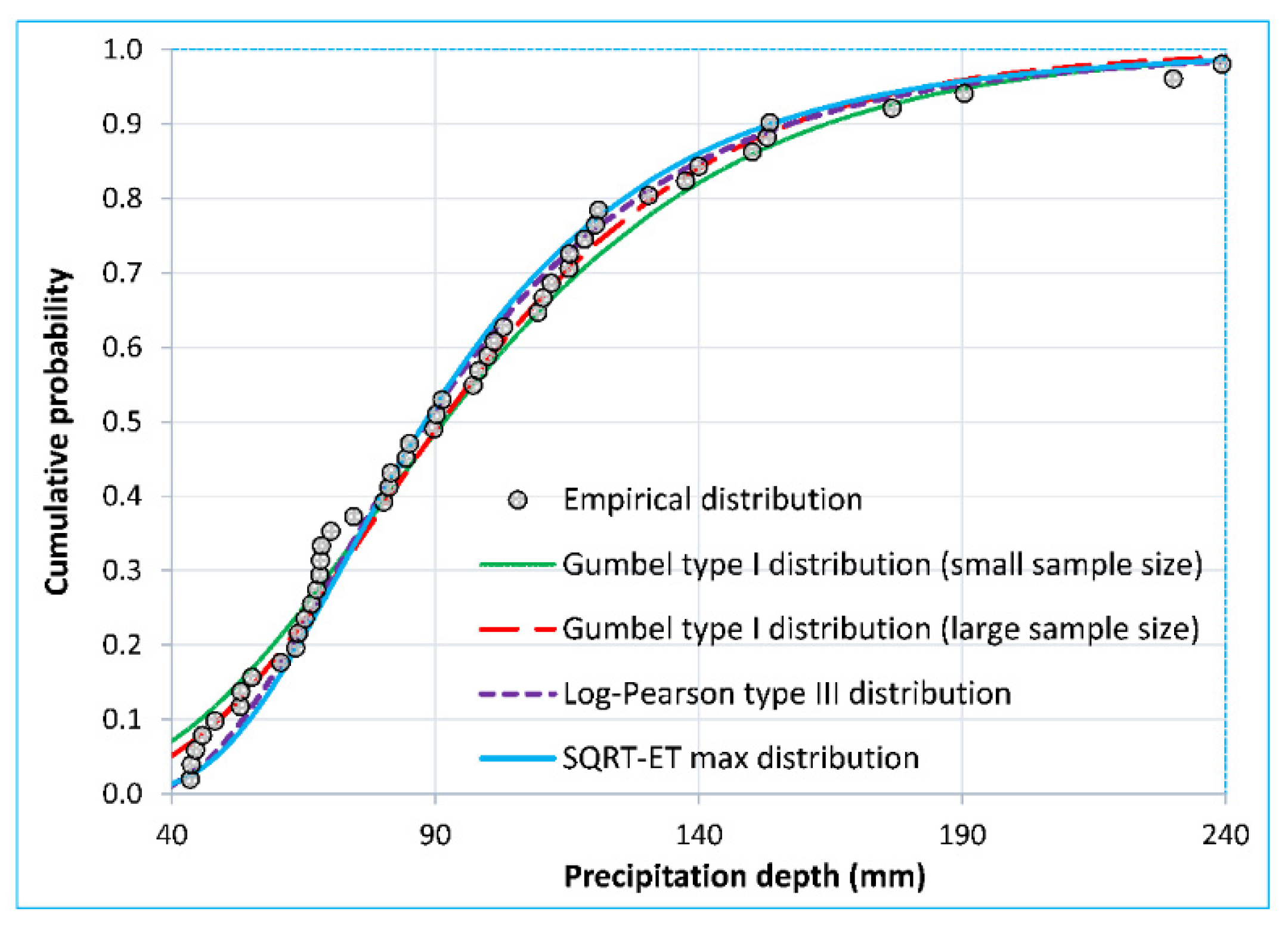
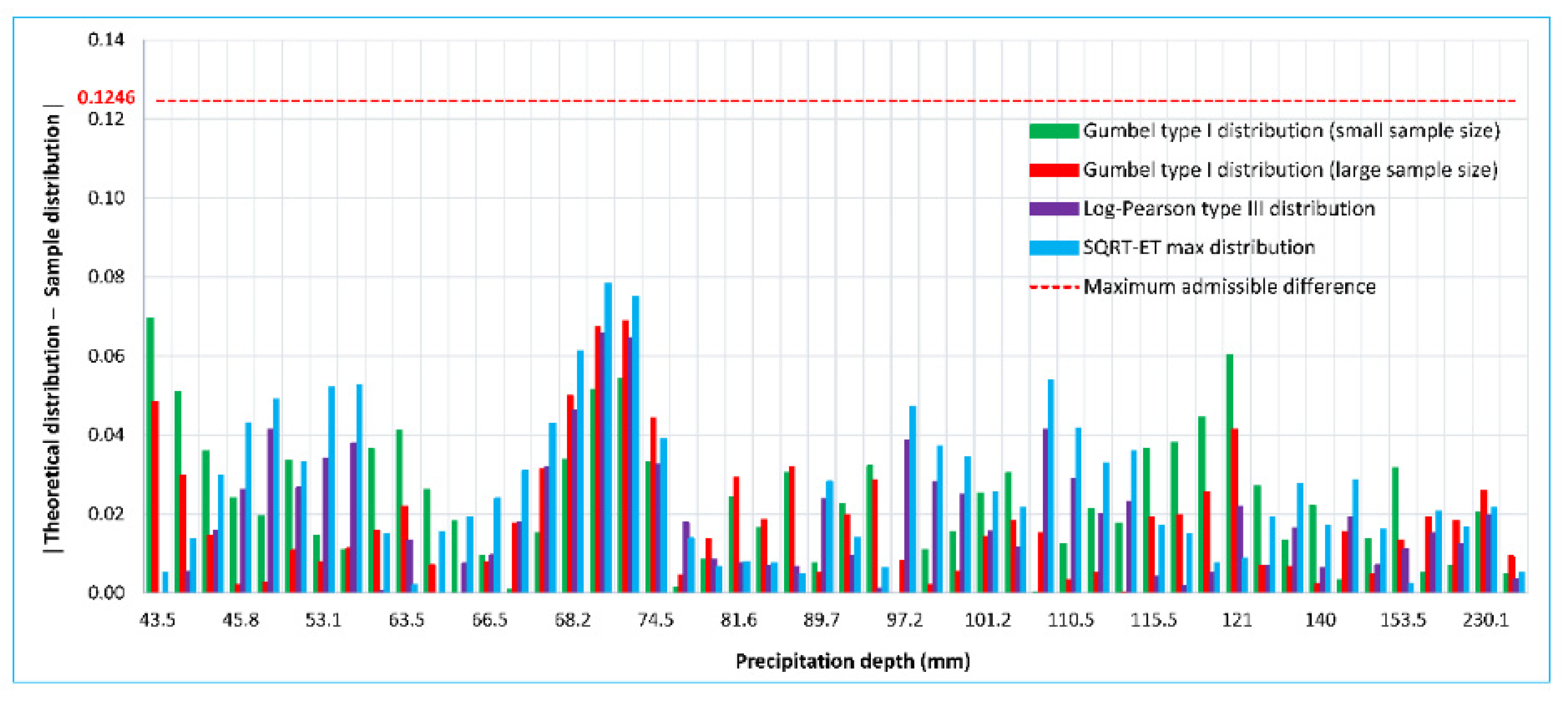
3.1. Definition and Adjustment of Probability Distribution Functions
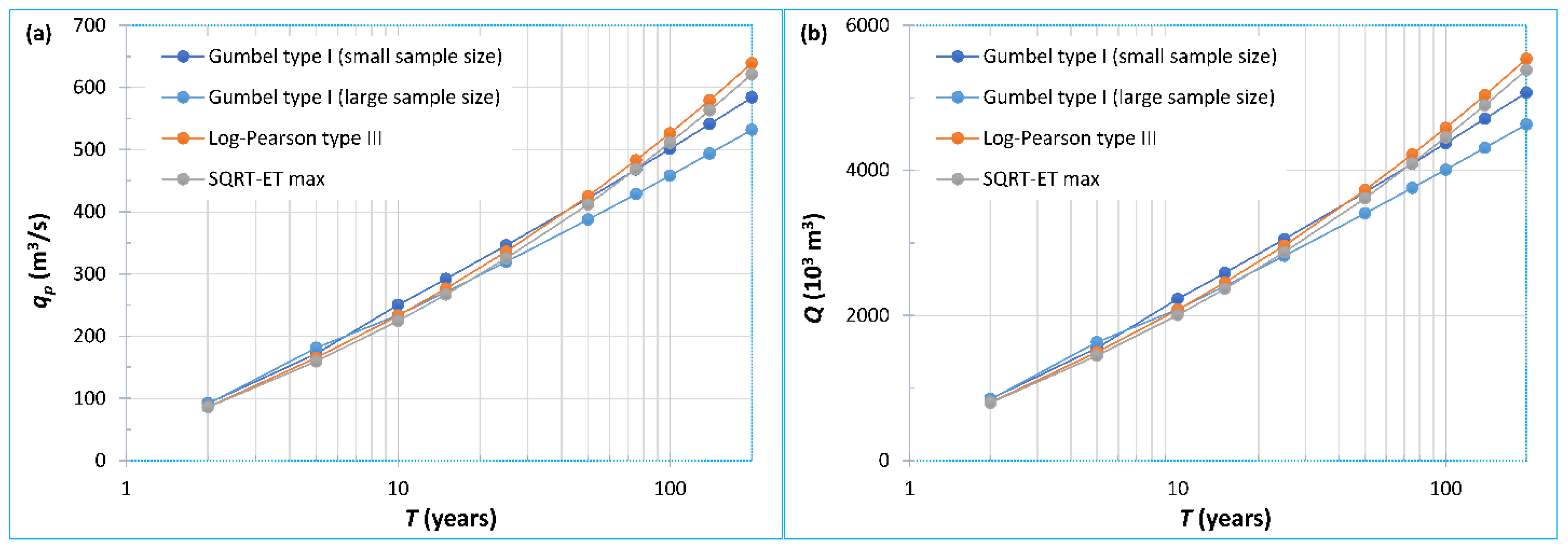
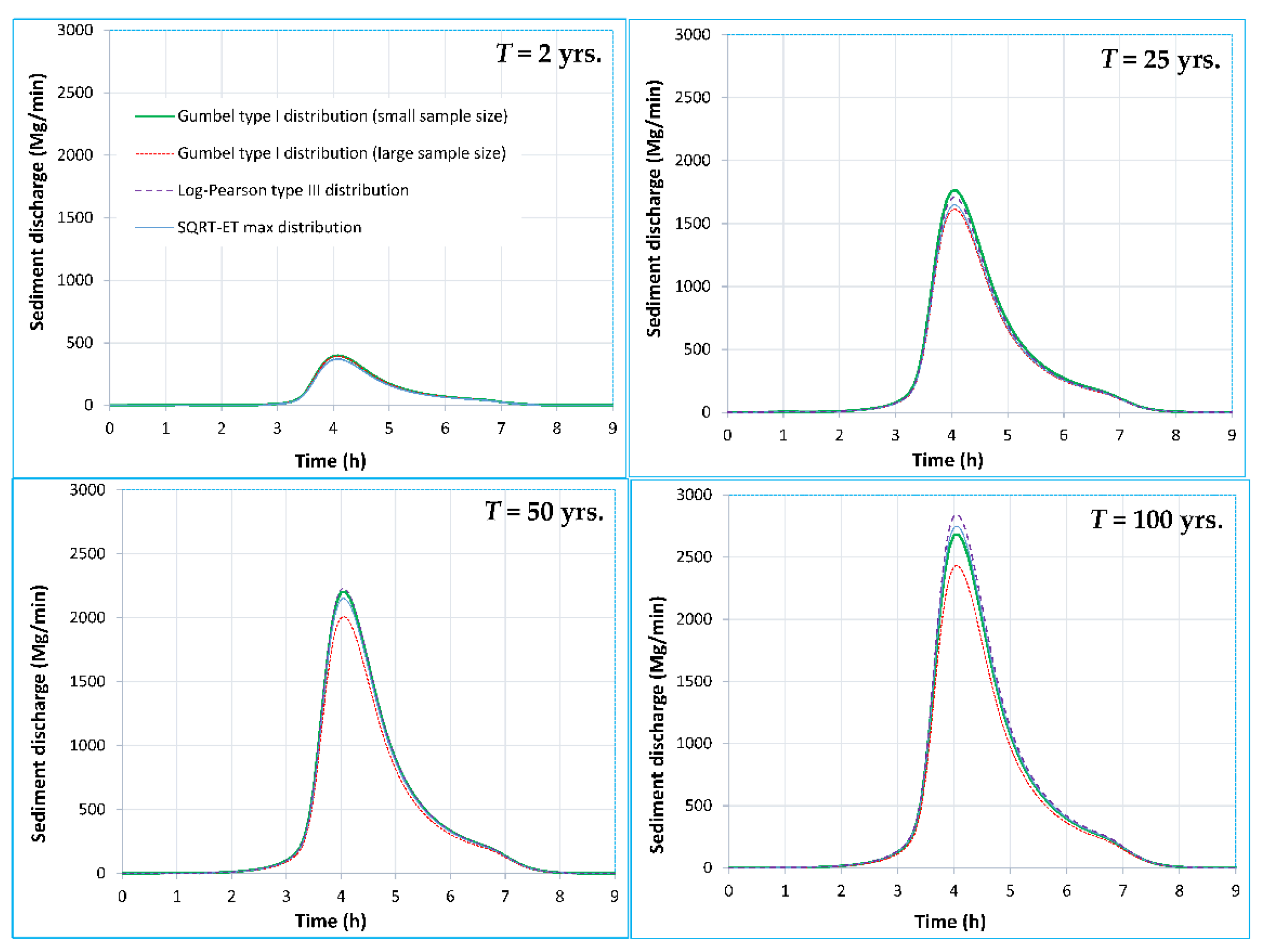
3.2. Sediment Yield for Different Return Periods
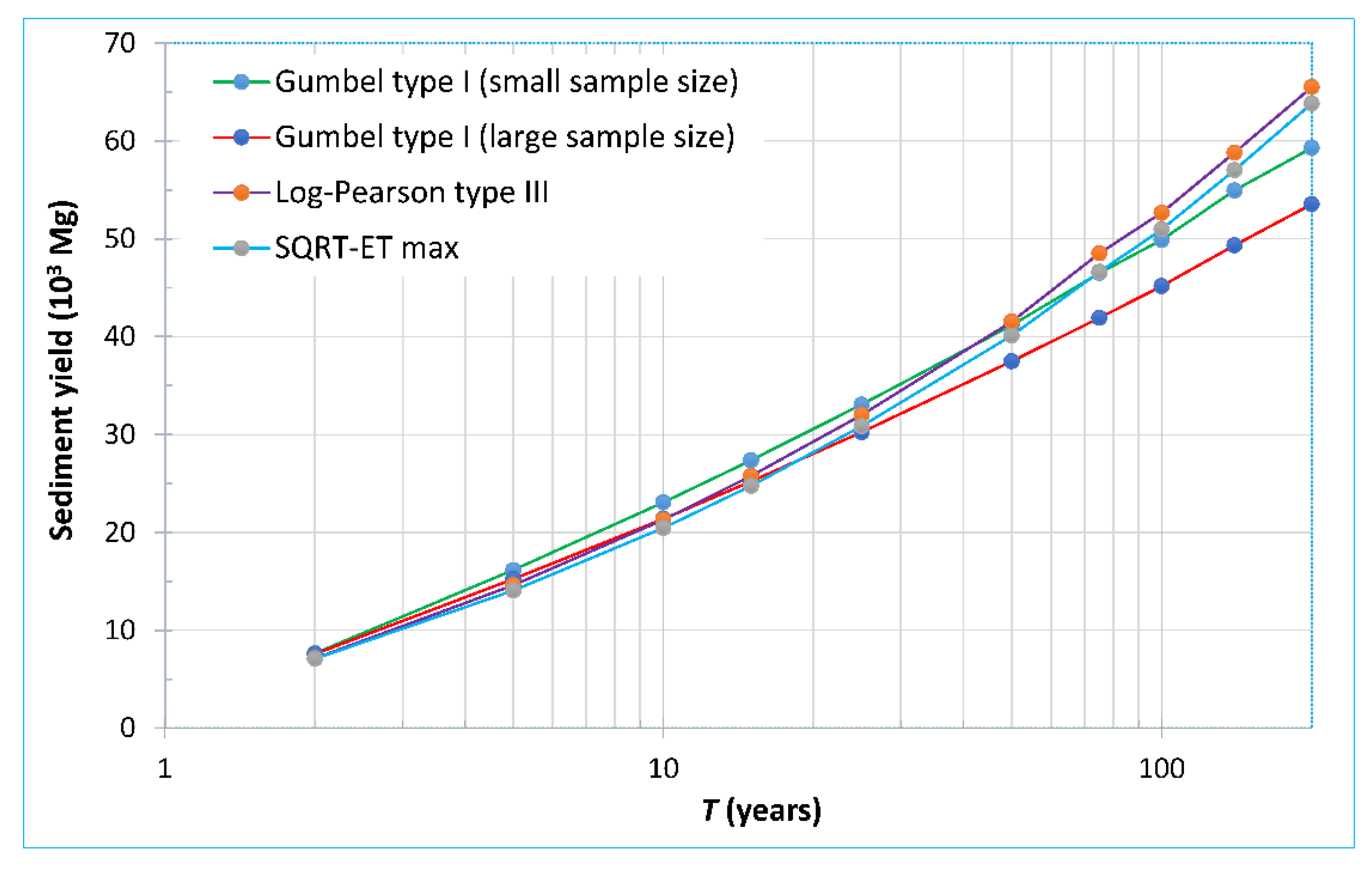
3.3. Mean Annual Sediment Yield According to Each Distribution Function
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nearing, M.A.; Xie, Y.; Liu, B.; Ye, Y. Natural and anthropogenic rates of soil erosion. Int. Soil Water Conserv. Res. 2017, 5, 77–84. [Google Scholar] [CrossRef]
- Quine, T.A.; Walling, D.E.; Zhang, X. Tillage erosion, water erosion and soil quality on cultivated terraces near Xifeng in the Loess Plateau, China. Land Degrad. Dev. 1999, 10, 251–274. [Google Scholar] [CrossRef]
- Mishra, P.K.; Rai, A.; Abdelrahman, K.; Rai, S.C.; Tiwari, A. Land Degradation, Overland Flow, Soil Erosion, and Nutrient Loss in the Eastern Himalayas, India. Land 2022, 11, 179. [Google Scholar] [CrossRef]
- Butt, M.J.; Waqas, A.; Mahmood, R. The combined effect of vegetation and soil erosion in the water resource management. Water Resour. Manag. 2010, 24, 3701–3714. [Google Scholar] [CrossRef]
- Gemitzi, A.; Petalas, C.; Tsihrintzis, V.A.; Pisinaras, V. Assessment of groundwater vulnerability to pollution: A combination of GIS, fuzzy logic and decision making techniques. Environ. Geol. 2006, 49, 653–673. [Google Scholar] [CrossRef]
- Halbac-Cotoara-Zamfir, R.; Smiraglia, D.; Quaranta, G.; Salvia, R.; Salvati, L.; Giménez-Morera, A. Land degradation and mitigation policies in the Mediterranean region: A brief commentary. Sustainability 2020, 12, 8313. [Google Scholar] [CrossRef]
- European Parlament. Procedure File: 2021/2548(RSP)|Legislative Observatory. 2021. Available online: https://oeil.secure.europarl.europa.eu/oeil/popups/ficheprocedure.do?reference=2021/2548(RSP)&l=en (accessed on 5 November 2022).
- Djoukbala, O.; Hasbaia, M.; Benselama, O.; Mazour, M. Comparison of the erosion prediction models from USLE, MUSLE and RUSLE in a Mediterranean watershed, case of Wadi Gazouana (NW of Algeria). Model. Earth Syst. Environ. 2019, 5, 725–743. [Google Scholar] [CrossRef]
- Busari, M.A.; Kukal, S.S.; Kaur, A.; Bhatt, R.; Dulazi, A.A. Conservation tillage impacts on soil, crop and the environment. Int. Soil Water Conserv. Res. 2015, 3, 119–129. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. A Universal Soil-Loss Equation to guide conservation farm planning. Trans. 7th Int. Congr. Soil Sci. 1960, 1, 418–425. [Google Scholar]
- RUSLE2. Conservation Planning, Inventory Erosion Rates and Estimate Sediment Delivery. NRCS, USDA, USA. Available online: https://fargo.nserl.purdue.edu/rusle2_dataweb/About_RUSLE2_Technology.htm (accessed on 11 November 2022).
- Akoko, G.; Le, T.H.; Gomi, T.; Kato, T. A review of SWAT model application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT model special section: Overview and insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Toral, F.; Pérez-Nieto, S.; Ibáñez-Castillo, L.A.; Hernández-Saucedo, F.R. Aplicabilidad del Modelo SWAT para la estimación de la erosión hídrica en las cuencas de México. Agrociencia 2012, 46, 101–105. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1405-31952012000200001&lng=es&nrm=iso (accessed on 4 September 2022).
- Sadeghi, S.H.R.; Gholami, L.; Khaledi Darvishan, A.; Saeidi, P. A review of the application of the MUSLE model worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef]
- Williams, J.R.; Berndt, H.D. Sediment yield prediction based on watershed hydrology. Trans. ASAE 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Arekhi, S.; Shabani, A.; Rostamizad, G. Application of the Modified Universal Soil Loss equation (MUSLE) in prediction of sediment yield (Case study: Kengir Watershed, Iran). Arab. J. Geosci. 2012, 5, 1259–1267. [Google Scholar] [CrossRef]
- Berteni, F.; Dada, A.; Grossi, G. Application of the MUSLE model and potential effects of climate change in a small alpine catchment in northern Italy. Water 2021, 13, 2679. [Google Scholar] [CrossRef]
- Pongsai, S.; Schmidt Vogt, D.; Shrestha, R.P.; Clemente, R.S.; Eiumnoh, A. Calibration and validation of the Modified Universal Soil Loss Equation for estimating sediment yield on sloping plots: A case study in Khun Satan catchment of northern Thailand. Can. J. Soil Sci. 2010, 90, 585–596. [Google Scholar] [CrossRef]
- Odongo, V.O.; Onyando, J.O.; Mutua, B.M.; Becht, R. Sensitivity analysis and calibration of the Modified Universal Soil Loss Equation (MUSLE) for the upper Malewa catchment, Kenya. Int. J. Sediment Res. 2013, 28, 368–383. [Google Scholar] [CrossRef]
- Rodríguez, A.; García, J.L.; Robredo, J.C.; López, D. Specific sediment yield model for reservoirs with medium-sized basins in Spain: An empirical and statistical approach. Sci. Total Environ. 2019, 681, 82–101. [Google Scholar] [CrossRef]
- Hrissanthou, V. Estimate of sediment yield in a basin without sediment data. Catena 2005, 64, 333–347. [Google Scholar] [CrossRef]
- García, C.; Robredo, J.C. Metodología para la evaluación de la emisión interanual de sedimentos por una cuenca vertiente. Rev. Montes 1996, 45, 22–24. [Google Scholar]
- Rodríguez, C.A.; Rodríguez-Pérez, Á.M.; Mancera, J.; Torres, J.; Carmona, N.; Bahamonde García, M. Applied methodology based on HEC-HMS for reservoir filling estimation due to soil erosion. J. Hydrol. Hydromech. 2022, 70, 341–356. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; US Department of Agriculture, Agriculture Research Service: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
- Lu, J.; Zheng, F.; Li, G.; Bian, F.; An, J. The effects of raindrop impact and runoff detachment on hillslope soil erosion and soil aggregate loss in the Mollisol region of Northeast China. Soil Tillage Res. 2016, 161, 79–85. [Google Scholar] [CrossRef]
- HEC–HMS (Hydrologic Engineering Center–Hydrologic Modeling System), 4.10 [Computer Software] ed; Army Corps of Engineers: Davis, CA, USA, 2022; Available online: http://www.hec.usace.army.mil/ (accessed on 10 October 2022).
- HEC-HMS (Hydrologic Engineering Center–Hydrologic Modeling System). Technical Reference Manual. CN Tables. Available online: https://www.hec.usace.army.mil/confluence/hmsdocs/hmstrm/cn-tables (accessed on 14 November 2022).
- Shi, W.; Chen, T.; Yang, J.; Lou, Q.; Liu, M. An improved MUSLE model incorporating the estimated runoff and peak discharge predicted sediment yield at the watershed scale on the Chinese Loess Plateau. J. Hydrol. 2022, 614, 128598. [Google Scholar] [CrossRef]
- Chimene, C.A.; Campos, J.N.B. The design flood under two approaches: Synthetic storm hyetograph and observed storm hyetograph. J. Appl. Water Eng. Res. 2020, 8, 171–182. [Google Scholar] [CrossRef]
- Watt, E.; Marsalek, J. Critical review of the evolution of the design storm event concept. Can. J. Civ. Eng. 2013, 40, 105–113. [Google Scholar] [CrossRef]
- Yen, B.C.; Chow, V.T. Design hyetographs for small drainage structures. J. Hydraul. Div. 1980, 106, 1055–1076. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Ilić, A.; Plavšić, J.; Radivojević, D. Rainfall-runoff simulation for design flood estimation in small river catchments. Facta Universitatis. Ser. Archit. Civ. Eng. 2018, 16, 029–043. [Google Scholar] [CrossRef]
- Maity, R. Probability Distributions and Their Applications. In Civil and Environmental Engineering; Springer: Singapore, 2018; pp. 93–143. [Google Scholar] [CrossRef]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Iowa State University Press: Ames, IA, USA, 2002. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Chapter 18. Frequency analysis of extreme events. In Handbook of Hydrology; Editor in Chief David R. Maidment; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Ministerio Para la Transición Ecológica y el Reto Demográfico. Gobierno de España. Reserva Natural Fluvial Alto Palmones. Available online: https://www.miteco.gob.es/es/agua/temas/delimitacion-y-restauracion-del-dominio-publico-hidraulico/Catalogo-Nacional-de-Reservas-Hidrologicas/informacion/andalucia/alto-palmones/default.aspx (accessed on 8 November 2022).
- Ministerio Para la Transición Ecológica y el Reto Demográfico. Gobierno de España. Agencia Estatal de Meteorología. Available online: https://www.aemet.es/en/serviciosclimaticos (accessed on 3 September 2021).
- Consejería de Agricultura, Ganadería, Pesca y Desarrollo Sostenible. Junta de Andalucía. Catálogo de la Red de Información Ambiental de Andalucía (REDIAM). Available online: https://www.juntadeandalucia.es/medioambiente/portal/acceso-rediam (accessed on 29 November 2022).
- Ministerio de Ciencia de Innovación. CSIC. Instituto Geológico y Minero de España. Gobierno de España. Información Geocientífica del IGME. Available online: http://info.igme.es/catalogo/default.aspx?lang=spa (accessed on 11 November 2022).
- QGIS. A Free and Open Source Geographic Information System. Available online: https://www.qgis.org/en/site/ (accessed on 8 November 2022).
- Steinmetz, A.A.; Beskow, S.; Terra, F.D.S.; Nunes, M.C.M.; Vargas, M.M.; Horn, J.F.C. Spatial discretization influence on flood modeling using unit hydrograph theory. RBRH 2019, 24, 1–12. [Google Scholar] [CrossRef]
- Pak, J.H.; Fleming, M.; Scharffenberg, W.; Gibson, S.; Brauer, T. Modeling surface soil erosion and sediment transport processes in the upper North Bosque River Watershed, Texas. J. Hydrol. Eng. 2015, 20, 04015034. [Google Scholar] [CrossRef]
- Pak, J.H.; Ramos, K.; Fleming, M.; Scharffenberg, W.; Gibson, S. Sensitivity Analysis for Sediment Transport in the Hydrologic Modeling System (HEC-HMS). Proc., Joint Federal Interagency Conf. 2015. Available online: https://acwi.gov/sos/pubs/3rdJFIC/Contents/2A-Pak.pdf (accessed on 8 November 2022).
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. Available online: https://www.jstor.org/stable/2235766 (accessed on 9 November 2022). [CrossRef]
- Wanielista, M.; Robert, K.; Ron, E. Hydrology: Water Quantity and Quality Control; John Wiley and Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Molin, P.; Abdi, H. New Table and Numerical Approximations for Kolmogorov-Smirnov/Lilliefors/van Soest Normality Test; University of Bourgogne: Dijon, France, 1998; Available online: https://personal.utdallas.edu/~herve/MolinAbdi1998-LillieforsTechReport.pdf (accessed on 24 October 2022).
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. JASA 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Huang, Y.P.; Lee, C.H.; Ting, C.S. Improved estimation of hydrologic data using the chi-square goodness-of-fit test. J. Chin. Instig. Eng. 2008, 31, 515–521. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Merlano-Sabalza, E.; Díaz-Vergara, Z.; Coronado-Hernández, J.R. Selection of hydrological probability distributions for extreme rainfall events in the regions of Colombia. Water 2020, 12, 1397. [Google Scholar] [CrossRef]
- Zorraquino, C. La función SQRT-ET max. Revista de Obras Públicas 2004, 3447, 33–37. [Google Scholar]
- Ferrer, F.J. El Modelo de Función de Distribución SQRT et MAX en el Análisis Regional de Máximos Hidrológicos. Aplicación a Lluvias Diarias. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 1996. [Google Scholar]
- Carter, D.J.T.; Challenor, P.G. Methods of fitting the Fisher-Tippett type 1 extreme value distribution. Ocean Eng. 1983, 10, 191–199. [Google Scholar] [CrossRef]
- Gumbel, E.J. Les valeurs extrêmes des distributions statistiques. Annales de l’institut Henri Poincaré 1935, 5, 115–158. Available online: http://www.numdam.org/item/AIHP_1935__5_2_115_0.pdf (accessed on 9 November 2022).
- Lehmer, D.H. Euler constants for arithmetical progressions. Acta Arith. 1975, 27, 25–142. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Burges, S.J. Gumbel’s extreme value I distribution: A new look. J. Hydraul. Eng. 1982, 108, 502–514. [Google Scholar] [CrossRef]
- Pearson, K. Contributions to the mathematical theory of evolution. Philos. Trans. R. Soc. 1894, 185, 71–110. [Google Scholar] [CrossRef]
- Huynh, N.P.; Thambirajah, J.A. Applications of the log Pearson type-3 distribution in hydrology. J. Hydrol. 1984, 73, 359–372. [Google Scholar] [CrossRef]
- Bobee, B.B.; Robitaille, R. The use of the Pearson type 3 and log Pearson type 3 distributions revisited. Water Resour. Res. 1977, 13, 427–443. [Google Scholar] [CrossRef]
- Etoh, T.; Murota, A.; Nakanishi, M. SQRT-exponential type distribution of maximum. In Hydrologic Frequency Modeling; Springer: Dordrecht, The Netherlands, 1987; pp. 253–264. [Google Scholar]
- Ferrer, F.J. Recomendaciones Para el Cálculo Hidrometeorológico de Avenidas. Ed. CEDEX, Spain. 2000. Available online: https://hispagua.cedex.es/node/92786 (accessed on 24 October 2022).
- Ministerio de Fomento. Dirección General de Carreteras. Gobierno de España. Máximas Lluvias Diarias en la España Peninsular. Ed. Secretaría de Estado de Infraestructuras y Transportes, Spain. 1999. Available online: https://www.mitma.gob.es/recursos_mfom/0610300.pdf (accessed on 24 October 2022).
- Kaffas, K.; Hrissanthou, V. Annual sediment yield prediction by means of three soil erosion models at the basin scale. In Proceedings of the 10th World Congress of EWRA “Panta Rhei”, Athens, Greece, 5–9 July 2017; pp. 5–9. Available online: https://www.ewra.net/ew/pdf/EW_2017_58_46.pdf (accessed on 10 November 2022).
- Gómez-Zotano, J.; Alcántara-Manzanares, J.; Olmedo-Cobo, J.A.; Martínez-Ibarra, E. La sistematización del clima mediterráneo: Identificación, clasificación y caracterización climática de Andalucía (España). Rev. Geogr. Norte Gd. 2015, 61, 161–180. [Google Scholar] [CrossRef]
- Trinh, T.; Kavvas, M.L.; Ishida, K.; Ercan, A.; Chen, Z.Q.; Anderson, M.L.; Nguyen, T. Integrating global land-cover and soil datasets to update saturated hydraulic conductivity parameterization in hydrologic modeling. Sci. Total Environ. 2018, 631, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Allue Andrade, J.L. Atlas Fitoclimático de España. Taxonomías; Ministerio de Agricultura Pesca y Alimentación: Madrid, Spain, 1990. [Google Scholar]
- Dysarz, T.; Wicher-Dysarz, J. Application of Hydrodynamic Simulation and Frequency Analysis for Assessment of Sediment Deposition and Vegetation Impacts on Floodplain Inundation. Pol. J. Environ. Stud. 2011, 20, 1441–1451. Available online: http://www.pjoes.com/Application-of-Hydrodynamic-Simulation-r-nand-Frequency-Analysis-for-Assessment-r,88695,0,2.html (accessed on 11 November 2022).
- Témez, J.R. Facetas del cálculo hidrometeorológico y estadístico de máximos caudales. Rev. Obras Públicas 2003, 3430, 47–51. [Google Scholar]
- Lai, C.-D.; Murthy, D.N.; Xie, M. Weibull distributions and their applications. In Springer Handbooks; Springer: Berlin/Heidelberg, Germany, 2006; pp. 63–78. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. JOSMA 2011, 2, 21–33. [Google Scholar]



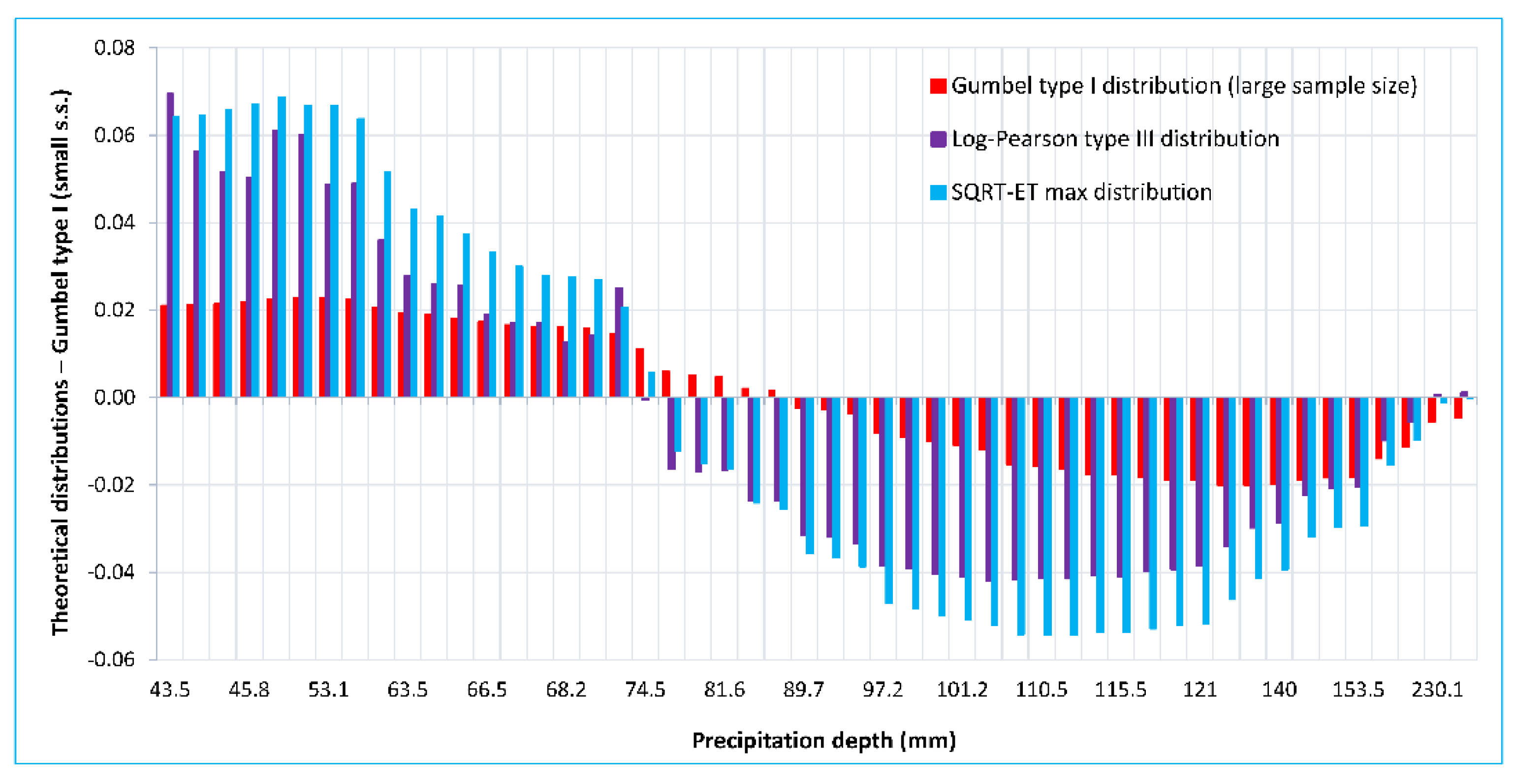
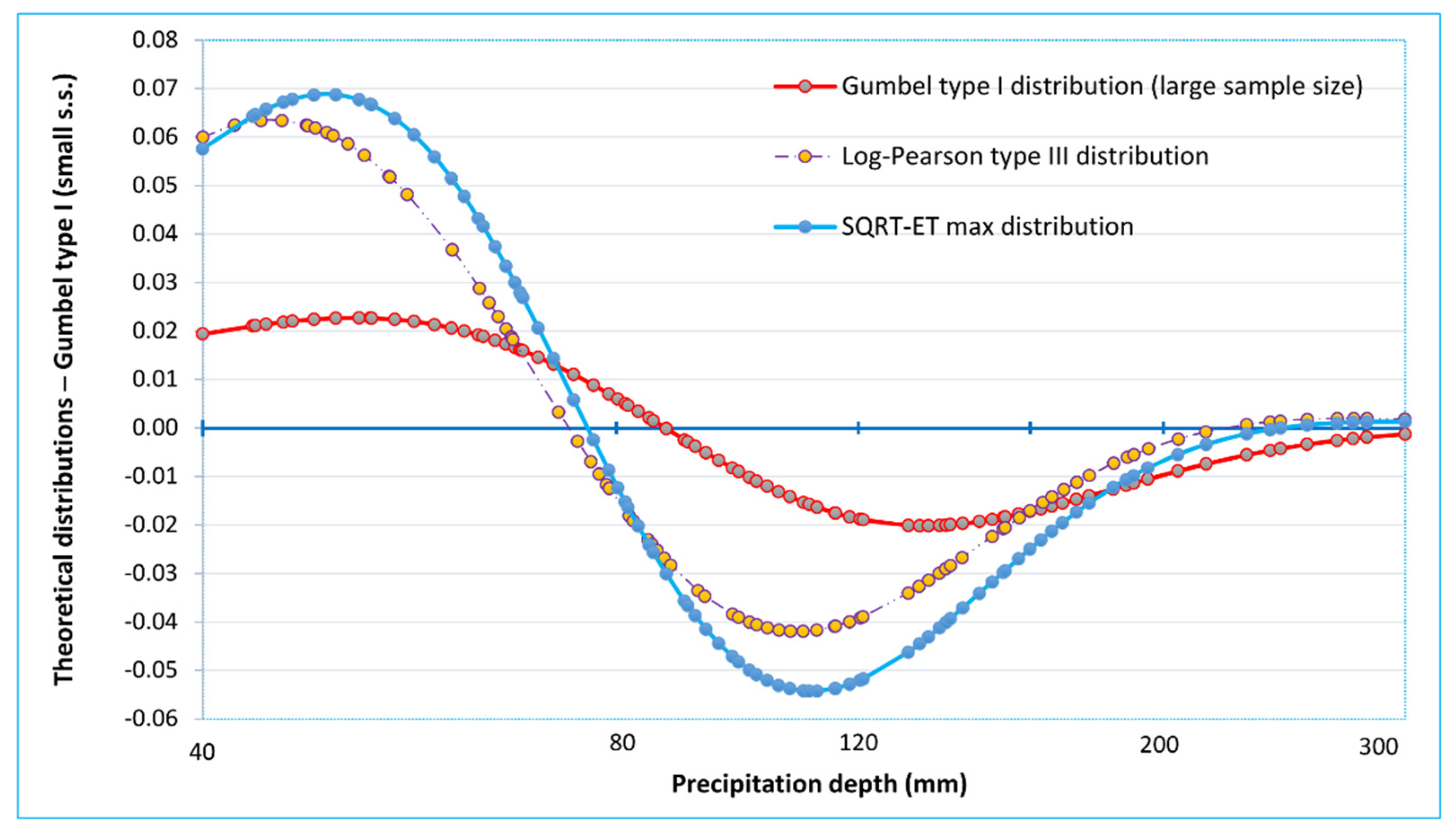
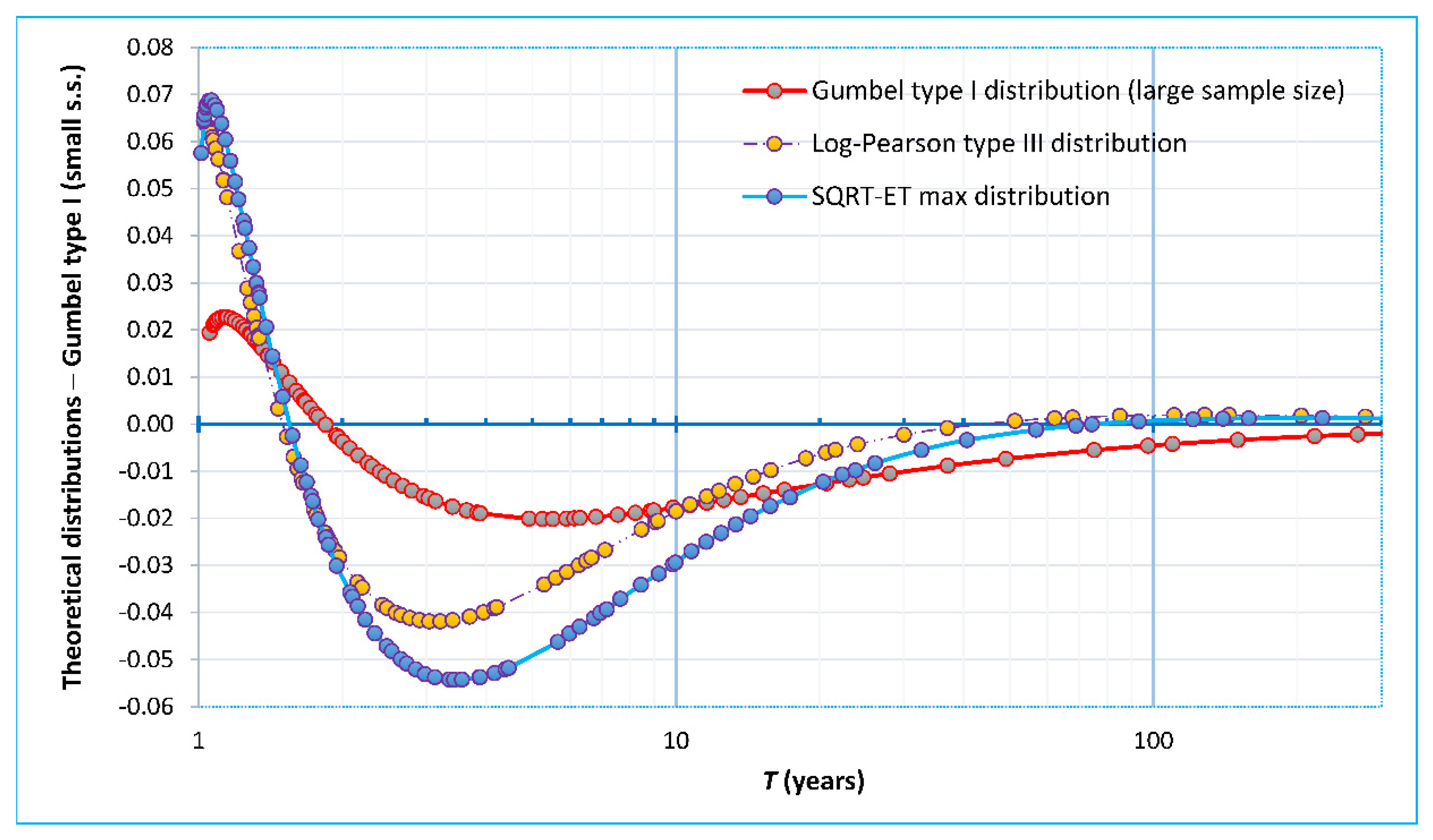
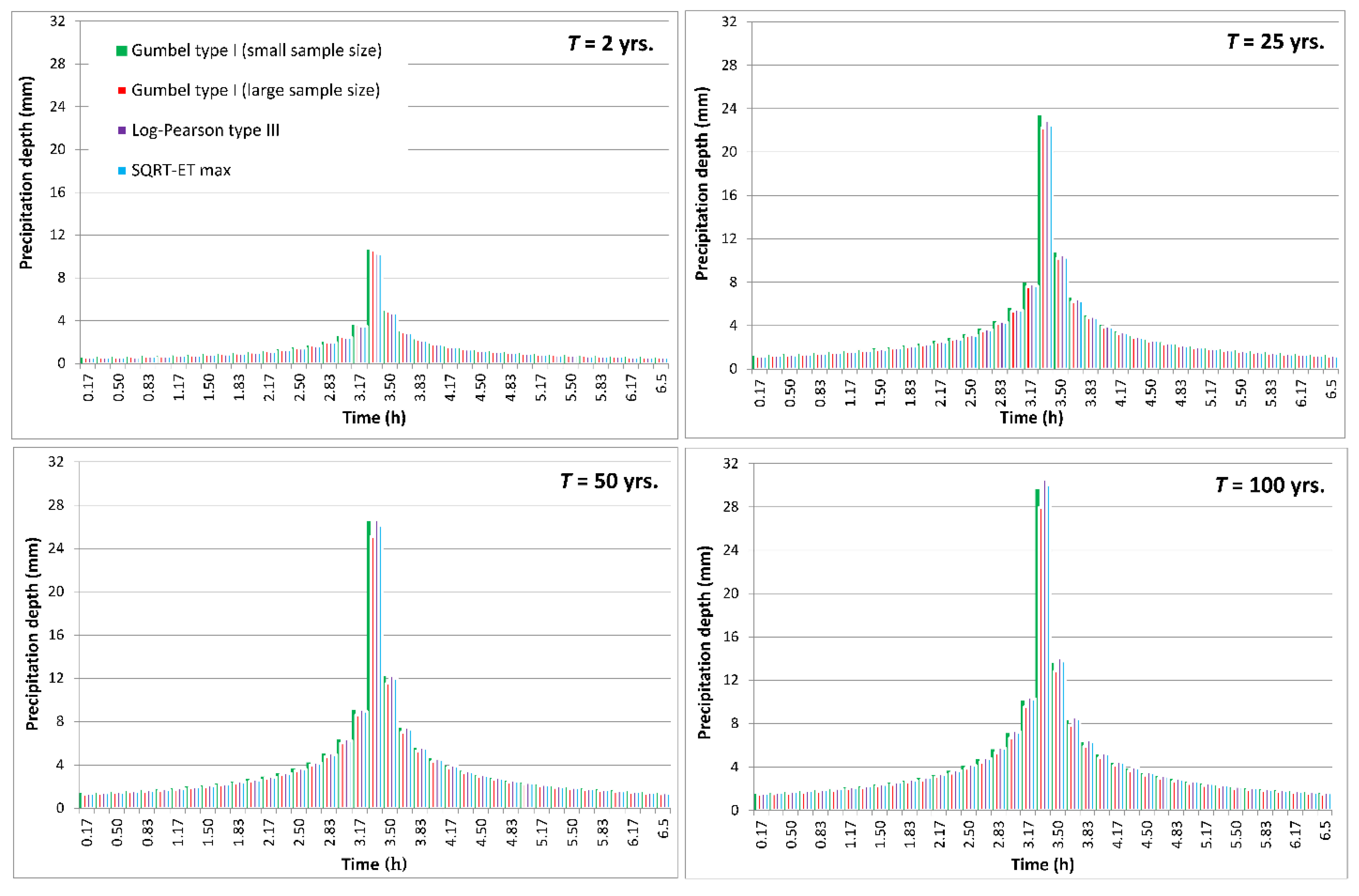
| Sample Size n | Mean (mm) | Standard Deviation (mm) | Covariance | Skewness Coefficient |
|---|---|---|---|---|
| 50 | 98.62 | 45.15 | 0.46 | 0.24 |
| Sandy Algibe | Campo de Gibraltar Clays | |
|---|---|---|
| Diameter (mm) | Percentage Lower Than | |
| 0.0005 | 0 | 0 |
| 0.0009 | 6 | 15 |
| 0.002 | 10 | 40 |
| 0.005 | 15 | 45 |
| 0.01 | 20 | 50 |
| 0.063 | 42 | 56 |
| 0.1 | 70 | 63 |
| 0.25 | 90 | 75 |
| 0.5 | 95 | 85 |
| 1 | 100 | 100 |
| Properties | Type of Soil | |
|---|---|---|
| Sandy Algibe | Clays of the Campo de Gibraltar | |
| Soil texture | Sandy loam | Clayey |
| Soil structure | Simple grain, weak and thin | Crumbly and lumpy on the surface. Arranged in blocks below the surface. |
| Percent of organic matter | 1.72 | 1.93 |
| Soil permeability | Moderate | Very slow |
| K factor | 0.30 | 0.41 |
| Gumbel Type I with a Small Sample Size | Gumbel Type I with a Large Sample Size | Log-Pearson Type III | SQRT-ET Max | |||||
|---|---|---|---|---|---|---|---|---|
| α (n) | β (n) | α (∞) | β (∞) | β (LP3) | γ (LP3) | X0 (LP3) | α (SQRT) | k (SQRT) |
| 0.02597 | 77.4991 | 0.0284 | 78.3037 | 0.0521 | 67.5027 | 0.9818 | 0.4993 | 69.3027 |
| Interval (Years) | Probability of Occurrence a | Average Yield b (Mg) | Sediment Yield Per Interval c (Mg·y−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GBS | GBL | LP3 | SQRT-ET | GBS | GBL | LP3 | SQRT-ET | ||
| 2–5 | 0.300 | 35,707 | 34,208 | 32,584 | 31,711 | 10,712 | 10,262 | 9775 | 9513 |
| 5–10 | 0.100 | 58,835 | 54,911 | 53,844 | 51,755 | 5884 | 5491 | 5384 | 5175 |
| 10–15 | 0.033 | 75,658 | 69,869 | 70,608 | 67,806 | 2522 | 2329 | 2354 | 2260 |
| 15–25 | 0.027 | 90,637 | 83,158 | 86,639 | 83,413 | 2417 | 2218 | 2310 | 2224 |
| 25–50 | 0.020 | 111,345 | 101,598 | 110,285 | 106,459 | 2227 | 2032 | 2206 | 2129 |
| 50–75 | 0.007 | 131,540 | 119,114 | 135,093 | 130,102 | 877 | 794 | 901 | 867 |
| 75–100 | 0.003 | 144,622 | 130,639 | 151,789 | 146,387 | 482 | 435 | 506 | 488 |
| 100–140 | 0.003 | 157,266 | 141,779 | 167,217 | 161,991 | 449 | 405 | 478 | 463 |
| 140–200 | 0.002 | 171,394 | 154,354 | 186,507 | 181,300 | 367 | 331 | 400 | 388 |
| Total sum of mean annual sediment yield (Mg) | 25,937 | 24,297 | 24,313 | 23,509 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez González, C.A.; Rodríguez-Pérez, Á.M.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. Sensitivity Analysis in Mean Annual Sediment Yield Modeling with Respect to Rainfall Probability Distribution Functions. Land 2023, 12, 35. https://doi.org/10.3390/land12010035
Rodríguez González CA, Rodríguez-Pérez ÁM, López R, Hernández-Torres JA, Caparrós-Mancera JJ. Sensitivity Analysis in Mean Annual Sediment Yield Modeling with Respect to Rainfall Probability Distribution Functions. Land. 2023; 12(1):35. https://doi.org/10.3390/land12010035
Chicago/Turabian StyleRodríguez González, César Antonio, Ángel Mariano Rodríguez-Pérez, Raúl López, José Antonio Hernández-Torres, and Julio José Caparrós-Mancera. 2023. "Sensitivity Analysis in Mean Annual Sediment Yield Modeling with Respect to Rainfall Probability Distribution Functions" Land 12, no. 1: 35. https://doi.org/10.3390/land12010035
APA StyleRodríguez González, C. A., Rodríguez-Pérez, Á. M., López, R., Hernández-Torres, J. A., & Caparrós-Mancera, J. J. (2023). Sensitivity Analysis in Mean Annual Sediment Yield Modeling with Respect to Rainfall Probability Distribution Functions. Land, 12(1), 35. https://doi.org/10.3390/land12010035








