Multi-Agent-Based Model for the Urban Macro-Level Impact Factors of Building Energy Consumption on Different Types of Land
Abstract
:1. Introduction
1.1. Urban Macro-Level Impact Factors of Building Energy Consumption
1.2. Building Energy Consumption Simulation Models
1.3. Research Objectives
- The first objective of this study is to use agent-based modeling technology to establish a simulation model of building energy consumption on the urban scale, which includes various urban macro-level impact factors and can realize the internal dynamic interaction between the factors. This model focuses on supporting urban planning, with the elements that can be adjusted by planning means as the core.
- The second objective is to use scenario simulation to identify the energy-saving potential of different types of land when the urban macro-level factors change. This will help planning decision-makers determine the priority areas for urban-scale building energy conservation through urban planning means.
- The third objective is to propose planning strategies for urban macro-level impact factors for each type of land based on the discussion of simulation results to provide a scientific basis and quantitative support for constructing the low-carbon city of Harbin.
2. Materials and Methods
2.1. Energy Consumption Data
2.2. Urban Macro-Level Impact Parameters
2.2.1. Urban Morphology Parameters
2.2.2. Climate Parameters
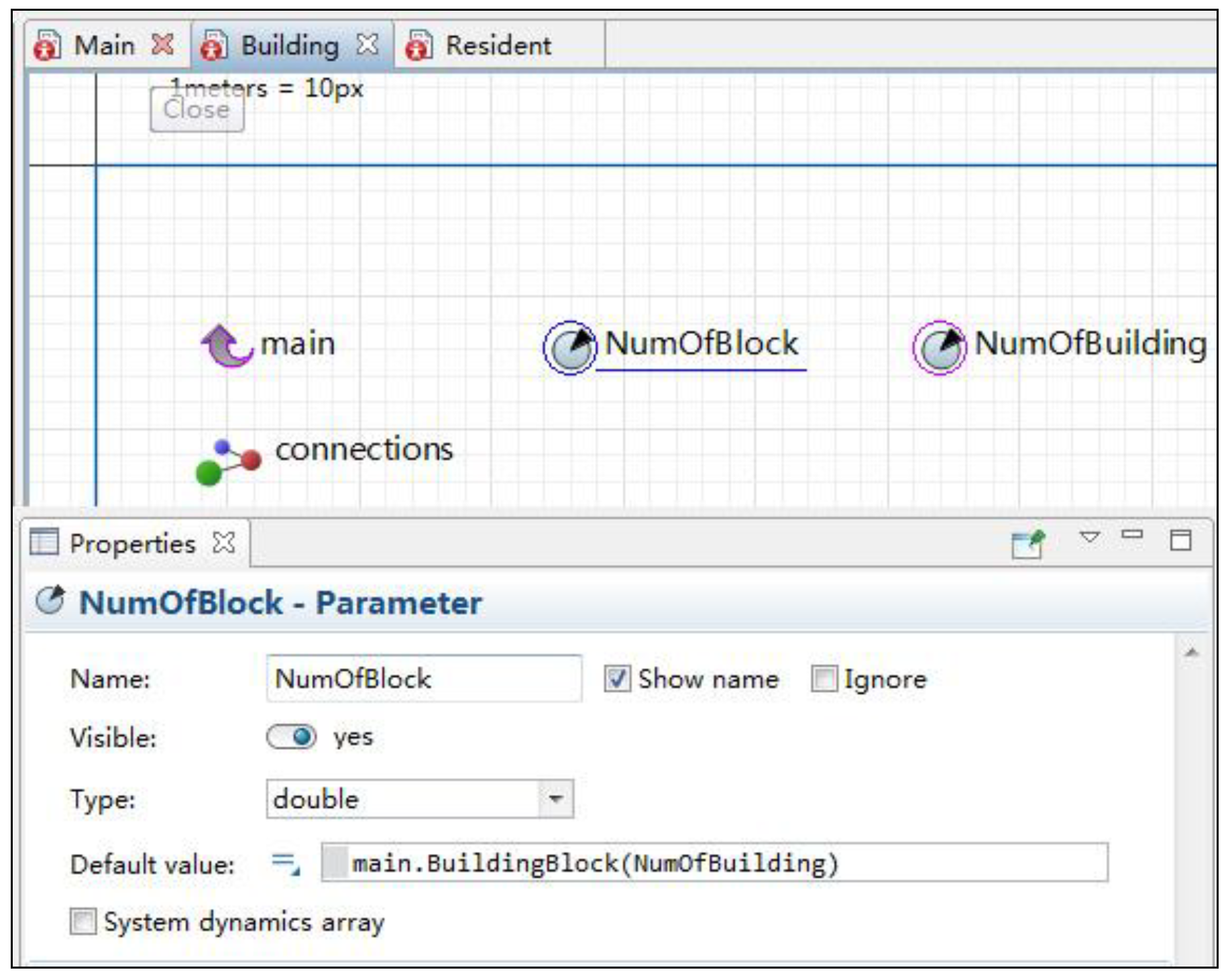
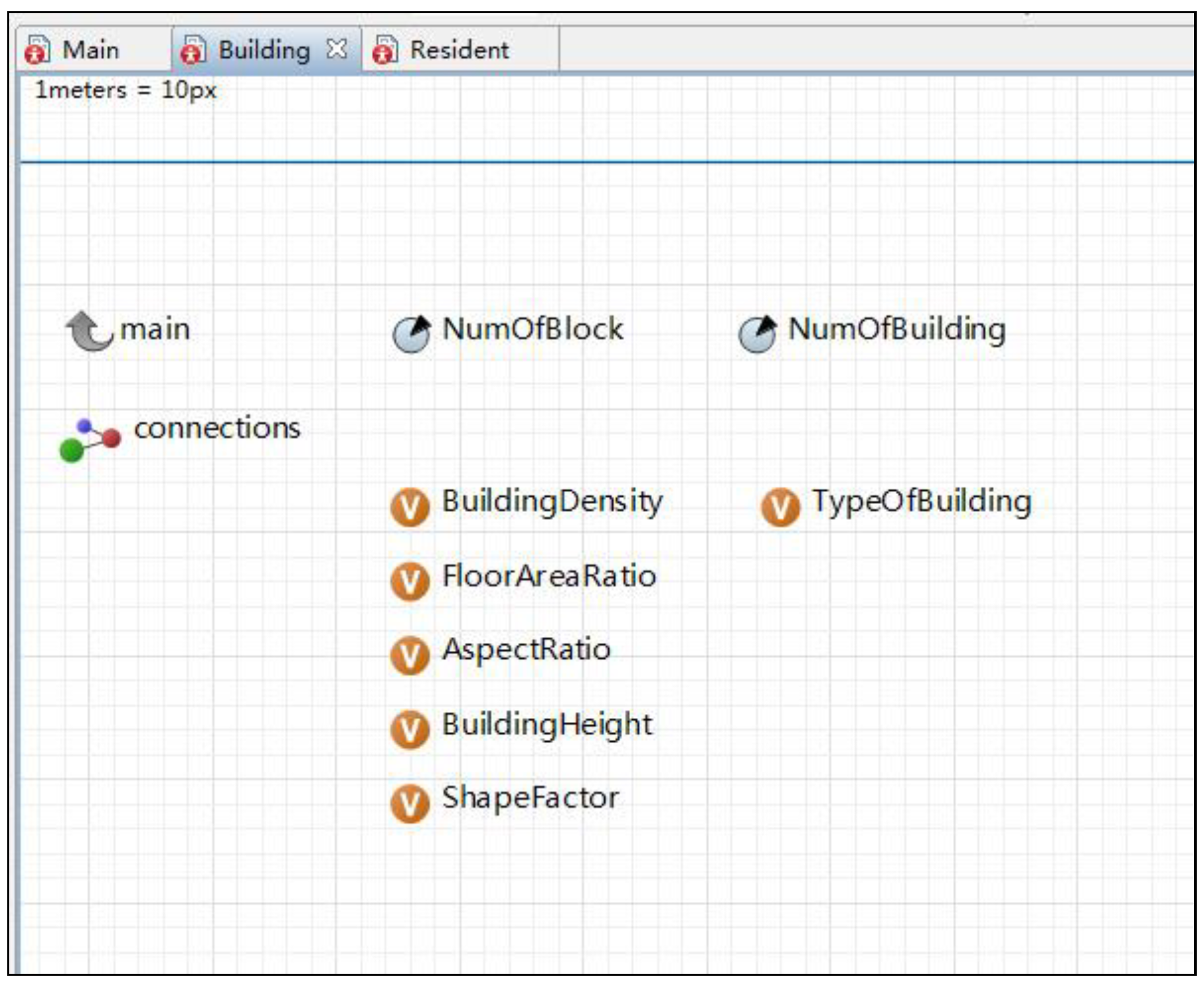
2.3. Model Structure and Parameterization
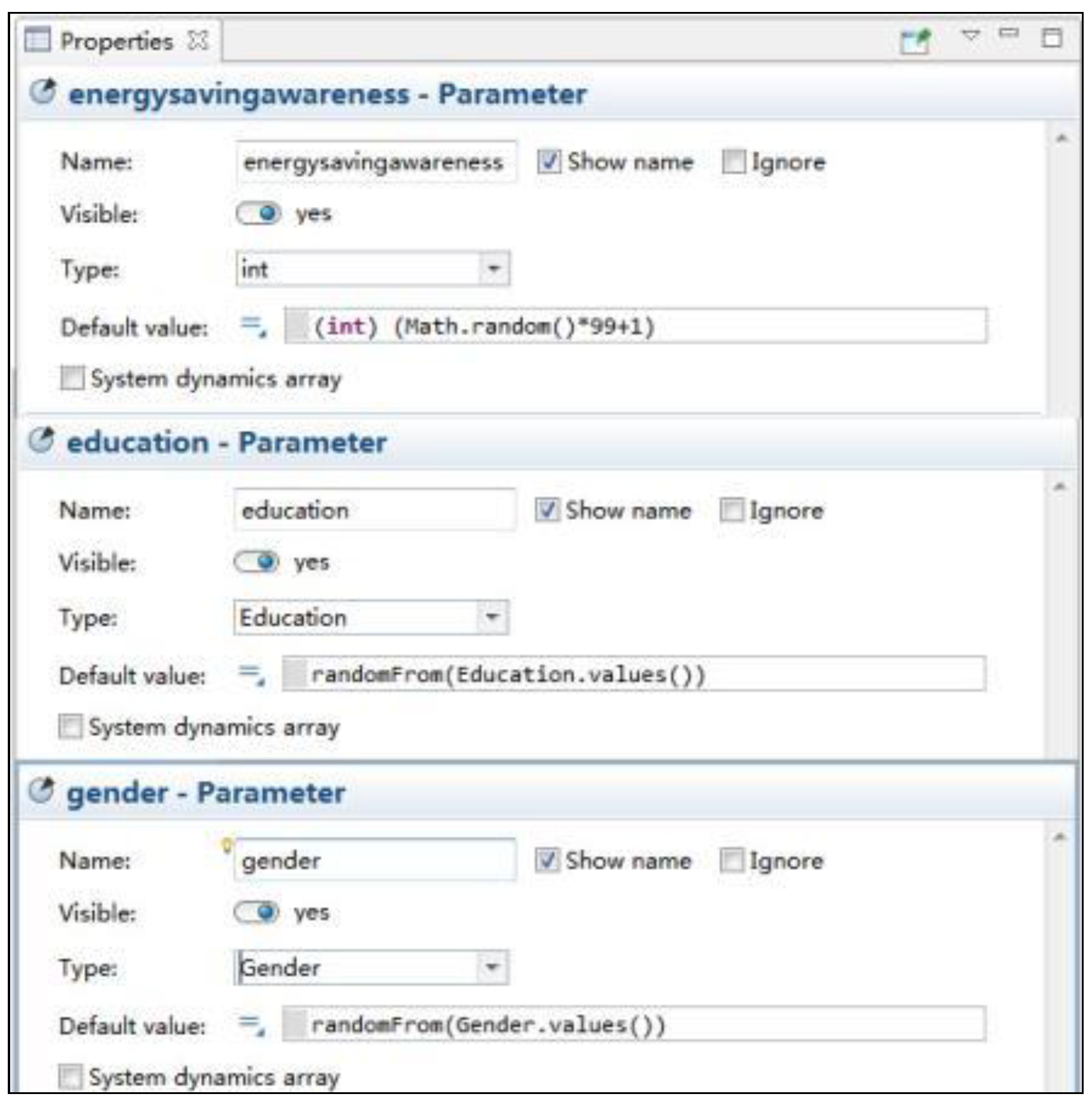
2.3.1. Input Data
2.3.2. Urban Morphology Sub-Model
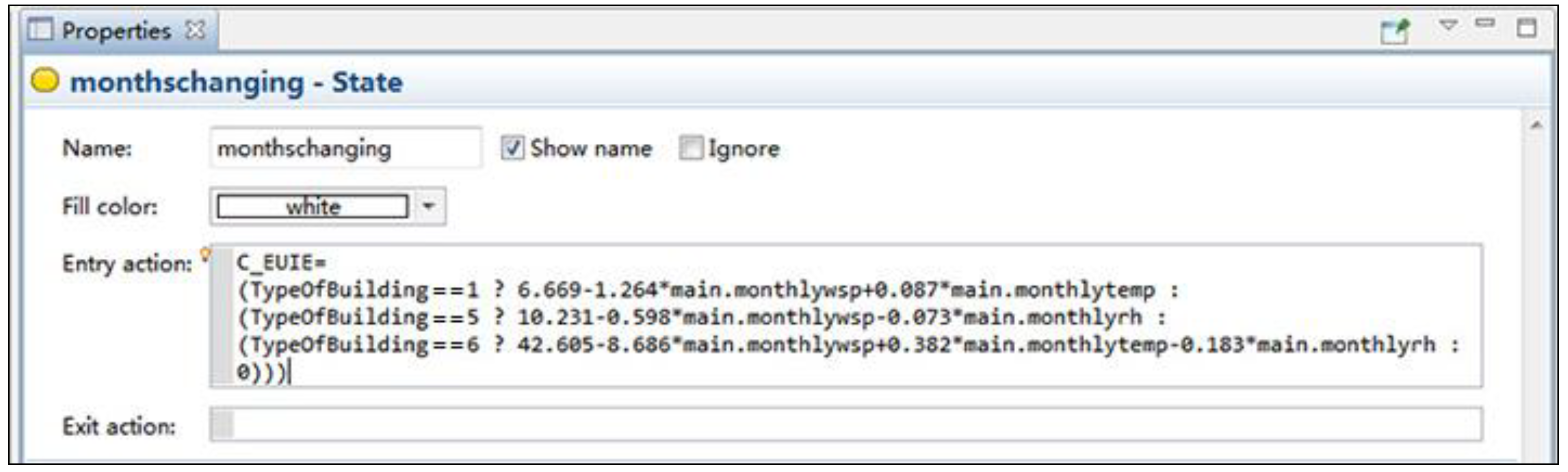
2.3.3. Climate Sub-Model
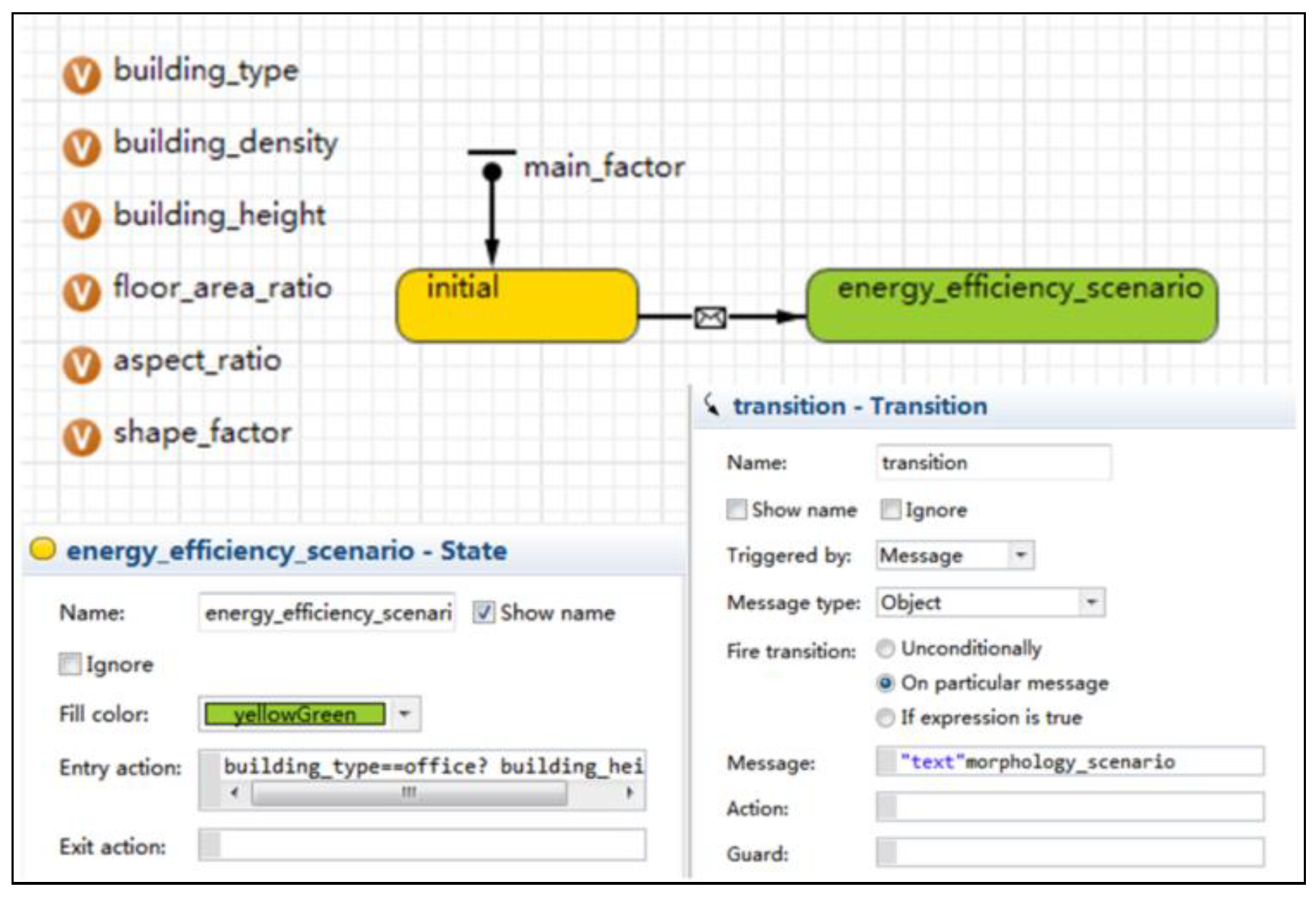
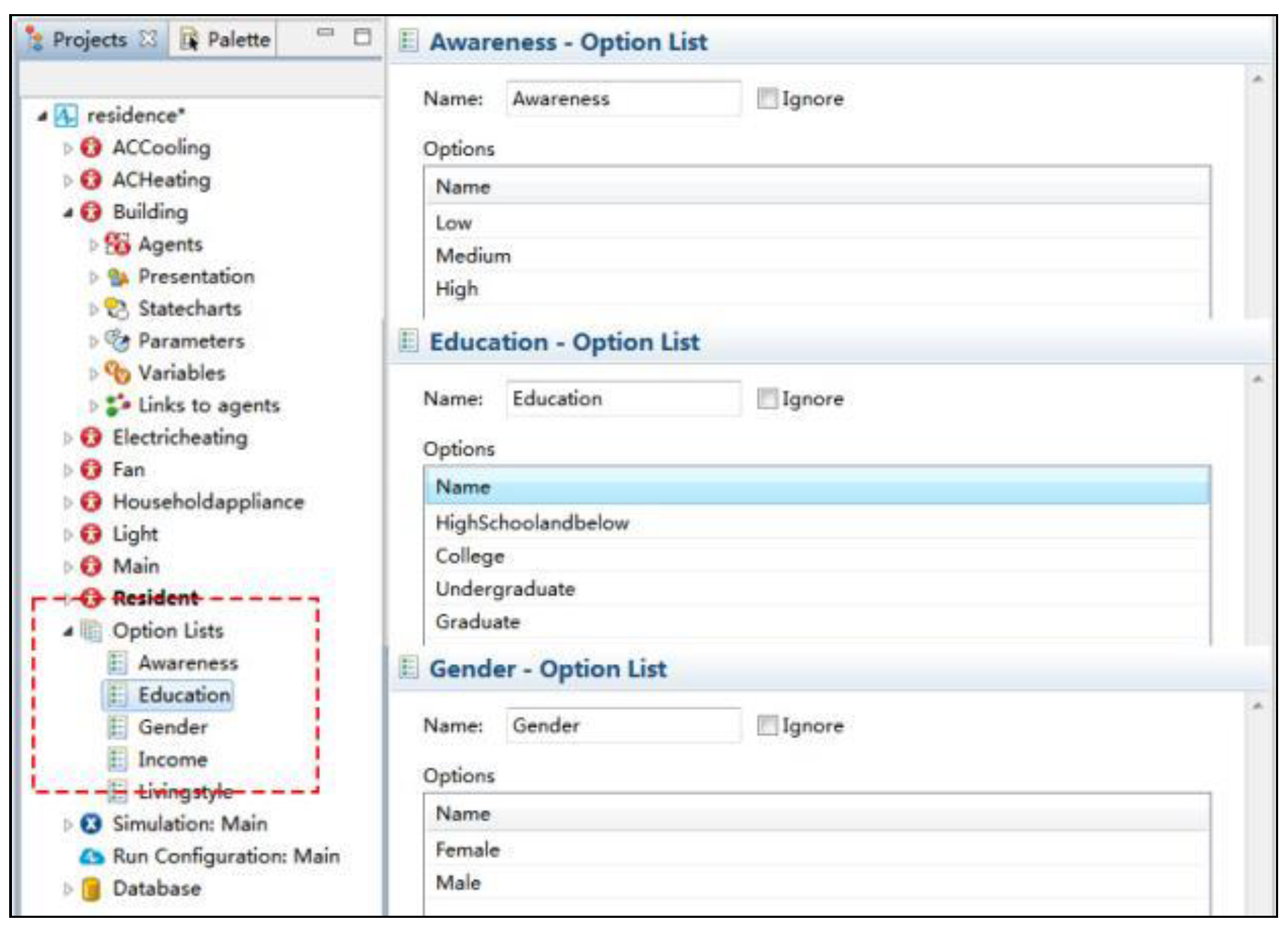
2.3.4. Energy Use Behavior Sub-Model
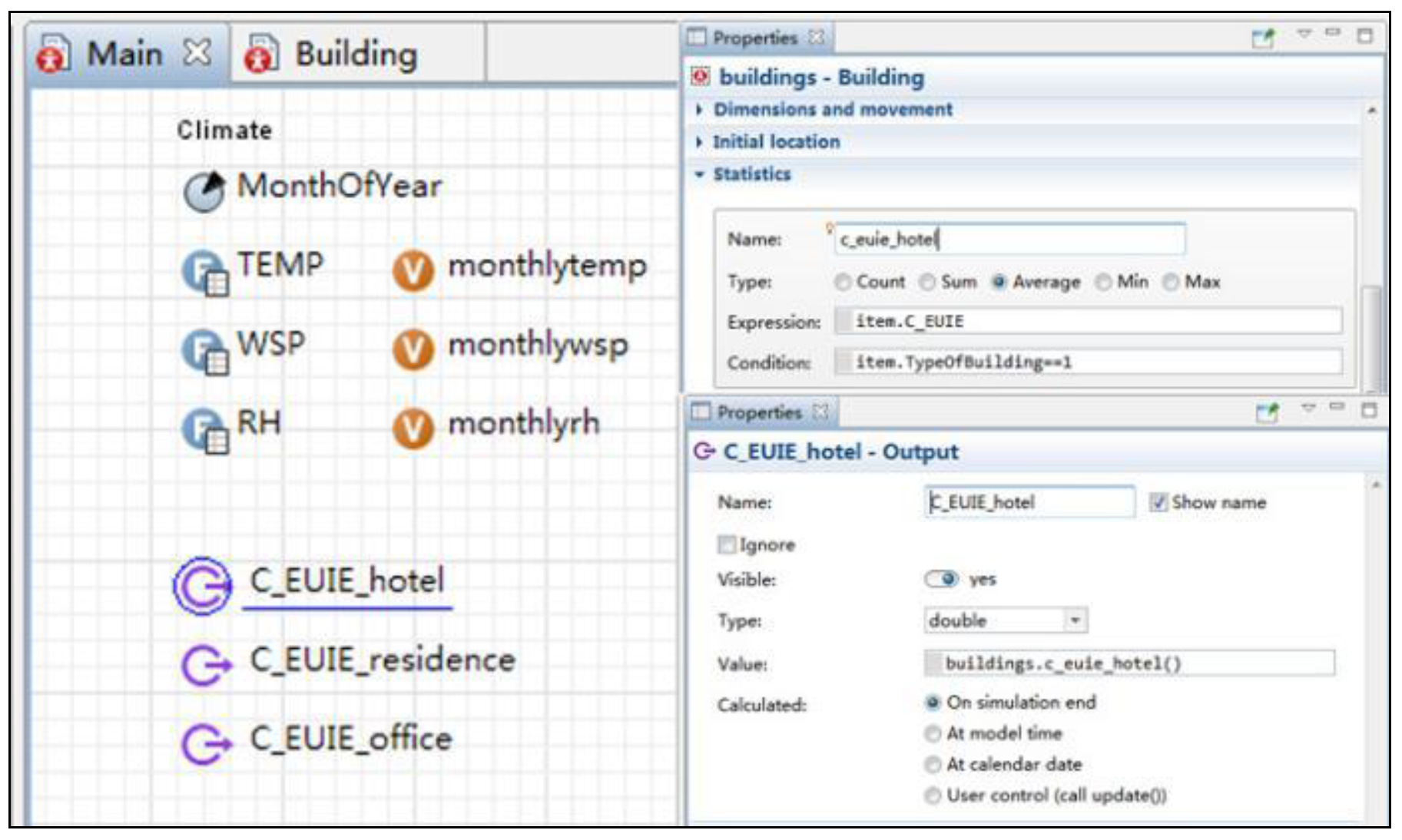
2.3.5. Simulation Output
2.4. Model Validation
2.4.1. Statistical Method
2.4.2. Agent Tracking
3. Simulation Results and Discussion
3.1. Simulation Scenarios and Calculation Output
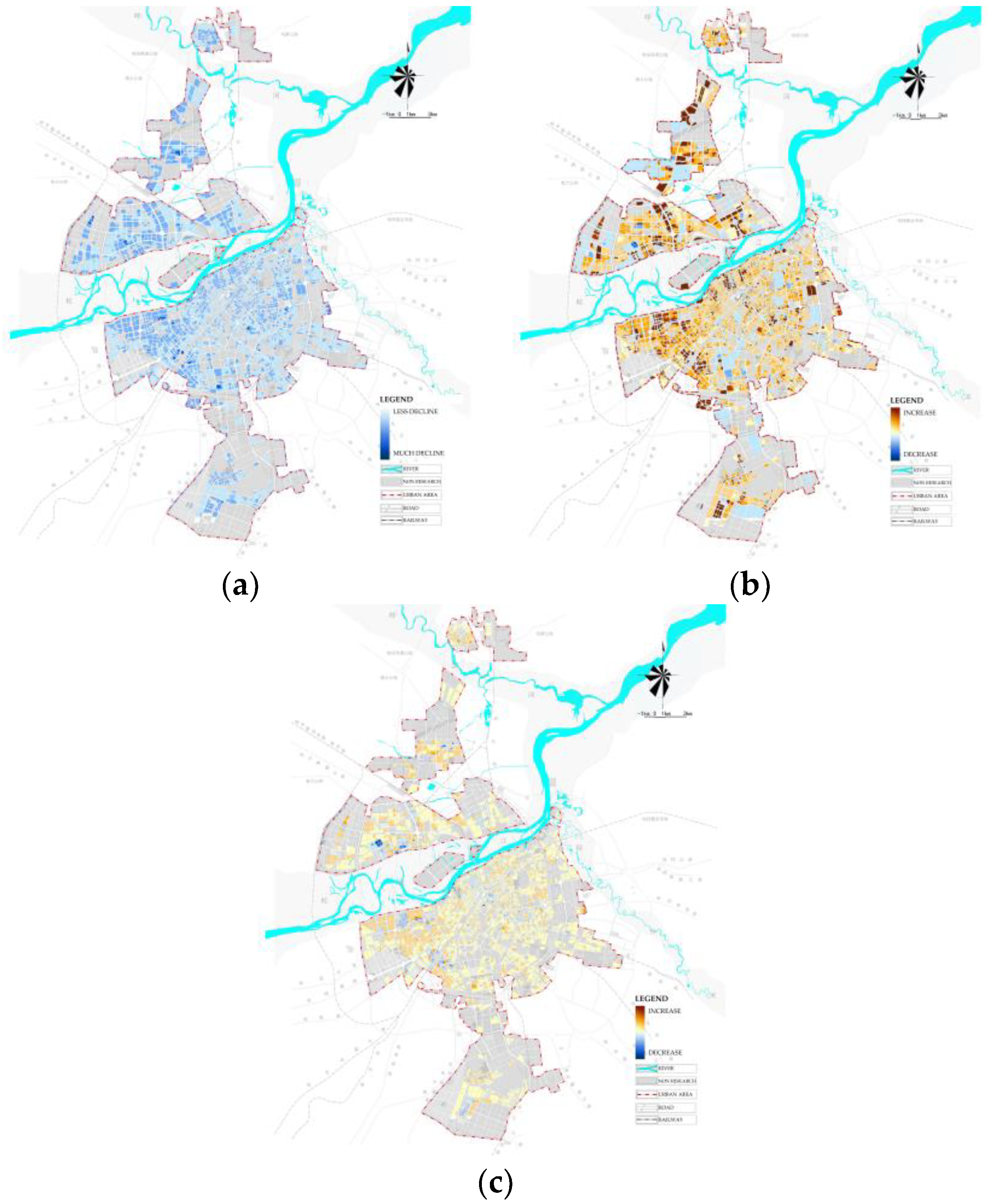
3.2. Energy-Saving Potential of Urban Morphology on the Different Types of Land
3.3. Energy-Saving Potential of Climate on the Different Types of Land
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Department of Economic and Social Affairs. World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420); United Nations Department of Economic and Social Affairs: New York, NY, USA, 2019. [Google Scholar]
- International Energy Agency. Energy Technology Perspectives 2016; International Energy Agency: Paris, France, 2016. [Google Scholar]
- Yang, L.; Yan, H.; Lam, J.C. Thermal comfort and building energy consumption implications–A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Oh, M.; Jang, K.M.; Kim, Y. Empirical analysis of building energy consumption and urban form in a large city: A case of Seoul, South Korea. Energy Build. 2021, 245, 111046. [Google Scholar] [CrossRef]
- Dibene-Arriola, L.M.; Carrillo-González, F.M.; Quijas, S.; Rodríguez-Uribe, M.C. Energy efficiency indicators for hotel buildings. Sustainability 2021, 13, 1754. [Google Scholar] [CrossRef]
- William, M.A.; Suárez-López, M.J.; Soutullo, S.; Hanafy, A.A. Building envelopes toward energy-efficient buildings: A balanced multi-approach decision making. Int. J. Energy Res. 2021, 15, 21096–21113. [Google Scholar] [CrossRef]
- Franco, A.; Miserocchi, L.; Testi, D. HVAC energy saving strategies for public buildings based on heat pumps and demand controlled ventilation. Energies 2021, 14, 5541. [Google Scholar] [CrossRef]
- De Rubeis, T.; Giacchetti, L.; Paoletti, D.; Ambrosini, D. Building energy performance analysis at urban scale: A supporting tool for energy strategies and urban building energy rating identification. Sustain. Cities Soc. 2021, 74, 103220. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Augenbroe, G. Development of prototypical buildings for urban scale building energy modeling: A reduced order energy model approach. Sci. Technol. Built Environ. 2018, 24, 33–42. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, J.; Luo, X. Parallel computational building-chain model for rapid urban-scale energy simulation. Energy Build. 2019, 201, 37–52. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Y.; Yang, J.; Chen, Z. Archetype identification and urban building energy modeling for city-scale buildings based on GIS datasets. Build. Simul. 2022, 15, 1547–1559. [Google Scholar] [CrossRef]
- Delmastro, C.; Gargiulo, M. Capturing the long-term interdependencies between building thermal energy supply and demand in urban planning strategies. Appl. Energy 2020, 268, 114774. [Google Scholar] [CrossRef]
- Yu, H.; Wang, M.; Lin, X.; Guo, H.; Liu, H.; Zhao, Y.; Wang, H.; Li, C.; Jing, R. Prioritizing urban planning factors on community energy performance based on GIS-informed building energy modeling. Energy Build. 2021, 249, 111191. [Google Scholar] [CrossRef]
- Moghadam, S.T.; Delmastro, C.; Corgnati, S.P.; Lombardi, P. Urban energy planning procedure for sustainable development in the built environment: A review of available spatial approaches. J. Clean. Prod. 2017, 165, 811–827. [Google Scholar] [CrossRef]
- Zanon, B.; Verones, S. Climate change, urban energy and planning practices: Italian experiences of innovation in land management tools. Land Use Policy 2013, 32, 343–355. [Google Scholar] [CrossRef]
- Yeo, I.-A.; Yoon, S.-H.; Yee, J.-J. Development of an urban energy demand forecasting system to support environmentally friendly urban planning. Appl. Energy 2013, 110, 304–317. [Google Scholar] [CrossRef]
- Wang, M.; Kexin, L. Transportation model application for the planning of low carbon city–take Xining city in China as example. Procedia Comput. Sci. 2013, 19, 835–840. [Google Scholar] [CrossRef] [Green Version]
- Shareef, S. The impact of urban morphology and building’s height diversity on energy consumption at urban scale. The case study of Dubai. Build. Environ. 2021, 194, 107675. [Google Scholar] [CrossRef]
- Lee, G.; Jeong, Y. Impact of urban and building form and microclimate on the energy consumption of buildings-based on statistical analysis. J. Asian Archit. Build. Eng. 2017, 16, 565–572. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xie, Y.; Luan, B.; Chen, X. Urban macro-level impact factors on Direct CO2 Emissions of urban residents in China. Energy Build. 2015, 107, 131–143. [Google Scholar] [CrossRef]
- Shen, P.; Wang, Z. How neighborhood form influences building energy use in winter design condition: Case study of Chicago using CFD coupled simulation. J. Clean. Prod. 2020, 261, 121094. [Google Scholar] [CrossRef]
- Ramponi, R.; Blocken, B.; Laura, B.; Janssen, W.D. CFD simulation of outdoor ventilation of generic urban configurations with different urban densities and equal and unequal street widths. Build. Environ. 2015, 92, 152–166. [Google Scholar] [CrossRef]
- Mouzourides, P.; Kyprianou, A.; Neophytou, M.K.-A.; Ching, J.; Choudhary, R. Linking the urban-scale building energy demands with city breathability and urban form characteristics. Sustain. Cities Soc. 2019, 49, 101460. [Google Scholar] [CrossRef]
- Liu, J.; Heidarinejad, M.; Gracik, S.; Srebric, J. The impact of exterior surface convective heat transfer coefficients on the building energy consumption in urban neighborhoods with different plan area densities. Energy Build. 2015, 86, 449–463. [Google Scholar] [CrossRef]
- Allen-Dumas, M.R.; Rose, A.N.; New, J.R.; Omitaomu, O.A.; Yuan, J.; Branstetter, M.L.; Sylvester, L.M.; Seals, M.B.; Carvalhaes, T.M.; Adams, M.B. Impacts of the morphology of new neighborhoods on microclimate and building energy. Renew. Sustain. Energy Rev. 2020, 133, 110030. [Google Scholar] [CrossRef]
- Steemers, K. Energy and the city: Density, buildings and transport. Energy Build. 2003, 35, 3–14. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F.; Nakhaie, A.A.; Yagouti, A.; Giguère, M.; Keusseyan, R.; Coman, A. Indoor thermal condition in urban heat Island–Development of a predictive tool. Build. Environ. 2012, 57, 7–17. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Olsthoorn, D.; Torjan, M.; Haghighat, F. Urban neighborhood characteristics influence on a building indoor environment. Sustain. Cities Soc. 2015, 19, 403–413. [Google Scholar] [CrossRef] [Green Version]
- Ahn, Y.; Sohn, D.-W. The effect of neighbourhood-level urban form on residential building energy use: A GIS-based model using building energy benchmarking data in Seattle. Energy Build. 2019, 196, 124–133. [Google Scholar] [CrossRef]
- De Lemos Martins, T.A.; Adolphe, L.; Bastos, L.E.G.; de Lemos Martins, M.A. Sensitivity analysis of urban morphology factors regarding solar energy potential of buildings in a Brazilian tropical context. Sol. Energy 2016, 137, 11–24. [Google Scholar] [CrossRef]
- Ashtiani, A.; Mirzaei, P.A.; Haghighat, F. Indoor thermal condition in urban heat island: Comparison of the artificial neural network and regression methods prediction. Energy Build. 2014, 76, 597–604. [Google Scholar] [CrossRef]
- Giridharan, R.; Lau, S.; Ganesan, S.; Givoni, B. Urban design factors influencing heat island intensity in high-rise high-density environments of Hong Kong. Build. Environ. 2007, 42, 3669–3684. [Google Scholar] [CrossRef]
- Song, S.; Leng, H.; Xu, H.; Guo, R.; Zhao, Y. Impact of urban morphology and climate on heating energy consumption of buildings in severe cold regions. Int. J. Environ. Res. Public Health 2020, 17, 8354. [Google Scholar] [CrossRef]
- Reinhart, C.F.; Davila, C.C. Urban building energy modeling—A review of a nascent field. Build. Environ. 2016, 97, 196–202. [Google Scholar] [CrossRef] [Green Version]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Johari, F.; Peronato, G.; Sadeghian, P.; Zhao, X.; Widén, J. Urban building energy modeling: State of the art and future prospects. Renew. Sustain. Energy Rev. 2020, 128, 109902. [Google Scholar] [CrossRef]
- Johari, F.; Munkhammar, J.; Shadram, F.; Widén, J. Evaluation of simplified building energy models for urban-scale energy analysis of buildings. Build. Environ. 2022, 211, 108684. [Google Scholar] [CrossRef]
- Kämpf, J.H.; Robinson, D. A simplified thermal model to support analysis of urban resource flows. Energy Build. 2007, 39, 445–453. [Google Scholar] [CrossRef]
- Dogan, T.; Reinhart, C. Shoeboxer: An algorithm for abstracted rapid multi-zone urban building energy model generation and simulation. Energy Build. 2017, 140, 140–153. [Google Scholar] [CrossRef]
- Sola, A.; Corchero, C.; Salom, J.; Sanmarti, M. Simulation tools to build urban-scale energy models: A review. Energies 2018, 11, 3269. [Google Scholar] [CrossRef] [Green Version]
- Rasheed, A. Multiscale Modelling of Urban Climate; EPFL: Lausanne, Switzerland, 2009. [Google Scholar]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; James, O.D.; Finn, D. Data driven approaches for prediction of building energy consumption at urban level. Energy Procedia 2015, 78, 3378–3383. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Fumo, N. A review on the basics of building energy estimation. Renew. Sustain. Energy Rev. 2014, 31, 53–60. [Google Scholar] [CrossRef]
- Li, Z.; Han, Y.; Xu, P. Methods for benchmarking building energy consumption against its past or intended performance: An overview. Appl. Energy 2014, 124, 325–334. [Google Scholar] [CrossRef]
- Ashrae, A.H. Fundamentals; IP Edition; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2009. [Google Scholar]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, D.; Liu, Y.; Han, Z.; Lun, L.; Gao, J.; Jin, G.; Cao, G. Accuracy analyses and model comparison of machine learning adopted in building energy consumption prediction. Energy Explor. Exploit. 2019, 37, 1426–1451. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.-h.; Braun, J.E. Development of methods for determining demand-limiting setpoint trajectories in buildings using short-term measurements. Build. Environ. 2008, 43, 1755–1768. [Google Scholar] [CrossRef]
- Wang, S.; Xu, X. Simplified building model for transient thermal performance estimation using GA-based parameter identification. Int. J. Therm. Sci. 2006, 45, 419–432. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [Green Version]
- Macal, C.M.; North, M.J. Agent-based modeling and simulation: ABMS examples. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 101–112. [Google Scholar]
- Berger, C.; Mahdavi, A. Review of current trends in agent-based modeling of building occupants for energy and indoor-environmental performance analysis. Build. Environ. 2020, 173, 106726. [Google Scholar] [CrossRef]
- Nägeli, C.; Jakob, M.; Catenazzi, G.; Ostermeyer, Y. Towards agent-based building stock modeling: Bottom-up modeling of long-term stock dynamics affecting the energy and climate impact of building stocks. Energy Build. 2020, 211, 109763. [Google Scholar] [CrossRef]
- Railsback, S.F.; Grimm, V. Agent-Based and Individual-Based Modeling: A Practical Introduction; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Hurtado, L.; Nguyen, P.; Kling, W. Agent-based control for building energy management in the smart grid framework. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- De Durana, J.M.G.; Barambones, O.; Kremers, E.; Varga, L. Agent based modeling of energy networks. Energy Convers. Manag. 2014, 82, 308–319. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.N.; Chi, H.-L.; Wei, H.-H.; Lee, M.; Ni, M. Influence of interior layouts on occupant energy-saving behaviour in buildings: An integrated approach using agent-based modelling, system dynamics and building information modelling. Renew. Sustain. Energy Rev. 2022, 161, 112382. [Google Scholar] [CrossRef]
- Ding, Z.; Hu, T.; Li, M.; Xu, X.; Zou, P.X. Agent-based model for simulating building energy management in student residences. Energy Build. 2019, 198, 11–27. [Google Scholar] [CrossRef]
- Song, S.-Y.; Leng, H. Modeling the household electricity usage behavior and energy-saving management in severely cold regions. Energies 2020, 13, 5581. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Azar, E. Integrating building performance simulation in agent-based modeling using regression surrogate models: A novel human-in-the-loop energy modeling approach. Energy Build. 2016, 128, 214–223. [Google Scholar] [CrossRef]
- Azar, E.; Menassa, C.C. Agent-based modeling of occupants and their impact on energy use in commercial buildings. J. Comput. Civ. Eng. 2012, 26, 506–518. [Google Scholar] [CrossRef]
- Walter, T.; Sohn, M.D. A regression-based approach to estimating retrofit savings using the building performance database. Appl. Energy 2016, 179, 996–1005. [Google Scholar] [CrossRef] [Green Version]
- Tellier, L.-N. Characterizing urban form by means of the urban metric system. Land Use Policy 2021, 111, 104672. [Google Scholar] [CrossRef]
- Equere, V.; Mirzaei, P.A.; Riffat, S. Definition of a new morphological parameter to improve prediction of urban heat island. Sustain. Cities Soc. 2020, 56, 102021. [Google Scholar] [CrossRef]
- Xu, X.; AzariJafari, H.; Gregory, J.; Norford, L.; Kirchain, R. An integrated model for quantifying the impacts of pavement albedo and urban morphology on building energy demand. Energy Build. 2020, 211, 109759. [Google Scholar] [CrossRef]
- Batty, M.; Torrens, P.M. Modelling and prediction in a complex world. Futures 2005, 37, 745–766. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, H. Urban planning for low-carbon sustainable development. Sustain. Comput. Inform. Syst. 2020, 28, 100398. [Google Scholar] [CrossRef]
- Lu, M.; Sun, G.; He, Z. Analysis and evaluation of factors influencing the low-carbon effect of urban high-rise settlement planning schemes based on AHP-fuzzy comprehensive evaluation method. Math. Probl. Eng. 2022, 2022, 9529110. [Google Scholar] [CrossRef]
- Wang, G.; Han, Q.; de Vries, B. The multi-objective spatial optimization of urban land use based on low-carbon city planning. Ecol. Indic. 2021, 125, 107540. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y. Study of key factors influencing low carbon urban environmental planning strategy. J. Environ. Prot. Ecol. 2021, 22, 893–900. [Google Scholar]
- Penazzi, S.; Accorsi, R.; Manzinia, R. Planning low carbon urban-rural ecosystems: An integrated transport land-use model. J. Clean. Prod. 2019, 235, 96–111. [Google Scholar] [CrossRef]
- Yu, Y. Explore the theoretical basis and implementation strategy of low-carbon urban community planning. Front. Environ. Sci. 2022, 10, 989318. [Google Scholar] [CrossRef]
- Hukkalainen, M.; Virtanen, M.; Paiho, S.; Airaksinen, M. Energy planning of low carbon urban areas—Examples from Finland. Sustain. Cities Soc. 2017, 35, 715–728. [Google Scholar] [CrossRef]
- Llantoy, N.; Chafer, M.; Cabeza, L.F. A comparative life cycle assessment (LCA) of different insulation materials for buildings in the continental Mediterranean climate. Energy Build. 2020, 225, 110323. [Google Scholar] [CrossRef]
- Heravi, G.; Salehi, M.M.; Rostami, M. Identifying cost-optimal options for a typical residential nearly zero energy building’s design in developing countries. Clean Technol. Environ. Policy 2020, 22, 2107–2128. [Google Scholar] [CrossRef]


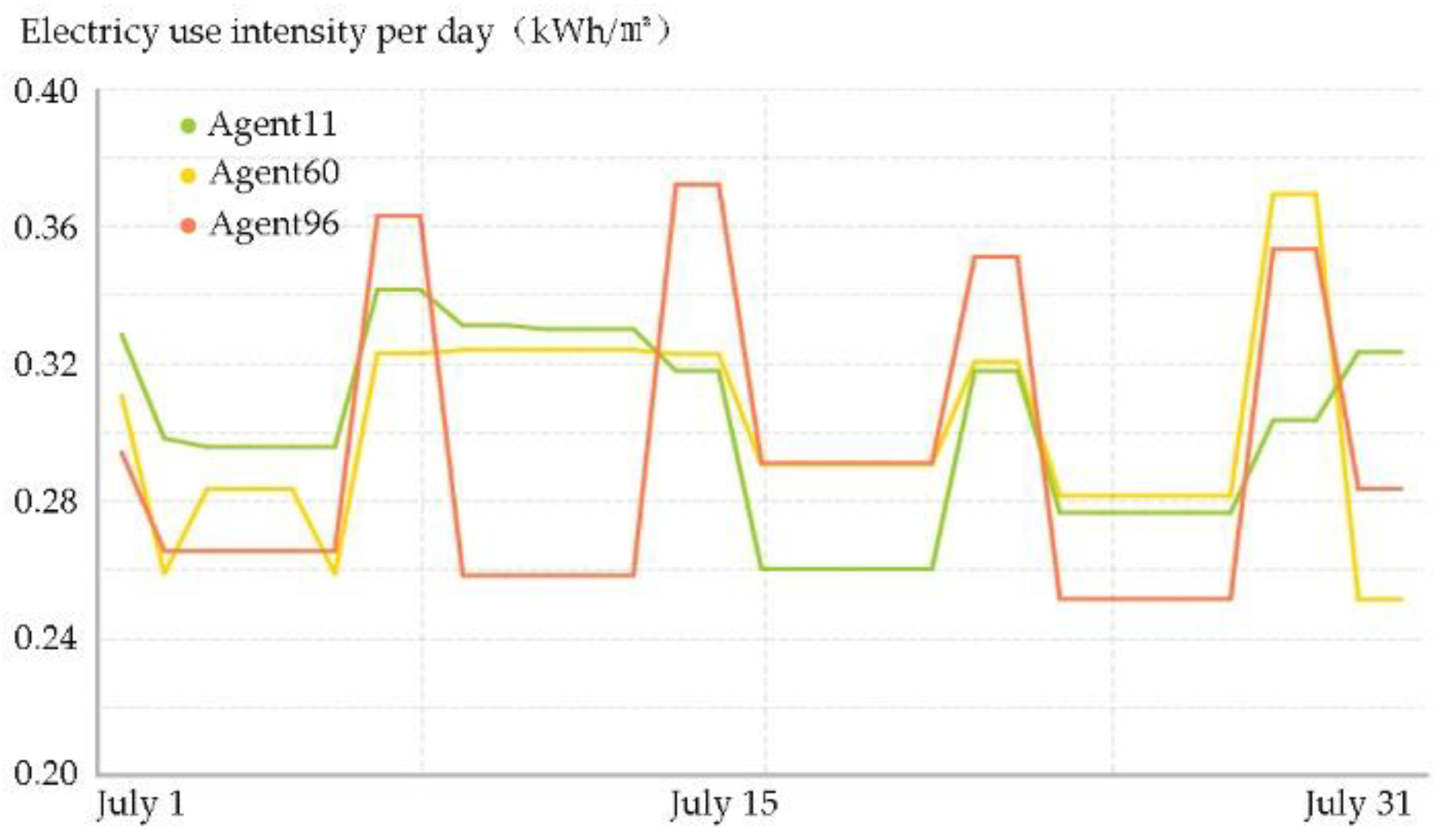
| Type | Building Height (m) | Total Building Area (m2) | Building Floor Area (m2) |
|---|---|---|---|
| Hotel | 5.92–108.73 | 941.13–6036.59 | 172.00–4018.23 |
| Retail building | 6.00–97.00 | 1536.60–238437.16 | 269.12–101453.12 |
| Hospital | 3.29–57.42 | 810.65–76286.13 | 223.51–3632.20 |
| Educational building | 3.49–57.00 | 503.04–85500.63 | 174.10–6276.32 |
| Residential building | 11.39–111.84 | 158.06-45679.20 | 158.06–5279.00 |
| Office building | 4.00–115.25 | 941.61–106209.65 | 50.30–5373.42 |
| Norma Distribution Test | Minimum Value (kWh/m2) | Maximum Value (kWh/m2) | Average Value (kWh/m2) | Standard Deviation (kWh/m2) |
|---|---|---|---|---|
| Sig | ||||
| 0.06 | 104.72 | 622.93 | 216.25 | 77.44 |
| Building Type | Building Density (%) | Building Height (m) | Floor Area Ratio | Aspect Ratio | Shape Factor |
|---|---|---|---|---|---|
| Hotel | 14.65–73.44 | 5.96–108.73 | 0.60–4.40 | 0.11–3.62 | 0.15–0.54 |
| Retail building | 12.39–58.79 | 6.20–97.00 | 0.73–5.96 | 0.15–1.76 | 0.09–0.55 |
| Hospital | 17.12–63.43 | 3.29–57.42 | 0.49–5.01 | 0.06–1.92 | 0.14–0.53 |
| Educational Building | 1.61–64.68 | 3.49–121.01 | 0.03–4.06 | 0.10–2.20 | 0.09–0.54 |
| Residential Building | 10.38–56.74 | 11.39–111.84 | 0.45–4.06 | 0.22–3.61 | 0.14–0.47 |
| Office building | 12.23–78.27 | 4.00–115.25 | 0.46–5.62 | 0.06–3.65 | 0.11–0.53 |
| Building Type | Variable | Denormalization Coefficient | Standardization Coefficient | R2 |
|---|---|---|---|---|
| Retail building | (constant) | 21.081 | — | 0.119 |
| Shape factor | 357.346 | 0.345 | ||
| Hospital | (constant) | −17.89 | — | 0.146 |
| Building density (%) | 2.514 | 0.382 | ||
| Educational building | (constant) | 50.964 | — | 0.103 |
| Building height (m) | −0.775 | −0.320 | ||
| Residential building | (constant) | −18.732 | — | 0.102 |
| Shape factor | 266.632 | 0.320 | ||
| Office building | (constant) | 51.519 | — | 0.105 |
| Building height (m) | −0.279 | −0.223 |
| Building Type | Variable | Denormalization Coefficient | Standardization Coefficient | R2 |
|---|---|---|---|---|
| Hotel | (constant) | 192.037 | — | 0.189 |
| Building height (m) | −0.601 | −0.435 | ||
| Retail building | (constant) | 105.508 | — | 0.522 |
| Aspect ratio | 51.45 | 0.376 | ||
| Shape factor | 239.71 | 0.413 | ||
| Educational building | (constant) | 170.211 | — | 0.176 |
| Building height (m) | −0.65 | −0.271 | ||
| Residential building | (constant) | 99.013 | — | 0.190 |
| Floor area ratio | 9.516 | 0.247 | ||
| Shape factor | 217.762 | 0.350 | ||
| Office building | (constant) | 179.642 | — | 0.126 |
| Building height (m) | −0.369 | −0.355 |
| Month | Temperature (°C) | Wind Speed (m/s) | Relative Humidity (%) |
|---|---|---|---|
| 1 | 2.57 | −16.56 | 71.48 |
| 2 | 3 | −11 | 67.9 |
| 3 | 2.6 | −1.7 | 62.2 |
| 4 | 3.84 | 9.13 | 45.52 |
| 5 | 4.68 | 16.64 | 49.2 |
| 6 | 2.8 | 19.9 | 67.9 |
| 7 | 2.6 | 24.7 | 70 |
| 8 | 3 | 22.1 | 76 |
| 9 | 2.8 | 15 | 69.7 |
| 10 | 3.3 | 6.2 | 53.9 |
| 11 | 3.3 | −5.7 | 61.6 |
| 12 | 2.3 | −17.1 | 66.6 |
| Building Type | Variable | Denormalization Coefficient | Standardization Coefficient | R2 |
|---|---|---|---|---|
| Hotel | (constant) | 6.669 | — | 0.151 |
| Wind speed | −1.264 | −0.244 | ||
| Temperature | 0.087 | 0.389 | ||
| Residential building | (constant) | 10.231 | — | 0.117 |
| Wind speed | −0.598 | −0.111 | ||
| Relative humidity | −0.073 | −0.196 | ||
| Office building | (constant) | 42.605 | — | 0.150 |
| Wind speed | −8.686 | −0.38 | ||
| Temperature | 0.382 | 0.386 | ||
| Relative humidity | −0.183 | −0.115 |
| Building Type | Variable | Denormalization Coefficient | Standardization Coefficient | R2 |
|---|---|---|---|---|
| Hotel | (constant) | −1.074 | — | 0.394 |
| Wind speed | 6.856 | 0.296 | ||
| Temperature | −1.003 | −0.843 | ||
| Retail building | (constant) | 57.233 | — | 0.127 |
| Wind speed | −10.281 | −0.357 | ||
| Hospital | (constant) | 23.458 | — | 0.196 |
| Temperature | −0.639 | −0.442 | ||
| Educational building | (constant) | 43.923 | — | 0.121 |
| Wind speed | −7.303 | −0.301 | ||
| Residential building | (constant) | 0.553 | — | 0.134 |
| Wind speed | −7.187 | −0.280 | ||
| Temperature | 0.627 | 0.475 | ||
| Relative humidity | 0.792 | 0.515 | ||
| Office building | (constant) | 44.302 | — | 0.558 |
| Wind speed | −2.342 | −0.099 | ||
| Temperature | −1.060 | −0.871 | ||
| Relative humidity | −0.315 | −0.222 |
| Building Type | Standardized Residual | MAE | MAPE | MSE | RMSE | |
|---|---|---|---|---|---|---|
| Identification Set | Validation Set | |||||
| Hotel | (−1.5, 1.9) | (−1.6, 1) | 24.7 | 16.1 | 937.3 | 30.6 |
| Retail building | (−2, 1.3) | (−0.9, 1.5) | 32.7 | 19.6 | 1810.8 | 42.6 |
| Hospital | / | / | / | / | / | / |
| Educational building | (−1.3, 2) | (−1.6, 1.6) | 25.0 | 15.9 | 1169.0 | 34.2 |
| Residential building | (−1.8, 1.8) | (−1.6, 1.2) | 20.7 | 12.7 | 692.8 | 26.3 |
| Office building | (−1.9, 2) | (−1.7, 1.5) | 22.2 | 14.0 | 793.7 | 28.0 |
| Building Type | Standardized Residual | MAE | MAPE | MSE | RMSE | |
|---|---|---|---|---|---|---|
| Identification Set | Validation Set | |||||
| Hotel | (−1.6, 1.9) | (−1.5, 1.7) | 7.4 | 15.9 | 80.7 | 9.0 |
| Retail building | (−1.8, 2) | (−1.8, 1) | 10.6 | 21.7 | 179.2 | 13.4 |
| Hospital | (−1.7, 2) | (−1.6, 1.4) | 10.2 | 22.1 | 158.1 | 12.6 |
| Educational building | (−1.9, 1.9) | (−1.9, 1) | 8.9 | 21.0 | 132.0 | 11.5 |
| Residential building | (−2,2) | (−1.9, 1.2) | 9.2 | 19.2 | 140.7 | 11.9 |
| Office building | (−2, 2) | (−1.7, 1.8) | 6.6 | 16.3 | 61.2 | 7.8 |
| F | Sig. | t | df | Sig. | |
|---|---|---|---|---|---|
| Equal variances assumed | 0.211 | 0.651 | −0.545 | 22 | 0.591 |
| Equal variances not assumed | / | / | −0.55 | 21.895 | 0.588 |
| Building Type | Building Density (%) | Building Height (m) | Floor Area Ratio | Aspect Ratio | Shape Factor |
|---|---|---|---|---|---|
| Hotel | — | +1.00 | — | — | — |
| Retail building | — | — | — | −0.10 | −0.10 |
| Hospital | −1.00 | — | — | — | — |
| Educational building | — | +1.00 | — | — | — |
| Residential building | — | — | −0.10 | — | −0.10 |
| Office building | — | +1.00 | — | — | — |
| Land Use Type | Average Annual EUI of Electricity (kWh/m2) | Average Annual EUI of Heating (kWh/m2) | Average Annual EUI (kWh/m2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Building Density (%) | Building Height (m) | Shape Factor | Building Height (m) | Shape Factor | Floor Area Ratio | Aspect Ratio | Building Density (%) | Building Height (m) | Shape Factor | Floor Area Ratio | Aspect Ratio | |
| Residential | — | — | 24.32 | — | 20.95 | 0.97 | — | — | — | 45.27 | 0.97 | — |
| Commercial | — | — | 36.45 | — | 24.21 | — | 5.56 | — | — | 60.66 | — | 5.56 |
| Office | — | 0.28 | — | 0.37 | — | — | — | — | 0.65 | — | — | — |
| Educational | — | 0.81 | — | 0.64 | — | — | — | — | 1.45 | — | — | — |
| Medical | 2.52 | — | — | — | — | — | — | 2.52 | — | — | — | — |
| Land Use Type | Average Annual EUI of Electricity (kWh/m2) | Average Annual EUI of Heating (kWh/m2) | Average Annual EUI (kWh/m2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Average Temperature (°C) | Average Wind Speed (m/s) | Average Relative Humidity (%) | Average Temperature (°C) | Average Wind Speed (m/s) | Average Relative Humidity (%) | Average Temperature (°C) | Average Wind Speed (m/s) | Average Relative Humidity (%) | |
| Residential | — | — | 24.32 | — | 20.95 | 0.97 | — | — | 45.27 |
| Commercial | — | — | 36.45 | — | 24.21 | — | — | — | 60.66 |
| Office | — | 0.28 | — | 0.37 | — | — | — | 0.65 | — |
| Educational | — | 0.81 | — | 0.64 | — | — | — | 1.45 | — |
| Medical | 2.52 | — | — | — | — | — | 2.52 | — | — |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Leng, H.; Guo, R. Multi-Agent-Based Model for the Urban Macro-Level Impact Factors of Building Energy Consumption on Different Types of Land. Land 2022, 11, 1986. https://doi.org/10.3390/land11111986
Song S, Leng H, Guo R. Multi-Agent-Based Model for the Urban Macro-Level Impact Factors of Building Energy Consumption on Different Types of Land. Land. 2022; 11(11):1986. https://doi.org/10.3390/land11111986
Chicago/Turabian StyleSong, Shiyi, Hong Leng, and Ran Guo. 2022. "Multi-Agent-Based Model for the Urban Macro-Level Impact Factors of Building Energy Consumption on Different Types of Land" Land 11, no. 11: 1986. https://doi.org/10.3390/land11111986
APA StyleSong, S., Leng, H., & Guo, R. (2022). Multi-Agent-Based Model for the Urban Macro-Level Impact Factors of Building Energy Consumption on Different Types of Land. Land, 11(11), 1986. https://doi.org/10.3390/land11111986






