Assessing the Impact of Urban Expansion on Surrounding Forested Landscape Connectivity across Space and Time
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Target Species
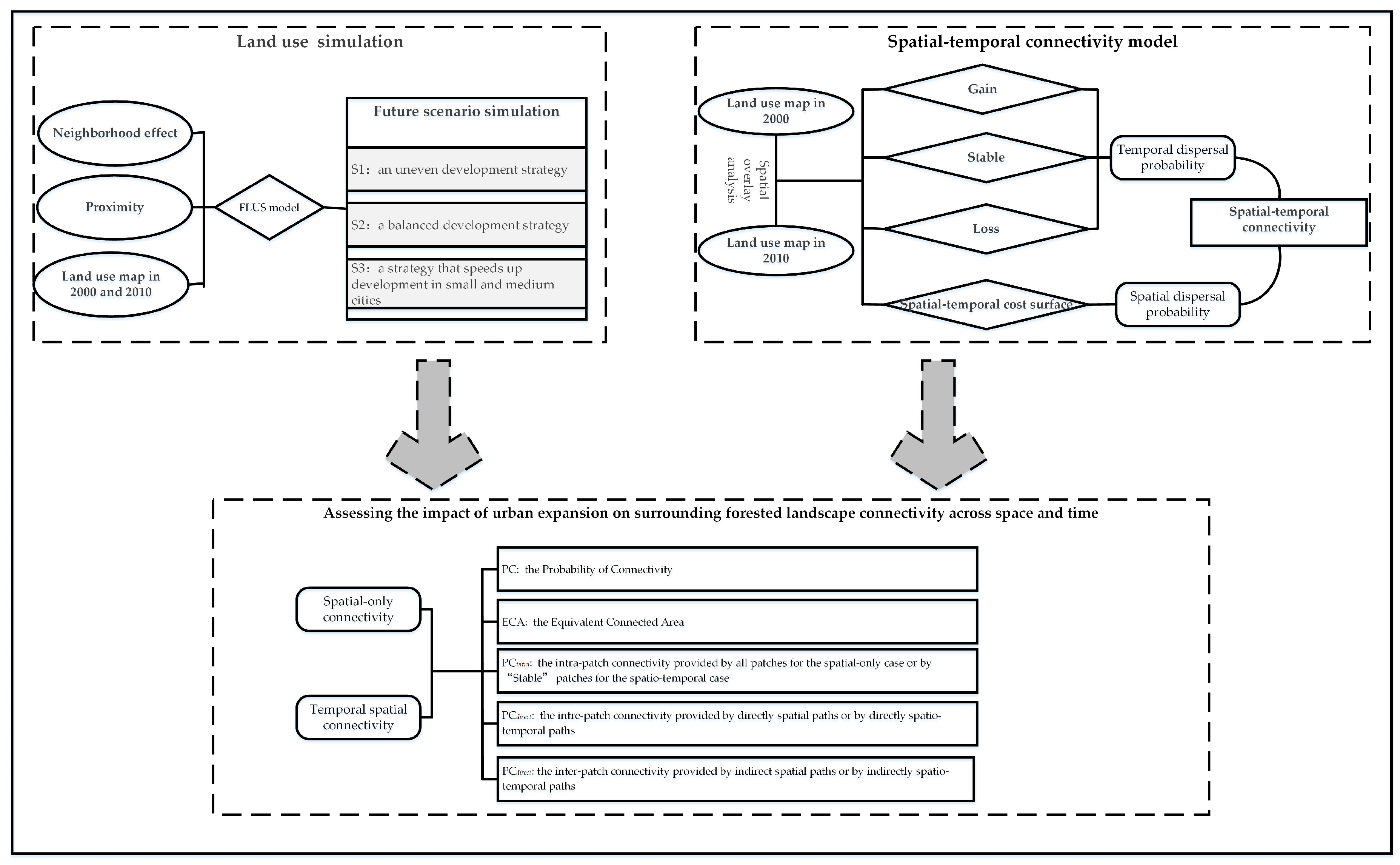
2.2. Research Framework
2.3. The Future Land Use Simulation Model
2.4. Simulating Different Regional Urban Development Strategies
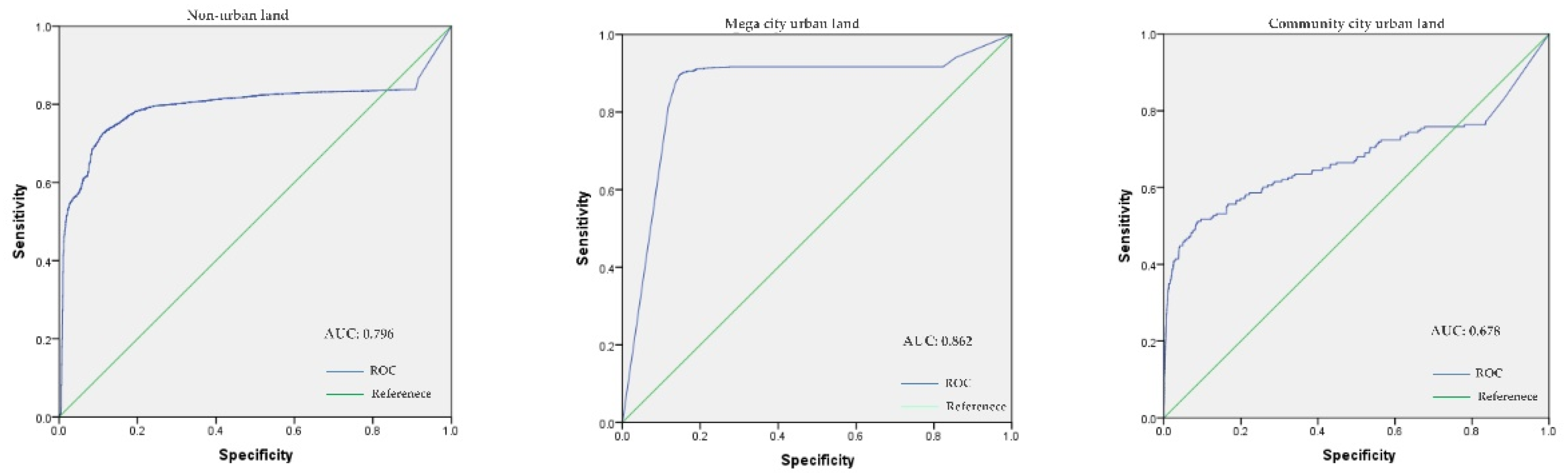
2.5. Model Validation
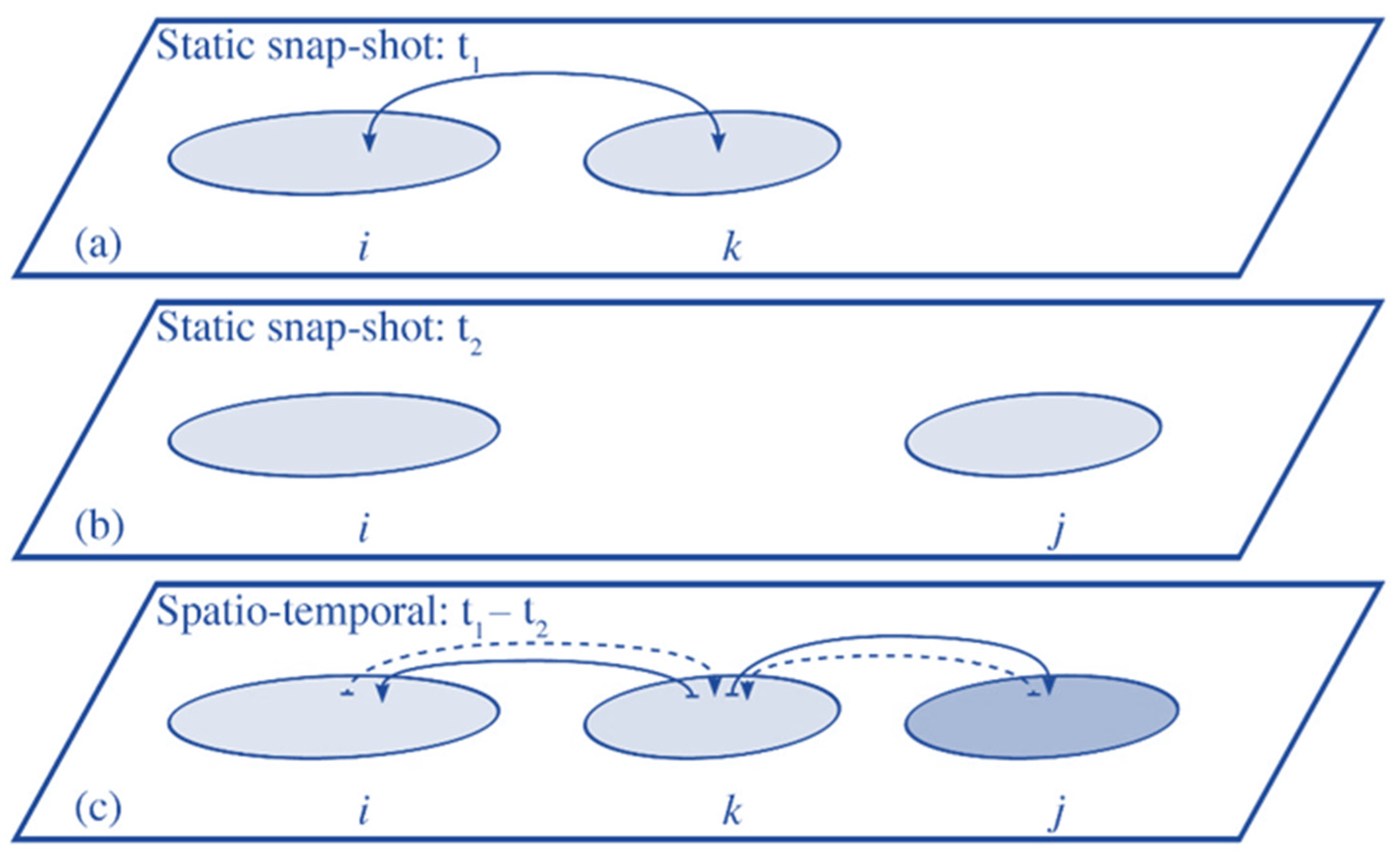
2.6. Spatial-Temporal Connectivity Model
2.7. Connectivity Metrics
3. Results
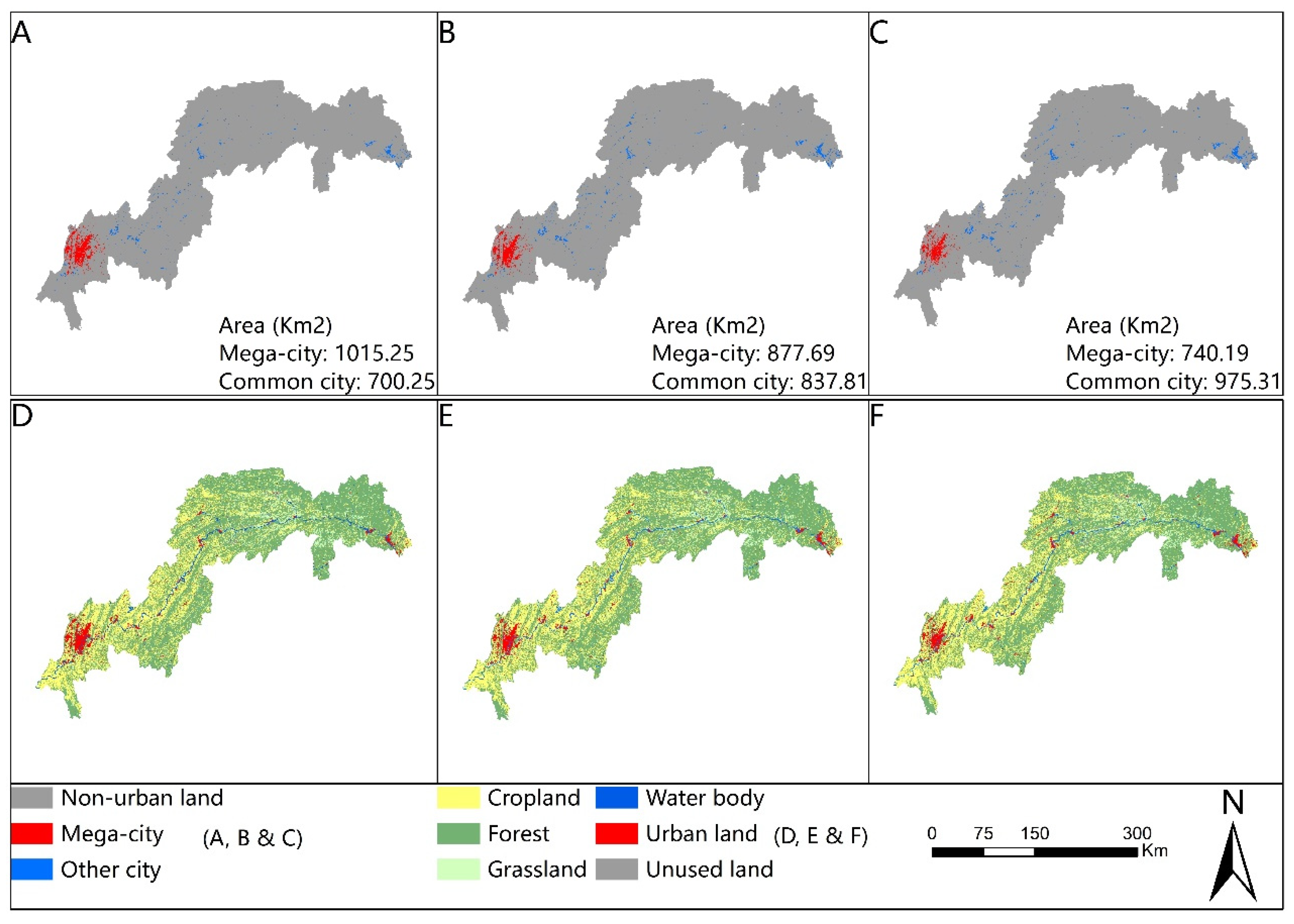
3.1. Urban Expansion and Habitat Change in Different Urban Development Scenarios
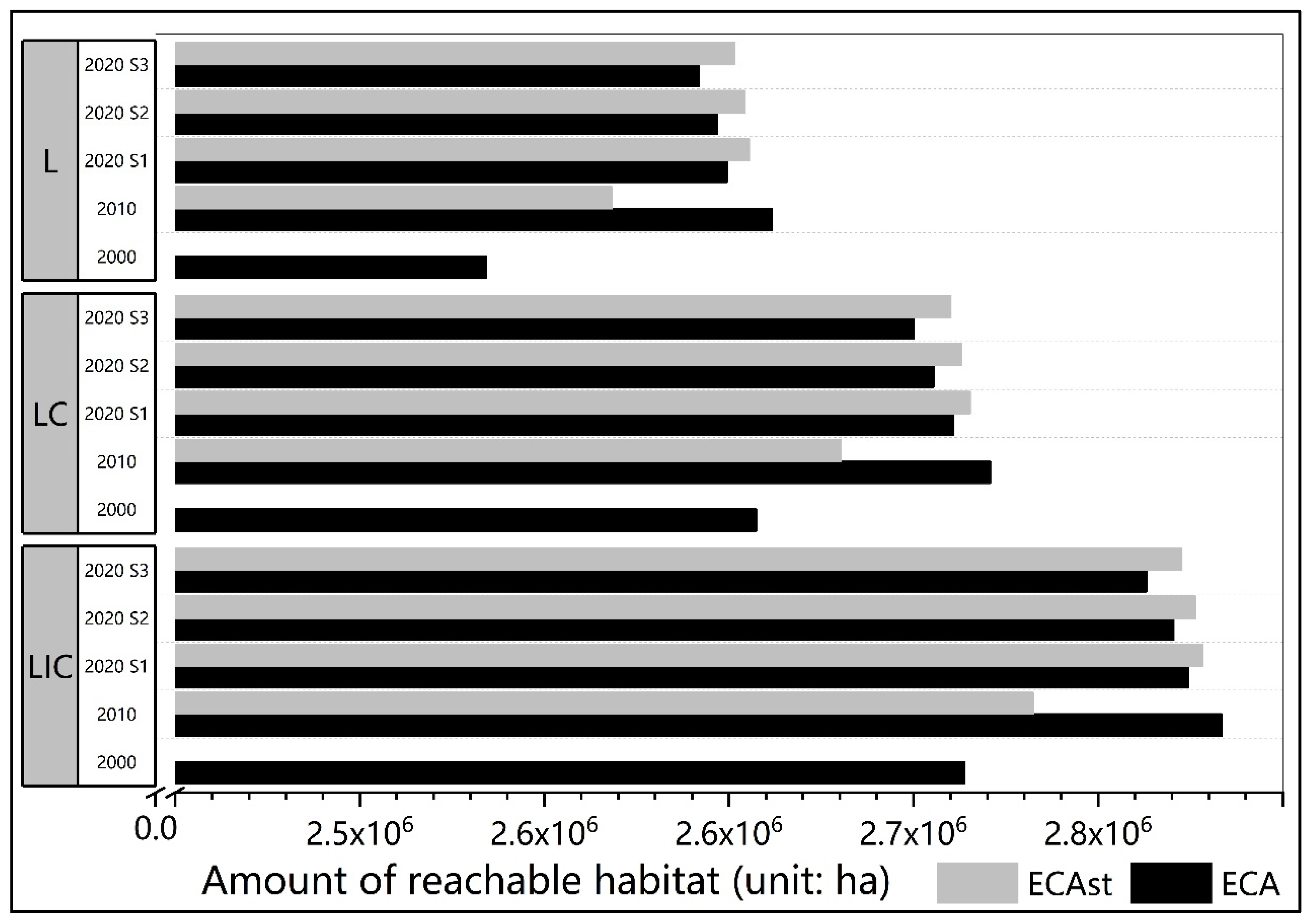
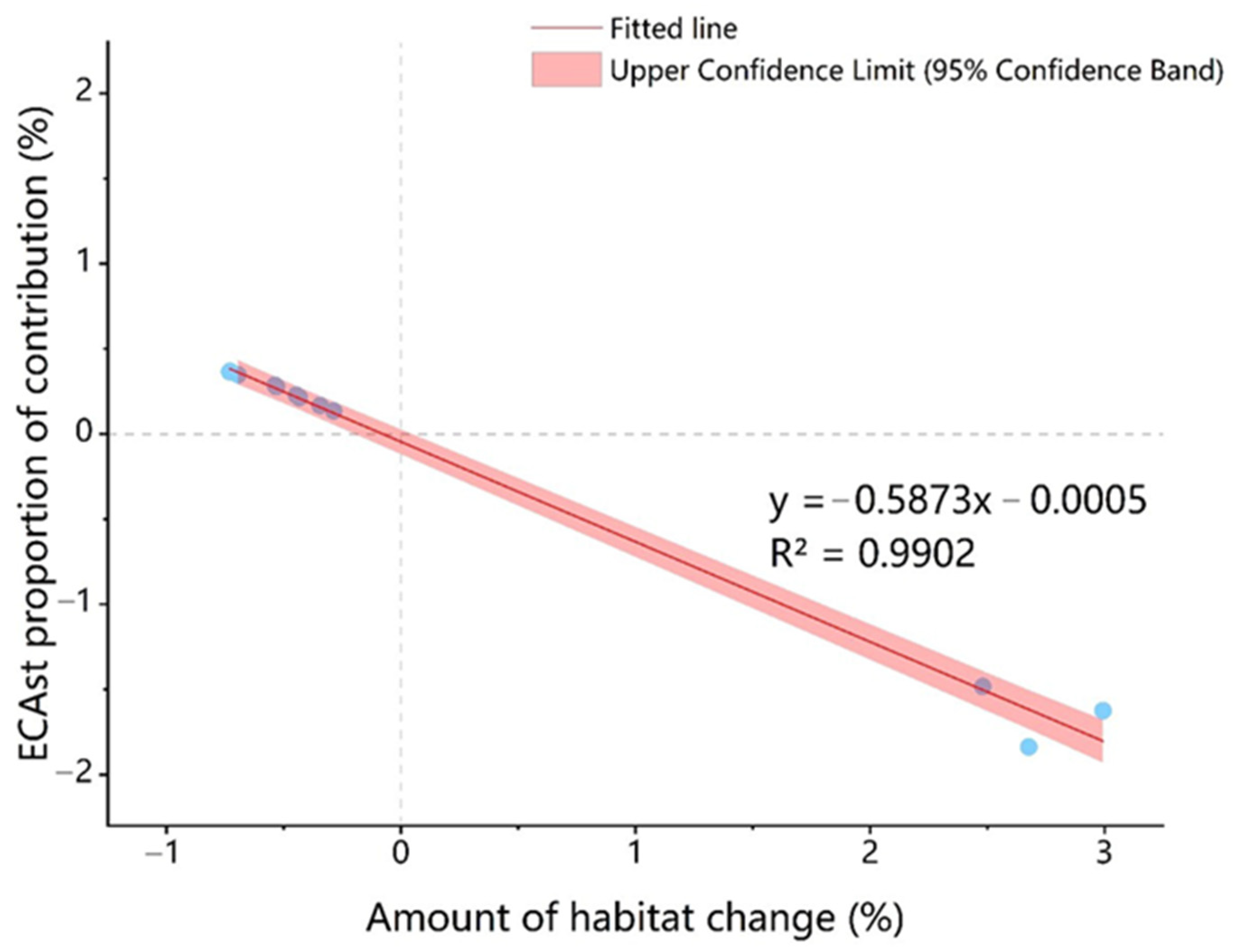
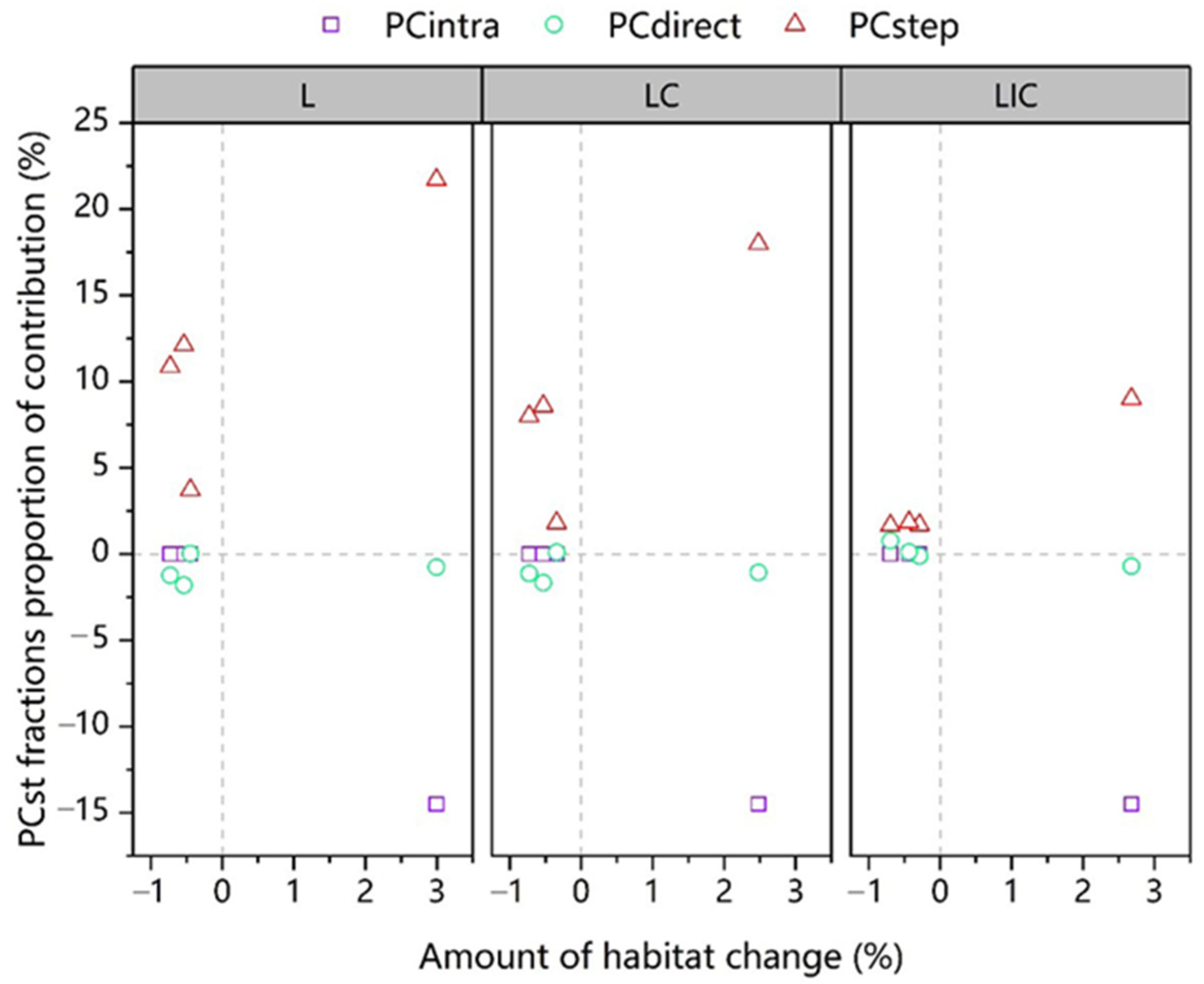
3.2. The Spatial-Only and Spatiotemporal Connectivity in Different Scenarios
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seto, K.C.; Guneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed]
- Sala, O.E.; Chapin, F.S., 3rd; Armesto, J.J.; Berlow, E.; Bloomfield, J.; Dirzo, R.; Huber-Sanwald, E.; Huenneke, L.F.; Jackson, R.B.; Kinzig, A.; et al. Global biodiversity scenarios for the year 2100. Science 2000, 287, 1770–1774. [Google Scholar] [CrossRef]
- McKinney, M.L. Urbanization as a major cause of biotic homogenization. Biol. Conserv. 2006, 127, 247–260. [Google Scholar] [CrossRef]
- Bauer, S.; Hoye, B.J. Migratory animals couple biodiversity and ecosystem functioning worldwide. Science 2014, 344, 1242552. [Google Scholar] [CrossRef]
- Allen, C.R.; Angeler, D.G.; Cumming, G.S.; Folke, C.; Twidwell, D.; Uden, D.R. Quantifying spatial resilience. J. Appl. Ecol. 2016, 53, 625–635. [Google Scholar] [CrossRef]
- Perkl, R.; Norman, L.M.; Mitchell, D.; Feller, M.; Smith, G.; Wilson, N.R. Urban growth and landscape connectivity threats assessment at Saguaro National Park, Arizona, USA. J. Land Use Sci. 2018. [Google Scholar] [CrossRef]
- Troupin, D.; Carmel, Y. Landscape patterns of development under two alternative scenarios: Implications for conservation. Land Use Policy 2016, 54, 221–234. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, J.-L.; Liao, T.-J.; Liang, X.; Tian, H. Simulating urban expansion and its impact on functional connectivity in the Three Gorges Reservoir Area. Sci. Total Environ. 2018, 643, 1553–1561. [Google Scholar] [CrossRef]
- Bierwagen, B.G. Connectivity in urbanizing landscapes: The importance of habitat configuration, urban area size, and dispersal. Urban. Ecosyst. 2006, 10, 29–42. [Google Scholar] [CrossRef]
- Mitsova, D.; Shuster, W.; Wang, X.H. A cellular automata model of land cover change to integrate urban growth with open space conservation. Landsc. Urban. Plann. 2011, 99, 141–153. [Google Scholar] [CrossRef]
- Grafius, D.R.; Corstanje, R.; Siriwardena, G.M.; Plummer, K.E.; Harris, J.A. A bird’s eye view: Using circuit theory to study urban landscape connectivity for birds. Landsc. Ecol. 2017, 32, 1771–1787. [Google Scholar] [CrossRef]
- Huang, J.L.; He, J.H.; Liu, D.F.; Li, C.; Qian, J. An ex-post evaluation approach to assess the impacts of accomplished urban structure shift on landscape connectivity. Sci. Total Environ. 2018, 622, 1143–1152. [Google Scholar] [CrossRef]
- Aguilera, F.; Valenzuela, L.M.; Botequilha-Leitao, A. Landscape metrics in the analysis of urban land use patterns: A case study in a Spanish metropolitan area. Landsc. Urban. Plann. 2011, 99, 226–238. [Google Scholar] [CrossRef]
- Marulli, J.; Mallarach, J.M. A GIS methodology for assessing ecological connectivity: Application to the Barcelona Metropolitan Area. Landsc. Urban. Plann. 2005, 71, 243–262. [Google Scholar] [CrossRef]
- Tannier, C.; Bourgeois, M.; Houot, H.; Foltete, J.C. Impact of urban developments on the functional connectivity of forested habitats: A joint contribution of advanced urban models and landscape graphs. Land Use Policy 2016, 52, 76–91. [Google Scholar] [CrossRef]
- Huang, J.L.; Andrello, M.; Martensen, A.C.; Saura, S.; Liu, D.F.; He, J.H.; Fortin, M.J. Importance of spatio–temporal connectivity to maintain species experiencing range shifts. Ecography 2020, 43, 591–603. [Google Scholar] [CrossRef]
- Martensen, A.C.; Saura, S.; Fortin, M.-J. Spatio-temporal connectivity: Assessing the amount of reachable habitat in dynamic landscapes. Methods Ecol. Evol. 2017, 8, 1253–1264. [Google Scholar] [CrossRef]
- Saura, S.; Bodin, Ö.; Fortin, M.-J. Stepping stones are crucial for species’ long-distance dispersal and range expansion through habitat networks. J. Appl Ecol. 2014, 51, 171–182. [Google Scholar] [CrossRef]
- Watts, A.; Schlichting, P.; Billerman, S.; Jesmer, B.; Micheletti, S.; Fortin, M.-J.; Funk, C.; Hapeman, P.; Muths, E.; Murphy, M. How spatio-temporal habitat connectivity affects amphibian genetic structure. Front. Genet. 2015, 6. [Google Scholar] [CrossRef]
- Hanski, I.; Ovaskainen, O. The metapopulation capacity of a fragmented landscape. Nature 2000, 404, 755–758. [Google Scholar] [CrossRef]
- Moilanen, A.; Nieminen, M. Simple Connectivity Measures in Spatial Ecology. Ecology 2002, 83, 1131–1145. [Google Scholar] [CrossRef]
- Pascual-Hortal, L.; Saura, S. Comparison and development of new graph-based landscape connectivity indices: Towards the priorization of habitat patches and corridors for conservation. Landsc. Ecol. 2006, 21, 959–967. [Google Scholar] [CrossRef]
- Saura, S.; Pascual-Hortal, L. A new habitat availability index to integrate connectivity in landscape conservation planning: Comparison with existing indices and application to a case study. Landsc. Urban. Plann. 2007, 83, 91–103. [Google Scholar] [CrossRef]
- Mui, A.B.; Caverhill, B.; Johnson, B.; Fortin, M.J.; He, Y.H. Using multiple metrics to estimate seasonal landscape connectivity for Blanding’s turtles (Emydoidea blandingii) in a fragmented landscape. Landsc. Ecol. 2017, 32, 531–546. [Google Scholar] [CrossRef]
- Wu, J.G.; Huang, J.H.; Han, X.G.; Xie, Z.Q.; Gao, X.M. Three-Gorges Dam—Experiment in habitat fragmentation? Science 2003, 300, 1239–1240. [Google Scholar] [CrossRef] [PubMed]
- The State Council of the People’s Republic of China. The Notification on Adjusting the Classification Standard of Urban Size; The State Council of the People’s Republic of China: Beijing, China, 2014.
- Xu, X.; Yang, G.; Tan, Y.; Liu, J.; Hu, H. Ecosystem services trade-offs and determinants in China’s Yangtze River Economic Belt from 2000 to 2015. Sci. Total Environ. 2018, 634, 1601–1614. [Google Scholar] [CrossRef] [PubMed]
- Hua, F.; Wang, X.; Zheng, X.; Fisher, B.; Wang, L.; Zhu, J.; Tang, Y.; Yu, D.W.; Wilcove, D.S. Opportunities for biodiversity gains under the world’s largest reforestation programme. Nat. Commun. 2016, 7, 12717. [Google Scholar] [CrossRef]
- Rabinowitz, A.R. Behavior and movements of sympatric civet species in HUAI-KHA-KHAENG Wildlife Sanctuary, Thailand. J. Zool. 1991, 223, 281–298. [Google Scholar] [CrossRef]
- Grassman, L.I.; Tewes, M.E.; Silvy, N.J.; Kreetiyutanont, K. Spatial organization and diet of the leopard cat (Prionailurus bengalensis) in north-central Thailand. J. Zool. 2005, 266, 45–54. [Google Scholar] [CrossRef]
- Odden, M.; Athreya, V.; Rattan, S.; Linnell, J.D.C. Adaptable Neighbours: Movement Patterns of GPS-Collared Leopards in Human Dominated Landscapes in India. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Bowman, J.; Jaeger, J.A.G.; Fahrig, L. Dispersal distance of mammals is proportional to home range size. Ecology 2002, 83, 2049–2055. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled Seamless SRTM Data V4. International Centre for Tropical Agriculture (CIAT). Available online: http://srtm.csi.cgiar.org (accessed on 19 December 2020).
- Center for International Earth Science Information Network—CIESIN—Columbia University; Information Technology Outreach Services—ITOS—University of Georgia. Global Roads Open Access Data Set, Version 1 (gROADSv1); NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2013. [Google Scholar]
- Liu, X.P.; Liang, X.; Li, X.; Xu, X.C.; Ou, J.P.; Chen, Y.M.; Li, S.Y.; Wang, S.J.; Pei, F.S. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban. Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Openshaw, S.; Openshaw, C. Artificial Intelligence in Geography; John Wiley & Sons: Chichester, UK, 1997. [Google Scholar]
- Lin, Y.P.; Chu, H.J.; Wu, C.F.; Verburg, P.H. Predictive ability of logistic regression, auto-logistic regression and neural network models in empirical land-use change modeling—A case study. Int. J. Geogr. Inf. Sci. 2011, 25, 65–87. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Liu, X.; Liang, X.; Wang, S.; Chen, Y.; Pei, F.; Xu, X. A New Global Land-Use and Land-Cover Change Product at a 1-km Resolution for 2010 to 2100 Based on Human–Environment Interactions. Ann. Am. Assoc. Geogr. 2017, 107, 1040–1059. [Google Scholar] [CrossRef]
- Liang, X.; Liu, X.P.; Li, D.; Zhao, H.; Chen, G.Z. Urban growth simulation by incorporating planning policies into a CA-based future land-use simulation model. Int. J. Geogr. Inf. Sci. 2018, 32, 2294–2316. [Google Scholar] [CrossRef]
- He, J.; Li, C.; Yu, Y.; Liu, Y.; Huang, J. Measuring urban spatial interaction in Wuhan Urban Agglomeration, Central China: A spatially explicit approach. Sustain. Cities Soc. 2017, 32, 569–583. [Google Scholar] [CrossRef]
- Hanley, J.A.; Mcneil, B.J. The Meaning and Use of the Area under a Receiver Operating Characteristic (Roc) Curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Vliet, J.V.; Bregt, A.K.; Hagen-Zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Visser, H.; de Nijs, T. The Map Comparison Kit. Environ. Model. Softw. 2006, 21, 346–358. [Google Scholar] [CrossRef]
- Bishop-Taylor, R.; Tulbure, M.G.; Broich, M. Surface-water dynamics and land use influence landscape connectivity across a major dryland region. Ecol. Appl. 2017, 27, 1124–1137. [Google Scholar] [CrossRef]
- Ruiz, L.; Parikh, N.; Heintzman, L.J.; Collins, S.D.; Starr, S.M.; Wright, C.K.; Henebry, G.M.; van Gestel, N.; McIntyre, N.E. Dynamic connectivity of temporary wetlands in the southern Great Plains. Landsc. Ecol. 2014, 29, 507–516. [Google Scholar] [CrossRef]
- Gurrutxaga, M.; Rubio, L.; Saura, S. Key connectors in protected forest area networks and the impact of highways: A transnational case study from the Cantabrian Range to the Western Alps (SW Europe). Landsc. Urban. Plann. 2011, 101, 310–320. [Google Scholar] [CrossRef]
- McRae, B.H.; Kavanagh, D.M. Linkage Mapper Connectivity Analysis Software; The Nature Conservancy: Seattle, WA, USA, 2011. [Google Scholar]
- Dale, M.R.T.; Fortin, M.J. From Graphs to Spatial Graphs. Annu. Rev. Ecol. Evol. Syst. 2010, 41, 21–38. [Google Scholar] [CrossRef]
- Saura, S.; Estreguil, C.; Mouton, C.; Rodríguez-Freire, M. Network analysis to assess landscape connectivity trends: Application to European forests (1990–2000). Ecol. Indic. 2011, 11, 407–416. [Google Scholar] [CrossRef]
- Saura, S.; Rubio, L. A common currency for the different ways in which patches and links can contribute to habitat availability and connectivity in the landscape. Ecography 2010, 33, 523–537. [Google Scholar] [CrossRef]
- Saura, S. Node self-connections in network metrics. Ecol. Lett. 2018, 21, 319–320. [Google Scholar] [CrossRef]
- Fu, W.; Liu, S.; Degloria, S.D.; Dong, S.; Beazley, R. Characterizing the “fragmentation–barrier” effect of road networks on landscape connectivity: A case study in Xishuangbanna, Southwest China. Landsc. Urban. Plann. 2010, 95, 122–129. [Google Scholar] [CrossRef]
- Liu, S.; Dong, Y.; Deng, L.; Liu, Q.; Zhao, H.; Dong, S. Forest fragmentation and landscape connectivity change associated with road network extension and city expansion: A case study in the Lancang River Valley. Ecol. Indic. 2014, 36, 160–168. [Google Scholar] [CrossRef]
- Essl, F.; Dullinger, S.; Rabitsch, W.; Hulme, P.E.; Pysek, P.; Wilson, J.R.; Richardson, D.M. Delayed biodiversity change: No time to waste. Trends Ecol. Evol 2015, 30, 375–378. [Google Scholar] [CrossRef]
- Kuussaari, M.; Bommarco, R.; Heikkinen, R.K.; Helm, A.; Krauss, J.; Lindborg, R.; Ockinger, E.; Partel, M.; Pino, J.; Roda, F.; et al. Extinction debt: A challenge for biodiversity conservation. Trends Ecol. Evol. 2009, 24, 564–571. [Google Scholar] [CrossRef]
- Jackson, S.T.; Sax, D.F. Balancing biodiversity in a changing environment: Extinction debt, immigration credit and species turnover. Trends Ecol. Evol 2010, 25, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.H.; Kodricbrown, A. Turnover Rates in Insular Biogeography—Effect of Immigration on Extinction. Ecology 1977, 58, 445–449. [Google Scholar] [CrossRef]
- Wimberly, M.C. Species dynamics in disturbed landscapes: When does a shifting habitat mosaic enhance connectivity? Landsc. Ecol. 2006, 21, 35–46. [Google Scholar] [CrossRef]
| Name | Data Type & Resolution | Source |
|---|---|---|
| The information of target species | Html & pdf | International Union for Conservation of Nature (IUCN) Red List |
| Land use data (2000 & 2010) | Raster, 30 m | CAS (http://www.resdc.cn/, accessed on 19 December 2020) |
| Population (2010) | Raster 1 km | |
| GDP (2010) | ||
| DEM | Raster, 90 m | SRTM 90 m Digital Elevation Data [33] |
| Traffic network | Shapefile | [34] |
| Ecological redline | Shapefile | Chongqing Environment Protection Bureau |
| Population statistical data | Pdf & Xls | The statistical yearbook of Chongqing and of Hubei |
| Source Node: Individual Location at for the Essential Links or at for the Auxiliary Links | Target Node: Individual Location after | |||||
|---|---|---|---|---|---|---|
| Essential Link (Individual Location at ) | Auxiliary Link (Individual Location in < < ) | |||||
| Stable | Loss | Gain | Stable | Loss | Gain | |
| Stable | 1 | 0 | 1 | N/A | 1 | N/A |
| Loss | 1 | 0 | 0.5 | N/A | 1 | N/A |
| Gain | 0 | 0 | 0 | 1 | 0.5 | 1 |
| Year | LIC | LC | L | |||
|---|---|---|---|---|---|---|
| Area | Change Rate | Area | Change Rate | Area | Change Rate | |
| 2000 | 27504 | N/A | 26,843 | N/A | 26,043 | N/A |
| 2010 | 28241 | 2.68% | 27,509 | 2.48% | 26,823 | 2.99% |
| 2020 S1 | 28160 | −0.29% | 27,414 | −0.34% | 26,703 | −0.45% |
| 2020 S2 | 28118 | −0.43% | 27,363 | −0.53% | 26,679 | −0.54% |
| 2020 S3 | 28045 | −0.69% | 27,309 | −0.73% | 26,627 | −0.73% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; He, J.; Yue, Q. Assessing the Impact of Urban Expansion on Surrounding Forested Landscape Connectivity across Space and Time. Land 2021, 10, 359. https://doi.org/10.3390/land10040359
Ren Z, He J, Yue Q. Assessing the Impact of Urban Expansion on Surrounding Forested Landscape Connectivity across Space and Time. Land. 2021; 10(4):359. https://doi.org/10.3390/land10040359
Chicago/Turabian StyleRen, Zhouqiao, Jianhua He, and Qiaobing Yue. 2021. "Assessing the Impact of Urban Expansion on Surrounding Forested Landscape Connectivity across Space and Time" Land 10, no. 4: 359. https://doi.org/10.3390/land10040359
APA StyleRen, Z., He, J., & Yue, Q. (2021). Assessing the Impact of Urban Expansion on Surrounding Forested Landscape Connectivity across Space and Time. Land, 10(4), 359. https://doi.org/10.3390/land10040359







