The Resilient Recurrent Behavior of Mediterranean Semi-Arid Complex Adaptive Landscapes
Abstract
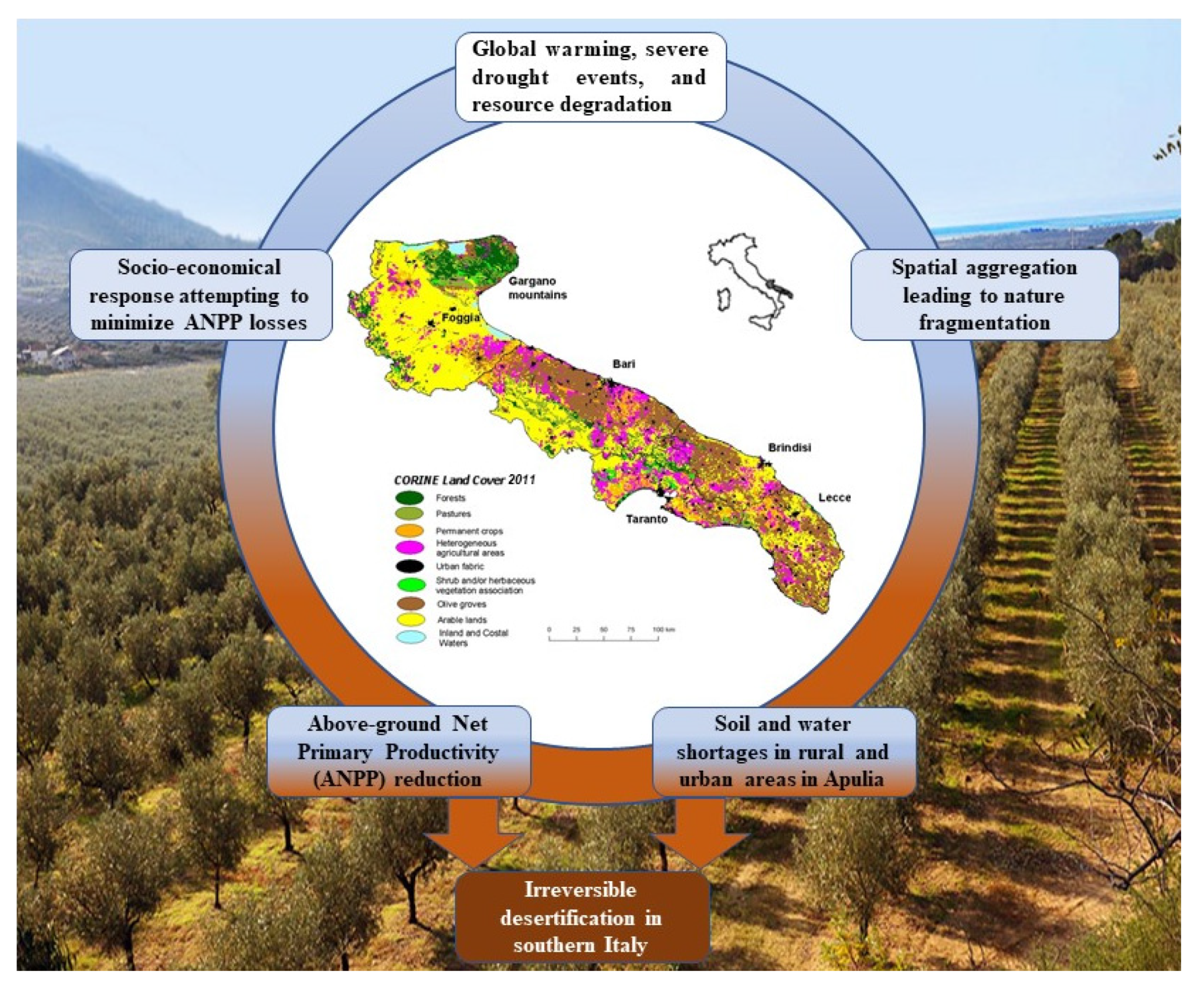
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Materials: Real World Time Series of Vegetation Indices
2.3. Methods
3. Results
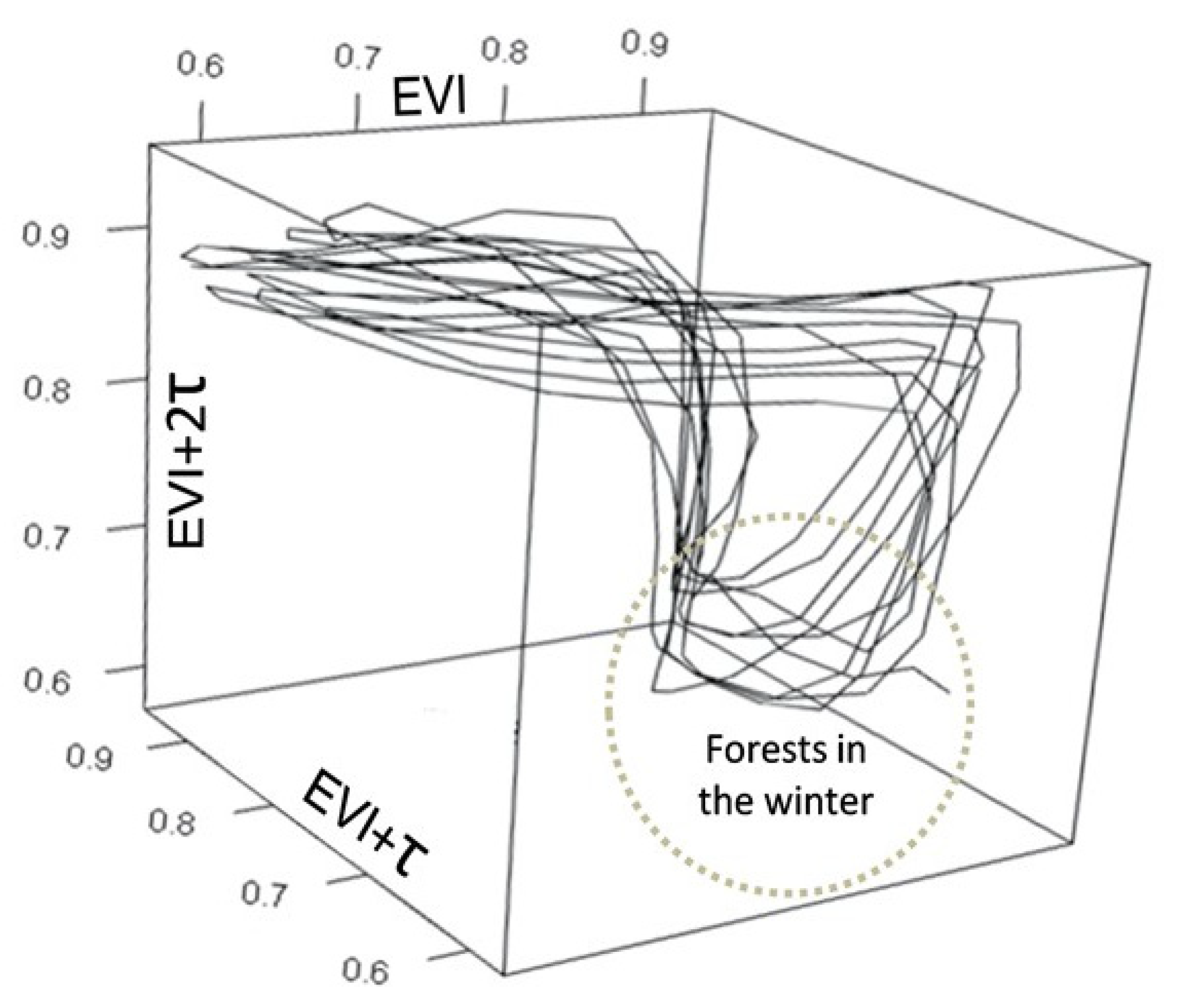
3.1. EVI Time Series and Cross-Correlations with Climate Data
3.2. RP and RQA Analysis
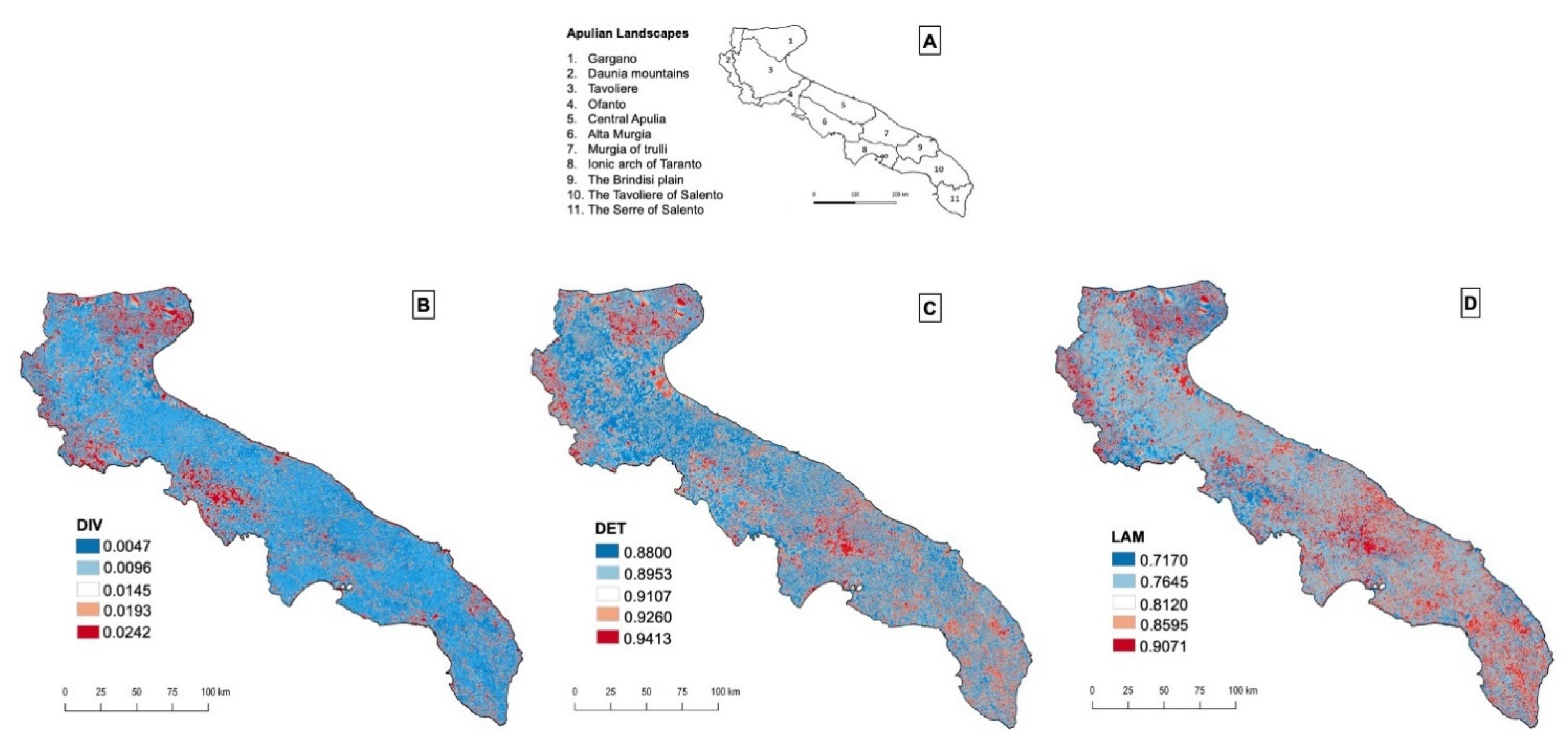
3.3. Maps of Recurrence Variables and Hot Spots Undergoing Degradation and Desertification (LDD)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levin, S.A. Ecosystems and the biosphere as complex adaptive systems. Ecosystems 1998, 1, 431–436. [Google Scholar] [CrossRef]
- Berkes, F.; Colding, J.; Folke, E. Navigating Social–Ecological Systems: Building Resilience for Complexity and Change; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Zaccarelli, N.; Petrosillo, I.; Zurlini, G.; Riitters, K.H. Source/sink patterns of disturbance and cross-scale mismatches in a panarchy of social-ecological landscapes. Ecol. Soc. 2008, 13, 26. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R. Catastrophic regime shifts in ecosystems: Linking theory to observation. Trends Ecol. Evol. 2003, 18, 648–656. [Google Scholar] [CrossRef]
- Reynolds, J.F.; Smith, D.M.S.; Lambin, E.F.; Turner, B.L., II; Mortimore, M.; Batterbury, S.P.J.; Downing, T.E.; Dowlatabadi, H.; Fernández, R.J.; Herrick, J.E.; et al. Global Desertification: Building a Science for Dryland Development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Reid, W.V.; Mooney, H.A.; Cropper, A.; Capistrano, D.; Carpenter, S.R.; Chopra, K.; Dasgupta, P.; Dietz, T.; Duraiappah, A.K.; Hassan, R.; et al. Ecosystems and Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Termorshuizen, J.W.; Opdam, P. Landscape services as a bridge between landscape ecology and sustainable development. Landsc. Ecol. 2009, 24, 1037–1052. [Google Scholar] [CrossRef]
- Costanza, R.; Fisher, B.; Mulder, K.; Liu, S.; Christopher, T. Biodiversity and ecosystem services: A multi-scale empirical study of the relationship between species richness and net primary production. Ecol. Econ. 2007, 61, 478–491. [Google Scholar] [CrossRef]
- Odum, H. Environment, Power, and Society; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Gaston, K.J. Global patterns in biodiversity. Nature 2000, 405, 220–227. [Google Scholar] [CrossRef]
- Vogt, J.V.; Safriel, U.; von Maltitz, G.; Sokona, Y.; Zougmore, R.; Bastin, G.; Hill, J. Monitoring and assessment of land degradation and desertification: Towards new conceptual and integrated approaches. Land Degrad. Dev. 2011, 22, 150–165. [Google Scholar] [CrossRef]
- Dubovyk, O. The role of Remote Sensing in land degradation assessments: Opportunities and challenges. Eur. J. Remote Sens. 2017, 50, 601–613. [Google Scholar] [CrossRef]
- Zhang, G.; Biradar, C.M.; Xiao, X.; Dong, J.; Zhou, Y.; Qin, Y.; Zhang, Y.; Liu, F.; Ding, M.; Thomas, R.J. Exacerbated grassland degradation and desertification in Central Asia during 2000–2014. Ecol. Appl. 2018, 28, 442–456. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Peterson, G.D. Estimating Resilience Across Landscapes. Conserv. Ecol. 2002, 6, 17. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Petrosillo, I.; Semeraro, T.; Zaccarelli, N.; Aretano, R.; Zurlini, G. The possible combined effects of land-use changes and climate conditions on the spatial-temporal patterns of primary production in a natural protected area. Ecol. Indic. 2013, 29, 25. [Google Scholar] [CrossRef]
- Zurlini, G.; Li, B.-L.; Zaccarelli, N.; Petrosillo, I. Spectral entropy, ecological resilience, and adaptive capacity for understanding, evaluating, and managing ecosystem stability and change. Glob. Chang. Biol. 2015, 21, 1377–1378. [Google Scholar] [CrossRef] [PubMed]
- Ladisa, G.; Todorovic, M.; Liuzzi, G.T. A GIS-based approach for desertification risk assessment in Apulia region, SE Italy. Phys. Chem. Earth Parts A B C 2012, 49, 103–113. [Google Scholar] [CrossRef]
- Nieto-Romero, M.; Oteros-Rozas, E.; González, J.A.; Martín-López, B. Exploring the knowledge landscape of ecosystem services assessments in Mediterranean agroecosystems: Insights for future research. Environ. Sci. Policy 2014, 37, 121–133. [Google Scholar] [CrossRef]
- Zurlini, G.; Marwan, N.; Semeraro, T.; Jones, K.B.; Aretano, R.; Pasimeni, M.R.; Valente, D.; Mulder, C.; Petrosillo, I. Investigating landscape phase transitions in Mediterranean rangelands by recurrence analysis. Landsc. Ecol. 2018, 33, 1617–1631. [Google Scholar] [CrossRef]
- Tarrasón, D.; Ravera, F.; Reed, M.S.; Dougill, A.J.; Gonzalez, L. Land degradation assessment through an ecosystem services lens: Integrating knowledge and methods in pastoral semi-arid systems. J. Arid Environ. 2016, 124, 205–213. [Google Scholar] [CrossRef]
- Smith, W.K.; Dannenberg, M.P.; Yan, D.; Herrmann, S.; Barnes, M.L.; Barron-Gafford, G.A.; Biederman, J.A.; Ferrenberg, S.; Fox, A.M.; Hudson, A.; et al. Remote sensing of dryland ecosystem structure and function: Progress, challenges, and opportunities. Remote Sens. Environ. 2019, 233, 111401. [Google Scholar] [CrossRef]
- Pueyo, Y.; Alados, C.L. Effects of fragmentation, abiotic factors and land use on vegetation recovery in a semi-arid Mediterranean area. Basic Appl. Ecol. 2007, 8, 158–170. [Google Scholar] [CrossRef]
- Kapur, B.; Pasquale, S.; Tekin, S.; Todorovic, M.; Sezen, S.M.; Özfidaner, M.; Gümü, Z. Prediction of climatic change for the next 100 years in Southern Italy. Sci. Res. Essays 2010, 5, 1470. [Google Scholar]
- Caroli, I.; Caldara, M. Vegetation history of Lago Battaglia (eastern Gargano coast, Apulia, Italy) during the middle-late Holocene. Veg. Hist. Archaeobotany 2007, 16, 317–327. [Google Scholar] [CrossRef]
- Di Rita, F.; Simone, O.; Caldara, M.; Gehrels, W.R.; Magri, D. Holocene environmental changes in the coastal Tavoliere Plain (Apulia, southern Italy): A multiproxy approach. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2011, 310, 139–151. [Google Scholar] [CrossRef]
- Perini, L.; Ceccarelli, T.; Zitti, M.; Salvati, L. Insight desertification process: Bio-physical and socio-economic drivers in Italy. Ital. J. Agrometeorol. 2009, 3, 45–55. [Google Scholar]
- Benassi, F.; Cividino, S.; Cudlin, P.; Alhuseen, A.; Lamonica, G.R.; Salvati, L. Population trends and desertification risk in a Mediterranean region, 1861–2017. Land Use Policy 2020, 95, 104626. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Salvati, L.; Mavrakis, A.; Colantoni, A.; Mancino, G.; Ferrara, A. Complex Adaptive Systems, soil degradation and land sensitivity to desertification: A multivariate assessment of Italian agro-forest landscape. Sci. Total Environ. 2015, 521–522, 235–245. [Google Scholar] [CrossRef]
- Metzger, M.J.; Rounsevell, M.D.A.; Acosta-Michlik, L.; Leemans, R.; Schröter, D. The vulnerability of ecosystem services to land use change. Agric. Ecosyst. Environ. 2006, 114, 69–85. [Google Scholar] [CrossRef]
- Petrosillo, I.; Zaccarelli, N.; Zurlini, G. Multi-scale vulnerability of natural capital in a panarchy of social-ecological landscapes. Ecol. Complex. 2010, 7, 359–367. [Google Scholar] [CrossRef]
- Salvati, L.; Bajocco, S.; Ceccarelli, T.; Zitti, M.; Perini, L. Towards a process-based evaluation of land vulnerability to soil degradation in Italy. Ecol. Indic. 2011, 11, 1216–1227. [Google Scholar] [CrossRef]
- Briassoulis, H. Mediterranean Desertification—Framing The Policy Context. EU DG for Research: Sustainable Development, Global Change and Ecosystem; Publications Office of the EU: Luxembourg, 2003. [Google Scholar]
- Acosta-Michlik, L.A.; Kumar, K.S.K.; Klein, R.J.T.; Campe, S. Application of fuzzy models to assess susceptibility to droughts from a socio-economic perspective. Reg. Environ. Chang. 2008, 8, 151–160. [Google Scholar] [CrossRef]
- Potter, C.; Tan, P.N.; Steinbach, M.; Klooster, S.; Kumar, V.; Myneni, R.; Genovese, V. Major disturbance events in terrestrial ecosystems detected using global satellite data sets. Glob. Chang. Biol. 2003, 9, 1005–1021. [Google Scholar] [CrossRef]
- Fu, X.; Tang, C.; Zhang, X.; Fu, J.; Jiang, D. An improved indicator of simulated grassland production based on MODIS NDVI and GPP data: A case study in the Sichuan province, China. Ecol. Indic. 2014, 40, 102–108. [Google Scholar] [CrossRef]
- Yan, D.; Scott, R.L.; Moore, D.J.P.; Biederman, J.A.; Smith, W.K. Understanding the relationship between vegetation greenness and productivity across dryland ecosystems through the integration of PhenoCam, satellite, and eddy covariance data. Remote Sens. Environ. 2019, 223, 50–62. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Potter, C.; Klooster, S.; Genovese, V. Net primary production of terrestrial ecosystems from 2000 to 2009. Clim. Chang. 2012, 115, 365–378. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Xiao, X.; Braswell, B.; Zhang, Q.; Boles, S.; Frolking, S.; Moore, B. Sensitivity of vegetation indices to atmospheric aerosols: Continental-scale observations in Northern Asia. Remote Sens. Environ. 2003, 84, 385–392. [Google Scholar] [CrossRef]
- Wallace, C.; Thomas, K. An Annual Plant Growth Proxy in the Mojave Desert Using MODIS-EVI Data. Sensors 2008, 8, 7792–7808. [Google Scholar] [CrossRef]
- Zaccarelli, N.; Li, B.-L.; Petrosillo, I.; Zurlini, G. Order and disorder in ecological time-series: Introducing normalized spectral entropy. Ecol. Indic. 2013, 28, 22–30. [Google Scholar] [CrossRef]
- Li, B.-L. Why is the holistic approach becoming so important in landscape ecology? Landsc. Urban Plan. 2000, 50, 27–41. [Google Scholar] [CrossRef]
- Strang, G. Wavelets. Am. Sci. 1994, 83, 250–255. [Google Scholar]
- Marwan, N. A historical review of recurrence plots. Eur. Phys. J. Spec. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef]
- Soudani, K.; Maire, G.; Dufrêne, E.; François, C.; Delpierre, N.; Ulrich, E.; Cecchini, S. Evaluation of the onset of green-up in temperate deciduous broadleaf forests derived from Moderate Resolution Imaging Spectroradiometer (MODIS) data. Remote Sens. Environ. 2008, 112, 2643–2655. [Google Scholar] [CrossRef]
- Vretenar, D.; Paar, N.; Ring, P.; Lalazissis, G.A. Nonlinear dynamics of giant resonances in atomic nuclei. Phys. Rev. E 1999, 60, 308–319. [Google Scholar] [CrossRef]
- Rustici, M.; Caravati, C.; Petretto, E.; Branca, M.; Marchettini, N. Transition Scenarios during the Evolution of the Belousov−Zhabotinsky Reaction in an Unstirred Batch Reactor. J. Phys. Chem. A 1999, 103, 6564–6570. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef]
- Belaire-Franch, J.; Contreras, D.; Tordera-Lledó, L. Assessing nonlinear structures in real exchange rates using recurrence plot strategies. Phys. D Nonlinear Phenom. 2002, 171, 249–264. [Google Scholar] [CrossRef]
- Marwan, N.; Kurths, J.; Foerster, S. Analysing spatially extended high-dimensional dynamics by recurrence plots. Phys. Lett. A 2015, 379, 894–900. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Wang, Y.; Wang, Y. Identifying spatial patterns of synchronization between NDVI and climatic determinants using joint recurrence plots. Environ. Earth Sci. 2011, 64, 851–859. [Google Scholar] [CrossRef]
- Gallopín, G.C. Linkages between vulnerability, resilience, and adaptive capacity. Glob. Environ. Chang. 2006, 16, 293–303. [Google Scholar] [CrossRef]
- Tonkin, J.D.; Bogan, M.T.; Bonada, N.; Rios-Touma, B.; Lytle, D.A. Seasonality and predictability shape temporal species diversity. Ecology 2017, 98, 1201–1216. [Google Scholar] [CrossRef]
- Colwell, R.K. Predictability, Constancy, and Contingency of Periodic Phenomena. Ecology 1974, 55, 1148–1153. [Google Scholar] [CrossRef]
- Walker, B.; Holling, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, Adaptability and Transformability in Social—Ecological Systems. Ecol. Soc. 2004, 9, 5. [Google Scholar] [CrossRef]
- Carpenter, S.; Walker, B.; Anderies, J.M.; Abel, N. From Metaphor to Measurement: Resilience of What to What? Ecosystems 2001, 4, 765–781. [Google Scholar] [CrossRef]
- Wuertz, D.; Setz, T.; Chalabi, Y. R Package ‘fNonlinear’. Available online: http://cran.r-project.org/web/packages/fNonlinear/index.html (accessed on 25 June 2020).
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficienciesA review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Heymann, Y.; Steenmans, C.; Croissille, G.; Bossard, M. Corine Land Cover. Technical Guide; Commission of the European Communities: Luxembourg, 1994. [Google Scholar]
- Santarsiero, V.; Nolè, G.; Lanorte, A.; Tucci, B.; Saganeiti, L.; Pilogallo, A.; Scorza, F.; Murgante, B. Assessment of Post Fire Soil Erosion with ESA Sentinel-2 Data and RUSLE Method in Apulia Region. (Southern Italy); Springer: Cham, Germany, 2020; pp. 590–603. [Google Scholar]
- Salvati, L.; Zitti, M.; Perini, L. Fifty Years on: Long-term Patterns of Land Sensitivity to Desertification in Italy. Land Degrad. Dev. 2016, 27, 97–107. [Google Scholar] [CrossRef]
- Fracchiolla, M.; Terzi, M.; D’Amico, F.S.; Tedone, L.; Cazzato, E. Conservation and pastoral value of former arable lands in the agro-pastoral system of the Alta Murgia National Park (Southern Italy). Ital. J. Agron. 2017, 11. [Google Scholar] [CrossRef]
- Tarantino, C.; Adamo, M.; Blonda, P. Long-Term Change Monitoring of Natural Grasslands Ecosystem in Support Of SDG 15.3.1. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Australia , 3–8 May 2020. [Google Scholar]
- Zurlini, G.; Petrosillo, I.; Jones, K.B.; Zaccarelli, N. Highlighting order and disorder in social-ecological landscapes to foster adaptive capacity and sustainability. Landsc. Ecol. 2013, 28, 1161–1173. [Google Scholar] [CrossRef]
- Pellicani, R.; Spilotro, G. Evaluating the quality of landslide inventory maps: Comparison between archive and surveyed inventories for the Daunia region (Apulia, Southern Italy). Bull. Eng. Geol. Environ. 2015, 74, 357–367. [Google Scholar] [CrossRef]
- Pisano, L.; Dragone, V.; Vennari, C.; Vessia, G.; Parise, M. The Influence of Slope Instability Processes in Demographic Dynamics of Landslide-Prone Rural Areas. In Landslides and Engineered Slopes. Experience, Theory and Practice; Cascini, L., Aversa, S., Picarelli, L., Scavia, C., Eds.; Associazione Geotecnica Italiana: Rome, Italy, 2016. [Google Scholar]
- Ferrara, A.; Kosmas, C.; Salvati, L.; Padula, A.; Mancino, G.; Nolè, A. Updating the MEDALUS-ESA Framework for Worldwide Land Degradation and Desertification Assessment. Land Degrad. Dev. 2020, 31, 1593–1607. [Google Scholar] [CrossRef]
- Higginbottom, T.; Symeonakis, E. Assessing Land Degradation and Desertification Using Vegetation Index Data: Current Frameworks and Future Directions. Remote Sens. 2014, 6, 9552–9575. [Google Scholar] [CrossRef]
- Yiran, G.A.B.; Kusimi, J.M.; Kufogbe, S.K. A synthesis of remote sensing and local knowledge approaches in land degradation assessment in the Bawku East District, Ghana. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 204–213. [Google Scholar] [CrossRef]
- Ghazaryan, G.; Dubovyk, O.; Kussul, N.; Menz, G. Towards an Improved Environmental Understanding of Land Surface Dynamics in Ukraine Based on Multi-Source Remote Sensing Time-Series Datasets from 1982 to 2013. Remote Sens. 2016, 8, 617. [Google Scholar] [CrossRef]
- Santos, F.; Dubovyk, O.; Menz, G. Monitoring Forest Dynamics in the Andean Amazon: The Applicability of Breakpoint Detection Methods Using Landsat Time-Series and Genetic Algorithms. Remote Sens. 2017, 9, 68. [Google Scholar] [CrossRef]
- Aprile, A.; Havlickova, L.; Panna, R.; Marè, C.; Borrelli, G.M.; Marone, D.; Perrotta, C.; Rampino, P.; de Bellis, L.; Curn, V.; et al. Different stress responsive strategies to drought and heat in two durum wheat cultivars with contrasting water use efficiency. BMC Genom. 2013, 14, 821. [Google Scholar] [CrossRef] [PubMed]
- Garbulsky, M.F.; Filella, I.; Verger, A.; Peñuelas, J. Photosynthetic light use efficiency from satellite sensors: From global to Mediterranean vegetation. Environ. Exp. Bot. 2014, 103, 3–11. [Google Scholar] [CrossRef]
- Rennenberg, H.; Loreto, F.; Polle, A.; Brilli, F.; Fares, S.; Beniwal, R.S.; Gessler, A. Physiological Responses of Forest Trees to Heat and Drought. Plant Biol. 2006, 8, 556–571. [Google Scholar] [CrossRef]
- Pignatti, S. Flora d’Italia; Edagricole: Bologna, Italy, 1982. [Google Scholar]
- Biondi, E.; Casavecchia, S.; Guerra, V.; Medagli, P.; Beccarisi, L.; Zuccarello, V. A contribution towards the knowledge of semideciduous and evergreen woods of Apulia (southeastern Italy). Fitosociologia 2004, 41, 3–28. [Google Scholar]
- Ortega, M.; Pascual, S.; Elena-Rosselló, R.; Rescia, A.J. Land-use and spatial resilience changes in the Spanish olive socio-ecological landscape. Appl. Geogr. 2020, 117, 102171. [Google Scholar] [CrossRef]
- Angelopoulos, K.; Dichio, B.; Xiloyannis, C. Inhibition of photosynthesis in olive trees (Olea europaea L.) during water stress and rewatering. J. Exp. Bot. 1996, 47, 1093–1100. [Google Scholar] [CrossRef]
- Huxman, T.E.; Cable, J.M.; Ignace, D.D.; Eilts, J.A.; English, N.B.; Weltzin, J.; Williams, D.G. Response of net ecosystem gas exchange to a simulated precipitation pulse in a semi-arid grassland: The role of native versus non-native grasses and soil texture. Oecologia 2004, 141, 295–305. [Google Scholar] [CrossRef] [PubMed]




| Recurrence Variable—Stability Metrics | System’s Adaptability Theoretical Descriptors |
|---|---|
| Determinism (DET): the percentage of recurrence points, which form diagonal lines. It gauges the stability and predictability of the dynamical system [14]. | Stability: concentrates on the adaptive capacity of the system to remain within the same domain because of mutually reinforcing structures and processes [56]. |
| Resilience: the probability that a system’s multiple states will persist [15]. | |
| Predictability: the reliability of event recurrence [57]. | |
| Laminarity (LAM): the percentage of recurrence points, which form vertical lines (laminar phases) in the system where some states do not change or change slowly (intermittency) and, hence, the state is trapped for some time [14]. | Constancy: when the state of the system remains the same [58]. |
| Divergence (DIV): the inverse of the length of the longest diagonal line (L max). It gauges the rate at which trajectories diverge and is the hallmark for critical transitions and dynamic chaos [14]. | Precariousness: the proximity or trajectory of an ecosystem state to a threshold that if crossed will result in a regime shift or critical transition [4,59]. Chaoticity: The condition of being chaotic. |
| The longest diagonal line in the plot (L max): the maximum predictability time; the smaller the divergence, the higher the system’s trajectory stability and predictability [14]. | Stability: qualities of a stability domain that resist changes in state or shifts in regime [60]. |
| Resilience: the probability that a system’s multiple states will persist [15]. | |
| Predictability: the reliability of event recurrence [57]. |
| Forests | Arable Lands | Olive Groves | Grasslands | |
|---|---|---|---|---|
| DET | 0.948 (0.940–0.956) | 0.930 (0.920–0.938) | 0.880 (0.870–0.890) | 0.891 (0.880–0.901) |
| REC | 0.125 (0.115–0.130) | 0.084 (0.077–0.091) | 0.056 (0.050–0.062) | 0.038 (0.030–0.040) |
| LAM | 0.932 (0.922–0.942) | 0.888 (0.878–0.898) | 0.768 (0.760–0.776) | 0.717 (0.705–0.729) |
| Lmax | 227.03 (218.40–235.60) | 195.10 (187.68–202.50) | 117.20 (112.75–121.65) | 41.3 (39.73–42.87) |
| DIV | 0.0041 (0.0044–0.0040) | 0.0051 (0.0053–0.0049) | 0.0085 (0.0089–0.0080) | 0.0250 (0.0262–0.0242) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrosillo, I.; Valente, D.; Mulder, C.; Li, B.-L.; Jones, K.B.; Zurlini, G. The Resilient Recurrent Behavior of Mediterranean Semi-Arid Complex Adaptive Landscapes. Land 2021, 10, 296. https://doi.org/10.3390/land10030296
Petrosillo I, Valente D, Mulder C, Li B-L, Jones KB, Zurlini G. The Resilient Recurrent Behavior of Mediterranean Semi-Arid Complex Adaptive Landscapes. Land. 2021; 10(3):296. https://doi.org/10.3390/land10030296
Chicago/Turabian StylePetrosillo, Irene, Donatella Valente, Christian Mulder, Bai-Lian Li, K. Bruce Jones, and Giovanni Zurlini. 2021. "The Resilient Recurrent Behavior of Mediterranean Semi-Arid Complex Adaptive Landscapes" Land 10, no. 3: 296. https://doi.org/10.3390/land10030296
APA StylePetrosillo, I., Valente, D., Mulder, C., Li, B.-L., Jones, K. B., & Zurlini, G. (2021). The Resilient Recurrent Behavior of Mediterranean Semi-Arid Complex Adaptive Landscapes. Land, 10(3), 296. https://doi.org/10.3390/land10030296







