Investigating Hydrochemical Groundwater Processes in an Inland Agricultural Area with Limited Data: A Clustering Approach
Abstract
:1. Introduction
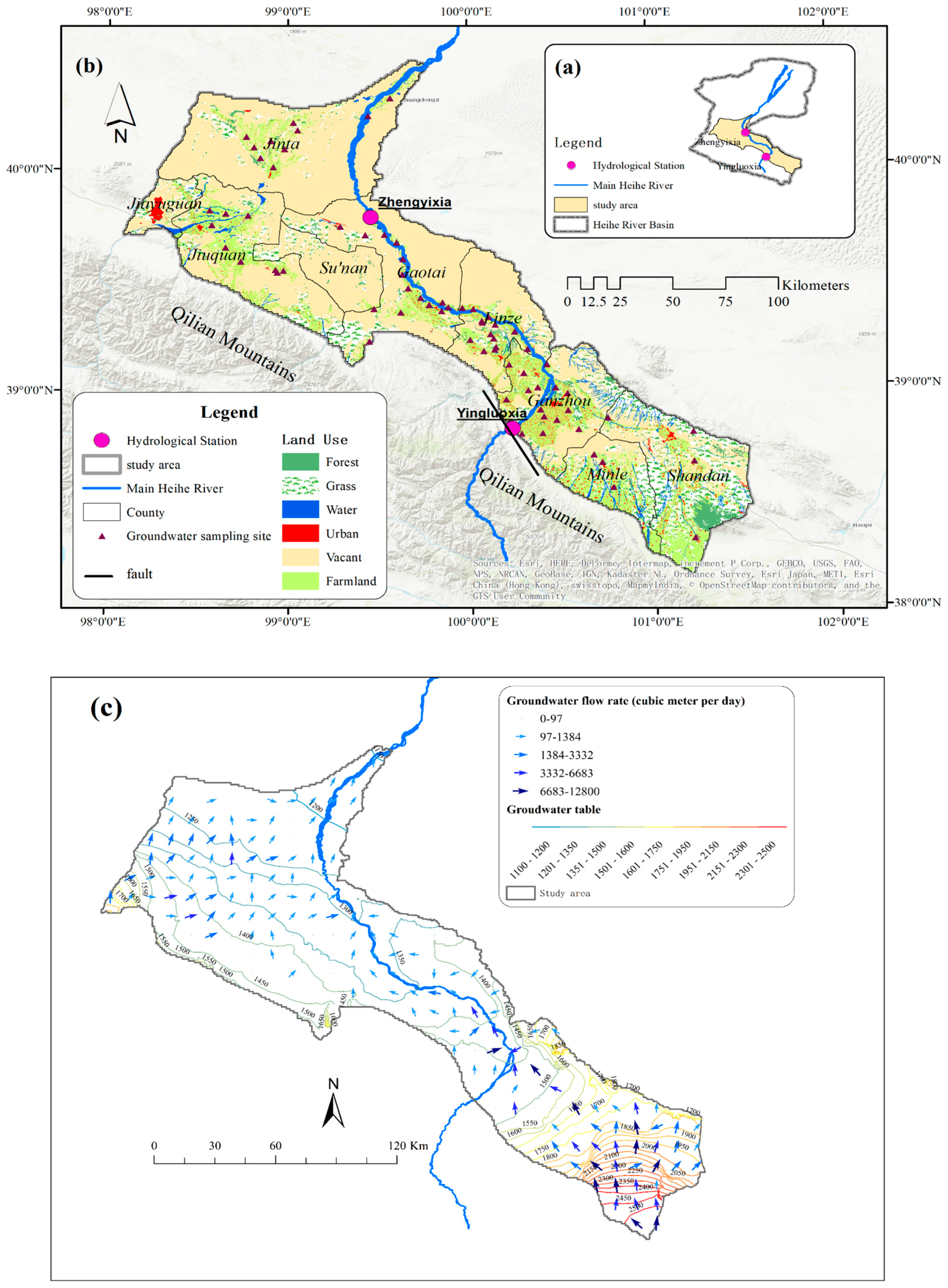
2. Study Area
3. Materials and Methods
3.1. Sample Collection and Treatment
3.2. GMM Clustering
3.3. Model Selection
3.4. Expectation-Maximization Algorithm
4. Results and Discussion
4.1. Descriptive Statistics
4.2. PCA Results
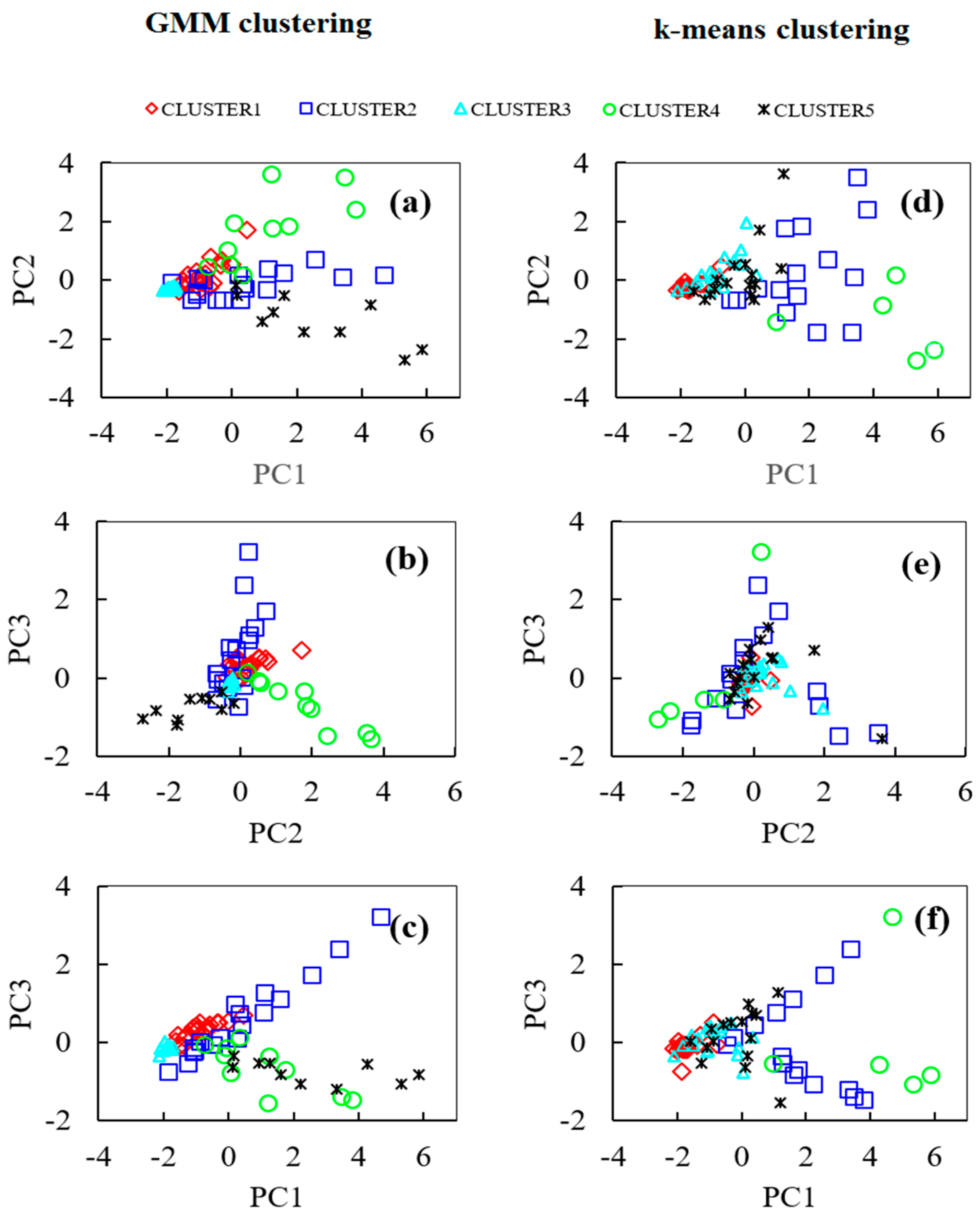
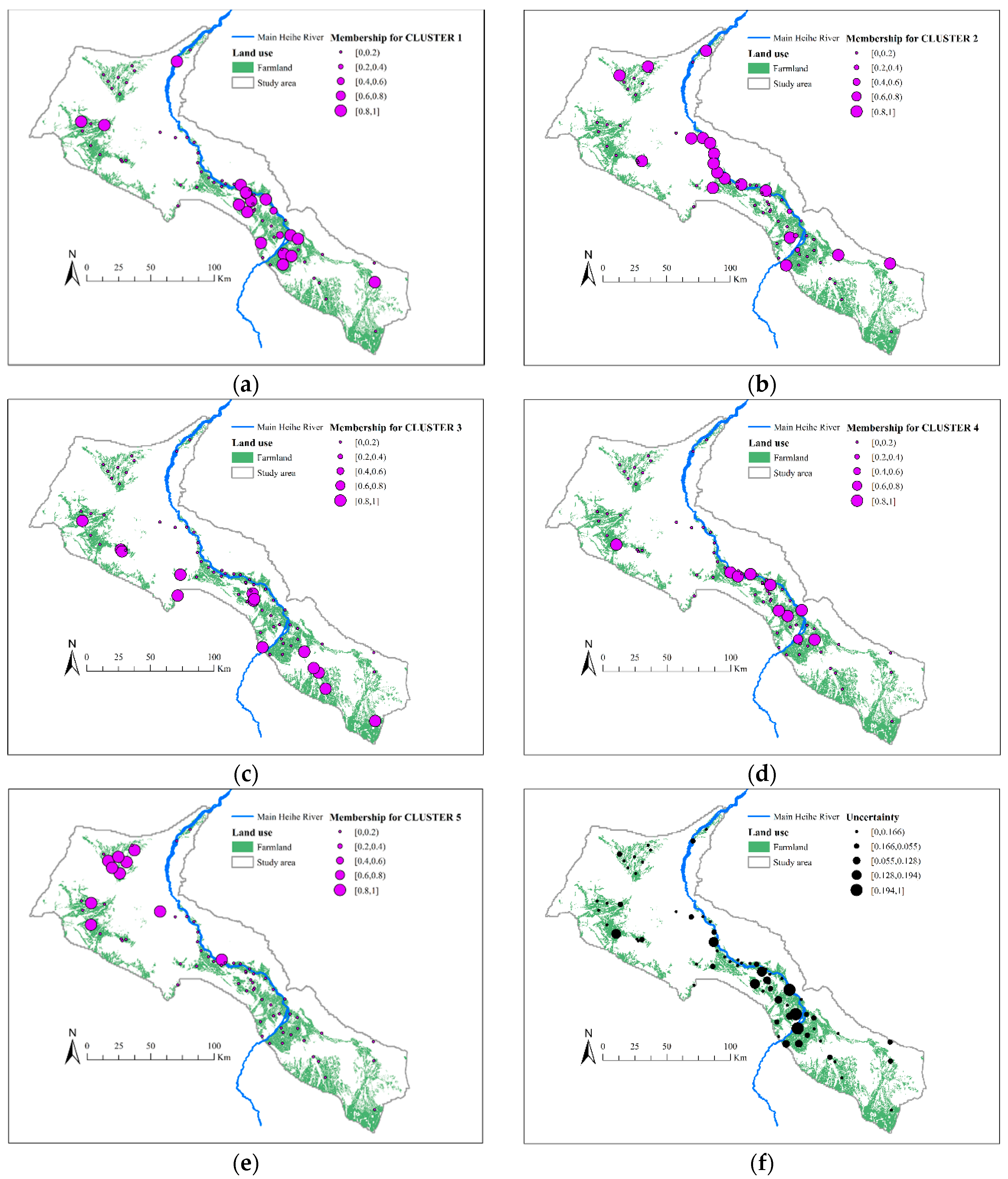
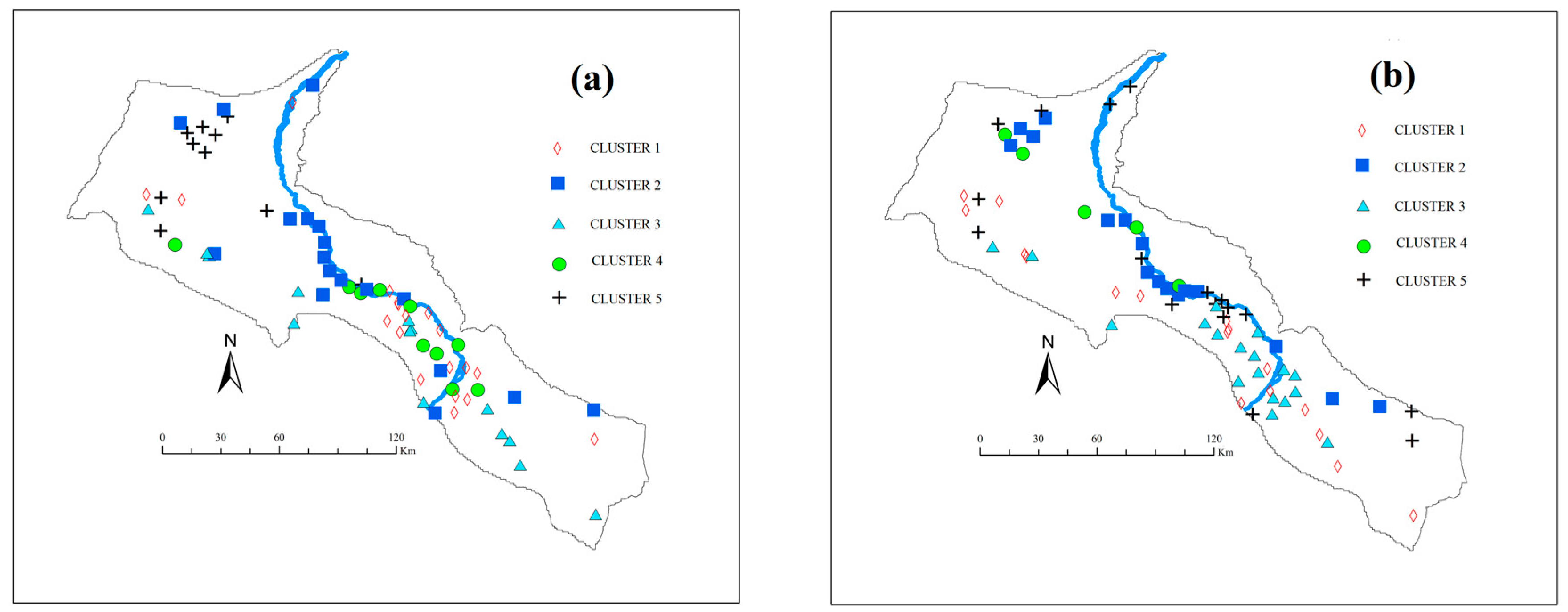
4.3. Clustering Results
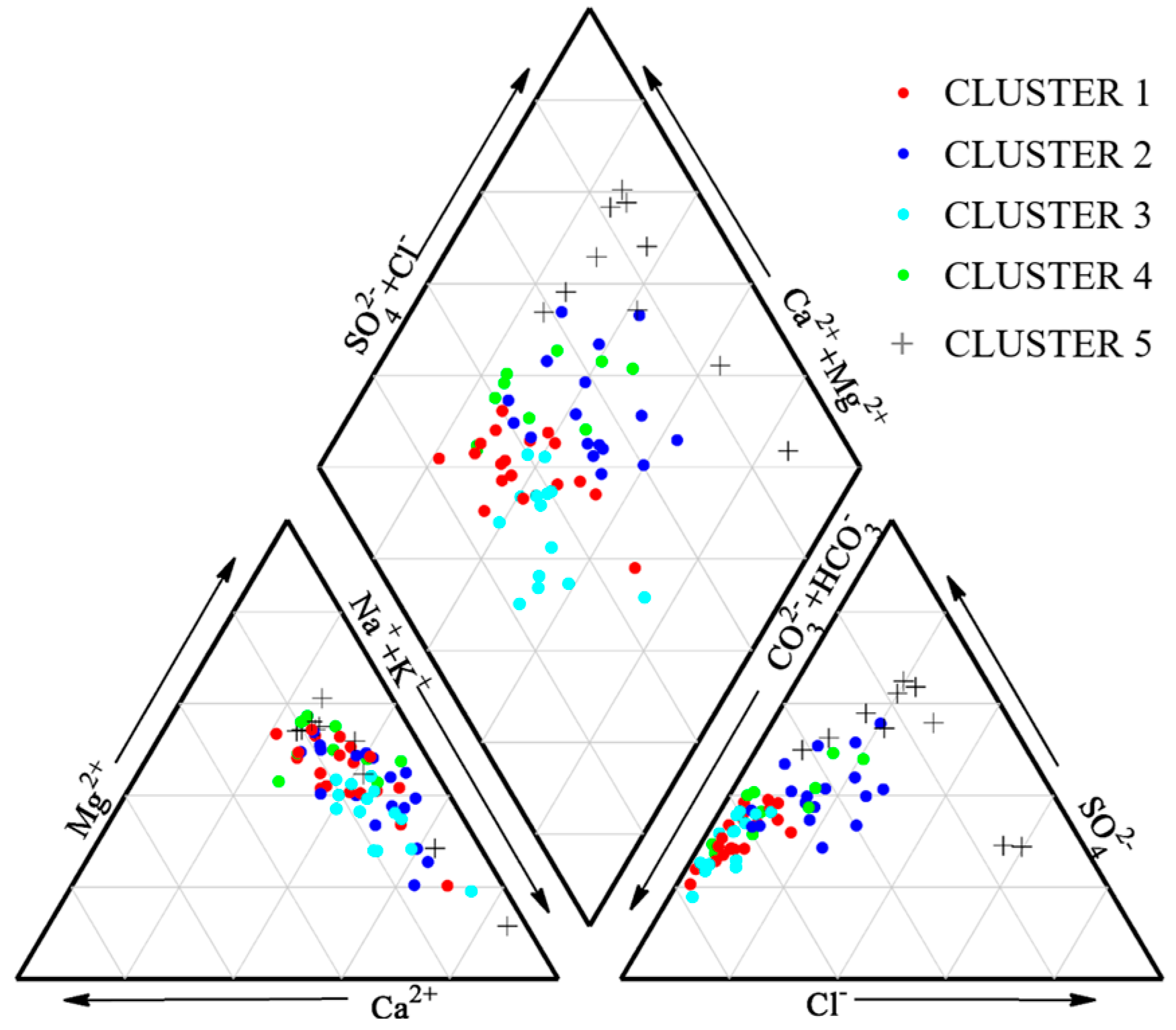
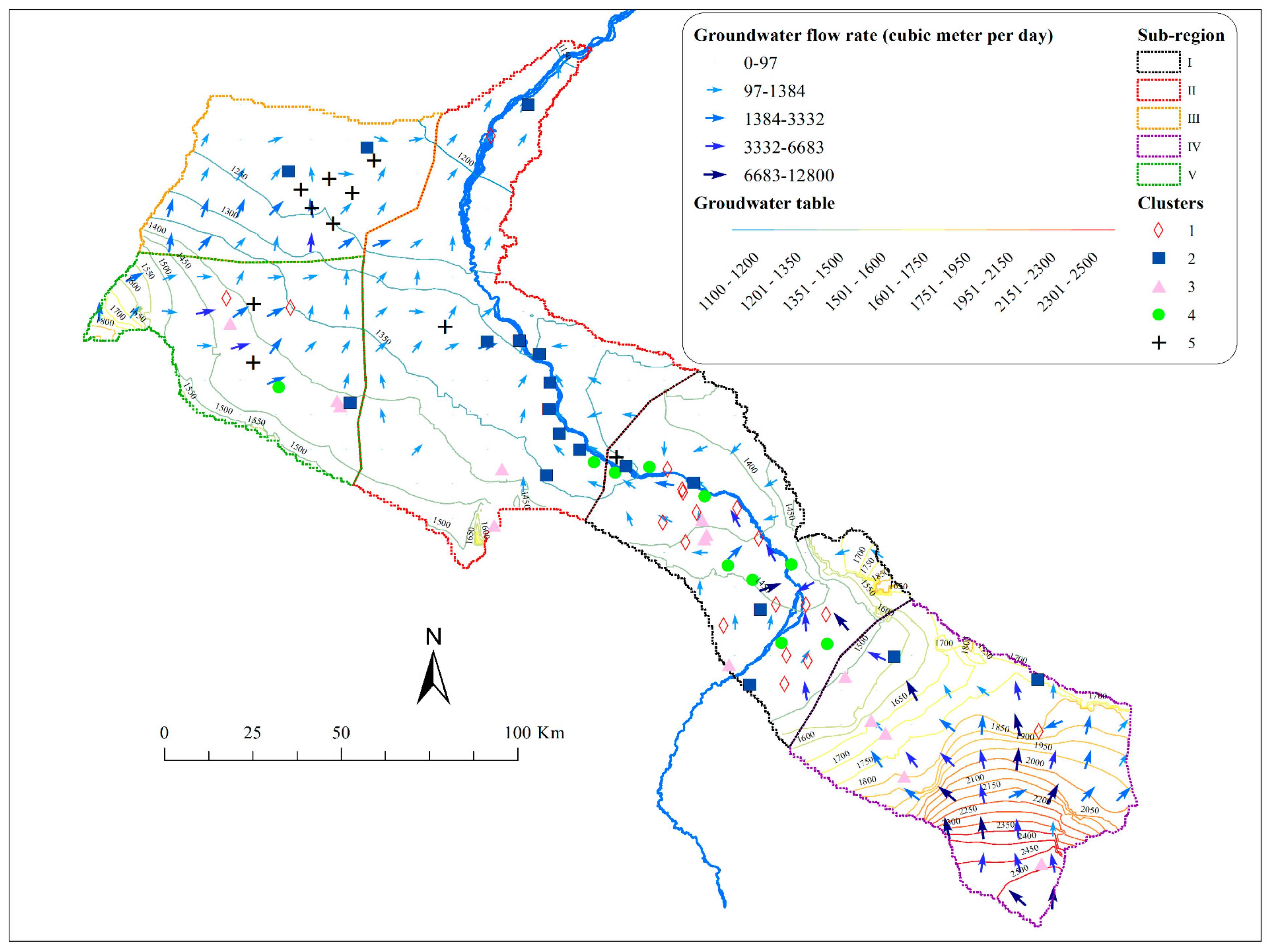
4.4. Regionalization of Groundwater Chemistry
4.5. Impact of Regional Water Cycle
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cloutier, V.; Lefebvre, R.; Therrien, R.; Savard, M.M. Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. J. Hydrol. 2008, 353, 294–313. [Google Scholar] [CrossRef]
- Hussein, M. Hydrochemical evaluation of groundwater in the Blue Nile basin, eastern Sudan, using conventional and multivariate techniques. Hydrogeol. J. 2003, 12, 144–158. [Google Scholar] [CrossRef]
- Suk, H.; Lee, K.-K. Characterization of a ground water hydrochemical system through multivariate analysis: Clustering into ground water zones. Ground Water 1999, 37, 358–366. [Google Scholar] [CrossRef]
- Lee, J.Y.; Cheon, J.Y.; Lee, K.K.; Lee, S.Y.; Lee, M.H. Statistical evaluation of geochemical parameter distribution in a ground water system contaminated with petroleum hydrocarbons. J. Environ. Qual. 2001, 30, 1548–1563. [Google Scholar] [CrossRef] [PubMed]
- Güler, C.; Thyne, G.D.; McCray, J.E.; Turner, A.K. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeol. J. 2002, 10, 455–474. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P. A regionalization method based on a cluster probability model. Water Resour. Res. 2011, 47, W11525. [Google Scholar] [CrossRef]
- Yoo, J.; Kwon, H.-H.; Kim, T.-W.; Ahn, J.-H. Drought frequency analysis using cluster analysis and bivariate probability distribution. J. Hydrol. 2012, 420, 102–111. [Google Scholar] [CrossRef]
- Mather, A.L.; Johnson, R.L. Event-based prediction of stream turbidity using a combined cluster analysis and classification tree approach. J. Hydrol. 2015, 530, 751–761. [Google Scholar] [CrossRef]
- Rao, A.R.; Srinivas, V.V. Regionalization of watersheds by fuzzy cluster analysis. J. Hydrol. 2006, 318, 57–79. [Google Scholar] [CrossRef]
- Zhu, G.; Su, Y.; Huang, C.; Qi., F.; Liu, Z. Hydrogeochemical processes in the groundwater environment of Heihe River Basin, Northwest China. Environ. Earth Sci. 2010, 60, 139–153. [Google Scholar]
- Kumar, M.; Ramanathan, A.; Keshari, A.K. Understanding the extent of interactions between groundwater and surface water through major ion chemistry and multivariate statistical techniques. Hydrol. Process. 2009, 23, 297–310. [Google Scholar] [CrossRef]
- Alvarez, M.D.P.; Carol, E.; Dapena, C. The role of evapotranspiration in the groundwater hydrochemistry of an arid coastal wetland (Peninsula Valdes, Argentina). Sci. Total Environ. 2015, 506, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Lee, K.-S.; Koh, D.-C.; Lee, D.-H.; Lee, S.-G.; Park, W.-B.; Koh, G.-W.; Woo, N.-C. Hydrogeochemical and isotopic evidence of groundwater salinization in a coastal aquifer: A case study in Jeju Volcanic Island, Korea. J. Hydrol. 2003, 270, 282–294. [Google Scholar] [CrossRef]
- Kim, K.-H.; Yun, S.-T.; Park, S.-S.; Joo, Y.; Kim, T.-S. Model-based clustering of hydrochemical data to demarcate natural versus human impacts on bedrock groundwater quality in rural areas, South Korea. J. Hydrol. 2014, 519, 626–636. [Google Scholar] [CrossRef]
- Güler, C.; Kurt, M.A.; Alpaslan, M.; Akbulut, C. Assessment of the impact of anthropogenic activities on the groundwater hydrology and chemistry in tarsus coastal plain (Mersin, Turkey) using fuzzy clustering, multivariate statistics and GIS techniques. J. Hydrol. 2012, 414, 435–451. [Google Scholar] [CrossRef]
- Güler, C.; Thyne, G.D. Delineation of hydrochemical facies distribution in a regional groundwater system by means of fuzzy c-means clustering. Water Resour. Res. 2004, 40, W12503. [Google Scholar] [CrossRef]
- Yidana, S.M.; Banoeng-Yakubo, B.; Akabzaa, T.; Asiedu, D. Characterization of the groundwater flow regime and hydrochemistry of groundwater from the buem formation, Eastern Ghana. Hydrol. Process. 2011, 25, 2288–2301. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modelling of chemical oxygen demand by using ANNS, ANFIS and k-means clustering techniques. J. Hydrol. 2014, 511, 279–289. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236. [Google Scholar] [CrossRef]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Maugis, C.; Celeux, G.; Martin-Magniette, M.-L. Variable selection for clustering with Gaussian mixture models. Biometrics 2009, 65, 701–709. [Google Scholar] [CrossRef] [PubMed]
- Bouveyron, C.; Brunet-Saumard, C. Model-based clustering of high-dimensional data: A review. Comput. Stat. Data Anal. 2014, 71, 52–78. [Google Scholar] [CrossRef] [Green Version]
- Biernacki, C.; Govaert, G. Choosing models in model-based clustering and discriminant analysis. J. Stat. Comput. Simul. 1999, 64, 49–71. [Google Scholar] [CrossRef]
- Fraley, C. How many clusters? Which clustering method? Answers via model-based cluster analysis. Comput. J. 1998, 41, 578–588. [Google Scholar] [CrossRef]
- Templ, M.; Filzmoser, P.; Reimann, C. Cluster analysis applied to regional geochemical data: Problems and possibilities. Appl. Geochem. 2008, 23, 2198–2213. [Google Scholar] [CrossRef]
- Law, M.H.C.; Figueiredo, M.A.T.; Jain, A.K. Simultaneous feature selection and clustering using mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1154–1166. [Google Scholar] [CrossRef] [PubMed]
- He, J. Mixture model based multivariate statistical analysis of multiply censored environmental data. Adv. Water Resour. 2013, 59, 15–24. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, Y.; Zheng, C.; Xiao, H.; Fan, W.; Zou, S.; Wu, B.; Yao, Y.; Zhang, A.; Liu, J. Exploring scale-dependent ecohydrological responses in a large endorheic river basin through integrated surface water-groundwater modeling. Water Resour. Res. 2015, 51, 4065–4085. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, Y.; Wu, X.; Tian, Y.; Han, F.; Liu, J.; Zheng, C. Optimizing water resources management in large river basins with integrated surface water-groundwater modeling: A surrogate-based approach. Water Resour. Res. 2015, 51, 2153–2173. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C. Optimizing conjunctive use of surface water and groundwater for irrigation to address human-nature water conflicts: A surrogate modeling approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, Y.; Tian, Y.; Wu, X.; Yao, Y.; Han, F.; Liu, J.; Zheng, C. Systematic assessment of the uncertainty in integrated surface water-groundwater modeling based on the probabilistic collocation method. Water Resour. Res. 2014, 50, 5848–5865. [Google Scholar] [CrossRef]
- Chang, J.A.; Wang, G.X. Major ions chemistry of groundwater in the arid region of Zhangye Basin, northwestern China. Environ. Earth Sci. 2010, 61, 539–547. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, W.; Su, Y.H.; Zhang, Y.W.; Si, J.H. Distribution and evolution of water chemistry in Heihe River basin. Environ. Geol. 2004, 45, 947–956. [Google Scholar] [CrossRef]
- Michael, L.M.; Leonard, F.K. Documentation of a Computer Program to Simulate Lake-Aquifer Interaction Using the MODFLOW Ground-Water Flow Model and the MOC3d Solute-Transport Model; Water-Resources Investigations Report; U.S. Geological Survey, Wisconsin Science Center: Middleton, WI, USA, 2000.
- Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
- Hu, L.T.; Chen, C.X.; Jiao, J.J.; Wang, Z.J. Simulated groundwater interaction with rivers and springs in the Heihe river basin. Hydrol. Process. 2007, 21, 2794–2806. [Google Scholar] [CrossRef]
- Hu, L.; Xu, Z.; Huang, W. Development of a river-groundwater interaction model and its application to a catchment in northwestern China. J. Hydrol. 2016, 543, 483–500. [Google Scholar] [CrossRef]
- Kang, E.; Cheng, G.; Lan, Y.; Jin, H. A model for simulating the response of runoff from the mountainous watersheds of inland river basins in the arid area of northwest China to climatic changes. Sci. China Ser. D Earth Sci. 1999, 42, 52–63. [Google Scholar] [CrossRef]
- Cao, G.; Zheng, C.; Craig, T.S. Groundwater recharge and mixing in arid and semiarid regions: Heihe river basin, Northwest China. Acta Geol. Sin. Engl. Ed. 2016, 90, 971–987. [Google Scholar]
- APHA; AWWA; WPCF. Standard Methods for the Examination of Water and Waste Water, 21st ed.; American Public Health Association: Washington, DC, USA, 2001; Available online: https://www.mwa.co.th/download/file_upload/SMWW_1000-3000.pdf (accessed on 18 September 2017).
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 38. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Phillips, S.J. Acceleration of k-means and related clustering algorithms. In Algorithm Engineering and Experiments, Proceedings of the 4th International Workshop, ALENEX 2002, San Francisco, CA, USA, 4–5 January 2002; Revised Papers; Springer: Berlin/Heidelberg, Germany, 2002; pp. 166–177. [Google Scholar]
- Raftery, A.E.; Dean, N. Variable selection for model-based clustering. J. Am. Stat. Assoc. 2006, 101, 168–178. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Brain, E. Cluster Analysis; Heinemann Educational: London, UK, 1974. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Molinari, A.; Guadagnini, L.; Marcaccio, M.; Guadagnini, A. Natural background levels and threshold values of chemical species in three large-scale groundwater bodies in northern Italy. Sci. Total Environ. 2012, 425, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Lei, L. A novel split and merge EM algorithm for Gaussian mixture model. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; pp. 479–483. [Google Scholar]
- Rhoades, J.D.; Kandiah, A.; Mashali, A.M. The Use of Saline Waters for Crop Production; FAO: Rome, Italy, 1992; Available online: http://www.fao.org/3/a-t0667e.pdf (accessed on 18 September 2017).
- Hollander, M.; Wolfe, D.A. Nonparametric Statistical Methods; Wiley: New York, NY, USA, 1973. [Google Scholar]
- LaBaugh, J.W. Groundwater chemistry A2—Likens, Gene E. In Encyclopedia of Inland Waters; Academic Press: Oxford, UK, 2009; pp. 703–713. [Google Scholar]
- Cronan, C.S. Major cations (Ca2+, Mg2+, Na+, K+,) A2—Likens, Gene E. In Encyclopedia of Inland Waters; Academic Press: Oxford, UK, 2009; pp. 45–51. [Google Scholar]
- Choi, B.Y.; Yun, S.T.; Kim, K.H.; Kim, J.W.; Kim, H.M.; Koh, Y.K. Hydrogeochemical interpretation of South Korean groundwater monitoring data using self-organizing maps. J. Geochem. Explor. 2014, 137, 73–84. [Google Scholar] [CrossRef]
- Farid, I.; Zouari, K.; Rigane, A.; Beji, R. Origin of the groundwater salinity and geochemical processes in detrital and carbonate aquifers: Case of Chougafiya basin (central Tunisia). J. Hydrol. 2015, 530, 508–532. [Google Scholar] [CrossRef]
- Zhu, G.F.; Su, Y.H.; Feng, Q. The hydrochemical characteristics and evolution of groundwater and surface water in the Heihe river basin, northwest China. Hydrogeol. J. 2008, 16, 167–182. [Google Scholar] [CrossRef]
- Farid, I.; Trabelsi, R.; Zouari, K.; Abid, K.; Ayachi, M. Hydrogeochemical processes affecting groundwater in an irrigated land in central Tunisia. Environ. Earth Sci. 2012, 68, 1215–1231. [Google Scholar] [CrossRef]
- Gowing, J.W.; Rose, D.A.; Ghamarnia, H. The effect of salinity on water productivity of wheat under deficit irrigation above shallow groundwater. Agric.Water Manag. 2009, 96, 517–524. [Google Scholar] [CrossRef]
- Petheram, C.; Bristow, K.L.; Nelson, P.N. Understanding and managing groundwater and salinity in a tropical conjunctive water use irrigation district. Agric.Water Manag. 2008, 95, 1167–1179. [Google Scholar] [CrossRef]
- Wang, J. Analysis and improving measures of saline soil in Gaotai County. Gausu Water Resour. Hydropower Technol. 2013, 49, 51–54. (In Chinese) [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Identification of homogeneous regions for the purposes of regionalisation. J. Hydrol. 1990, 121, 217–238. [Google Scholar] [CrossRef]
| Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | NO3− | HCO3− | TDS | |
|---|---|---|---|---|---|---|---|---|---|
| Na+ | 1.000 | 0.252 | 0.720 | 0.611 | 0.953 | 0.890 | −0.109 | 0.489 | 0.913 |
| K+ | 1.000 | 0.558 | 0.505 | 0.235 | 0.454 | −0.012 | 0.435 | 0.440 | |
| Mg2+ | 1.000 | 0.891 | 0.698 | 0.887 | 0.123 | 0.657 | 0.905 | ||
| Ca2+ | 1.000 | 0.581 | 0.786 | 0.041 | 0.571 | 0.815 | |||
| Cl− | 1.000 | 0.884 | −0.074 | 0.413 | 0.870 | ||||
| SO42− | 1.000 | −0.002 | 0.595 | 0.959 | |||||
| NO3− | 1.000 | 0.019 | 0.015 | ||||||
| HCO3− | 1.000 | 0.718 | |||||||
| TDS | 1.000 |
| Ions | PC1 | PC2 | PC3 | PC4 |
|---|---|---|---|---|
| Na+ | 0.402 | −0.203 | 0.160 | 0.411 |
| K+ | 0.391 | 0.118 | −0.064 | −0.327 |
| Mg2+ | 0.424 | 0.155 | −0.090 | −0.254 |
| Ca2+ | 0.384 | 0.180 | 0.031 | −0.478 |
| Cl− | 0.395 | −0.202 | 0.158 | 0.480 |
| SO42− | 0.437 | −0.049 | 0.062 | 0.093 |
| NO3− | 0.060 | 0.768 | −0.453 | 0.138 |
| HCO3− | −0.088 | 0.505 | 0.853 | 0.026 |
| Variance explained | 61.5% | 14.4% | 11.5% | 7.5% |
| Cumulative variance explained | 61.5% | 75.8% | 87.3% | 94.8% |
| Model ID | K | p | Attributes | L | BIC |
|---|---|---|---|---|---|
| 1 | 3 | 2 | PC1, PC2 | −177.74 | 367.27 |
| 2 | 3 | 3 | PC1, PC2, PC3 | −187.02 | 405.90 |
| 3 | 4 | 2 | PC1, PC2 | −169.92 | 355.78 |
| 4 | 4 | 3 | PC1, PC2, PC3 | −119.71 | 282.26 |
| 5 | 4 | 4 | PC1, PC2, PC3, PC4 | −143.77 | 369.33 |
| 6 | 5 | 3 | PC1, PC2, PC3 | −87.12 | 228.07 |
| 7 | 6 | 3 | PC1, PC2, PC3 | −65.09 | 195.00 |
| 8 | 7 | 3 | PC1, PC2, PC3 | −78.33 | 232.47 |
| 9 | 6 | 4 | PC1, PC2, PC3, PC4 | −146.6 | 416.58 |
| 10 | 4 | 3 | Cl−, NO3−, HCO3− | −111.787 | 266.42 |
| 11 | 3 | 3 | Cl−, NO3−, HCO3− | −158.52 | 346.88 |
| 12 | 3 | 7 | K+, Mg2+, Ca2+, Cl−, NO3−, HCO3−, pH | −535.41 | 1279 |
| Cluster | Salinity Level (PC1 Score) | Impact of Surface Water (PC2 Score) | Impact of Fertilization (PC3 Score) | Salinity Change Due to Recharge (PC1-PC2) | Fertilization-Impacted Recharge (PC2-PC3) | Groundwater Quality vs. Agricultural Development (PC1-PC3) * |
|---|---|---|---|---|---|---|
| CLUSTER 1 | Low to medium | Medium | Medium | Enhanced | No | Limiting |
| CLUSTER 2 | Low to high | Low to medium | Low to medium | Insignificant | No | Limiting |
| CLUSTER 3 | Low | Medium | Medium | Insignificant | No | Insignificant |
| CLUSTER 4 | Medium to high | Medium to high | Medium to high | Enhanced | Yes | Degrading |
| CLUSTER 5 | Medium to high | Low | Medium to high | Reduced | No | Degrading |
| Hydrological Variables | m1 | m2 | m3 | m4 | m5 |
|---|---|---|---|---|---|
| Potential ET | −0.128 | −0.089 | −0.270 | 0.092 | 0.307 |
| Groundwater ET | −0.152 | −0.076 | −0.186 | −0.191 | 0.282 |
| Precipitation | 0.316 | 0.006 | 0.257 | 0.268 | −0.184 |
| Infiltration | 0.095 | 0.010 | −0.106 | 0.235 | 3 × 10−4 |
| Irrigation | −0.028 | 0.044 | −0.284 | 0.157 | −0.140 |
| Groundwater depth | 0.178 | −0.031 | 0.455 | 0.027 | 0.214 |
| UZ recharge | −0.084 | 0.004 | −0.182 | 0.064 | −0.244 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Zheng, Y.; Zhang, J.; Wu, B.; Wang, S.; Tian, Y.; Li, J.; Meng, X. Investigating Hydrochemical Groundwater Processes in an Inland Agricultural Area with Limited Data: A Clustering Approach. Water 2017, 9, 723. https://doi.org/10.3390/w9090723
Wu X, Zheng Y, Zhang J, Wu B, Wang S, Tian Y, Li J, Meng X. Investigating Hydrochemical Groundwater Processes in an Inland Agricultural Area with Limited Data: A Clustering Approach. Water. 2017; 9(9):723. https://doi.org/10.3390/w9090723
Chicago/Turabian StyleWu, Xin, Yi Zheng, Juan Zhang, Bin Wu, Sai Wang, Yong Tian, Jinguo Li, and Xue Meng. 2017. "Investigating Hydrochemical Groundwater Processes in an Inland Agricultural Area with Limited Data: A Clustering Approach" Water 9, no. 9: 723. https://doi.org/10.3390/w9090723





