Assessment of the Combined Effects of Threshold Selection and Parameter Estimation of Generalized Pareto Distribution with Applications to Flood Frequency Analysis

Abstract

Floods are costly natural disasters that are projected to increase in severity and frequency into the future. Exceedances over a high threshold and analysis of their distributions, as determined through the Peak Over Threshold (POT) method and approximated by a Generalized Pareto Distribution (GPD), respectively, are widely used for flood frequency analysis. This study investigates the combined effects of threshold selection and GPD parameter estimation on the accuracy of flood quantile estimates, and develops a new, widely-applicable framework that significantly improves the accuracy of flood quantile estimations. First, the performance of several parameter estimators (i.e., Maximum Likelihood; Probability Weighted Moments; Maximum Goodness of Fit; Likelihood Moment; Modified Likelihood Moment; and Nonlinear Weighted Least Square Error) for the GPD was compared through Monte Carlo simulation. Then, a calibrated Soil and Water Assessment Tool (SWAT) model for the province of Alberta, Canada, was used to reproduce daily streamflow series for 47 watersheds distributed across the province, and the POT was applied to each. The Goodness of Fit for the resulting flood frequency models was measured by the upper tail Anderson-Darling (AD) test and the root-mean-square error (RMSE) and demonstrated improvements for more than one-third of stations by averages of 65% (AD) and 47% (RMSE), respectively.

1. Introduction

Floods are considered the most destructive and wide-spread natural disaster, and account annually for about 50 percent of all natural disasters world-wide [1,2]. Further, intensification of the hydrological cycle with climate change may lead to larger and more frequent floods [3,4,5,6], and land use change may increase flood risk through expansion of urban areas, which typically limit soil permeability [7], or through development in the flood plain. Examples of recent extreme flood events include flooding in the Calgary, Alberta, area in 2013, which created the costliest natural disaster in Canadian history, with damage of approximately $6 billion [8], and the largest number of flood events recorded in a single year in the United States in 2016, the most catastrophic of which occurred in Louisiana [9]. In Europe, the May–June 2013 flooding of the Elbe, Oder, and Danube rivers in Germany produced the third ‘‘flood of the century’’ since 1997 [10].

To mitigate flood risks, understanding the relationship between flood events and their probability of occurrence is a critical first step from both economic and environmental points of view [1,11]. A systematic assessment of flood risks is therefore vital for sustainable watershed management and planning. More specifically, a rigorous analysis of flood events helps to identify the risk of flooding at various locations and aids in selection of appropriate design periods for structures such as dams and levees [12,13,14]. Thus, reliable predictions of flood magnitude will improve both the sustainability and economic efficiency of water resources systems.

Flood Frequency Analysis (FFA) is a standard method used to detect relationships between flood magnitudes and the corresponding frequency of occurrence. FFA has largely been applied in four categories: on-site FFA, climate/weather-informed on-site FFA, historical and paleo-flood analyses, and regional FFA [13]. In this paper, the focus is on-site FFA, which is performed by fitting a chosen probability distribution to flood events sampled from streamflow records at the site of interest [15]. Three different approaches are available for flood event sampling from a streamflow record: the annual maxima (AM), the partial duration series, and the peaks over a threshold (POT) [16,17,18,19,20,21]. Although the AM is the most common because of its simplicity, it samples only one event per year [14,17,19]; therefore, it may result in a loss of information, if the second or third peak within a year—which can be greater than the flood peak in other years—is ignored. This situation is particularly problematic in regions where the record of historical streamflow is short. In contrast, the POT includes all peaks above a certain flow value (the threshold), which provides flexibility in controlling the number of events included in the analysis. Comparisons between AM and POT series have found that POT offers a smaller uncertainty of estimated values, because of the larger quantity of data involved in the analysis [18,22,23]. More specifically, Cunnane [24] conducted a statistical analysis that showed greater statistical efficiency, or more precise estimation of the parameters, for POT where the average number of peaks per year included in the POT series was greater than 1.65.

The standard practice in POT fits a distribution to exceedances above a selected threshold. In selecting this threshold, it must be high enough to identify the distribution underlying the excess series and to maintain the independent and identically distributed (IID) flood variables assumption. It also should not be so high as to increase the variance by reducing the number of events needed for reliable inferences [13,25]. Therefore, the optimal threshold detection has been of interest in earlier studies [19,25,26,27,28,29,30,31,32,33,34,35], which have suggested various approaches based on graphical and/or analytical methods. An example of the graphical approach is the Mean Residual Life plot (MRL), while analytical approaches include the Square Error method (SE), the Multiple Threshold Method (MTM), and the Likelihood Ratio Test method (LRT). Numerous studies have stated that the performance of FFA with POT is dependent upon the threshold selection method applied but its effect was not studied (e.g., [36,37,38]). Zoglat et al. [25] noted the subjectivity of the graphical methods and therefore compared different analytical methods towards threshold selection, with the LRT method found to be the best and SE second-best, with satisfactory performance. However, it is difficult to generalize this approach because the comparison was performed for only one hydrometric station.

After sampling the flood peaks, a distribution is chosen for the FFA model. There are several probability distribution methods used to model extreme events. Generalized Pareto Distribution (GPD) is widely used to model extreme floods over a threshold. It has been used successfully to estimate return values of flood events in conjunction with a POT method. Pickands [39] first introduced the GPD as a two-parameter family of distributions for exceedances over a threshold and showed that it is a stable distribution for excesses over thresholds. To determine appropriate parameter values, numerous estimators for the GPD have been proposed in the literature, with the Maximum Likelihood Estimator (MLE) [39], Method of Moments (MOM) [40], and the Probability Weighted Moments (PWM) used most widely. Additional methods have also been proposed, including Likelihood Moment Estimations (LME) [41], the modified Likelihood Moment Estimator (NEWLME) [42], and the Nonlinear Weighted Least Squares estimator (NWLS) [43]. For an extensive discussion of the various methods see de Zea Bermudez and Kotz [44]. Estimator performance has been found to vary considerably with both the flood-event sample sizes and the value of the GPD shape-parameter, such that estimators that perform well in some situations may perform poorly in others. For example, Hosking and Wallis [40] introduced the PWM estimators for the GPD and compared them to the MOM and MLE estimators. They showed that the MOM and PWM estimators have lower bias and variance than MLE estimators for sample sizes less than 500; however, both are sensitive to threshold choice and sometimes result in infeasible estimates [29]. Many other simulation studies have provided a quantitative comparison of the performance of different estimators (e.g., [36,37,38,45]). These simulation studies pointed out that estimator performance depends on the threshold selection method without a quantitative measure of this effect.

Overall, there are numerous factors influencing the accuracy of the modeled return period of an extreme flood. Among them are the length and accuracy of flow records, the criteria used to identify independent flood peaks, the threshold selection method, and the estimator of the selected probability distribution. Moreover, the performance of various parameter and quantile estimators can vary greatly in terms of their bias, variance, and sensitivity to threshold choice; and consequently affect the accuracy of the estimated return values [37,46]. Given the key role of threshold selection in reducing uncertainty prediction, the POT method is still under-employed, particularly for studying the impacts of climate change. In climate change studies, application of the POT method can be beneficial as it provides useful information about the time of floods along with their magnitudes. Accordingly, it is important to measure the performance of the GPD estimator quantitatively along with the effect of threshold selection (POT) on its performance.

The purpose of this study is to propose a novel systematic procedure for assessing the combined effect of the threshold selection method and GPD parameter estimator on the accuracy of flood frequency distribution calculations. First, a comparison between older and more recent methods proposed for the GPD over a wide range of flood event sample sizes and shape parameters was undertaken. Further, POT was applied to a large number of streamflow series using different combinations of threshold selection methods and parameter estimators and the goodness of fit of the flood frequency distributions were assessed. We hypothesize that more accurate flood frequency models can be obtained by improving threshold selection and GPD parameter estimator selection.

This paper is organized as follows. Section 2 describes the study area, data used for the analysis, and the methods employed in this study. Section 3 presents the results from applying POT on simulated streamflow records from SWAT model along with the analysis and discussion of these results. Section 4 includes the summary and conclusions of the study.

2. Materials and Methods

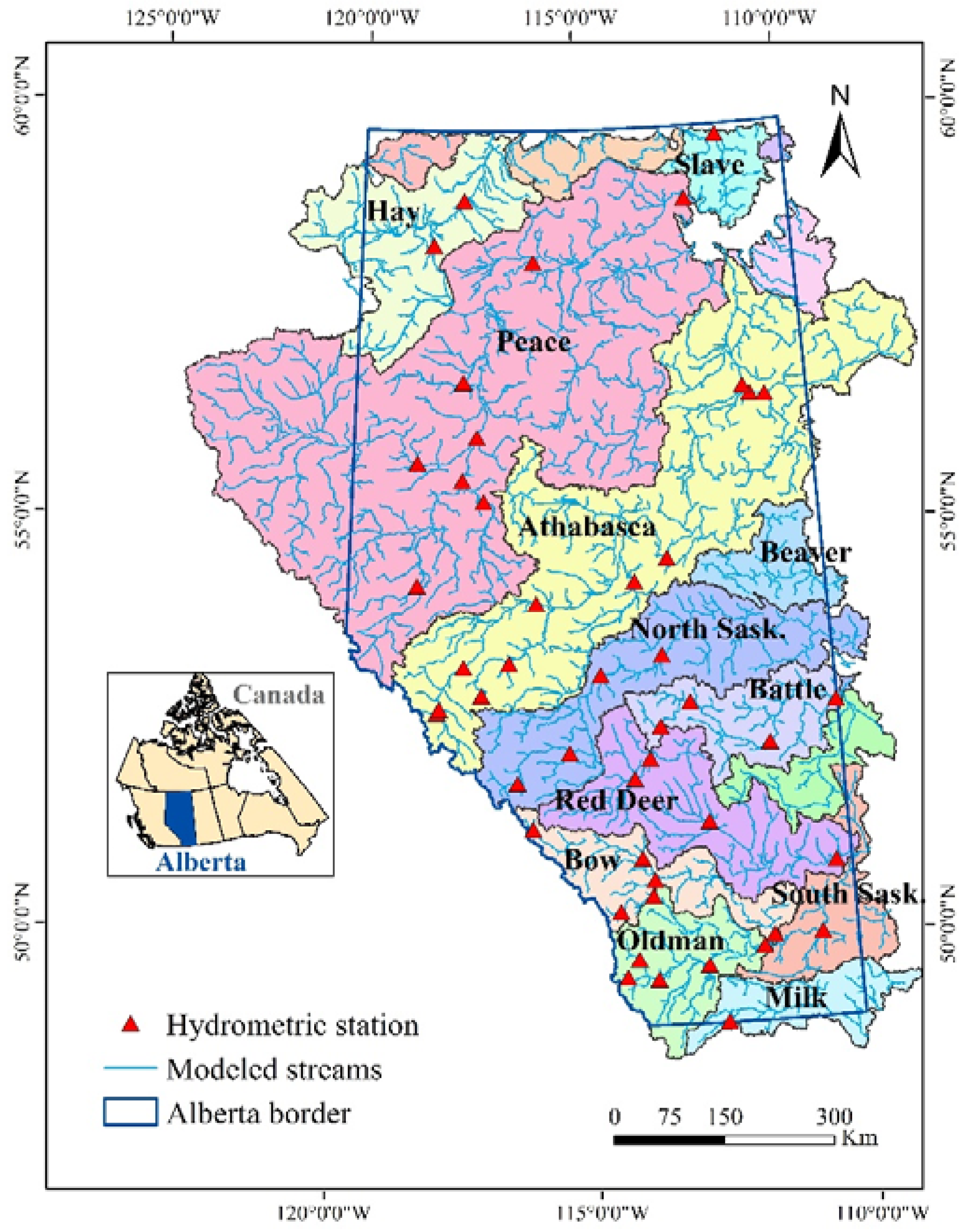
2.1. Study Area, Hydrologic Model, and Data Overview

Given the large spatial extent of Alberta, the variability of the hydro-meteorological conditions, and the availability of a calibrated Soil and Water Assessment Tool (SWAT) model [47] for the province of Alberta, Canada for the period 1986–2007 that allows us to obtain streamflow records across the entire province, Alberta presented an ideal study region. One of the three Canadian Prairie Provinces, Alberta has an area of about 661,000 km² that encompasses 17 river basins principally originating from the east slopes of the Canadian Rockies, and that drain eastward to Hudson Bay through the provinces of Saskatchewan and Manitoba or northward to the Arctic Ocean [48]. Alberta has a relatively dry climate. In the north, the average annual precipitation ranges from 400 mm in the northeast to over 500 mm in the northwest, while in the south, it ranges from 450 mm to less than 350 mm in the southeast. Northern Alberta is dominated by Boreal forests and was wet for the 100 years between 1900 and 2000 [49]. Southern Alberta is dominated by grassland that has experienced progressively decreasing precipitation for the period 1960–2000 [49]. Alberta has cold winters and warm summers with a mean annual temperature ranging from 3.6 °C to 4.4 °C.

Despite its relatively low average precipitation, Alberta is experiencing increasing flooding trends mainly because of high variability in precipitation [50]. For example, flooding in the city of Calgary in 2013 is considered to have been the costliest natural disaster in Canadian history [8]. Thus, the province makes an interesting case study because of its heterogeneous hydro-climatic conditions, diverse land management practices, and the occurrence of extreme hydrologic events (e.g., floods). Alberta forms the basis of an assessment of our research objectives and the development of a comprehensive practical guideline for the most suitable methods for threshold selection and parameter estimation methods under diverse hydro-climatic conditions.

The stream flow data used for the study are daily average discharges as simulated by the SWAT model [48]. Input variables for the SWAT hydrologic model of Alberta have been carefully selected to represent the actual physical processes related to natural and anthropogenic features (e.g., snow, potholes, glaciers, reservoirs, dams, and irrigated agriculture), and to minimize input data uncertainties [48]. The model has been extensively calibrated and validated using the discharge data of about 130 hydrometric stations for the 1983–2007 period in the province [47] (See Table S1), and can simulate stream flow and other water resource components in 2255 sub-basins across the province. In this study we used a subset of 47 stations/outlets spread across the province (see Figure 1), based on efficiency criteria that were used to assess the calibrated performance of the model based on simulated versus observed discharges e.g., bR², NSE, and R² [48]. Only the stations with bR², NSE, and R² greater than 0.6 were considered, because these values provide both reliable streamflow records and a sufficient number of stations to cover various river basins that encompass a diverse range of topographic, hydrologic, and climatic conditions.

2.2. Probability Modeling

In flood probability modeling, a distribution is fitted to excesses above a high threshold (POT) for a selected streamflow sample. For flood peak flows, extreme value theory shows that the distribution of exceedances of a high-enough threshold will tend to follow a Generalized Pareto distribution [37,51]. The theoretical development of the GPD can be found in Coles [17]. The cumulative distribution frequency (CDF) for the GPD is derived from the following equation:

$$F_u\left(x\right)=Pr\left(X-u<x|X>u\right)=\{\begin{array}{c}1-{\left(1+\frac{\xi \left(x-u\right)}{\mathsf{\sigma }}\right)}^{\frac{-1}{\xi }}\xi \ne 0\\ 1-e^{\left(-\frac{x-u}{\sigma }\right)}\xi =0\end{array},$$

(1)

where x is the flood peak flow in m³/s, $\xi$ is the shape parameter, u is the location parameter, also known as the threshold, and $\sigma$ is the scale parameter. In special cases, $\xi$ = 0 and $\xi$ = 1 yield an exponential distribution and a uniform distribution, respectively, while a Pareto distribution is obtained when $\xi$ < 0. Note that selection of the threshold, u, reduces the three-parameter GPD to a two-parameter distribution. To evaluate the Goodness of Fit, a comparison between the modeled CDF and the empirical distribution function (EDF) was performed. The EDF is calculated from,

$$\tilde{F}\left(x_{\left(i\right)}\right)=\frac{i}{n+1},$$

(2)

where i is the rank of the flood event and n is the sample size [17].

In this study, the data were sampled from 47 streamflow gauges using two threshold selection methods (see Section 2.2.3). The sampled data were then fitted to GPD using each of the parameter estimators considered in this study (see Section 2.2.1), and the fitted distributions were compared with the empirical distribution. To assess the Goodness of Fit, the root-mean-square error (RMSE) and p-value of the Anderson-Darling test (AD) were computed. The Anderson Darling statistic allots extra weight to floods in the tail of the distribution [30], which are of importance when estimating floods with high return periods.

2.2.1. GPD Parameter Estimators

Several techniques are available for the estimation of GPD parameters, including MLE [39], PWM [40], LME [41], NEWLME [42], MGFAD [27], and NWLS [43].

• Maximum Likelihood Estimator (MLE): MLE is the most efficient method of parameter estimation, particularly for large streamflow sample sizes. It maximizes the likelihood function (L) for the sampled independent flood peaks (x), and is derived from,

  $$L\left(\xi ,\sigma \right)={\prod }_{j=1}^{n}f\left(x_j,\xi ,\sigma \right),$$

  (3)

  where $f=\frac{dF}{dx}$. The estimated parameters are the values that maximize Equation (3). Although the algorithms used to compute MLE estimated parameters run into convergence problems, Ashkar and Tatsambon [36] argue that this behavior is simply due to incorrect choice of the numerical algorithm.
• Probability Weighted Moments Estimator (PWM): The PWM estimator has a lower bias and variance than the MLE estimator for sample sizes less than 500 [40]. The PWM of a sampled flood peak (x) with distribution function F is derived from the following equation:

  $$M_{p,q,r}=E\left(x^P{F}^q{\left(1-F\right)}^r\right)={\int }_0^1{\left[x\left(F\right)\right]}^P{F}^q{\left(1-F\right)}^{r}dF,$$

  (4)
  PWM always exists, is computationally straightforward, and is a function of the plotting position, which makes it more stable. However, PWM estimates are sensitive to the threshold choice [37,40].
• The Likelihood Moment Estimator (LME): LME is a hybrid between likelihood and moment estimators, and was proposed by Zhang [41]. The LME for a streamflow sample size of n is derived from the following equation:

  $$\frac{1}{n}{\sum }_{j=1}^n{\left(1-\theta X_i\right)}^P-\frac{1}{1-r}=0,\theta <X_{\left(n\right)}^{-1},$$

  (5)

  where $\theta =\xi /\sigma$ and $P=\frac{-rn}{{\sum }_{j=1}^n\log \left(1-\theta x_j\right)}$. In this equation the parameter r < 1 is chosen before the estimation [42].
  Zhang [41] shows that when $r=\xi$, the LME and MLE asymptotic variances are the same. The LME is simple to compute and less sensitive than other parameter estimators to threshold choice [37]. In this study, an initial guess of the value of $\xi$ was made by the PWM as recommended by Mackay et al. [37].
• The Modified Likelihood Moment Estimator (NEWLME): The NEWLME method was proposed by Zhang and Stephens [42] to address complexities in the MLE numerical solution and to avoid computational problems. The method is similar to the Bayesian methods [37] and its solution is calculated as follows:

  $$\widehat{\theta }=\frac{\int \theta ·\pi \left(\theta \right)L\left(\theta \right)d\theta }{\int \pi \left(\theta \right)L\left(\theta \right)d\theta },$$

  (6)

  where $L\left(\theta \right)=n\left[\log \left(\frac{\theta }{\xi }\right)\right]+\xi -1$ with $\xi =-n^{-1}{\sum }_{i=1}^n\log \left(1-\theta x_i\right)$ is the profile log-likelihood function, and $\pi \left(\theta \right)$ is a data-driven density function for $\theta$ [42]. This allows the parameters to be computed very efficiently [37].
• The Maximum Goodness of Fit–Anderson-Darling Estimator (MGFAD): Moharram et al. [52] proposed least-square type estimators, which are found by minimizing the sum of squared difference between the empirical and the model quantiles. Luceño [27] proposed an estimator with a similar approach, in which the estimates are obtained by minimizing the square differences between the empirical and the model distribution functions using various Goodness of Fit statistics. Luceño [27] included the Cramer-von Mises [30], the Anderson-Darling [30], and the right-tail weighted Anderson-Darling statistics [53]. The different statistics considered by Luceño [27] were found to have strong positive bias and high root-mean-square error (RMSE) in estimating high quantiles for small sample sizes [37]. Only the Maximum Goodness of Fit estimator with Anderson-Darling statistic (MGFAD) was considered in this study.
• The Nonlinear Weighted Least Squares Estimator (NWLS): A new estimator based on the nonlinear weighted least squares estimator (NWLS) was recently proposed by Song and Song [38], and revised and improved by Park and Kim [43]. The calculation of the NWLS estimator is a two-step procedure that is calculated using Equations (7) and (8) as follows:

  $$\left({\widehat{\xi }}_1,{\widehat{\sigma }}_1\right)=\arg {\min }_{\left(\xi ,\sigma \right)}{\sum }_{i=1}^n{\left[\log \frac{1-F_n\left(x_i\right)}{1-F_n\left(u\right)}-\log \left(1-G_{\xi ,u,\sigma }\left(x_i\right)\right)\right]}^2,$$

  (7)

  $$\left({\widehat{\xi }}_2,{\widehat{\sigma }}_2\right)=\arg {\min }_{\left(\xi ,\sigma \right)}{\sum }_{i=1}^n{\left[\frac{i\left(n-i+1\right)}{{\left(n+1\right)}^2\left(n+2\right)}\right]}^{-1}{\left[\frac{F_n\left(x_i\right)-F_n\left(u\right)}{1-F_n\left(u\right)}-G_{\xi ,u,\sigma }\left(x_i\right)\right]}^2,$$

  (8)

Park and Kim [43] compared the performance of the NWLS with some other estimators, and it was found to be highly competitive for heavy-tailed data ($\xi >0)$. In this study, the performance of the NWLS was tested for the case $\xi <0$.

2.2.2. Performance Analyses of the GPD Estimators and the Monte Carlo (MC) Sampling Experiments

Performance of the GPD parameter estimators depends on both the sample size, n, and the value of the GPD shape parameter, $\xi$ [37]. Since the streamflow records did not provide a sufficient range of events to yield reasonable estimates for the entire range of possible values in a given GPD model, a Monte Carlo sampling technique [54] was used to generate different samples in order to evaluate the performance of the six GPD parameter estimators described in Section 2.2.1. A total of 10,000 random samples of different n, $\xi$, and $\sigma$ combinations was generated. Samples of size n = 40, 50, ..., 200, 500, and 1000 were used for the parameter estimation, with the $\xi$ values ranging from −0.5 to 0.5 ($\xi$ = −0.5, −0.4, −0.3, −0.2, −0.1, 0, 0.1, 0.2, 0.3, 0.4, 0.5), and of the scale parameter $\sigma$ ranging from 20 to 1000. Then, from each sample, the shape and scale parameters were computed by the parameter estimator and the 0.99 quantile was obtained from the resulting distribution. To evaluate the performance of the six parameter estimation methods, four statistics were computed: the average biases in estimating the shape and scale parameters, the 0.99 quantile (upper quantile), and the average root-mean-square error (RMSE). The comparison between different estimators for each threshold selection method focused on the upper tail Anderson-Darling test (AD), as it evaluates the ability of the model to estimate high quantiles. The other statistics (e.g., RMSE) were used to evaluate the model performance further, if the AD test values were similar.

In the application of flood frequency analysis, the value of the scale parameter can vary significantly, from 100 to 1000 or more; therefore, we examined the effect of varying scale parameter values on the accuracy of estimating the 0.99 quantile.

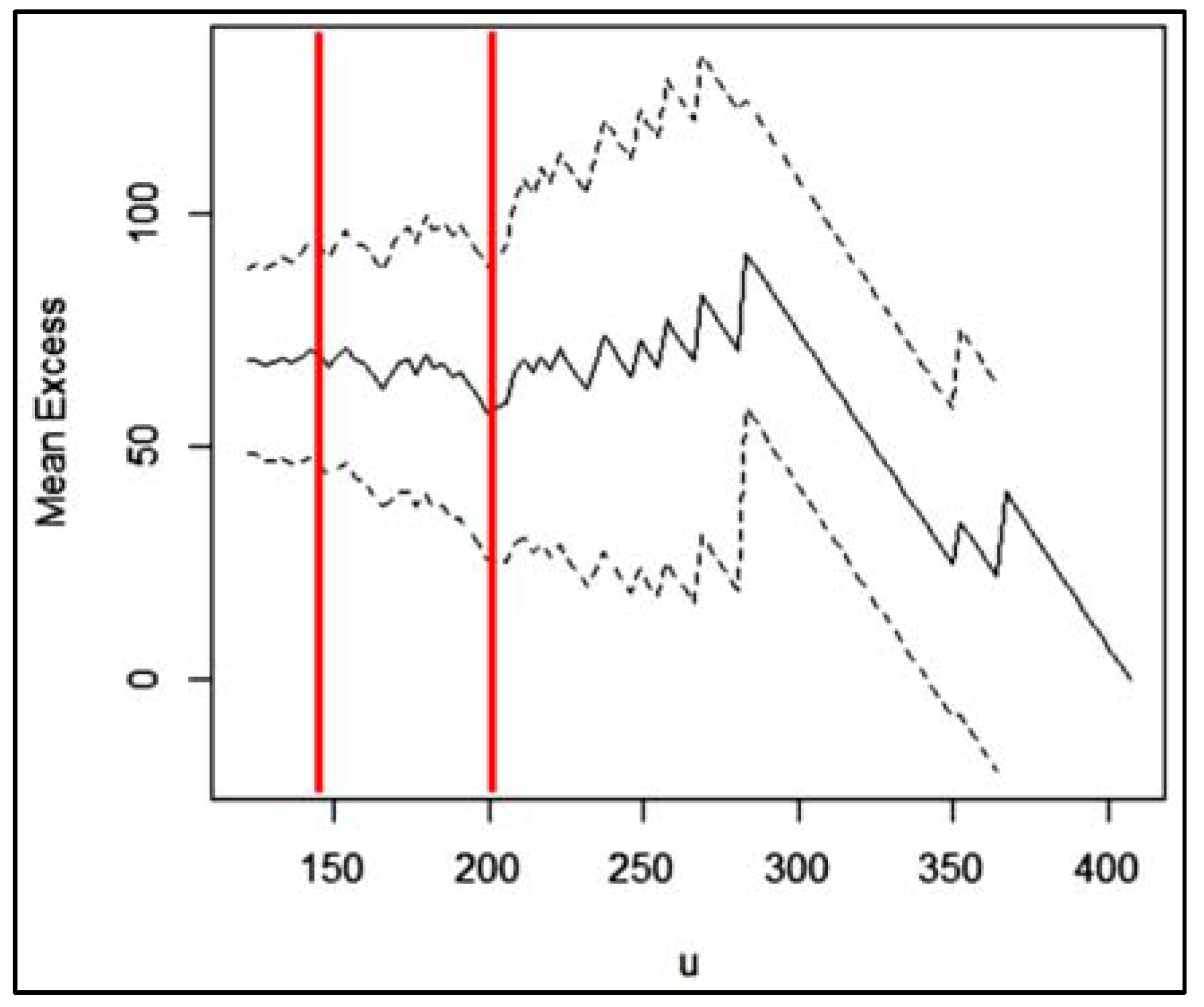
2.2.3. Threshold Selection Methods

The choice of a threshold is an important practical problem with a solution that is primarily based on a compromise between estimator bias and variance. In other words, it affects the performance of the different GPD parameter estimators. To investigate further the effect of the threshold selection method on the performance of the GPD parameter estimators, data were sampled from 47 streamflow gauges using the threshold selection methods. Various methods to select thresholds have been proposed in the literature. For the application, one option includes graphical methods, which are relatively easy to apply. However, they have some shortcomings. First, the interpretation of these plots is unclear in practice [17], and it is clearly difficult to determine which portion of the curve is completely linear. Second, graphical techniques cannot be automated and the uncertainty associated with threshold selection cannot be estimated [55]. Figure 2 shows a range of potential optimum threshold values, making the use of a single value from the range in the analysis subjective. Compared to graphical methods, analytical methods are less subjective and the computations can easily be programmed. Zoglat et al. [25] compared various threshold selection techniques. Two analytical methods outperformed the other techniques and were employed in our study: The Square Error Method (SE) and Likelihood Ratio Test method (LRT). A brief description of the two methods is provided as follows:

The SE optimal threshold value is the value for which the mean square error of the EDF and CDF is the minimum for an estimator. Zoglat et al. [25] suggested an algorithm based on the work of Beirlant et al. [51]. The main steps of the algorithms are as follows (Adapted from Zoglat et al. [25]):

• Let $u_1,\dots ,u_m$ be m equally spaced increasing threshold candidates ($u_m$ is the threshold corresponding to the minimum number of exceedances—the number of years in the record multiplied by 1.65 [24]). For $j=1,\dots ,m$, let ${\widehat{\xi }}_{uj},{\widehat{\sigma }}_{uj}$ be the estimates from any of the six parameter estimators employed in the study of the scale and shape parameters of the GPD underlying the exceedances over the threshold $u_j$.
• Find $N_{uj}$, the number of exceedances over $u_j$.
• Simulate $\nu$ independent samples of size $N_{uj}$ from GPD with parameter ${\widehat{\xi }}_{uj},{\widehat{\sigma }}_{uj}$.
• For each $\alpha \in A=\left\{0.05,0.1,0.15,\dots ,0.95\right\}$, and each $i=1,\dots ,\nu$, calculate the quantile $q_{\left(\alpha ,u_j\right)}^i$ of the $i$th simulated sample compute Equation (9).

  $$q_{\left(\alpha ,u_j\right)}^{sim}=\frac{1}{\nu }{\sum }_{i=1}^{\nu }{q}_{\left(\alpha ,u_j\right)}^i,$$

  (9)
• For $j=1,\dots ,m$ calculate the square error, $S{E}_{u_j}=\sum _{\alpha \in A}{(\frac{q_{\left(\alpha ,u_j\right)}^{sim}}{q_{\left(\alpha ,u_j\right)}^{obs}})}^2$, where $q_{\left(\alpha ,u_j\right)}^{obs}$ is the observed quantile corresponding to the simulated quantile.
• The optimal threshold value is the value of minimum $S{E}_{u_j}$.

LRT was proposed by Zoglat e al. [25]. It is based on using the likelihood ration test statistic to test the hypothesis $H_0:u_i$ is the optimal threshold against $H_1:u_k$ is the optimal threshold. The LRT statistic is given by:

$$LR\left(u_i,u_k\right)=-2\log \frac{f({\widehat{\xi }}_{u_i},{\widehat{\sigma }}_{u_i},{\mathrm{X}}_{u_i})}{f({\widehat{\xi }}_{u_k},{\widehat{\sigma }}_{u_k},{\mathrm{X}}_{u_i})},$$

(10)

where LR is the likelihood ratio, $f(\dots )$ is the likelihood function, ${\mathrm{X}}_{u_i}$ is the vector of observations exceeding $u_i$, and ${\mathrm{X}}_{u_k}$ is the vector of observations exceeding $u_k$. For LRT application, the maximum threshold is selected to correspond to 36 exceedances—the number of years in the record multiplied by 1.65 [24]. For more details on LRT method see Zoglat et al. [25].

Further, to meet the requirements for the POT method, an independence test is applied to ensure that peaks identified with the POT method correspond to different flood events. The test is conditional for the set of sampled peaks and is a prerequisite to any statistical frequency analysis and to the Poisson process assumption [17,19]. To assess the degree of dependence between flood peaks, we examined autocorrelation coefficients. Specifically, when the absolute values of autocorrelation coefficients for different lag times, in time series with n observations, are less than or equal to the critical values, the flood peaks can be regarded as being independent from each other [22,56]. The critical values are equal to $\pm 1.96/\sqrt{n}$, corresponding to the 0.05 significance level, where n is the sample size. If more than two values exceed the critical values, this means the flood peaks are dependent; therefore, a higher threshold level without a restriction on the duration between flood peaks must be tried, as recommended by Ashkar and Rouselle [57]. In addition, the number of the sampled peaks was compared to 1.65 times the number of years in the record to ensure that it exceeds this lower bound and that the POT is therefore more effective than the AM series, as recommended by Cunnane [24]. The peaks were sampled automatically by an algorithm we developed in R [58]. Then the autocorrelation values of peaks were calculated and the figures were plotted using the “forecast” package in R [59] and visually checked.

In application, it is more convenient to interpret the POT flood frequency model in terms of quantiles or return levels [17,22]. Flood estimates can be made based on Poisson model, negative binomial, and binomial models. It is not necessary to prefer one model to the other models. Regardless of accepting or rejecting the Poisson hypothesis any of the three models can be used [60,61]. For more details on modeling the quantiles and return levels please refer to Cunnane [60] and Coles [17].

3. Results and Discussion

Quantile estimates and shape parameter estimates ($\xi$) are presented here, with a focus on the accuracy of the predicted high quantiles (floods with high return periods) rather than on the estimated parameters of the distribution.

3.1. Performance Analyses Results of the GPD Estimators Using MC Sampling Data

The average biases of the 99% quantile and shape parameter ($\xi$) for sample sizes ranging from n = 40 to 500 for different parameter estimators are presented in Figure 3 and Figure 4, respectively. The results can be summarized as follows (also see

Table 1. Sensitivity analyses of the parameter estimators to the sample size (n) for estimating the shape parameter ($\xi$) and the 99% quantile. Low represents an average bias range of 0–10% of the highest calculated bias, Medium represents the range 10–30% of the highest calculated bias, High represents values greater than 30%. Abbreviations are as follows: PWM—probability weighted moments, LME—likelihood moment estimator, MLE—maximum likelihood estimator, NEWLME—modified likelihood moment estimator, MGFAD—maximum goodness of fit-Anderson Darling estimator, NWLS—Nonlinear weighted least square estimator.

Parameter Estimator	Shape Parameter		99% Quantile
	$\mathit{\xi }$ > 0	$\mathit{\xi }$ < 0	$\mathit{\xi }$ > 0	$\mathit{\xi }$ < 0
PWM	Medium	Low	Low	Low
LME	Low	High	Low	High
MLE	High	High	Low	Low
NEWLME	Low	Medium	Medium	Low
MGFAD	Low	Low	High	High
NWLS	High	Medium	High	High

):

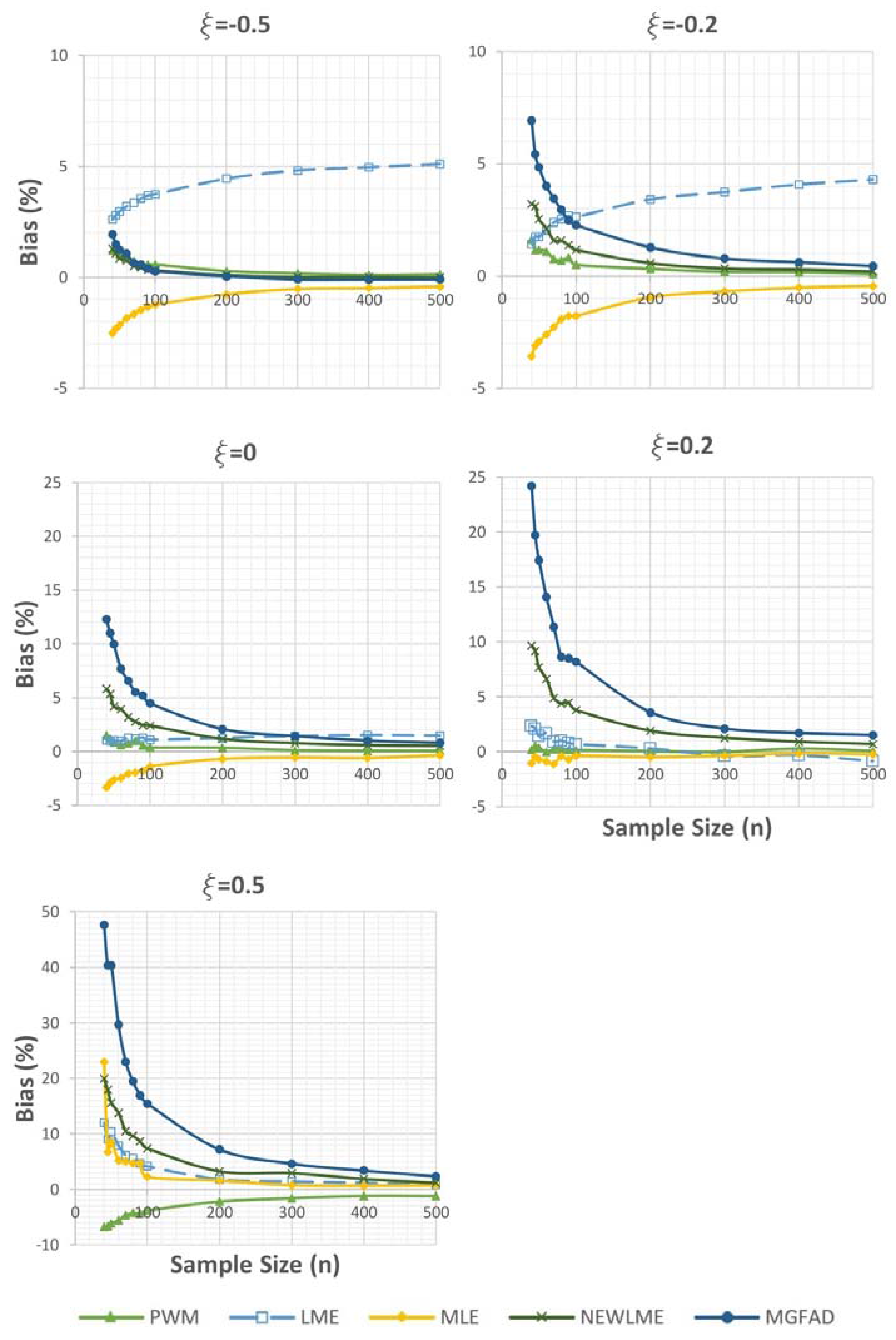
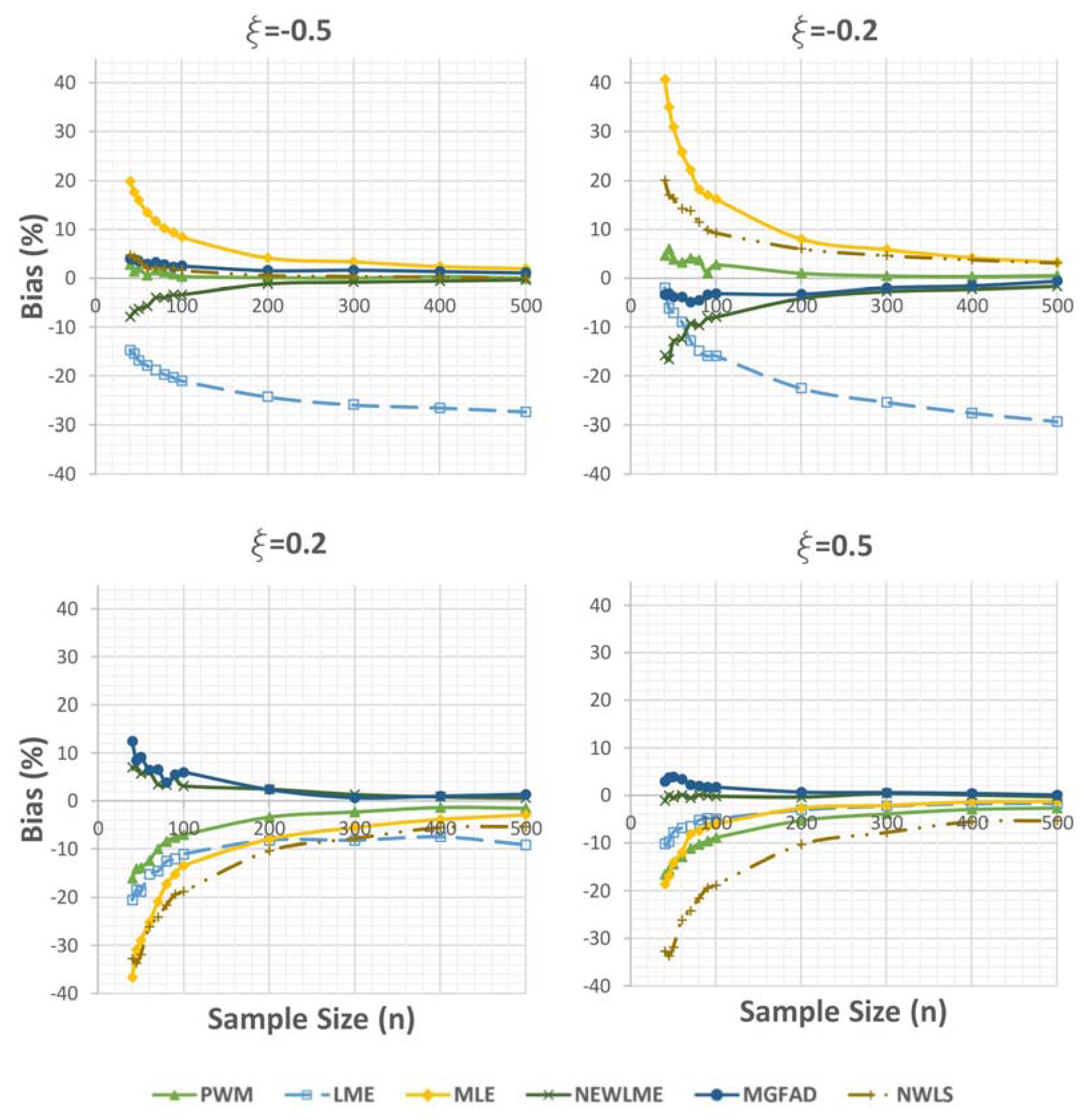
• Generally, the relative bias of estimated parameter values and the 99% quantile decreased with increasing sample size (n). However, for short tails ($\xi$ < 0) the bias was still high in the case of MLE and LME, even if the sample size was increased to 300.
• PWM: Very consistent and among all methods the least sensitive to sample size (n). However, it had a medium sensitivity to the sample size and medium bias for heavy tails with respect to estimating the shape parameter.
• LME: For heavy tails, LME was among the parameter estimators that had the lowest bias and sensitivity to the sample size. However, for short tails the biases in estimating the 99% quantile and shape parameter were very high.
• MLE: Very accurate in estimating the 99% quantile. However, it had a high bias in estimating the shape parameter and was very sensitive to the sample size for heavy and short tailed distributions.
• NEWLME: Average performance in estimating the 99% quantile for heavy tails and the shape parameter for short tails. In contrast, NEWLME excelled when estimating the shape parameter for heavy tails and estimating the 99% quantile for short tails.
• MGFAD: The most accurate and the least sensitive to sample size in estimating the shape parameter. However, it had a very high bias and sensitivity to the sample size when estimating the 99% quantile.
• NWLS: No trend of decreasing bias with increasing sample size (n) in predicting the 99% quantile. However, it showed a similar trend in the case of shape parameter estimations with average bias compared to the other methods.

In the application of flood frequency analysis, the value of the scale parameter can vary significantly, from 10 to 1000 or more; therefore, we examined the effect of varying scale parameter values on the accuracy of estimation of the 0.99 quantile. Surprisingly, the LME method, often reported as one of the better methods for GPD fitting in previous comparative studies [41,42,62], was found to be sensitive to high values of the scale parameter. In contrast, the other methods did not show the same sensitivity to the scale parameter value.

3.2. Application of POT to Observed Streamflows

The six parameter estimators were applied for the thresholds selected by both LRT and SE methods to the 47 stations from the study area. Accuracy of shape parameter estimation and the Goodness of Fit obtained with respect to AD and RMSE for different ranges of the shape parameter value are summarized in

Table 2. Goodness of Fit that can be achieved by a combination of the likelihood ratio test method (LRT) and different parameter estimators for different ranges of the shape parameter ($\xi$) in terms of (1) the bias in predicting the shape parameter, (2) Anderson-Darling (AD) test, and (3) the root-mean-square error (RMSE). High represents a variance ranges from 0% to 3% of the lowest possible RMSE or AD, Medium represents the range 3–10% of the lowest possible RMSE or AD, Low represents values greater than 10%. Abbreviations are as follows: AD—Anderson-Darling, RMSE—root-mean-square error, PWM—probability weighted moments, LME—likelihood moment estimator, MLE—maximum likelihood estimator, NEWLME—modified likelihood moment estimator, MGFAD—maximum goodness of fit-Anderson Darling estimator, NWLS—Nonlinear weighted least square estimator.

Parameter Estimator		PWM	LME	MLE	NEWLME	MGFAD	NWLS
Ξ	ξ > 0	Low	Low	Low	Low	Medium	High
	ξ < 0	Low	Medium	High	Medium	High	Medium
AD	ξ > 0.4	Low	Low	Low	Low	Low	Low
	0.4 > ξ > 0.2	Low	High	High	Low	Low	Low
	0.2 > ξ > 0	Low	Low	High	Low	Low	Low
	0 > ξ > −0.15	Low	Low	High	Medium	Medium	Low
	−0.15 > ξ > −0.25	Low	Low	Low	High	Low	Low
	ξ < −0.25	Medium	Low	Low	High	Medium	Medium
RMSE	ξ > 0.4	Low	Low	Low	Low	Low	Low
	0.4 > ξ > 0.2	Low	Low	Low	Low	Low	Low
	0.2 > ξ > 0	Low	Low	Low	Low	Low	Low
	0 > ξ > −0.15	Low	Low	Low	Low	Low	Low
	−0.15 > ξ > −0.25	Low	Low	Medium	Low	Low	Low
	ξ < −0.25	Low	Low	Low	Low	Low	Low

for LRT and

Table 3. Goodness of Fit that can be achieved by a combination of the square error method (SE) and different parameter estimators for different ranges of the shape parameter ($\xi$) in terms of (1) the bias in predicting the shape parameter, (2) Anderson-Darling (AD) test, and (3) the root-mean-square error (RMSE). High represents a variance ranges from 0% to 3% of the lowest possible RMSE or AD, Medium represents the range 3–10% of the lowest possible RMSE or AD, Low represents values greater than 10%.

Parameter Estimator		PWM	LME	MLE	NEWLME	MGFAD	NWLS
Ξ	ξ > 0	Low	Low	Low	Low	Low	Low
	ξ < 0	Low	Low	Low	Low	Low	Low
AD	ξ > 0.4	Low	Low	Low	Low	Low	High
	0.4 > ξ > 0.2	Low	Low	Low	Low	Low	Low
	0.2 > ξ > 0	Low	Low	Low	Low	Low	Low
	0 > ξ > −0.15	Low	Low	Low	Low	Low	Low
	−0.15 > ξ > −0.25	Low	Low	Low	Medium	Low	Low
	ξ < −0.25	High	Medium	Low	High	Medium	High
RMSE	ξ > 0.4	High	High	High	High	Medium	Low
	0.4 > ξ > 0.2	High	High	High	Medium	High	High
	0.2 > ξ > 0	High	High	High	Low	Low	Low
	0 > ξ > −0.15	High	High	High	Medium	Medium	Medium
	−0.15 > ξ > −0.25	High	High	High	Low	Medium	Medium
	ξ < −0.25	Low	High	Medium	Medium	Medium	High

for SE. Models developed for thresholds chosen by the SE method generally could not accurately estimate the shape parameter value. In contrast, models developed with NWLS with thresholds selected by the LRT method had high goodness of fit for heavy tails. Furthermore, models developed by MGFAD with thresholds selected by LRT method had high Goodness of Fit for short tails.

Generally, models developed with thresholds selected by the LRT had better Goodness of Fit with respect to the Anderson Darling (AD) test and higher RMSE. In contrast, models developed with thresholds selected by the SE had lower RMSE and higher AD statistics. The behavior of the parameter estimators was found to be similar within the ranges of the shape parameter identified in Table 2 and Table 3.

We investigated different combinations of threshold selection methods and parameter estimators to develop a new framework that improves the Goodness of Fit and minimizes the AD statistic and RMSE and, consequently, obtains more accurate predictions of flood return periods. We found that the combination of LRT and MLE outperformed other combinations for shape parameter values ranging from −0.15 to 0.4, while the LRT and NEWLME combination was the best for short tails for the range of shape parameter values from −0.25 to −0.15. For short tails with shape parameter values less than −0.25 and for heavy tails with shape parameter values greater than 0.4, the SE and NWLS gave the best fit compared to the other methods.

Our results demonstrate that the choice of best combination of parameter estimation and threshold selection methods depends on the range of values of the shape parameter. Hence, it is critical to have an accurate estimate of the shape parameter value prior to fitting the distribution. The combination of LRT and NWLS was found to perform best in predicting shape parameter values greater than zero, while the LRT with MGFAD was the best among other combinations to predict the shape parameter for short tails. Overall, based on the above findings, we have created a new framework for obtaining a more accurate flood frequency distribution that considers both the effect of threshold selection method and parameter estimator, as illustrated in the flow chart of Figure 5.

It could be argued that the MLE convergence problem may constrain the applicability of the resulting framework, because the MLE method for shape parameter values from −0.15 to 0.4 may produce solutions for MLE that do not converge. Although it is theoretically possible to have datasets for which no solution exists to the likelihood equations, it appears to be a very rare case in practical applications in hydrology [30].

The models for 47 hydrometric station records were fitted using the framework developed in this work (Figure 5). The resulting fitted models were compared to the models using the approach proposed by Zoglat et al. [25] (LRT-MLE). When the new framework was applied (e.g., Figure 4), a significant improvement in AD and RMSE was achieved. The Anderson-Darling (AD) test results was improved for 38% of the stations by an average of 65%. In addition, the RMSE was decreased for 35% of the stations by an average of 47% (see supplemental Table S2 for percentage improvements).

Further, the relationship between the sample size, i.e., the number of peaks, and the variance in the estimated shape and scale parameters was investigated. For the two parameters, the variance was found to increase with a decrease in the sample size, a result that agrees with those of other studies [13,25]. See supplemental Table S2 for the estimated parameters and their variance, and Figure S1 and Figure S2 for the relationship between the variance in shape and scale and the sample size. In addition, we investigated the sample size and variance of the two parameters versus the drainage area. We found that the variance in scale parameter increases with increasing drainage area, since—under the same hydrological conditions—increasing the drainage area increases the flow, which in turn increases the scale parameter value. A larger scale parameter value results in a larger variance in the scale parameter estimation (see Figure S3 for the relationship between the variance in scale and the drainage area). Further, the variance in the shape parameter decreases with increasing drainage area (see Figure S4 for the relationship between the variance in scale and the drainage area). Finally, the sample size decreases with increasing drainage area (see Figure S5 for the relationship between the sample size and drainage area).

4. Conclusions

The performance of the POT method and the accuracy of estimated floods depend on both the selected threshold and the parameter estimator. In this paper, we proposed a systematic and flexible procedure to assess the combined effect of the threshold selection method and the GPD parameter estimator on the accuracy of the flood frequency distribution. The accuracy of estimating the shape parameter value and the 0.99 quantile were investigated for the MLE, PWM, LME, NEWLME, MGFAD, NWLS estimators by conducting a series of Monte Carlo simulation studies. We found that NWLS and MLE are better parameter estimation methods for heavy tails, while MLE, NEWLME, and NWLS are better parameter estimation methods for short tails. Furthermore, in addition to the tail behavior effect, the value of the scale parameter can also significantly influence the accuracy of LME.

In our study, the six parameter estimators were applied for the thresholds selected by both LRT and SE methods to each of 47 streamflow records. Our results demonstrated that the effects of variations in parameter estimators and threshold selection method must be performed a priori to allow for the most accurate estimates of flood frequency.

We tested our hypothesis by trying different combinations of threshold selection methods and parameter estimators to minimize the AD statistic and RMSE of the developed models. A new framework resulted from this minimization process. The new framework was then applied to each of 47 stations and the developed models using the new framework were compared to the models developed using MLE for parameter estimator and LRT as the threshold selection method. Using the new framework, the AD test results improved for 38% of the stations by an average of 65%. In addition, the RMSE was decreased for 35% of the stations by an average of 47%. Hence, more accurate flood frequency models and flood estimates can be obtained using the new framework, with its improved threshold selection and GPD parameter estimator selection.

The framework developed in this study is widely applicable since it is based on the analysis of data of 47 watersheds with diverse geo-hydro-climatic conditions. More importantly, given that the assumption of independent and identically distributed flood variables is maintained, it will be applicable in other catchments irrespective of their location and other hydrological conditions. Two main reasons can explain our conclusion: (i) from a statistical point of view, the sampled data covered a sufficient range of the shape parameter values that can be found in any catchment irrespective of the location of the catchment, as suggested by Hosking and Wallis [40] and later confirmed by Choulakian and Stephens [30]. In addition, the methods that were concluded to be dependent on the scale parameter value were not considered in the framework; (ii) the framework suggested in Figure 5 was generated from a combination of Monte-Carlo simulations and datasets sampled from streamflow. The results of the sampled streamflow peaks are in accordance with the findings from Monte-Carlo simulations that were based on generated datasets and covered a broader range of values of thresholds, shape parameter, and scale parameter.

The findings of this study can be applied to a wide range of situations. First, our systematic assessment procedure can be used to investigate the combined effect of new GPD parameter estimators and threshold selection methods, leading to better estimations for all POT applications in general, and specifically to flood frequency analysis. More accurate flood estimates are important for climate change adaptation requirements including insurance applications, establishment of the design flood for hydraulic and flood protection structures, and the projection of climate change impacts on flood events.