Forecasting of Industrial Water Demand Using Case-Based Reasoning—A Case Study in Zhangye City, China
Abstract
:1. Introduction
2. Study Area and Data Sources
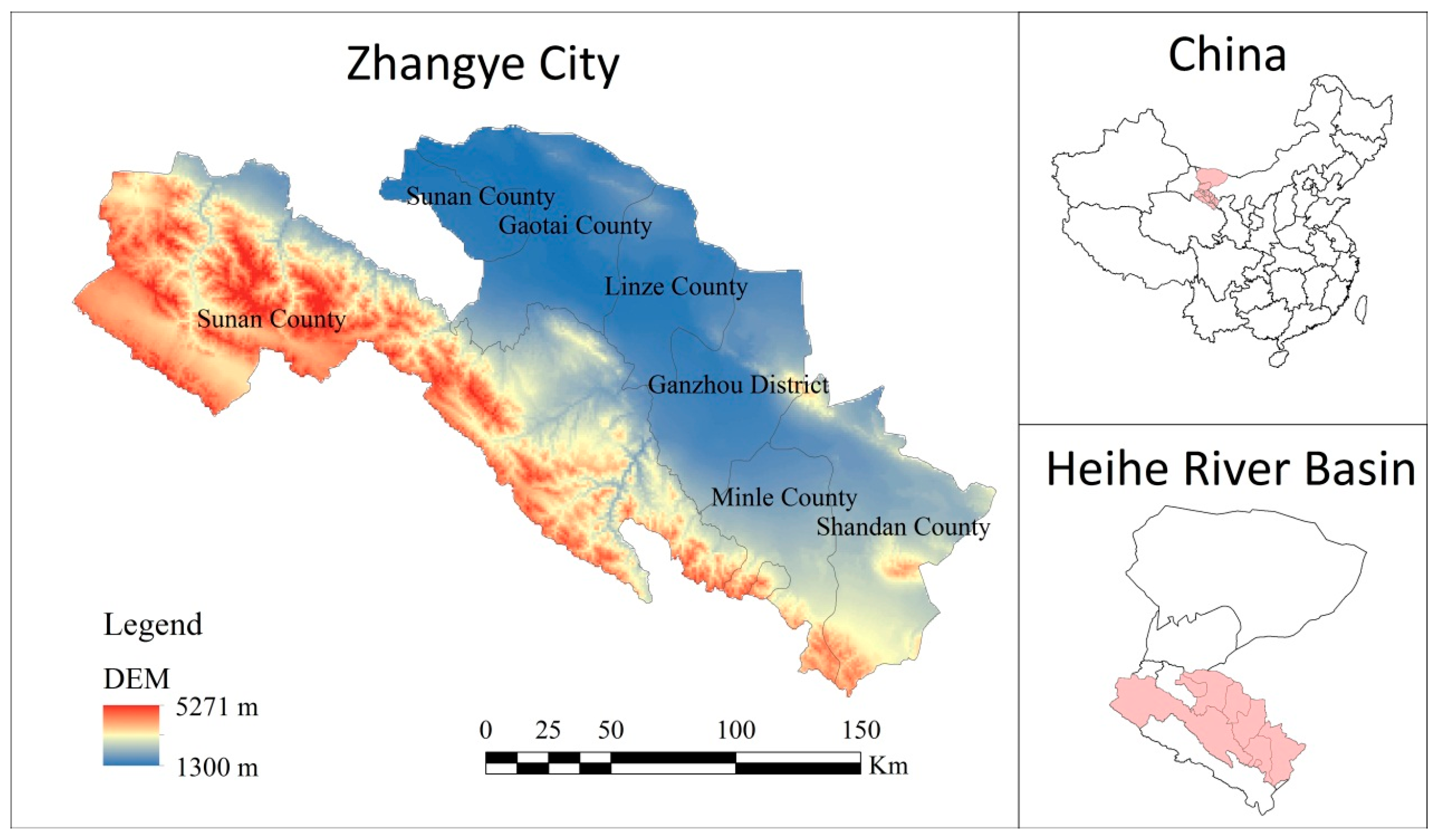
2.1. Study Area
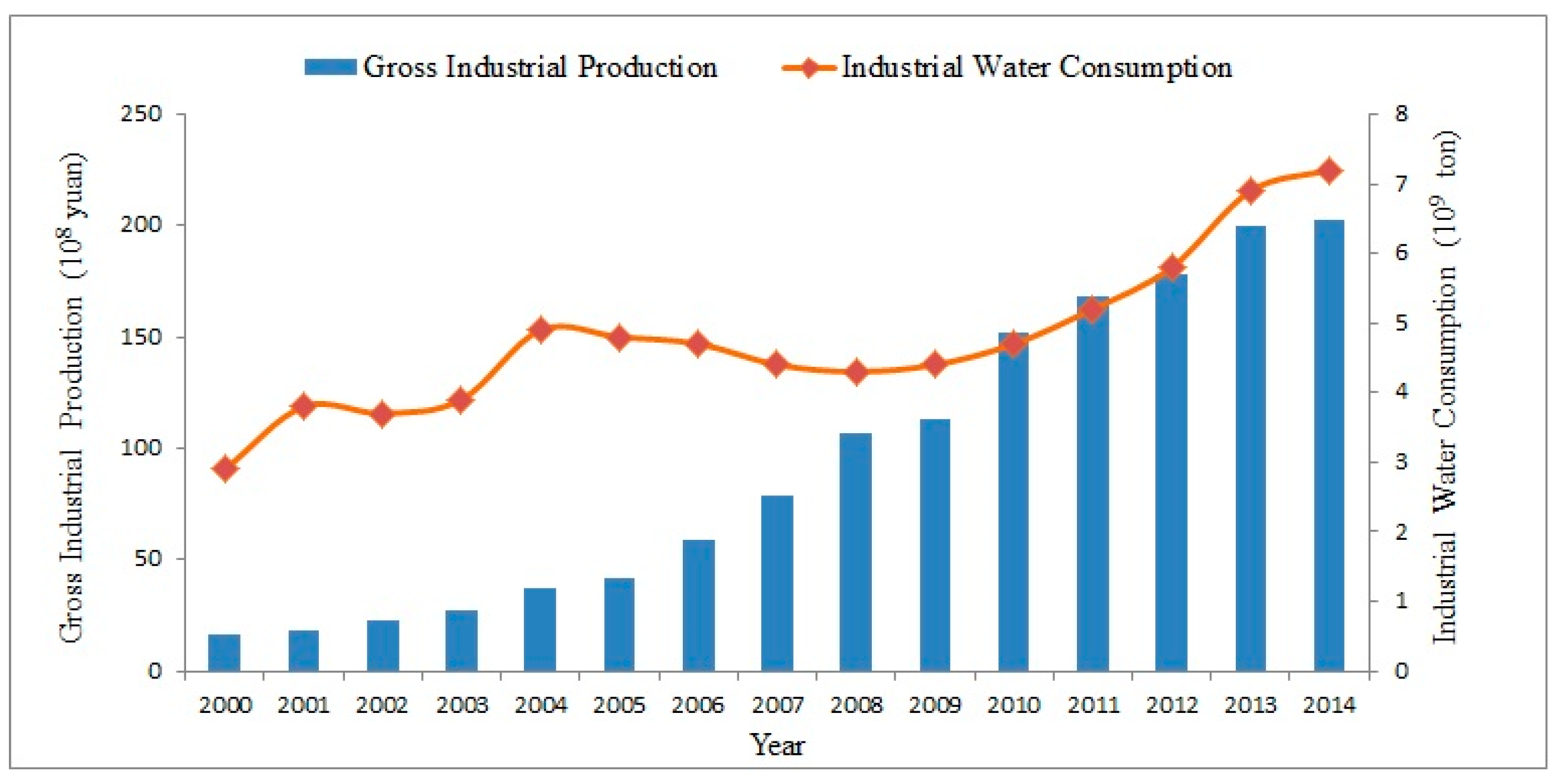
2.2. Data Sources
3. Methodology
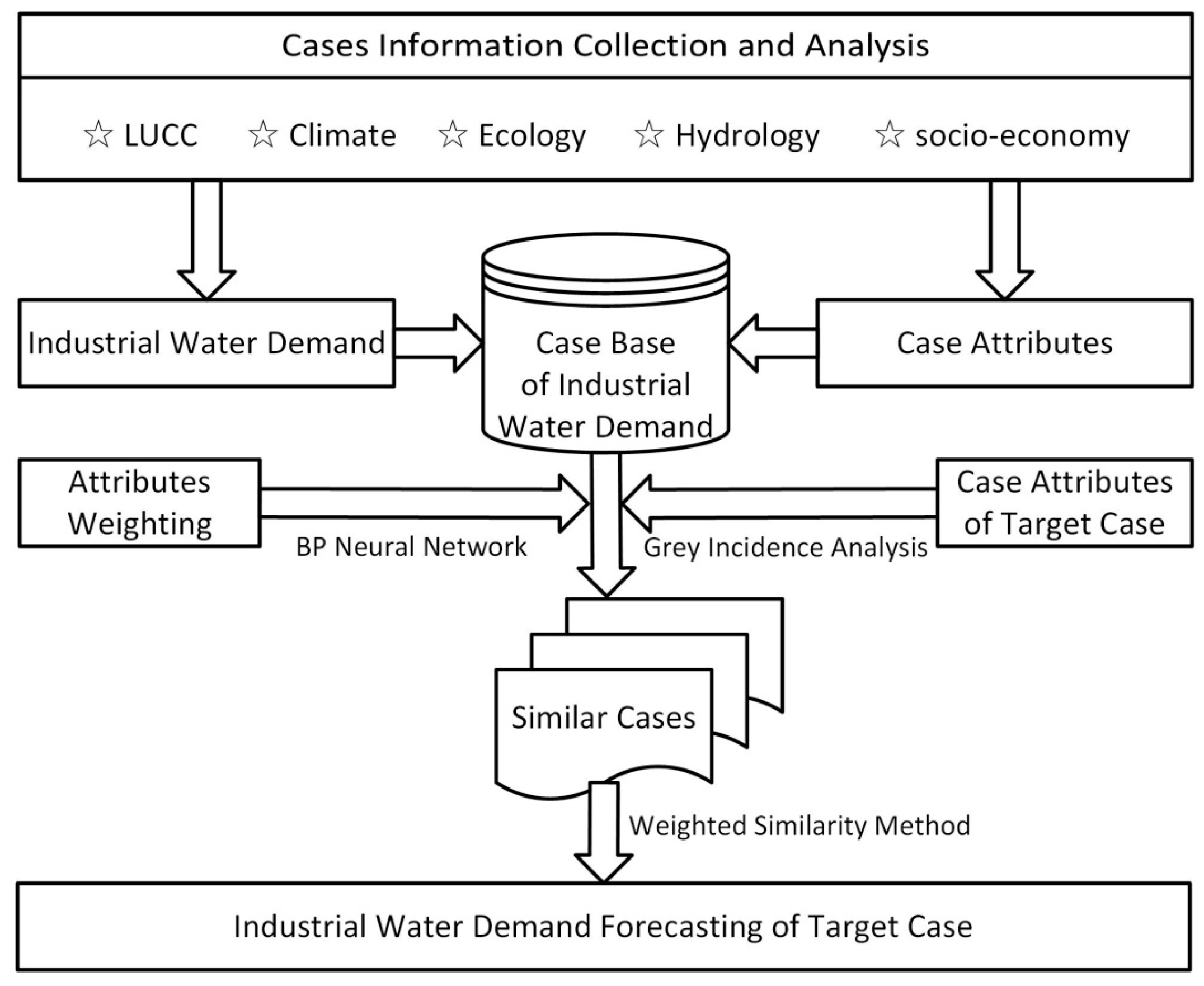
3.1. CBR Forecasting Framework
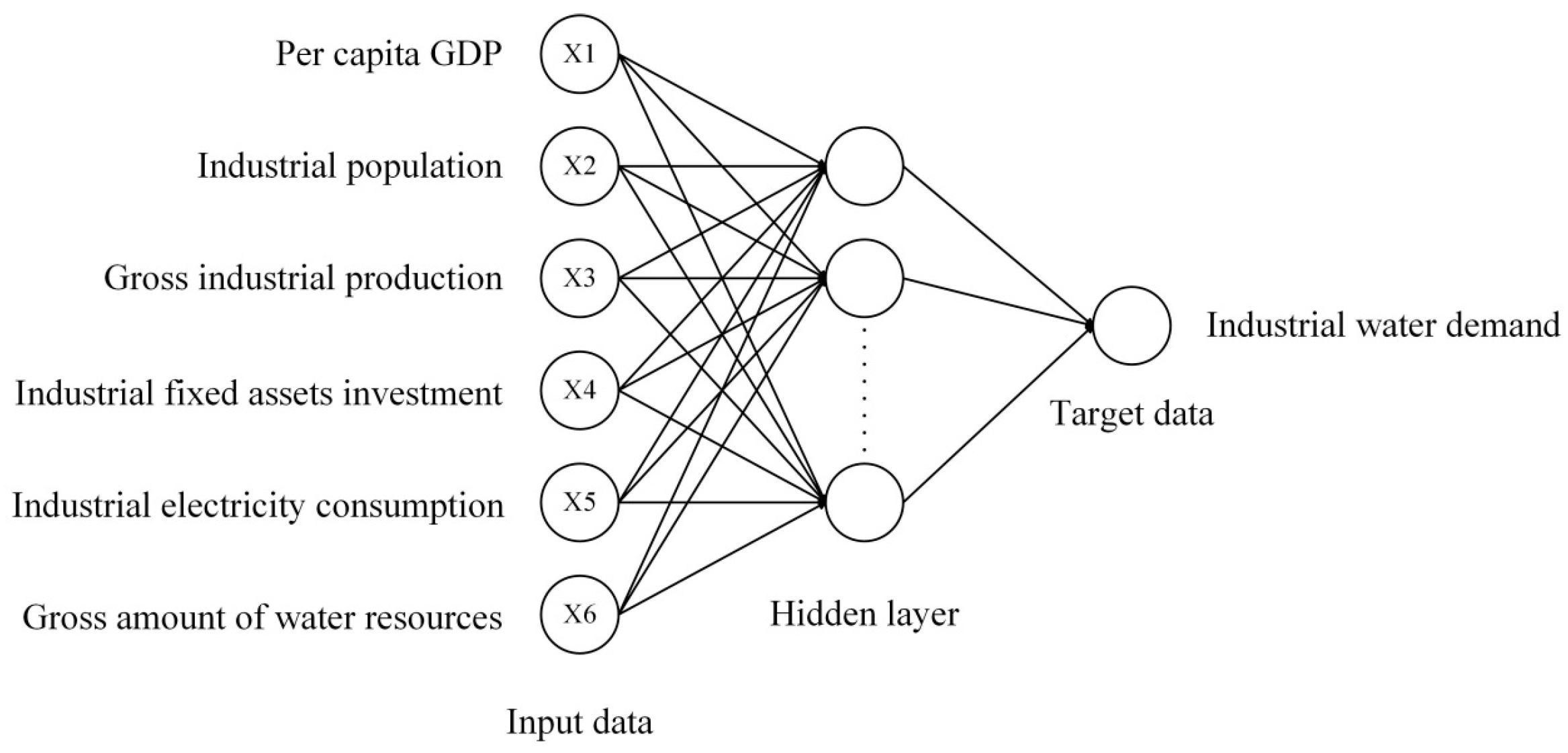
3.2. Extraction of Case Attributes
3.3. Attributes Weighting Based on the Back Propagation Neural Network (BPN)
3.4. Similarities Calculation Based on Grey Incidence Analysis
3.5. Industrial Water Demand Forecasting
4. Results
4.1. Validation of the CBR Model
4.2. Forecasting of the Target Case
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Cities | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hefei | 0.9057 | 0.9109 | 0.9070 | 0.9072 | 0.9052 | 0.9090 | 0.9209 | 0.9066 | 0.9093 | 0.9100 | 0.8582 | 0.8371 | 0.8042 | 0.7794 | 0.7104 |
| Guangzhou | 0.7721 | 0.7963 | 0.7949 | 0.7248 | 0.7150 | 0.7122 | 0.7547 | 0.7502 | 0.7167 | 0.6338 | 0.6845 | 0.6931 | 0.6740 | 0.6559 | 0.6122 |
| Fuzhou | 0.8711 | 0.8686 | 0.8691 | 0.8820 | 0.8508 | 0.8371 | 0.8404 | 0.8117 | 0.7913 | 0.8182 | 0.8044 | 0.7972 | 0.7769 | 0.7473 | 0.7062 |
| Guiyang | 0.8908 | 0.8854 | 0.8834 | 0.8910 | 0.8991 | 0.8825 | 0.8933 | 0.8898 | 0.8743 | 0.8940 | 0.8894 | 0.8877 | 0.9123 | 0.8821 | 0.8821 |
| Xining | 0.9023 | 0.9019 | 0.9020 | 0.9057 | 0.9067 | 0.8956 | 0.8898 | 0.8975 | 0.8954 | 0.9312 | 0.9418 | 0.9512 | 0.9530 | 0.9520 | 0.9376 |
| Yinchuan | 0.9047 | 0.9061 | 0.9073 | 0.9116 | 0.9179 | 0.9227 | 0.9312 | 0.9453 | 0.9560 | 0.9600 | 0.9677 | 0.9401 | 0.9215 | 0.8841 | 0.8748 |
| Qingdao | 0.8367 | 0.8397 | 0.8275 | 0.8247 | 0.8081 | 0.7875 | 0.7927 | 0.7838 | 0.7461 | 0.7221 | 0.6951 | 0.6694 | 0.6378 | 0.6105 | 0.6053 |
| Suzhou | 0.8239 | 0.8235 | 0.8103 | 0.7577 | 0.7258 | 0.6989 | 0.6631 | 0.6332 | 0.6132 | 0.5992 | 0.5531 | 0.5405 | 0.5212 | 0.5030 | 0.5058 |
| Kunming | 0.8654 | 0.8675 | 0.8672 | 0.8730 | 0.8762 | 0.8589 | 0.8660 | 0.8587 | 0.8630 | 0.8709 | 0.8697 | 0.8746 | 0.8669 | 0.8506 | 0.8471 |
| Shenyang | 0.8752 | 0.8844 | 0.8923 | 0.8989 | 0.8970 | 0.8842 | 0.8769 | 0.8804 | 0.8526 | 0.8249 | 0.7979 | 0.7802 | 0.7558 | 0.7454 | 0.7380 |
| Changchun | 0.8943 | 0.8979 | 0.9077 | 0.9154 | 0.9186 | 0.9141 | 0.9047 | 0.8942 | 0.8927 | 0.8842 | 0.8700 | 0.8594 | 0.8346 | 0.8123 | 0.7866 |
| Urumqi | 0.9106 | 0.9119 | 0.9153 | 0.9193 | 0.9234 | 0.9279 | 0.9330 | 0.9384 | 0.9523 | 0.9585 | 0.9566 | 0.9268 | 0.8957 | 0.8923 | 0.8802 |
| Chongqing | 0.7586 | 0.7605 | 0.7406 | 0.7352 | 0.7229 | 0.7130 | 0.7086 | 0.6593 | 0.6400 | 0.6316 | 0.6110 | 0.6114 | 0.6183 | 0.6053 | 0.5642 |
| Tianjin | 0.8076 | 0.8063 | 0.8035 | 0.8021 | 0.8016 | 0.8057 | 0.8005 | 0.7612 | 0.7126 | 0.6760 | 0.6274 | 0.5952 | 0.5849 | 0.5554 | 0.5399 |
| Zhengzhou | 0.8300 | 0.8241 | 0.8165 | 0.8216 | 0.8252 | 0.8296 | 0.8223 | 0.8034 | 0.8022 | 0.7851 | 0.7600 | 0.7297 | 0.7395 | 0.7256 | 0.7125 |
| Chengdu | 0.8349 | 0.8283 | 0.8224 | 0.8158 | 0.8073 | 0.7968 | 0.7981 | 0.7740 | 0.7570 | 0.7742 | 0.7424 | 0.7022 | 0.6598 | 0.6475 | 0.6617 |
| Dalian | 0.8859 | 0.8779 | 0.8917 | 0.9040 | 0.9200 | 0.9081 | 0.9050 | 0.8817 | 0.8386 | 0.8042 | 0.7790 | 0.7715 | 0.7331 | 0.7254 | 0.7127 |
| Shanghai | 0.7132 | 0.7093 | 0.7135 | 0.7128 | 0.7025 | 0.6817 | 0.6606 | 0.6315 | 0.6087 | 0.6054 | 0.5858 | 0.5721 | 0.5665 | 0.5550 | 0.5521 |
| Wuhan | 0.8295 | 0.8314 | 0.8371 | 0.8259 | 0.8386 | 0.8406 | 0.8350 | 0.8345 | 0.8134 | 0.7899 | 0.7408 | 0.7123 | 0.6725 | 0.6430 | 0.6239 |
| Beijing | 0.8001 | 0.8008 | 0.8025 | 0.8049 | 0.8078 | 0.7887 | 0.7715 | 0.7408 | 0.7489 | 0.7372 | 0.7108 | 0.6855 | 0.6833 | 0.6698 | 0.6639 |
| Changsha | 0.8558 | 0.8552 | 0.8557 | 0.8576 | 0.8568 | 0.8624 | 0.8693 | 0.8728 | 0.8700 | 0.8343 | 0.7890 | 0.7686 | 0.7187 | 0.6982 | 0.6872 |
| Nanchang | 0.8558 | 0.8643 | 0.8593 | 0.8647 | 0.8779 | 0.8747 | 0.8850 | 0.8934 | 0.8922 | 0.8848 | 0.8597 | 0.8391 | 0.7886 | 0.7707 | 0.7528 |
| Nanjing | 0.8688 | 0.8637 | 0.8640 | 0.8665 | 0.8700 | 0.8643 | 0.8604 | 0.7396 | 0.8040 | 0.7861 | 0.7461 | 0.7134 | 0.6813 | 0.6642 | 0.6656 |
| Jinan | 0.8462 | 0.8490 | 0.8519 | 0.8606 | 0.8629 | 0.8607 | 0.8642 | 0.8654 | 0.8455 | 0.8277 | 0.8023 | 0.7949 | 0.7831 | 0.7598 | 0.7495 |
| Wuxi | 0.8582 | 0.8564 | 0.8551 | 0.8329 | 0.7904 | 0.7708 | 0.7421 | 0.7212 | 0.6861 | 0.6729 | 0.6403 | 0.6264 | 0.6091 | 0.5997 | 0.5959 |
| Shijiazhuang | 0.8810 | 0.8847 | 0.8851 | 0.8827 | 0.8835 | 0.8659 | 0.8605 | 0.8517 | 0.8495 | 0.8434 | 0.8353 | 0.8341 | 0.8204 | 0.8002 | 0.7826 |
| Xi’an | 0.8899 | 0.8928 | 0.8907 | 0.8911 | 0.8922 | 0.8962 | 0.8990 | 0.8950 | 0.8930 | 0.8975 | 0.9022 | 0.9091 | 0.8821 | 0.8605 | 0.8553 |
| Zhangye | 0.9061 | 0.9082 | 0.9100 | 0.9087 | 0.9090 | 0.9136 | 0.9157 | 0.9179 | 0.9192 | 0.9236 | 0.9293 | 0.9347 | 0.9447 | 0.9465 | 0.9525 |
References
- Rijsberman, F.R. Water scarcity: Fact or fiction? Agric. Water Manag. 2006, 80, 5–22. [Google Scholar] [CrossRef]
- Deng, X.; Zhao, C. Identification of water scarcity and providing solutions for adapting to climate changes in the Heihe River Basin of China. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed]
- Katz, D. Water use and economic growth: Reconsidering the Environmental Kuznets Curve relationship. J. Clean. Prod. 2015, 88, 205–213. [Google Scholar] [CrossRef]
- Johannsen, I.M.; Hengst, J.C.; Goll, A.; Höllermann, B.; Diekkrüger, B. Future of Water Supply and Demand in the Middle Drâa Valley, Morocco, under Climate and Land Use Change. Water 2016, 8, 313. [Google Scholar] [CrossRef]
- Nian, Y.; Li, X.; Zhou, J.; Hu, X. Impact of land use change on water resource allocation in the middle reaches of the Heihe River Basin in northwestern China. J. Arid Land 2014, 6, 273–286. [Google Scholar] [CrossRef]
- Connor, R. The United Nations World Water Development Report 2015: Water for a Sustainable World; UNESCO Publishing: Paris, France, 2015. [Google Scholar]
- Bai, M.; Zhou, S.; Zhao, M.; Yu, J. Water use efficiency improvement against a backdrop of expanding city agglomeration in developing countries—A case study on industrial and agricultural water use in the Bohai Bay region of China. Water 2017, 9, 89. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, F.; Wang, Z.; Li, X.; Zhang, T. An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China. Sustainability 2014, 6, 3301–3320. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting: Evaluation of different ANN learning algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Zhai, Y.; Wang, J.; Teng, Y.; Zuo, R. Water demand forecasting of Beijing using the time series forecasting method. J. Geogr. Sci. 2012, 22, 919–932. [Google Scholar] [CrossRef]
- Mohamed, M.M.; Almualla, A.A. Water demand forecasting in Umm Al-Quwain (UAE) using the the IWR-MAIN specify forecasting mode. Water Resour. Manag. 2010, 24, 4093–4120. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Kibria, G. Principal component regression analysis in water demand forecasting: An application to the blue mountains, NSW, Australia. J. Hydrol. Environ. Res. 2016, 1, 49–59. [Google Scholar]
- Jain, A.; Varshney, A.K.; Joshi, U.C. Short-term water demand forecast modelling at IIT Kanpur using artificial neural networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Liu, J.; Savenije, H.H.; Xu, J. Forecast of water demand in Weinan City in China using WDF-ANN model. Phys. Chem. Earth Parts A/B/B 2003, 28, 219–224. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Adamowski, J.F. Peak daily water demand forecast modeling using artificial neural networks. J. Water Resour. Plan. Manag. 2008, 134, 119–128. [Google Scholar] [CrossRef]
- Zhang, Q.; Diao, Y.; Dong, J. Regional water demand prediction and analysis based on Cobb-Douglas model. Water Resour. Manag. 2013, 27, 3103–3113. [Google Scholar] [CrossRef]
- Weatherhead, E.K.; Knox, J.W. Predicting and mapping the future demand for irrigation water in England and Wales. Agric. Water Manag. 2000, 43, 203–218. [Google Scholar] [CrossRef]
- Gato, S.; Jayasuriya, N.; Roberts, P. Temperature and rainfall thresholds for base use urban water demand modelling. J. Hydrol. 2007, 337, 364–376. [Google Scholar] [CrossRef]
- Mo, X.; Liu, S.; Lin, Z.; Xu, Y.; Xiang, Y.; Mcvicar, T.R. Prediction of crop yield, water consumption and water use efficiency with a SVAT-crop growth model using remotely sensed data on the north China plain. Ecol. Model. 2005, 183, 301–322. [Google Scholar] [CrossRef]
- Pulido-Calvo, I.; Montesinos, P.; Roldán, J.; Ruiznavarro, F. Linear regressions and neural approaches to water demand forecasting in irrigation districts with telemetry systems. Biosyst. Eng. 2007, 97, 283–293. [Google Scholar] [CrossRef]
- Bello-Tomás, J.J.; González-Calero, P.A.; Díaz-Agudo, B. Jcolibri: An object-oriented framework for building CBR systems. In Advances in Case-Based Reasoning, Proceedings of the 7th European Conference on Case-Based Reasoning, Madrid, Spain, 30 August–2 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 29–39. [Google Scholar]
- Bergmann, R.; Stahl, A. Similarity measures for object-oriented case representations. In Proceedings of the Forth European Workshop on Case-Based Reasoning, Dublin, Ireland, 23–25 September 1998; Springer: Berlin/Heidelberg, Germany; pp. 25–36. [Google Scholar]
- Reyes, E.R.; Negny, S.; Robles, G.C.; Le Lann, J.M. Improvement of online adaptation knowledge acquisition and reuse in case-based reasoning: Application to process engineering design. Eng. Appl. Artif. Intell. 2015, 41, 1–16. [Google Scholar] [CrossRef]
- Shin, K.S.; Han, I. Case-based reasoning supported by genetic algorithms for corporate bond rating. Expert Syst. Appl. 1999, 16, 85–95. [Google Scholar] [CrossRef]
- Kolodner, J. Case-Based Reasoning; Morgan Kaufmann Publishers Inc.: San Meteo, CA, USA, 1993. [Google Scholar]
- Leake, D.B. Problem solving and reasoning: Case-based. Int. Encycl. Soc. Behav. Sci. 2015, 2015, 56–60. [Google Scholar]
- Zhao, K.; Yu, X. A case based reasoning approach on supplier selection in petroleum enterprises. Expert Syst. Appl. 2011, 38, 6839–6847. [Google Scholar] [CrossRef]
- Olsson, E.; Funk, P.; Xiong, N. Fault diagnosis in industry using sensor readings and case-based reasoning. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2004, 15, 41–46. [Google Scholar]
- Yang, B.S.; Han, T.; Kim, Y.S. Integration of ART-Kohonen neural network and case-based reasoning for intelligent fault diagnosis. Expert Syst. Appl. 2004, 26, 387–395. [Google Scholar] [CrossRef]
- Madhusudan, T.; Zhao, J.L.; Marshall, B. A case-based reasoning framework for workflow model management. Data Knowl. Eng. 2004, 50, 87–115. [Google Scholar] [CrossRef]
- Li, Y.F.; Xie, M.; Goh, T.N. A study of mutual information based feature selection for case based reasoning in software cost estimation. Expert Syst. Appl. 2009, 36, 5921–5931. [Google Scholar] [CrossRef]
- Shin, K.S.; Han, I. A case-based approach using inductive indexing for corporate bond rating. Decis. Support Syst. 2001, 32, 41–52. [Google Scholar] [CrossRef]
- Fan, C.Y.; Chang, P.C.; Lin, J.J.; Hsieh, J.C. A hybrid model combining case-based reasoning and fuzzy decision tree for medical data classification. Appl. Soft Comput. 2011, 11, 632–644. [Google Scholar] [CrossRef]
- Holt, A.; Bichindaritz, I.; Schmidt, R.; Perner, P. Medical applications in case-based reasoning. Knowl. Eng. Rev. 2005, 20, 289–292. [Google Scholar] [CrossRef]
- Huang, M.J.; Chen, M.Y.; Lee, S.C. Integrating data mining with case-based reasoning for chronic diseases prognosis and diagnosis. Expert Syst. Appl. 2007, 32, 856–867. [Google Scholar] [CrossRef]
- Amailef, K.; Lu, J. Ontology-supported case-based reasoning approach for intelligent m-Government emergency response services. Decis. Support Syst. 2013, 55, 79–97. [Google Scholar] [CrossRef]
- Liu, W.; Hu, G.; Li, J. Emergency resources demand prediction using case-based reasoning. Saf. Sci. 2012, 50, 530–534. [Google Scholar] [CrossRef]
- Du, Y.; Wen, W.; Cao, F.; Ji, M. A case-based reasoning approach for land use change prediction. Expert Syst. Appl. 2010, 37, 5745–5750. [Google Scholar] [CrossRef]
- Li, X.; Liu, X. An extended cellular automaton using case-based reasoning for simulating urban development in a large complex region. Int. J. Geogr. Inf. Sci. 2006, 20, 1109–1136. [Google Scholar] [CrossRef]
- Jonassen, D.H.; Hernandez-Serrano, J. Case-based reasoning and instructional design: Using stories to support problem solving. Educ. Technol. Res. Dev. 2002, 50, 65–77. [Google Scholar] [CrossRef]
- Shen, Y.; Colloc, J.; Jacquet-Andrieu, A.; Kai, L. Emerging medical informatics with case-based reasoning for aiding clinical decision in multi-agent system. J. Biomed. Inf. 2015, 56, 307–317. [Google Scholar] [CrossRef] [PubMed]
- De Mantaras, R.L.; McSherry, D.; Bridge, D.; Leake, D.; Smyth, B.; Craw, S.; Keane, M. Retrieval, reuse, revision and retention in case-based reasoning. Knowl. Eng. Rev. 2005, 20, 215–240. [Google Scholar] [CrossRef]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Guan, Q.; Wang, L.; Clarke, K.C. An artificial-neural-network-based, constrained CA model for simulating urban growth. Cartogr. Geogr. Inf. Sci. 2005, 32, 369–380. [Google Scholar] [CrossRef]
- Chen, G.; Yu, J. Two Sub-swarms Particle Swarm Optimization Algorithm. In Advances in Natural Computation, Procedings of the International Conference on Natural Computation, Changsha, China, 27–29 August 2005; Springer: Berlin/Heidelberg, Germany; pp. 515–524.
- Venkatesan, R.; Kumar, V. A genetic algorithms approach to growth phase forecasting of wireless subscribers. Int. J. Forecast. 2002, 18, 625–646. [Google Scholar] [CrossRef]
- Harpham, C.; Dawson, C.W.; Brown, M.R. A review of genetic algorithms applied to training radial basis function networks. Neural Comput. Appl. 2004, 13, 193–201. [Google Scholar] [CrossRef]
- Salajegheh, E.; Gholizadeh, S. Optimum design of structures by an improved genetic algorithm using neural networks. Adv. Eng. Softw. 2005, 36, 757–767. [Google Scholar] [CrossRef]

| Case Attributes | Weight | Predicted Value of Zhangye in 2030 |
|---|---|---|
| industrial population | 0.2200 | 39.10 × 103 |
| per capita GDP | 0.1874 | 41.91 × 103 yuan |
| gross industrial production | 0.1176 | 37.53 × 109 yuan |
| industrial fixed assets investment | 0.1951 | 19.06 × 109 yuan |
| industrial electricity consumption | 0.1247 | 2.37 × 109 kw·h |
| gross amount of water resources | 0.1553 | 3.63 × 109 ton |
| Year | Forecast | Observed | Relative Error |
|---|---|---|---|
| 2013 | 65 | 69 | −5.80% |
| 2014 | 73 | 72 | 1.39% |
| Methods | Forecast | Observed | Relative Error |
|---|---|---|---|
| CBR | 65 | 69 | −5.80% |
| GM(1, 1) | 81 | 69 | 17.39% |
| BPN | 55 | 69 | −20.29% |
| City_Year | Similarity | City_Year | Similarity |
|---|---|---|---|
| Yinchuan_2008 | 0.9560 | Urumqi_2010 | 0.9566 |
| Urumqi_2008 | 0.9523 | Xining_2011 | 0.9512 |
| Yinchuan_2009 | 0.9600 | Xining_2012 | 0.9530 |
| Urumqi_2009 | 0.9585 | Xining_2013 | 0.9520 |
| Yinchuan_2010 | 0.9677 | Zhangye_2014 | 0.9525 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Zheng, W.; Ke, X. Forecasting of Industrial Water Demand Using Case-Based Reasoning—A Case Study in Zhangye City, China. Water 2017, 9, 626. https://doi.org/10.3390/w9080626
Yang B, Zheng W, Ke X. Forecasting of Industrial Water Demand Using Case-Based Reasoning—A Case Study in Zhangye City, China. Water. 2017; 9(8):626. https://doi.org/10.3390/w9080626
Chicago/Turabian StyleYang, Bohan, Weiwei Zheng, and Xinli Ke. 2017. "Forecasting of Industrial Water Demand Using Case-Based Reasoning—A Case Study in Zhangye City, China" Water 9, no. 8: 626. https://doi.org/10.3390/w9080626
APA StyleYang, B., Zheng, W., & Ke, X. (2017). Forecasting of Industrial Water Demand Using Case-Based Reasoning—A Case Study in Zhangye City, China. Water, 9(8), 626. https://doi.org/10.3390/w9080626





