Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives
Abstract
:1. Introduction
2. Methodology
- Obtain the matrix of relative membership grades , where rij is defined as the relative membership grade. corresponds to bigger means better indexes, and corresponds to smaller means better indexes;
- Obtain the transposed matrix of , that is,;
- Calculate non-normalized weighting vectors as follows:where p is the distance parameter, in which p = 1 means Hamming distance and p = 2 means Euclidean distance. In this paper, p = 2.
- Calculate the maximum relative membership grade for the comprehensive benefits of sample j, which is named as the comprehensive benefit coefficient (uj) as follows:where is the normalized weight, , and .
- Transform the multiple objectives into a single one. The following formula can be used to replace Formula (1a):
3. Application
3.1. Study Area and Problem Statement
3.2. Data Source and Processing
3.3. Model Establishment
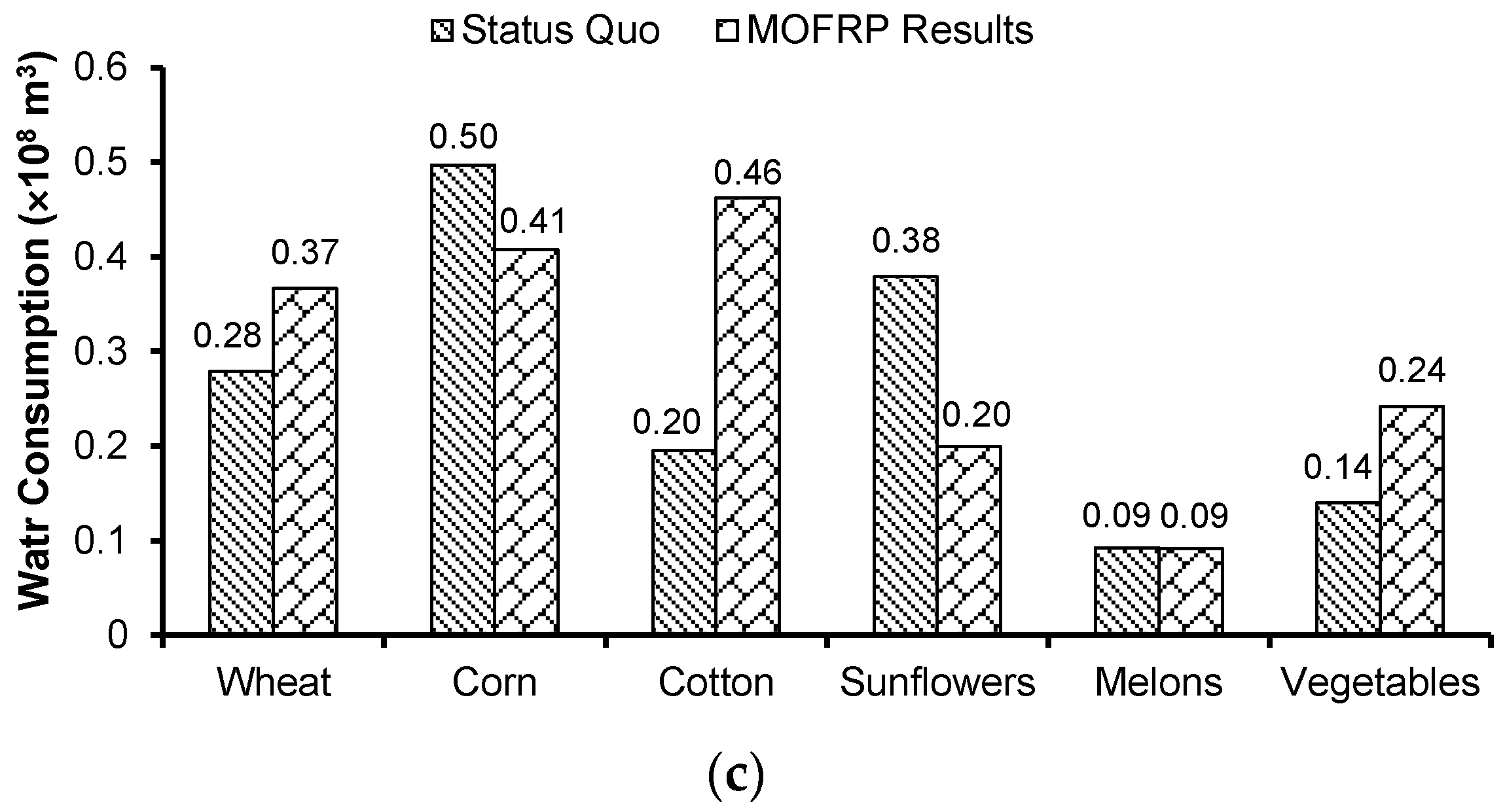
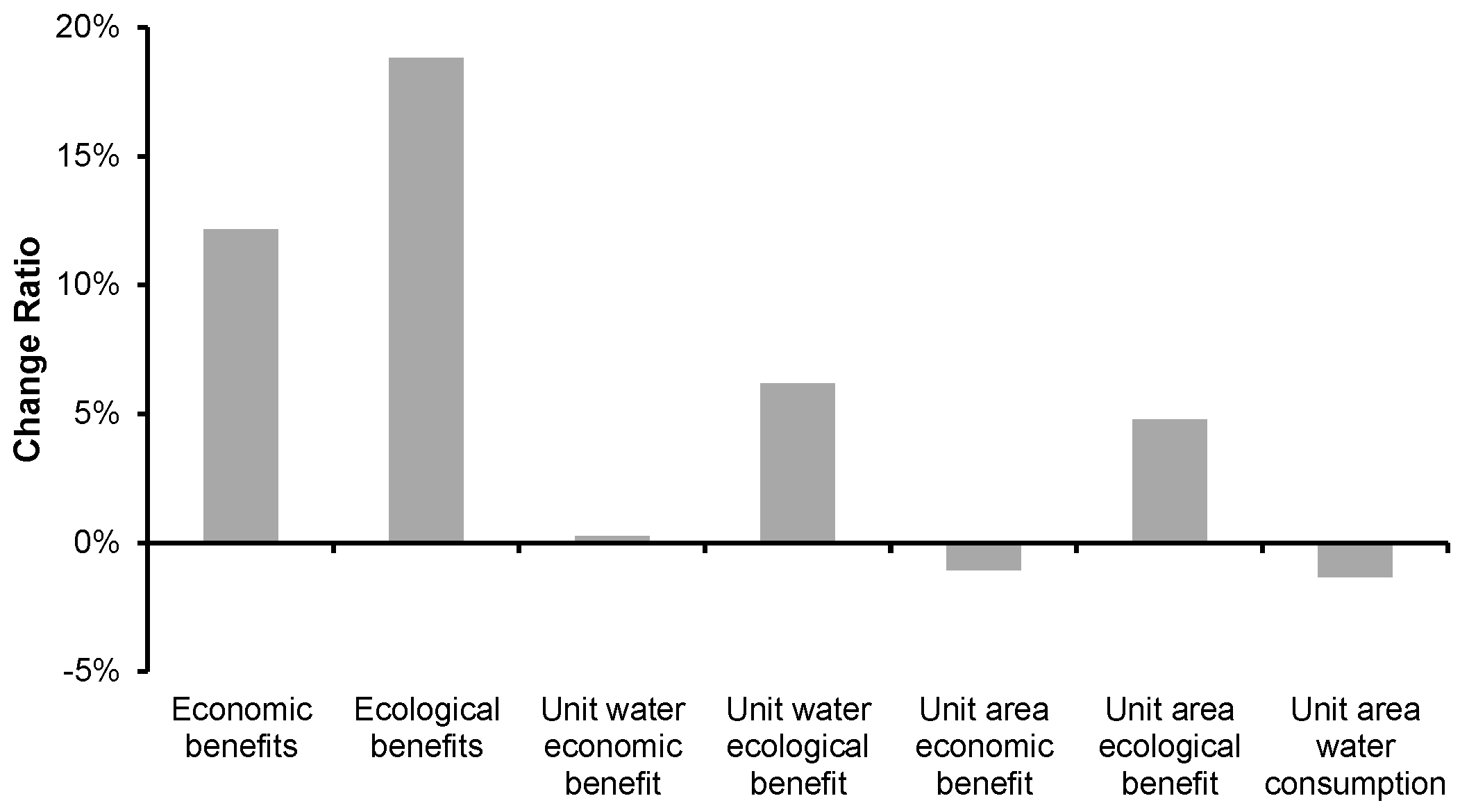
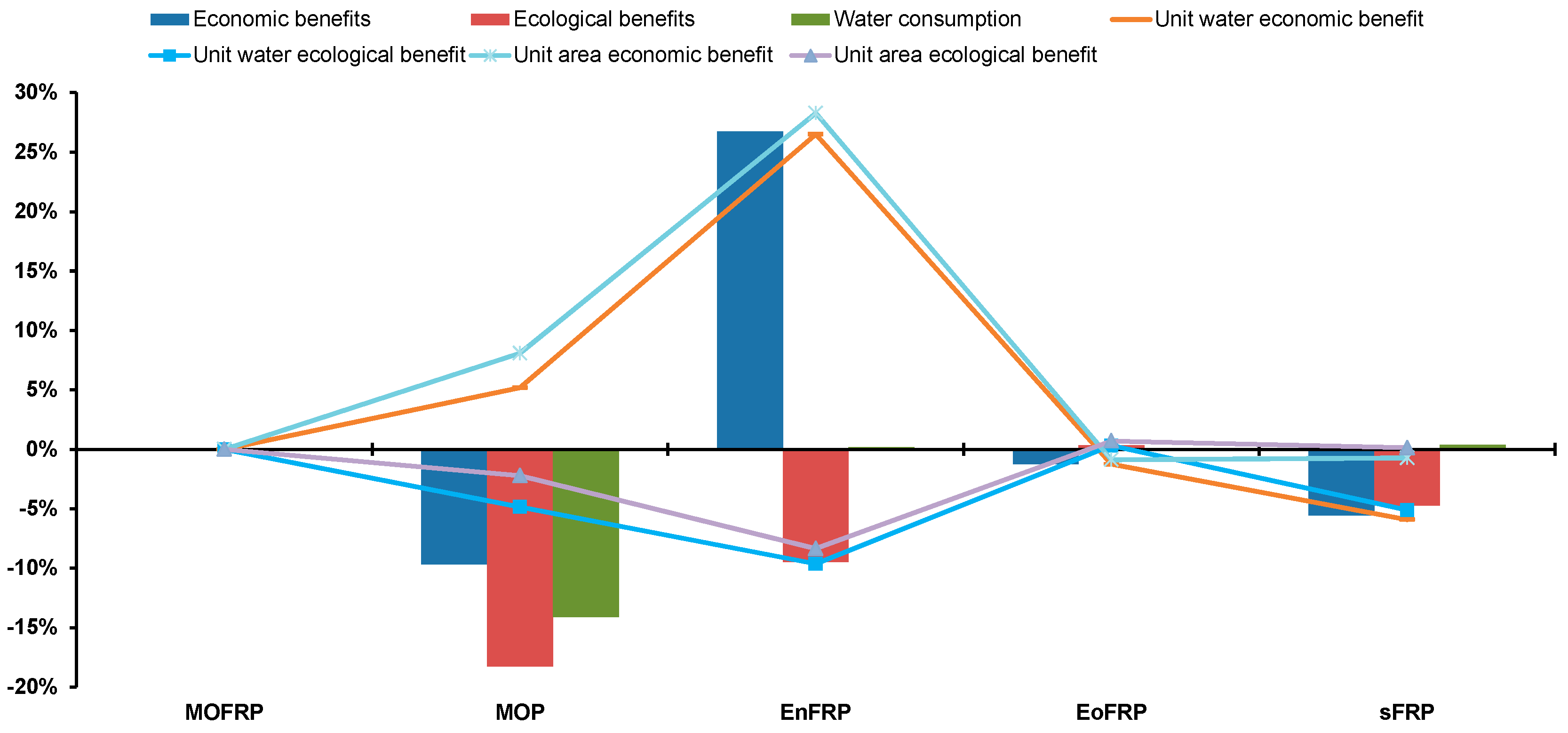
4. Results and Discussion
4.1. Results Analysis and Comparisons with the Status Quo
4.2. Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aregay, F.A.; Yao, L.Y.; Zhao, M.J. Spatial preference heterogeneity for integrated river basin management: The case of the Shiyang River basin, China. Sustainability 2016, 8, 970. [Google Scholar] [CrossRef]
- Zhou, W.; Li, J.L.; Mu, S.J.; Gang, C.C.; Sun, Z.G. Effects of ecological restoration-induced land-use change and improved management on grassland net primary productivity in the shiyanghe river basin, North-West China. Grass Forage Sci. 2014, 69, 596–610. [Google Scholar] [CrossRef]
- Kang, S.Z.; Hao, X.M.; Du, L.; Tong, T.S.; Su, X.L.; Lu, H.N.; Li, X.L.; Huo, Z.L.; Li, S.E.; Ding, R.S. Improving agricultural water productivity to ensure food security in China under changing environment: From research to practice. Agric. Water Manag. 2017, 179, 5–17. [Google Scholar] [CrossRef]
- Todorovic, M.; Lamaddalena, N.; Jovanovic, N.; Pereira, L.S. Agricultural water management: Priorities and challenges. Agric. Water Manag. 2015, 147, 1–3. [Google Scholar] [CrossRef]
- Rong, Q.Q.; Liu, J.T.; Cai, Y.P.; Lu, Z.H.; Zhao, Z.Z.; Yue, W.C.; Xia, J.B. Leaf carbon, nitrogen and phosphorus stoichiometry of tamarix chinensis lour. In the laizhou bay coastal wetland, China. Ecol. Eng. 2015, 76, 57–65. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. Radial interval chance-constrained programming for agricultural non-point source water pollution control under uncertainty. Agric. Water Manag. 2011, 98, 1595–1606. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Hsing, Y.T.; Huang, C.H.; Liu, F.M. Policies, land use, and water resource management in an arid oasis ecosystem. Environ. Manag. 2015, 55, 1036–1051. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Chen, X.H.; Tong, L.; Li, J.B.; Li, M. An optimization model for a crop deficit irrigation system under uncertainty. Eng. Optim. 2014, 46, 1–14. [Google Scholar] [CrossRef]
- Das, B.; Singh, A.; Panda, S.N.; Yasuda, H. Optimal land and water resources allocation policies for sustainable irrigated agriculture. Land Use Policy 2015, 42, 527–537. [Google Scholar] [CrossRef]
- Schutze, N.; Kloss, S.; Lennartz, F.; al Bakri, A.; Schmitz, G.H. Optimal planning and operation of irrigation systems under water resource constraints in oman considering climatic uncertainty. Environ. Earth Sci. 2012, 65, 1511–1521. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. Radial-Interval linear programming for environmental management under varied protection levels. J. Air Waste Manag. Assoc. 2010, 60, 1078–1093. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. Review: Computer-based models for managing the water-resource problems of irrigated agriculture. Hydrogeol. J. 2015, 23, 1217–1227. [Google Scholar] [CrossRef]
- Wang, X.W.; Cai, Y.P.; Xu, Y.; Zhao, H.Z.; Chen, J.J. Optimal strategies for carbon reduction at dual levels in China based on a hybrid nonlinear grey-prediction and quota-allocation model. J. Clean. Prod. 2014, 83, 185–193. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Yeh, S.C.; Liu, L.; Li, G.C. A modeling approach for investigating climate change impacts on renewable energy utilization. Int. J. Energy Res. 2012, 36, 764–777. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. A fuzzy evacuation management model oriented toward the mitigation of emissions. J. Environ. Inf. 2015, 25, 117–125. [Google Scholar] [CrossRef]
- Groot, J.C.J.; Oomen, G.J.M.; Rossing, W.A.H. Multi-objective optimization and design of farming systems. Agric. Syst. 2012, 110, 63–77. [Google Scholar] [CrossRef]
- Kennedy, C.M.; Hawthorne, P.L.; Miteva, D.A.; Baumgarten, L.; Sochi, K.; Matsumoto, M.; Evans, J.S.; Polasky, S.; Hamel, P.; Vieira, E.M.; et al. Optimizing land use decision-making to sustain brazilian agricultural profits, biodiversity and ecosystem services. Biol. Conserv. 2016, 204, 221–230. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S.R. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Galan-Martin, A.; Vaskan, P.; Anton, A.; Esteller, L.J.; Guillen-Gosalbez, G. Multi-objective optimization of rainfed and irrigated agricultural areas considering production and environmental criteria: A case study of wheat production in Spain. J. Clean. Prod. 2017, 140, 816–830. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. Multi-source multi-sector sustainable water supply under multiple uncertainties: An inexact fuzzy-stochastic quadratic programming approach. Water Resour. Manag. 2013, 27, 451–473. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Wang, X.; Li, G.C.; Tan, Q. An inexact programming approach for supporting ecologically sustainable water supply with the consideration of uncertain water demand by ecosystems. Stoch. Environ. Res. Risk Assess. 2011, 25, 721–735. [Google Scholar] [CrossRef]
- Wang, R.; Li, Y.; Tan, Q. A review of inexact optimization modeling and its application to integrated water resources management. Front. Earth Sci. 2015, 9, 51–64. [Google Scholar] [CrossRef]
- Zeng, X.T.; Kang, S.Z.; Li, F.S.; Zhang, L.; Guo, P. Fuzzy multi-objective linear programming applying to crop area planning. Agric. Water Manag. 2010, 98, 134–142. [Google Scholar] [CrossRef]
- Yue, W.C.; Cai, Y.P.; Rong, Q.Q.; Li, C.H.; Ren, L.J. A hybrid life-cycle and fuzzy-set-pair analyses approach for comprehensively evaluating impacts of industrial wastewater under uncertainty. J. Clean. Prod. 2014, 80, 57–68. [Google Scholar] [CrossRef]
- Chen, S.Y.; Ma, J.Q.; Zhang, Z.W. A multi-objective fuzzy optimization model for planting structure and its method. J. Dalian Univ. Technol. 2003, 43, 12–15. [Google Scholar]
- Leung, Y. Spatial Analysis and Planning under Imprecision; Studies in Regional Science and Urban Economics; North-Holland Publishing Co.: Amsterdam, The Netherlands; New York, NY, USA, 1988. [Google Scholar]
- Inuiguchi, M.; Sakawa, M. Robust optimization under softness in a fuzzy linear programming problem. Int. J. Approx. Reason. 1998, 18, 21–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Li, Z.; Quan, J.; Li, X.Y.; Wu, X.C.; Wu, H.W.; Li, Y.T.; Li, G.Y. Establishing a model of conjunctive regulation of surface water and groundwater in the arid regions. Agric. Water Manag. 2016, 174, 30–38. [Google Scholar] [CrossRef]
- Feng, Q.; Miao, Z.; Li, Z.X.; Li, J.G.; Si, J.H.; Yonghong, S.; Chang, Z.Q. Public perception of an ecological rehabilitation project in inland river basins in Northern China: Success or failure. Environ. Res. 2015, 139, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Nie, X.H.; Huang, G.H.; Li, Y.P.; Liu, L. Ifrp: A hybrid interval-parameter fuzzy robust programming approach for waste management planning under uncertainty. J. Environ. Manag. 2007, 84, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Huang, G.H.; Wu, C.Z.; Cai, Y.P. If-Em: An interval-parameter fuzzy linear programming model for environment-oriented evacuation planning under uncertainty. J. Adv. Transp. 2011, 45, 286–303. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Tan, Q.; Liu, L. An integrated approach for climate-change impact analysis and adaptation planning under multi-level uncertainties. Part II. Case study. Renew. Sustain. Energy Rev. 2011, 15, 3051–3073. [Google Scholar] [CrossRef]
- Chang, Z.F.; Wang, D.W.; Duan, X.F.; Wang, Q.Q.; Zhang, J.H.; Yang, M. Relative ecological values of several major plants in minqin desert area. J. Arid Land Resour. Environ. 2015, 29, 86–91. [Google Scholar]
- Cai, Y.P.; Huang, G.H.; Yang, Z.F.; Sun, W.; Chen, B. Investigation of public’s perception towards rural sustainable development based on a two-level expert system. Expert Syst. Appl. 2009, 36, 8910–8924. [Google Scholar] [CrossRef]

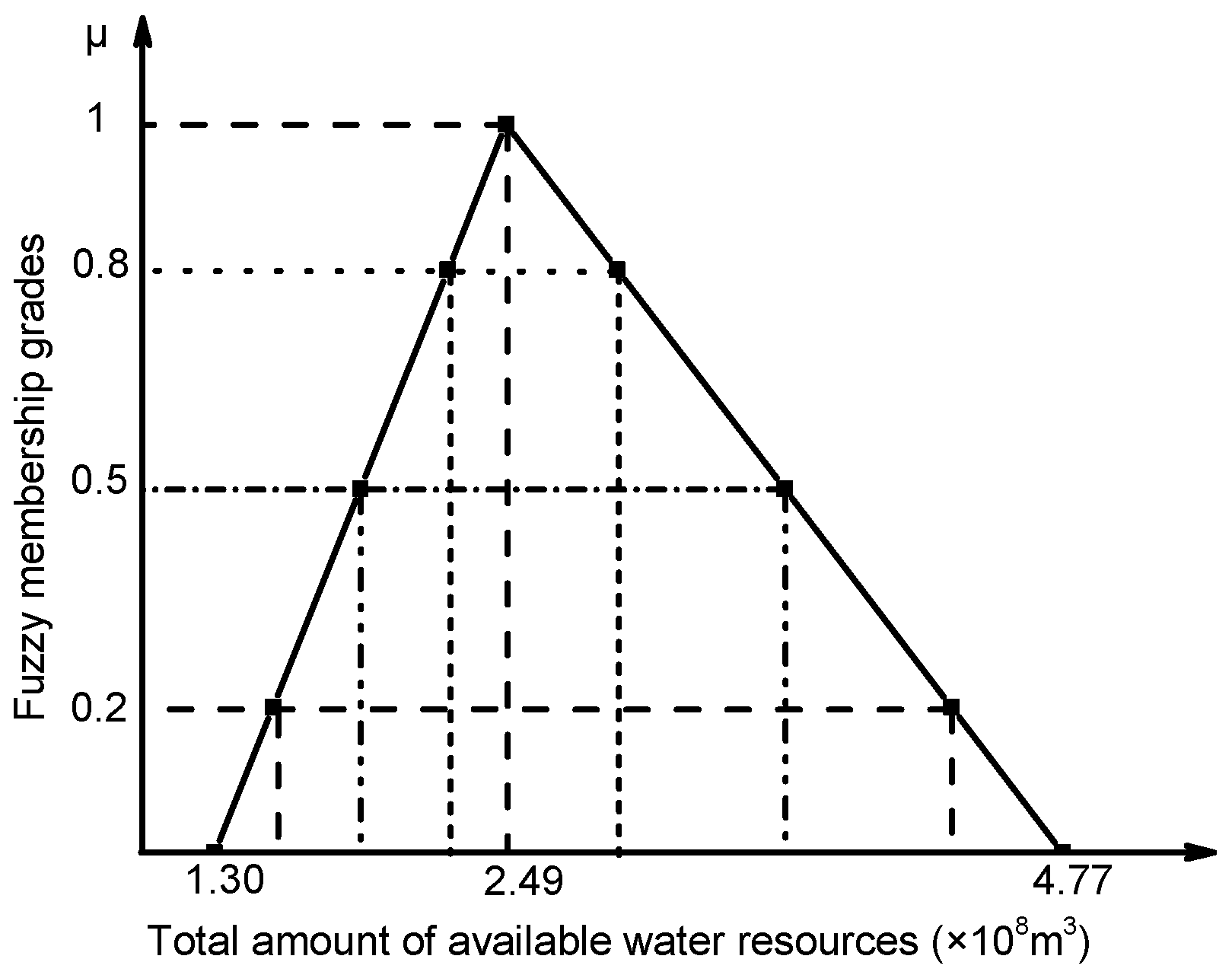
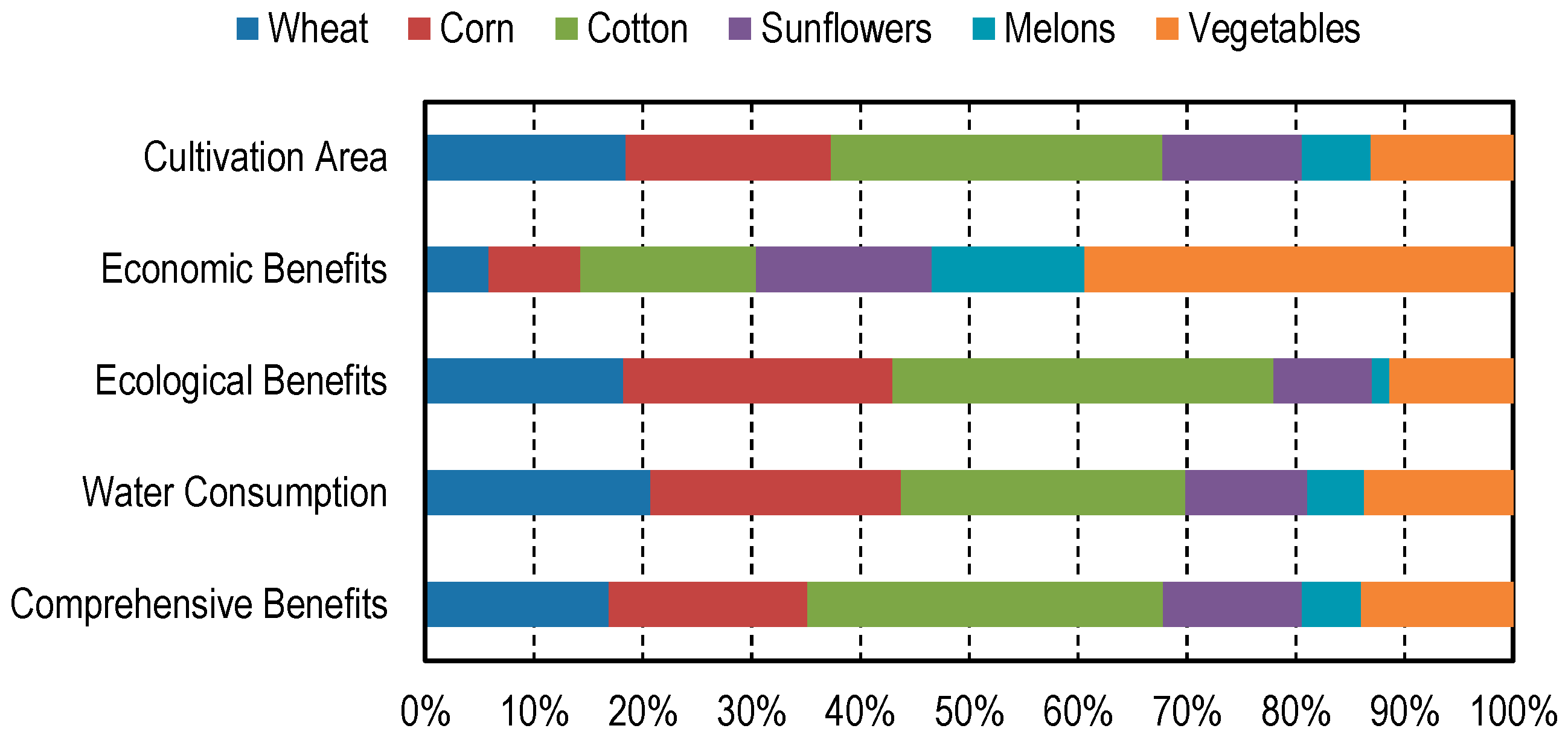
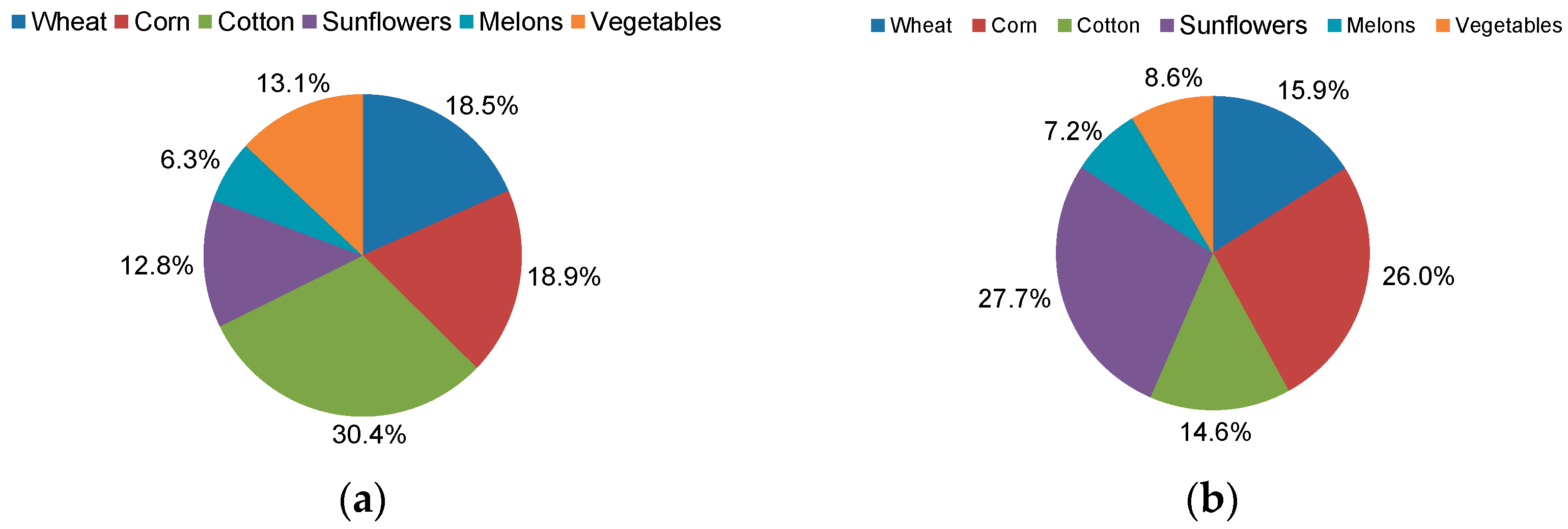
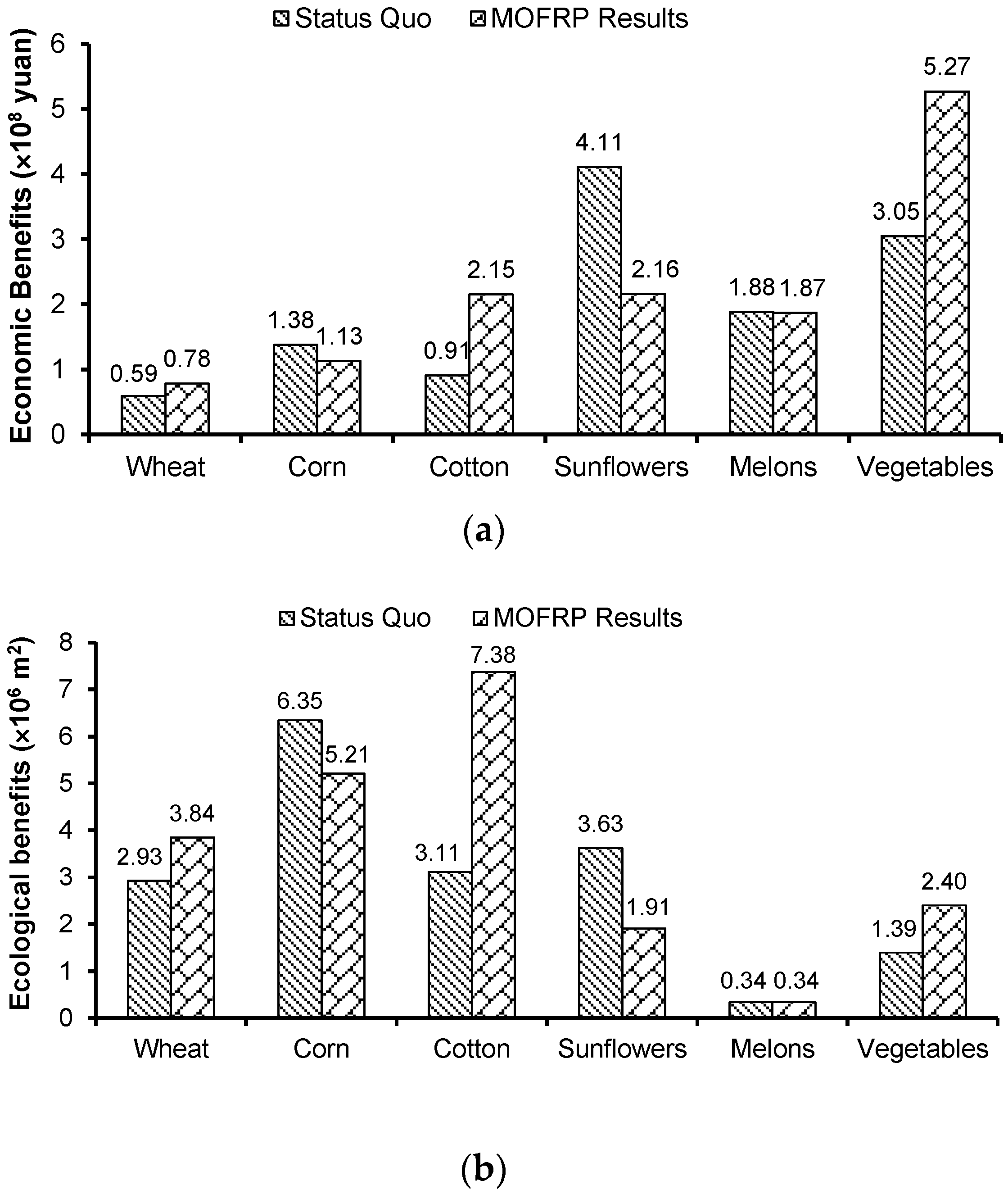
| Crop | Wheat | Corn | Cotton | Sunflowers | Melons | Vegetables |
|---|---|---|---|---|---|---|
| Yield (kg/hm2) | 7695 | 10,544 | 1800 | 5566 | 6532 | 54,462 |
| Cost (yuan/hm2) | 5250 | 9520 | 11,340 | 3598 | 13,265 | 21,547 |
| Price (yuan/kg) | 2.09 | 2.36 | 16.40 | 8.41 | 13.71 | 2.29 |
| Demand (kg/person) | 250 | 350 | 40 | 113 | 72 | 164 |
| Minimum Area (hm2) | 5200 | 5000 | 4000 | 3883 | 1973 | 5099 |
| Maximum Area (hm2) | 140,000 | 10,452 | 11,856 | 11,650 | 3960 | 7648 |
| Water Consumption (m3/hm2) | 5100 | 5550 | 3900 | 3981 | 3750 | 4750 |
| Current Cultivated Area (hm2) | 5473 | 8947 | 5000 | 9513 | 2467 | 2947 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Q.; Zhang, S.; Li, R. Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives. Water 2017, 9, 488. https://doi.org/10.3390/w9070488
Tan Q, Zhang S, Li R. Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives. Water. 2017; 9(7):488. https://doi.org/10.3390/w9070488
Chicago/Turabian StyleTan, Qian, Shan Zhang, and Ran Li. 2017. "Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives" Water 9, no. 7: 488. https://doi.org/10.3390/w9070488
APA StyleTan, Q., Zhang, S., & Li, R. (2017). Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives. Water, 9(7), 488. https://doi.org/10.3390/w9070488




