Using Modeling Tools to Better Understand Permafrost Hydrology
Abstract
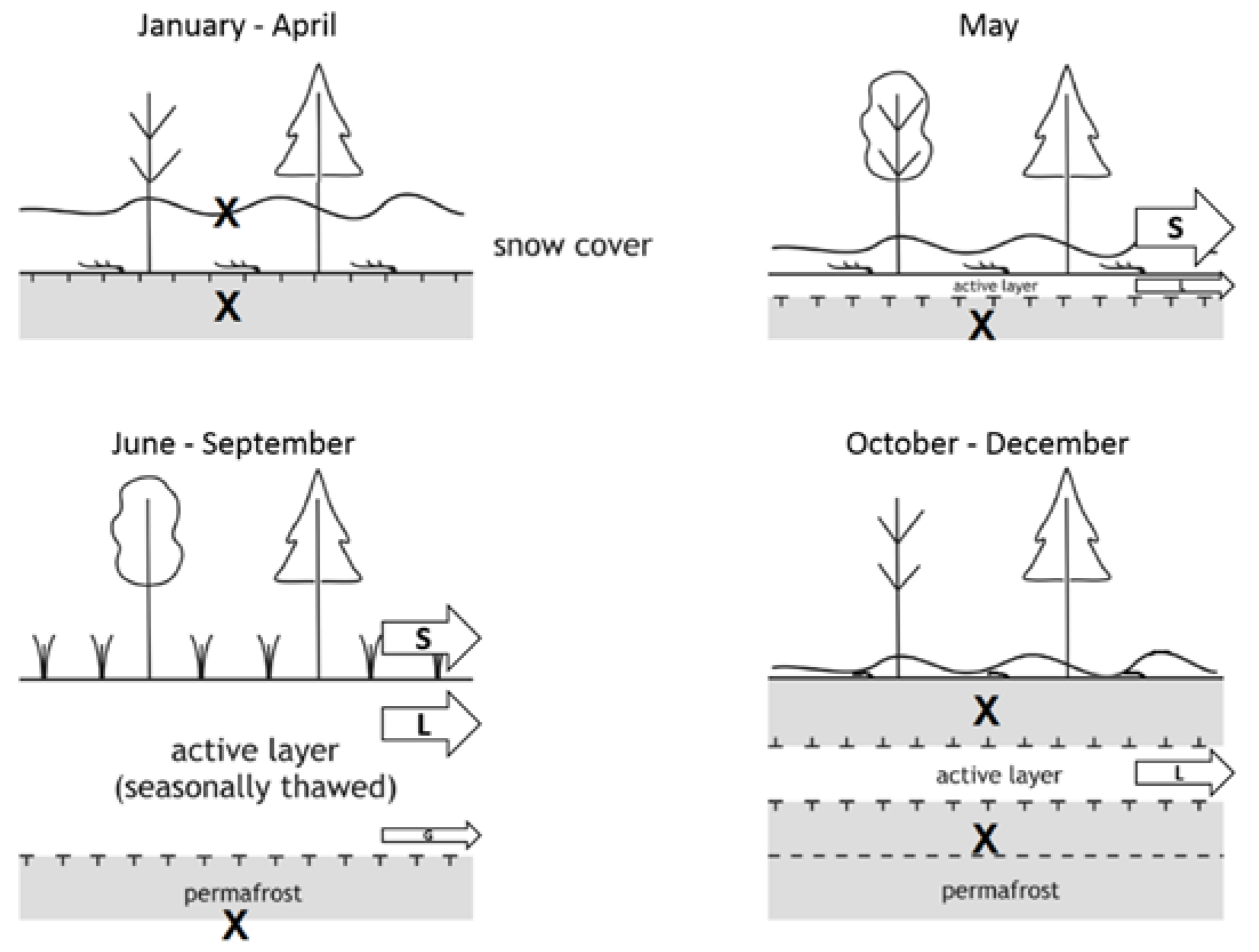
:1. Introduction
- to evaluate the role of permafrost soils in water transfer,
- to identify the hydrologically relevant features for each permafrost class, and the runoff routing through a large Arctic watershed of the Yenisei River,
- to characterize and quantify the different hydrological pathways,
- to perform hydrological modeling of the Yenisei River at daily time step, accounting for the hydrological functions of permafrost, in order to allow predictions under non-stationary conditions.
2. Results
2.1. Hydrological Response
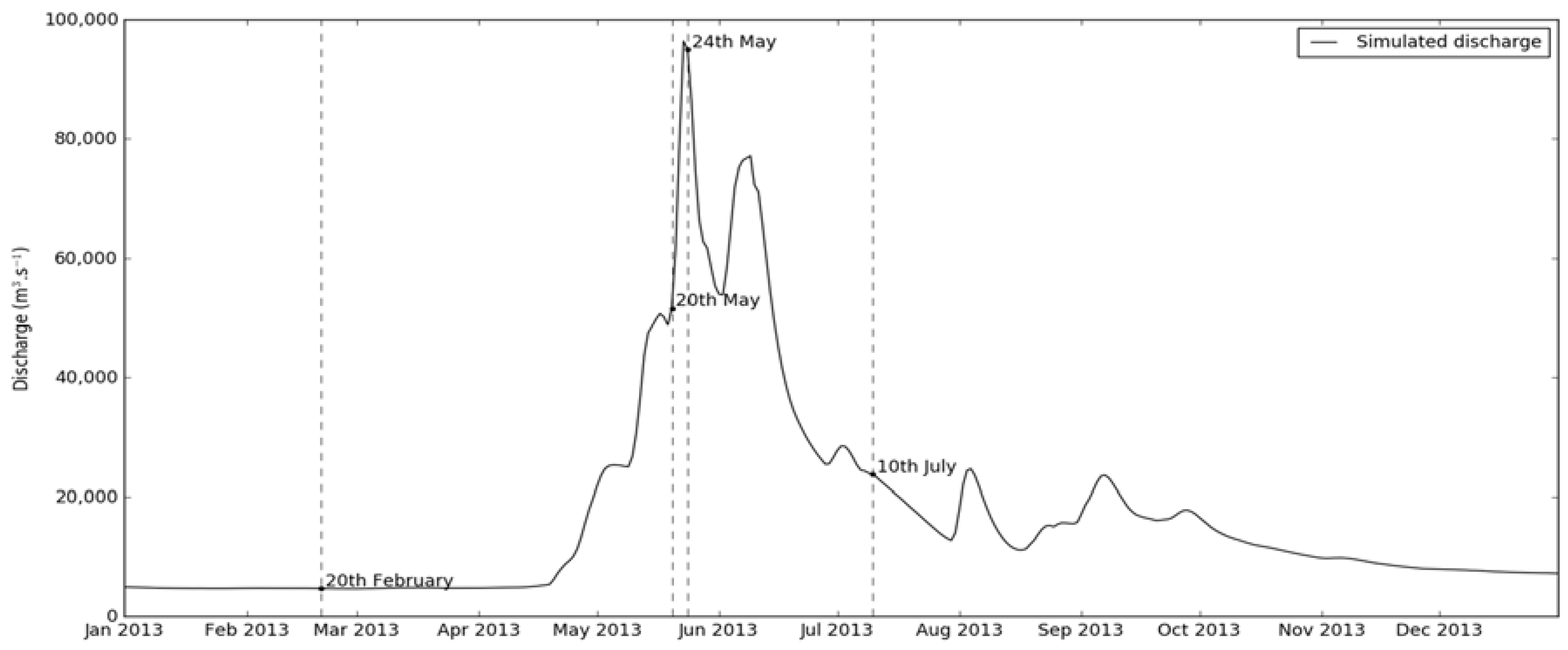
2.1.1. Daily Modeled Discharge
2.1.2. Comparison with the Modeling at a Monthly Time Step
2.2. Modeled Water Balance
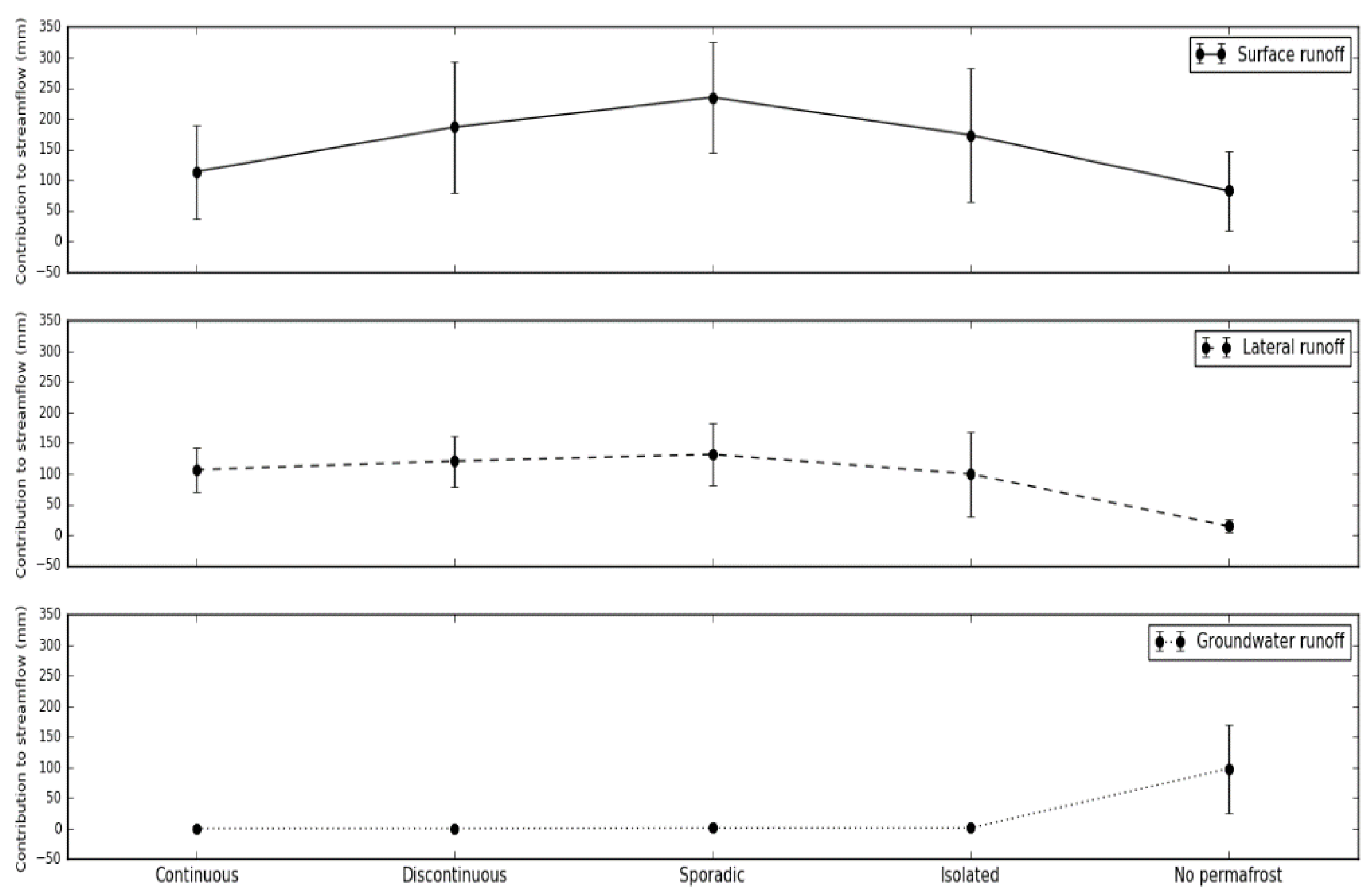
2.3. Spatial Water Transfer
3. Discussion
3.1. Conceptualization of Permafrost Hydrology in the Yenisei Watershed and Outputs
3.2. Future Modeling Improvements for the Arctic Rivers
3.3. Limit of the Model for Permafrost Soils
4. Materials and Methods
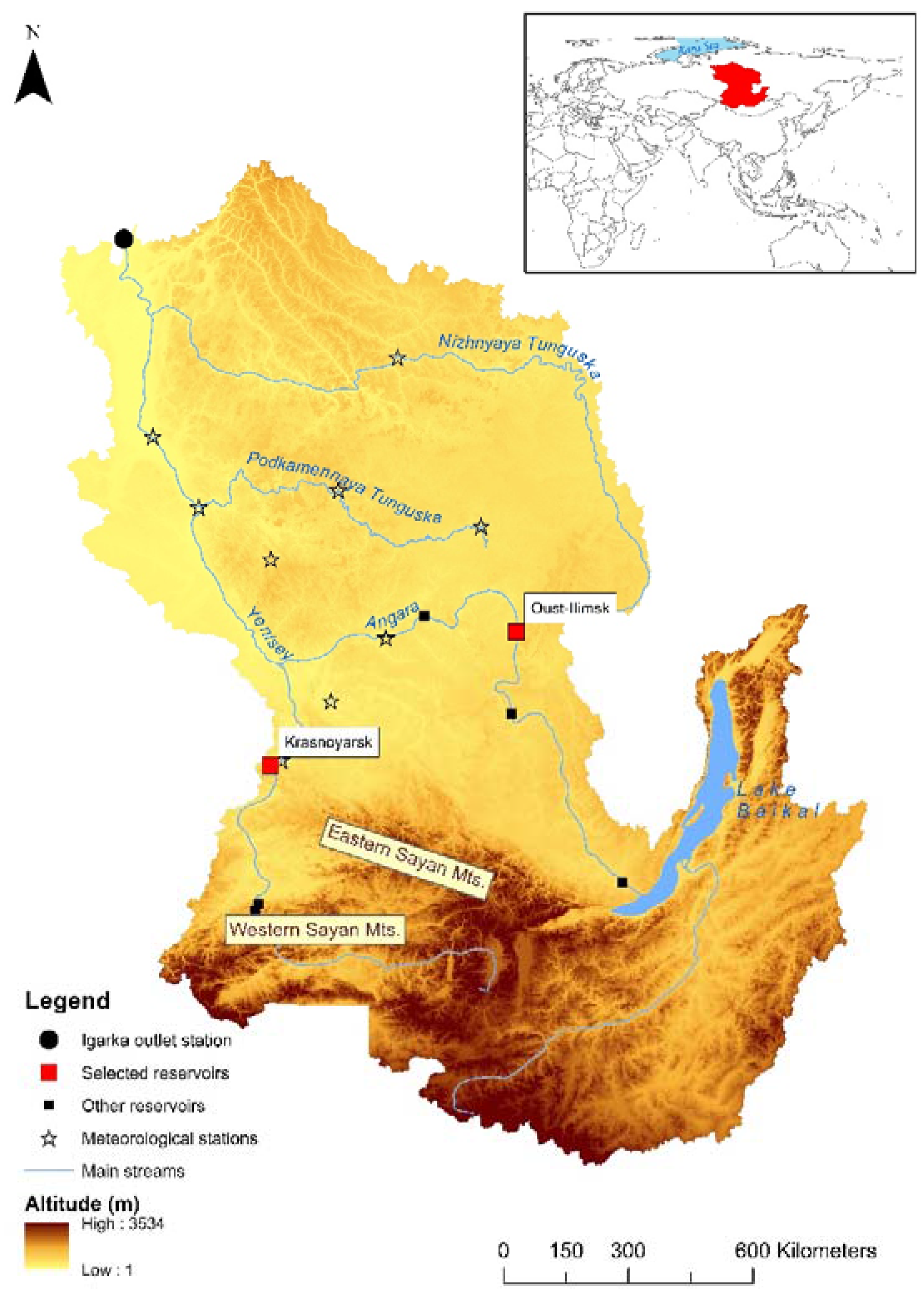
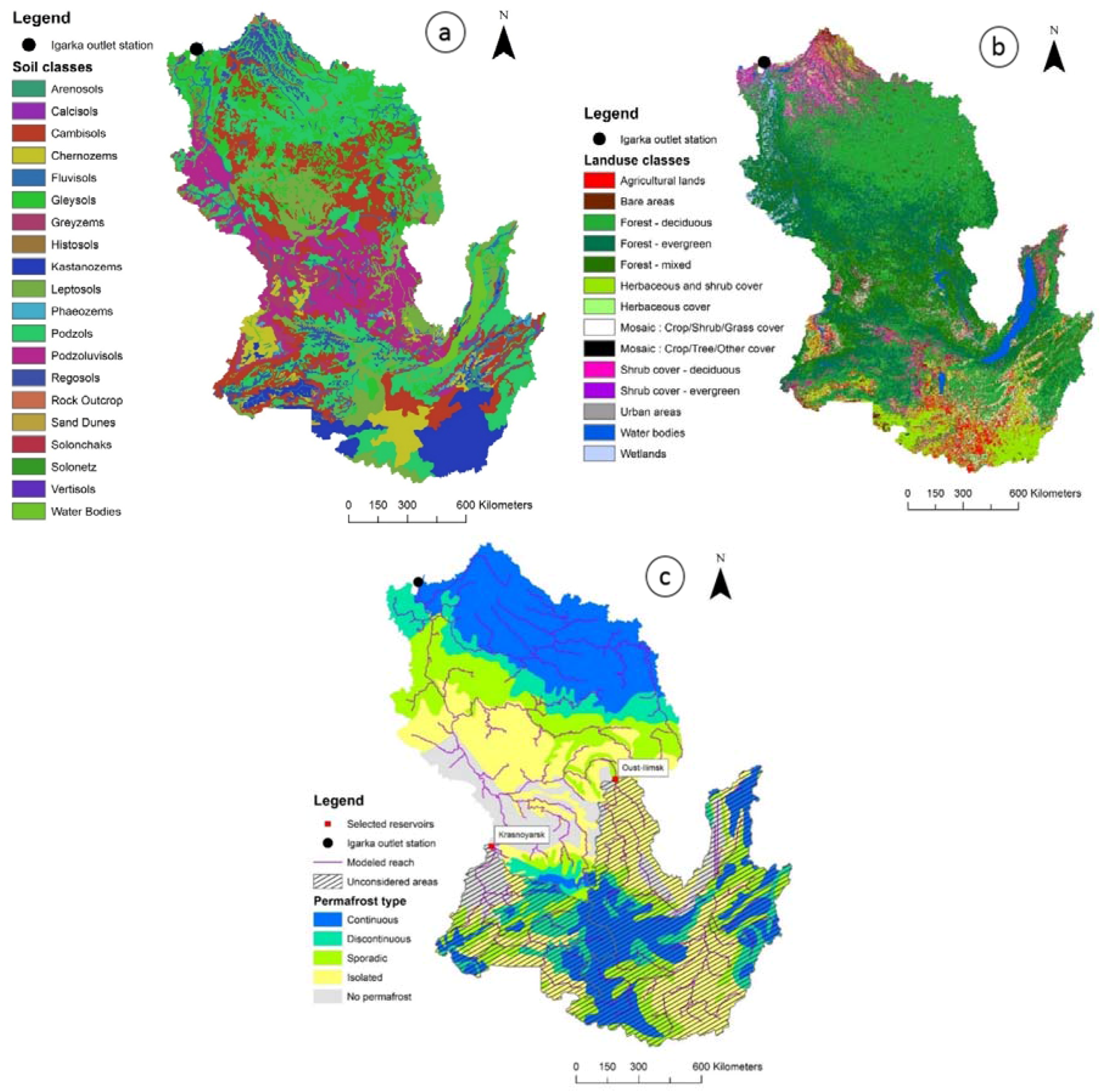
4.1. Study Area
4.2. Observed Data
4.3. Model Choice
4.4. Modeling Data Inputs
4.5. Conceptualization
4.5.1. Climate Approach
4.5.2. Distribution of the Flows Returning to the River
4.5.3. Permafrost Approach
4.6. Model Calibration and Validation
4.7. Model Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, United Kingdom and New York, NY, USA, 2013; ISBN 978-1-107-66182-0. [Google Scholar]
- Serreze, M.; Barry, R. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet. Chang. 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Stocker, T.F.; Raible, C.C. Climate change: Water cycle shifts gear. Nature 2005, 434, 830–833. [Google Scholar] [CrossRef] [PubMed]
- Francis, J.; White, D.; Cassano, J.; Gutowski, W.; Hinzman, L.; Holland, M.; Steele, M.; Vörösmarty, C. An arctic hydrologic system in transition: Feedbacks and impacts on terrestrial, marine, and human life. J. Geophys. Res. 2005, 114. [Google Scholar] [CrossRef]
- Frey, K.; McClelland, J. Impacts of permafrost degradation on arctic river biogeochemistry. Hydrol. Process. 2009, 23, 169–182. [Google Scholar] [CrossRef]
- Kuzin, V.I.; Platov, G.A.; Golubeva, E.N. Influence that interannual variations in Siberian river discharge have on redistribution of freshwater fluxes in Arctic Ocean and North Atlantic. Izv. Atmos. Ocean. Phys. 2010, 46, 770–783. [Google Scholar] [CrossRef]
- Woo, M.-K.; Kane, D.L.; Carey, S.K.; Yang, D. Progress in permafrost hydrology in the new millennium. Permafr. Periglac. Process. 2008, 19, 237–254. [Google Scholar] [CrossRef]
- Briggs, M.A.; Campbell, S.; Nolan, J.; Walvoord, M.; Ntarlagiannis, D.; Day-Lewis, F.; Lane, J. Surface geophysical methods for characterizing frozen ground in transitional permafrost landscapes. Permafr. Periglac. Process. 2016, 28, 52–65. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Buttle, J.; Carey, S.K.; McGuire, K.; Laudon, H.; Soulsby, C. Tracer-based assessment of flow paths, storage and runoff generation in northern catchments: A review: Tracers in Northern catchments. Hydrol. Process. 2015, 29, 3475–3490. [Google Scholar] [CrossRef]
- McClelland, J.W.; Tank, S.E.; Spencer, R.G.M.; Shiklomanov, A.I. Coordination and sustainability of river observing activities in the Arctic. Arctic 2015, 68, 59–68. [Google Scholar] [CrossRef]
- Beltaos, S.; Prowse, T.D. River-ice hydrology in a shrinking cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Streletskiy, D.A.; Tananaev, N.I.; Opel, T.; Shiklomanov, N.I.; Nyland, K.E.; Streletskaya, I.D.; Tokarev, I.; Shiklomanov, A.I. Permafrost hydrology in changing climatic conditions: Seasonal variability of stable isotope composition in rivers in discontinuous permafrost. Environ. Res. Lett. 2015, 10, 95003. [Google Scholar] [CrossRef]
- Woo, M. Permafrost hydrology in North America. Atmos. Ocean. 1986, 24, 201–234. [Google Scholar] [CrossRef]
- Burt, T.P.; Williams, P.J. Hydraulic conductivity in frozen soils. Earth Surf. Process. 1976, 1, 349–360. [Google Scholar] [CrossRef]
- Zhang, T.; Frauenfeld, O.; Serreze, M.; Etringer, A. Spatial and temporal variability in active layer thickness over the Russian Arctic drainage basin. J. Geophys. Res. 2005, 110, D16101. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; Bockheim, J.; Canadell, J.G.; Euskirchen, E.; Field, C.B.; Goryachkin, S.V.; Hagemann, S.; Kuhry, P.; Lafleur, P.M.; Lee, H.; et al. Vulnerability of Permafrost Carbon to Climate Change: Implications for the Global Carbon Cycle. BioScience 2008, 58, 701–714. [Google Scholar] [CrossRef]
- Carey, S.K.; Woo, M.-K. Hydrology of two slopes in subarctic Yukon, Canada. Hydrol. Process. 1999, 13, 2549–2562. [Google Scholar] [CrossRef]
- Bense, V.F.; Kooi, H.; Ferguson, G.; Read, T. Permafrost degradation as a control on hydrogeological regime shifts in a warming climate: Groundwater and degrading permafrost. J. Geophys. Res. 2012, 117, F03036. [Google Scholar] [CrossRef]
- Woo, M. Permafrost Hydrology; Springer: Heidelberg, Germany, 2012; ISBN 9783642234620. [Google Scholar]
- McKenzie, J.M.; Voss, C.I. Permafrost thaw in a nested groundwater-flow system. Hydrogeol. J. 2013, 21, 299–316. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic Impacts of Thawing Permafrost—A Review. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Su, F.; Adam, J.C.; Trenberth, K.E.; Lettenmaier, D.P. Evaluation of surface water fluxes of the pan-Arctic land region with a land surface model and ERA-40 reanalysis. J. Geophys. Res. 2006, 111, D05110. [Google Scholar] [CrossRef]
- Amon, R.M.W.; Rinehart, A.J.; Duan, S.; Louchouarn, P.; Prokushkin, A.; Guggenberger, G.; Bauch, D.; Stedmon, C.; Raymond, P.A.; Holmes, R.M.; et al. Dissolved organic matter sources in large Arctic rivers. Geochim. Cosmochim. Acta 2012, 94, 217–237. [Google Scholar] [CrossRef]
- Tarnocai, C.; Canadell, J.G.; Schuur, E.A.G.; Kuhry, P.; Mazhitova, G.; Zimov, S. Soil organic carbon pools in the northern circumpolar permafrost region: Soil organic carbon pools. Glob. Biogeochem. Cycles 2009, 23, GB2023. [Google Scholar] [CrossRef]
- Boike, J.; Roth, K.; Overduin, P.P. Thermal and hydrologic dynamics of the active layer at a continuous permafrost site (Taymyr Peninsula, Siberia). Water Resour. Res. 1998, 34, 355–363. [Google Scholar] [CrossRef]
- Jafarov, E.E.; Marchenko, S.S.; Romanovsky, V.E. Numerical modeling of permafrost dynamics in Alaska using a high spatial resolution dataset. Cryosphere 2012, 6, 613–624. [Google Scholar] [CrossRef]
- Weismüller, J.; Wollschläger, U.; Boike, J.; Pan, X.; Yu, Q.; Roth, K. Modeling the thermal dynamics of the active layer at two contrasting permafrost sites on Svalbard and on the Tibetan Plateau. Cryosphere 2011, 5, 741–757. [Google Scholar] [CrossRef]
- Schramm, I.; Boike, J.; Bolton, W.R.; Hinzman, L.D. Application of TopoFlow, a spatially distributed hydrological model, to the Imnavait Creek watershed, Alaska. J. Geophys. Res. 2007, 112, G04S46. [Google Scholar] [CrossRef]
- Rigon, R.; Bertoldi, G.; Over, T.M. GEOtop: A Distributed Hydrological Model with Coupled Water and Energy Budgets. J. Hydrometeorol. 2006, 7, 371–388. [Google Scholar] [CrossRef]
- Gusev, E.M.; Nasonova, O.N.; Dzhogan, L.Y. Reproduction of Pechora runoff hydrographs with the help of a model of heat and water exchange between the land surface and the atmosphere (SWAP). Water Resour. 2010, 37, 182–193. [Google Scholar] [CrossRef]
- Semenova, O.; Vinogradov, Y.; Vinogradova, T.; Lebedeva, L. Simulation of soil profile heat dynamics and their integration into hydrologic modelling in a permafrost zone. Permafr. Periglac. Process. 2013, 25, 257–269. [Google Scholar] [CrossRef]
- Zhou, J.; Kinzelbach, W.; Cheng, G.; Zhang, W.; He, X.; Ye, B. Monitoring and modeling the influence of snow pack and organic soil on a permafrost active layer, Qinghai–Tibetan Plateau of China. Cold Reg. Sci. Technol. 2013, 90–91, 38–52. [Google Scholar] [CrossRef]
- Finney, D.L.; Blyth, E.; Ellis, R. Improved modelling of Siberian river flow through the use of an alternative frozen soil hydrology scheme in a land surface model. Cryosphere 2012, 6, 859–870. [Google Scholar] [CrossRef]
- Arora, V.K. Streamflow simulations for continental scale river basins in a global atmospheric general circulation model. Adv. Water Resour. 2001, 24, 775–791. [Google Scholar] [CrossRef]
- Fukutomi, Y.; Igarashi, H.; Masuda, K.; Yasunari, T. Interannual variability of summer water balance components in three major river basins of Northern Eurasia. J. Hydrometeorol. 2003, 4, 283–296. [Google Scholar] [CrossRef]
- Nakai, T.; Kim, Y.; Busey, R.C.; Suzuki, R.; Nagai, S.; Kobayashi, H.; Park, H.; Sugiura, K.; Ito, A. Characteristics of evapotranspiration from a permafrost black spruce forest in interior Alaska. Polar Sci. 2013, 7, 136–148. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, Y.; Armstrong, R.; Robinson, D.; Brodzik, M.-J. Streamflow response to seasonal snow cover mass changes over large Siberian watersheds. J. Geophys. Res. 2007, 112, F02S22. [Google Scholar] [CrossRef]
- Hülsmann, L.; Geyer, T.; Schweitzer, C.; Priess, J.; Karthe, D. The effect of subarctic conditions on water resources: Initial results and limitations of the SWAT model applied to the Kharaa River Basin in Northern Mongolia. Environ. Earth Sci. 2015, 73, 581–592. [Google Scholar] [CrossRef]
- Vinogradov, Y.B.; Semenova, O.M.; Vinogradova, T.A. An approach to the scaling problem in hydrological modelling: The deterministic modelling hydrological system. Hydrol. Process. 2011, 25, 1055–1073. [Google Scholar] [CrossRef]
- Ludwig, W.; Probst, J.-L.; Kempe, S. Predicting the oceanic input of organic carbon by continental erosion. Glob. Biogeochem. Cycle 1996, 10, 23–41. [Google Scholar] [CrossRef]
- Raymond, P.A.; McClelland, J.W.; Holmes, R.M.; Zhulidov, A.V.; Mull, K.; Peterson, B.J.; Striegl, R.G.; Aiken, G.R.; Gurtovaya, T.Y. Flux and age of dissolved organic carbon exported to the Arctic Ocean: A carbon isotopic study of the five largest arctic rivers. Glob. Biogeochem. Cycles 2007, 21, GB4011. [Google Scholar] [CrossRef]
- Holmes, R.M.; McClelland, J.W.; Peterson, B.J.; Tank, S.E.; Bulygina, E.; Eglinton, T.I.; Gordeev, V.V.; Gurtovaya, T.Y.; Raymond, P.A.; Repeta, D.J.; et al. Seasonal and Annual Fluxes of Nutrients and Organic Matter from Large Rivers to the Arctic Ocean and Surrounding Seas. Estuar. Coasts 2012, 35, 369–382. [Google Scholar] [CrossRef]
- Lake Baikal. Available online: http://whc.unesco.org/en/list/754 (accessed on 23 May 2017).
- McClelland, J.W. Increasing river discharge in the Eurasian Arctic: Consideration of dams, permafrost thaw, and fires as potential agents of change. J. Geophys. Res. 2004, 109, D18102. [Google Scholar] [CrossRef]
- Brown, J.; Ferrians, J.A.; Melnikov, E. Circum.-Arctic Map of Permafrost and Ground-Ice Conditions; Version 2; National Snow and Ice Data Center (NSIDC): Boulder, CO, USA, 2002. [Google Scholar]
- Roshydromet, Russian Federal Service for Hydrometeorology and Environmental Monitoring. Available online: https://gmvo.skniivh.ru (accessed on 6 June 2017).
- Herschy, R. The velocity-area method. Flow Meas. Instrum. 1993, 4, 7–10. [Google Scholar] [CrossRef]
- Stieglitz, M.; Hobbie, J.; Giblin, A.; Kling, G. Hydrologic modeling of an arctic tundra watershed: Toward Pan-Arctic predictions. J. Geophys. Res. 1999, 104, 27507–27518. [Google Scholar] [CrossRef]
- Ducharne, A.; Golaz, C.; Leblois, E.; Laval, K.; Polcher, J.; Ledoux, E.; de Marsily, G. Development of a high resolution runoff routing model, calibration and application to assess runoff from the LMD GCM. J. Hydrol. 2003, 280, 207–228. [Google Scholar] [CrossRef]
- Nohara, D.; Kitoh, A.; Hosaka, M.; Oki, T. Impact of Climate Change on River Discharge Projected by Multimodel Ensemble. J. Hydrometeorol. 2006, 7, 1076–1089. [Google Scholar] [CrossRef]
- Alkama, R.; Kageyama, M.; Ramstein, G. Freshwater discharges in a simulation of the Last Glacial Maximum climate using improved river routing. Geophys. Res. Lett. 2006, 33, L21709. [Google Scholar] [CrossRef]
- Yang, H.; Piao, S.; Zeng, Z.; Ciais, P.; Yin, Y.; Friedlingstein, P.; Sitch, S.; Ahlström, A.; Guimberteau, M.; Huntingford, C.; et al. Multicriteria evaluation of discharge simulation in Dynamic Global Vegetation Models: Evaluation on simulation of discharge. J. Geophys. Res. Atmos. 2015, 120, 7488–7505. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Yang, H.; Srinivasan, R.; Zehnder, A.J.B. Modeling blue and green water availability in Africa: Modeling blue and green water availability in Africa. Water Resour. Res. 2008, 44, W07406. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. Am. Soc. Agric. Biol. Eng. 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Faramarzi, M.; Abbaspour, K.C.; Ashraf Vaghefi, S.; Farzaneh, M.R.; Zehnder, A.J.B.; Srinivasan, R.; Yang, H. Modeling impacts of climate change on freshwater availability in Africa. J. Hydrol. 2013, 480, 85–101. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—An overview. Hydrol. Sci. J. 2015, 60, 771–783. [Google Scholar] [CrossRef]
- Hutton, C.; Wagener, T.; Freer, J.; Han, D.; Duffy, C.; Arheimer, B. Most computational hydrology is not reproducible, so is it really science? Water Resour. Res. 2016, 52, 7548–7555. [Google Scholar] [CrossRef]
- Flügel, W.-A. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process. 1995, 9, 423–436. [Google Scholar] [CrossRef]
- Soil and Water Assessment Tool. Available online: http://swatmodel.tamu.edu/ (accessed on 6 June 2017).
- ESRI. Available online: http://www.esri.com/ (accessed on 6 June 2017).
- Climate Forecast System Reanalysis. Available online: http://rda.ucar.edu/pub/cfsr.html (accessed on 6 June 2017).
- Information System of Russian Water Surveys. Available online: https://gmvo.skniivh.ru/ (accessed on 6 June 2017).
- Tananaev, N. Permafrost Hydrology under Changing Climate; P.I. Melnikov Permafrost Institute: Yakutsk, Sakha Republic, Russia, 2015. [Google Scholar]
- Suzuki, K. Estimation of Snowmelt Infiltration into Frozen Ground and Snowmelt Runoff in the Mogot Experimental Watershed in East Siberia. Int. J. Geosci. 2013, 4, 1346–1354. [Google Scholar] [CrossRef]
- Suzuki, K.; Liston, G.E.; Matsuo, K. Estimation of Continental-Basin-Scale Sublimation in the Lena River Basin, Siberia. Adv. Meteorol. 2015, 2015, 286206. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C. Swat-Cup2: SWAT Calibration and Uncertainty Programs Manual Version 2, Department of Systems Analysis, Integrated Assessment and Modelling (SIAM), Eawag; Swiss Federal Institute of Aquatic Science and Technology: Duebendorf, Switzerland, 2011. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
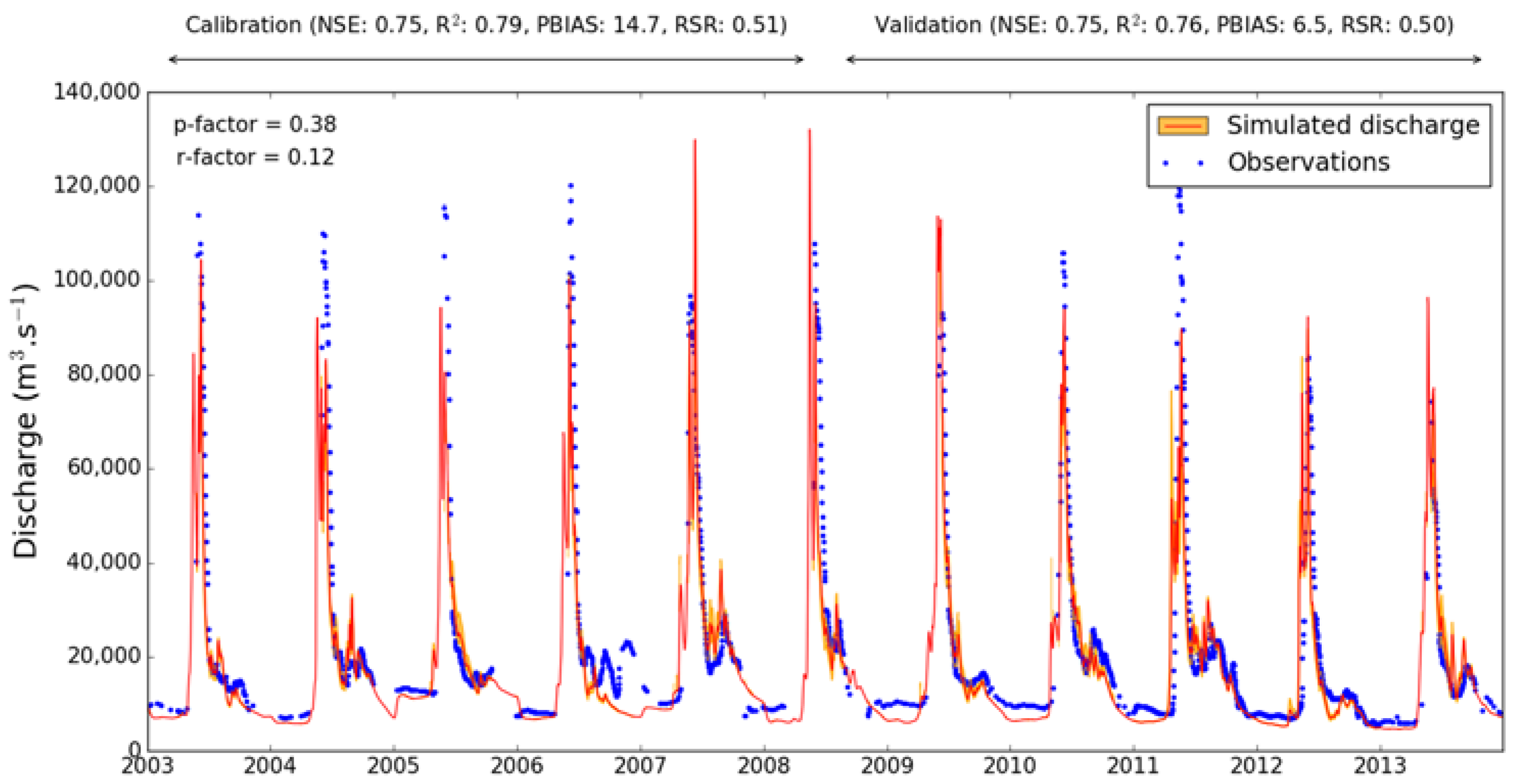
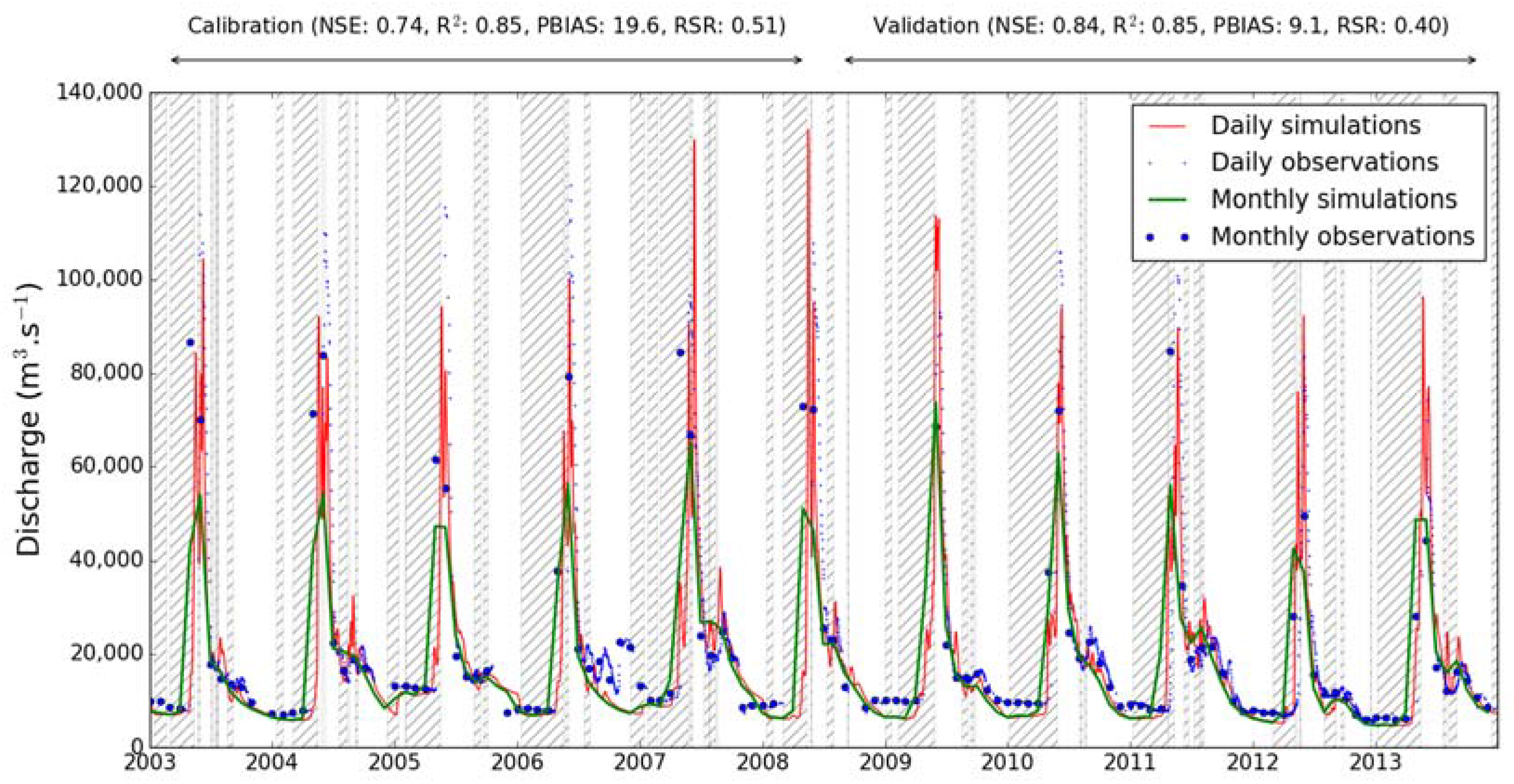
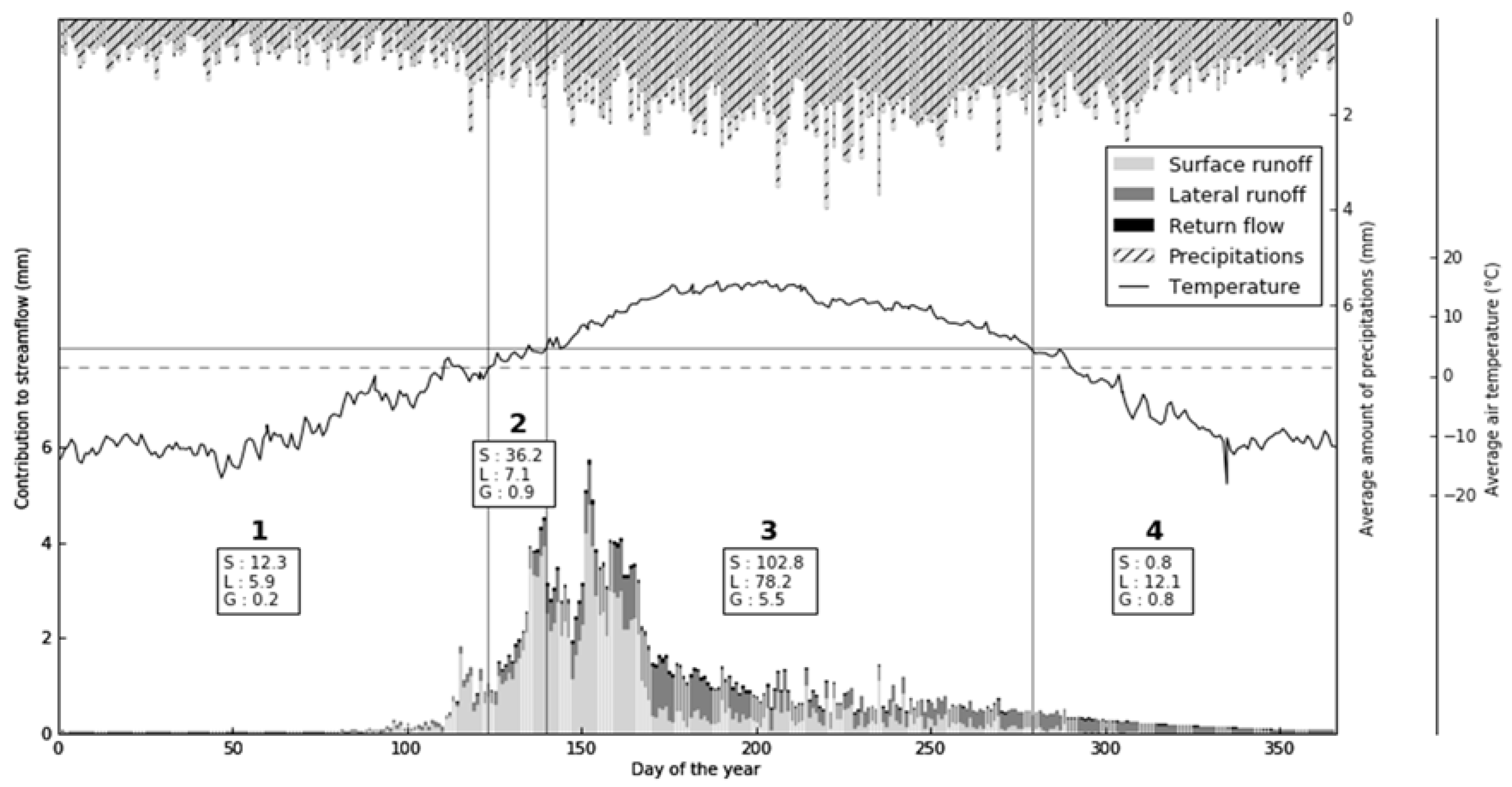
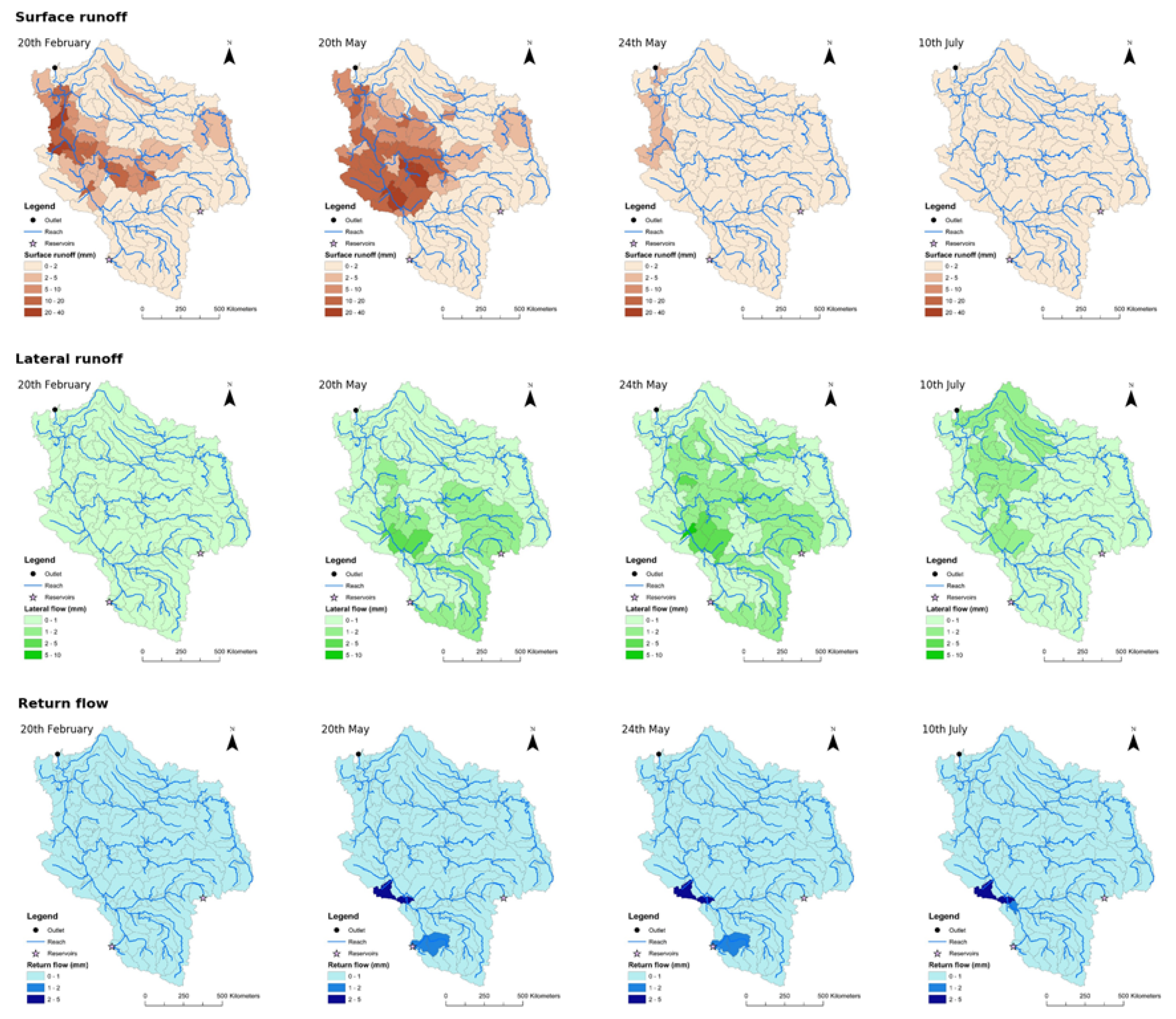
| Daily Time Step Modeling | Monthly Time Step Modeling | |||||
|---|---|---|---|---|---|---|
| Number of Values | Calibration | Validation | Calibration | Validation | ||
| Low flow periods | 1175 | NSE | 0.70 | 0.66 | 0.87 | 0.74 |
| R2 | 0.55 | 0.50 | 0.57 | 0.80 | ||
| PBIAS | 2.0 | −1.0 | 7.6 | 2.0 | ||
| RSR | 0.43 | 0.67 | 0.36 | 0.51 | ||
| High flow periods | 189 | NSE | 0.75 | 0.78 | 0.71 | 0.86 |
| R2 | 0.37 | 0.44 | 0.08 | 0.56 | ||
| PBIAS | 25.7 | 22.0 | 30.5 | 19.2 | ||
| RSR | 0.52 | 0.45 | 0.54 | 0.37 | ||
| Source | ArcticGRO Dataset | This Study | Finney et al. (2012) | Ducharne et al. (2003) | Alkama et al. (2006) | Nohara et al. (2006) | Arora (2001) | Yang et al. (2015) |
|---|---|---|---|---|---|---|---|---|
| Years | 2003–2013 | 2003–2013 | 1989–1999 | 1980–1988 | 1980–1994 | 1901–2010 | ||
| Data | Observed | Simulated | Simulated | Simulated | Simulated | Simulated | Simulated | Simulated |
| Model | SWAT | TOPMODEL | RiTHM | LMDZ | TRIP | AMIP2 | SDGVM | |
| Runoff (mm yr−1) | 241.6 ± 31.3 | 237.8 ± 38.7 | 140 | 140.6 | 151.7 ± 44.3 | 179 | 189 | 273.8 |
| Discharge (109 m3 yr−1) | 589.5 ± 76.4 | 580.2 ± 94.4 | 341.6 | 343.1 | 370.1 ± 108.1 | 436.8 | 461.2 | 668.1 |
| Difference with observed data (%) | 1.6 | 42.1 | 41.8 | 37.2 | 26.0 | 21.8 | 13.3 |
| Data Type | Observations | Resolution | Source |
|---|---|---|---|
| Digital Elevation (DEM) | - | 500 m | Digital Elevation Data (http://www.viewfinderpanoramas.org/dem3.html) |
| Soil dataset | - | 1 km | Harmonized World Soil Database v 1.1 (http://webarchive.iiasa.ac.at/Research/LUC/External-World-soil-database/HTML/index.html?sb=1) |
| Land use dataset | - | 1 km | Global Land Cover 2000 Database (http://forobs.jrc.ec.europa.eu/products/glc2000/products.php) |
| River network dataset | - | - | Natural Earth (http://www.naturalearthdata.com) |
| River discharge | 2003–2013 | - | Arctic Great Rivers Observatory (http://arcticgreatrivers.org/) |
| Reservoirs deliveries | 2008–2014 | - | Roshydromet (https://gmvo.skniivh.ru/) |
| Meteorological dataset | 1999–2014 | - | Observed: Global center for meteorological data, VNIIGMI-MCD, Region of Moscou (http://aisori.meteo.ru/ClimateR) Simulated: Climate Forecast System Reanalysis (CFSR) Model (http://globalweather.tamu.edu/) |
| Parameter | Name | Input File | Literature Range | Calibrated Value | Sensitivity Rank |
|---|---|---|---|---|---|
| SMTMP | Snow melt base temperature (°C) | .bsn | −5–5 | 4.75 | 1 |
| SMFMN | Melt factor for snow on December 21 (mm H2O/°C-day) | .bsn | 0–10 | 0.25 | 2 |
| TIMP | Snow pack temperature lag factor | .bsn | 0–1 | 0.42 | 3 |
| SMFMX | Melt factor for snow on June 21 (mm H2O/°C-day) | .bsn | 0–10 | 8.26 | 4 |
| SNO50COV | Fraction of SNOCOVMX that corresponds to 50% snow cover | .bsn | 0–1 | 0.57 | 5 |
| LAT_TTIME | Lateral flow travel time (days) | .hru | 0–180 | 9.06 | 6 |
| SFTMP | Snowfall temperature (°C) | .bsn | −5–5 | 1.52 | 7 |
| SNOCOVMX | Minimum snow water content that corresponds to 100% snow cover (mm H2O) | .bsn | 0–500 | 67.73 | 8 |
| ESCO | Soil evaporation compensation factor | .bsn | 0–1 | 0.86 | 9 |
| CANMX | Maximum canopy storage (mm H2O) | .hru | 0–100 | 1.90 | 10 |
| SLSOIL | Slope length for lateral subsurface flow (m) | .hru | 0–150 | 3 | X |
| DEP_IMP | Depth to impervious layer in soil profile (mm) | .hru | 0–6000 | 800–2000 | X |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabre, C.; Sauvage, S.; Tananaev, N.; Srinivasan, R.; Teisserenc, R.; Sánchez Pérez, J.M. Using Modeling Tools to Better Understand Permafrost Hydrology. Water 2017, 9, 418. https://doi.org/10.3390/w9060418
Fabre C, Sauvage S, Tananaev N, Srinivasan R, Teisserenc R, Sánchez Pérez JM. Using Modeling Tools to Better Understand Permafrost Hydrology. Water. 2017; 9(6):418. https://doi.org/10.3390/w9060418
Chicago/Turabian StyleFabre, Clément, Sabine Sauvage, Nikita Tananaev, Raghavan Srinivasan, Roman Teisserenc, and José Miguel Sánchez Pérez. 2017. "Using Modeling Tools to Better Understand Permafrost Hydrology" Water 9, no. 6: 418. https://doi.org/10.3390/w9060418
APA StyleFabre, C., Sauvage, S., Tananaev, N., Srinivasan, R., Teisserenc, R., & Sánchez Pérez, J. M. (2017). Using Modeling Tools to Better Understand Permafrost Hydrology. Water, 9(6), 418. https://doi.org/10.3390/w9060418










