A Simplified Simulation Method for Flood-Induced Bend Scour—A Case Study Near the Shuideliaw Embankment on the Cho-Shui River
Abstract
:1. Introduction
2. Field Data Collection and Formula Derivation
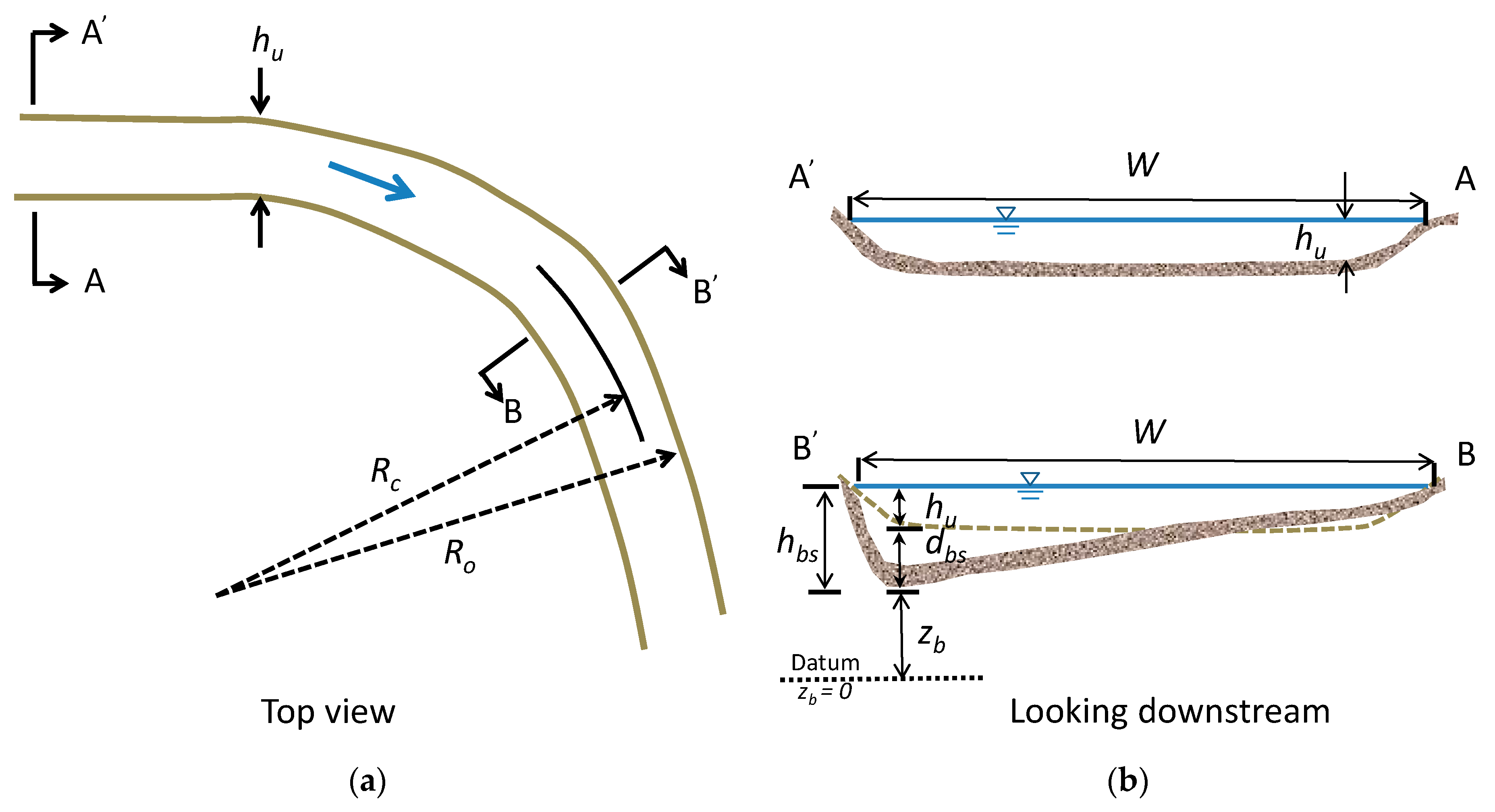
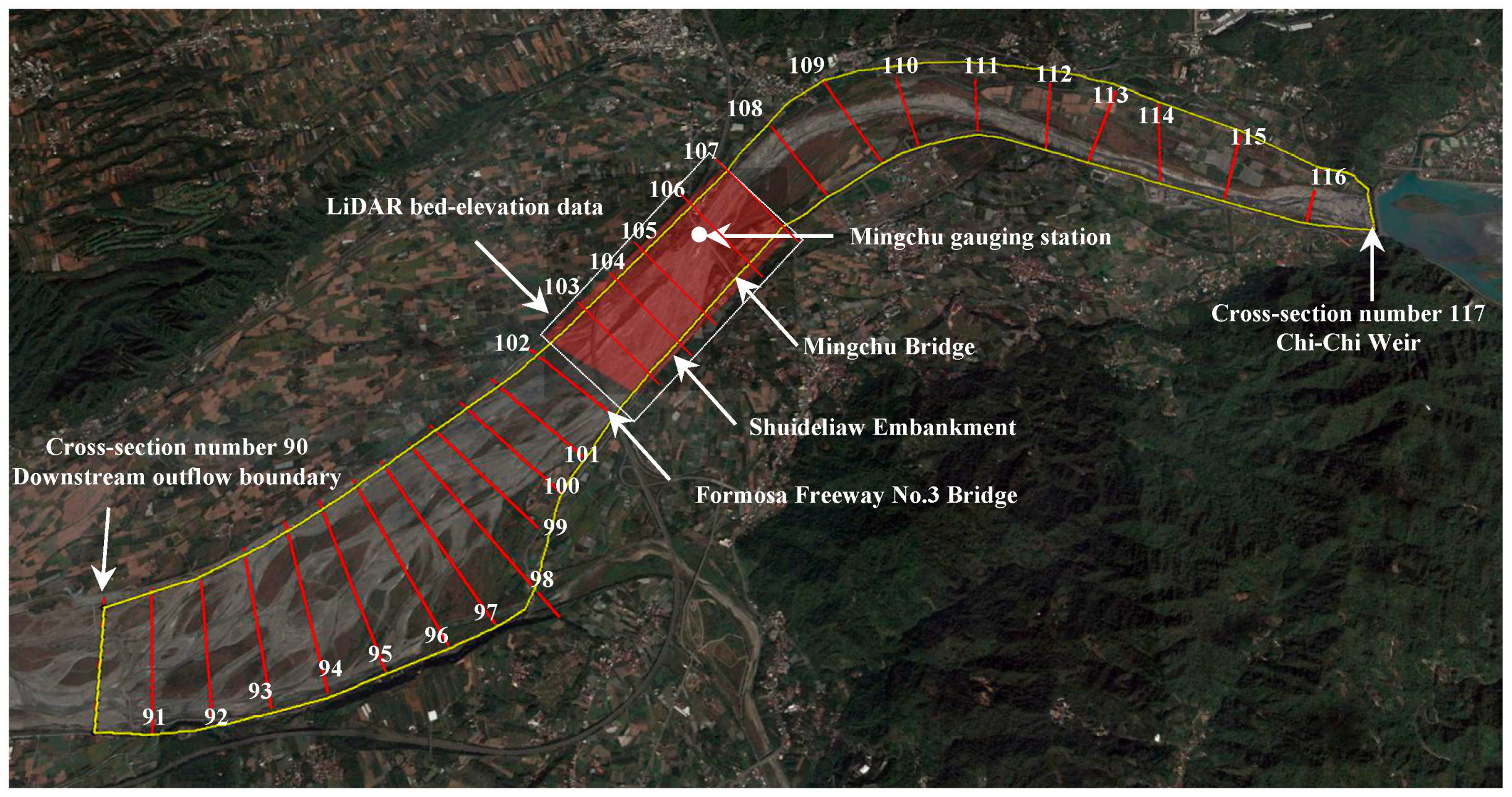
2.1. Site Description
2.2. Field Data
2.3. Proposed Bend Scour Computation Equation
3. Method for Embankment Toe Scour Simulation
3.1. 2D Finite-Volume Hydraulic Model
- The cell interface is the dry edge, when and , in which and are the left and right water depths at the center of the cell interface, respectively. There is no flux estimation.
- The cell interface is the wet edge, when and . The upstream flux-splitting finite-volume scheme coupled with the hydrostatic reconstruction method [24] is adopted to estimate the well-balanced numerical fluxes.
- The cell interface is the partially wet edge with flux, when , , and , where zb is the bed elevation. The momentum flux is set at 0 and the mass flux (hu)LR at cell interface LR is estimated as:
- The cell interface is the partially wet edge without flux, when , , and . According to the bed elevation condition, there is no flux across the cell interface. Thus, no flux estimation is required.
3.2. General Scour Computation Equation
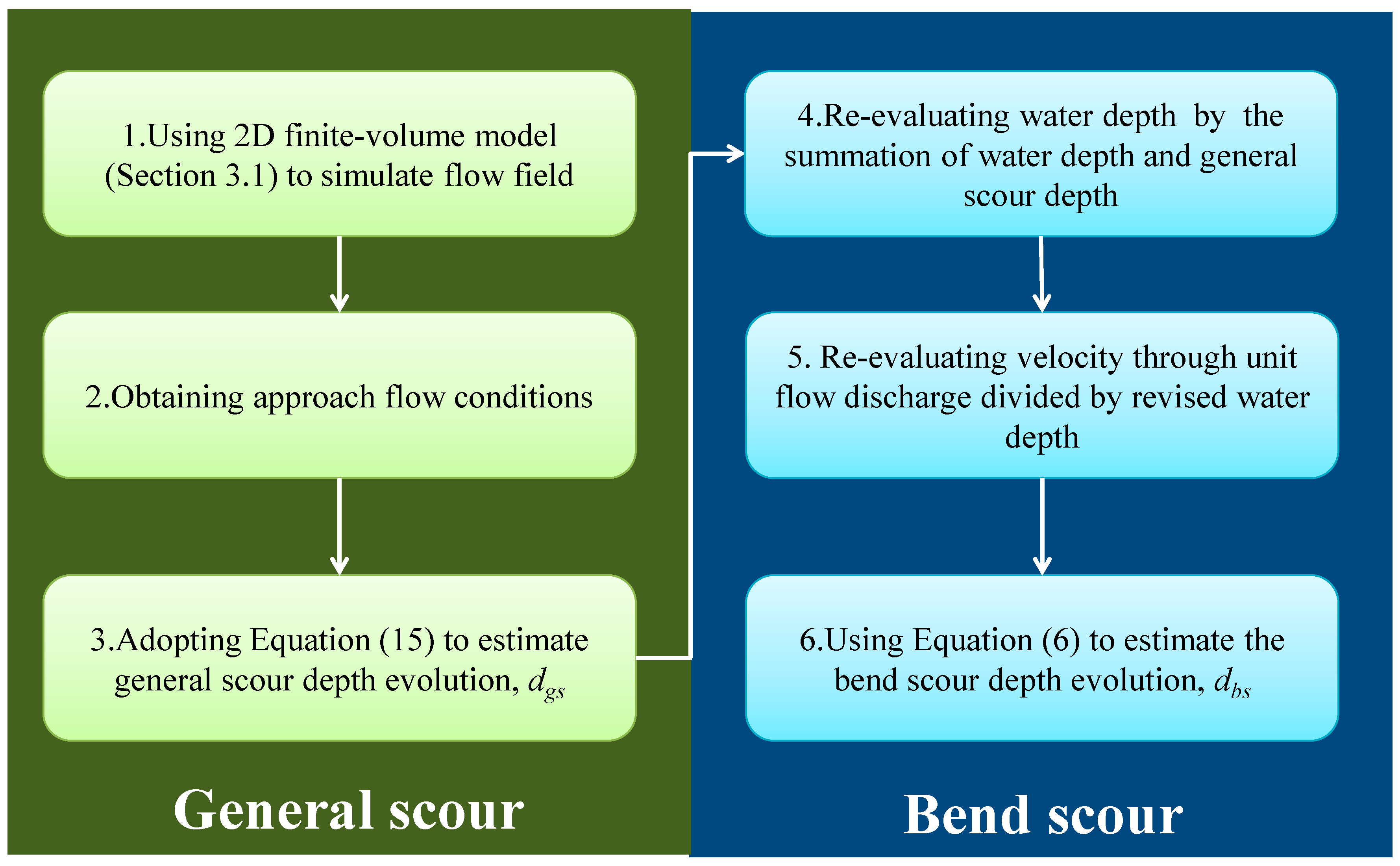
3.3. Method for Simulating Bend Scour Depth Evolution
- Inputting flow hydrographs (simulation time step is 1 h), setting model parameters (i.e., numerical time step and Manning roughness coefficients), and then simulating the 2D flow field in the bend reach through the proposed 2D finite-volume hydraulic model (Section 3.1). At the end of each simulation time step, the water depth and velocity in each computational cell are outputted.
- After 2D flow simulation, one obtains the approach flow conditions (i.e., entire hydrographs) at the specific computational cell, including water depth, velocities, water surface width, and the centerline radius of the bend.
- For each simulation time step (1 h), one substitutes the approach flow conditions into the general scour computation equation (i.e., Equation (15)) to achieve the estimated general scour depth. After the entire general scour simulation, the evolution of the estimated general scour depth is thus obtained.
- For each simulation time step (1 h), one re-evaluates the water depth by adding the water depth and the estimated general scour depth to obtain the revised water depth: .
- For each simulation time step (1 h), one re-evaluates velocity through unit flow discharge divided by revised water depth and obtains the revised velocity as .
- For each simulation time step (1 h), one substitutes the revised flow conditions (i.e., ) into Equations (1)–(3) and (6) to obtain the bend scour depth. After entire bend scour simulation, the evolution of the estimated bend scour depth is thus obtained.
4. Flow Field and Embankment Toe Scour Simulations
4.1. Verifications of 2D Finite-Volume Model
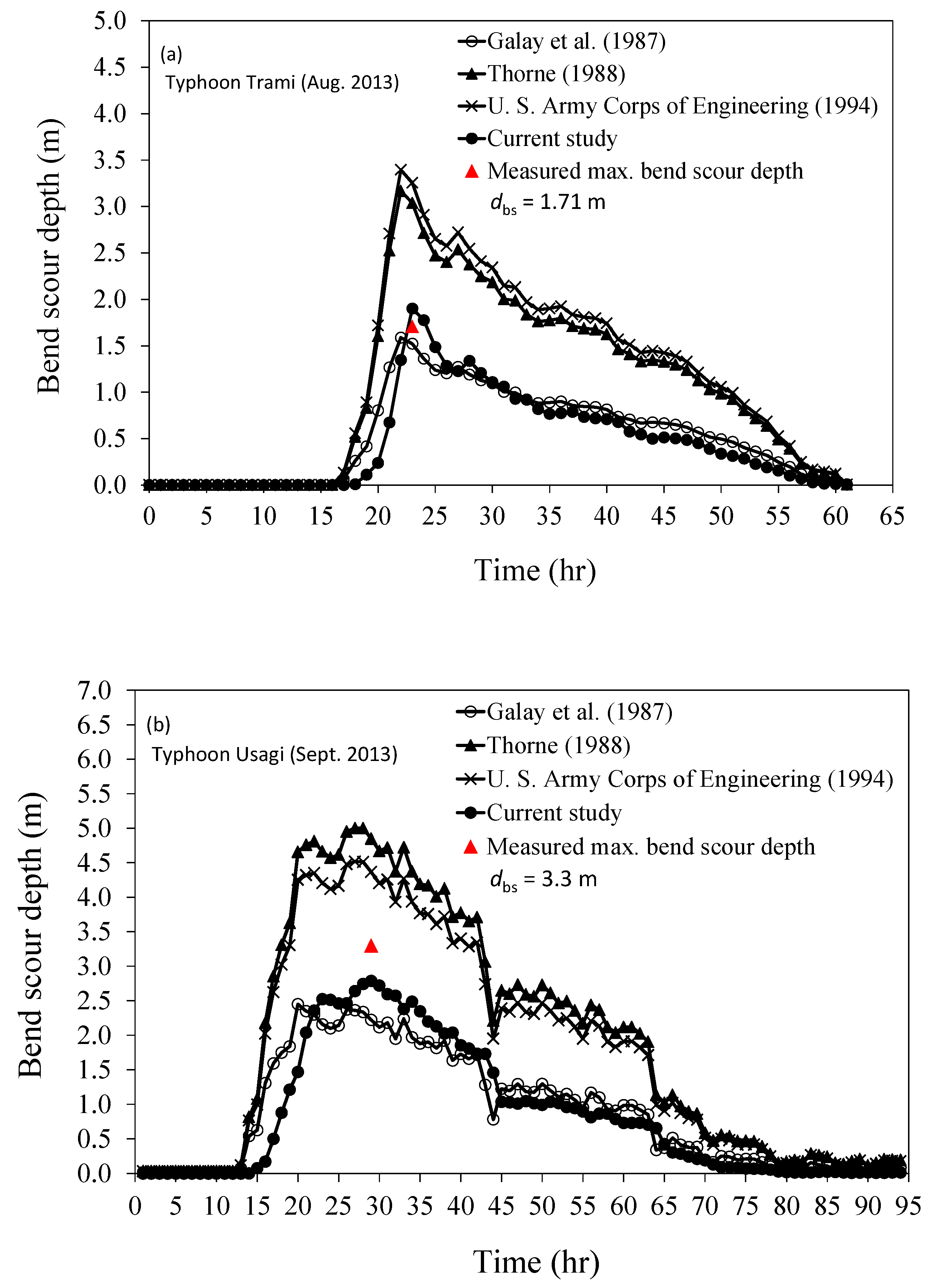
4.2. Verifications of Proposed Method for Bend Scour Depth
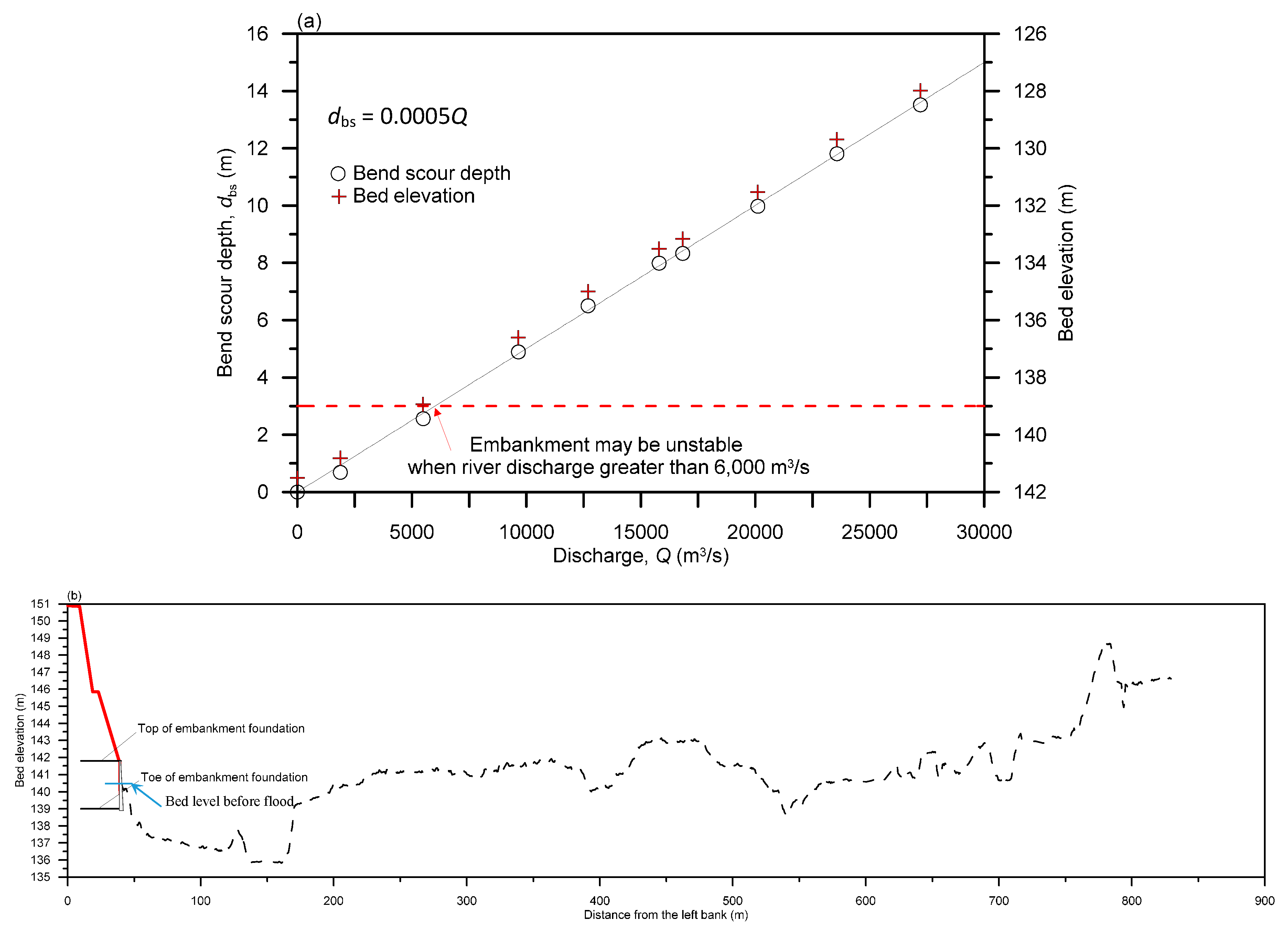
4.3. Practical Embankment Safety Curve
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ojha, C.; Singh, V.; Adrian, D. Influence of porosity on piping models of levee failure. J. Geotech. Geoenviron. Eng. 2001, 127, 1071–1074. [Google Scholar] [CrossRef]
- Vrijling, J.K.; Schweckendiek, T.; Kanning, W. Safety standards of flood defenses. In Proceedings of the 3rd International Symposium on Geotechnical Safety and Risk, Munich, Germany, 2–3 June 2011. [Google Scholar]
- Dos Santos, R.N.C.; Caldeira, L.M.M.S.; Serra, J.P.B. FMEA of a tailings dam. Georisk 2012, 6, 89–104. [Google Scholar] [CrossRef]
- Zhang, L.M.; Xu, Y.; Liu, Y.; Peng, M. Assessment of flood risks in Pearl River Delta due to levee breaching. Georisk 2013, 7, 122–133. [Google Scholar] [CrossRef]
- Lin, C. Study on Related Countermeasures of Scour Vulnerable Levees along Cho-Shui River; Fourth River Management Office, Water Resources Agency, Ministry of Economic Affairs: Changhua County, Taiwan, 2007.
- Wahl, T.L. Prediction of Embankment Dam Breach Parameters: A Literature Review and Needs Assessment; Dam Safety Research Report DSO-98-004; US Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1998.
- Morris, M.; Kortenhaus, A.; Visser, P.J.; Hassan, M. Breaching Processes: A State of the Art Review; FLOODsite Report T06-06-03; FLOODsite Consortium: Wallingford, UK, 2009. [Google Scholar]
- Morris, M.W.; Kortenhaus, A.; Visser, P.J. Modeling Breach Initiation and Growth; FLOODsite Report T06-08-02; FLOODsite Consortium: Wallingford, UK, 2009. [Google Scholar]
- Jia, D.D.; Shao, X.; Wang, H.; Zhou, G. Three-dimensional modeling of bank erosion and morphological changes in the Shishou bend of the middle Yangtze River. Adv. Water Resour. 2010, 33, 348–360. [Google Scholar] [CrossRef]
- ASCE/EWRI Task Committee on Dam/Levee Breaching. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar]
- Motta, D.; Abad, J.D.; Langendoen, E.J.; Garcia, M.H. A simplified 2D model for meander migration with physically-based bank evolution. Geomorphology 2012, 163–164, 10–25. [Google Scholar] [CrossRef]
- Viero, D.P.; D’Alpaos, A.; Carniello, L.; Defina, A. Mathematical modeling of flooding due to river bank failure. Adv. Water Resour. 2013, 59, 82–94. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Mendoza, A.; Abad, J.D.; Tassi, P.; Wang, D.C.; Ata, R.; Abderrezzak, K.E.K.; Hervouet, J.M. Improved numerical modeling of morphodynamics of rivers with steep banks. Adv. Water Resour. 2016, 93, 4–14. [Google Scholar] [CrossRef]
- Dodaro, G.; Tafarojnoruz, A.; Stefanucci, F.; Adduce, C.; Calomino, F.; Gaudio, R.; Sciortino, G. An experimental and numerical study on the spatial and temporal evolution of a scour hole downstream of a rigid bed. In Proceedings of the International Conference on Fluvial Hydraulics, River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 1415–1422. [Google Scholar]
- Yen, C.L.; Lai, J.S.; Chang, W.Y. Modeling of 3D flow and scouring around circular piers. Proc. Natl. Sci. Counc. A Phys. Sci. Eng. 2001, 25, 17–26. [Google Scholar]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsoe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Guo, W.D.; Hong, J.H.; Lee, F.Z.; Lai, J.S. Bridge scour prediction using 2D hydraulic model with empirical equations—A case study of Shuangyuan Bridge piers on the Kao-Ping River. In Proceedings of the 6th World Conference on Structural Control and Monitoring, Barcelona, Spain, 15–17 July 2014. [Google Scholar]
- Li, Z.W.; Yu, M.H. Numerical simulation of local flow field around spur dike. Wuhan Univ. J. Hydraul. Electr. Eng. 2000, 33, 18–22. [Google Scholar]
- Zhang, H.; Nakagawa, H.; Ishigaki, T.; Muto, Y. Prediction of 3D flow field and local scouring around spur dikes. J. Hydraul. Eng. 2005, 49, 1003–1008. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H.; Kawaike, Y.B.; Baba, Y. Experimental and simulation of turbulent flow in local scour around a spur dyke. Int. J. Sediment Res. 2009, 24, 33–45. [Google Scholar] [CrossRef]
- Hong, J.H.; Guo, W.D.; Chiew, Y.M.; Chen, C.H. A new practical method to simulate flood-induced bridge pier scour—A case study of Mingchu Bridge piers on the Cho-Shui River. Water 2016, 8, 238. [Google Scholar] [CrossRef]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Lai, J.S.; Guo, W.D.; Lin, G.F.; Tan, Y.C. A well-balanced upstream flux-splitting finite-volume scheme for shallow-water flow simulations with irregular bed topography. Int. J. Numer. Methods Fluids 2010, 62, 927–944. [Google Scholar] [CrossRef]
- Guo, W.D.; Lai, J.S.; Lin, G.F.; Lee, F.Z.; Tan, Y.C. Finite volume multi-stage scheme for advection-diffusion modeling in shallow water flow. J. Mech. 2011, 27, 415–430. [Google Scholar] [CrossRef]
- Guo, W.D.; Yang, T.H.; Chang, Y.C.; Shih, D.S.; Chen, C.H.; Ho, J.Y.; Lee, K.T.; Lin, G.F.; Hsiao, L.F.; Lee, C.S. Real-time scour depth predicting system based on ensemble quantitative precipitation forecast. In Proceedings of the 35th IAHR World Congress, Chengdu, China, 8–13 September 2013. [Google Scholar]
- Galay, V.J.; Yaremko, E.K.; Quazi, M.E. River Bed Scour and Construction of Stone Riprap Protection in Sediment Transport Gravel Bed Rivers; John Wiley and Sons, Ltd.: New York, NY, USA, 1987. [Google Scholar]
- Thorne, C.R. Bank Processes on the Red River between Index, Arkansas and Shreveport, Louisiana; Final Report to the US Army European Research Office, contract number DAJA45-88-C-0018; Department of Geography, Queen Mary College: London, UK, 1988. [Google Scholar]
- USA Army Corps of Engineering (USACE). Hydraulic Design of Flood Control Channels; Engineering Manual 1110-2-1601; Department of the Army, Corps of Engineers, Office of the Chief of Engineers: Washington, DC, USA, 1994. [Google Scholar]
- Lin, G.H.; Lin, C. Research in Foundation Erosion of Hazard Potential Levees in Jhuoshuei River; Fourth River Management Office, Water Resources Agency, Ministry of Economic Affairs: Changhua County, Taiwan, 2013.
- Lu, J.Y. Field Study of Short-Term Riverbed General Scour for Typhoon-Induced Floods; Water Resources Planning Institute, Water Resources Agency, Ministry of Economic Affairs: Taichung, Taiwan, 2014.
- Su, C.C.; Lu, J.Y. Measurements and prediction of typhoon-induced short-term general scours in intermittent rivers. Nat. Hazards 2013, 66, 671–687. [Google Scholar] [CrossRef]
- Abou-Seida, M.M.; Elsaeed, G.H.; Mostafa, T.M.; Elzahry, E.F. Local scour at bridge abutments in cohesive soil. J. Hydraul. Res. 2012, 50, 171–180. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Lai, J.S. Implementation and Application Study of the Achievements between WRA and USBR Cooperation (2/4); Water Resources Planning Institute, Water Resources Agency, Ministry of Economic Affairs: Taichung, Taiwan, 2010. (In Chinese)
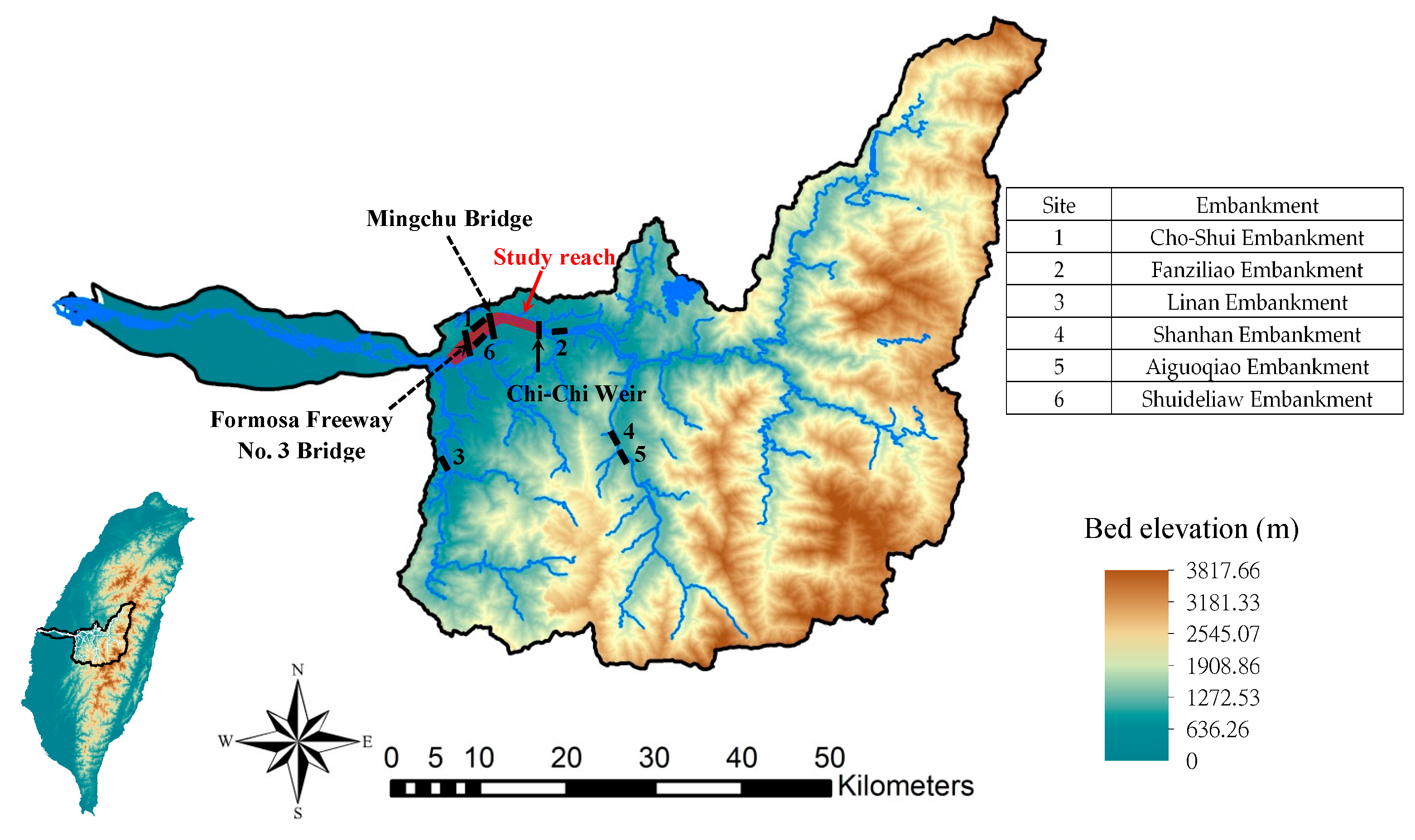
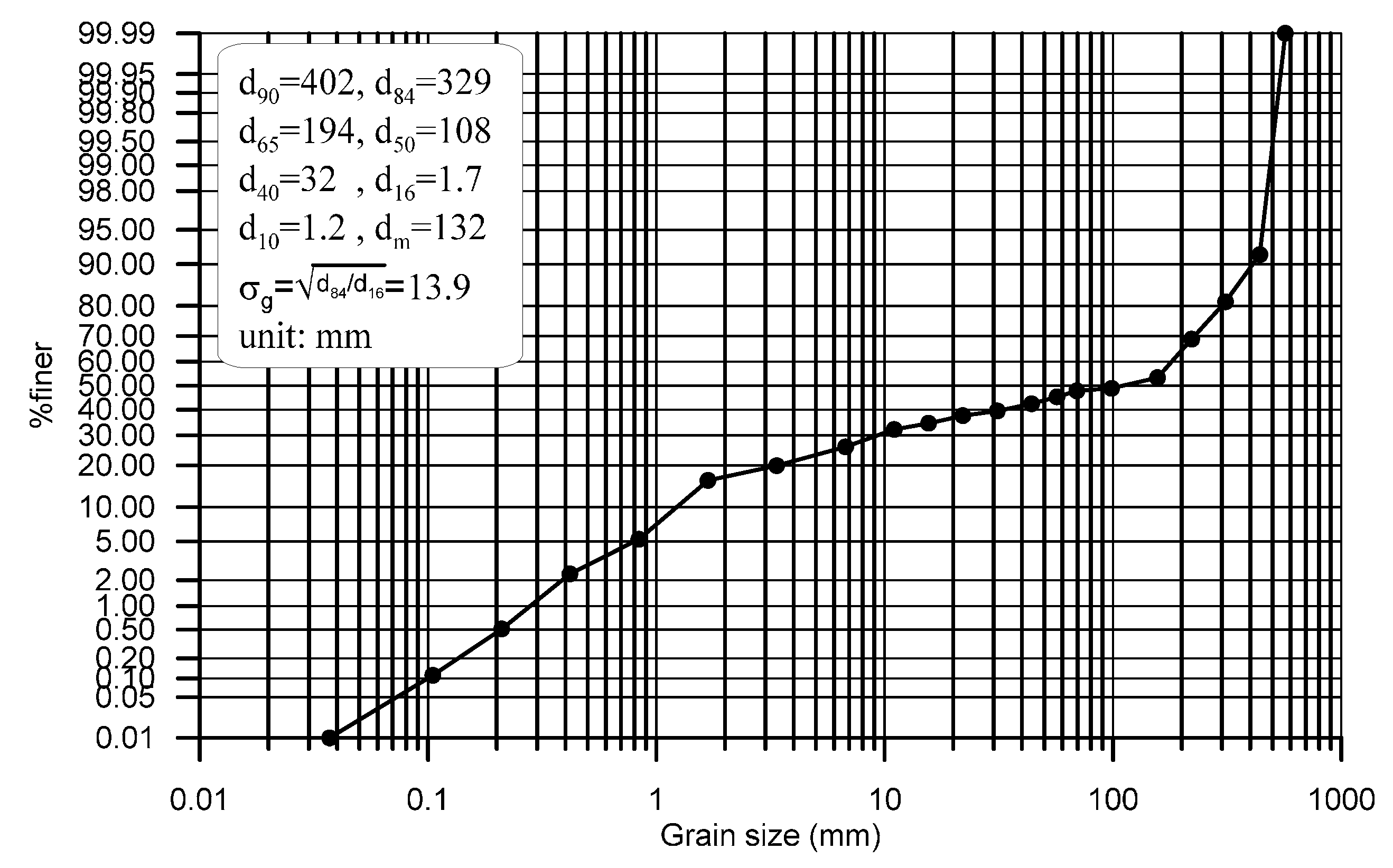
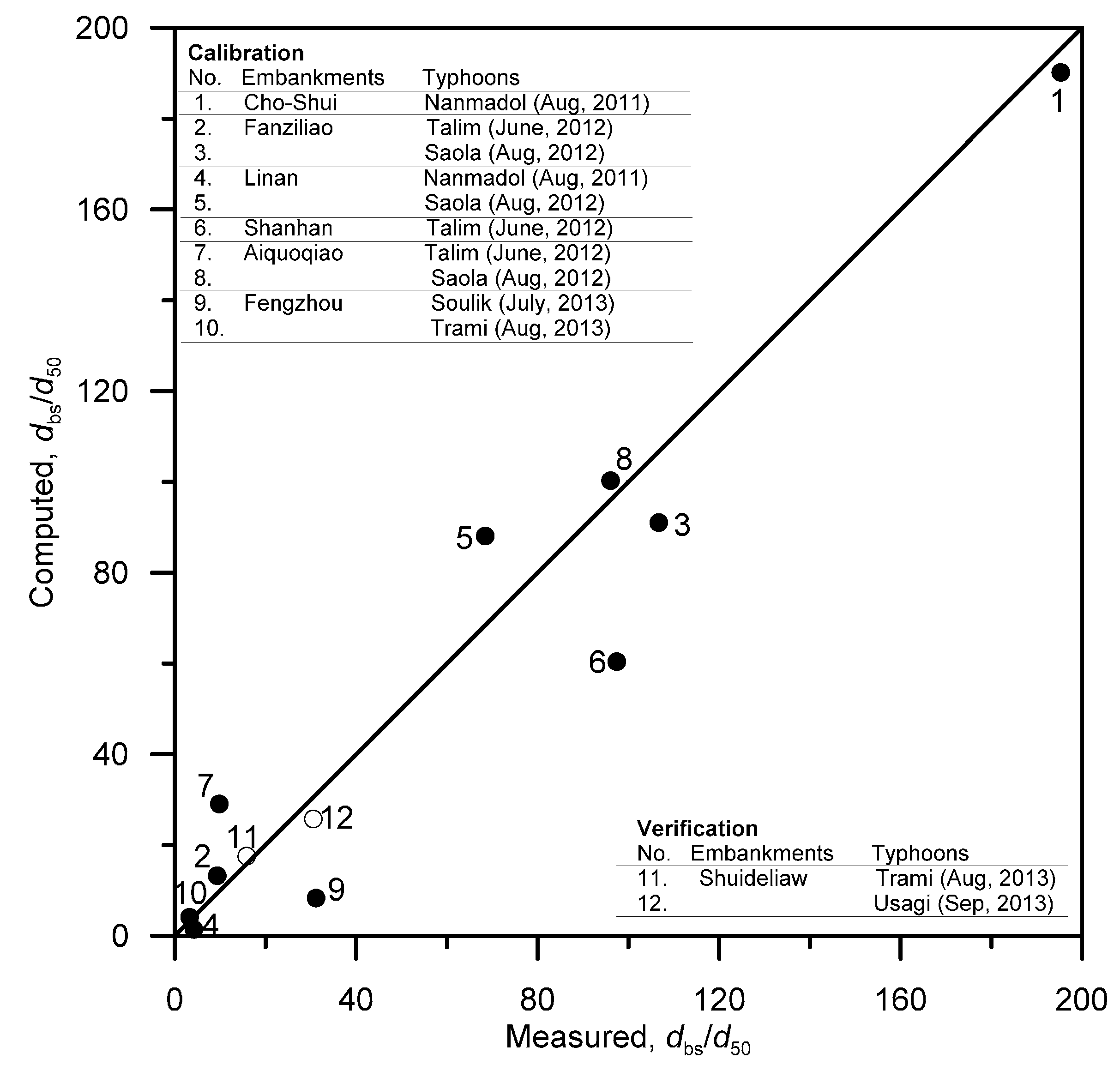
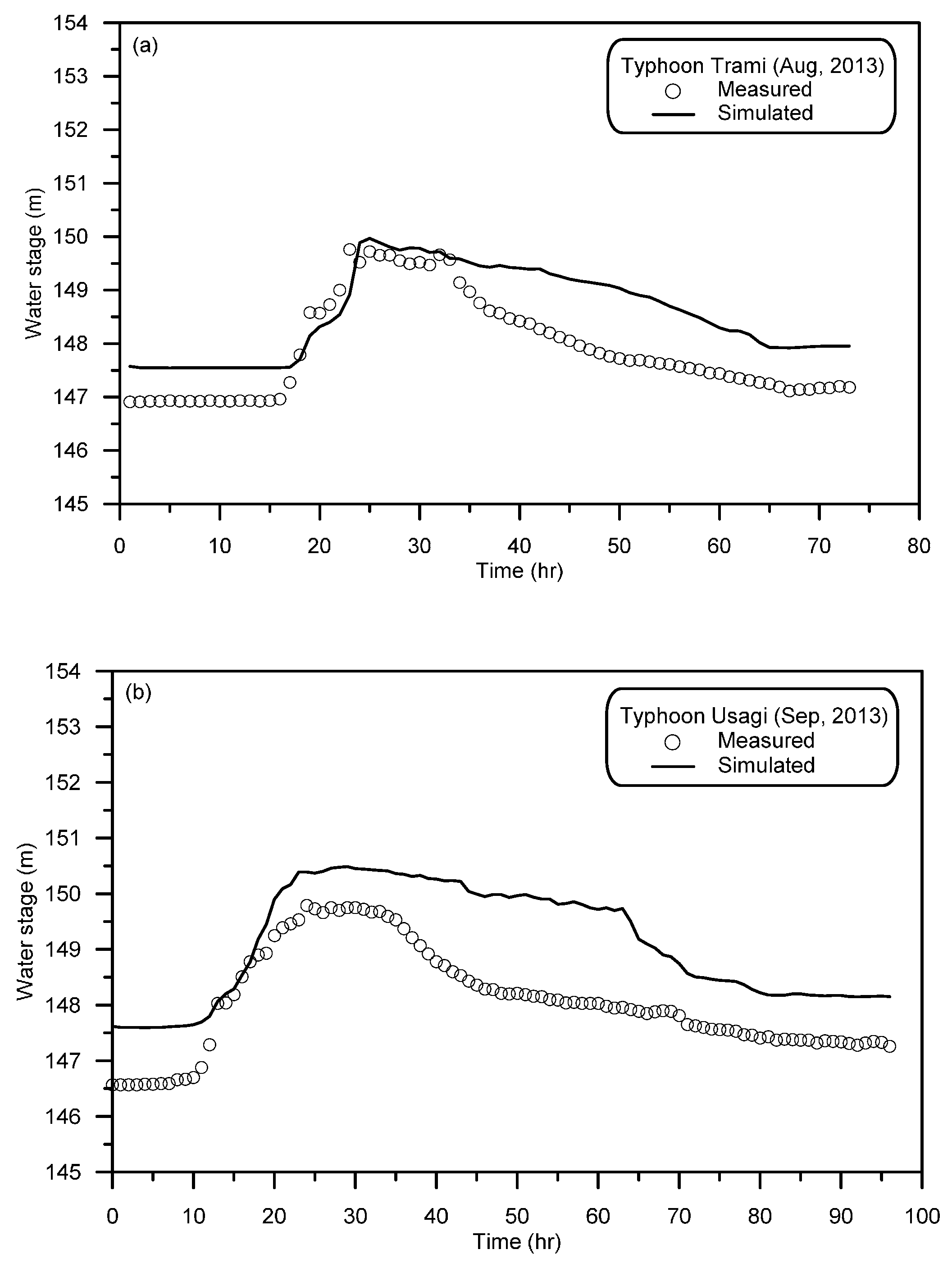
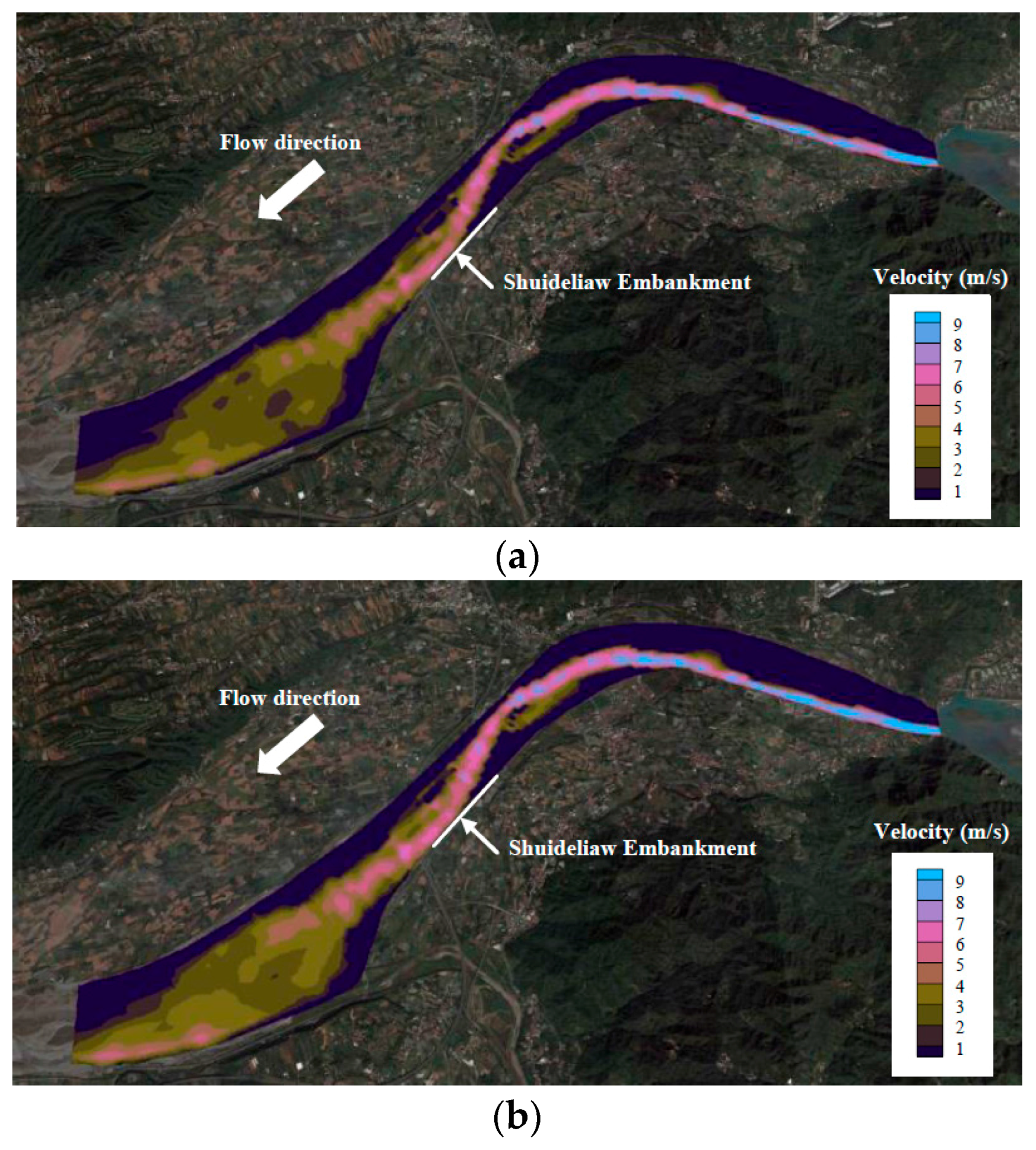
| River | Site | Flood Event | Qp (m3/s) | qp (m2/s) | s0 | d50 (mm) | R0 (m) | dbs (m) | Remark |
|---|---|---|---|---|---|---|---|---|---|
| Cho-Shui River | Cho-Shui Embankment | 1. Typhoon Nanmadol (August 2011) | 164 | 1.48 | 0.0063 | 3.43 | 605 | 0.67 | Lin and Lin [30] |
| Fanziliao Embankment | 2. Typhoon Talim (June 2012) | 346 | 1.86 | 0.0071 | 23.5 | 418 | 0.22 | ||
| 3. Typhoon Saola (August 2012) | 475 | 2.97 | 0.0057 | 7.5 | 418 | 0.8 | |||
| Linan Embankment | 4. Typhoon Nanmadol (August 2011) | 186 | 1.31 | 0.0066 | 85 | 558 | 0.36 | ||
| 5. Typhoon Saola (August 2012) | 2279 | 13.21 | 0.0066 | 34.5 | 558 | 2.36 | |||
| Shanhan Embankment | 6. Typhoon Talim (June 2012) | 562 | 4.44 | 0.0153 | 19.5 | 471 | 1.9 | ||
| Aiguoqiao Embankment | 7. Typhoon Talim (June 2012) | 1182 | 11.87 | 0.0112 | 48 | 169 | 0.47 | ||
| 8. Typhoon Saola (August 2012) | 1837 | 14.94 | 0.0148 | 25.5 | 169 | 2.45 | |||
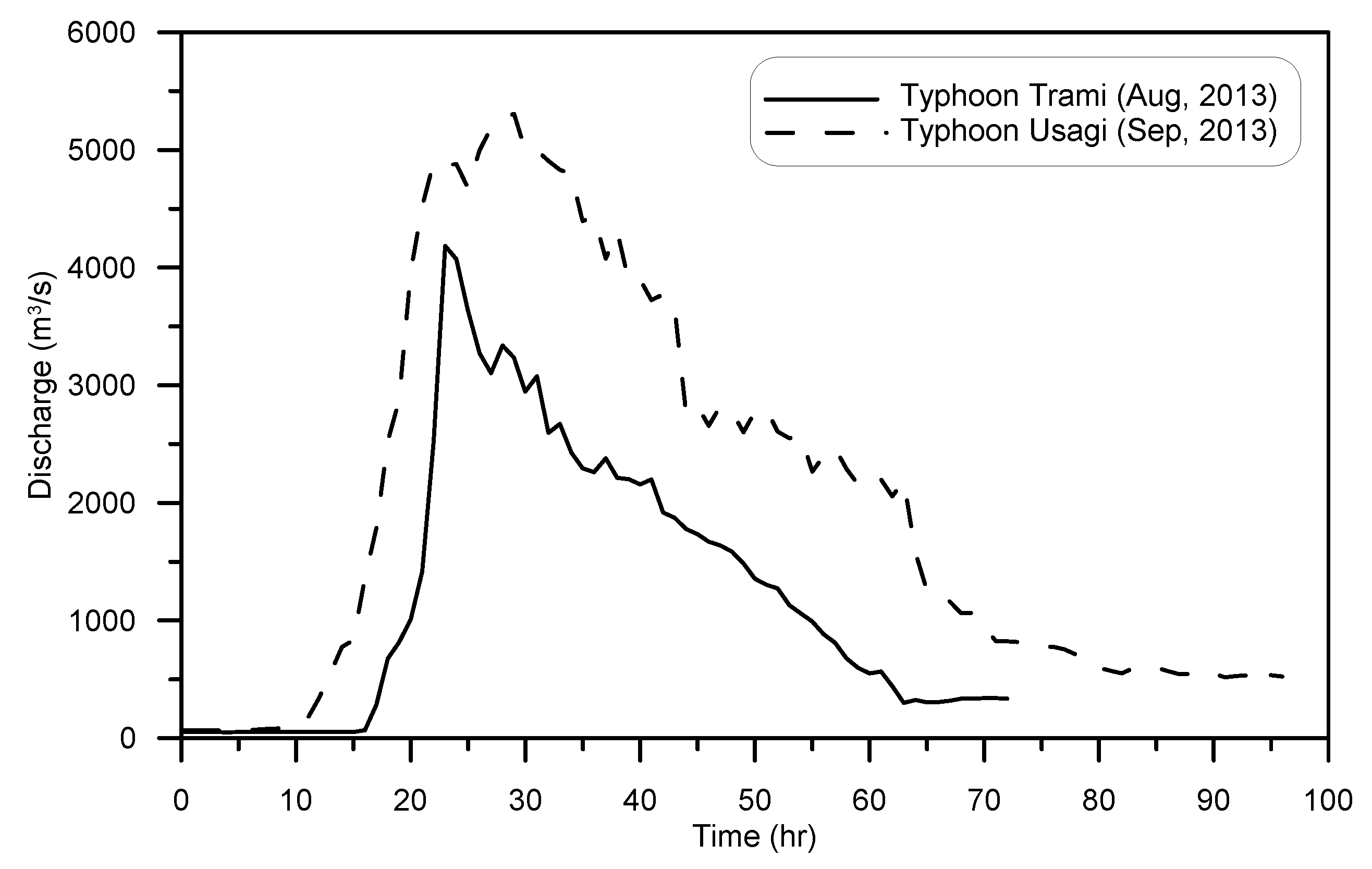
| Shuideliaw Embankment | 9. Typhoon Trami (August 2013) | 4186 | 25.37 | 0.00527 | 108 | 800 | 1.71 | Lu [31] | |
| 10. Typhoon Usagi (September 2013) | 5309 | 18.31 | 0.00527 | 108 | 800 | 3.30 | |||
| Da-Chia River | Fengzhou Embankment | 11. Typhoon Soulik (July 2013) | 6692 | 22.01 | 0.00755 | 168 | 500 | 5.23 | |
| 12. Typhoon Trami (August 2013) | 2393 | 10.64 | 0.00755 | 168 | 500 | 0.55 |
| Events | Three Criteria | ||
|---|---|---|---|
| Eηp (%) | ETp (%) | R2 | |
| Typhoon Trami (August 2013) | 0.1335 | 8.69 | 0.874 |
| Typhoon Usagi (September 2013) | 0.4600 | 8.33 | 0.889 |
| Methods | Typhoon Trami (Measured = 1.71 m) | Typhoon Usagi (Measured = 3.3 m) | ||
|---|---|---|---|---|
| Simulated | Simulated | |||
| Galay et al. [27] | 1.52 | −11.11 | 2.22 | −32.73 |
| Thorne [28] | 3.04 | 77.78 | 4.85 | 46.97 |
| U.S. Army Corps of Engineering [29] | 3.25 | 90.06 | 4.37 | 32.42 |
| Proposed method | 1.90 | 11.11 | 2.78 | −15.76 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.-D.; Hong, J.-H.; Chen, C.-H.; Su, C.-C.; Lai, J.-S. A Simplified Simulation Method for Flood-Induced Bend Scour—A Case Study Near the Shuideliaw Embankment on the Cho-Shui River. Water 2017, 9, 324. https://doi.org/10.3390/w9050324
Guo W-D, Hong J-H, Chen C-H, Su C-C, Lai J-S. A Simplified Simulation Method for Flood-Induced Bend Scour—A Case Study Near the Shuideliaw Embankment on the Cho-Shui River. Water. 2017; 9(5):324. https://doi.org/10.3390/w9050324
Chicago/Turabian StyleGuo, Wen-Dar, Jian-Hao Hong, Cheng-Hsin Chen, Chih-Chiang Su, and Jihn-Sung Lai. 2017. "A Simplified Simulation Method for Flood-Induced Bend Scour—A Case Study Near the Shuideliaw Embankment on the Cho-Shui River" Water 9, no. 5: 324. https://doi.org/10.3390/w9050324
APA StyleGuo, W.-D., Hong, J.-H., Chen, C.-H., Su, C.-C., & Lai, J.-S. (2017). A Simplified Simulation Method for Flood-Induced Bend Scour—A Case Study Near the Shuideliaw Embankment on the Cho-Shui River. Water, 9(5), 324. https://doi.org/10.3390/w9050324





