Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations
Abstract
:1. Introduction
2. FSL Monitoring
2.1. Study Area
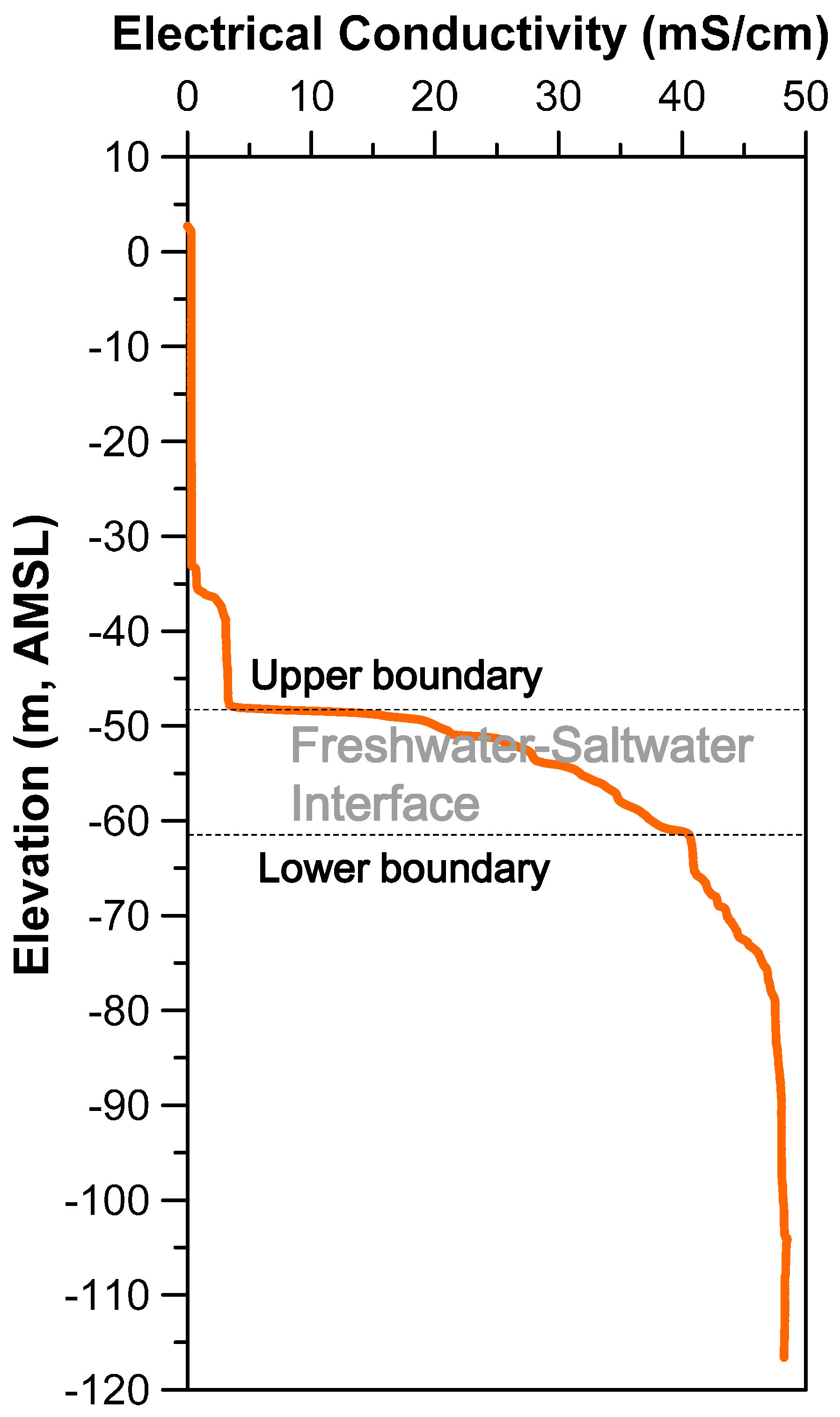
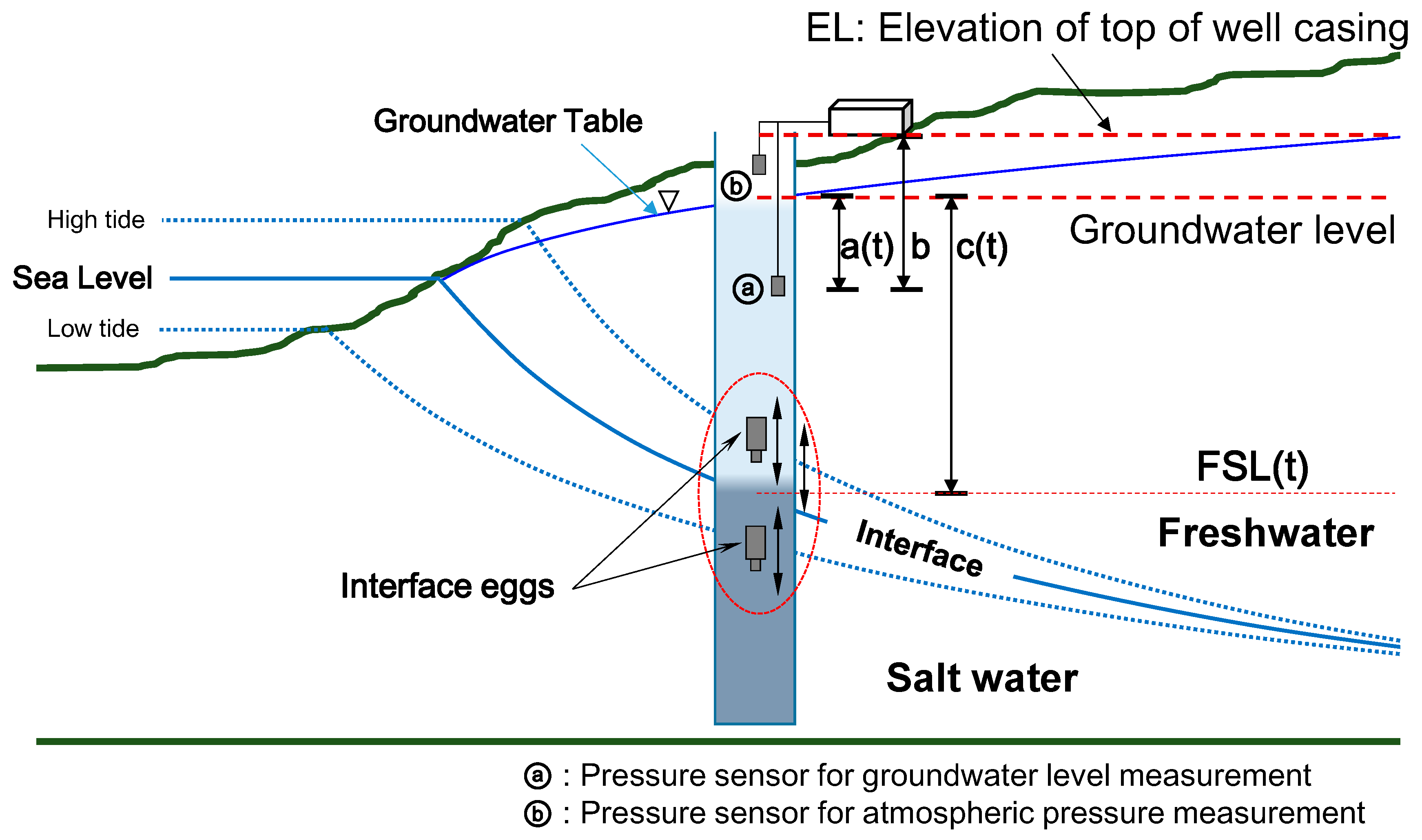
2.2. Monitoring Device and Data
3. FSL Prediction Model Development
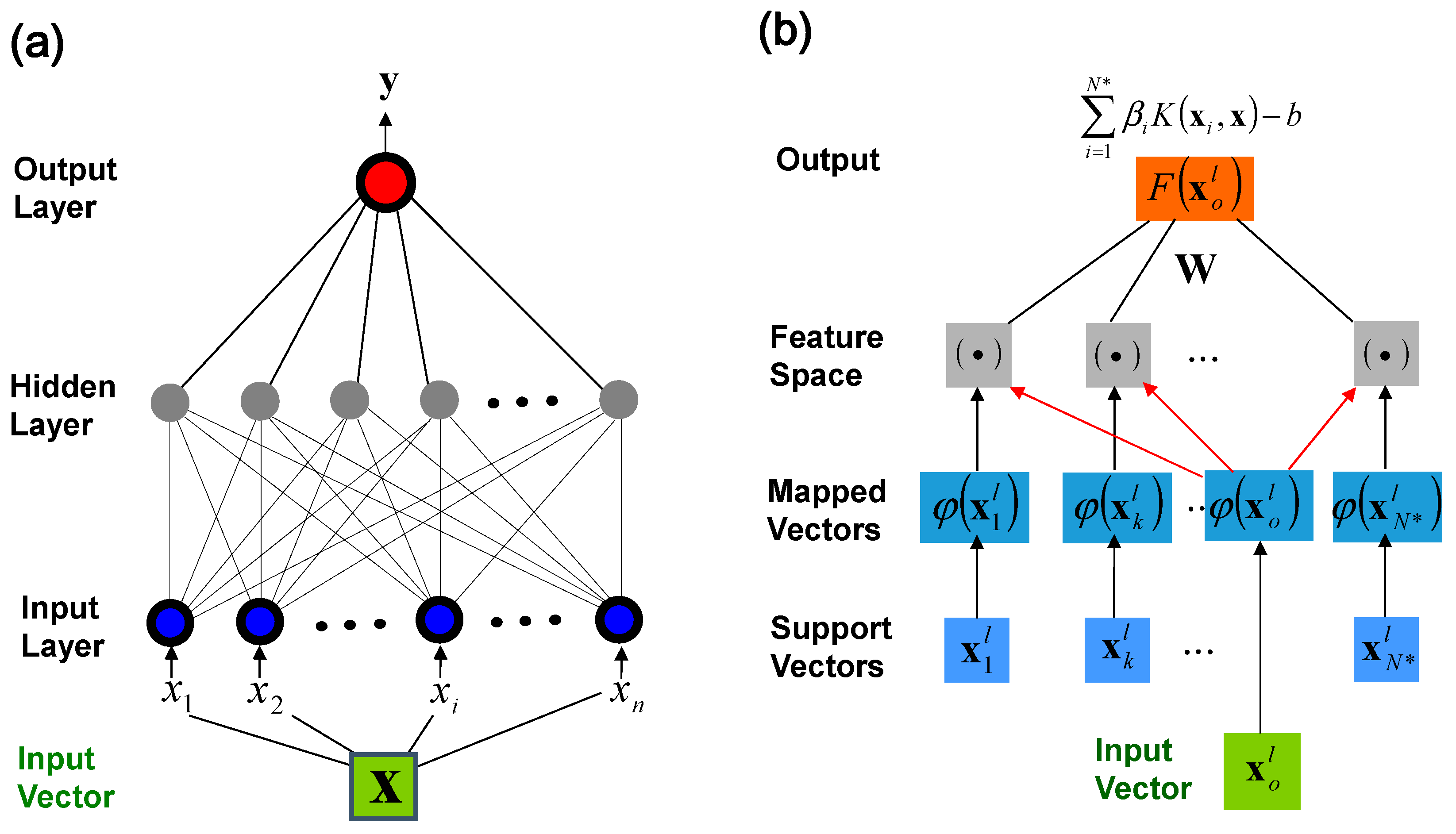
3.1. Aritificial Neural Network (ANN)
3.2. Suport Vector Machine (SVM)
3.3. Time Series Modeling Strategy
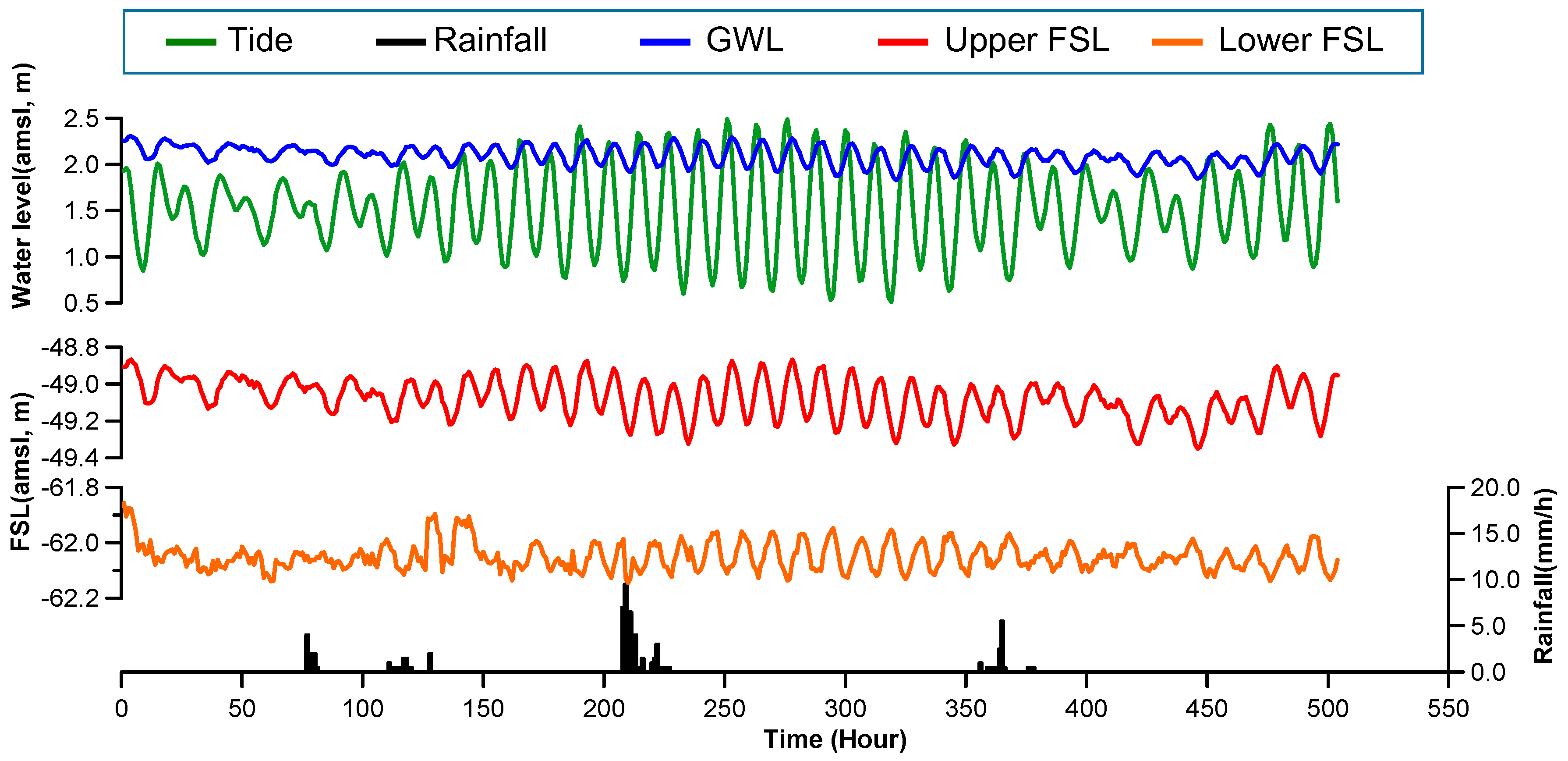
4. Results and Discussion
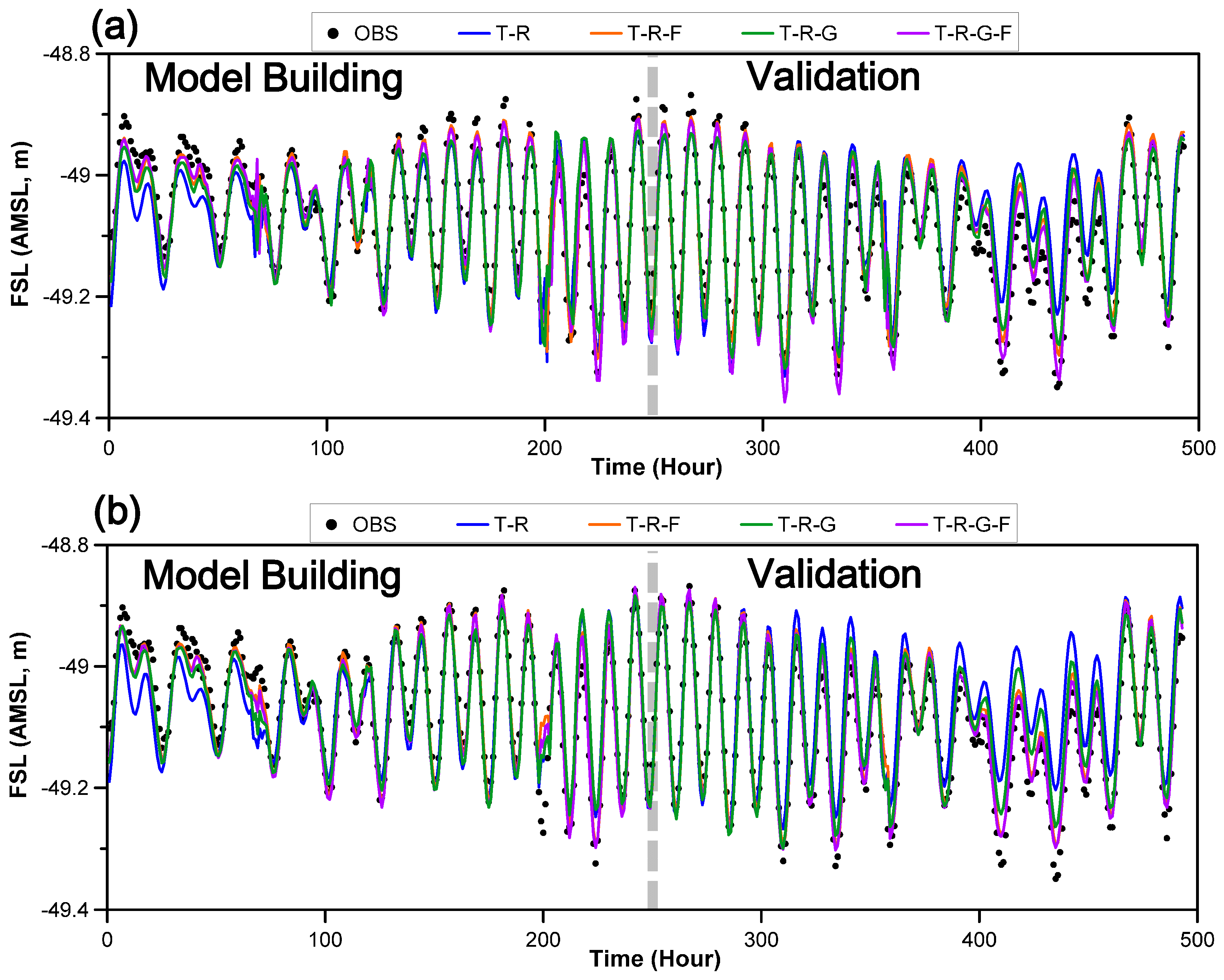
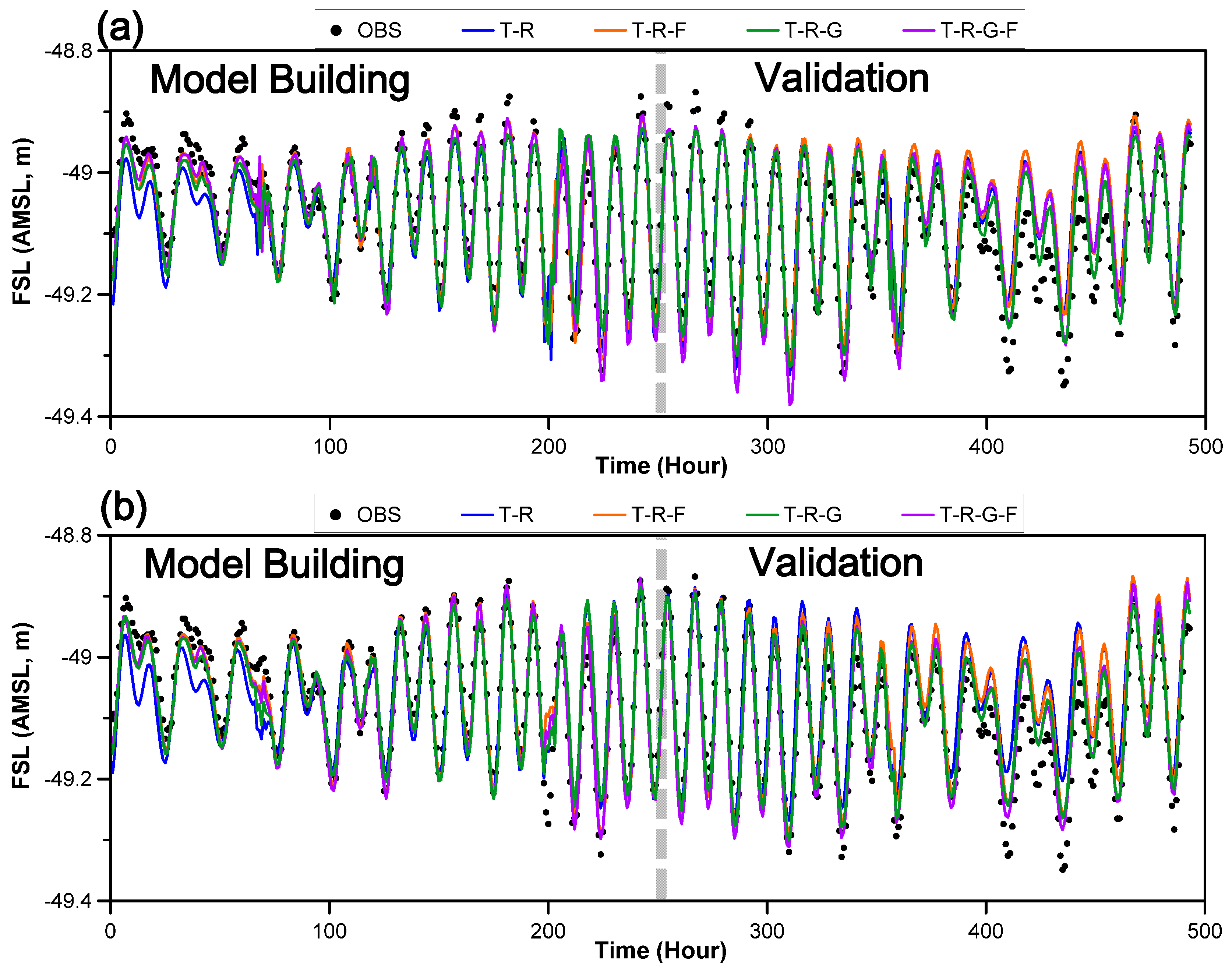
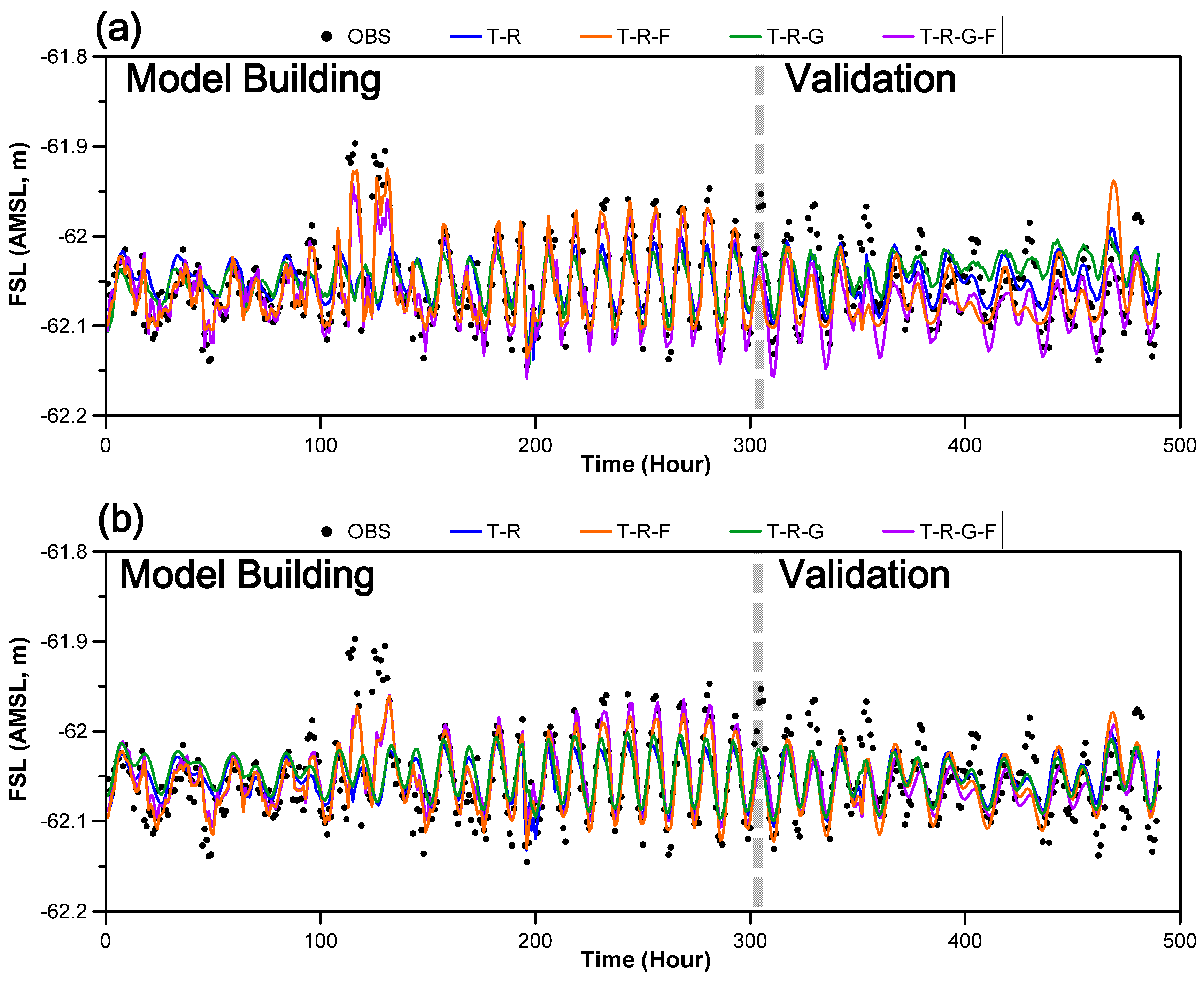
4.1. Direct Prediction of FSL
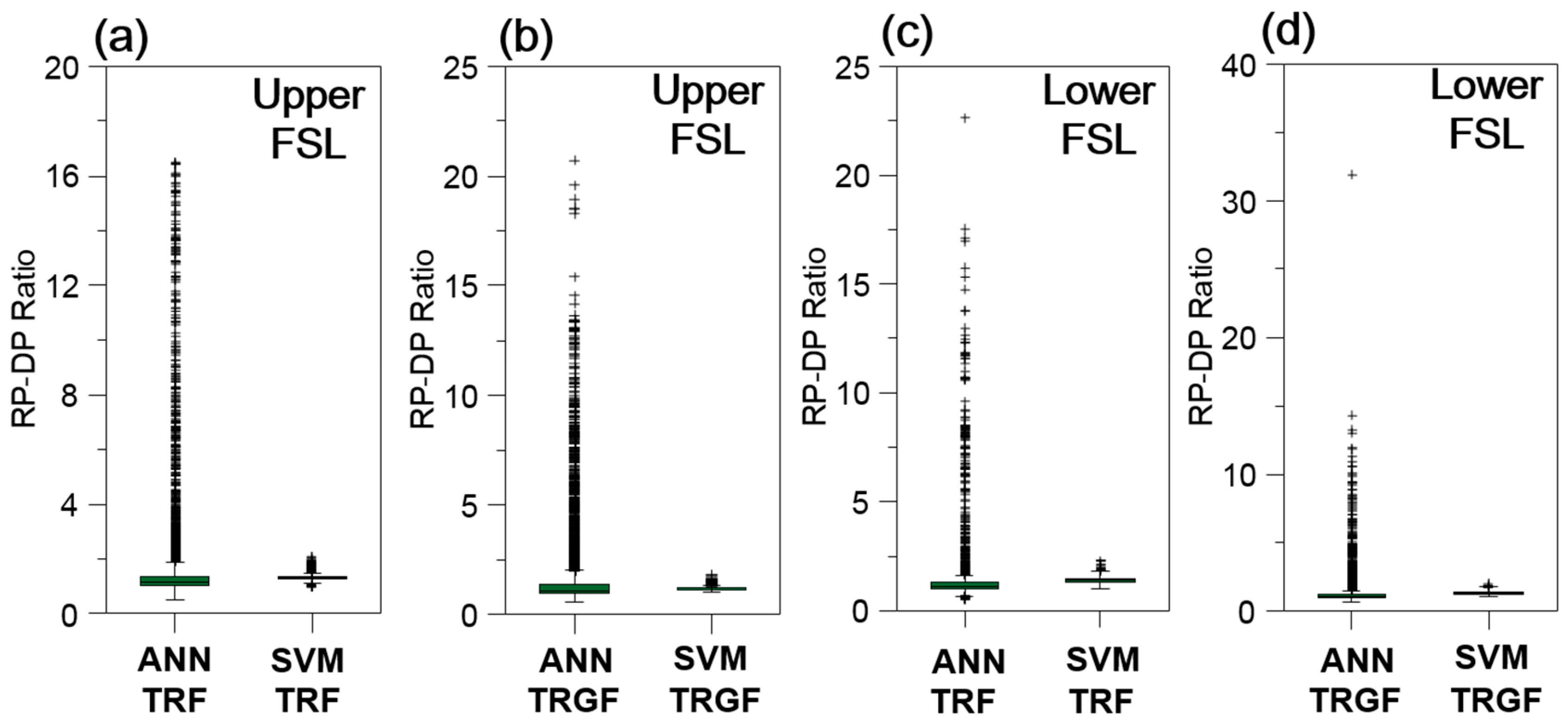
4.2. Recursive Prediction of FSL
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, K.; Seong, H.; Kim, T.; Park, K.; Woo, N.; Park, Y.; Koh, G.; Park, W. Tidal effects on variations of fresh-saltwater interface and groundwater flow in a multilayered coastal aquifer on a volcanic island (Jeju Island, Korea). J. Hydrol. 2006, 330, 525–542. [Google Scholar] [CrossRef]
- Liu, C.K.; Dai, J.J. Seawater intrusion and sustainable yield of basal aquifers. J. Am. Water Resour. Assoc. 2012, 48, 861–870. [Google Scholar] [CrossRef]
- Kim, Y.; Yoon, H.; Kim, K.P. Development of a novel method to monitor the temporal change in the location of the freshwater-saltwater interface and time series models for the prediction of the interface. Environ. Earth Sci. 2016, 75, 882–891. [Google Scholar] [CrossRef]
- Gingerich, S.B.; Voss, C.I. Thee-dimensional variable-density flow simulation of a coastal aquifer in southern Oahu, Hawaii, USA. Hydrogeol. J. 2005, 13, 436–450. [Google Scholar] [CrossRef]
- Wener, A.D.; Gallagher, M.R. Characterization of sea-water intrusion in the Pioneer Valley, Australia using hydrochemistry and three-dimensional numerical modelling. Hydrogeol. J. 2006, 14, 1452–1469. [Google Scholar] [CrossRef]
- Guo, W.; Langevin, C.D. User’s Guide to SEWAT: A Computer Program for Simulation of Three-Dimensional Variable-Density Ground-Water Flow; United States Geological Survey: Tallahassee, FL, USA, 2002; p. 73.
- Rozell, D.J.; Wong, T. Effects of climate change on groundwater resources at Shelter Island, New York State, USA. Hydrogeol. J. 2010, 18, 1657–1665. [Google Scholar] [CrossRef]
- Yechieli, Y.; Shalev, E.; Wollman, S.; Kiro, Y.; Kafri, U. Response of the Mediterranean and Dead Sea coastal aquifers to sea level variations. Water Resour. Res. 2010, 46, W12550. [Google Scholar] [CrossRef]
- Bardossy, A. Calibration of hydrological model parameters for ungauged catchments. Hydrol. Earth Syst. Sci. 2007, 11, 703–710. [Google Scholar] [CrossRef]
- Pollacco, J.A.P.; Ugalde, J.M.S.; Angulo-Jaramillo, R.; Braud, I.; Saugier, B. A linking test to reduce the number of hydraulic parameters necessary to simulate groundwater recharge in unsaturated zone. Adv. Water Resour. 2008, 31, 355–369. [Google Scholar] [CrossRef]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short-term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Akhtar, M.K.; Corzo, G.A.; van Andel, S.J.; Jonoski, A. River flow forecasting with artificial neural networks using satellite observed precipitation pre-processed with flow length and travel time information: Case study of the Ganges river basin. Hydrol. Earth Syst. Sci. 2009, 13, 1607–1618. [Google Scholar] [CrossRef]
- Hu, T.S.; Lam, K.C.; Ng, S.T. A modified neural network for improving river flow prediction. Hydrol. Sci. J. 2005, 50, 299–318. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobee, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef]
- Coppola, E.; Rana, A.J.; Poulton, M.M.; Szidarovszky, F.; Uhl, V.V. A neural network model for predicting aquifer water level elevations. Groundwater 2005, 43, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Sudheer, K.P. Artificial neural network modeling for groundwater level forecasting in a river island of eastern India. Water Resour. Manag. 2010, 24, 1845–1865. [Google Scholar] [CrossRef]
- Liong, S.Y.; Sivapragasam, C. Flood stage forecasting with support vector machines. J. Am. Water Resour. Assoc. 2002, 38, 173–186. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Asefa, T.; Kemblowski, M.W.; Urroz, G.; McKee, M.; Khalil, A. Support vectors-based groundwater head observation networks design. Water Resour. Res. 2004, 40, W1150901. [Google Scholar] [CrossRef]
- Gill, M.K.; Asefa, T.; Kaheil, Y.; McKee, M. Effect of missing data on performance of learning algorithms for hydrologic prediction: Implication to an imputation technique. Water Resour. Res. 2007, 43, W07416. [Google Scholar] [CrossRef]
- Yoon, H.; Hyun, Y.; Ha, K.; Lee, K.K.; Kim, G.B. A method to improve the stability and accuracy of ANN- and SVM-based time series models for long-term groundwater level predictions. Comput. Geosci. 2016, 90, 144–155. [Google Scholar] [CrossRef]
- Krishna, B.; Satyaji Rao, Y.R.; Vijaya, T. Modelling groundwater levels in an urban coastal aquifer using artificial neural networks. Hydrol. Process. 2008, 22, 1180–1188. [Google Scholar] [CrossRef]
- Nayak, P.C.; Satyaji Rao, Y.R.; Sudheer, K.P. Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour. Manag. 2006, 20, 77–90. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhou, H. A hybrid methodology for salinity time series forecasting based on wavelet transform and NARX neural networks. Arab. J. Sci. Eng. 2014, 39, 6895–6905. [Google Scholar] [CrossRef]
- Wan, Y.; Wan, C.; Hedgepeth, M. Elucidating multidecadal saltwater intrusion vegetation dynamics in a coastal floodplain with artificial neural networks and aerial photography. Ecohydology 2015, 8, 309–324. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modeling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L. The PDP Research Group, Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Platt, J.C. Fast training of support vector machines using sequential minimal optimization. In Advances in Kernel Methods-Support Vector Learning, 2nd ed.; Schölkopf, B., Burges, C., Smola, A., Eds.; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Ji, Y.; Hao, J.; Reyhani, N.; Lendasse, A. Direct and recursive prediction of time series using mutual information selection. In Proceedings of the International Work-Conference on Artificial Neural Networks, Barcelona, Spain, 8–10 June 2005; Volume 3512, pp. 1010–1017. [Google Scholar]
- Herrera, L.J.; Pomares, H.; Rojas, I.; Guillen, A.; Prieto, A.; Valenzuela, O. Recursive prediction for long term time series forecasting using advanced models. Neurocomputing 2007, 70, 2870–2880. [Google Scholar] [CrossRef]


| Variables | Max. Correlation Coefficient | Lag Time (Hour) |
|---|---|---|
| T-G | 0.85 | 2 |
| R-G | 0.14 | 43 |
| T-F (upper) | 0.83 | 2 |
| R-F (upper) | 0.11 | 47 |
| G-F (upper) | 0.97 | 0 |
| T-F (Lower) | 0.56 | 6 |
| R-F (Lower) | 0.27 | 19 |
| G-F (Lower) | 0.54 | 4 |
| Input Structures (Model Type) | Number of Components for Variables | |||||
|---|---|---|---|---|---|---|
| T | R | G | F | Total | ||
| Upper FSL | T-R | 4 | 4 | – | – | 8 |
| T-R-F | 4 | 4 | – | 4 | 12 | |
| T-R-G | 4 | 4 | 3 | – | 15 | |
| T-R-G-F | 4 | 4 | 3 | 4 | 19 | |
| Lower FSL | T-R | 8 | 4 | – | – | 12 |
| T-R-F | 8 | 4 | – | 4 | 16 | |
| T-R-G | 8 | 4 | 5 | – | 17 | |
| T-R-G-F | 8 | 4 | 5 | 4 | 21 | |
| Data Type | Data Allocation | ||
|---|---|---|---|
| Model Building | Model Validation | ||
| Upper FSL | Num. data | 250 | 247 |
| Time | 7:00 15 September–12:00 21 September | 13:00 21 September–23:00 5 October | |
| Lower FSL | Num. data | 300 | 197 |
| Time | 7:00 15 September–17:00 27 September | 18:00 27 September–23:00 5 October | |
| Model Type | ANN | SVM | |||||
|---|---|---|---|---|---|---|---|
| HN | LR | MM | C | Eps | Sig | ||
| Upper FSL | T-R | 2 | 0.001 | 0.0 | 7.0 | 0.13 | 3.0 |
| T-R-F | 15 | 0.020 | 0.0 | 5.0 | 0.05 | 2.5 | |
| T-R-G | 2 | 0.005 | 0.3 | 7.0 | 0.10 | 3.0 | |
| T-R-G-F | 5 | 0.005 | 0.0 | 10.0 | 0.05 | 3.0 | |
| Lower FSL | T-R | 15 | 0.001 | 0.9 | 3.0 | 0.11 | 2.0 |
| T-R-F | 15 | 0.001 | 0.3 | 5.0 | 0.13 | 3.0 | |
| T-R-G | 20 | 0.001 | 0.9 | 0.5 | 0.13 | 2.5 | |
| T-R-G-F | 10 | 0.001 | 0.0 | 5.0 | 0.13 | 3.0 | |
| Model | Index | T-R | T-R-F | T-R-G | T-R-G-F | Average |
|---|---|---|---|---|---|---|
| ANN | RMSE (m) | 0.061 | 0.034 | 0.042 | 0.032 | 0.042 |
| MARE (%) | 10.329 | 5.901 | 7.083 | 5.613 | 7.232 | |
| CORR | 0.888 | 0.965 | 0.935 | 0.964 | 0.938 | |
| SVM | RMSE (m) | 0.072 | 0.029 | 0.038 | 0.023 | 0.040 |
| MARE (%) | 12.335 | 4.959 | 6.221 | 3.944 | 6.865 | |
| CORR | 0.882 | 0.982 | 0.954 | 0.980 | 0.949 |
| Model | Index | T-R | T-R-F | T-R-G | T-R-G-F | Average |
|---|---|---|---|---|---|---|
| ANN | RMSE (m) | 0.034 | 0.020 | 0.040 | 0.020 | 0.028 |
| MARE (%) | 15.314 | 8.438 | 18.494 | 8.623 | 12.717 | |
| CORR | 0.593 | 0.885 | 0.549 | 0.908 | 0.734 | |
| SVM | RMSE (m) | 0.028 | 0.022 | 0.030 | 0.021 | 0.025 |
| MARE (%) | 12.630 | 9.229 | 12.654 | 9.104 | 10.904 | |
| CORR | 0.777 | 0.859 | 0.733 | 0.867 | 0.809 |
| Model | Index | T-R | T-R-F | T-R-G | T-R-G-F | Average |
|---|---|---|---|---|---|---|
| ANN | RMSE (m) | 0.061 | 0.061 | 0.042 | 0.056 | 0.055 |
| MARE (%) | 10.329 | 10.582 | 7.083 | 9.852 | 9.462 | |
| CORR | 0.888 | 0.965 | 0.935 | 0.892 | 0.902 | |
| SVM | RMSE (m) | 0.072 | 0.069 | 0.038 | 0.040 | 0.055 |
| MARE (%) | 12.335 | 12.255 | 6.221 | 7.043 | 9.463 | |
| CORR | 0.882 | 0.920 | 0.954 | 0.943 | 0.925 |
| Model | Index | T-R | T-R-F | T-R-G | T-R-G-F | Average |
|---|---|---|---|---|---|---|
| ANN | RMSE (m) | 0.034 | 0.042 | 0.040 | 0.034 | 0.037 |
| MARE (%) | 15.314 | 16.837 | 18.494 | 14.937 | 16.395 | |
| CORR | 0.593 | 0.420 | 0.549 | 0.806 | 0.592 | |
| SVM | RMSE (m) | 0.028 | 0.034 | 0.030 | 0.035 | 0.032 |
| MARE (%) | 12.630 | 14.347 | 12.654 | 14.773 | 13.601 | |
| CORR | 0.777 | 0.611 | 0.733 | 0.592 | 0.678 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, H.; Kim, Y.; Ha, K.; Lee, S.-H.; Kim, G.-P. Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations. Water 2017, 9, 323. https://doi.org/10.3390/w9050323
Yoon H, Kim Y, Ha K, Lee S-H, Kim G-P. Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations. Water. 2017; 9(5):323. https://doi.org/10.3390/w9050323
Chicago/Turabian StyleYoon, Heesung, Yongcheol Kim, Kyoochul Ha, Soo-Hyoung Lee, and Gee-Pyo Kim. 2017. "Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations" Water 9, no. 5: 323. https://doi.org/10.3390/w9050323
APA StyleYoon, H., Kim, Y., Ha, K., Lee, S.-H., & Kim, G.-P. (2017). Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations. Water, 9(5), 323. https://doi.org/10.3390/w9050323





