Temporal Distribution Characteristics of Alpine Precipitation and Their Vertical Differentiation: A Case Study from the Upper Shule River
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Date Acquisition
2.3. Methods
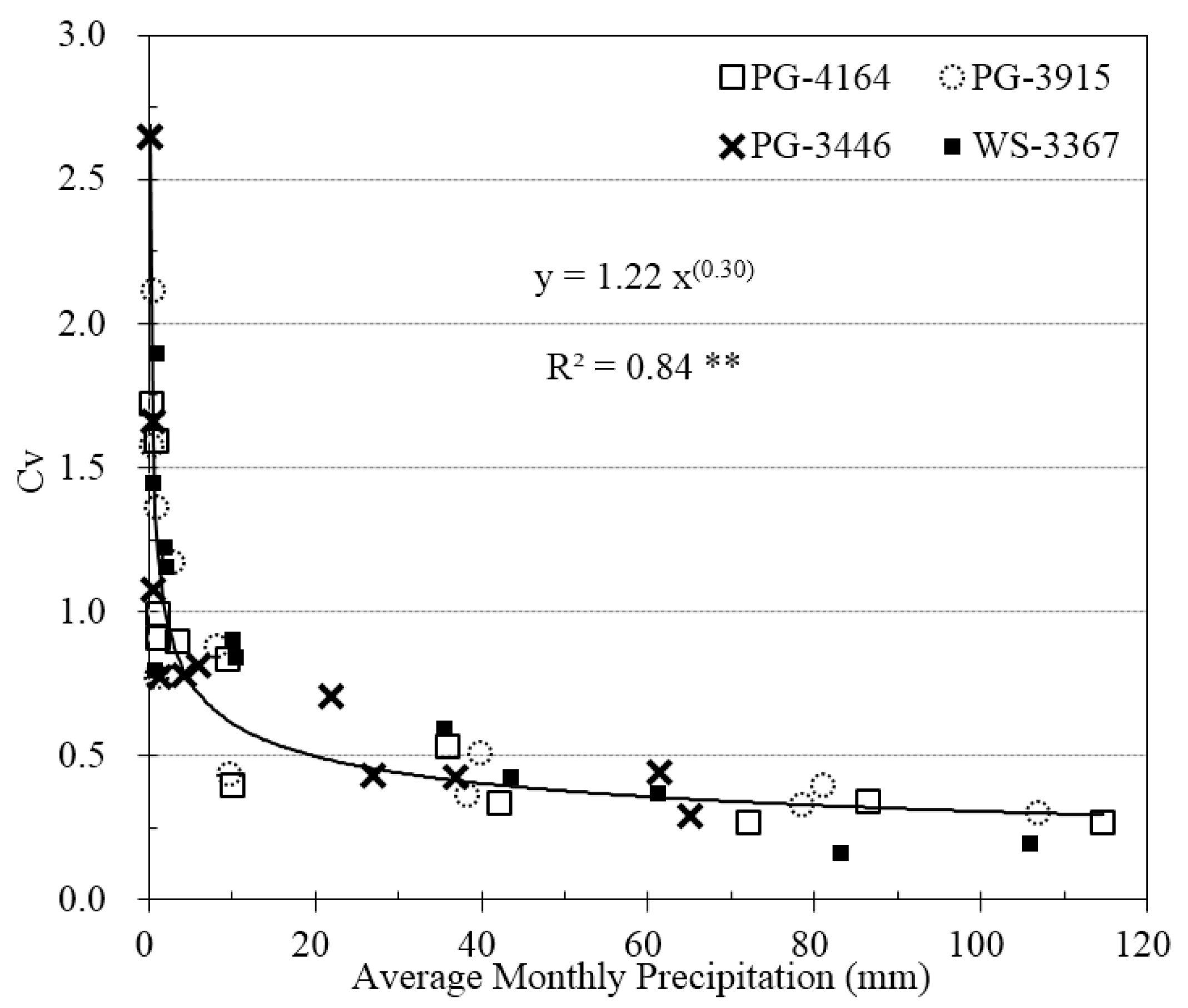
3. Results and Discussion
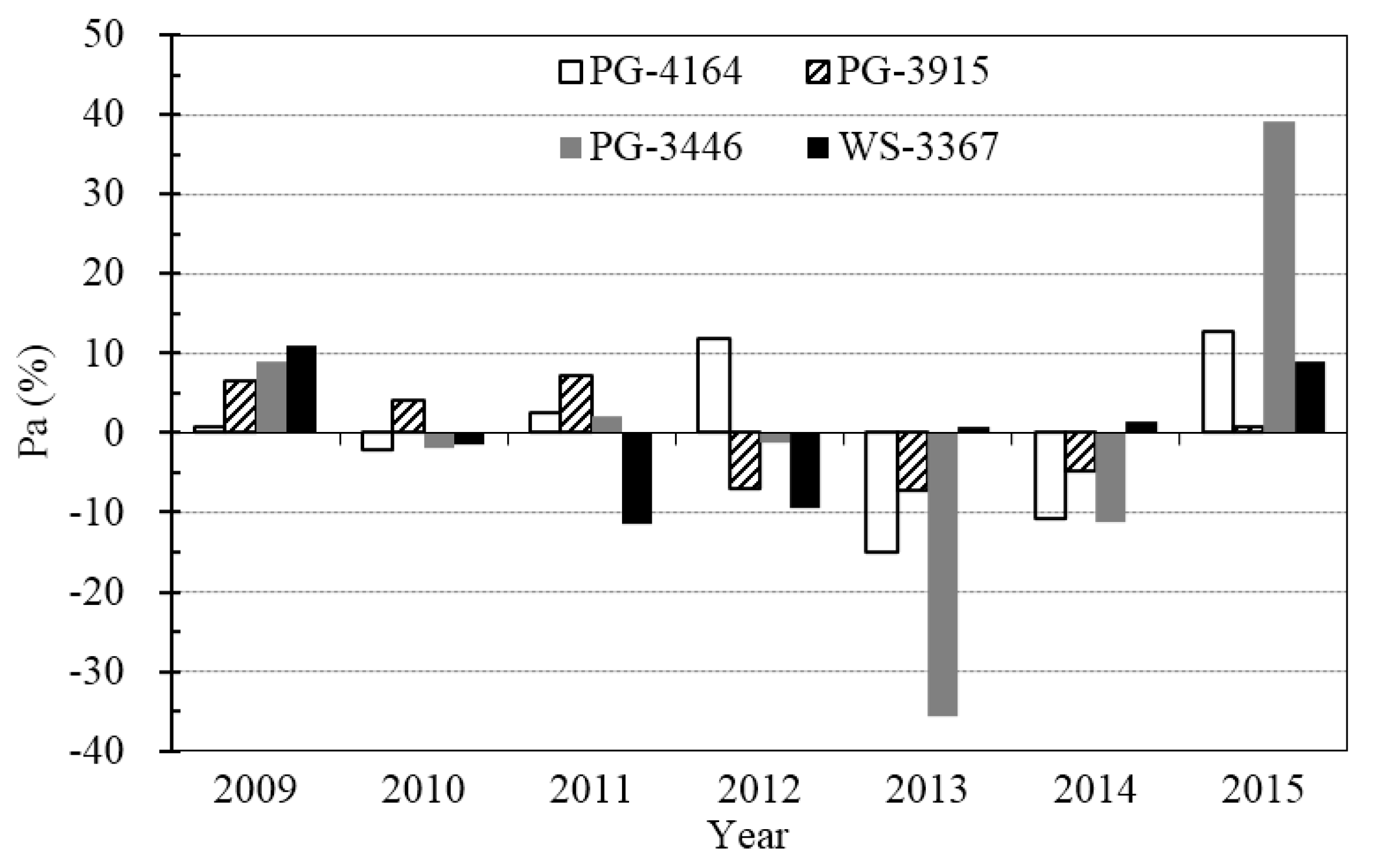
3.1. Inter-Annual Fluctuation
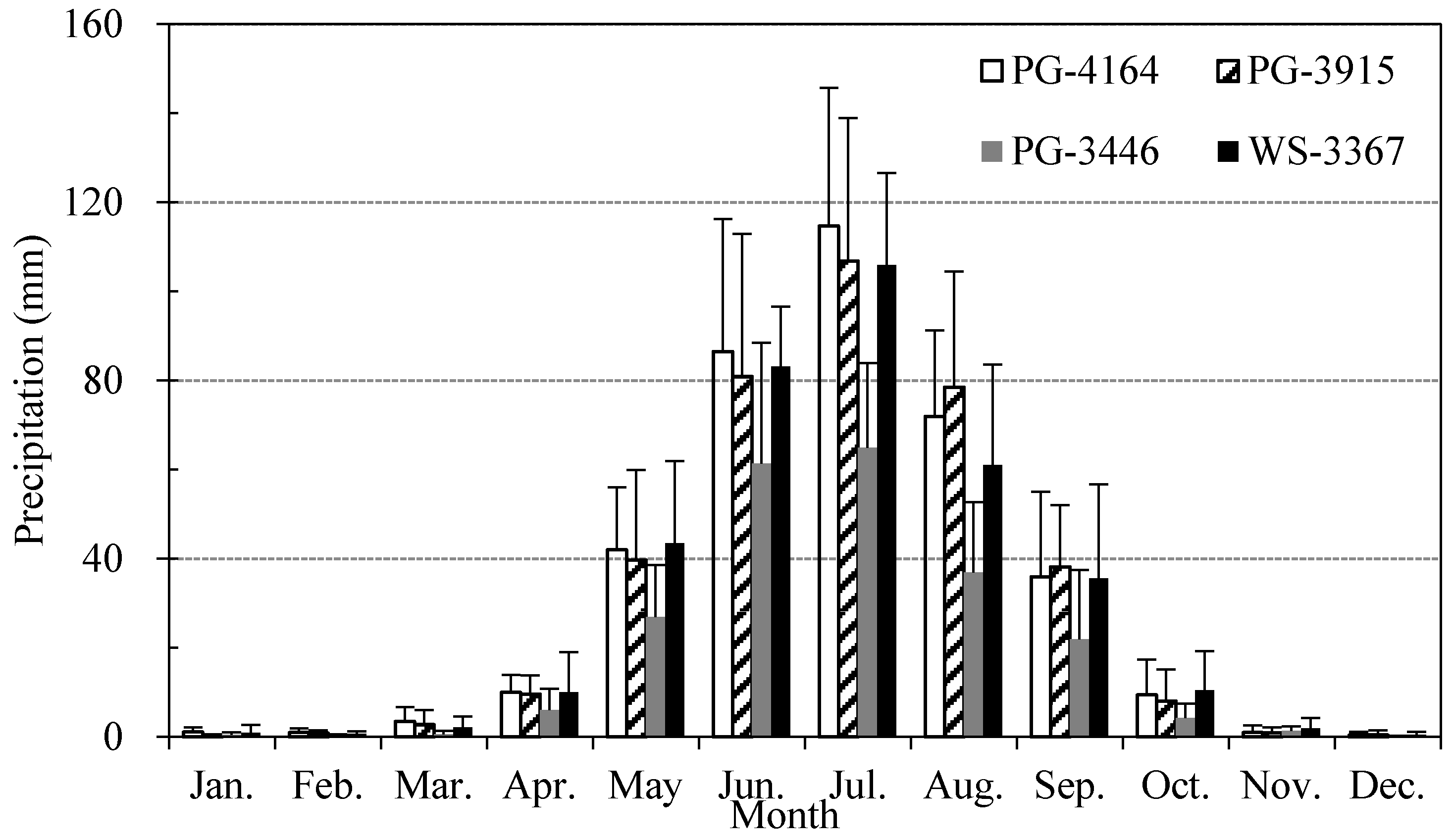
3.2. Annual Distribution
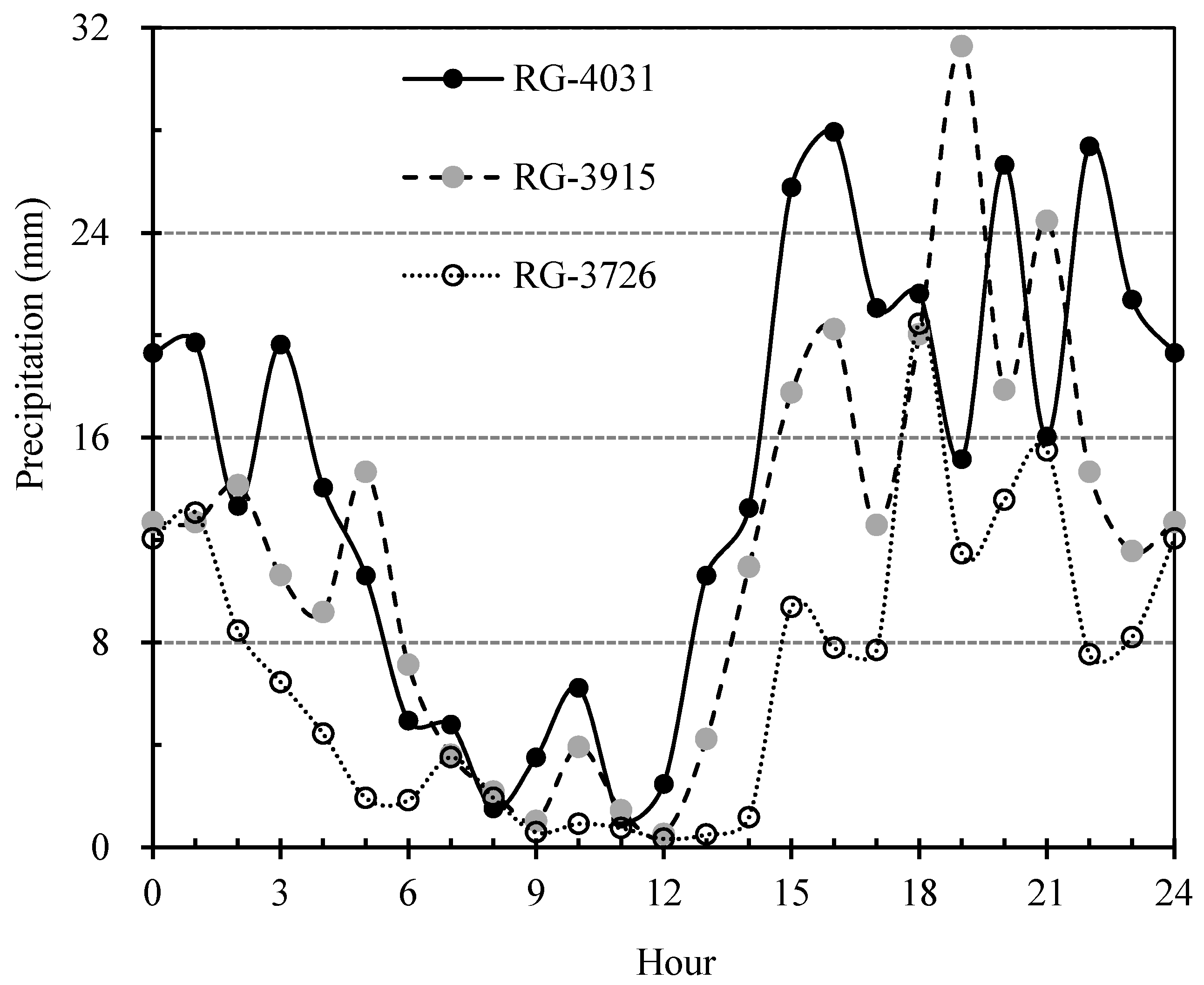
3.3. Diurnal Variation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Allan, R.P.; Soden, B.J. Atmospheric warming and the amplification of precipitation extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef] [PubMed]
- Terzago, S.; Cassardo, C.; Cremonini, R.; Fratianni, S. Snow Precipitation and Snow Cover Climatic Variability for the Period 1971–2009 in the Southwestern Italian Alps: The 2008–2009 Snow Season Case Study. Water 2010, 2, 773–787. [Google Scholar] [CrossRef]
- Bala, G.; Caldeira, K.; Nemani, R.; Cao, L.; Ban-Weiss, G.; Shin, H.J. Albedo enhancement of marine clouds to counteract global warming: Impacts on the hydrological cycle. Clim. Dynam. 2011, 37, 915–931. [Google Scholar] [CrossRef]
- Coppola, E.; Verdecchia, M.; Giorgi, F.; Colaiuda, V.; Tomassetti, B.; Lombardi, A. Changing hydrological conditions in the Po basin under global warming. Sci. Total Environ. 2014, 493, 1183–1196. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Deng, X.Z.; Song, W.; Li, Z.H.; Chen, J.C. What is the main cause of grassland degradation? A case study of grassland ecosystem service in the middle-south Inner Mongolia. Catena 2017, 150, 100–107. [Google Scholar] [CrossRef]
- Davis, J.; Pavlova, A.; Thompson, R.; Sunnucks, P. Evolutionary refugia and ecological refuges: Key concepts for conserving Australian arid zone freshwater biodiversity under climate change. Glob. Chang. Biol. 2013, 19, 1970–1984. [Google Scholar] [CrossRef] [PubMed]
- Son, K.H.; Bae, D.H. Drought analysis according to shifting of climate zones to arid climate zone over Asia monsoon region. J. Hydrol. 2015, 529, 1021–1029. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Hasani, K.; Bavani, A.R.M.; Asgari, K. A framework for the assessment of reservoir operation adaptation to climate change in an arid region. Int. J. Glob. Warm. 2016, 9, 286–305. [Google Scholar] [CrossRef]
- Yin, Z.L.; Feng, Q.; Zou, S.B.; Yang, L.S. Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Deng, X.Z.; Zhao, C.H. Identification of Water Scarcity and Providing Solutions for Adapting to Climate Changes in the Heihe River Basin of China. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
- Shinohara, Y.; Kumagai, T.; Otsuki, K.; Kume, A.; Wada, N. Impact of climate change on runoff from a mid-latitude mountainous catchment in central Japan. Hydrol. Process. 2009, 23, 1418–1429. [Google Scholar] [CrossRef]
- Smith, P.C.; Calanca, P.; Fuhrer, J. A Simple Scheme for Modeling Irrigation Water Requirements at the Regional Scale Applied to an Alpine River Catchment. Water 2012, 4, 869–886. [Google Scholar] [CrossRef]
- Deng, X.Z.; Gibson, J.; Wang, P. Quantitative measurements of the interaction between net primary productivity and livestock production in Qinghai Province based on data fusion technique. J. Clean Prod. 2017, 142, 758–766. [Google Scholar] [CrossRef]
- Kunz, M. Characteristics of large-scale orographic precipitation in a linear perspective. J. Hydrometeorol. 2011, 12, 27–44. [Google Scholar] [CrossRef]
- Hoover, J.D.; Doesken, N.; Elder, K.; Laituri, M.; Liston, G.E. Temporal trend analyses of alpine data using North American regional reanalysis and In Situ data: Temperature, wind Speed, precipitation, and derived blowing snow. J. Appl. Meteorol. Clim. 2014, 53, 676–693. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.G.; Yang, D.Q.; Hao, Z.C. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Saghafian, B.; Bondarabadi, S.R. Validity of regional rainfall spatial distribution methods in mountainous areas. J. Hydrol. Eng. 2008, 13, 531–540. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bievre, B.; Wyseure, G. Spatial and Temporal Rainfall Variability in Mountainous Areas: A Case Study from the South Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Yang, M.X.; Yao, T.D.; Gou, X.H.; Wang, H.J.; Ha, L.S. Comparison analysis of the summer monsoon precipitation between northern and southern slopes of Tanggula Mountains, Qinghai–Xizang (Tibetan) Plateau: A case study in summer 1998. Hydrol. Process. 2007, 21, 1841–1847. [Google Scholar] [CrossRef]
- Chen, S.Y.; Liu, W.J.; Qin, X.; Liu, Y.S.; Zhang, T.Z.; Chen, K.L.; Hu, F.Z.; Ren, J.W.; Qin, D.H. Response characteristics of vegetation and soil environment to permafrost degradation in the upstream regions of the Shule River Basin. Environ. Res. Lett. 2012, 7, 045406. [Google Scholar] [CrossRef]
- Luo, K.S.; Tao, F.L.; Deng, X.Z.; Moiwo, J.P. Changes in potential evapotranspiration and surface runoff in 1981–2010 and the driving factors in Upper Heihe River Basin in Northwest China. Hydrol. Process. 2017, 31, 90–103. [Google Scholar] [CrossRef]
- Deng, X.Z.; Singh, R.B.; Liu, J.G.; Guneralp, B. Water productivity and integrated water resources management. Phys. Chem. Earth 2016, 96, 1. [Google Scholar] [CrossRef]
- Yesilirmak, E.; Atatanir, L. Spatiotemporal variability of precipitation concentration in western Turkey. Nat. Hazards 2016, 81, 687–704. [Google Scholar] [CrossRef]
- Zhang, L.; Miao, Q.L. Precipitation changes in the Tibetan Plateau during the last four decades. Arid Land Geogr. 2007, 30, 240–246. [Google Scholar]
- Zhou, S.W.; Wang, Q.H.; Du, J.; Ma, Z.F. Characteristics of spatial and temporal distribution of precipitation in flood season over the Tibetan Plateau. Clim. Environ. Res. 2011, 16, 723–732. (In Chinese) [Google Scholar]
- Lin, H.B.; You, Q.L.; Jiao, Y.; Min, J.Z. Spatial and temporal characteristics of the precipitation over the Tibetan Plateau from 1961 to 2010 based on high resolution grid-observation dataset. J. Nat. Resour. 2015, 30, 271–281. [Google Scholar]
- Lan, Y.C.; Hu, X.L.; Xiao, S.C.; Wen, J.; Wang, G.Y.; Zou, S.B.; La, C.F.; Song, J. Study on climate change in mountainous region of Shulehe River Basin in past 50 years and its effect to mountainous runoff. Plateau Meteorol. 2012, 31, 1636–1644. (In Chinese) [Google Scholar]
- Hua, L.J.; Zhong, L.H.; Ke, Z.J. Characteristics of the precipitation recycling ratio and its relationship with regional precipitation in China. Theor. Appl. Climatol. 2017, 127, 513–531. [Google Scholar] [CrossRef]
- Hua, L.J.; Zhong, L.H.; Ke, Z.J. Precipitation recycling and soil–precipitation interaction across the arid and semi-arid regions of China. Int. J. Climatol. 2016, 36, 3708–3722. [Google Scholar] [CrossRef]
- Yang, W.; He, J.H.; Wang, P.X.; Wang, C.H. Inhomogeneity characteristics of intra-annual precipitation over the Tibetan Plateau in recent 42 years. Acta Geogr. Sin. 2011, 66, 376–384. [Google Scholar]
- Meng, X.J.; Zhang, S.F.; Zhang, Y.Y.; Wang, C.C. Temporal and spatial changes of temperature and precipitation in Hexi Corridor during 1955–2011. J. Geogr. Sci. 2013, 23, 653–667. [Google Scholar] [CrossRef]
- Xu, X.D.; Zhao, T.L.; Lu, C.G.; Shi, X.H. Characteristics of the water cycle in the atmosphere over the Tibetan Plateau. Acta Meteorol. Sin. 2014, 72, 1079–1095. [Google Scholar]
- Zhou, S.W.; Wu, P.; Wang, C.H.; Han, J.C. Spatial distribution of atmospheric water vapor and its relationship with precipitation in summer over the Tibetan Plateau. J. Geogr. Sci. 2012, 22, 795–809. [Google Scholar] [CrossRef]
- Tanaka, L.M.D.S.; Satyamurty, P.; Machado, L.A.T. Diurnal variation of precipitation in central Amazon Basin. Int. J. Climatol. 2014, 34, 3574–3584. [Google Scholar] [CrossRef]
- Mao, J.Y.; Wu, G.X. Diurnal variations of summer precipitation over the Asian monsoon region as revealed by TRMM satellite data. Sci. China Earth Sci. 2012, 55, 554–566. [Google Scholar] [CrossRef]
- Yu, R.C.; Zhou, T.J.; Xiong, A.Y.; Zhu, Y.J.; Li, J.M. Diurnal variations of summer precipitation over contiguous China. Geophys. Res. Lett. 2007, 34, L01704. [Google Scholar] [CrossRef]
- Yu, R.C.; Yuan, W.H.; Li, J.; Fu, Y.F. Diurnal phase of late-night against late-afternoon of stratiform and convective precipitation in summer southern contiguous China. Clim. Dynam. 2010, 35, 567–576. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Germann, U.; Panziera, L. Diurnal cycle of precipitation over complex Alpine orography: Inferences from high-resolution radar observations. Q. J. R. Meteorol. Soc. 2013, 139, 1025–1046. [Google Scholar] [CrossRef]
- Long, Q.C.; Chen, Q.L.; Gui, K.; Zhang, Y. A Case Study of a Heavy Rain over the Southeastern Tibetan Plateau. Atmosphere 2016, 7, 118. [Google Scholar] [CrossRef]

| Site | Longitude (°E) | Latitude (°N) | Altitude (m) | Record Period | Years |
|---|---|---|---|---|---|
| PG-4164 | 98.36 | 38.56 | 4164 | Whole Year | 2009–2015 |
| PG-3915 | 98.31 | 38.42 | 3915 | ||
| PG-3446 | 97.72 | 38.84 | 3446 | ||
| RG-4031 | 98.26 | 38.30 | 4031 | Rain Season | 2012–2015 |
| RG-3915 | 98.31 | 38.42 | 3915 | ||
| RG-3726 | 98.03 | 38.70 | 3726 |
| Site | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | Average |
|---|---|---|---|---|---|---|---|---|
| PG-4164 | 0.77 | 0.75 | 0.78 | 0.81 | 0.77 | 0.73 | 0.75 | 0.77 |
| PG-3915 | 0.77 | 0.77 | 0.80 | 0.80 | 0.79 | 0.75 | 0.75 | 0.78 |
| PG-3446 | 0.75 | 0.71 | 0.82 | 0.83 | 0.79 | 0.79 | 0.79 | 0.78 |
| WS-3367 | 0.73 | 0.75 | 0.77 | 0.83 | 0.80 | 0.73 | 0.73 | 0.76 |
| Site | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | Average |
|---|---|---|---|---|---|---|---|---|
| PG-4164 | 191.9 | 183.8 | 182.7 | 185.5 | 189.1 | 191.2 | 193.0 | 188.2 |
| PG-3915 | 197.8 | 180.9 | 193.7 | 188.0 | 190.7 | 194.5 | 182.7 | 189.8 |
| PG-3446 | 193.8 | 183.0 | 183.6 | 182.2 | 182.3 | 182.9 | 185.6 | 184.8 |
| WS-3367 | 191.9 | 187.8 | 191.1 | 182.3 | 181.5 | 196.7 | 183.8 | 187.9 |
| Site | Precipitation Frequency | Precipitation Intensity (mm/h) | ||||
|---|---|---|---|---|---|---|
| H24 | HLP | HLP/H24 | H24 | HLP | HLP/H24 | |
| RG-4031 | 563 | 207 | 36.8% | 0.58 | 0.40 | 68.9% |
| RG-3915 | 410 | 165 | 40.2% | 0.63 | 0.38 | 60.0% |
| RG-3726 | 284 | 157 | 55.3% | 0.63 | 0.15 | 24.2% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Yang, G. Temporal Distribution Characteristics of Alpine Precipitation and Their Vertical Differentiation: A Case Study from the Upper Shule River. Water 2017, 9, 284. https://doi.org/10.3390/w9040284
Li Q, Yang G. Temporal Distribution Characteristics of Alpine Precipitation and Their Vertical Differentiation: A Case Study from the Upper Shule River. Water. 2017; 9(4):284. https://doi.org/10.3390/w9040284
Chicago/Turabian StyleLi, Qingfeng, and Guojing Yang. 2017. "Temporal Distribution Characteristics of Alpine Precipitation and Their Vertical Differentiation: A Case Study from the Upper Shule River" Water 9, no. 4: 284. https://doi.org/10.3390/w9040284
APA StyleLi, Q., & Yang, G. (2017). Temporal Distribution Characteristics of Alpine Precipitation and Their Vertical Differentiation: A Case Study from the Upper Shule River. Water, 9(4), 284. https://doi.org/10.3390/w9040284







