Space–Time Characterization of Rainfall Field in Tuscany
Abstract
:1. Introduction
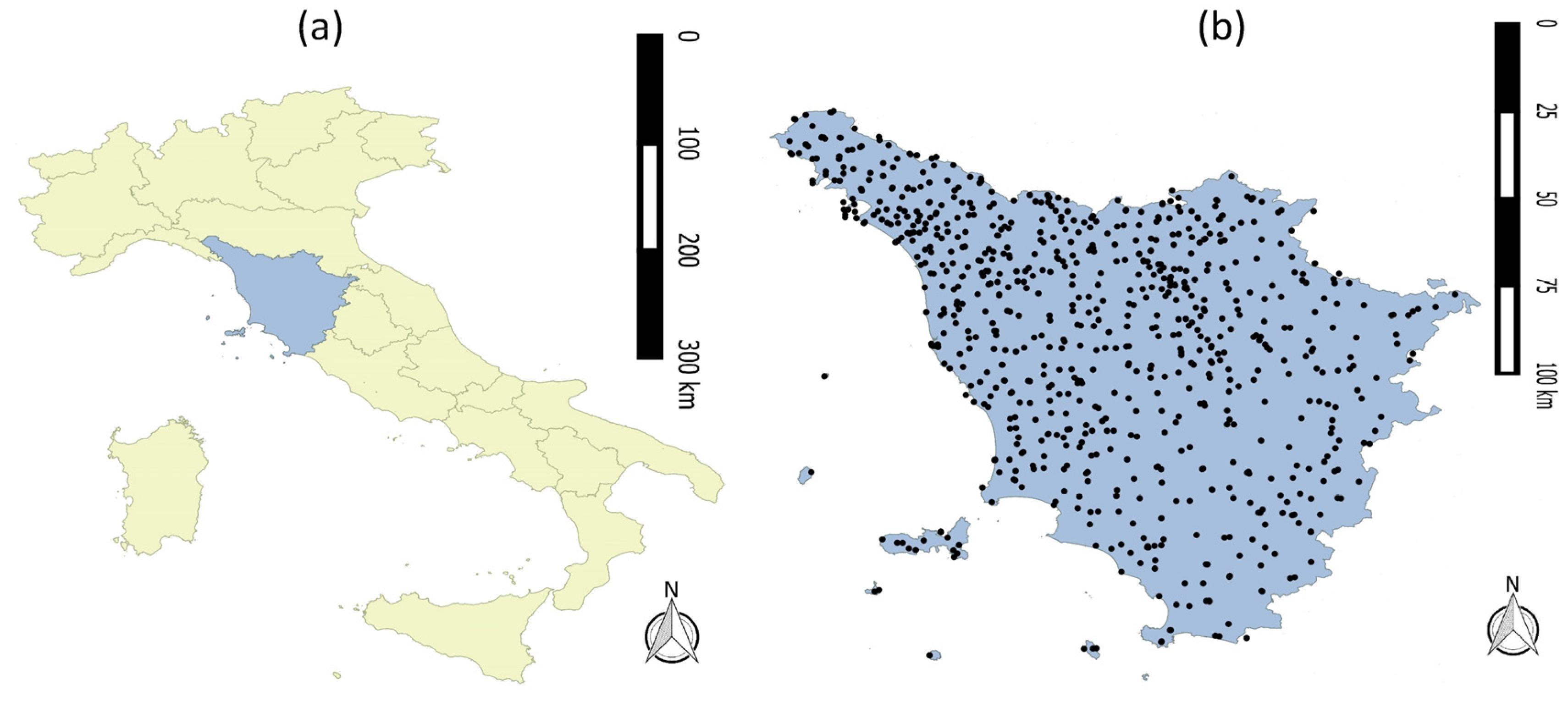
2. Data and Methodology
2.1. Data
2.2. The NPOBK Technique
2.3. ACR Estimation
2.4. Local Rainfall Regime
2.4.1. Time Average of Local Rainfall
2.4.2. Trend Analysis of Local Rainfall
2.5. Global Rainfall Regime
2.5.1. Global Rainfall
2.5.2. Observables for the Study of the Global Rainfall Regime
3. Results
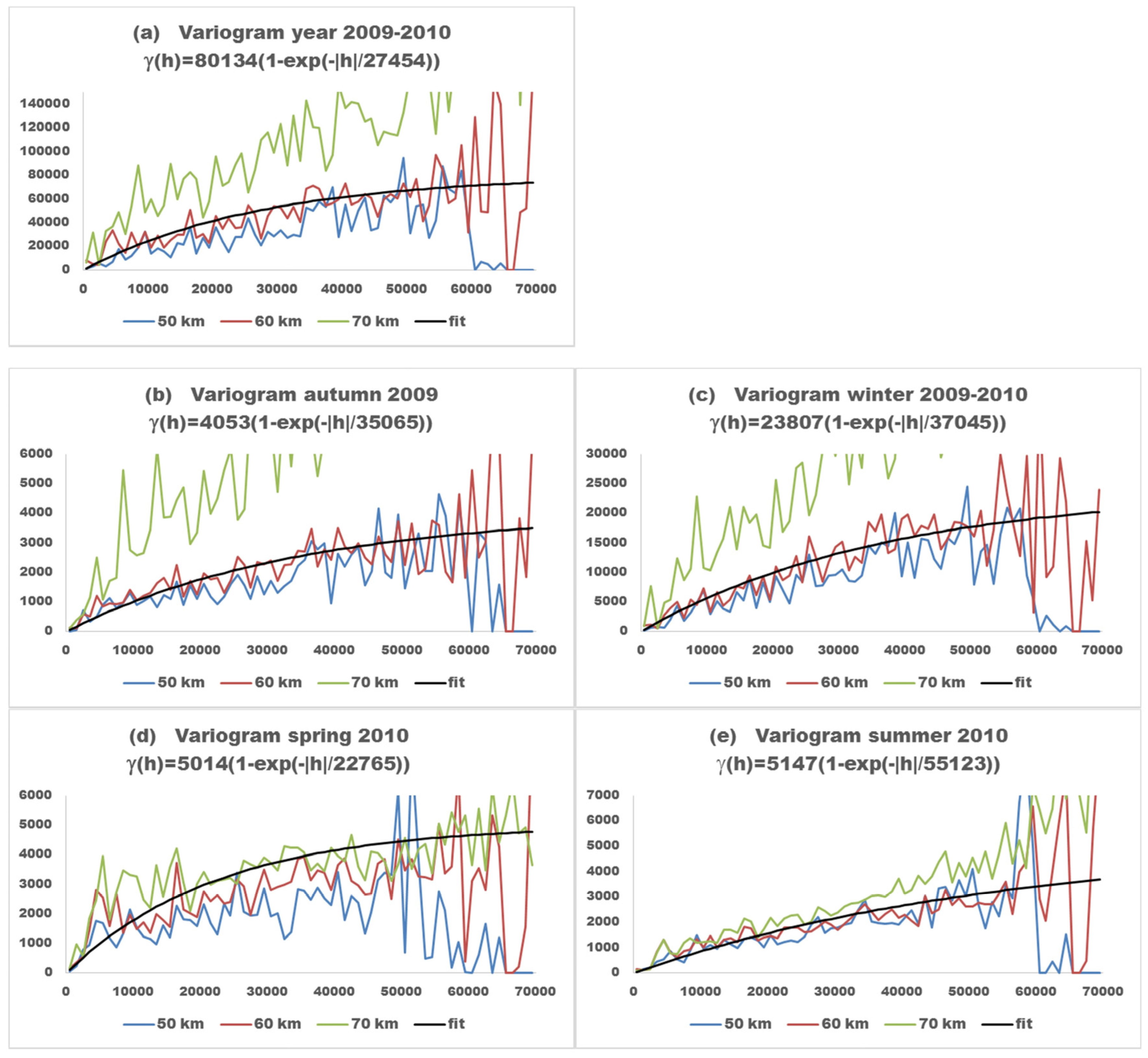
3.1. Evaluation of the Variogram
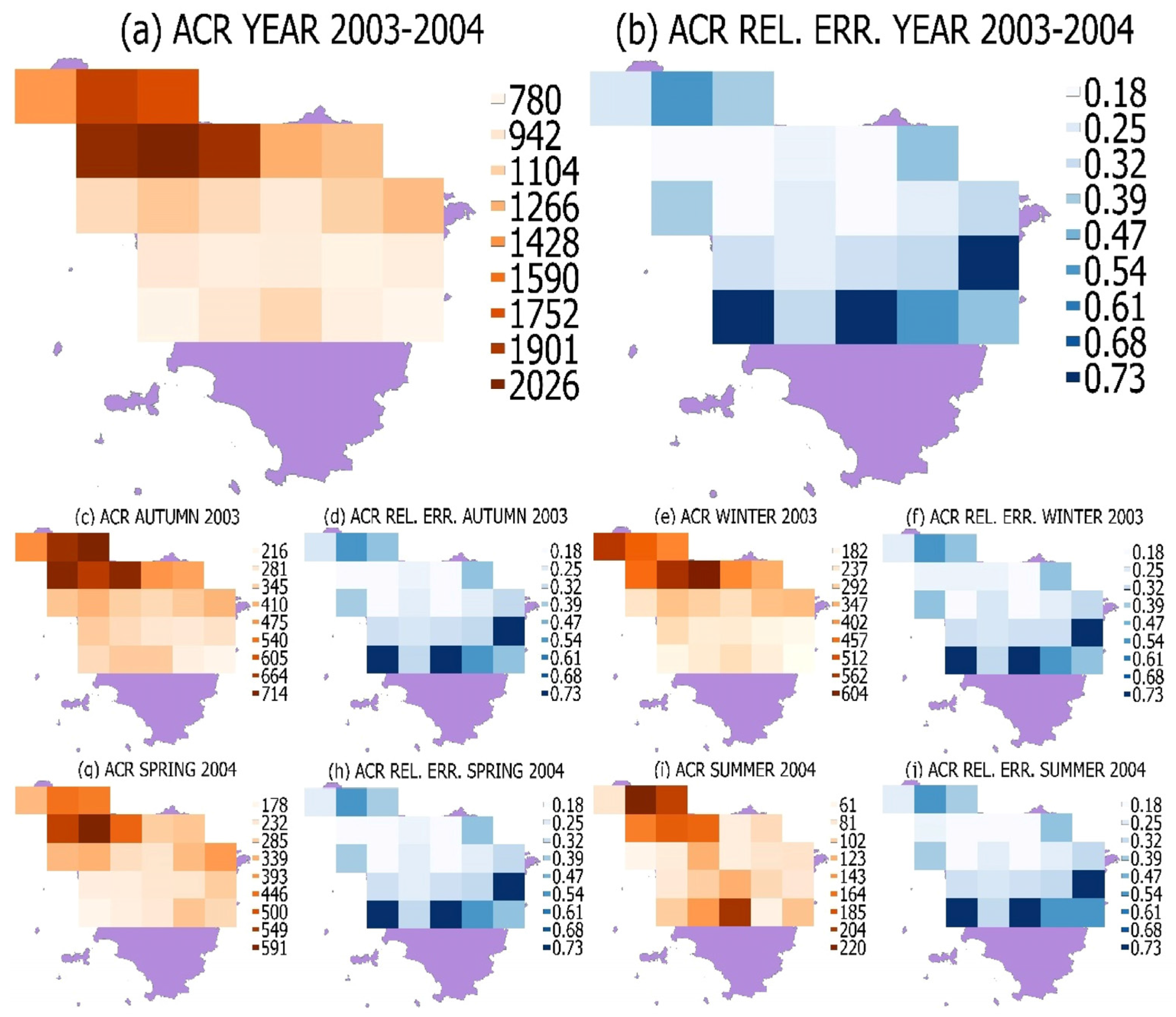
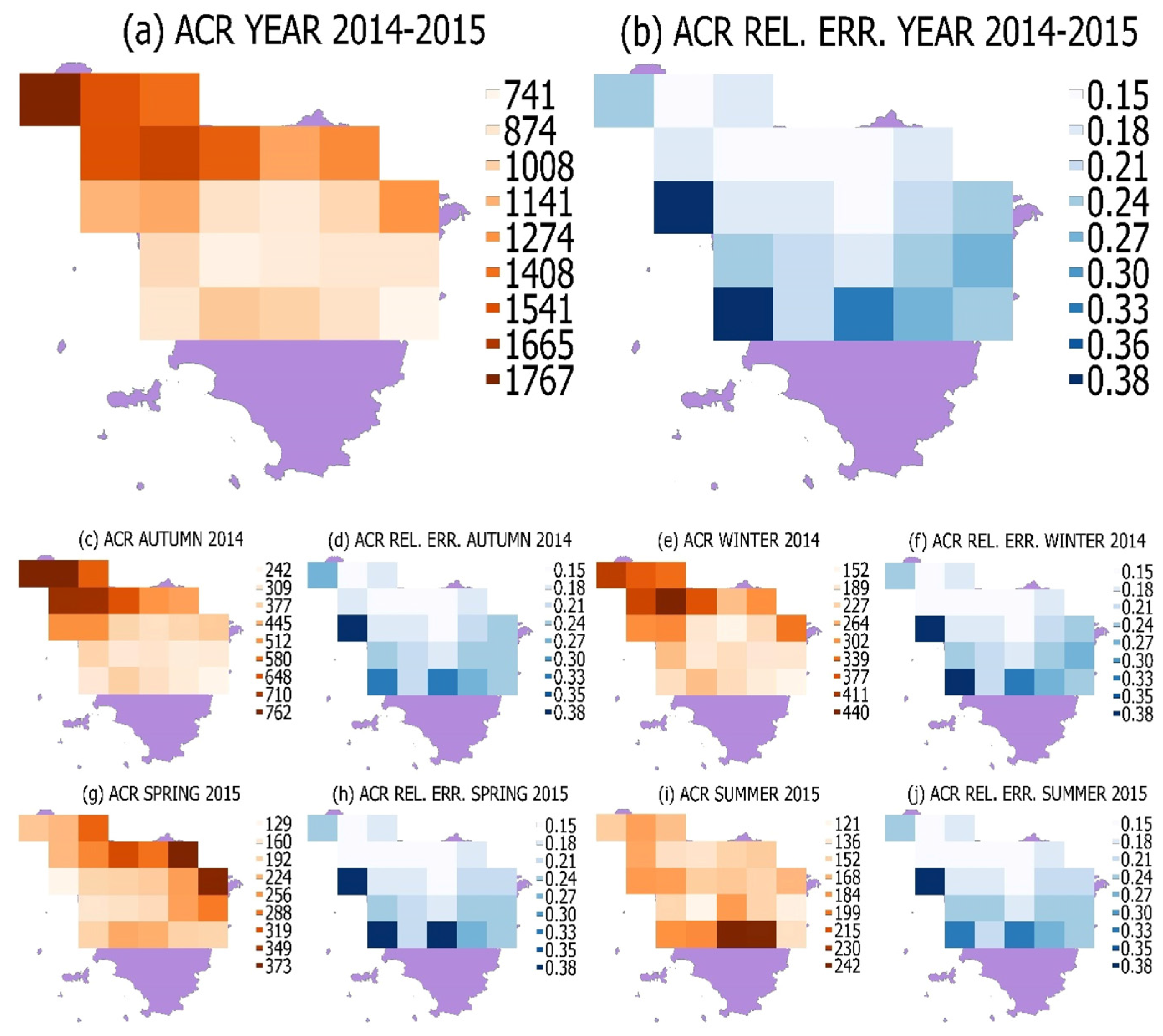
3.2. Estimation of Rainfall Amount
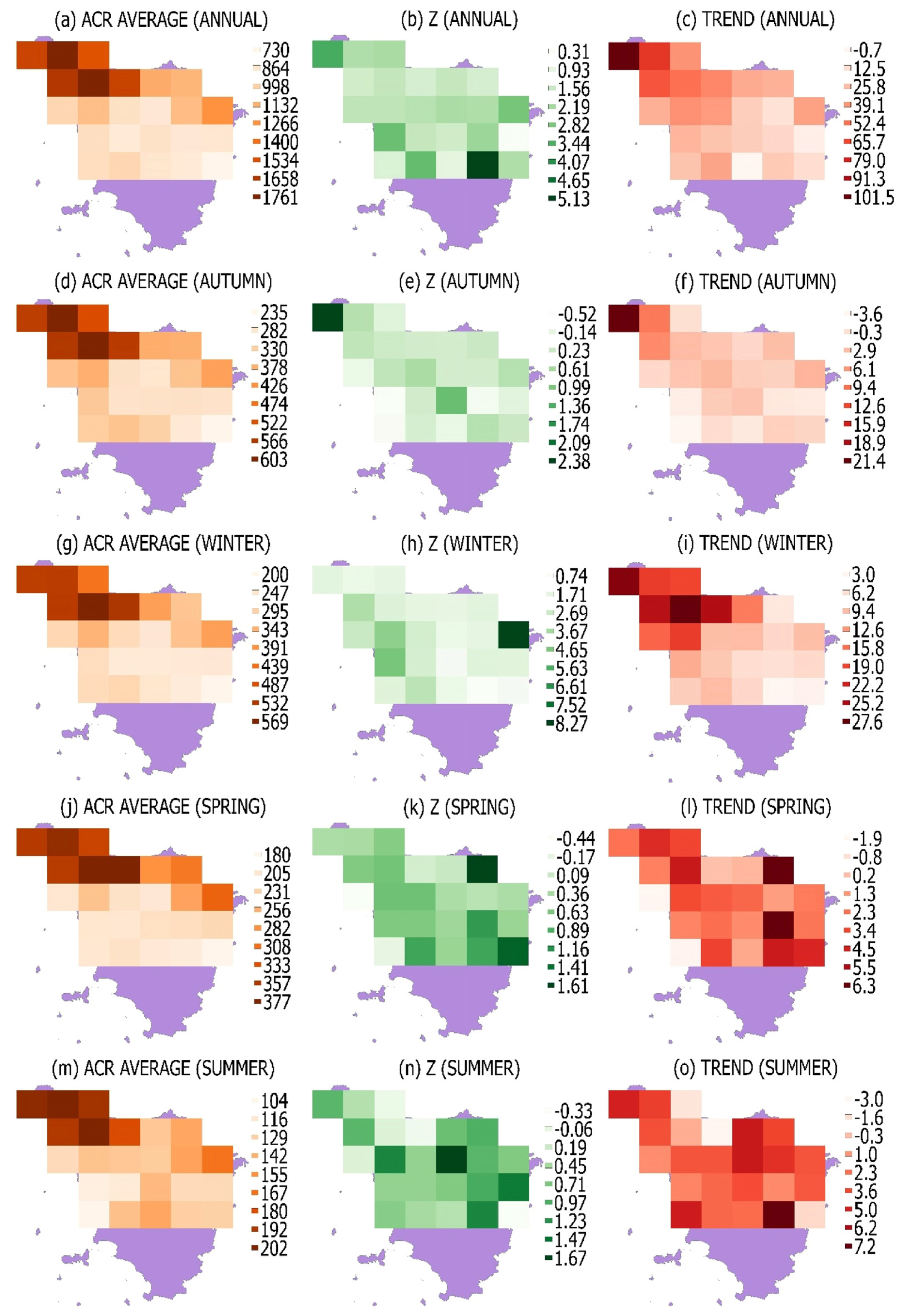
3.3. Characterization of the Local Rainfall Regime
3.3.1. Estimation of the Time Average of the Local Rainfall
3.3.2. Evolution of the Local Rainfall Regime
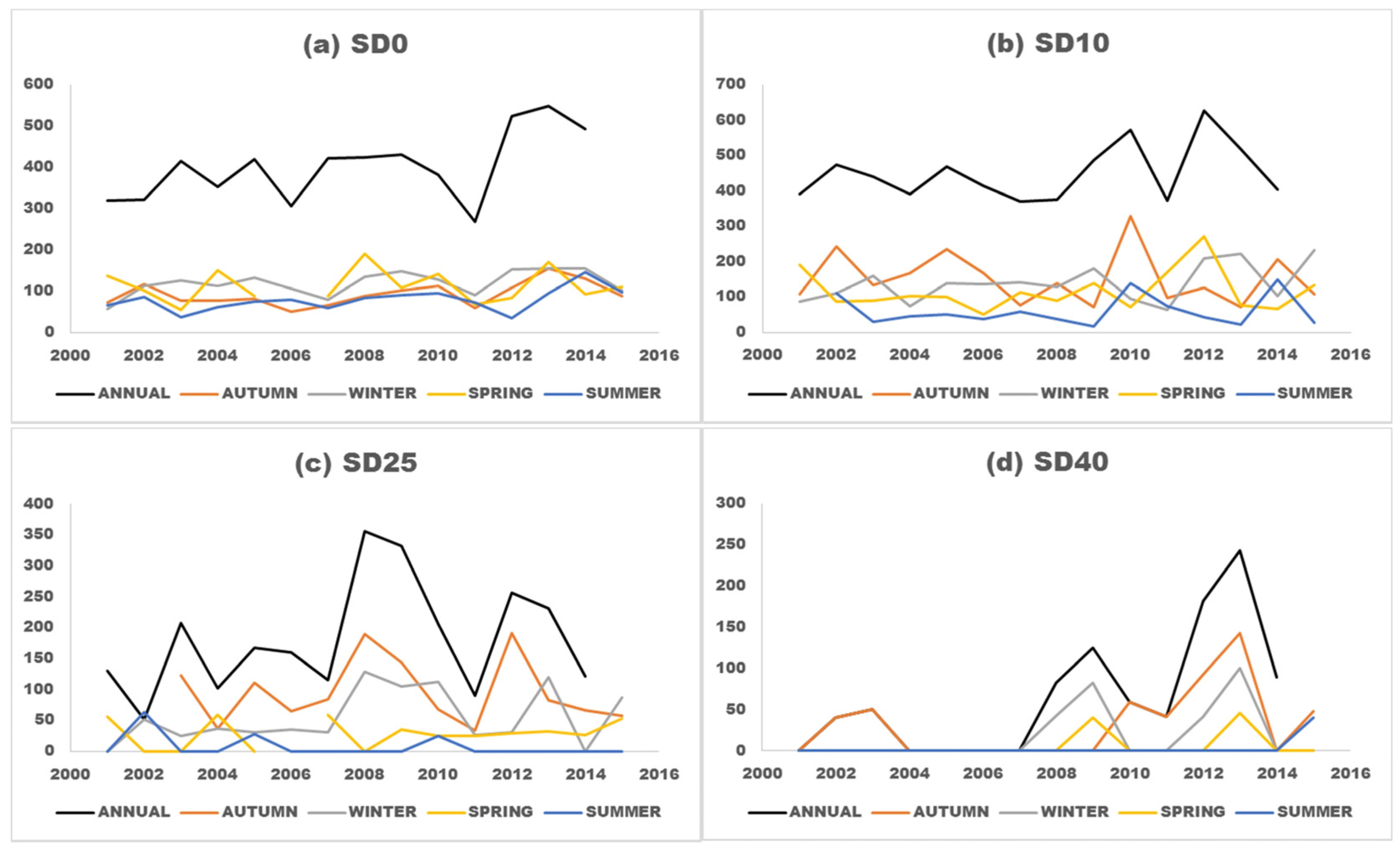
3.4. Characterization of the Global Rainfall Regime
4. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Romero, R.; Guijarro, J.A.; Ramis, C.; Alonso, S. A 30-year (1964–1993) daily rainfall data base for the Spanish Mediterranean regions: First exploratory study. Int. J. Climatol. 1998, 18, 541–560. [Google Scholar] [CrossRef]
- Alpert, P. The paradoxical increase of Mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29, 31.1–31.4. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T. Changes in total precipitation, rainy days and extreme events in northeastern Italy. Int. J. Climatol. 2001, 21, 861–871. [Google Scholar] [CrossRef]
- Martínez, M.D.; Lana, X.; Burgueño, A.; Serra, C. Spatial and temporal daily rainfall regime in Catalonia (NE Spain) derived from four precipitation indices, years 1950–2000. Int. J. Climatol. 2007, 27, 123–138. [Google Scholar] [CrossRef]
- Brunetti, M.; Colacino, M.; Maugeri, M.; Nanni, T. Trends in the daily intensity of precipitation in Italy from 1951 to 1996. Int. J. Climatol. 2001, 21, 299–316. [Google Scholar] [CrossRef]
- Jang, J.H. An advanced method to apply multiple rainfall thresholds for urban flood warnings. Water 2015, 7, 6056–6078. [Google Scholar] [CrossRef]
- Notaro, V.; Liuzzo, L.; Freni, G.; La Loggia, G. Uncertainty analysis in the evaluation of extreme rainfall trends and its implications on urban drainage system design. Water 2015, 7, 6931–6945. [Google Scholar] [CrossRef]
- Pedersen, L.; Jensen, N.E.; Christensen, L.E.; Madsen, H. Quantification of the spatial variability of rainfall based on a dense network of rain gauges. Atmos. Res. 2010, 95, 441–454. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Krajewski, W.F.; Ciach, G.J.; Villarini, G.; Smith, J.A. Estimation of radar-rainfall error spatial correlation. Adv. Water Resour. 2009, 32, 1020–1030. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F. On the estimation of radar rainfall error variance. Adv. Water Resour. 1999, 22, 585–595. [Google Scholar] [CrossRef]
- Mazza, A.; Antonini, A.; Melani, S.; Ortolani, A. Recalibration of cumulative rainfall estimates by weather radar over a large area. J. Appl. Remote Sens. 2015, 9, 095993. [Google Scholar] [CrossRef]
- Mazza, A.; Antonini, A.; Melani, S.; Ortolani, A. Estimates of cumulative rainfall over a large area by weather radar. In Proceedings of the SPIE Remote Sensing and Security, Remote Sensing of Clouds and the Atmosphere XIX and Optics in Atmospheric Propagation and Adaptive Systems XVII, Amsterdam, The Netherlands, 22–25 September 2014.
- Chiles, J.P.; Delfiner, P.B. Structural analysis. In Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Balding, D.J., Cressie, N.A., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 28–146. [Google Scholar]
- Chiles, J.P.; Delfiner, P.B. Kriging. In Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Balding, D.J., Cressie, N.A., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 147–237. [Google Scholar]
- Wackemagel, H. Geostatistics. In Multivariate. Geostatistics an Introduction with Applications, 3rd ed.; Springer: Berlin, Germany, 2003; pp. 35–120. [Google Scholar]
- Armstrong, M. The theory of kriging. In Basic Linear Geostatistics, 1st ed.; Springer: Berlin, Germany, 1998; pp. 83–102. [Google Scholar]
- Doneaud, A.; Ionescu-Niscov, S.; Priegnitz, D.L.; Smith, P.L. The area-time integral as an indicator for convective rain volumes. J. Clim. Appl. Meteorol. 1984, 23, 555–561. [Google Scholar] [CrossRef]
- Doneaud, A.A.; Smith, P.L.; Dennis, A.S.; Sengupta, S. A simple method for estimating convective rain volume over an area. Water Resour. Res. 1981, 17, 1676–1682. [Google Scholar] [CrossRef]
- Griffith, C.G.; Woodley, W.L.; Grube, P.G.; Martin, D.W.; Stout, J.; Sikdar, D.N. Rain estimation from geosynchronous satellite imagery—Visible and infrared studies. Mon. Weather Rev. 1978, 106, 1153–1171. [Google Scholar] [CrossRef]
- Fatichi, S.; Caporali, E. A comprehensive analysis of changes in precipitation regime in Tuscany. Int. J. Climatol. 2009, 29, 1883–1893. [Google Scholar] [CrossRef]
- Bartolini, G.; Grifoni, D.; Torrigiani, T.; Vallorani, R.; Meneguzzo, F.; Gozzini, B. Precipitation changes from two long-term hourly datasets in Tuscany, Italy. Int. J. Climatol. 2014, 34, 3977–3985. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Non parametric test for trend detection. In Time Series Modelling of Water Resources and Environmental Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1994; pp. 853–938. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Qu, B.; Lv, A.; Jia, S.; Zhu, W. Daily precipitation changes over large river basins in China. 1960–2013. Water 2016, 8, 185. [Google Scholar] [CrossRef]
- Romano, E.; Preziosi, E. Precipitation pattern analysis in the Tiber River basin (central Italy) using standardized indices. Int. J. Climatol. 2013, 33, 1781–1792. [Google Scholar] [CrossRef]
- Crisci, A.; Gozzini, B.; Meneguzzo, F.; Pagliara, S.; Maracchi, G. Extreme rainfall in a changing climate: Regional analysis and hydrological implications in Tuscany. Hydrol. Process. 2002, 16, 1261–1274. [Google Scholar] [CrossRef]
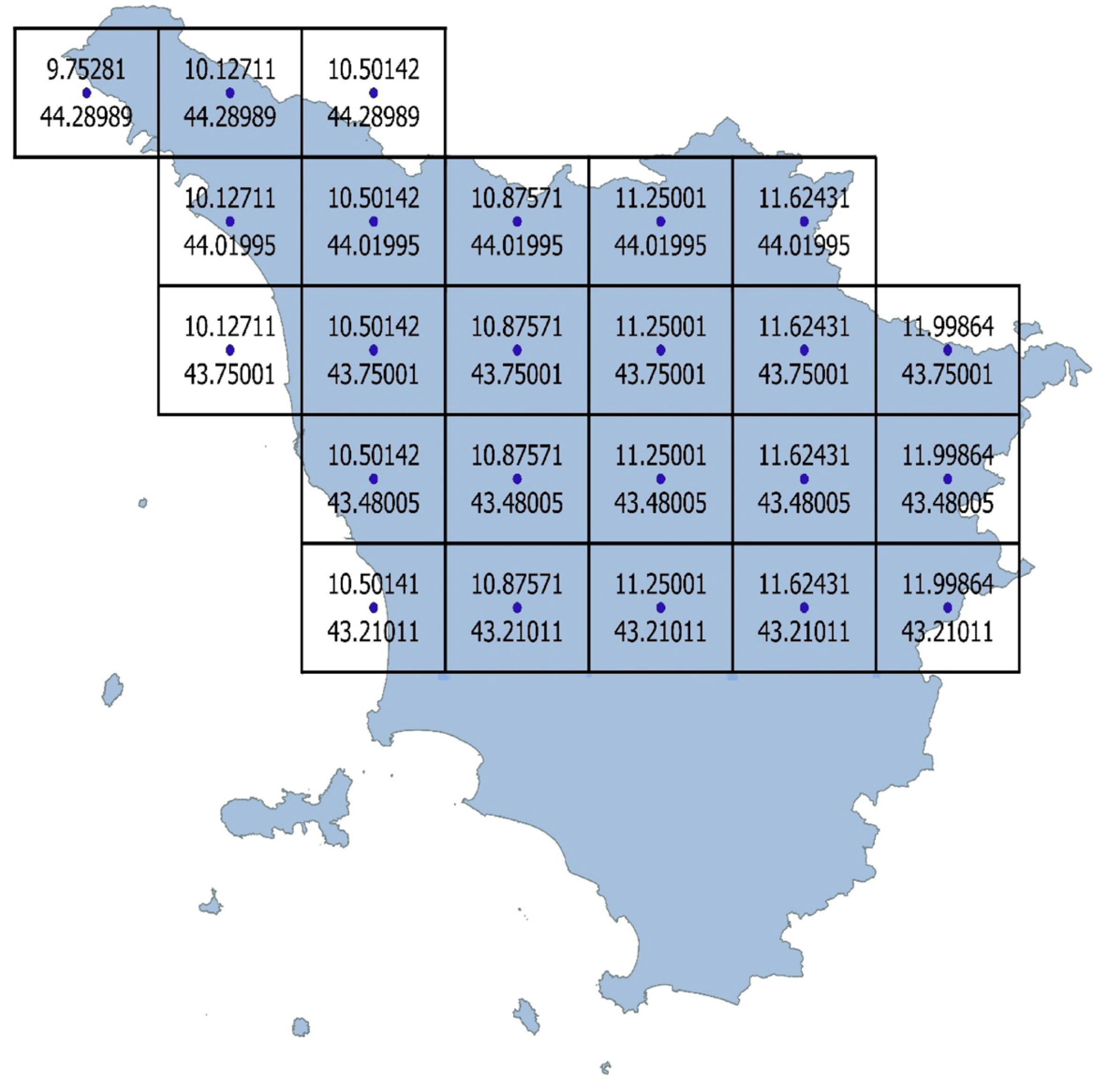

| lat.: 43.480053 lon.: 11.250000 | |||||||||||||||
| YEAR | ANNUAL | AUTUMN | WINTER | SPRING | SUMMER | ||||||||||
| ACR | σ | ERR | ACR | σ | ERR | ACR | σ | ERR | ACR | σ | ERR | ACR | σ | ERR | |
| 2001–2002 | 795 | 99 | 0.38 | 229 | 29 | 0.38 | 117 | 17 | 0.43 | 197 | 25 | 0.38 | 172 | 43 | 0.75 |
| 2002–2003 | 780 | 80 | 0.31 | 290 | 30 | 0.31 | 238 | 24 | 0.31 | 158 | 16 | 0.31 | 104 | 26 | 0.75 |
| 2003–2004 | 870 | 89 | 0.31 | 278 | 28 | 0.31 | 238 | 24 | 0.31 | 227 | 23 | 0.31 | 208 | 52 | 0.75 |
| 2004–2005 | 798 | 89 | 0.34 | 143 | 36 | 0.75 | 222 | 25 | 0.34 | 158 | 18 | 0.34 | 226 | 57 | 0.75 |
| 2005–2006 | 983 | 110 | 0.34 | 513 | 57 | 0.34 | 220 | 25 | 0.34 | M | M | M | 100 | 11 | 0.34 |
| 2006–2007 | 842 | 86 | 0.31 | 240 | 18 | 0.23 | 189 | 14 | 0.22 | 200 | 13 | 0.19 | 78 | 9 | 0.34 |
| 2007–2008 | 681 | 51 | 0.23 | 135 | 11 | 0.25 | 188 | 14 | 0.23 | 224 | 16 | 0.22 | 109 | 11 | 0.31 |
| 2008–2009 | 931 | 95 | 0.31 | 324 | 23 | 0.22 | 272 | 17 | 0.19 | 221 | 14 | 0.19 | 139 | 14 | 0.31 |
| 2009–2010 | 982 | 61 | 0.19 | 200 | 13 | 0.19 | 365 | 23 | 0.19 | 265 | 15 | 0.17 | 96 | 10 | 0.31 |
| 2010–2011 | 937 | 60 | 0.19 | 443 | 30 | 0.20 | 230 | 15 | 0.19 | 123 | 8 | 0.19 | 138 | 14 | 0.31 |
| 2011–2012 | 541 | 36 | 0.20 | 127 | 8 | 0.20 | 114 | 8 | 0.21 | 224 | 15 | 0.20 | 64 | 6 | 0.28 |
| 2012–2013 | 1155 | 83 | 0.22 | 446 | 31 | 0.21 | 261 | 19 | 0.22 | 309 | 21 | 0.20 | 136 | 34 | 0.75 |
| 2013–2014 | 1266 | 95 | 0.23 | 418 | 29 | 0.21 | 330 | 24 | 0.22 | 170 | 13 | 0.23 | 233 | 41 | 0.53 |
| 2014–2015 | 824 | 51 | 0.19 | 316 | 19 | 0.18 | 203 | 12 | 0.18 | 176 | 10 | 0.18 | 246 | 27 | 0.34 |
| lat.: 44.019947 lon.: 10.875702 | |||||||||||||||
| YEAR | ANNUAL | AUTUMN | WINTER | SPRING | SUMMER | ||||||||||
| ACR | σ | ERR | ACR | σ | ERR | ACR | σ | ERR | ACR | σ | ERR | ACR | S | ERR | |
| 2001–2002 | 1375 | 243 | 0.53 | 386 | 97 | 0.75 | 284 | 35 | 0.38 | 324 | 21 | 0.19 | 359 | 24 | 0.20 |
| 2002–2003 | 1434 | 96 | 0.20 | 750 | 48 | 0.19 | 408 | 27 | 0.20 | 194 | 13 | 0.21 | 63 | 5 | 0.22 |
| 2003–2004 | 1940 | 130 | 0.20 | 701 | 47 | 0.20 | 617 | 45 | 0.22 | 464 | 31 | 0.20 | 171 | 11 | 0.19 |
| 2004–2005 | 1036 | 116 | 0.34 | M | M | M | 251 | 17 | 0.20 | 291 | 19 | 0.19 | 194 | 20 | 0.31 |
| 2005–2006 | 1459 | 94 | 0.19 | 509 | 33 | 0.19 | 490 | 33 | 0.20 | M | M | M | 199 | 11 | 0.17 |
| 2006–2007 | 1328 | 83 | 0.19 | 364 | 21 | 0.17 | 504 | 29 | 0.17 | 251 | 14 | 0.16 | 159 | 10 | 0.18 |
| 2007–2008 | 1231 | 71 | 0.17 | 341 | 20 | 0.17 | 353 | 20 | 0.17 | 427 | 23 | 0.16 | 105 | 6 | 0.16 |
| 2008–2009 | 1843 | 109 | 0.18 | 677 | 37 | 0.16 | 700 | 37 | 0.16 | 392 | 21 | 0.16 | 111 | 6 | 0.15 |
| 2009–2010 | 1906 | 97 | 0.15 | 453 | 23 | 0.15 | 786 | 39 | 0.15 | 361 | 18 | 0.15 | 317 | 16 | 0.15 |
| 2010–2011 | 1744 | 89 | 0.15 | 740 | 38 | 0.15 | 575 | 29 | 0.15 | 233 | 11 | 0.15 | 210 | 10 | 0.15 |
| 2011–2012 | 1162 | 59 | 0.15 | 384 | 20 | 0.15 | 287 | 15 | 0.16 | 424 | 21 | 0.15 | 80 | 4 | 0.15 |
| 2012–2013 | 2193 | 112 | 0.15 | 744 | 37 | 0.15 | 570 | 29 | 0.15 | 815 | 40 | 0.15 | 140 | 7 | 0.15 |
| 2013–2014 | 2241 | 117 | 0.16 | 599 | 31 | 0.15 | 1057 | 54 | 0.15 | 290 | 15 | 0.16 | 300 | 15 | 0.15 |
| 2014–2015 | 1478 | 75 | 0.15 | 643 | 33 | 0.15 | 374 | 19 | 0.15 | 325 | 17 | 0.15 | 138 | 7 | 0.15 |
| Lat. | Lon. | Day_Month_Year | ACR AM | ACR NPOBK |
|---|---|---|---|---|
| 43.75 | 10.13 | 11_11_2001 | 4.4 | 5.2 |
| 44.02 | 10.88 | 7_10_2003 | 0.8 | 0.5 |
| 44.02 | 10.13 | 29_10_2004 | 44.1 | 37.0 |
| 44.29 | 9.75 | 22_3_2006 | 12.2 | 8.9 |
| 44.20 | 10.13 | 29_2_2008 | 1.2 | 1.9 |
| 43.75 | 12.00 | 24_7_2011 | 7.5 | 11.0 |
| 43.21 | 11.25 | 5_10_2013 | 17.1 | 18.7 |
| ANNUAL | AUTUMN | WINTER | SPRING | SUMMER | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Lon | ACR AV | Z | T | ACR AV | Z | T | ACR AV | Z | T | ACR AV | Z | T | ACR AV | Z | T |
| 43.21 | 10.50 | 914 | 1.17 | 23.1 | 335 | −0.48 | −3.6 | 269 | 1.89 | 7.9 | 202 | −0.21 | −1.8 | 104 | 0.62 | 5.2 |
| 43.21 | 10.88 | 955 | 3.09 | 34.3 | 350 | 0.06 | −0.1 | 284 | 3.03 | 9.5 | 210 | 0.99 | 3.5 | 136 | 0.44 | 2.6 |
| 43.21 | 11.25 | 870 | 0.95 | −0.7 | 329 | −0.22 | −1.8 | 249 | 1.31 | 7.0 | 199 | 0.43 | 0.8 | 146 | 0.33 | 2.5 |
| 43.21 | 11.62 | 827 | 5.28 | 20.9 | 273 | 0.44 | 1.1 | 229 | 0.74 | 3.0 | 196 | 0.99 | 4.7 | 130 | 1.31 | 7.6 |
| 43.21 | 12.00 | 730 | 2.01 | 13.3 | 235 | 0.22 | 0.6 | 200 | 0.90 | 3.5 | 180 | 1.48 | 4.3 | 129 | −0.33 | −1.4 |
| 43.48 | 10.50 | 910 | 3.02 | 28.1 | 343 | −0.52 | −2.5 | 268 | 4.70 | 10.7 | 205 | 0.59 | 1.8 | 109 | 0.55 | 1.6 |
| 43.48 | 10.88 | 824 | 1.64 | 23.3 | 289 | 0.11 | 1.5 | 235 | 2.24 | 8.4 | 203 | 0.59 | 2.4 | 113 | 0.55 | 2.6 |
| 43.48 | 11.25 | 885 | 1.42 | 19.6 | 290 | 1.12 | 2.2 | 234 | 0.89 | 6.3 | 213 | 0.40 | 1.6 | 139 | 0.66 | 3.4 |
| 43.48 | 11.62 | 838 | 2.31 | 15.8 | 293 | −0.44 | −1.6 | 236 | 1.90 | 6.0 | 215 | 1.09 | 6.6 | 123 | 0.99 | 1.4 |
| 43.48 | 12.00 | 852 | 0.31 | 3.4 | 288 | −0.11 | −2.0 | 239 | 1.82 | 6.8 | 222 | 0.43 | 2.2 | 124 | 1.40 | 3.1 |
| 43.75 | 10.13 | 956 | 1.75 | 30.2 | 352 | −0.32 | 0.3 | 279 | 2.67 | 16.6 | 203 | −0.44 | −1.9 | 123 | 0.00 | 1.3 |
| 43.75 | 10.50 | 1075 | 1.75 | 40.6 | 380 | 0.32 | 2.0 | 339 | 4.22 | 19.6 | 242 | 0.69 | 3.3 | 135 | 1.31 | 3.2 |
| 43.75 | 10.88 | 896 | 1.86 | 37.8 | 292 | 0.55 | 3.2 | 270 | 2.35 | 9.3 | 210 | 0.69 | 2.9 | 133 | 0.55 | 3.2 |
| 43.75 | 11.25 | 841 | 2.08 | 19.1 | 286 | 0.10 | 1.3 | 242 | 1.39 | 9.5 | 201 | 0.30 | 2.6 | 132 | 1.73 | 5.4 |
| 43.75 | 11.62 | 1079 | 2.01 | 11.2 | 351 | 0.10 | 1.0 | 318 | 1.66 | 7.0 | 268 | 0.20 | 1.1 | 148 | 0.89 | 4.3 |
| 43.75 | 12.00 | 1264 | 2.87 | 35.3 | 402 | 0.44 | 3.6 | 371 | 8.50 | 9.3 | 317 | 0.30 | 2.1 | 166 | 0.66 | 3.2 |
| 44.02 | 10.13 | 1652 | 1.40 | 60.4 | 565 | 0.33 | 7.1 | 523 | 3.39 | 24.3 | 354 | 0.58 | 1.9 | 192 | 0.88 | 3.3 |
| 44.02 | 10.50 | 1777 | 1.65 | 52.1 | 614 | 0.18 | 3.0 | 580 | 1.98 | 28.4 | 383 | 0.66 | 4.8 | 202 | 0.00 | 0.2 |
| 44.02 | 10.88 | 1598 | 1.31 | 44.2 | 557 | 0.11 | 2.0 | 533 | 1.68 | 24.7 | 378 | 0.00 | 0.1 | 182 | −0.22 | −3.0 |
| 44.02 | 11.25 | 1156 | 1.64 | 31.8 | 383 | 0.10 | 0.4 | 371 | 1.58 | 14.8 | 282 | 0.10 | 0.4 | 133 | 0.79 | 5.4 |
| 44.02 | 11.62 | 1113 | 1.31 | 29.6 | 378 | 0.22 | 2.8 | 313 | 1.85 | 5.0 | 301 | 1.68 | 6.5 | 146 | 0.95 | 3.7 |
| 44.29 | 9.75 | 1588 | 3.50 | 104.6 | 554 | 2.47 | 22.2 | 521 | 1.78 | 26.5 | 355 | 0.30 | 2.3 | 199 | 0.88 | 5.0 |
| 44.29 | 10.13 | 1792 | 1.99 | 70.8 | 608 | 0.43 | 8.7 | 522 | 1.31 | 19.7 | 369 | 0.33 | 4.2 | 205 | 0.34 | 3.9 |
| 44.29 | 10.50 | 1517 | 2.12 | 40.0 | 525 | −0.06 | −0.4 | 434 | 1.64 | 18.9 | 345 | 0.55 | 3.4 | 195 | −0.18 | −2.0 |
| ANNUAL | AUTUMN | WINTER | SPRING | SUMMER | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z | T | Z | T | Z | T | Z | T | Z | T | |
| ACR_TOT | 1.86 | 35.4 | 0.49 | 2.9 | 3.57 | 14.8 | 0.20 | 1.1 | 1.48 | 3.9 |
| NRD | 1.20 | 2.2 | 0.00 | −0.1 | 3.37 | 1.1 | 0.69 | 0.4 | 1.14 | 0.5 |
| MIP | 1.86 | 0.1 | 1.29 | 0.2 | 1.58 | 0.1 | 0.00 | 0.0 | 0.79 | 0.1 |
| SD0 | 2.36 | 13.3 | 1.68 | 3.3 | 1.78 | 3.1 | 0.40 | 0.6 | 4.16 | 2.7 |
| SD10 | 0.71 | 4.3 | −0.79 | −1.6 | 1.48 | 6.5 | 0.10 | 0.5 | 0.40 | 1.7 |
| SD25 | 0.88 | 7.6 | 0.30 | 0.5 | 0.94 | 2.8 | 0.10 | 0.0 | −1.14 | 0.0 |
| SD40 | 2.58 | 10.5 | 1.51 | 0.2 | 3.96 | 2.689 | 0.68 | 0.0 | 1.50 | 0.0 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazza, A. Space–Time Characterization of Rainfall Field in Tuscany. Water 2017, 9, 86. https://doi.org/10.3390/w9020086
Mazza A. Space–Time Characterization of Rainfall Field in Tuscany. Water. 2017; 9(2):86. https://doi.org/10.3390/w9020086
Chicago/Turabian StyleMazza, Alessandro. 2017. "Space–Time Characterization of Rainfall Field in Tuscany" Water 9, no. 2: 86. https://doi.org/10.3390/w9020086
APA StyleMazza, A. (2017). Space–Time Characterization of Rainfall Field in Tuscany. Water, 9(2), 86. https://doi.org/10.3390/w9020086




