Assessment of Optional Sediment Transport Functions via the Complex Watershed Simulation Model SWAT

Abstract

The Soil and Water Assessment Tool 2012 (SWAT2012) offers four sediment routing methods as optional alternatives to the default simplified Bagnold method. Previous studies compared only one of these alternative sediment routing methods with the default method. The proposed study evaluated the impacts of all four alternative sediment transport methods on sediment predictions: the modified Bagnold equation, the Kodoatie equation, the Molinas and Wu equation, and the Yang equation. The Arroyo Colorado Watershed, Texas, USA, was first calibrated for daily flow. The sediment parameters were then calibrated to monthly sediment loads, using each of the four sediment routing equations. An automatic calibration tool—Integrated Parameter Estimation and Uncertainty Analysis Tool (IPEAT)—was used to fit model parameters. The four sediment routing equations yielded substantially different sediment sources and sinks. The Yang equation performed best, followed by Kodoatie, Bagnold, and Molinas and Wu equations, according to greater model goodness-of-fit (represented by higher Nash–Sutcliffe Efficiency coefficient and percent bias closer to 0) as well as lower model uncertainty (represented by inclusion of observed data within 95% confidence interval). Since the default method (Bagnold) does not guarantee the best results, modelers should carefully evaluate the selection of alternative methods before conducting relevant studies or engineering projects.

1. Introduction

The semi-distributed watershed simulation model, Soil and Water Assessment Tool (SWAT) [1] has been applied worldwide to identify critical source areas of water quality impairments and evaluate potential solutions through land use change and water resource planning and management [2,3,4,5,6,7,8,9]. Various SWAT applications have been conducted to explore sediment loading from watersheds [10,11,12,13]. Most SWAT sediment studies have focused on sediment transport in surface and bank erosion [13,14,15], while comparatively few studies have taken into account sediment transport within streams [16,17]. In addition, excess sediment loads can cause silting problems and damage aquatic habitats [18]. In recent years, research related to sediment yield and transportation has increased considerably [19]. Challenges such as erosion of fertile topsoil, blocking stream channels, and filling reservoirs have the potential to impact agricultural productivity [20].

In SWAT version 2012 (SWAT2012), the simulation of sediment transport in channels was updated by including four equations for sediment routing by particle size along with the simplified Bagnold equation [21] incorporated in SWAT since the 2005 version [22]. The alternative methods are (1) modified Bagnold equation [21]; (2) Kodoatie equation [23]; (3) Molinas and Wu equation [24]; and (4) Yang equation [25]. The four sediment transport equations were developed based on different theories and bed materials. The Bagnold equation was modified by Williams [26] to calculate the maximum sediment transport capacity via the velocity function of peak stream. The Kodoatie equation calculates the maximum transport capacity with flow depths, stream geometry, and bed materials, beside flow velocity. The Molinas and Wu equation calculates the maximum transport capacity with universal stream power, which is related to flow depth and particle fall velocity. The Yang equation calculates the maximum transport capacity with unit stream power and includes mean and critical velocity, shear velocity, material fall velocity, kinematic viscosity, critical stream power for incipient motion, and particle size.

Each of the four alternative sediment transport functions in SWAT calculates sediment transport mechanisms differently [22]. SWAT applies the principle of sediment transport capacity to further route sediment processes through main reaches or channels. Sediment deposition or streambed degradation is determined based on the current sediment concentration in the channel system and the estimated sediment transport capacity. Only the modified Bagnold equation will be examined in this study. Comparisons between the simplified and modified version, which both have the same equation for maximum transport capacity, were previously conducted to evaluate the effect on sediment predictions [19,27]. The major difference between the two equations is that the modified Bagnold equation is able to simulate the mechanism of bank erosion. In addition, the modified Bagnold equation may provide better predictions of low sediment concentrations than the simplified version (which is also the default sediment transport function) [19,27]. Selection of alternative methods could be justified based on the river bed materials (particle types), specified ranges of particle size, physical assumptions of mathematical equations and the associated impacts on model calibration and predictions.

The four alternative sediment transport routing methods (modified Bagnold, Kodoatie, Molinas and Wu, and Yang) have not previously been compared or investigated with respect to maximum sediment transport capacity in SWAT2012. The goal of this study is to evaluate the potential influence of the four alternative sediment transport methods on sediment loads and concentrations using a SWAT model developed for the Arroyo Colorado watershed (ACW), in Southern Texas, USA. Specifically, the following objectives were pursued: (i) to assess the performance of each respective sediment transport routing method on predicting flow and sediment in SWAT; and (ii) to quantify and to evaluate the corresponding predictive uncertainty associated with these methods.

2. Materials and Methods

2.1. The SWAT Model

The SWAT model is a spatially distributed, semi-physically-based watershed simulation model developed and maintained by the Agricultural Research Service, United States Department of Agriculture to evaluate the impact of land management and climate change on flow and water quality processes [2]. Relevant functions of SWAT include weather components, hydrology, land use, crop growth, sediment transport routines, fate of nutrients, and conservation practices, which are capable of evaluating various hydrological, hydrochemical, and biophysical processes [3,6,28]. SWAT is a complex watershed simulation model conducted on daily time steps. In addition, large-scale, long-term simulations/predictions are available in alternative time scales (e.g., daily, monthly and annual). Implementations of SWAT can be found in various subjects including sediments transport, nutrients processes, and pesticide applications in varying watersheds of the world [29,30,31]. Modifications of SWAT and comparisons among alternative routing methods are available in literature [32,33,34,35,36].

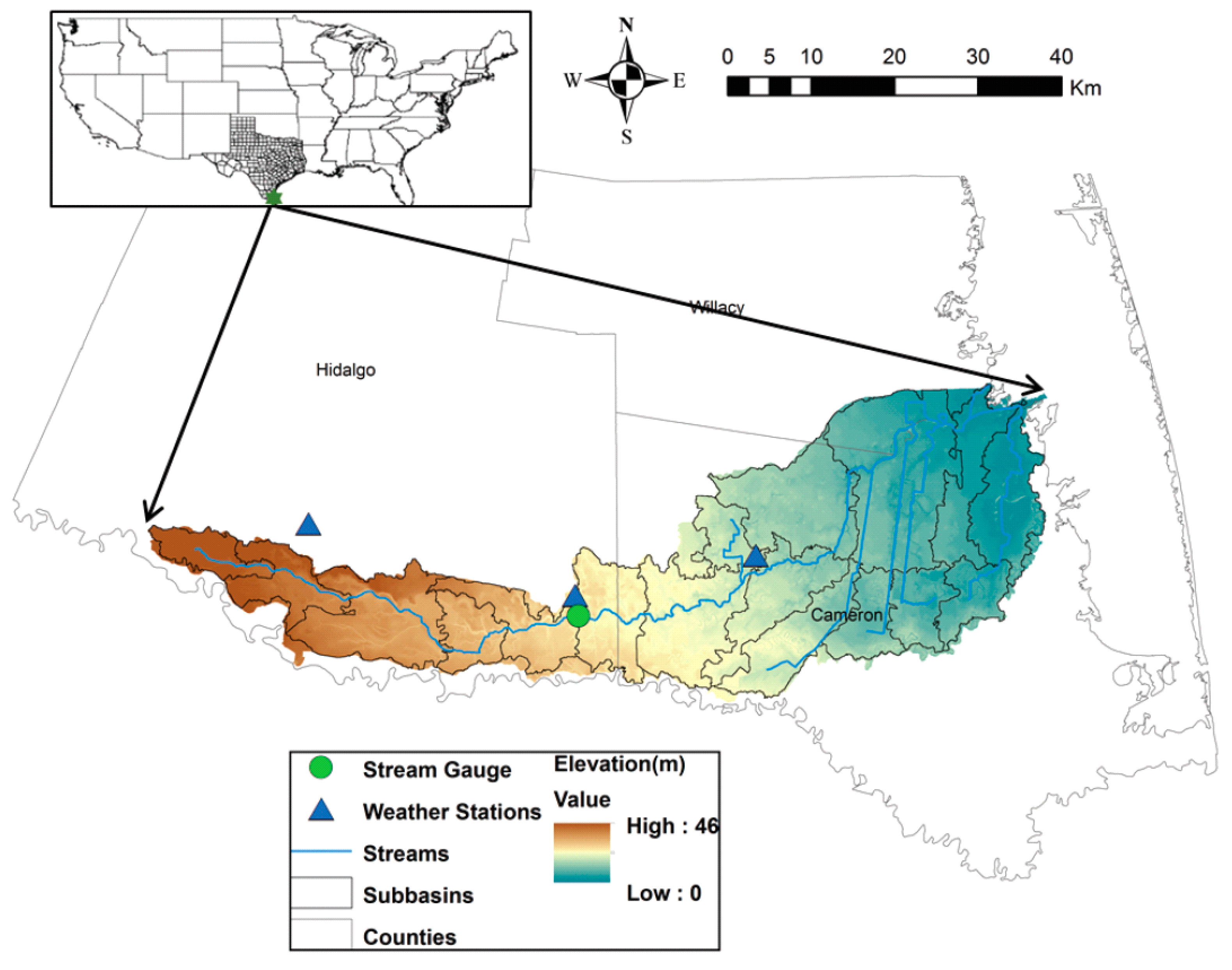
2.2. Study Area

The Arroyo Colorado watershed (ACW) is a part of the Nueces-Rio Grande Coastal Basin located in Southern Texas, USA (sharing its border with Mexico, see Figure 1). The Arroyo Colorado River (ACR) in ACW is a branch of the Rio Grande River and the drainage area of 1692 km² within three counties (Cameron, Hidalgo, and Willacy Counties) [37]. In general, the ACW is comprehensively developed in terms of agricultural activities and urbanization. Specifically, more anthropogenic development can be found in the central and the western parts of the ACW (e.g., cities such as Donna, Harlingen, McAllen, Mercedes, Mission, Pharr, San Benito, and Weslaco) [37].

As shown in Figure 2, agriculture (54%), rangeland (18.5%) and urban areas (12.5%) are the three major land use categories in the ACW, whereas the commonly cultivated crops are cane, cotton, citrus, sorghum, and vegetables. The predominant soils in the ACW are sandy loams (0.06–2 mm), clay loams (0.002–0.006 mm), and clays (<0.002 mm), whereas the depth of soil layers is ranging from 1600 mm to 2000 mm. In SWAT, temperature and precipitation are the two major climate model inputs. The average annual temperature in the ACW is 28.9 °C in July and 14.5 °C in January which can also be considered as the reference data for summer and winter. The average annual precipitation ranges from 530 mm to 680 mm which can also be categorized as the semi-arid climate region. More details of the ACW can also be found in [37].

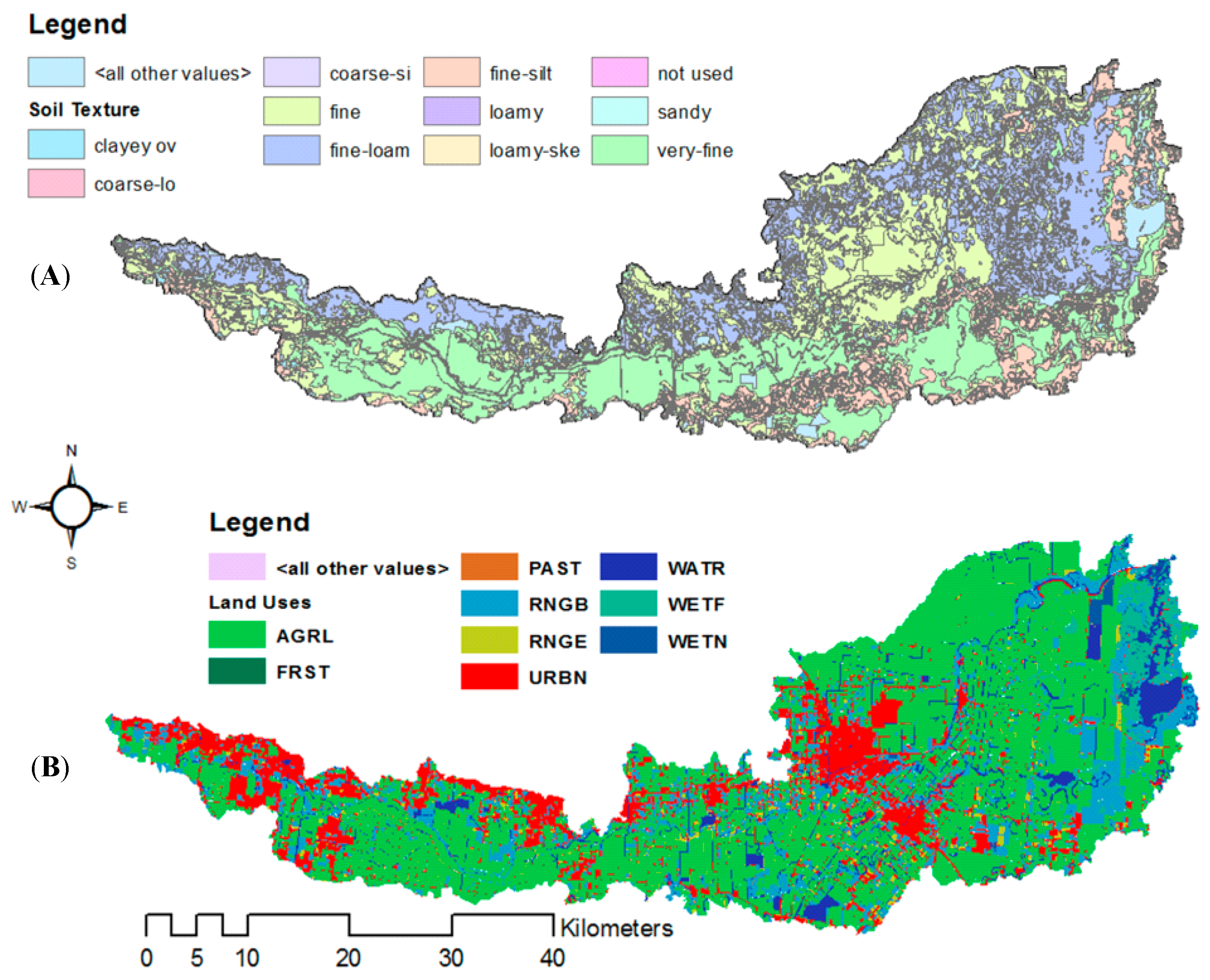
2.3. Sources of Input Data

Meteorological records (e.g., precipitation, temperature), anthropogenic activities (e.g., agricultural operation, urban usage), and measured hydrological data were integrated by the ArcSWAT system (ArcSWAT 2012.10.18, Texas A&M University, College Station, Texas, USA) which is a platform that incorporates the SWAT model and GIS (Geographic Information System) with a user-friendly interface. A Digital Elevation Model (DEM) with a spatial resolution of 30 m × 30 m downloaded from the National Elevation Dataset of the U.S. Geological Survey (USGS) [39], was used to generate sub-basins of the SWAT model in the ACW [40]. Additional information of SWAT included a land use map representing land cover conditions for 2004–2007 and the soil map from the Soil Survey Geographic Database (SSURGO), USDA-NRCS (United States Department of Agriculture-Natural Resources Conservation Service). In the SWAT model, the watershed was divided into 17 sub-basins comprising 475 Hydrological Response Units (HRUs) further subdivided by land use, soil and slope combinations. Crops and management practices including tillage practices, irrigation management, and nutrient application rate and timing were obtained by local agencies including Texas Commission of Environmental Quality (TCEQ), Texas AgriLife Research, Texas State Soil and Water Conservation Board (TSSWCB), and Natural Resources Conservation Service (NRCS). In addition, best management practices involving land leveling, irrigation management, nutrient management methods in the period of 1999–2006 were provide by TSSWCB.

Daily weather data (minimum–maximum air temperature and precipitation during the period 2000–2005) were collected for model inputs from three stations: COOPID 413943 near Harlingen; COOPID 415836 near Mercedes; and COOPID 419588 near Weslaco (managed by Texas State Climatologist Office located at Texas A&M University at College Station). The stream flow data of a gauge station (near Llano Grande at FM (Farm-to-Market Road) 1015 south of Weslaco) was provided by International Boundary and Water Commission. In addition, there was a total of 21 permitted point sources with discharges in the ACW, including 16 municipal districts with discharge permit limits ranging from 0.4 to 10 million gallons per day, three industrial areas, and two shrimp farms with infrequent discharge [41].

The watershed modeling work conducted in this study was designed to enhance the living quality of local colonia residents [37]. However, one of the challenging issues was the lack of observation data especially for sediment loads (substantially restricted by available funding supported). It was stated in Harmel et al. [42] and Yen et al. [43] that model performance (in terms of statistics) of watershed modeling could be substantially affected by the quality of measurement data. For sediment loadings alone, measurement uncertainty may reach up to 117%. Therefore, the selection of alternative functions should be even more carefully examined while an insufficient amount of data was acquired. We tried to make the best use of the available measurement data in the sense of fulfilling a complete watershed modeling project. In this study, suspended sediment (SS) was evaluated by water quality data from limited grab samples (7–8 times per year). LOAD ESTimator (LOADEST) is a software package developed by USGS that can automatically conduct regression analysis to generate estimated water quality data. Available observation records are used to fill gaps at time steps with missing data. In this case, LOADEST was used to convert the grab-samples into time series loads with monthly mean values within the 95% confidence interval [44], as observed data to calibrate SWAT. For more information on the input and sampling data of the ACW, see the research by Seo et al. [38].

2.4. Sediment Transport Methods in SWAT

SWAT2012 offers four alternative sediment routing methods to the model’s standard method. All sediment routing equations share the same in-stream sediment routing (sediment transport capacity is routed in main reaches/channels) but calculate the maximum sediment transport capacity (maximum concentration of transportable sediment) differently. A brief introduction of the four methods is described as follows, and further details can be found in the SWAT User’s Manual [22].

2.4.1. Modified Bagnold Equation

The Bagnold equation is the default choice for calculating maximum transport capacity from a reach segment in SWAT. This method determines the maximum transport capacity as a function of channel slope and velocity. The equation was developed by Williams [26] based on stream power as defined by Bagnold [21]. The maximum transport capacity from a reach segment is calculated by Equation (1).

$$con{c}_{sed,ch,mx}=c_{sp}·{v_{ch,pk}}^{SPEXP}$$

(1)

where, $con{c}_{sed,ch,mx}$ is the sediment concentration (maximum) transported by water (ton/m³); $c_{sp}$ (SPCON) is the user defined sediment coefficient; $v_{ch,pk}$ is the peak channel velocity (m/s); and SPEXP is the user defined coefficient in the exponential term [1]. In SWAT2012, extension of the Bagnold stream power function served as a separate modeling option from the default Bagnold method. The modified Bagnold equation includes consideration of the shear stress deployed by the water on the river bank as well as the stream bed that dislodges sediment particles based on the concept of critical shear stress [45].

2.4.2. Kodoatie Equation

The Kodoatie equation is suitable for streams that have bed materials of sizes ranging from silt to gravel. The equation was modified by Kodoatie [23] based on the equation developed by Posada [46] via the nonlinear optimization approach to categorize data from the field in various riverbed sediment sizes. The maximum transport capacity is represented as Equation (2).

$$con{c}_{sed,ch,mx}=\left(\frac{a·{v_{ch}}^b·y^c·S^d}{Q_{in}}\right)·\left(\frac{W+W_{bm}}{2}\right)$$

(2)

where, $v_{ch}$ is the mean flow velocity (m/s); y is the mean flow depth (m); $S$ is the energy slope (m/m) (in SWAT, the value of $S$ is projected the same as bed slope in all cases); regression coefficients for the Kodoatie equation are defined as a, b, c and d in categorizing four different bed materials; $Q_{in}$ is the daily water volume that enters each sub-basin (m³); W is the channel width at water surface (m); and $W_{bm}$ is the bottom channel width (m).

2.4.3. Molinas and Wu Equation

By the application of universal stream power, the Molinas and Wu equation was designed for simulating large sand-bed rivers. The equation was developed by Molinas and Wu [24] using universal stream power to calculate the maximum transport capacity.

$$C_w=M{\psi }^N$$

(3)

where, $C_w$ is the sediment concentration by weight (mg/L); $\psi$ is the universal stream power; M and N are user defined coefficients. The equation was calibrated using large river basins as test cases and the following equation is derived:

$$C_w=\frac{1430·\left(0.86+\sqrt{\psi }\right)·{\psi }^{1.5}}{0.016+\psi }·{10}^{-6}$$

(4)

The universal stream power $\psi$, can be expressed as:

$$\psi =\frac{{v_{ch}}^3}{\left(S_g-1\right)·g·depth·{\omega }_{50}·{\left[{\log }_{10}\left(\frac{depth}{D_{50}}\right)\right]}^2}$$

(5)

where, $S_g$ is the solid relative density (2.65 g/cm³ for this study); g is the gravity acceleration (9.81 m/s²); depth is the flow depth (m); ${\omega }_{50}$ is the fall velocity (m/s) for median size particles; $D_{50}$ is the median of sediment size (mm).

2.4.4. Yang Sand and Gravel Equation

The method was developed mainly for simulation of sand and gravel materials. Yang [47] calculated the total sand transport rate as excess unit stream power (the unit stream power is defined as the time rate of potential energy dissipation per unit weight of water), which is a product of velocity and slope. Yang [48] extended the unit stream power equation for sand to gravel loading. Equations for sand and gravel were separately developed based on regression of critical unit stream power, fall velocity, kinematic viscosity, sediment size, shear velocity, and unit stream power. The equations for sand (median sizes $D_{50}$, less than 2 mm) are as follows:

$$\log C_{w,ppm}=5.435-0.286\log \frac{{\omega }_{50}{D}_{50}}{\nu }-0.457\log \frac{V_{*}}{{\omega }_{50}}+\left(1.799 -0.409\log \frac{{\omega }_{50}{D}_{50}}{\nu } -0.314\log \frac{V_{*}}{{\omega }_{50}}\right)\log \left(\frac{{\upsilon }_{ch}S}{{\omega }_{50}}-\frac{V_{ch}S}{{\omega }_{50}}\right)$$

(6)

and for gravel ($D_{50}$ between 2 mm and 10 mm) are:

$$\log C_{w,ppm}=6.681-0.633\log \frac{{\omega }_{50}{D}_{50}}{\nu }-4.816\log \frac{V_{*}}{{\omega }_{50}}+\left(2.784-0.305\log \frac{{\omega }_{50}{D}_{50}}{\nu } - 0.282\log \frac{V_{*}}{{\omega }_{50}}\right)\log \left(\frac{{\upsilon }_{ch}S}{{\omega }_{50}}-\frac{V_{ch}S}{{\omega }_{50}}\right)$$

(7)

where $C_{w,ppm}$ is the sediment concentration (mg/L); $\nu$ is the kinematic viscosity (m²/s); $V_{*}$ is the shear velocity (m/s); $V_{ch}$ is the critical velocity (m/s); and ${\upsilon }_{ch}$ is the mean channel velocity (m/s). The results of sediment concentration in mg/L are divided by 10⁶ to convert to concentration by weight, and then the conversion equation for Molinas and Wu is used to convert to maximum bed load concentration in metric ton/m³.

2.5. Model Calibration and Validation

In this study, calibration consisted of testing each of the four scenarios in SWAT whereas alternative sediment routing equations were tested. The scenario name and equation tested in each scenario were (i) Scenario 01: Modified Bagnold equation; (ii) Scenario 02: Kodoatie model; (iii) Scenario 03: Molinas and Wu model; and (iv) Scenario 04: Yang sand and gravel model. Calibration of the SWAT model for the ACW was conducted from 2002 to 2003 (warmup years from 2000 to 2001) and the validation period was from 2004 to 2005. Daily streamflow and monthly sediment were calibrated via the Integrated Parameter Estimation and Uncertainty Analysis Tool (IPEAT) [49]. IPEAT is a framework for both auto-calibration and uncertainty analysis which adopts Dynamically Dimensioned Search (DDS) as the major parameter estimation technique [50] (however, DDS can be replaced by other methods under the IPEAT framework). In addition, IPEAT has been demonstrated to have superior performance (e.g., convergence speed and the ability to find better solutions) over other commonly implemented auto-calibration techniques such as Shuffle Complex Evolution (SCE-UA) and DiffeRential Evolution Adaptive Metropolis (DREAM) [51].

In this study, the SWAT model was calibrated/validated by the measurement data from the gauge station (U.S.G.S. 08470142), which is 58 km west of the ACW outlet. A total 14 parameters were altered for flow calibration, and for sediment. The same set of calibrated streamflow parameters was used for all scenarios and the sediment parameters were calibrated in each scenario. The parameters and the recommended ranges are listed in Appendix A and Appendix B.

The Nash–Sutcliffe Efficiency coefficient (NSE) was used as the objective function to determine model goodness-of-fit. NSE has been implemented broadly as the primary statistical measure in the field of watershed modeling [52,53]. The values of NSE may range from −∞ to one which represent the worst and the best model performance. In Equation (8), $y_i^{Obs}$ is the observation data at time step $i$; $y_i^{Sim}$ is the model predictions at time step $i$; $y_i^{Mean}$ is the mean of observation data at time step $i$; and $N$ is the time span of total time steps. Perfect simulation is achieved when NSE equals one, while negative values of NSE are generally regarded as poor performance. In this study, NSE was modified for the auto-calibration process [38] so that a value of zero indicates a perfect fit. In Equation (9), the objective function represents the integrated value of (1 − NSE) for targeted output variables (e.g., streamflow and sediment), where $OF$ is the value of the objective function; NSE_v is the value of NSE of variable $v$; and $V$ is the total number of variables.

$$NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^N{\left(y_i^{Obs}-y_i^{Sim}\right)}^2}{{{\displaystyle \sum }}_{i=1}^N{\left(y_i^{Obs}-y_i^{Mean}\right)}^2}$$

(8)

$$OF={{\displaystyle \sum }}_{v=1}^V\left(1-NS{E}_v\right)$$

(9)

It is difficult to estimate uncertainty in a deterministic model such as SWAT, therefore, the inclusion rate and spread were exerted to quantify the comparative level of uncertainty among scenarios. Spread is the average width of the 95% confidence interval along simulated temporal series. Since the width of confidence intervals may change over temporal series, it is a lot easier to compare levels of uncertainty by averaged width (which is defined as “spread”). On the other hand, the inclusion rate is calculated by the percentage of observed data located within 95% confidence intervals of modeling outputs (calculated by sorting simulation outputs at each time step using empirical probability density function). If there are 10 observation points and only seven of the total are located within the confidence intervals, the inclusion rate is going to be 70%. More details and applications of the inclusion rate and spread can be found in Yen [50], Yen et al. [49].

3. Results

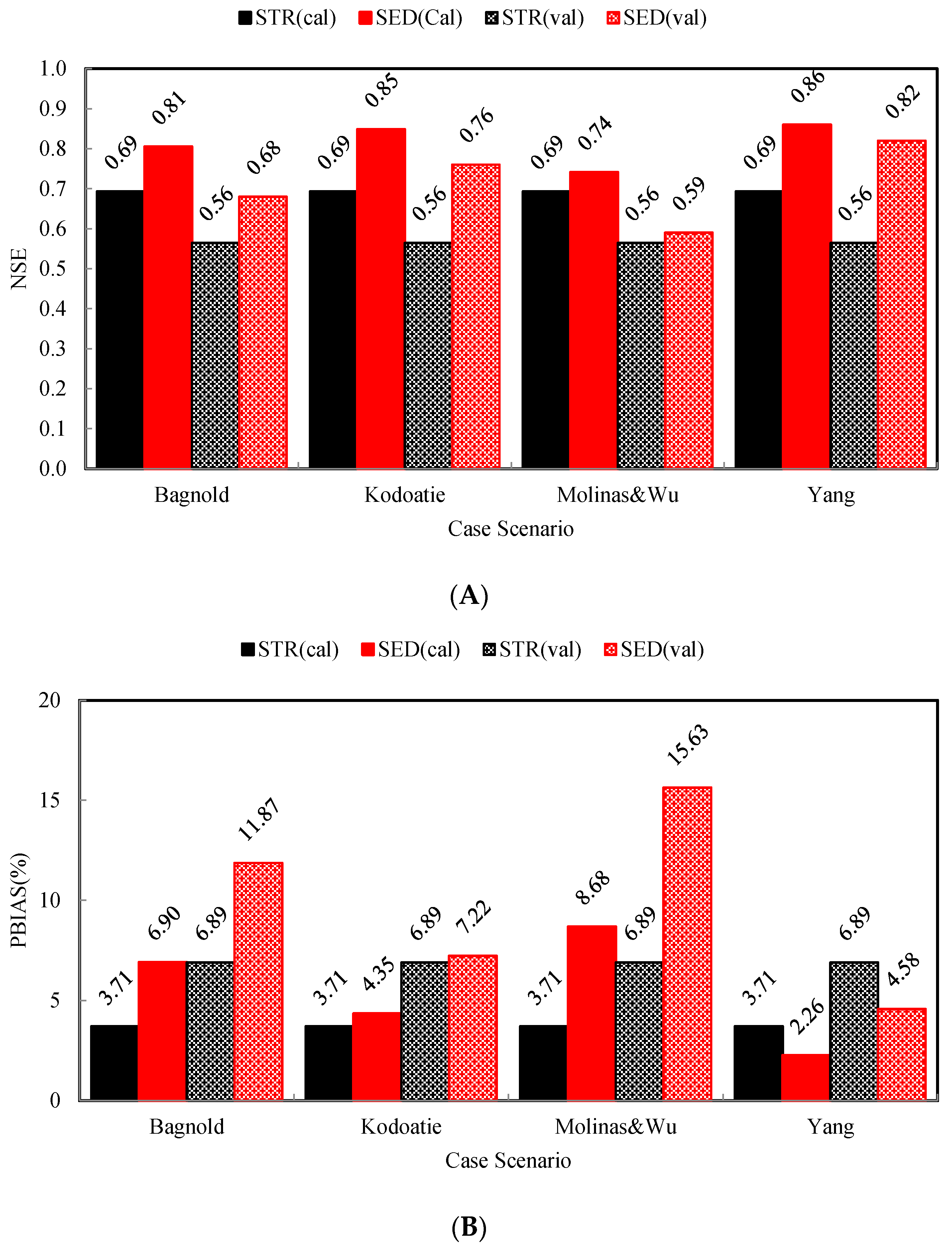
3.1. Comprehensive Comparisons by Objective Function Values

Figure 3A presents the overall performance for objective functions (optimized for sediment calibration) along with the model iteration for all four scenarios. The convergence speed was fairly varied with different scenarios where Scenario 02 reached a stable objective function value slower than other scenarios. After 1500 iteration times, no improvements (in terms of objective function values that did not change for more than 0.1% of the previous one within 1000 runs) were made in any of the scenarios. Figure 3B shows the best objective function values among the four scenarios. Scenario 04 (Yang equation) generated the best objective function, while Scenario 3 (Molinas and Wu equation) yielded the worst objective function. By comparing the performance of objective function values, the Yang equation fitted the measured data best. On the other hand, it is also necessary to consider other statistical measures (since there are other methods used to evaluate model performance in this study), which will be further discussed in later sections.

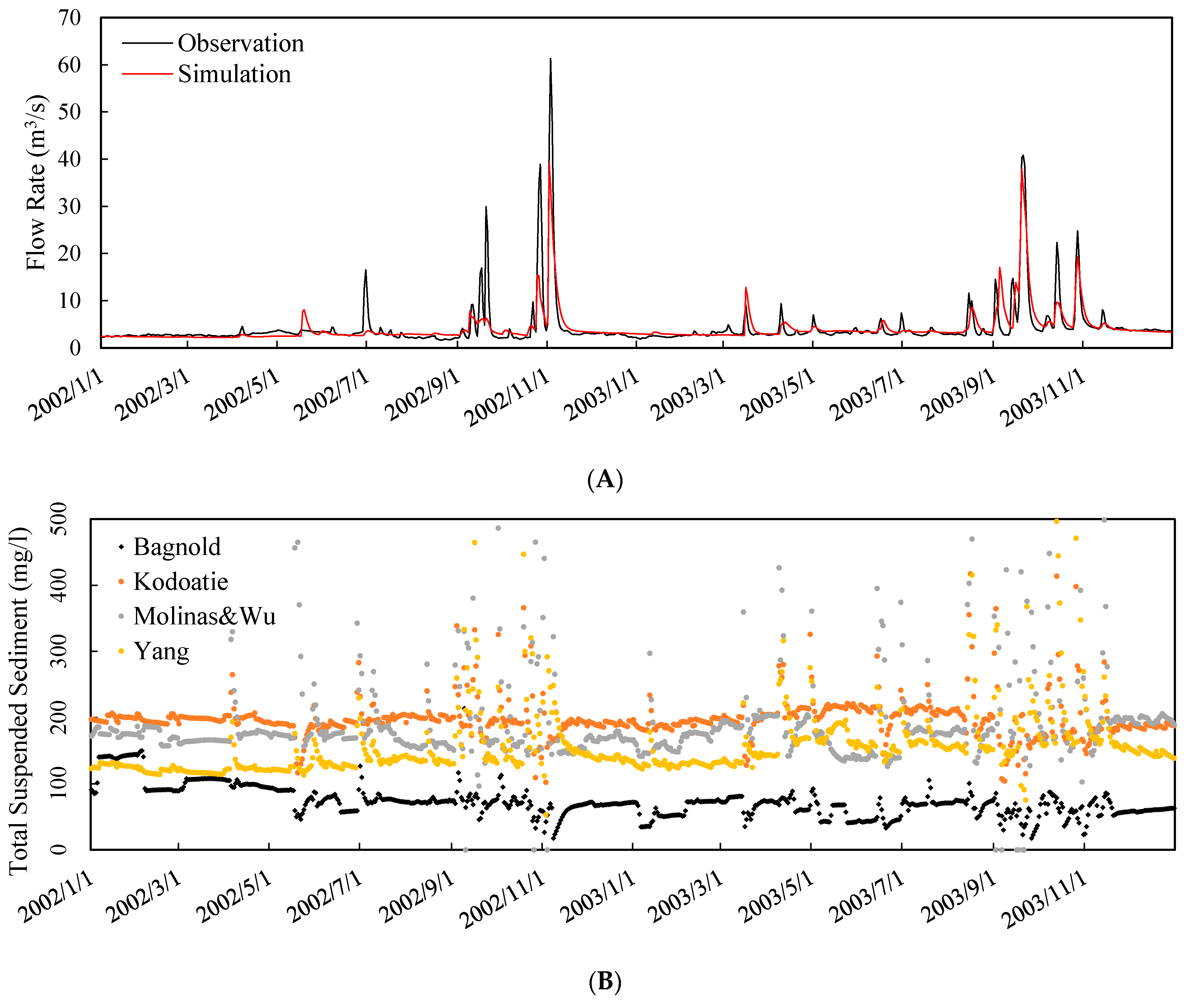
3.2. Evaluation of Model Performance on Streamflow and Sediment Predictions

In Figure 3A,B, model predictions of streamflow and sediment loadings were evaluated in terms of NSE and PBIAS (percent bias). NSE values for streamflow were close to 0.69 and 0.56 for calibration and validation periods, respectively, in all four scenarios (Figure 4A). PBIAS was relatively low at less than or equal to 7% for streamflow for both evaluation periods in all four scenarios (Figure 4B). NSE values for sediment, however, were better for Scenarios 02 (Kodoatie), and 04 (Yang)—at approximately 0.85—than for Scenarios 01 (Bagnold) and 03 (Molinas and Wu).

PBIAS values for sediment exhibited the same trend (in terms of statistical values and also the relative differences among scenarios) in both the calibration and validation periods. In the calibration period, PBIAS for sediment was less than 5% for Scenarios 02 (Kodoatie) and 04 (Yang), compared to 7% for Scenario 01 (Bagnold) and almost 9% for Scenario 03 (Molinas and Wu). In the validation period, Scenario 04 (Yang) performed the best, followed by Scenarios 02, 01, and 03. According to the guidelines for model performance, statistics recommended by Moriasi et al. [54] (one may also take advantage of the latest and more detailed guidelines in Moriasi et al. [55]), the best results from Scenarios 02 and 04 were considered “Very Good,” while results from Scenarios 01 and 03 were classified as “Good.” The results of error statistics were consistent with the overall performance of objective function values. The Yang equation generated the best sediment predictions, while the Molinas and Wu equation yielded the worst sediment predictions. Details of each method were further investigated in the following section.

Comparisons of simulated and observed values were shown in Figure 5A,B. As stated previously, streamflow predictions were fairly close among all scenarios either in NSE or PBIAS. In Figure 5A, the simulated streamflow approximated observed flow in all four scenarios. The peak flows in September and December 2002 were slightly underestimated, while the recession limbs during August and September 2003 were slightly overestimated. In general, the simulated daily streamflow performed well in both low and high conditions. In Figure 5B, simulated sediment under Scenarios 02 and 04 showed similar trends to the other two scenarios in time series. Considerable underestimation (around 50% underestimation between Scenario 03 and the observation) can be found in the early stage of Scenario 03. The performance of sediment predictions during high flow conditions was closer to observed data than during low flow periods, which can be explained by the fact that the objective function (NSE) was designed to capture peak events. The differences of streamflow and sediment processes among scenarios were consistent with the corresponding statistics.

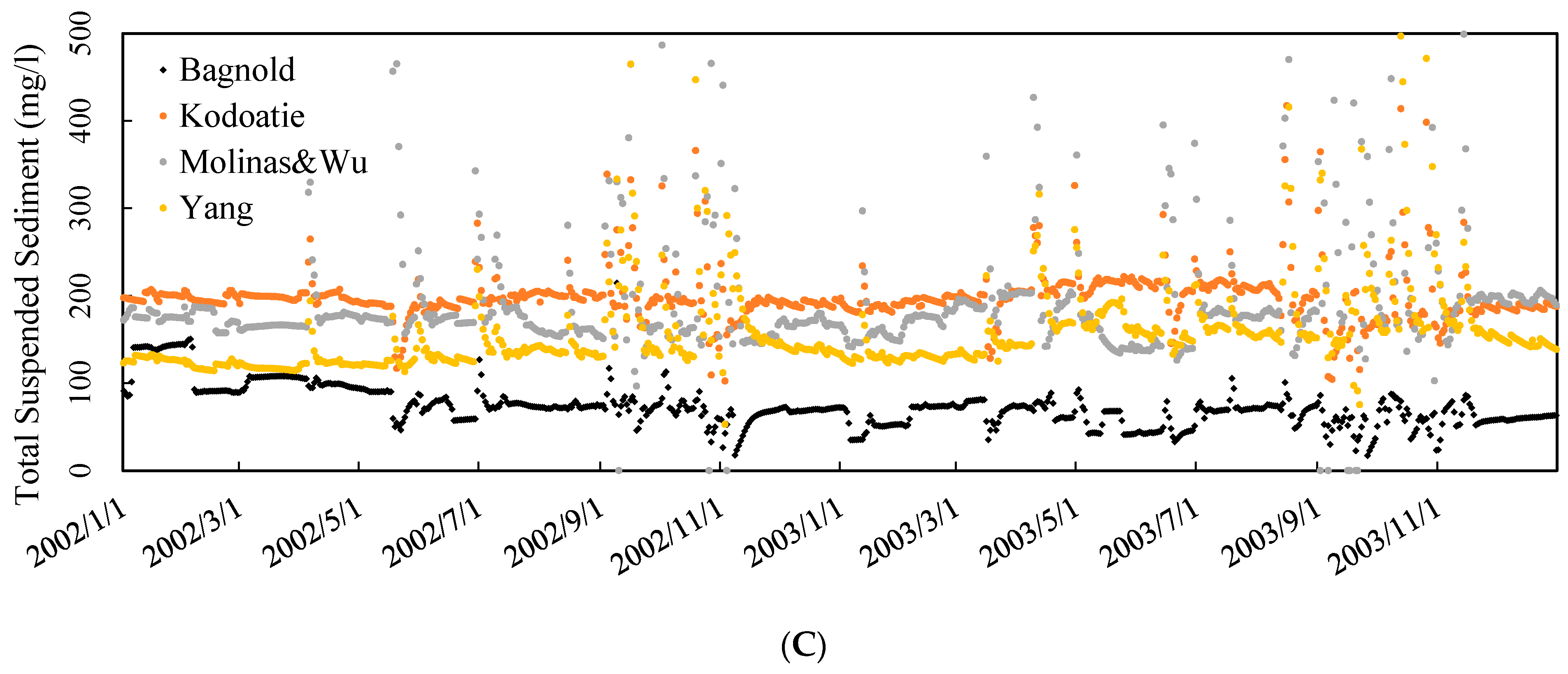
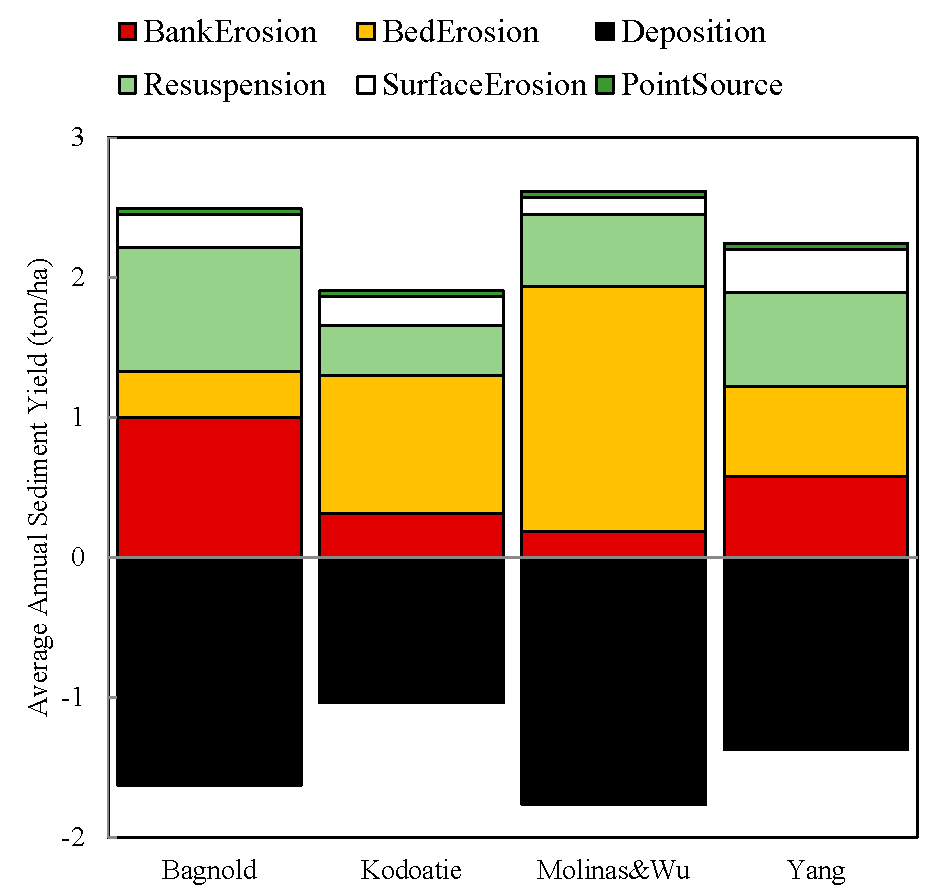
3.3. Evaluation of Sediment Concentration and Sediment Budget

Figure 5A–C demonstrated that, while all four equations generated comparable streamflow and sediment load trends, the total suspended sediment (TSS) concentration varied significantly between equations. In SWAT, TSS consisted only of silt and clay, while the total sediment loads contained all particles. Only 35% of the total sediment loads from the Yang equation were silt and clay, while almost all total sediment loads from the other three equations were silt and clay. Accordingly, the Yang equation, which was developed to simulate large particles such as sand and gravel, generated lower sediment concentrations than did the Molinas and Wu equation and the Kodoatie equation. The Bagnold equation yielded the lowest TSS concentrations overall, but it is important to note that, during high flow conditions, TSS concentrations rose when applying the Bagnold equation (Figure 5B).

In considering why four equations that generated comparable sediment loads can yield different TSS concentrations, it is important to consider sediment sources and sinks associated with each respective equation. As shown in Figure 6, the Bagnold equation had significant bank erosion and minimal bed erosion, while bed erosion exceeded bank erosion in all three other equations. The Molinas and Wu equation generated the most sediment movement (2.62 ton/ha), as well as the greatest erosion (1.76 ton/ha), resuspension, and deposition. In general, surface erosion and point sources contributed an unsubstantial portion of sediment yield. Notable findings here will be further investigated in the next section.

3.4. Uncertainty Analysis

The predictive uncertainty for streamflow and sediment were evaluated using the inclusion rate and spread, and the results were shown in

Table 1. Inclusion rate and spread of measured streamflow and sediment within the 95% confidence intervals of the simulation period (2002–2003).

Scenario	Inclusion Rate (%)		Spread
	Streamflow	Sediment	Streamflow	Sediment
Scenario 01	49.59	62.50	1.815	0.046
Scenario 02	49.59	35.42	1.815	0.033
Scenario 03	49.59	54.17	1.815	0.040
Scenario 04	49.59	31.25	1.815	0.029

Notes: Inclusion rate (%): Percentage of measured data located within the 95% confidence intervals. Spread: Average width of the corresponding uncertainty band along the predicted time series. The units for streamflow and sediment are m³/s (cubic meter per second), and tons/ha (tons per hectare) respectively.

. Since all scenarios share mutual streamflow calibration results, the inclusion rate and spread are essentially the same. For sediment predictions, Scenarios 02 and 04 (the best two scenarios) performed similarly while a considerable increase of spread and the inclusion rate can be found in Scenario 01 and 03. In general, the wider spread identified in Scenarios 01 and 03 increased the corresponding inclusion rate.

A higher inclusion rate means that more of the observed data set is located within the 95% confidence interval of the model simulation, which seems to indicate reduced uncertainty. However, the associated spread increases with higher inclusion rates, suggesting that it is harder for the auto-calibration technique to find better solutions in the given watershed modeling project. Therefore, a higher inclusion rate may also indicate that the corresponding uncertainty has increased. In this study, the importance of greater or lesser uncertainty relied upon relative comparisons among scenarios instead of a quantified, stand-alone measurement. Accordingly, it is not feasible to objectively identify which scenario is superior based on the available evidence. Scientists and stakeholders should consider the potential margins while conducting alternative approaches.

4. Discussion

4.1. Similarities and Differences during Calibration

In this study, it was found that all four sediment routing methods produced similar calibrated sediment yields in the targeted watershed, but sediment concentration differed substantially. The four sediment routing methods estimated quite different sources and sinks of sediment throughout the watershed. In the Bagnold equation, erosion occurred mainly on the stream banks, while it was primarily bed erosion in the other equations. In the Yang equation, bed materials were calibrated to better simulate sandy conditions; therefore, the total sediment loads contained more coarse materials, which SWAT excluded from TSS concentrations, than silt and clay. In the other equations, bank and bed materials were calibrated to be loamy, and total sediment loads were essentially silt and clay, which was a part of the primary sources to TSS concentrations in SWAT.

The discrepancies in sediment load composition are not completely due to the differences in equation theory. The auto-calibration approach, which selects parameter values without any regard of physical meaning (see Appendix A for the best parameter sets in the four scenarios), may contribute to erroneous differences in sediment load composition. The mechanism for stream bank and stream bed erosion was controlled by CH_COV1 and CH_COV2 in the routing (*.rte) files, which are more prone to erosion with lower parameter values (if CH_EQU > 0). Therefore, one may control erroneous erosion of the river bank and bed by specifying different ranges for stream bank and stream bed.

The fractions of silt and clay in total sediment loads were controlled by CH_BNK_D50 and CH_BED_D50, respectively. In terms of calibrated bed sediment size, the Bagnold and the Kodoatie equations performed well during the auto-calibration processes. CH_BED_D50 values (which were not yet available in literature) were 1.267 μm, medium clay, and 49.24 μm, coarse silt, for Kodoatie and Bagnold, respectively. However, the former was developed for sediment from silt to gravel, while the latter was for sandy rivers. The other two scenarios included suitable bed sediment sizes for the application sediment transport equations.

For study areas with missing TSS data or expert knowledge of sediment transport pathways, one cannot conclusively judge which results best suit the catchment. As stated in a previous study [56], selection of alternative functions within a complex watershed simulation model could significantly impact model predictions. Ideally, users should apply both extensive TSS data and thorough knowledge of a study area as they choose a sediment routing equation and parameter ranges measurements that suit their specific goals. When complete data are not available, users should consider how their sediment routing equation and parameter range choices may affect results.

4.2. Comparisons of Equation Theories and Applications

There were both resuspension and deposition by all equations, due to the sediment routing processes in the SWAT model, which were the same for all equations (SWAT conducts sediment routing in main reaches and channels according to the sediment transport capacity). In studies of the field isotope investigation, most stream erosion was redeposited within the streams, and much of the TSS in the water column came from resuspended sediments within streams [57,58]. The Kodoatie equation has been tested against stream bed materials of all sizes, whereas Bagnold, Molinas and Wu and Yang equations were developed for large sand-bed rivers [24,25,59]. In addition, the Bagnold and Yang equations were widely applied in large rivers. The Kodoatie equation and the Molinas and Wu equations were not applied as much as the other two equations. Intuitively, the Kodoatie equation should have performed the best because it could incorporate the full range of sediment sizes. However, Yang’s equation performed overall the best, followed by the Kodoatie, Bagnold, and Molinas and Wu equations. It implied that the selection of sediment transport equations should be determined based on more than which equation can incorporate more sediment material sizes. One should also consider other issues such as (i) how many associated parameters are available to properly reflect actual watershed behavior (e.g., actual measured values of bank erosion parameters are available or perhaps an additional calibration process is required); and (ii) how well the integrated watershed model (in this case, the SWAT model) could simulate the sediment transport process by alternative methods (e.g., in other cases, surface runoff routines can be calculated by curve number procedure [60] or the Green and Ampt infiltration approach [61] via SWAT [56]).

In SWAT, the optional modified Bagnold equation is associated with the highest inclusion rate of sediment (Table 1) as well as the highest level of uncertainty. SWAT allowed more parameters to be calibrated for the modified Bagnold equation than for the other three alternative equations, because it shared the same parameters as the default simplified Bagnold equation [27]. Many parameters in the three other equations were hard coded in the SWAT model and thus cannot be calibrated. Parameters for the Bagnold equation should be more dependent on field survey data than the three other equations to reduce uncertainty using SWAT as the modeling tool.

The fundamental approach to improve the simulation results is to have more observation data of the targeted watershed, such as sediment sizes, channel erosion factors, and channel cover factors. It is advised to use measured data (parameters) to conduct relevant comparisons and analysis. However, it is difficult to evaluate some equations in depth due to limited information about the study area. In many cases, it may not be feasible economically or due to time constraints. These challenges may be addressed by automatic calibration techniques, which were developed to address the growing number of unknown values of model parameters.

5. Conclusions

In this study, the impacts of alternative maximum sediment transport functions on sediment prediction in the SWAT model were evaluated by IPEAT. Four sediment routing methods (modified Bagnold equation, Kodoatie equation, Molinas and Wu equation, and Yang sand and gravel equation) in the SWAT model were calibrated and validated via daily flow and monthly sediment loads in the ACW using IPEAT as the primary tool in conducting parameter estimation and uncertainty analysis. The Yang and the Kodoatie equations generated better predictions in terms of commonly used statistical measures. In addition, the associated uncertainty is relatively lower for the Yang and the Kodoatie equations. Uncertainty of model results from these two equations was smaller, with a higher inclusion rate and smaller spread, than results from other equations. In the Yang equation, both sand and gravel are applicable with calibrated sediment size, while the Kodoatie equation is not suitable for the calibrated values.

The major finding of this study is that it is possible for the four sediment transport equations to yield similar sediment yields, even in a watershed that does not have a complete set of observation data (e.g., measurement of sediment sizes, channel bank information). However, the use of alternative functions may not directly impact desired results due to varying TSS concentrations, the associated source and sink terms, or a complex watershed simulation model with multiple calculation procedures in specific output variables. In practice, it may be difficult to measure or even estimate values of channel or river bed parameters. Auto-calibration may provide an efficient technology to calibrate model parameters within a limited timeframe. However, the embedded physical meanings could contribute to erroneous, biased results if the tool (e.g., IPEAT in this study) is implemented blindly. As scientists, engineers, and decision makers (not limited to politicians) contemplate policy issues related to sediment transport, they should evaluate the applicability of model results to policy on a case-by-case basis. Input data, parameter estimation, and selection of sediment transport equation contribute to what one can and cannot conclusively determine from the results of a SWAT modeling study.