Next Article in Journal
Maximizing Infiltration Rates by Removing Suspended Solids: Results of Demonstration Testing of Riverbed Filtration in Orange County, California †
Next Article in Special Issue
Modelling Hydrology and Sediment Transport in a Semi-Arid and Anthropized Catchment Using the SWAT Model: The Case of the Tafna River (Northwest Algeria)
Previous Article in Journal
From Surface Flow Velocity Measurements to Discharge Assessment by the Entropy Theory
Previous Article in Special Issue
Statistical Analysis of the Spatial Distribution of Multi-Elements in an Island Arc Region: Complicating Factors and Transfer by Water Currents
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 2
10.3390/w9020121
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment

by
Thomas R. Mortlock
1,*,
Ian D. Goodwin
2,
John K. McAneney
1 and
Kevin Roche
1
1
Risk Frontiers, Macquarie University, North Ryde, NSW 2109, Australia
2
Marine Climate Risk Group, Department of Environmental Sciences, Macquarie University, North Ryde, NSW 2109, Australia
*
Author to whom correspondence should be addressed.
Water 2017, 9(2), 121; https://doi.org/10.3390/w9020121
Submission received: 5 December 2016 / Revised: 24 January 2017 / Accepted: 6 February 2017 / Published: 14 February 2017
(This article belongs to the Special Issue Sediment Transport in Coastal Waters)
Browse Figures
Versions Notes

Abstract

:
In June 2016, an unusual East Coast Low storm affected some 2000 km of the eastern seaboard of Australia bringing heavy rain, strong winds and powerful wave conditions. While wave heights offshore of Sydney were not exceptional, nearshore wave conditions were such that beaches experienced some of the worst erosion in 40 years. Hydrodynamic modelling of wave and current behaviour as well as contemporaneous sand transport shows the east to north-east storm wave direction to be the major determinant of erosion magnitude. This arises because of reduced energy attenuation across the continental shelf and the focussing of wave energy on coastal sections not equilibrated with such wave exposure under the prevailing south-easterly wave climate. Narrabeen–Collaroy, a well-known erosion hot spot on Sydney’s Northern Beaches, is shown to be particularly vulnerable to storms from this direction because the destructive erosion potential is amplified by the influence of the local embayment geometry. We demonstrate the magnified erosion response that occurs when there is bi-directionality between an extreme wave event and preceding modal conditions and the importance of considering wave direction in extreme value analyses.

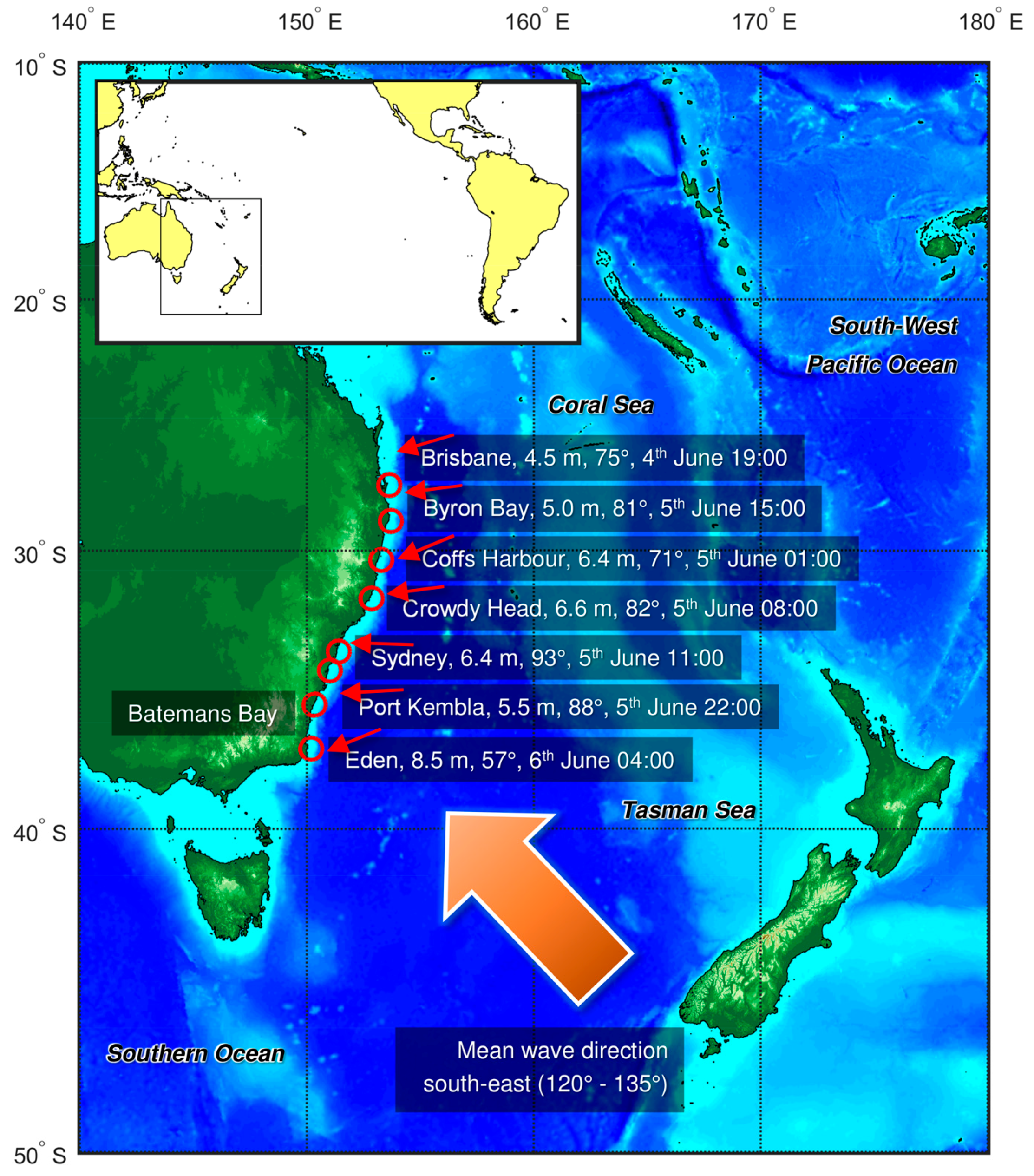
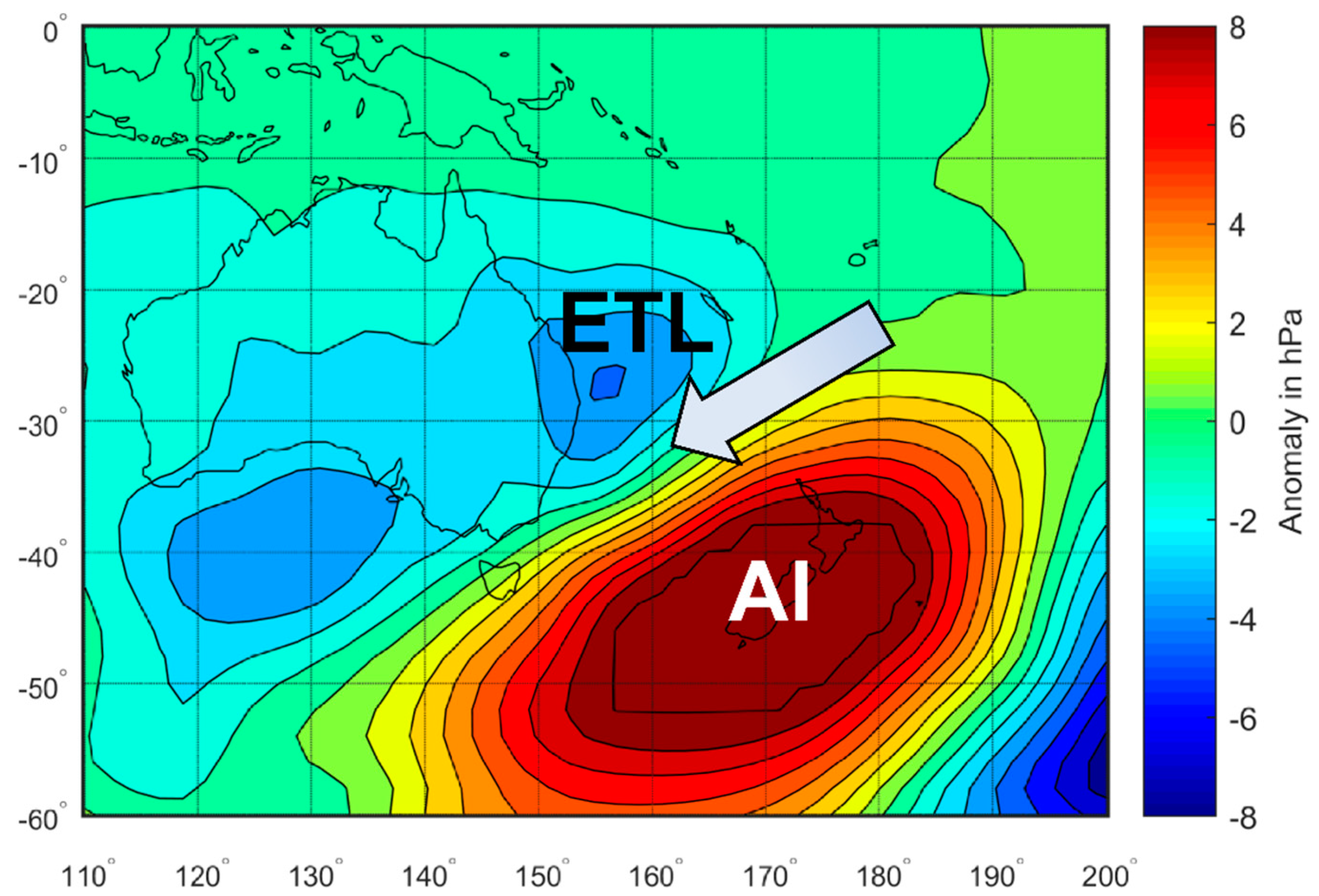
1. Introduction

East Coast Low (ECL) storms bring heavy rain, strong winds and powerful coastal wave conditions to the Southeast Australian coast. They are often responsible for significant beach erosion and lowland inundation and pose a threat to coastal infrastructure and public safety. The ‘Pasha Bulker’ storm in June 2007, for example, was responsible for normalised insurance losses of AUD$1.97 billion [1,2]; economic losses arising from that event are likely to have been at least double this figure.
ECLs are a common feature across the Southern Hemisphere extra-tropics [3,4]. In Australia, they typically form in the late Austral autumn to early winter and are a regular feature of the winter climate [5]. They typically bring storm wave conditions over a 3-day period before decaying eastwards into the Tasman Sea [6]. Their steep build up to peak storm wave conditions makes them one of the more dangerous weather systems affecting the New South Wales coast (NSW) and poses difficulties for forecasting.
The weather pattern of the June 2016 event was unusual in the context of the last few decades and is referred to as a “Black Nor’easter” because the black skies and north-easterly winds recorded by mariners in the late 1800s. The heavy rainfall and unusual wave direction coincided with some of the highest tides of the year further amplifying impacts at the coast. During most ECLs, the rotation of the low-pressure cell (clockwise flow in the Southern Hemisphere) and extra-tropical origin usually produce a south to south-easterly wave direction. The June 2016 event, however, produced east to north-east storm waves along the entire east coast (~2000 km of shoreline length) (Figure 1). Wave heights increased from north to south and the Eden buoy (far south coast of NSW) recorded a maximum individual wave height of 17.7 m—the largest wave ever recorded along the NSW coast [7]. Peak storm significant wave heights offshore of Sydney were considerably smaller (1-hourly Hs 6.4 m) yet still led to significant erosion at the coast.
The north-easterly wave direction was the result of a hybrid Anticyclonic Intensification (AI)/Easterly Trough Low (ETL) synoptic weather pattern as described in [5]. The low-pressure cell developed over the Coral Sea and northern Tasman Sea and was directed down the east coast by a strong blocking anticyclone which intensified over the South Island of New Zealand (Figure 2). The long fetch of approximately 1500 km produced sustained long wave periods (in excess of 14 s) that are unusual for the Tasman Sea from this direction and further contributed to powerful wave conditions at the coast.
Storm wave events from the north-east are uncommon, having occurred on average twice per decade at Sydney over the past 40 years [9]. The long-term mean annual wave direction is 135° (south-easterly), and waves approaching clockwise of east constitute almost 70% of observations. The south-easterly wave climate is moderately oblique to the shoreline and leads to increasing south-to-north alongshore wave energy and littoral transport [10]. The beach morphology is equilibrated to this wave energy gradient [11] and provides a natural buffer to erosion when the storm wave direction is similar to the modal (non-storm) wave direction. A more extreme erosion response occurs when the storm and modal wave directions are different, as occurred in June 2016. Even a relatively subtle change in wave obliquity can make a big difference to the magnitude and direction of littoral transport, as demonstrated empirically [12], and can drive a significant shoreline response on wave-dominated sandy coasts [13].
One of the worst affected areas was Collaroy, a suburb situated at the south end of the Narrabeen–Collaroy embayment on Sydney’s Northern Beaches (Figure 3). Beach erosion and accretion trends have been monitored here since 1976 [15] and have been shown to be synchronous with other beach compartments along the NSW coast [16,17]. Despite being well recognised as an erosion hot spot, the shorefront of Collaroy is characterised by a legacy of inappropriate development into the active beach zone [18]. How to best to manage this legacy poses a significant challenge and fraught policy area for governments [19]. Management decisions are purportedly based on cost-benefit analyses, which are chiefly controlled by the value of the land and property at risk. As population density and demand for coastal property continues to increase, the cost of not providing ongoing protection also rises. Contemporaneously, the hazard threatening coastal communities is also likely to increase with climate change.
The primary focus of our study is to demonstrate the importance of storm wave direction for coastal erosion impacts, using Narrabeen–Collaroy as an example of regional significance. The hydrodynamics controlling the erosion risk are examined, by comparing impacts from the June 2016 event with another ECL event that impacted Sydney in April 2015 but with a different offshore wave direction. A re-assessment of extreme wave conditions at Sydney, combined with nearshore buoy observations, also demonstrates the importance of wave direction considerations when assessing erosion potential in a changing climate.

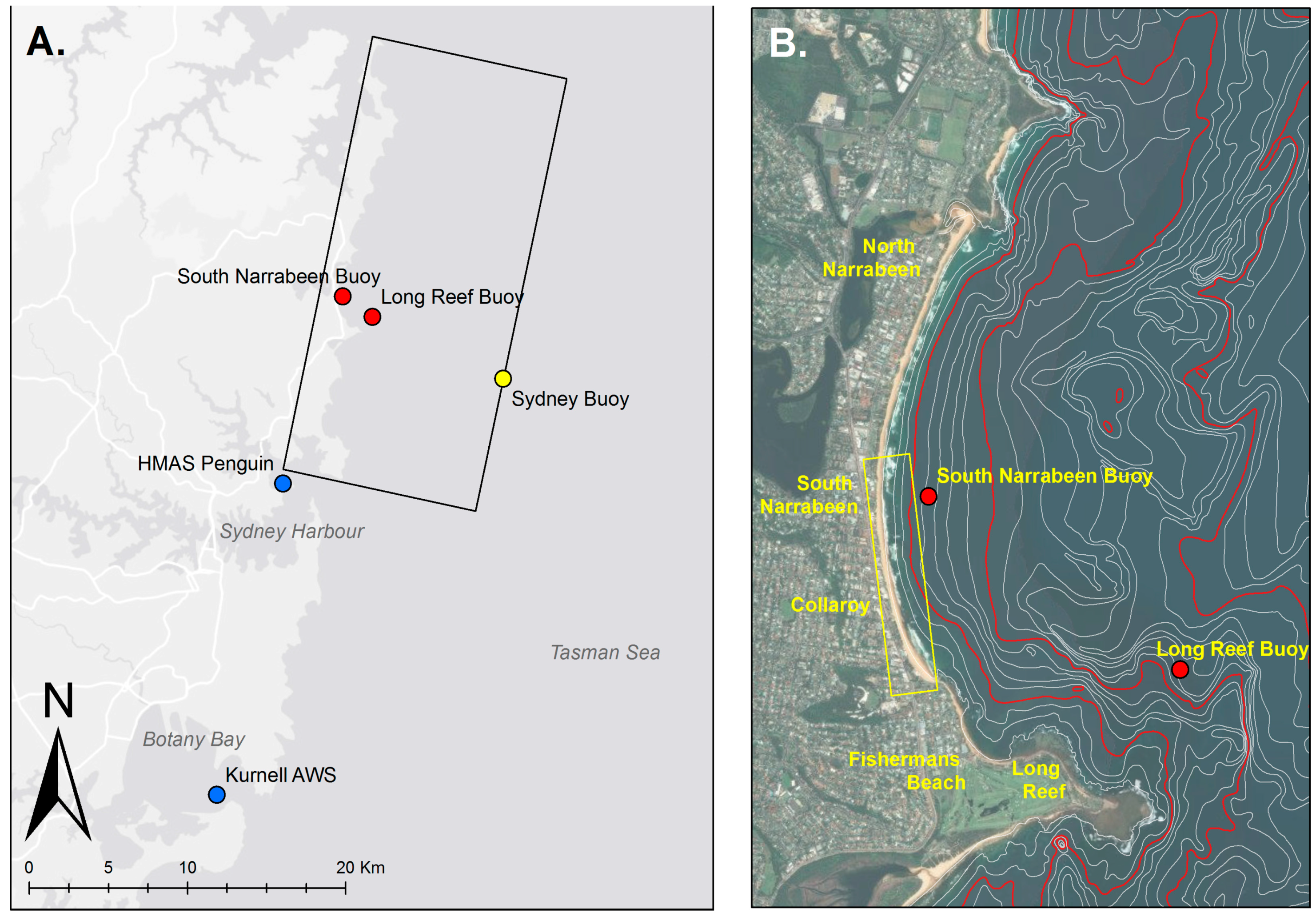
2. Observational Data

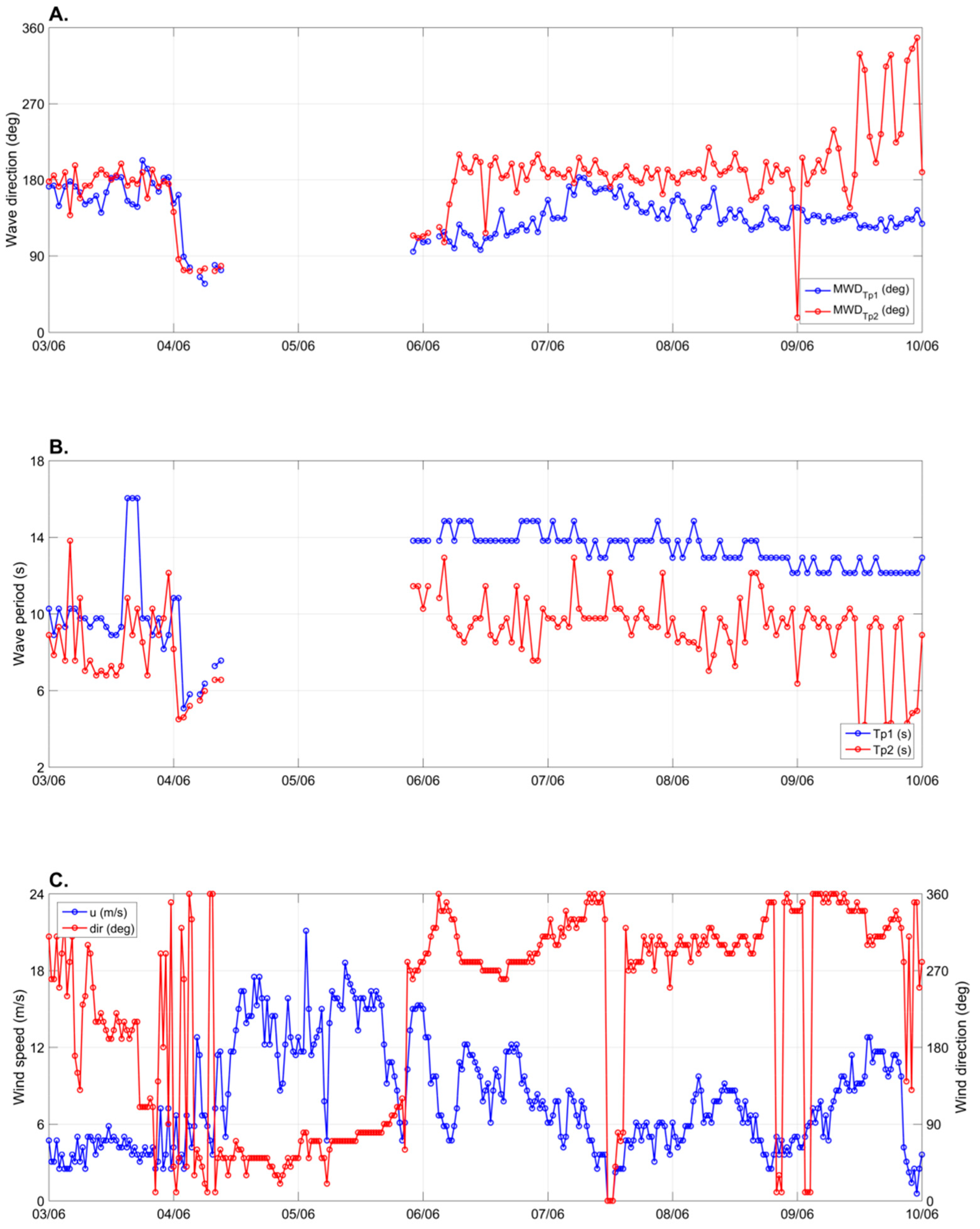
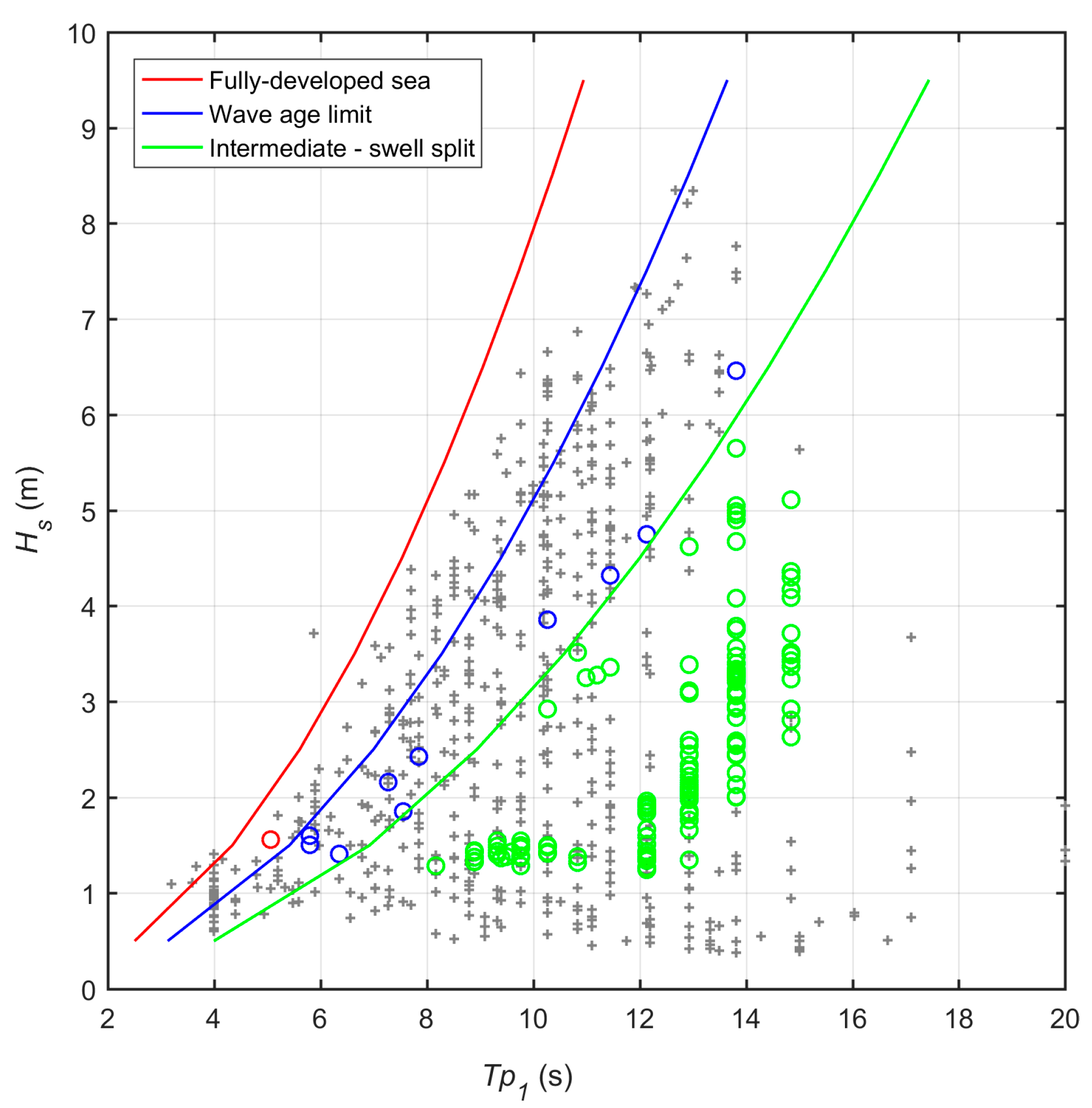
2.1. Wave Conditions

Hourly parametric wave data were sourced over the period 3 to 10 June 2016 from observations at the Sydney waverider buoy located approximately 9 km off the Narrabeen–Collaroy embayment in 90 m water depth (Figure 3). The significant wave height, Hs (m), maximum wave height, Hmax (m), peak wave period at the first and second spectral peak, Tp1 and Tp2 (s) and mean wave direction at the first and second spectral peak, MWDTp1 and MWDTp2 (degrees true north coming from) were the wave parameters used. The long-term parametric wave record from the Sydney buoy (non-directional since 1987, directional since 1992) was also used in this study. Observations from two other wave buoys deployed inside the Narrabeen embayment (Figure 3) between August and November 2011 were also used. These buoys were deployed at South Narrabeen (~12 m depth) and at Long Reef (~20 m depth). The South Narrabeen buoy was directional, while the Long Reef buoy was not.

2.2. Tide Conditions

Tide levels over the duration of the storm were taken at 15-min intervals from the gauge at the naval base of Her Majesty’s Australian Ship (HMAS) Penguin, Middle Head, Sydney Harbour (Figure 3). This station is considered representative of the open coast tide. Tides are semi diurnal and micro tidal (mean range of 1.3 m) along the NSW coast and approach almost perpendicular to the shelf, so that geographical differences in the timing of high and low tides across the state are negligible. Both forecast and observed tidal data were used to measure the surge component of the water level.

2.3. Wind Conditions

Half-hourly wind observations of velocity (m/s) and direction (degrees true north coming from) were obtained from the Kurnell weather station, 10 m above sea level, in Botany Bay (Figure 3). In the absence of over-sea wind measurements, Wood et al. [20] found the wind climate at Kurnell to best represent coastal ocean winds for the Sydney region.

2.4. Coastal Erosion

Pre- and post-storm beach surveys (above the water line) were undertaken at Narrabeen–Collaroy by University of New South Wales as part of a long-term beach monitoring program [15]. Shore-normal transects were surveyed at five locations along the beach using GPS, each extending from the dune behind the beach down to the water line. Pre- and post-storm hydrographic surveys (below the water line) were also undertaken at Narrabeen–Collaroy by NSW Office of Environment and Heritage [21]. Both surveys used a jet ski bottom-mounted single-beam echo sounder, narrow-beam transducer and GPS system and covered the shoreface from approximately 2 m to 15 m water depth with 50 m-spaced shore-normal survey lines.

3. Numerical Modelling

Wave, water level and wind observations over the duration of the storm were input to a coupled wave, flow and morphological model of the Sydney region to investigate coastal processes associated with the June 2016 event. A MIKE 21/3 Coupled Model developed by the Danish Hydraulic Institute (DHI) was used [22]. In this instance, the modelling system coupled a spectral wave model with a hydrodynamic flow model and a sediment transport model to simulate waves, currents, water levels and bed elevation change during the storm.
The wave model (MIKE 21 Spectral Wave, SW) simulates the growth, decay and transformation of wind-generated waves and swell in coastal locations. Directionally-decoupled and quasi-stationary formulations were used. Wave- and wind-driven currents and water level variations drive the hydrostatic flow model (MIKE 21 Flow Model), which is based on the two-dimensional Reynolds-averaged Navier–Stokes equations. Hydrodynamic conditions from the flow model and wave radiation stress terms from the wave model were used as input to the sand transport model (STPQ3D) to simulate morphological changes during the storm. The effect of bed ripples, bed slope, cross-current transport, rips and undertow were all included in the calculations. All model components were dynamically coupled, in other words a full feedback between the morphology, waves and currents took place at each time step. For a more detailed description of coupled model physics, the reader is referred to [22].

3.1. Model Bathymetry

The model domain covered the Sydney Northern Beaches area from North Head, Sydney Harbour in the south to Palm Beach in the north (Figure 3) and extended offshore to the 90-m isobath where the Sydney wave buoy is located. A mosaic of best-available bathymetries was used to generate a seabed topography in the model, including the pre-storm hydrographic survey undertaken at Narrabeen–Collaroy [21]. Bathymetric data also included a series of Single-Beam Echosounder (SBES) surveys of the upper shoreface of the Sydney Northern Beaches area undertaken by the Office of Environment and Heritage (OEH) between 2011 and 2016 (average 50 m line spacing); a Multi-Beam Echosounder (MBES) survey of the lower shoreface area offshore of the Northern Beaches undertaken by OEH in 2014 (5 m point density); and a series of SBES survey lines of the inner shelf offshore of the Northern Beaches area undertaken by the Royal Australian Navy (RAN) in the 1970s (average 200 m line spacing). The bathymetric data was mapped onto a flexible computational mesh, composed of a series of irregular Delaney triangles (elements), using a natural neighbor interpolation method. The interpolated bathymetric mesh was then refined based on a depth/gradient ratio to improve the computational resolution for shallow water and areas of complex subaqueous reef. This led to a computational mesh with an average element length of 200 m offshore (in approximately 90 m water depth), grading to 20 m at the shoreline. An approximate 20 m resolution at the shoreline was considered sufficient to resolve cross- and along-shore transport processes and ensured all available bathymetry soundings were used.
The coastal planform and elevation of the subaerial beach was idealized using the pre-storm cross-shore profile data from the Narrabeen beach monitoring program [15], and recent aerial photography. The dry beach was included in the model to provide a sediment source for storm cut and for flooding and drying at the shoreline.

3.2. Model Boundary Conditions

Boundary wind, wave and tide data were derived from point-source measurements close to or within the model domain, as described in Section 2. These time-series data (hourly waves, half-hourly winds, and 15-min tides) were applied at all three open boundaries of the model (south, east and north), apart from the waves which were only applied on the east (ocean) boundary. A depth-integrated approximation based on linear wave theory [22] was used for wave forcing on both lateral boundaries (north and south) to estimate waves entering the two sides of the model domain. Sensitivity testing ensured that the model domain was sufficiently wide to avoid potential errors propagating from the lateral boundaries into the area of interest. A computational time step of 15 min was used to resolve all boundary conditions, and a 12-h model spin up period was imposed.
An inherent assumption of the model was that the measured waves, tides and winds were representative of, and constant along, the length of the model boundaries on which they were applied. The east (ocean) boundary ran through the moored location of the Sydney waverider buoy and followed the same isobath (90 m). Wind data was sourced from the most representative source and was chosen over other wind hindcasts as the latter can under-estimate near-coast wind fields in this area [20,23]. Because an atmospheric model was not used, the wind field was spatially constant throughout the model domain for each time step, so localized variations were not captured. Tide measurements were applied as variations in the surface water elevation at each boundary. This included a barometric surge element as measured on top of the astronomical tide. Local wind and wave set-up were generated by the model.
Parametric wave data from the Sydney buoy (Hs, Tp1, MWDTp1) were used assuming a JONSWAP spectrum as full spectral conditions from the buoy during the storm were unavailable at the time of writing. Thus, any bi-modality during the storm was not replicated in the model and is likely to have contributed to residual errors after calibration (Section 3.5). Directional spreading of the parametric wave data was estimated for each time step based on wave-age curves generated using the method of [24]. The entire Sydney buoy record (1987–2016) was used to approximate wave steepness limits of wind-sea, intermediate sea-swell, and swell, based on Hs and Tp1 (Figure A2). All wave events classed as wind-sea were assigned a spreading of ~25°, intermediate sea-swell ~20°, and swell ~15°, after [22]. From Figure A2, it is interesting to note that most wave conditions during this event were theoretically swell waves because of the unusually long wave periods.

3.3. Model Bed Characteristics

Bed resistance, bottom friction and bed layer thickness varied spatially within the model domain in accord with a comprehensive set of observations of subaqueous reef areas and sediment samples collated in [25]. In this way, the influence of the roughness and non-erodibility of rock reefs was accounted for in the model. An estimate of the physical roughness height of rock reef was derived from Light Detection And Ranging (LiDAR) imagery of low-tide exposed rock platforms around Long Reef headland. Transects were taken through the reef sections, following the method of [26]. Results ranged from 0.08 m to 0.33 m with a mean of 0.16 m. These values are similar to those reported for coral reef platforms (e.g., 0.16 m [27]) with the upper values reflecting the greater rugosity of bare rock reef than that of coral. The mean value of 0.16 m was used to calculate bed resistance effects for all areas of rock reef within the model domain. A value of 0.05 m was used elsewhere to account for the effect of small sand ripples on flow resistance [22,28].
To describe the bottom frictional effects of reef, the physical roughness height, kw, was converted to a hydraulic (Nikuradse) roughness value, kn, using the approximation kn ≈ 2.kw [29], giving a kn of 0.32 m. Using similar logic, Huang et al. [30] arrived at a comparable value for kn of 0.27 m for coral reef. For non-reef areas, a kn of 0.04 m was used to approximate the effect of small sand ripples on the frictional dissipation of wave energy [31].
Where reef areas existed, the bed thickness was set to zero to ensure that no erosion could take place. Elsewhere, an infinite thickness was used. At the land boundary, areas of reef headland were assigned a reflection coefficient of 0.8 (1.0 being fully reflective) to describe the intensity of a reflected wave heights relative to incident wave heights against a headland [22]. Full wave reflection effects (such as standing waves) were not accounted for. Beach sections were fully absorptive.
A cross-shore gradation in the median grain diameter, d50, was used based on observations in [25]. d50 varied from 0.33 mm on the sub-aerial beach, to 0.22 mm in the surf zone, coarsening thereafter to 0.48 mm on the lower shoreface. Observations were not of sufficient density to derive any along-shore variation in grain size. Sediment samples from various sources collated in [25] suggest the grain size distribution around d50 did not vary significantly in a cross-shore direction, thus, a single grading coefficient of 1.34 was used. A porosity of 0.4 was used consistent with that of quartz sand. Carbonate material present in beach sediments along the Northern Beaches is likely to vary the porosity (and specific density) of sand in a cross-shore direction, but is not included here.

3.4. Model Calibration

The sensitivity of the model to varying mesh resolution, seabed substrate type, wave breaking, directional resolution and wave theory were examined. A Brier Skill Score (BSS) was used to assess the model’s morphological performance, and by inference the nearshore flow field, using observed bathymetric change from pre- and post-storm hydrographic surveys undertaken at Narrabeen–Collaroy [21]. A skill score was calculated for each mesh element within the survey area so the spatial variance in model error could be assessed. The scoring method and classification system described in Sutherland et al. [32] was used.
The most significant improvement in model skill was obtained by increasing the resolution of the computational mesh from the 30-m isobath to the shoreline. Changes to the mesh resolution seaward of this had negligible effects on model performance. A coarse resolution mesh grading from an approximate element length of 250 m along the 30-m isobath to 50 m at the shoreline, returned a median BSS across the survey area of −5 (‘Bad’). A more highly-resolved mesh covering the whole of the Narrabeen–Collaroy embayment (from 30-m isobath to shoreline) at a 20-m resolution, dramatically improved the median BSS to 0.22 (‘Good’).
The cost of not including areas of rock reef in the model, and their effect on flow resistance, bottom friction and erodible layer thickness, was a reduction in model skill from 0.22 (‘Good’) to 0.12 (‘Fair’). A wave breaking parameter, γ, of 0.9, best replicated the observed volume in the surf zone bar, as has been also found by [33] in a similar setting. Increasing the directional resolution of the wave forcing (from 10° to 5°) made no significant improvement, perhaps because the coarser binning in part compensated for deficiencies in the directionality of boundary wave forcing (Section 3.2).
The model sensitivity to two wave theories was tested; the first using a combination of Stokes and Cnoidal fifth-order classic wave theories, and another combining the semi-empirical wave theories of Doering and Bowen [34] and Isobe and Horikawa [35]. The Stokes/Cnoidal theories led to a wider area of small-scale bed lowering seaward of the surf zone bar but did not replicate the accretion volume in the bar as well as the Doering and Bowen/Isobe and Horikawa formulation. Thus, the latter was used here.

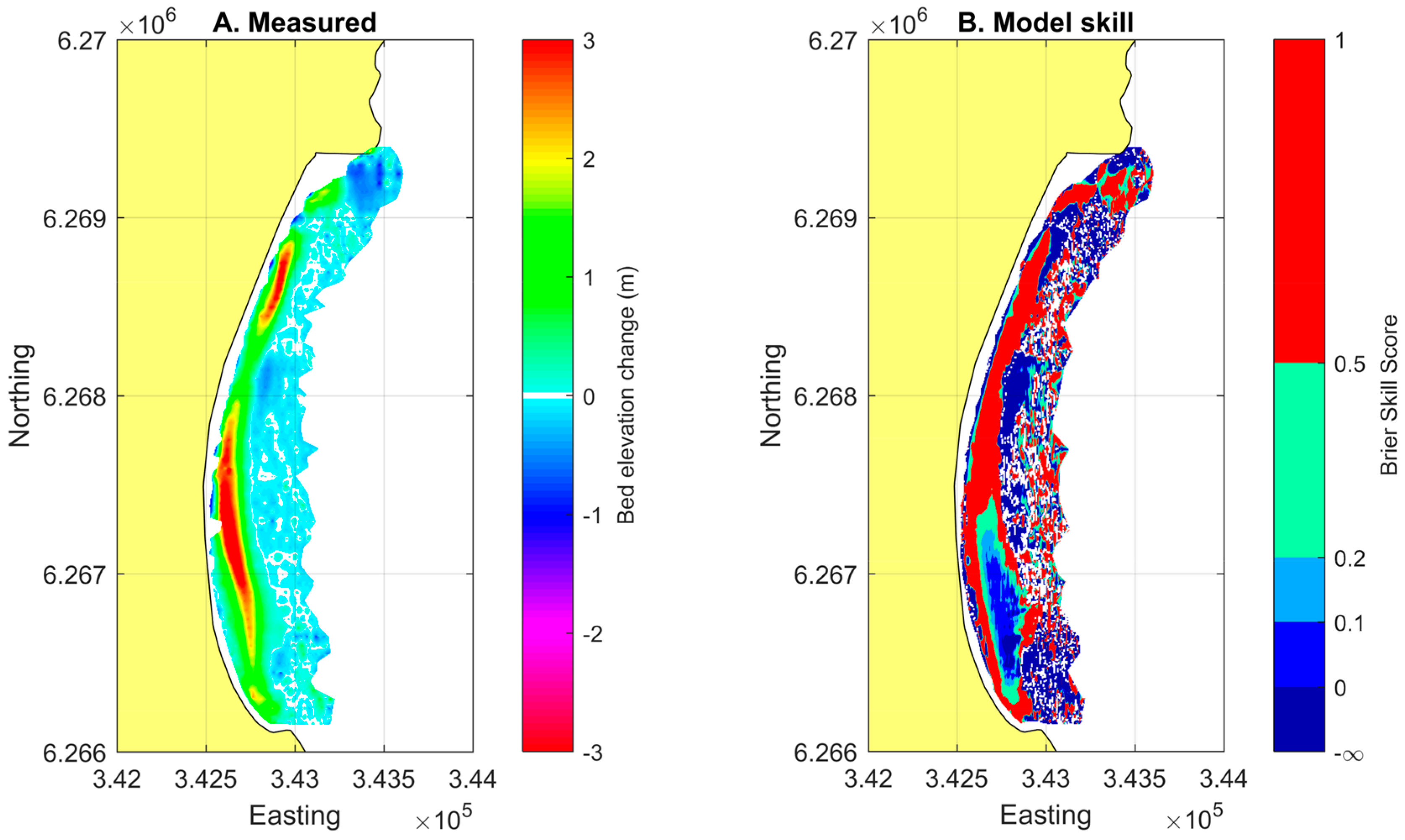
3.5. Model Verification

The wave component of the model was verified against the four months of directional, hourly wave buoy observations collected from the South Narrabeen and Long Reef nearshore wave buoys (described in Section 2.1, locations shown in Figure 3). The model showed good predictive skill for significant wave height (R2 = 0.9, slope = 0.9, at both buoy locations) and mean wave direction (R2 = 0.8, slope = 0.9) but exhibited a small positive bias in the mean wave period (1–2 s) at both buoy locations.
After calibration, the morphological model attained a median skill score across the surveyed area of 0.35, a figure considered ‘Good’ [32]. In describing the location and geometry of the surf zone storm bar, in most places the skill score exceeded 0.7, a rating considered ‘Excellent’ (Figure 4). However, morphological change at the southern end of the embayment was not well replicated. This may have been because data transmission issues at the buoy during the storm [7] meant the wave direction and period around the storm peak are interpolated values. Moreover, there was no spectral wave data available at the time of writing thus wave bi-modality was not accounted for in the model. These factors collectively may have led to an under-representation of north-easterly wave energy responsible for bar build-up at the south end of the embayment.

4. Coastal Conditions at Sydney

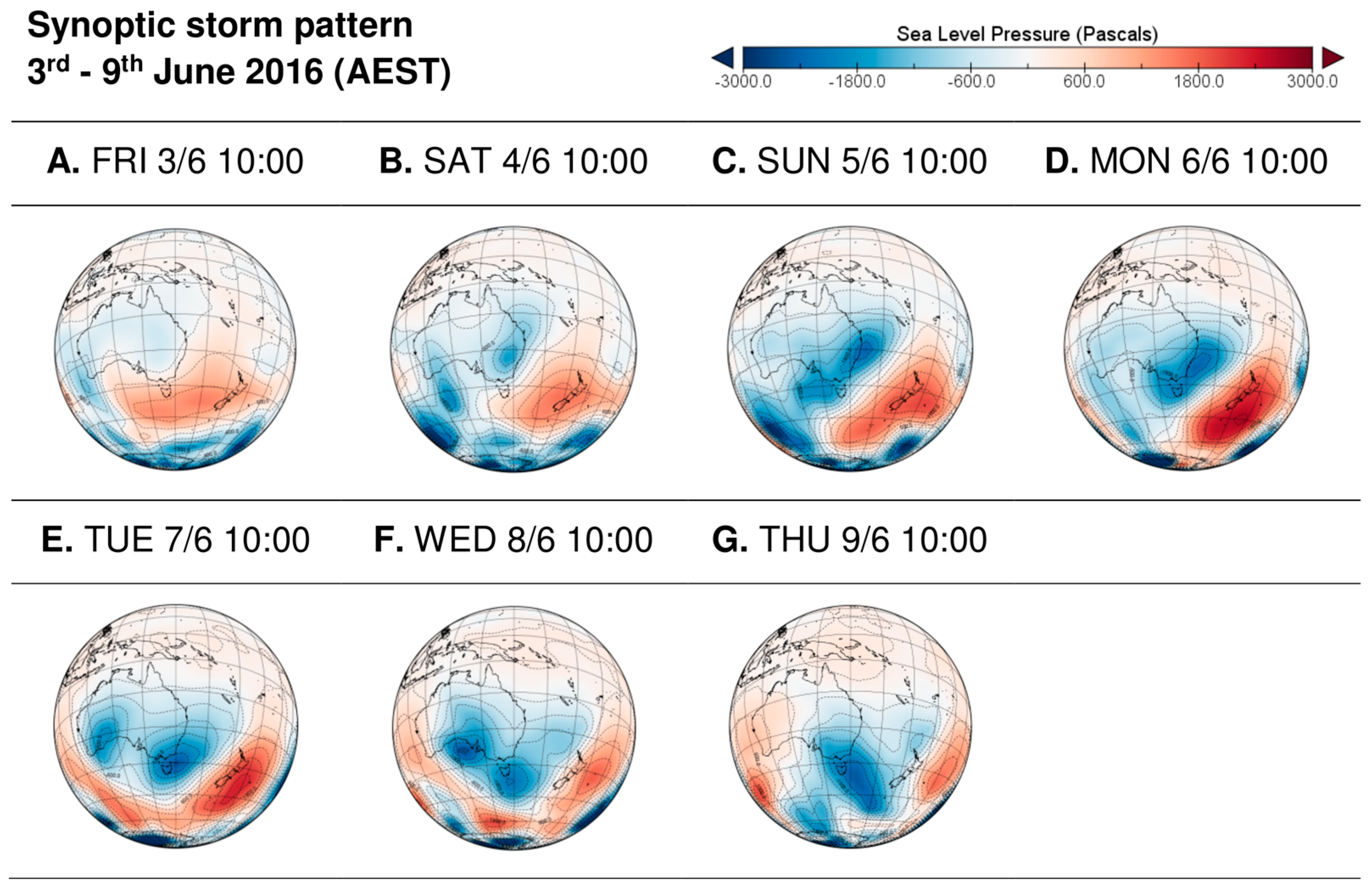
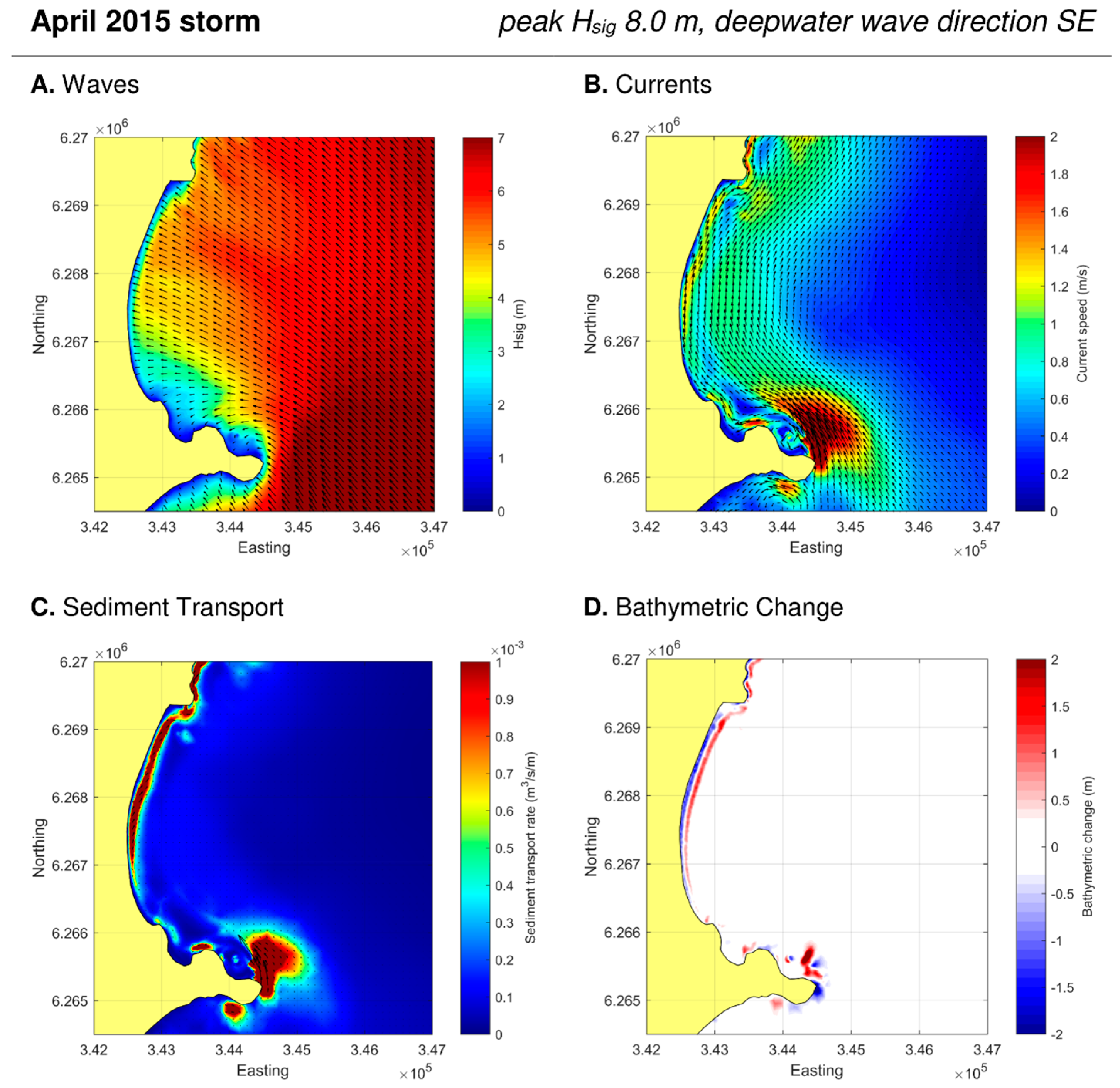
4.1. Peak Storm Conditions

Storm peak wave conditions coincided with the winter solstice spring tide, a period of strong onshore winds and heavy rainfall. Figure 5 shows the wave heights and water levels observed at Sydney during the storm. Wave period and direction and wind speed and direction observations are given in the Appendix A (Figure A1).
A maximum water level of 1.29 m Australian Height Datum (AHD) was recorded at the tide gauge at HMAS Penguin around 20:00 on 5 June, which represents an Average Recurrence Interval (ARI) of approximately 2.5 years [7]. This included a positive tidal residual of up to 0.34 m (storm surge). Water levels on the open coast would have variably been higher than this because of wave and wind set up. Modelling here suggests that maximum water levels may have exceeded 1.7 m AHD around 21:00 at Long Reef headland and North Narrabeen (comprising a ~0.6 m surge). This does not include wave run up which can easily be an order of magnitude greater than the surge component [36]. Onshore winds observed at the Kurnell weather station averaging 15 m·s−1 (~30 knots) were sustained for almost 20 h leading up to and during the storm peak, with gusts of up to 24 m·s−1 (~60 knots).
Storm wave conditions at Sydney (defined as the hourly Hs exceeding 2 m for a period of 72 h or more, after [9]) began around midday on Friday 4 June and lasted until late evening on Wednesday 8 June (106 h). A peak storm wave height (Hs) of 6.4 m was recorded at 11:00 on Sunday 5 June. Hs then remained around 6 m for the next 10 h (until 21:00), after which it began to gradually decline. Maximum wave heights (Hmax) exceeded 8 m between 06:00 on the Sunday to 03:00 the following morning peaking at 12 m at 15:00 on Sunday afternoon.
Some wave period and direction information was missing due to transmission problems at the buoy over the peak of the storm [7], but interpolated values suggest a storm peak direction (MWDTp1) of around 93°, and period (Tp1) of around 11.5 s. While the exact variation of MWDTp1 and Tp1 over the period of missing data is unknown, the interpolated values are in broad agreement with the peak direction and period of other mid-shelf wave buoys along the coast (Figure 1). As the storm intensified, the wave period at Sydney lengthened to around 14 s and the wave direction simultaneously rotated clockwise from north-east to east. Over this period, the synoptic weather pattern suggests that the deep-water wind and wave field was still north-east (Figure 6C,D).
The more easterly direction recorded at the buoy may be a result of the longer-period waves having already refracted around towards shore-normal by the time they reached the buoy location. Wave base—the depth at which surface waves begin to be influenced by the sea bed—was around 150 m, suggesting that waves had already refracted on the edge of the continental shelf far seawards of the buoy location (on the 90-m isobath).

4.2. Post Storm Conditions

As the low-pressure trough tracked south down the coast, the mean wave direction at Sydney rotated clockwise from around 70° (East–North–East) at the start of the storm to around 110° (East–South–East) by the early morning of Monday 6 June. Up until this point, buoy observations showed that wave conditions were largely uni-modal, meaning most wave energy was travelling at the same speed from the same direction. This suggests that wave conditions during the peak of the storm were generated from a single source (the low-pressure system). This can be seen in Figure A1 where wave periods and directions at the first and second spectral peaks have similar values. As the storm moved away from Sydney during Monday, the parametric wave data suggests that conditions became bi-modal as the amount of wave energy generated by the low-pressure system was replaced by longer period (Tp1–14 s) swell from the east. Figure 6D suggests that this long-period easterly swell was generated off the northern limb of the anticyclone situated over New Zealand. Long wave periods between 12 and 14 s were sustained for the following 96 h as wave heights decreased. At the same time, very oblique (southerly) waves were still being produced by the low-pressure system as it tracked south down the east coast (MWDTp2, Figure A1A).

5. The Importance of Wave Direction for Coastal Risk

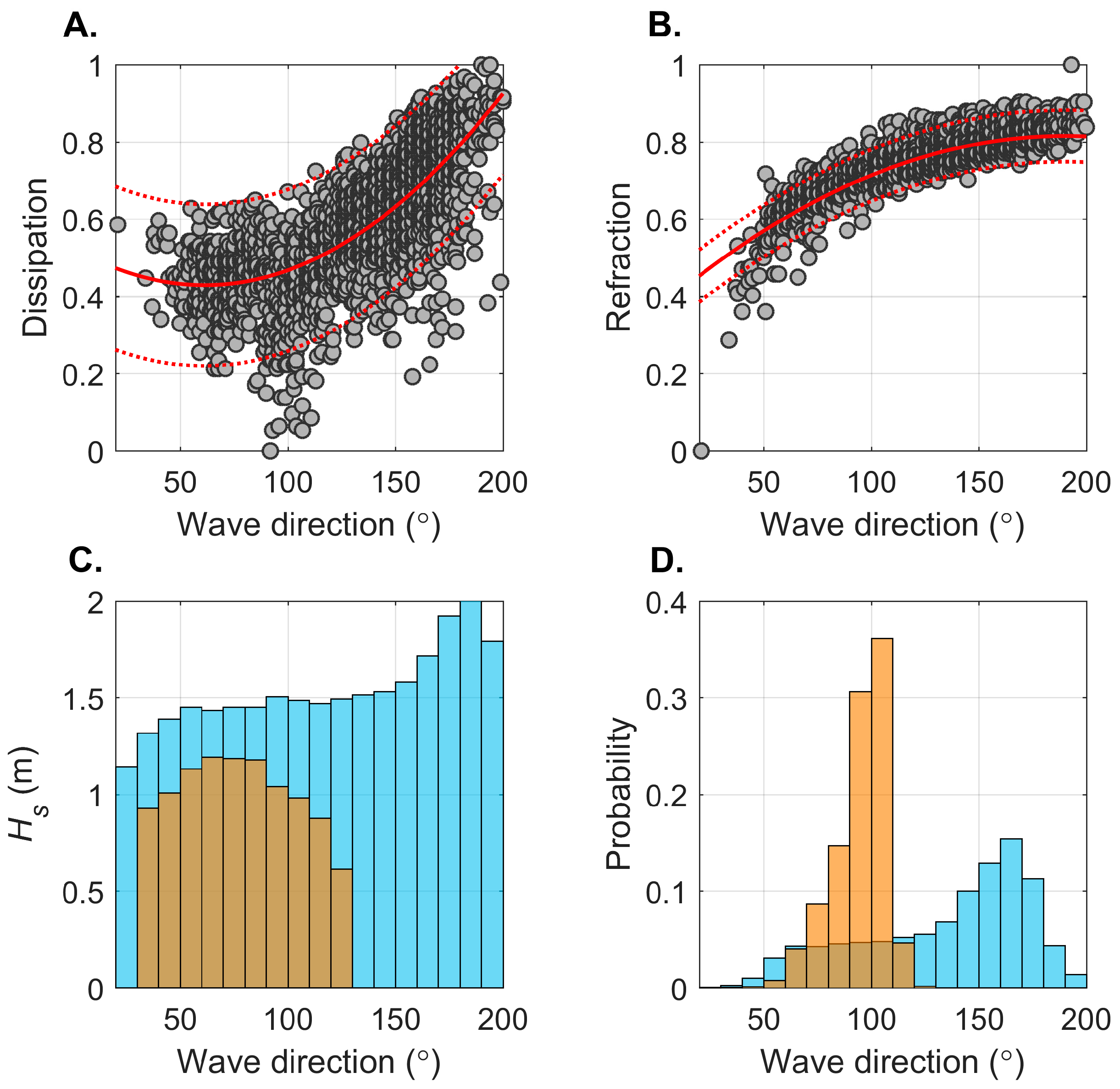
5.1. Wave Direction Control on Nearshore Wave Heights

Traditional assessments of coastal risk relate the offshore wave height to beach erosion and inundation with secondary, or no, consideration of wave direction. The June 2016 event highlighted the importance of storm wave direction for coastal impacts at Sydney. The peak storm offshore wave height (6.4 m) was unremarkable yet wave energy conditions at the coast were extra-ordinary (Figure 7).
The high-energy coastal wave conditions were a result of the unusual offshore wave direction rather than large offshore wave heights. Concurrent wave data previously recorded at the Sydney (mid-shelf) buoy and the nearshore buoy at South Narrabeen (over the period August to November 2011—not during the June 2016 storm), suggest that waves from the north-east to east undergo less energy dissipation (reduction in wave height) and refraction (change in wave direction) when travelling across the continental shelf towards the coast than do waves approaching from the south-east to south (Figure 8). The dissipation coefficients in Figure 8A were calculated as the nearshore Hs divided by the offshore Hs. Likewise, the refraction coefficients in Figure 8B were calculated as nearshore MWDTp1 divided by the offshore MWDTp1. These values were then normalized between 0 and 1 to make rates of dissipation and refraction comparable across wave directions.
Nearshore wave heights (seaward of shoaling in shallow water) are usually smaller than offshore wave heights because wave energy is dissipated across the shelf and shoreface, principally because of friction with the seabed. The South Narrabeen buoy was moored in ~12 m water depth, meaning most waves recorded at this location were only weakly shoaled and unbroken. Thus, most nearshore wave heights recorded over the observation period were lower than the offshore (mid-shelf) wave height because of energy dissipation across the shelf.
However, the rate of dissipation is often a function of wave direction. Figure 8A indicates that energy dissipation is lowest for waves from the north-east to east, and increases as the wave direction rotates towards the south. Likewise, Figure 8B shows that waves from the south-east to south undergo most refraction to reach the Sydney coast.
The dissipation and refraction coefficients (red lines Figure 8A) were applied to the entire directional wave record at the mid-shelf buoy (1992–2016) to obtain the likely long-term wave height distribution (Figure 8C) and probability of occurrence of wave directions (Figure 8D) at Narrabeen, compared to the offshore wave data. Figure 8C shows that the highest waves recorded offshore come from 160° to 190°, while the highest waves at Narrabeen (centre of embayment, ~12 m water depth) are from 70° to 90°. Similarly, Figure 8D shows that the most frequent waves offshore are from 160° to 180° while the most frequent waves at Narrabeen are from 90° to 110°.
This highlights two important points: first, that the offshore wave observations are not a good representation of the nearshore wave climate at Sydney. Second, that there is a strong directional control on coastal wave conditions at Sydney, which explains how extreme surf zone waves, as shown in Figure 7, can occur for modest offshore storm wave heights when approaching from the north-east to east.

5.2. Wave Direction Control on Nearshore Hydrodynamics

As shown above, the Sydney coast is most exposed to north-east to easterly wave energy, despite south-east to southerly waves being more powerful and frequent offshore. Modelling here shows that the geometry and aspect of the Narrabeen–Collaroy compartment further increases the vulnerability of the Collaroy beachfront to north-east to easterly storm waves because of the effect of wave direction on the nearshore hydrodynamics.
To demonstrate this, the model was run for the June 2016 storm and for another ECL event that impacted Sydney between 19 and 23 April 2015. The April 2015 event had a significantly larger peak storm wave height (Hs 8.0 m) and some of the strongest-ever winds recorded at the Kurnell weather station with gusts exceeding 130 km·h−1. It also produced a more ‘regular’ south-easterly storm wave direction (145° at the storm peak) than in June 2016. The wave refraction pattern, nearshore current field and sediment transport patterns at Narrabeen–Collaroy at the peak of the storm in April 2015 and June 2016 are shown in Figure 9A–C and Figure 10A–C, respectively. The modelled bathymetric change after each storm event is shown in Figure 9D and Figure 10D.
The modelled flow and transport pattern in June 2016 was very different. The easterly nearshore wave direction produced a southward, rather than northward, alongshore current for almost all beaches on Sydney’s Northern Beaches. The only exception to this regional pattern was the Long Reef to Collaroy coastal section where a strong northward littoral current exceeding 2 ms−1 at the peak of the storm occurred (Figure 10B). This current met a powerful southward current around Collaroy/South Narrabeen, which the model suggests produced an offshore-directed mega-rip extending out to ~20 m water depth offshore of Collaroy. This current then deflected south and re-entered the surf zone at Long Reef forming a large rip cell.
The positioning of rip currents is well known to correspond to ‘erosion hot spots’, as the offshore-directed flow scours a trough, lowering the beach level and leaving adjacent dunes (and property) more exposed to storm wave erosion. Figure 11 illustrates how the positioning of the modelled mega-rip current during the peak of the June storm aligns with locations of observed erosion damage. The northward-directed flow between Long Reef and Collaroy was unique within the Northern Beaches region because of the eastward extension of Long Reef headland, which bifurcated the wave-driven current south towards the neighbouring embayment, DeeWhy, and north towards Collaroy.
The modelled littoral flow velocities, sediment transport rates and volumes of offshore sand movement at Narrabeen–Collaroy were all greater in June 2016 than April 2015, despite significantly lower offshore wave heights in 2016. Long-term beach monitoring [15] also shows that the 2016 storm led to the largest eroded subaerial beach volume at Narrabeen–Collaroy since recording began in 1976. Erosion of the subaerial beach was not explicitly modelled here because of insufficient information on the pre-storm beach condition. On the other hand, the amount of sand moved below the water line within the surf zone is a robust indicator of erosion to the subaerial beach, since the surf zone and beach morphologies at Narrabeen are closely coupled [40]. The same starting bathymetry was used for both storm events, meaning any differences in post-storm surf zone bathymetry are primarily a result of nearshore wave conditions during the two storms.
Our modelling suggests that in April 2015 the surf-zone bar accreted by approximately 90,500 m3 (an average of ~25 m3 per m of alongshore length) compared to an accretion of approximately 205,000 m3 (~60 m3 per m of alongshore length) in June 2016. The ‘bar’ was defined as any positive post-storm cumulative bed elevation change over 0.3 m on the upper shoreface. These volumes may not reflect the actual change because of several factors not included in the model as discussed in Section 3. Moreover, not all sand that forms the storm bar comes from the beach. Some sand is also moved from depths seaward of the surf zone because of wave asymmetry leading to a net shoreward transport in depths where there are no breaking waves or undertow [41,42,43]. The ratio between the offshore/onshore sources depends on the dominance of alongshore or cross-shore transport, which in turn depends on the storm wave direction. Our modelling indicates that during April 2015 over 95% of sand that formed the storm bar originated from the beach, whereas in June 2016 around 85% came from the beach and the remainder from onshore transport outside the surf zone.
The beach monitoring program at Narrabeen shows a slightly lower but comparable ~40% difference between the amount of subaerial beach erosion in June 2016 and April 2015. This is based on the Subaerial Beach Volume Index (SVI), a ratio of the dry beach volume relative to the long-term mean [15]. Prior to the April 2015 event, the beach was close to the mean state (SVI + 2.6), but after the storm it had been reduced to −24.9 (a net change of 27.5). Prior to the June 2016 event, the early winter was characterised by a period of quiescent, southerly waves that had acted to considerably build up the beach (+13.6). After the storm, the beach was down to its lowest SVI value recorded (−34.0)—a net change of 47.6 (thus, a ~40% difference between the April 2015 and June 2016 storms). While this is not directly comparable to the ~50% difference derived from modelling in this study (the monitoring is of the subaerial beach while the modelling is of the subaqueous shoreface), it serves to highlight the magnitude differences in the erosion impacts between the events and is broadly in agreement with the modelled shoreface change.
Bathymetric surveys at Narrabeen (Section 3) and well as the modelling here indicate that sand removed from the subaerial beach during storms does not leave the embayment. Narrabeen and other embayments along the central and south coast of NSW are known to be essentially ‘closed’ each with a finite sediment budget [44]. Most sand during a storm is transferred down the upper shoreface to around 4–5 m water depth, after which it is progressively reworked shoreward during subsequent non-storm wave conditions. This loss/recovery cycle can be seen in the long-term beach monitoring record at Narrabeen, which shows no significant net change in the subaerial beach volume over the past 40 years [15]. Indeed, previous analyses of the Narrabeen record highlight the importance of time intervals between successive storms in allowing the post-storm recovery of the beach [45,46]. While the beach may recover after a storm, erosion to the foredune and damage sustained to property is lasting.

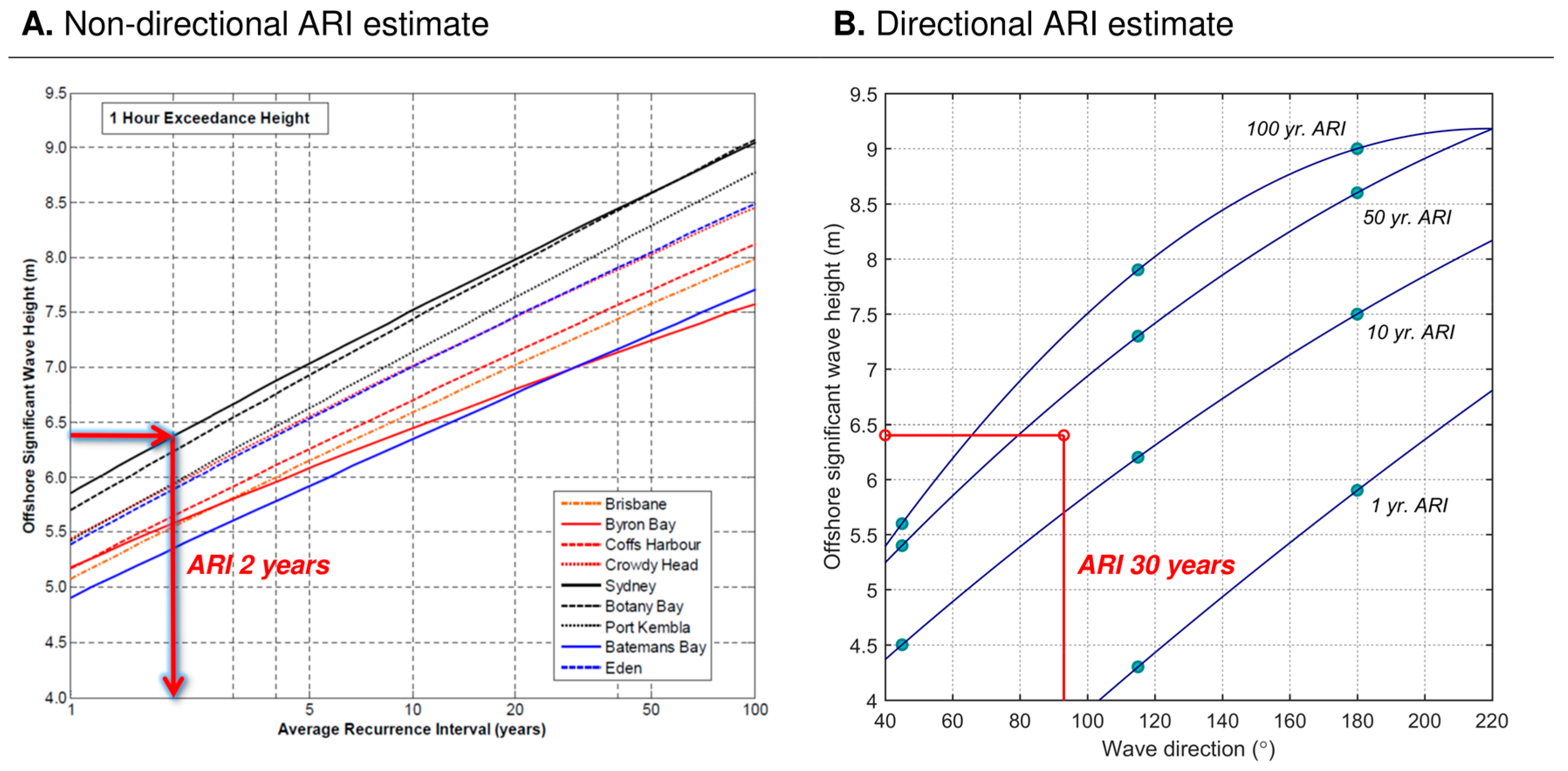
5.3. Wave Direction Control on Recurrence Estimates

Estimates of the return period, or Average Recurrence Interval (ARI), of storm wave conditions are usually derived from an extreme value analysis of storm peak wave heights from a long-term set of observations. Since wave height is the most important design parameter for coastal engineering, ARI estimates are traditionally non-directional; i.e., one extreme value curve is used for storm wave conditions from all directions. Per this approach, the ARI estimate for the June 2016 event is only ~2 years (Figure 12A). However, this estimate is misleading because the powerful inshore wave conditions generated by this event were far greater than that seen on average every two years.
A more relevant ARI of the June 2016 storm needs to consider wave direction. Shand et al. [47] re-examined ARI estimates at Sydney (up to 2009) for storm waves coming from three directional quadrants; <90° (north-east to east), 90°–135° (south-east), and >135° (south-east to south). We interpolated these results across directional bins (using a second-order polynomial) to obtain an indication of the ARI of peak storm wave heights across all wave directions (Figure 12B). Indicative results here suggest that the June 2016 peak storm conditions (6.4 m Hs from 93°) have an ARI of approximately 30 years when wave direction is considered. It is important to note that this estimate is derived from only 17 years of directional wave data (1992–2009, yet to be updated), which is not considered sufficient for reliable extreme value analysis on the NSW coast [7]. Nonetheless, it serves to demonstrate the importance of accounting for wave direction when estimating the likelihood of recurrence of storm wave conditions. Incorporating wave directional effects into extreme value analyses can significantly affect the design of coastal structures [48,49], especially when projecting future extreme conditions where there may be shifts in the directional wind and wave climate [50,51].

6. Implications for Coastal Management in a Changing Climate

The June 2016 East Coast Low was an unusual storm, both in terms of the synoptic configuration and wave conditions. However, storm wave events from this direction are projected to become more common in Southeast Australia in the future with tropical expansion [6]. One of the most robust signatures of present and near-future climate warming is a widening of the tropics, with a continued poleward expansion of ~1° to 2° projected for later this century [52]. This tropical expansion may lead to an increased frequency of easterly and north-easterly waves along the Southeast Australian coast [51] and, as a result, the regional wave climate is predicted to rotate anticlockwise [50].
It is unclear, however, whether this will be manifest in both the modal and storm wave climate, or whether tropical expansion will lead to an increase in bi-directionality between extreme wave events and the mean state. Currently, there is a ~10° difference between the long-term (past 40 years) modal and storm wave directions along the NSW coast, meaning beach systems are largely equilibrated with the distribution of wave energy during and between storms. However, when extreme wave events come from different directions to modal conditions, the erosion response is magnified. The June 2016 storm exemplified this, as the east to north-east wave conditions followed several months of quiescent southerly swell.
At present, the minimum criteria for estimating current and future rates of shoreline recession in coastal zone management plans in NSW include recession due to sediment budget deficits and projected sea level rise [53]. The requirements for beach erosion revolve around a storm bite magnitude arising from an event with an ARI of ~100 years [53]. The requirements for both shoreline recession and beach erosion ignore potential changes in wave direction. An allowance for beach rotation (resulting from inter-annual changes in wave direction associated with El Niño Southern Oscillation) is usually included, but this does not address the control that long-term changes in storm wave direction may have on the propagation of wave energy into the nearshore and, as demonstrated here and in previous studies [54,55], on coastal erosion response. Neither does it address the significant influence that wave direction has on the return period estimates of storm events and their resultant erosion potential.

7. Conclusions

The June 2016 East Coast Low storm demonstrates the importance of wave direction for coastal impacts in Southeast Australia. Our modelling shows that the direction of wave propagation across the shelf was the primary control on the amount of energy in the nearshore, rather than the magnitude of storm wave conditions offshore. Dissipation and refraction coefficients derived from simultaneous offshore and nearshore buoy observations also illustrate the importance of wave direction on the nearshore distribution of wave heights and indicate that the offshore wave record alone is a misleading proxy for erosion risk. Hydrodynamic modelling suggests that the Collaroy to South Narrabeen coastal section is particularly vulnerable to erosion impacts during storms from the east to north-east because of the local embayment geometry. A re-assessment of extreme wave heights at Sydney also demonstrates the importance of considering wave direction when deriving storm recurrence parameters for coastal engineering.
Both observational and climate model based studies suggest an anti-clockwise rotation in the mean wave direction for the South-West Pacific region over the coming decades in association with a poleward expansion of the tropics. It is unclear, however, whether these changes will lead to an increase in bi-directionality between the extreme and mean wave climate. As demonstrated in June 2016, the coastal erosion response is magnified when the modal and storm wave directions are different. Assessments of erosion risk in Southeast Australia do not yet consider impacts of future changes to the directional wave climate. This is symptomatic of the global emphasis on sea level rise over wave climate change, and should be identified as an important knowledge gap for coastal management. Our findings are also of relevance for other Southern Hemisphere east coasts in the sub-tropics, such as the Southern Brazil and Natal to Mozambique regions, where tropical expansion may lead to similar changes in the directional wave climate.

Acknowledgments

This research was part funded by a NSW Office for Environment and Heritage (OEH) grant to CI Goodwin as part of the OEH/Sydney Institute of Marine Science (SIMS), Coastal Processes and Response Research Node (Grant Project 1A Quantification of Sand Supply from the NSW Shoreface). Nearshore wave data from buoys deployed at South Narrabeen and Long Reef were collected as part of an Australian Research Council Linkage Project (grant number LP100200348). Wave data from these deployments are available on request from the authors. Wave data from waverider buoys in New South Wales (NSW) and tidal data from the HMAS Penguin tide gauge are collected as part of the NSW Coastal Data Network Program managed by the Office of Environment and Heritage (OEH) and was sourced from Manly Hydraulic Laboratory. Wave data from the Brisbane waverider buoy is funded by State of Queensland, Department of Science, Information Technology, Innovation and the Arts and is available from https://data.qld.gov.au/dataset/coastal-data-system-waves-brisbane. Wind data from the Kurnell automatic weather station was sourced from the Bureau of Meteorology. Beach profile information from the long-term monitoring program at Narrabeen–Collaroy beach was sourced from http://narrabeen.wrl.unsw.edu.au. Pre- and post-storm hydrographic surveys of Narrabeen–Collaroy beach were undertaken by OEH for the OEH/SIMS Coastal Processes and Response Research Node of the NSW Climate Change Adaptation Hub. All other bathymetric data used for modelling was obtained on request from OEH. A Macquarie University academic licence for MIKE by DHI software was used for modelling. Permission for reproduction of images of wave conditions in Figure 7 was kindly given by the photographer Mark Onorati for use in this publication only. Rights of reproduction of images of coastal damage in Figure 11 was purchased by Risk Frontiers from Australian Associated Press under a Multimedia Commercial Use agreement. The authors also thank the anonymous reviewers of this paper whose comments significantly improved the quality of the manuscript.

Author Contributions

All authors jointly conceived the idea for the paper; Thomas R. Mortlock performed all data analysis and modelling; Thomas R. Mortlock wrote the bulk of the paper; Ian D. Goodwin and Thomas R. Mortlock made observations of the storm meteorology, nearshore wave conditions and coastal impacts; Ian D. Goodwin, Kevin Roche and John K. McAneney made substantial edits to the final draft of the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Water 09 00121 g013 550
Figure A1. Observations of (A) mean wave direction at the first and second spectral peaks (MWDTp1 and MWDTp2); (B) wave period at the first and second spectral peaks (Tp1 and Tp2); and (C) wind speed (u) and direction (dir) from 3 to 10 June 2016. Wave data was recorded at the Sydney waverider buoy and wind data was recorded at the Kurnell Automatic Weather Station (locations Figure 3).
Figure A1. Observations of (A) mean wave direction at the first and second spectral peaks (MWDTp1 and MWDTp2); (B) wave period at the first and second spectral peaks (Tp1 and Tp2); and (C) wind speed (u) and direction (dir) from 3 to 10 June 2016. Wave data was recorded at the Sydney waverider buoy and wind data was recorded at the Kurnell Automatic Weather Station (locations Figure 3).
Water 09 00121 g013
Water 09 00121 g014 550
Figure A2. Wave age curves derived from all Hs and Tp1 values recorded at the Sydney waverider buoy (1987–2016). Grey crosses represent unique wave steepness occurrences at the buoy and circles represent wave conditions as measured during the June 2016 storm. The red line represents the Pierson–Moskowitz limit for fully-developed seas [56]; the green line represents the wave age limit between wind-sea and swell [57]; and the blue line is a line of constant steepness that divides the sea and swell components into two equal parts [24]. All wave events falling between the red and blue lines are ‘wind-sea’; between the blue and green lines are ‘intermediate sea-swell’; and beyond the green line are ‘swell’. In this way, the long-term wave climate defines the divisions between wave types. Values for directional spreading of parametric wave data can then be defined (Section 3.2).
Figure A2. Wave age curves derived from all Hs and Tp1 values recorded at the Sydney waverider buoy (1987–2016). Grey crosses represent unique wave steepness occurrences at the buoy and circles represent wave conditions as measured during the June 2016 storm. The red line represents the Pierson–Moskowitz limit for fully-developed seas [56]; the green line represents the wave age limit between wind-sea and swell [57]; and the blue line is a line of constant steepness that divides the sea and swell components into two equal parts [24]. All wave events falling between the red and blue lines are ‘wind-sea’; between the blue and green lines are ‘intermediate sea-swell’; and beyond the green line are ‘swell’. In this way, the long-term wave climate defines the divisions between wave types. Values for directional spreading of parametric wave data can then be defined (Section 3.2).
Water 09 00121 g014

References

  1. Crompton, R.P.; McAneney, K.J. Normalised Australian insured losses from meteorological hazards: 1967–2006. Environ. Sci. Policy 2008, 1, 371–378. [Google Scholar] [CrossRef]
  2. McAneney, J.; McAneney, D.; Musulin, R.; Walker, G.; Crompton, R. Government-sponsored natural disaster insurance pools: A view from down-under. Int. J. Disaster Risk Reduct. 2006, 15, 1–9. [Google Scholar] [CrossRef]
  3. Taljaard, J.J. Atmospheric Circulation Systems, Synoptic Climatology and Weather Phenomena of South Africa. Part 2: Atmospheric Circulation Systems in the South African Region; Department of Environmental Affairs and Tourism, South Africa, Report No. 27-32; South African Weather Bureau: Pretoria, South Africa, 1995. [Google Scholar]
  4. Cuchiara, D.C.; Fernandes, E.H.; Strauch, J.C.; Winterwerp, J.C.; Calliari, L.J. Determination of the wave climate for the southern Brazilian shelf. Cont. Shelf Res. 2009, 29, 545–555. [Google Scholar] [CrossRef]
  5. Browning, S.; Goodwin, I.D. Large-Scale Influences on the Evolution of Winter Subtropical Maritime Cyclones Affecting Australia’s East Coast. Mon. Weather Rev. 2013, 141, 2416–2431. [Google Scholar] [CrossRef]
  6. Goodwin, I.D.; Mortlock, T.R.; Browning, S. Tropical and Extratropical-Origin Storm Wave Types and Their Contrasting Directional Power Distribution on the Inner Shelf. J. Geophys. Res. Oceans 2016, 121, 4833–4853. [Google Scholar] [CrossRef]
  7. Louis, S.; Couriel, E.; Lewis, G.; Glatz, M.; Kulmar, M.; Golding, J.; Hanslow, D. NSW East Coast Low Event—3 to 7 June 2016 Weather, Wave and Water Level Matters. In Proceedings of the NSW Coastal Conference, Coffs Harbour, Australia, 9–11 November 2016.
  8. International Hydrographic Organization (IHO). Limits of Oceans and Seas; International Hydrographic Organization: Bremerhaven, Germany, 1953. [Google Scholar]
  9. Shand, T.D.; Goodwin, I.D.; Mole, M.A.; Carley, J.T.; Browning, S.; Coghlan, I.; Harley, M.D.; Pierson, W.J. NSW Coastal Inundation Hazards Study: Coastal Storms and Extreme Waves; Water Research Laboratory (WRL) & Climate Futures at Macquarie University, WRL Technical Report 2010/16; University of New South Wales: Sydney, Australia, 2011. [Google Scholar]
  10. Short, A.D. Role of geological inheritance in Australian beach morphodynamics. Coast. Eng. 2010, 57, 92–97. [Google Scholar] [CrossRef]
  11. Wright, L.D.; Short, A.D. Morphodynamic Variability of Surf Zones and Beaches: A Synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
  12. Rosati, J.D.; Walton, T.L.; Bodge, K. Chapter III-2 Longshore Sediment Transport. In Coastal Engineering Manual, Part III; Vincent, L., Demirbilek, Z., Eds.; U.S. Army Corp of Engineers: Washington, DC, USA, 2002; pp. III-2-1–III-2-109. [Google Scholar]
  13. Splinter, K.D.; Turner, I.L.; Reinhardt, M.; Ruessink, G. Rapid adjustment of shoreline behavior to changing seasonality of storms: Observations and modelling at an open-coast beach. Earth Surf. Process. Landf. 2017. [Google Scholar] [CrossRef]
  14. Poli, P.; Hersbach, H.; Dee, D.P.; Berrisford, P.; Simmons, A.J.; Vitart, F.; Laloyaux, P.; Tan, D.G.H.; Peubey, C.; Thépaut, N.; et al. ERA-20C: An Atmospheric Reanalysis of the Twentieth Century. J. Clim. 2016, 29, 4083–4097. [Google Scholar] [CrossRef]
  15. Turner, I.L.; Harley, M.D.; Short, A.D.; Simmons, J.A.; Bracs, M.A.; Phillips, M.S.; Splinter, K.D. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data 2016, 3, 160024. [Google Scholar] [CrossRef] [PubMed]
  16. Short, A.D.; Bracs, M.A.; Turner, I.L. Beach oscillation and rotation: Local and regional response on three beaches in southeast Australia. J. Coast. Res. 2014, 66, 712–717. [Google Scholar] [CrossRef]
  17. Bracs, M.; Turner, I.L.; Splinter, K.D.; Short, A.D.; Mortlock, T.R. Synchronised patterns of erosion and deposition observed at two beaches. Mar. Geol. 2016, 380, 196–204. [Google Scholar] [CrossRef]
  18. Nielsen Lord Associates. Narrabeen-Collaroy Fishermans Beach Coastal Management Strategy, Phase One: Hazard Definition; Nielsen Lord Associates Report No. 87020.01.003; Prepared for Warringah Shire Council; Wavelength Press: Sydney, Australia, 1988; p. 17. [Google Scholar]
  19. Roche, K.; Goodwin, I.D.; McAneney, J. Management of the coastal zone in Bryon Bay: The neglect of medium-term considerations. Agenda 2013, 20, 21–39. [Google Scholar]
  20. Wood, J.E.; Roughan, M.; Tate, P.M. Finding a proxy for wind stress over the coastal ocean. Mar. Freshw. Res. 2012, 63, 528–544. [Google Scholar] [CrossRef]
  21. Holtznagel, S.; Ingleton, T. Field Survey QAQC for Sydney Northern Beaches—Narrabeen Beach Hydro June 2016. In Single-Beam QAQC Metadata Sheet; NSW Office of Environment and Heritage: Sydney, Australia, 2016. [Google Scholar]
  22. Danish Hydraulics Institute (DHI). MIKE21/3 Coupled Model FM User Guide; MIKE by DHI; Danish Hydraulics Institute: Hørsholm, Denmark, 2016. [Google Scholar]
  23. Cardno. NSW Coastal Waves: Numerical Modelling Final Report; Cardno Report No. LJ2949/R2745; Prepared for Office of Environment and Heritage (NSW); Cardno: St Leonards, Australia, 2012; p. 281. [Google Scholar]
  24. Le Cozannet, G.; Lecacheux, S.; Delvallee, E.; Desramaut, N.; Oliveros, C.; Pedreros, R. Teleconnection Pattern Influence on Sea-Wave Climate in the Bay of Biscay. J. Clim. 2011, 24, 641–652. [Google Scholar] [CrossRef]
  25. Goodwin, I.D.; Mortlock, T.R.; Ribó, M.; O’Brien, P. Wave Climate and the Distribution of Inner to Middle Shelf Sand Bodies on the South-Eastern Australian Shelf; Prepared for NSW Office of Environment and Heritage; Marine Climate Risk Group, Macquarie University: Sydney, Australia, 2017. [Google Scholar]
  26. McCormick, M.I. Comparison of field methods for measuring surface topography and their associations with a tropical reef fish assemblage. Mar. Ecol. Prog. Ser. 1994, 112, 87–94. [Google Scholar] [CrossRef]
  27. Lowe, R.J.; Falter, J.L.; Bandet, M.D.; Pawlak, G.; Atkinson, M.J.; Monismith, S.G.; Koseff, J. Spectral wave dissipation over a barrier reef. J. Geophys. Res. 2005, 110, C04001. [Google Scholar] [CrossRef]
  28. Thornton, E.B.; Guza, R.T. Transformation of wave height distribution. J. Geophys. Res. 1983, 88, 5925–5938. [Google Scholar] [CrossRef]
  29. Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific: Singapore, 1992; Volume 4. [Google Scholar]
  30. Huang, Z.-C.; Lenain, L.; Kendall Melville, W.; Middleton, J.H.; Reineman, B.; Statom, N.; McCabe, R.M. Dissipation of wave energy and turbulence in a shallow coral reef lagoon. J. Geophys. Res. 2012, 117, C03015. [Google Scholar] [CrossRef]
  31. Weber, N. Bottom Friction for Wind Sea and Swell in Extreme Depth-Limited Situations. J. Phys. Oceanogr. 1991, 21, 149–172. [Google Scholar] [CrossRef]
  32. Sutherland, J.; Peet, A.H.; Soulsby, R.L. Evaluating the performance of morphological models. Coast. Eng. 2004, 51, 917–939. [Google Scholar] [CrossRef]
  33. Sedigh, M.; Tomlinson, R.; Cartwright, N.; Etemad-Shahidi, A. Numerical modelling of the Gold Coast Seaway area hydrodynamics and littoral drift. Ocean Eng. 2016, 121, 47–61. [Google Scholar] [CrossRef]
  34. Doering, J.C.; Bowen, A.J. Parameterization of orbital velocity asymmetries of shoaling and breaking waves using bispectral analysis. Coast. Eng. 1995, 26, 15–33. [Google Scholar] [CrossRef]
  35. Isobe, M.; Horikawa, K. Study on water particle velocities of shoaling and breaking waves. Coast. Eng. Jpn. 1982, 25, 109–123. [Google Scholar]
  36. Morris, B.; Foulsham, E.; Laine, R.; Wiecek, D.; Hanslow, D. Evaluation of Runup Characteristics on the NSW Coast. J. Coast. Res. 2016, 75, 1187–1191. [Google Scholar] [CrossRef]
  37. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
  38. Onorati, M. Images of Coastal Wave Conditions at South Narrabeen during the June 2016 Storm. Images taken 06/06/16 Reproduced with Permission from M. Onorati for This Publication Only. Available online: https://www.instagram.com/markonorati/ (accessed on 5 November 2016).
  39. Australian Associated Press (AAP). Images of Coastal Erosion Damage at South Narrabeen During the June 2016 Storm; Images Taken 07/06/16; Image ID 20160607001262647757 and 20160607001262620563, Purchased under Commercial Agreement by Risk Frontiers 02/12/16; Australian Associated Press: Sydney, Australia, 2016. [Google Scholar]
  40. Harley, M.D.; Turner, I.L.; Short, A.D. New insights into embayed beach rotation: The importance of wave exposure and cross-shore processes. J. Geophys. Res. Earth Surf. 2015, 120, 1470–1484. [Google Scholar] [CrossRef]
  41. Patterson, D.C.; Nielsen, P. Depth, bed slope and wave climate dependence of long term average sand transport across the lower shoreface. Coast. Eng. 2016, 117, 113–125. [Google Scholar] [CrossRef]
  42. O’Donoghue, T.; Wright, S. Flow tunnel measurements of velocities and sand flux in oscillatory sheet flow for well-sorted and graded sands. Coast. Eng. 2004, 51, 1163–1184. [Google Scholar] [CrossRef]
  43. Ruessink, B.G.; Michallet, H.; Abreu, T.; Sancho, F.; Van der A, D.A.; Van der Werf, J.J.; Silva, P.A. Observations of velocities, sand concentrations, and fluxes under velocity-asymmetric oscillatory flows. J. Geophys. Res. Oceans 2011, 116, 2156–2202. [Google Scholar] [CrossRef]
  44. Short, A.D. Beaches of the New South Wales Coast: A Guide to Their Nature, Characteristics, Surf and Safety, 2nd ed.; Sydney University Press: Sydney, Australia, 2007. [Google Scholar]
  45. Callaghan, D.P.; Nielsen, P.; Short, A.; Ranasinghe, R. Statistical simulation of wave climate and extreme beach erosion. Coast. Eng. 2008, 55, 375–390. [Google Scholar] [CrossRef]
  46. Karunarathna, H.; Pender, D.; Ranasinghe, R.; Short, A.D.; Reeve, D.E. The effects of storm clustering on beach profile variability. Mar. Geol. 2014, 348, 103–112. [Google Scholar] [CrossRef]
  47. Shand, T.; Mole, M.A.; Carley, J.T.; Peirson, W.L.; Cox, R.J. Coastal Storm Data Analysis: Provision of Extreme Wave Data for Adaptation Planning; Water Research Laboratory (WRL) Technical Report 2011/242; University of New South Wales: Sydney, Australia, 2011. [Google Scholar]
  48. Jonathon, P.; Ewans, K. The effect of directionality on extreme wave design criteria. Ocean Eng. 2007, 34, 1977–1994. [Google Scholar] [CrossRef]
  49. Thompson, P.; Cai, Y.; Reeve, D.; Stander, J. Automated threshold selection methods for extreme wave analysis. Coast. Eng. 2009, 10, 1013–1021. [Google Scholar] [CrossRef]
  50. Hemer, M.A.; Fan, Y.; Mori, N.; Semedo, A.; Wang, X.L. Projected changes in wave climate from a multi-model ensemble. Nat. Clim. Chang. 2013, 3, 471–476. [Google Scholar] [CrossRef]
  51. Mortlock, T.R.; Goodwin, I.D. Directional wave climate and power variability along the Southeast Australian shelf. Cont. Shelf Res. 2015, 98, 36–53. [Google Scholar] [CrossRef]
  52. Lucas, C.; Timbal, B.; Nguyen, H. The expanding tropics: A critical assessment of the observational and modeling studies. WIREs Clim. Chang. 2014, 5, 89–112. [Google Scholar] [CrossRef]
  53. Office of Environment and Heritage (OEH). Guidelines for Preparing Coastal Zone Management Plans; Report No. OEH 2013/0224; Office of Environment and Heritage: Sydney, Australia, 2013; p. 26. [Google Scholar]
  54. Splinter, K.D.; Davidson, M.A.; Golshani, A.; Tomlinson, R. Climate controls on longshore sediment transport. Cont. Shelf Res. 2012, 48, 146–156. [Google Scholar] [CrossRef]
  55. Zacharioudaki, A.; Reeve, D.E. Shoreline evolution under climate change wave scenarios. Clim. Chang. 2011, 108, 73–105. [Google Scholar] [CrossRef]
  56. Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of A.A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
  57. Carter, D.J.T. Prediction of wave height and period for a constant wind velocity using the JONSWAP results. Ocean. Eng. 1982, 9, 17–33. [Google Scholar] [CrossRef]
Water 09 00121 g001 550
Figure 1. Map of the Tasman and Coral Seas region with locations of waverider buoys in Southeast Australia (red circles). The Tasman Sea borders the east coast of Australia, and extends west to New Zealand. It extends north to where it meets the Coral Sea at approximately 30° S [8]. The peak storm hourly significant wave height, mean wave direction, and time of peak storm wave conditions during the June 2016 event, are given for each buoy location. The Batemans Bay buoy data transmission failed during the event [7]. Red arrows illustrate peak storm wave direction. Mean wave direction (range of averages for all buoys over portions of records having directional observations) is also shown. Inset shows the study region in relation to the Pacific Basin.
Figure 1. Map of the Tasman and Coral Seas region with locations of waverider buoys in Southeast Australia (red circles). The Tasman Sea borders the east coast of Australia, and extends west to New Zealand. It extends north to where it meets the Coral Sea at approximately 30° S [8]. The peak storm hourly significant wave height, mean wave direction, and time of peak storm wave conditions during the June 2016 event, are given for each buoy location. The Batemans Bay buoy data transmission failed during the event [7]. Red arrows illustrate peak storm wave direction. Mean wave direction (range of averages for all buoys over portions of records having directional observations) is also shown. Inset shows the study region in relation to the Pacific Basin.
Water 09 00121 g001
Water 09 00121 g002 550
Figure 2. Composite sea level pressure (SLP) anomaly (in hectopascals, hPa) for all east-northeast Anticyclonic Intensification (AI)/Easterly Trough Low (ETL) storm wave events since 1974, using events identified from buoy records in Shand et al. [9], and the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA 20th Century reanalysis (ERA-20C) [14]. The composite anomaly was calculated relative to the ERA-20C long-term mean (1900–2010).
Figure 2. Composite sea level pressure (SLP) anomaly (in hectopascals, hPa) for all east-northeast Anticyclonic Intensification (AI)/Easterly Trough Low (ETL) storm wave events since 1974, using events identified from buoy records in Shand et al. [9], and the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA 20th Century reanalysis (ERA-20C) [14]. The composite anomaly was calculated relative to the ERA-20C long-term mean (1900–2010).
Water 09 00121 g002
Water 09 00121 g003 550
Figure 3. (A) Regional map showing approximate extents of numerical model domain (black box); locations of nearshore wave buoys (red); location of Sydney wave buoy (yellow); and locations of tide and wind stations used in this study (blue); and (B) local map of Narrabeen–Collaroy beach with bathymetry (5, 15 and 30 m isobaths in red); locations of nearshore wave buoys shown in (A); and approximate area of erosion damage at Collaroy during the June 2016 storm (yellow box).
Figure 3. (A) Regional map showing approximate extents of numerical model domain (black box); locations of nearshore wave buoys (red); location of Sydney wave buoy (yellow); and locations of tide and wind stations used in this study (blue); and (B) local map of Narrabeen–Collaroy beach with bathymetry (5, 15 and 30 m isobaths in red); locations of nearshore wave buoys shown in (A); and approximate area of erosion damage at Collaroy during the June 2016 storm (yellow box).
Water 09 00121 g003
Water 09 00121 g004 550
Figure 4. Measured morphological change (in metres) during the June 2016 storm event (A) and model skill in replicating observed change (B). The pre- and post-storm surveys in (A) extend from ~2 m to ~15 m water depth. The colour scheme in (B) reflects the Brier skill assessment of [32]. Morphological change within the vertical error of the surveyed data (±0.03, [21]) was omitted from both plots.
Figure 4. Measured morphological change (in metres) during the June 2016 storm event (A) and model skill in replicating observed change (B). The pre- and post-storm surveys in (A) extend from ~2 m to ~15 m water depth. The colour scheme in (B) reflects the Brier skill assessment of [32]. Morphological change within the vertical error of the surveyed data (±0.03, [21]) was omitted from both plots.
Water 09 00121 g004
Water 09 00121 g005 550
Figure 5. Observations of significant and maximum hourly wave heights and 15-min water levels observed and predicted at the Sydney wave buoy and the tide gauge at Her Majesty’s Australian Ship (HMAS) Penguin, Sydney Harbour, from 3 to 10 June 2016. Water levels are given relative to Australian Height Datum (AHD) which approximates to the mean sea level.
Figure 5. Observations of significant and maximum hourly wave heights and 15-min water levels observed and predicted at the Sydney wave buoy and the tide gauge at Her Majesty’s Australian Ship (HMAS) Penguin, Sydney Harbour, from 3 to 10 June 2016. Water levels are given relative to Australian Height Datum (AHD) which approximates to the mean sea level.
Water 09 00121 g005
Water 09 00121 g006 550
Figure 6. Sea level pressure patterns over the Tasman Sea every 24 h from 3 to 9 June 2016 from the NCEP/NCAR reanalysis at a 2.5° resolution [37]. High pressure (red) is associated with anti-cyclonic winds and low pressure (blue) is associated with cyclonic winds. The low-pressure trough that formed in (A,B) was directed down the length of the New South Wales coast in (C,D) and into Tasmania in (E) by the anticyclone that intensified over New Zealand. Only when the anticyclone migrated eastwards into the South-West Pacific in (F) could the low-pressure cell move off the coast into the South Tasman Sea (G).
Figure 6. Sea level pressure patterns over the Tasman Sea every 24 h from 3 to 9 June 2016 from the NCEP/NCAR reanalysis at a 2.5° resolution [37]. High pressure (red) is associated with anti-cyclonic winds and low pressure (blue) is associated with cyclonic winds. The low-pressure trough that formed in (A,B) was directed down the length of the New South Wales coast in (C,D) and into Tasmania in (E) by the anticyclone that intensified over New Zealand. Only when the anticyclone migrated eastwards into the South-West Pacific in (F) could the low-pressure cell move off the coast into the South Tasman Sea (G).
Water 09 00121 g006
Water 09 00121 g007 550
Figure 7. Nearshore wave conditions at South Narrabeen on Monday 6 June 2016. Authors’ and photographer’s visual estimates of breaking wave heights from these images are between 4 and 5 m (~13 to 16 ft.). Reproduced with permission from Mark Onorati [38]. The images in (A,C) are of the beach section behind Narrabeen Fire Station (red brick building in foreground in (C)) approximately half the way along the Narrabeen-Collaroy embayment; the image in (B) is 100 m north of (A,C) adjacent to Robertson Street.
Figure 7. Nearshore wave conditions at South Narrabeen on Monday 6 June 2016. Authors’ and photographer’s visual estimates of breaking wave heights from these images are between 4 and 5 m (~13 to 16 ft.). Reproduced with permission from Mark Onorati [38]. The images in (A,C) are of the beach section behind Narrabeen Fire Station (red brick building in foreground in (C)) approximately half the way along the Narrabeen-Collaroy embayment; the image in (B) is 100 m north of (A,C) adjacent to Robertson Street.
Water 09 00121 g007
Water 09 00121 g008 550
Figure 8. Rates of energy dissipation (A) and refraction (B) for waves approaching Narrabeen between August and November 2011. Wave direction on the x-axis relates to the offshore (mid-shelf) wave direction as measured at the Sydney buoy. Polynomial functions (solid red lines) describe the dissipation/refraction curves with 95% confidence intervals (dashed red lines). The long-term wave height distribution (C) and occurrence probability of wave directions (D) are shown for the Sydney offshore (blue, observed) and Narrabeen nearshore (orange, modelled) for the period 1992–2016. The Narrabeen nearshore data was obtained by applying the dissipation and refraction coefficients in (A,B) to the offshore data.
Figure 8. Rates of energy dissipation (A) and refraction (B) for waves approaching Narrabeen between August and November 2011. Wave direction on the x-axis relates to the offshore (mid-shelf) wave direction as measured at the Sydney buoy. Polynomial functions (solid red lines) describe the dissipation/refraction curves with 95% confidence intervals (dashed red lines). The long-term wave height distribution (C) and occurrence probability of wave directions (D) are shown for the Sydney offshore (blue, observed) and Narrabeen nearshore (orange, modelled) for the period 1992–2016. The Narrabeen nearshore data was obtained by applying the dissipation and refraction coefficients in (A,B) to the offshore data.
Water 09 00121 g008
Water 09 00121 g009 550
Figure 9. Modelling results for (A) significant wave height and mean wave direction; (B) current velocity and direction (C) sediment transport rate and direction; and (D) bathymetric change at Narrabeen–Collaroy during the April 2015 storm event. Results shown in (A–C) are at the storm peak; while (D) is the cumulative change post-event. Bathymetric change in (D) less than ±0.03 m was omitted, consistent with limits of model calibration (Section 3).
Figure 9. Modelling results for (A) significant wave height and mean wave direction; (B) current velocity and direction (C) sediment transport rate and direction; and (D) bathymetric change at Narrabeen–Collaroy during the April 2015 storm event. Results shown in (A–C) are at the storm peak; while (D) is the cumulative change post-event. Bathymetric change in (D) less than ±0.03 m was omitted, consistent with limits of model calibration (Section 3).
Water 09 00121 g009
Water 09 00121 g010 550
Figure 10. As for Figure 9 but for the June 2016 storm event.
Figure 10. As for Figure 9 but for the June 2016 storm event.
Water 09 00121 g010
Water 09 00121 g011 550
Figure 11. Modelled nearshore current pattern (m/s) at Narrabeen–Collaroy during the peak of the June 2016 storm (as shown in Figure 10B), and locations of observed severe erosion damage at Collaroy. Area of most extreme erosion corresponds to the location of the modelled storm rip current. Source of images Australian Associated Press (rights for reproduction purchased) [39].
Figure 11. Modelled nearshore current pattern (m/s) at Narrabeen–Collaroy during the peak of the June 2016 storm (as shown in Figure 10B), and locations of observed severe erosion damage at Collaroy. Area of most extreme erosion corresponds to the location of the modelled storm rip current. Source of images Australian Associated Press (rights for reproduction purchased) [39].
Water 09 00121 g011
Water 09 00121 g012 550
Figure 12. (A) Average Recurrence Interval (ARI) estimates for storm wave heights not accounting for wave direction. The peak storm wave height and ARI estimate for the June 2016 event are highlighted (red) for the Sydney buoy (black solid line). Original figure reproduced from [47]; (B) ARI estimates for storm wave heights at Sydney accounting for wave direction. Original data from [47].
Figure 12. (A) Average Recurrence Interval (ARI) estimates for storm wave heights not accounting for wave direction. The peak storm wave height and ARI estimate for the June 2016 event are highlighted (red) for the Sydney buoy (black solid line). Original figure reproduced from [47]; (B) ARI estimates for storm wave heights at Sydney accounting for wave direction. Original data from [47].
Water 09 00121 g012

Share and Cite

MDPI and ACS Style

Mortlock, T.R.; Goodwin, I.D.; McAneney, J.K.; Roche, K. The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment. Water 2017, 9, 121. https://doi.org/10.3390/w9020121

AMA Style

Mortlock TR, Goodwin ID, McAneney JK, Roche K. The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment. Water. 2017; 9(2):121. https://doi.org/10.3390/w9020121

Chicago/Turabian Style

Mortlock, Thomas R., Ian D. Goodwin, John K. McAneney, and Kevin Roche. 2017. "The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment" Water 9, no. 2: 121. https://doi.org/10.3390/w9020121

APA Style

Mortlock, T. R., Goodwin, I. D., McAneney, J. K., & Roche, K. (2017). The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment. Water, 9(2), 121. https://doi.org/10.3390/w9020121

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop