System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan
Abstract
:1. Introduction
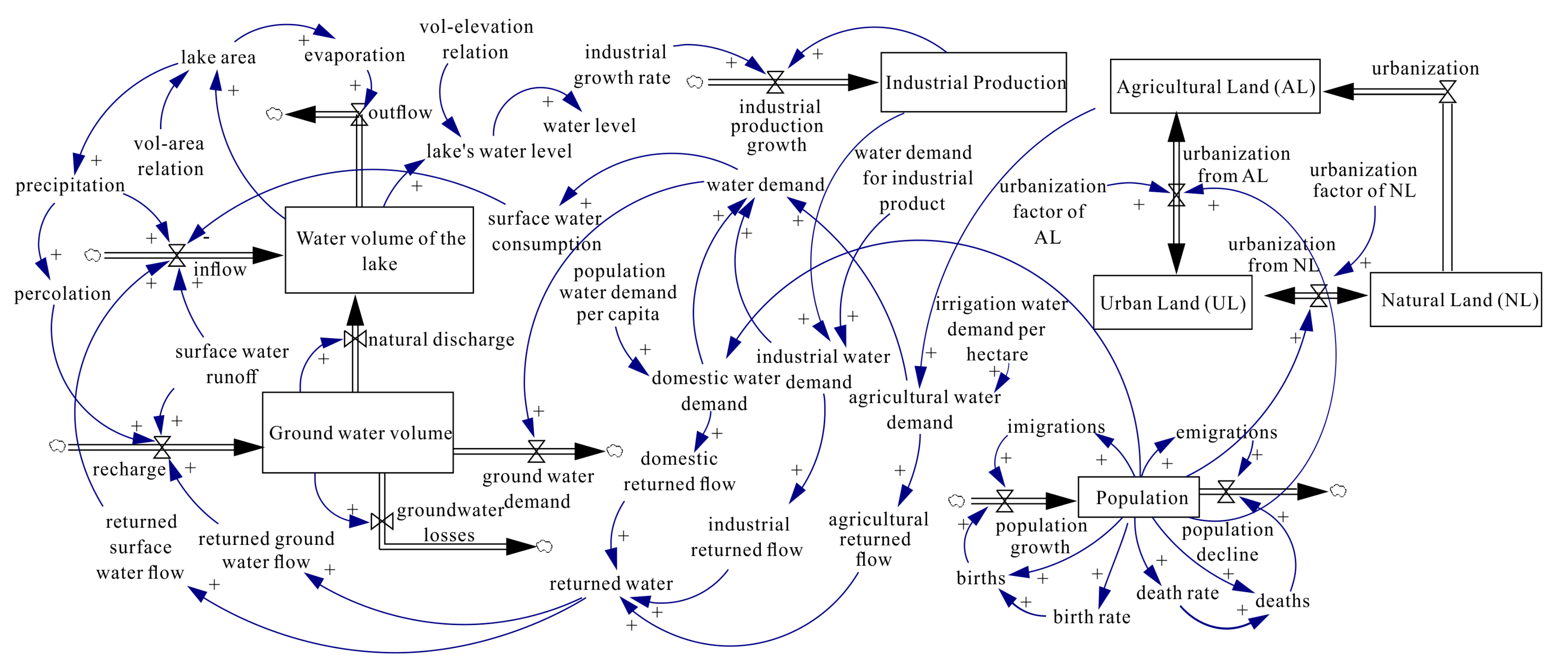
2. Model Structure
2.1. System Dynamics Model
2.2. Model Equations
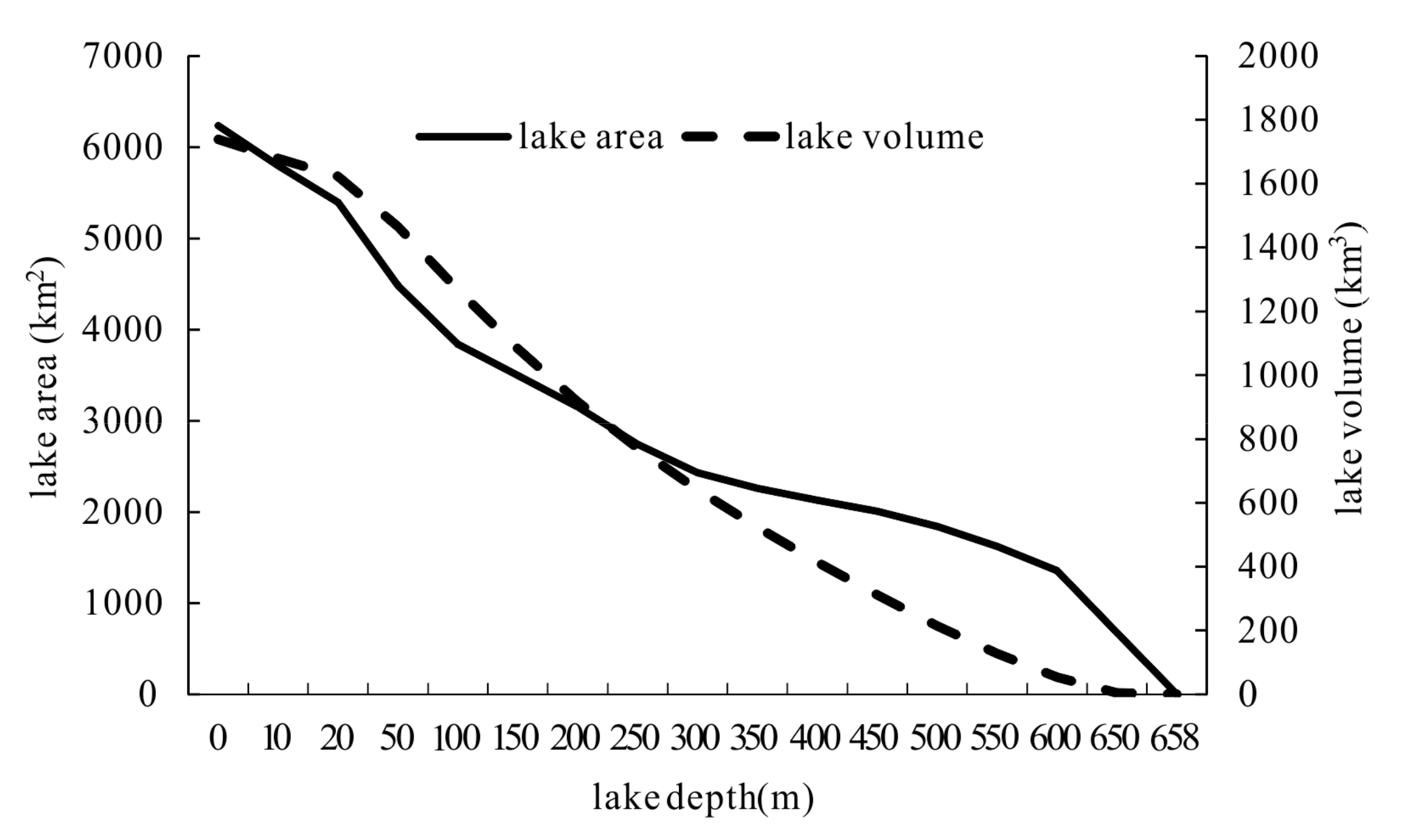
2.2.1. Lake Water Volume
2.2.2. Groundwater
2.2.3. Water Demand
2.2.4. Population
2.2.5. Land Use Changes
3. Materials and Methodology
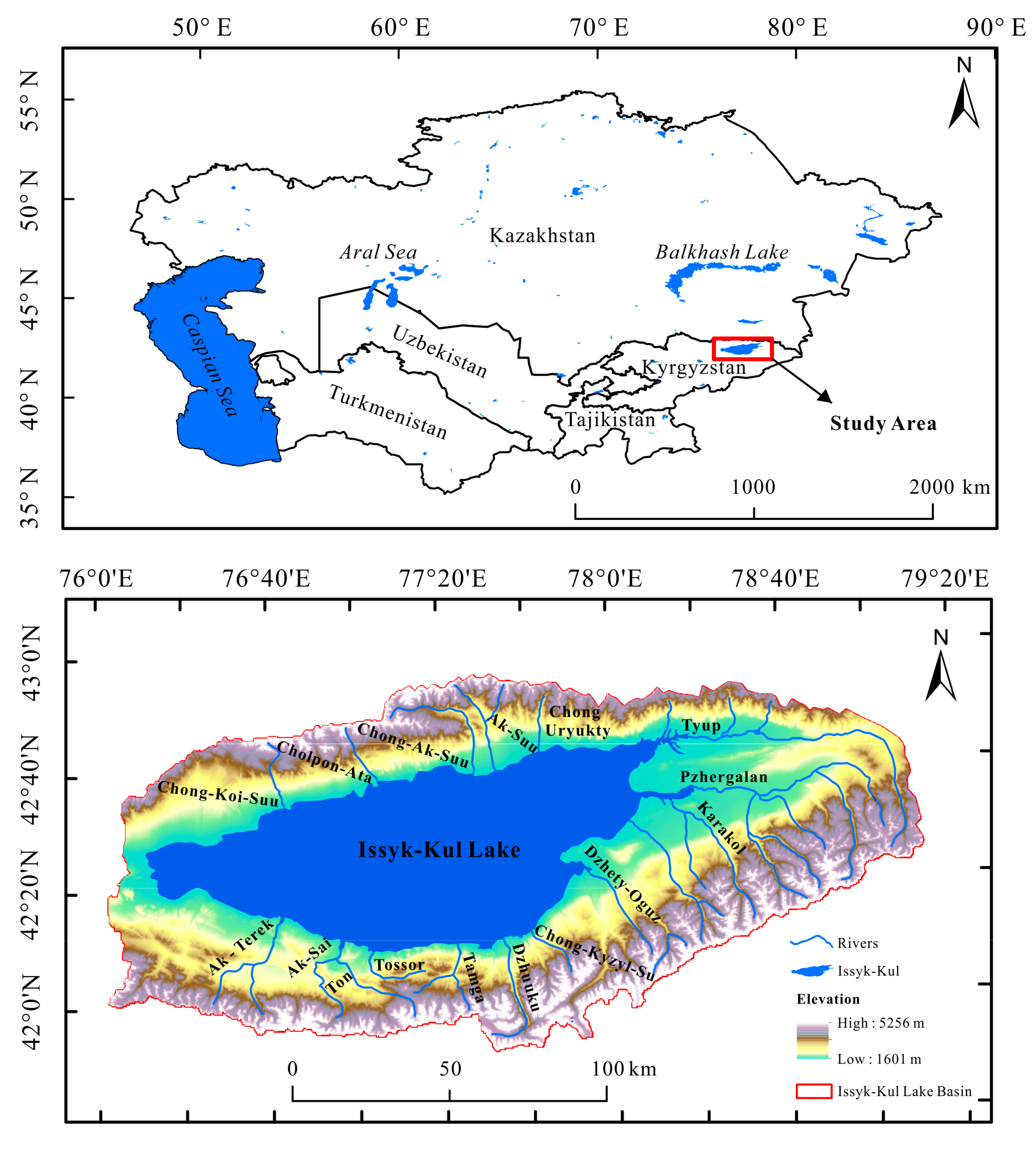
3.1. Study Area
3.2. Model Inputs
3.3. Model Calibration and Validation
4. Results
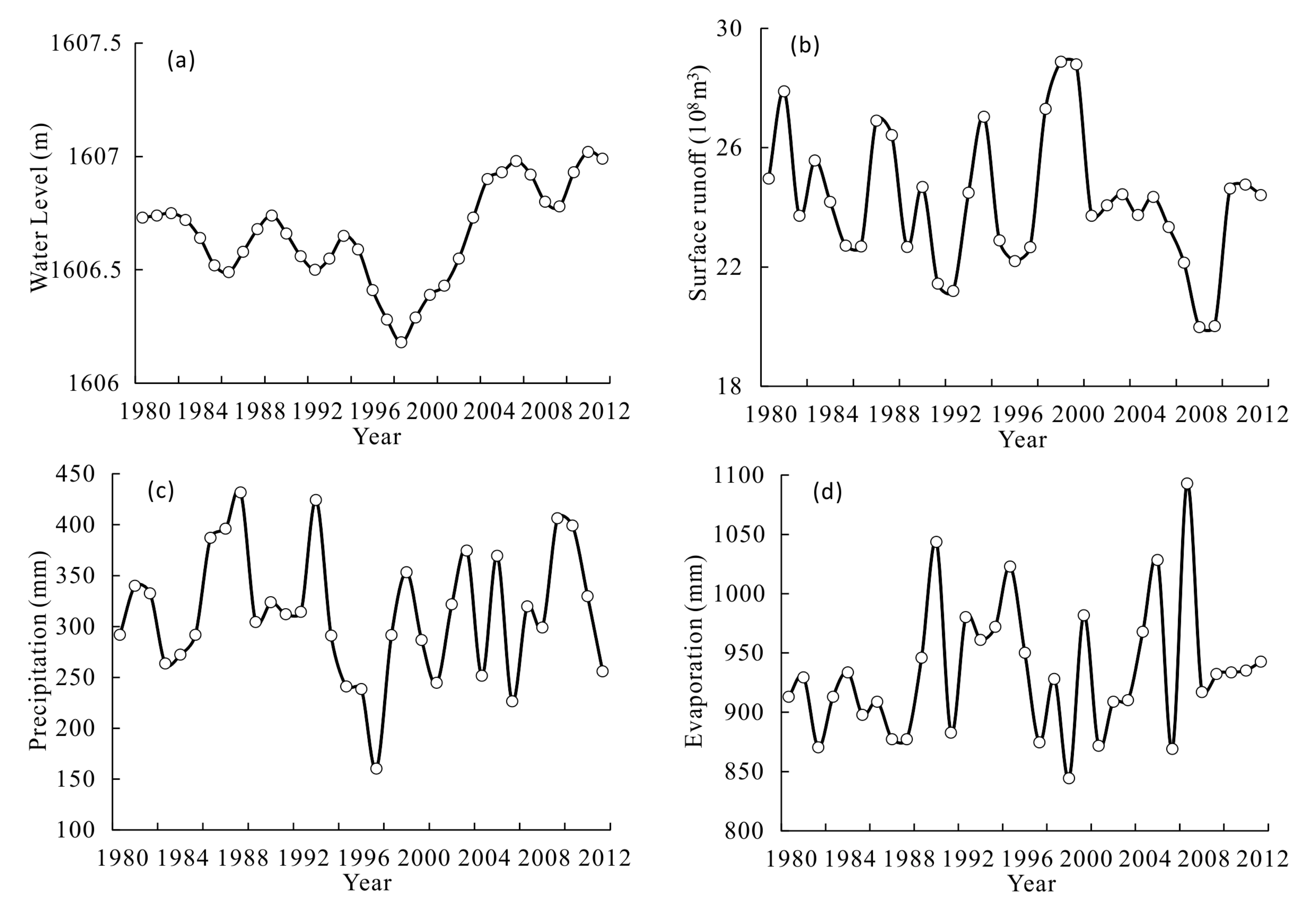
4.1. Water Level Variations of Issyk-Kul Lake
4.2. Factors Influencing the Water Balance
4.2.1. Climate-Hydrologic Change
4.2.2. Anthropogenic Activity
4.3. Calibration and Validation
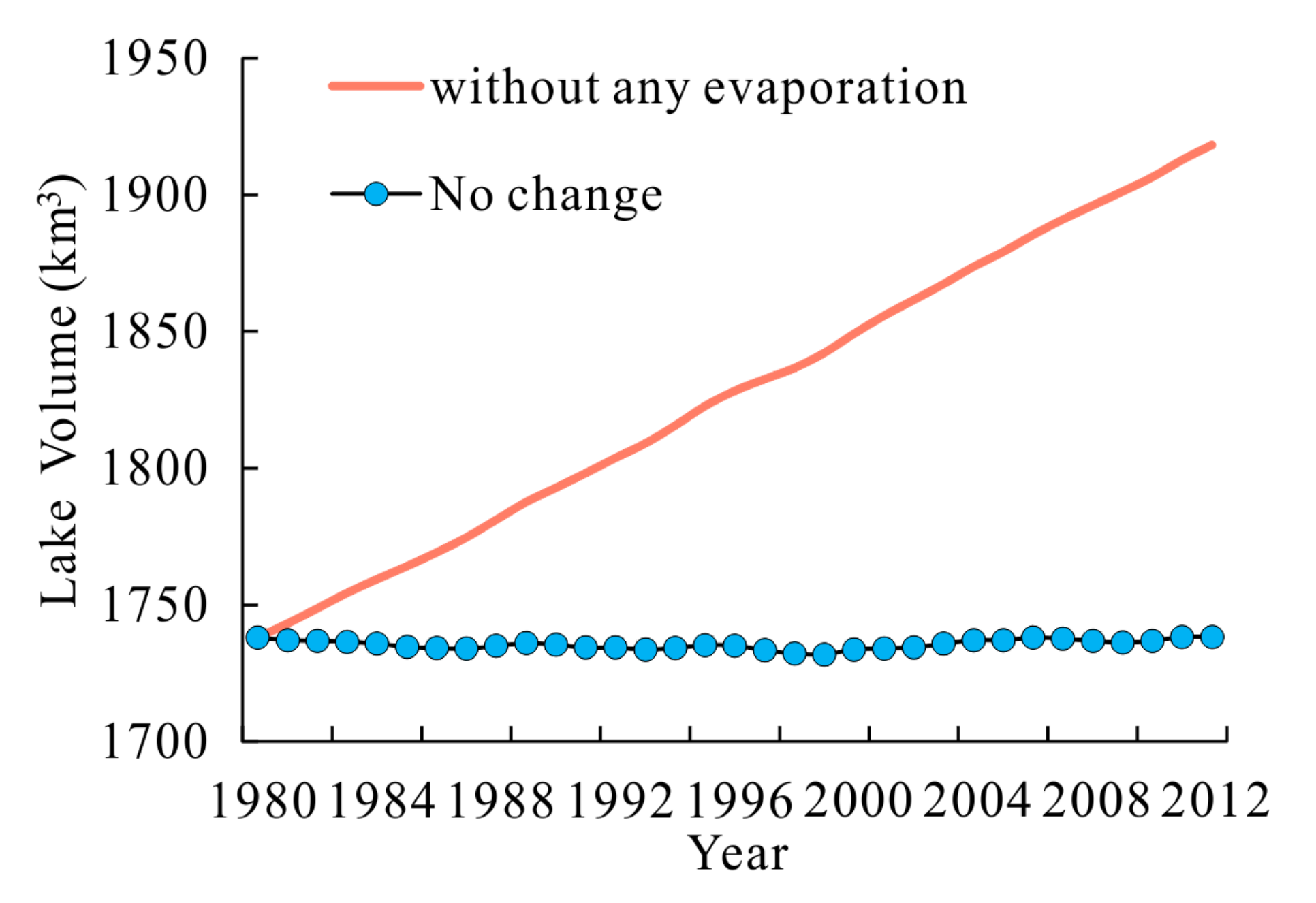
4.3.1. Extreme Condition Test
4.3.2. Behavior Reproduction Test
4.3.3. Sensitivity Degree Analysis
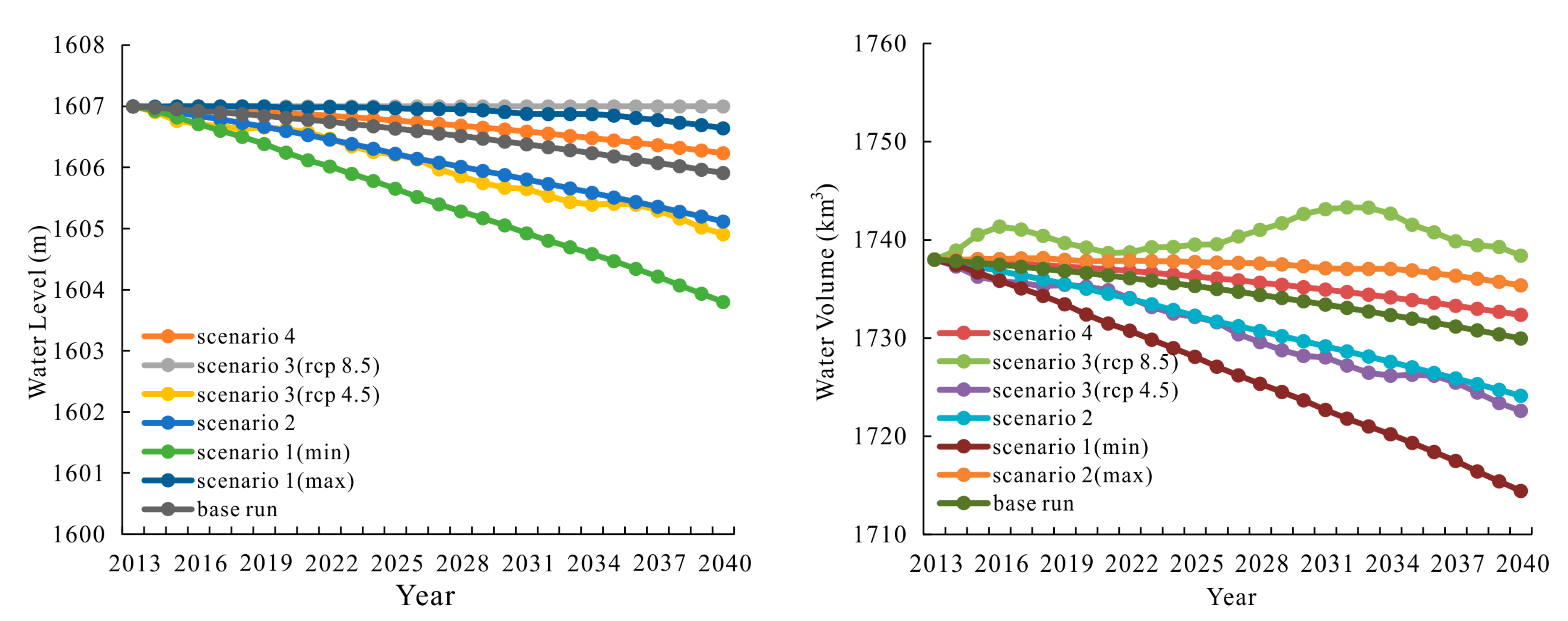
4.4. Simulation Scenarios and Results
- The behavior of the lake water level under the scenarios decrease in water consumption (scenarios 4) the annual lake water level will not change much; the annual average lake water level would increase from 1606.532 m to 1606.688 m (+0.156 m).
- The river flow and water cycle components scenarios (1, 2 and 3) have a greater influence on the water level. As the river runoff (scenario 1) close to its maximum runoff and minimum runoff during the past years, the annual average lake water level drops from 1606.532 m to 1605.460 m (−1.072 m), or increase to 1606.913 m (+0.381 m). Moreover, as the evaporation increases (scenario 2) by 1.76 mm during the future, the annual average lake water level drops from 1606.532 m to 1606.109 m (−0.423 m). Scenario 2, in combination with predicted precipitation changes (RCP 4.5 and RCP 8.5), as scenario 3, have a significant impact on the water level. This impact was greater than for scenario 2 and scenario 4, as the annual average lake water level would decrease from 1606.532 m to 1606.013 m (+0.519 m), or increase to 1607 m (+0.468 m).
- The analysis determines that the river inflow and the water cycle components scenarios significantly impact the lake water level. They are the key strategies for managing the lake water level. Reducing the water consumption in the catchment is indeed leading to an increase of the surface water inflow to the lake and in turn to a rising water level.
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vorosmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Meybeck, M. Global analysis of river systems: From earth system controls to anthropocene syndromes. Philos. Trans. R. Soc. B 2003, 358, 1935–1955. [Google Scholar] [CrossRef] [PubMed]
- Setegn, S.G.; Rayner, D.; Melesse, A.M.; Dargahi, B.; Srinivasan, R. Impact of climate change on the hydroclimatology of Lake Tana Basin, Ethiopia. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Faramarzi, M.; Ghasemi, S.S.; Yang, H. Assessing the impact of climate change on water resources in Iran. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Smiatek, G.; Kunstmann, H.; Heckl, A. High-resolution climate change impact analysis on expected future water availability in the Upper Jordan catchment and the Middle East. J. Hydrometeorol. 2014, 15, 1517–1531. [Google Scholar] [CrossRef]
- Ibatullin, S. Sector Report: The Impact of Climate Change on Water Resources in Central Asia; Eurasian Development Bank: Almaty, Kazakhstan, 2009. [Google Scholar]
- White, C.J.; Tanton, T.W.; Rycroft, D.W. The impact of climate change on the water resources of the Amu Darya basin in central Asia. Water Resour. Manag. 2014, 28, 5267–5281. [Google Scholar] [CrossRef]
- Yessekin, B.; Bogachev, V. Water resources and sustainable development in Central Asia: Roles of risk assessment and risk management. In Risk Assessment as a Tool for Water Resources Decision-Making in Central Asia; Teaf, C.M., Yessekin, B.K., Khankhasayev, M.K., Eds.; Springer: Dordrecht, The Netherlands, 2004; Volume 34, pp. 197–212. [Google Scholar]
- Ososkova, T.; Gorelkin, N.; Chub, V. Water resources of Central Asia and adaptation measures for climate change. Environ. Monit. Assess. 2000, 61, 161–166. [Google Scholar] [CrossRef]
- Karthe, D.; Chalov, S.; Borchardt, D. Water resources and their management in central Asia in the early twenty first century: Status, challenges and future prospects. Environ. Earth Sci. 2015, 73, 487–499. [Google Scholar] [CrossRef]
- Deng, H.J.; Chen, Y.N.; Wang, H.J.; Zhang, S.H. Climate change with elevation and its potential impact on water resources in the Tianshan Mountains, Central Asia. Glob. Planet. Chang. 2015, 135, 28–37. [Google Scholar] [CrossRef]
- Dukhovny, V.A.; Sokolov, V.I.; Ziganshina, D.R. Integrated water resources management in Central Asia, as a way of survival in conditions of water scarcity. Quat. Int. 2013, 311, 181–188. [Google Scholar] [CrossRef]
- Makhmudov, E.J.; Makhmudov, I.E.; Sherfedinov, L.Z. Problems of water resource management in Central Asia. In Transboundary Water Resources: A Foundation for Regional Stability in Central Asia; Moerlins, J.E., Khankhasayev, M.K., Leitman, S.F., Makhmudov, E.J., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 11–28. [Google Scholar]
- Badescu, V.; Schuiling, R.D. Aral Sea; irretrievable Loss or Irtysh imports? Water Resour. Manag. 2010, 24, 597–616. [Google Scholar] [CrossRef]
- Hwang, C.; Kao, Y.C.; Tangdamrongsub, N. Preliminary analysis of lake level and water storage changes over lakes Baikal and Balkhash from satellite altimetry and gravimetry. Terr. Atmos. Ocean. Sci. 2011, 22, 97–108. [Google Scholar] [CrossRef]
- Salamat, A.U.; Abuduwaili, J.; Shaidyldaeva, N. Impact of climate change on water level fluctuation of Issyk-Kul Lake. Arab. J. Geosci. 2015, 8, 5361–5371. [Google Scholar] [CrossRef]
- Song, C.Q.; Huang, B.; Ke, L.H.; Richards, K.S. Seasonal and abrupt changes in the water level of closed lakes on the Tibetan Plateau and implications for climate impacts. J. Hydrol. 2014, 514, 131–144. [Google Scholar] [CrossRef]
- Caruso, B.; Newton, S.; King, R.; Zammit, C. Modelling climate change impacts on hydropower lake inflows and braided rivers in a mountain basin. Hydrol. Sci. J. 2017, 62, 928–946. [Google Scholar] [CrossRef]
- Matsuyama, H.; Kezer, K. Long-term variation of precipitation around Lake Balkhash in Central Asia from the end of the 19th century. Sola 2009, 5, 73–76. [Google Scholar] [CrossRef]
- Bai, J.; Chen, X.; Li, J.; Yang, L.; Fang, H. Changes in the area of inland lakes in arid regions of central Asia during the past 30 years. Environ. Monit. Assess. 2011, 178, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Romanovsky, V.V. Water level variations and water balance of Lake Issyk-Kul. Lake Issyk-Kul Its Nat. Environ. 2002, 13, 45–57. [Google Scholar]
- Shabunin, G.D.; Shabunin, A.G. Climate and physical properties of water in Lake Issyk-Kul. Lake Issyk-Kul Its Nat. Environ. 2002, 13, 3–11. [Google Scholar]
- Vermeesch, P.; Poort, J.; Duchkov, A.D.; Klerkx, J.; de Batist, M. Lake Issyk-Kul (Tien Shan): Unusually low heat flow in an active intermontane basin. Geol. Geofiz. 2004, 45, 616–625. [Google Scholar]
- Karmanchuk, A.S. Water chemistry and ecology of Lake Issyk-Kul. Lake Issyk-Kul Its Nat. Environ. 2002, 13, 13–26. [Google Scholar]
- Yuan, Y.J.; Zeng, G.M.; Liang, J.; Huang, L.; Hua, S.S.; Li, F.; Zhu, Y.; Wu, H.P.; Liu, J.Y.; He, X.X.; et al. Variation of water level in dongting lake over a 50-year period: Implications for the impacts of anthropogenic and climatic factors. J. Hydrol. 2015, 525, 450–456. [Google Scholar] [CrossRef]
- Jalili, S.; Kirchner, I.; Livingstone, D.M.; Morid, S. The influence of large-scale atmospheric circulation weather types on variations in the water level of Lake Urmia, Iran. Int. J. Climatol. 2012, 32, 1990–1996. [Google Scholar] [CrossRef]
- Dusini, D.S.; Foster, D.L.; Shore, J.A.; Merry, C. The effect of Lake Erie water level variations on sediment resuspension. J. Gt. Lakes Res. 2009, 35, 1–12. [Google Scholar] [CrossRef]
- De Grave, J.; Glorie, S.; Buslov, M.M.; Stockli, D.F.; McWilliams, M.O.; Batalev, V.Y.; Van den Haute, P. Thermo-tectonic history of the Issyk-Kul basement (Kyrgyz northern Tien Shan, Central Asia). Gondwana Res. 2013, 23, 998–1020. [Google Scholar] [CrossRef]
- Macaulay, E.A.; Sobel, E.R.; Mikolaichuk, A.; Wack, M.; Gilder, S.A.; Mulch, A.; Fortuna, A.B.; Hynek, S.; Apayarov, F. The sedimentary record of the Issyk Kul basin, Kyrgyzstan: Climatic and tectonic inferences. Basin Res. 2016, 28, 57–80. [Google Scholar] [CrossRef]
- Ricketts, R.D.; Johnson, T.C.; Brown, E.T.; Rasmussen, K.A.; Romanovsky, V.V. The Holocene paleolimnology of Lake Issyk-Kul, Kyrgyzstan: Trace element and stable isotope composition of ostracodes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2001, 176, 207–227. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Global Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Vollmer, M.K.; Weiss, R.F.; Williams, R.T.; Falkner, K.K.; Qiu, X.; Ralph, E.A.; Romanovsky, V.V. Physical and chemical properties of the waters of saline lakes and their importance for deep-water renewal: Lake Issyk-Kul, Kyrgyzstan. Geochim. Cosmochim. Acta 2002, 66, 4235–4246. [Google Scholar] [CrossRef]
- Lyons, W.B.; Welch, K.A.; Bonzongo, J.C.; Graham, E.Y.; Shabunin, G.; Gaudette, H.E.; Poreda, R.J. A preliminary assessment of the geochemical dynamics of Issyk-Kul Lake, Kirghizstan. Limnol. Oceanogr. 2001, 46, 713–718. [Google Scholar] [CrossRef]
- Uralbekov, B.M.; Smodis, B.; Burkitbayev, M. Uranium in natural waters sampled within former uranium mining sites in Kazakhstan and Kyrgyzstan. J. Radioanal. Nucl. Chem. 2011, 289, 805–810. [Google Scholar] [CrossRef]
- Gavshin, V.M.; Melgunov, M.S.; Sukhorukov, F.V.; Bobrov, V.A.; Kalugin, I.A.; Klerkx, J. Disequilibrium between uranium and its progeny in the Lake Issyk-Kul system (Kyrgyzstan) under a combined effect of natural and manmade processes. J. Environ. Radioact. 2005, 83, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Alamanov, A.; Mikkola, H. Is biodiversity friendly fisheries management possible on Issyk-Kul Lake in the Kyrgyz Republic? AMBIO 2011, 40, 479–495. [Google Scholar] [CrossRef] [PubMed]
- Peeters, F.; Finger, D.; Hofer, M.; Brennwald, M.; Livingstone, D.M.; Kipfer, R. Deep-water renewal in Lake Issyk-Kul driven by differential cooling. Limnol. Oceanogr. 2003, 48, 1419–1431. [Google Scholar] [CrossRef]
- Hofer, M.; Peeters, F.; Aeschbach-Hertig, W.; Brennwald, M.; Holocher, J.; Livingstone, D.M.; Romanovski, V.; Kipfer, R. Rapid deep-water renewal in Lake Issyk-Kul (Kyrgyzstan) indicated by transient tracers. Limnol. Oceanogr. 2002, 47, 1210–1216. [Google Scholar] [CrossRef]
- Vollmer, M.K.; Weiss, R.F.; Schlosser, P.; Williams, R.T. Deep-water renewal in Lake Issyk-Kul. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Waugh, D.W.; Vollmer, M.K.; Weiss, R.F.; Haine, T.W.N.; Hall, T.M. Transit time distributions in Lake Issyk-Kul. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Mandychev, A.N. Groundwater in the Issyk Kul basin. Lake Issyk-Kul Its Nat. Environ. 2002, 13, 71–76. [Google Scholar]
- Qin, B.Q.; Yu, G. Implications of lake level variations at 6 ka and 18 ka in mainland Asia. Glob. Planet. Chang. 1998, 18, 59–72. [Google Scholar] [CrossRef]
- Romanovsky, V.V.; Tashbaeva, S.; Crétaux, J.-F.; Calmant, S.; Drolon, V. The closed Lake Issyk-Kul as an indicator of global warming in Tien-Shan. Nat. Sci. 2013, 5, 608–623. [Google Scholar] [CrossRef]
- Alymkulova, B.; Abuduwaili, J.; Issanova, G.; Nahayo, L. Consideration of water uses for its sustainable management, the case of Issyk-Kul Lake, Kyrgyzstan. Water 2016, 8, 298. [Google Scholar] [CrossRef]
- Winz, I.; Brierley, G.; Trowsdale, S. The use of system dynamics simulation in water resources management. Water Resour. Manag. 2009, 23, 1301–1323. [Google Scholar] [CrossRef]
- Kotir, J.H.; Smith, C.; Brown, G.; Marshall, N.; Johnstone, R. A system dynamics simulation model for sustainable water resources management and agricultural development in the Volta River Basin, Ghana. Sci. Total Environ. 2016, 573, 444–457. [Google Scholar] [CrossRef] [PubMed]
- Forrester, J.W. Counterintuitive behavior of social systems. Theor. Decis. 1971, 2, 109–144. [Google Scholar] [CrossRef]
- Ahmad, S.; Prashar, D. Evaluating municipal water conservation policies using a dynamic simulation model. Water Resour. Manag. 2010, 24, 3371–3395. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. Integration of heuristic knowledge with analytical tools for the selection of flood damage reduction measures. Can. J. Civ. Eng. 2001, 28, 208–221. [Google Scholar] [CrossRef]
- Qaiser, K.; Ahmad, S.; Johnson, W.; Batista, J. Evaluating the impact of water conservation on fate of outdoor water use: A study in an arid region. J. Environ. Manag. 2011, 92, 2061–2068. [Google Scholar] [CrossRef] [PubMed]
- Qaiser, K.; Ahmad, S.; Johnson, W.; Batista, J.R. Evaluating water conservation and reuse policies using a dynamic water balance model. Environ. Manag. 2013, 51, 449–458. [Google Scholar] [CrossRef] [PubMed]
- Rusuli, Y.; Li, L.; Ahmad, S.; Zhao, X. Dynamics model to simulate water and salt balance of bosten lake in Xinjiang, China. Environ. Earth Sci. 2015, 74, 2499–2510. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S.; Nayak, A. Increasing streamflow forecast lead time for snowmelt-driven catchment based on large-scale climate patterns. Adv. Water Resour. 2013, 53, 150–162. [Google Scholar] [CrossRef]
- Shrestha, E.; Ahmad, S.; Johnson, W.; Batista, J.R. The carbon footprint of water management policy options. Energy Policy 2012, 42, 201–212. [Google Scholar] [CrossRef]
- Dawadi, S.; Ahmad, S. Evaluating the impact of demand-side management on water resources under changing climatic conditions and increasing population. J. Environ. Manag. 2013, 114, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Butler, C.; Adamowski, J. Empowering marginalized communities in water resources management: Addressing inequitable practices in participatory model building. J. Environ. Manag. 2015, 153, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Ahmad, S.; Attarod, P. Drought forecasting in a semi-arid watershed using climate signals: A neuro-fuzzy modeling approach. J. Mt. Sci. 2014, 11, 1593–1605. [Google Scholar] [CrossRef]
- Yaeger, M.A.; Housh, M.; Cai, X.M.; Sivapalan, M. An integrated modeling framework for exploring flow regime and water quality changes with increasing biofuel crop production in the US Corn Belt. Water Resour. Res. 2014, 50, 9385–9404. [Google Scholar] [CrossRef]
- Valipour, M. Future of agricultural water management in Africa. Arch. Agron. Soil Sci. 2015, 61, 907–927. [Google Scholar] [CrossRef]
- Abadi, L.S.K.; Shamsai, A.; Goharnejad, H. An analysis of the sustainability of basin water resources using vensim model. KSCE J. Civ. Eng. 2015, 19, 1941–1949. [Google Scholar] [CrossRef]
- Ventana Systems (2012) Vensim DSS. Ventana Systems, Inc.: Harvard, MA, USA, 2012, 6.0b ed. Available online: http://vensim.com/vensim-software/ (accessed on 18 December 2017).
- Ragni, M.; Steffenhagen, F.; Klein, A. Generalized dynamic stock and flow systems: An AI approach. Cogn. Syst. Res. 2011, 12, 309–320. [Google Scholar] [CrossRef]
- Kaplinsky, M.I.; Timchenko, L.S. Water balance of Lake Issyk-Kul over many years. Bull. SARNIGMI iss 1997, 50, 87–101. (In Russion) [Google Scholar]
- Bolshakov, V.A.; Virina, E.I.; Faustov, S.S.; Chernova, L.M. Magnetic-properties of Issyk-Kul Lake bottom sediments. Izv. Akad. Nauk SSSR Fiz. Zemli 1986, 1, 99–105. [Google Scholar]
- De Batist, M.; Imbo, Y.; Vermeesch, P.; Klerkx, J.; Giralt, S.; Delvaux, D.; Lignier, V.; Beck, C.; Kalugin, I.; Abdrakhmatov, K.E. Bathymetry and sedimentary environments of Lake Issyk-Kul, Kyrgyz Republic (Central Asia): A large, high-altitude, tectonic lake. Lake Issyk-Kul Its Nat. Environ. 2002, 13, 101–123. [Google Scholar]
- Rykiel, E.J. Testing ecological models: The meaning of validation. Ecol. Model. 1996, 90, 229–244. [Google Scholar] [CrossRef]
- Mirchi, A.; Madani, K.; Watkins, D.; Ahmad, S. Synthesis of system dynamics tools for holistic conceptualization of water resources problems. Water Resour. Manag. 2012, 26, 2421–2442. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Hong, Y.; Yong, B.; Yang, X.L.; Yuan, F.; Ma, M.W. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the bayesian model averaging method. J. Hydrol. 2012, 452, 213–225. [Google Scholar] [CrossRef]
- Sidike, A.; Chen, X.; Liu, T.; Durdiev, K.; Huang, Y. Investigating alternative climate data sources for hydrological simulations in the upstream of the Amu Darya River. Water 2016, 8, 441. [Google Scholar] [CrossRef]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Comparison of PERSIANN and V7 TRMM Multi-satellite Precipitation Analysis (TMPA) products with rain gauge data over Iran. Int. J. Remote Sens. 2013, 34, 8156–8171. [Google Scholar] [CrossRef]
- Omlin, M.; Brun, R.; Reichert, P. Biogeochemical model of Lake Zurich: Sensitivity, identifiability and uncertainty analysis. Ecol. Model. 2001, 141, 105–123. [Google Scholar] [CrossRef]
- Propastin, P. Assessment of Climate and Human Induced Disaster Risk over Shared Water Resources in the Balkhash Lake Drainage Basin; Springer: Berlin/Heidelberg, Germany, 2013; pp. 41–54. [Google Scholar]
- Farre, I.; Faci, J.M. Deficit irrigation in maize for reducing agricultural water use in a mediterranean environment. Agric. Water Manag. 2009, 96, 383–394. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Alcamo, J.; Doll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rosch, T.; Siebert, S. Global estimates of water withdrawals and availability under current and future “business-as-usual” conditions. Hydrol. Sci. J. 2003, 48, 339–348. [Google Scholar] [CrossRef]
- Bayer, S. Business dynamics: Systems thinking and modeling for a complex world. Interfaces 2004, 34, 324–326. [Google Scholar]
- Ji, J.; Yang, R.; Sun, Z.H.; Yuan, H.Y. Validation and evaluation of large eddy simulation based field-zone model for smoke movement in building fires. Prog. Saf. Sci. Technol. 2006, 6, 721–724. [Google Scholar]
- Yuan, Q. Precipitation in Central Asia in the mid- and late-21st century. J. Clim. 2017. manuscript submitted for publication. [Google Scholar]
- Wang, G.Y.; Shen, Y.P.; Qin, D.H. Issyk-Kul Lake level fluctuation during 1860–2005 and its relation with regional climatic and hydrological changes. J. Glaciol. Geocryol. 2006, 28, 855–860. [Google Scholar]
- Wang, G.Y.; Shen, Y.P.; Wang, N.L.; Wu, Q.B. The effects of climate change and human activities on the lake level of the Issyk-Kul during the past 100 years. Glaciol. Geocryol. 2010, 32, 1097–1105. [Google Scholar]
- Guo, H.C.; Liu, L.; Huang, G.H.; Fuller, G.A.; Zou, R.; Yin, Y.Y. A system dynamics approach for regional environmental planning and management: A study for the Lake Erhai Basin. J. Environ. Manag. 2001, 61, 93–111. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.H.; Jin, H.L.; Zhao, S.W. Based on system dynamics model of evolvement of water resources and social economic system in Xinjiang Aibi Lake area. Model. Simul. 2010, 4, 122–125. [Google Scholar]
- Hassanzadeh, E.; Zarghami, M.; Hassanzadeh, Y. Determining the main factors in declining the Urmia Lake level by using system dynamics modeling. Water Resour. Manag. 2012, 26, 129–145. [Google Scholar] [CrossRef]
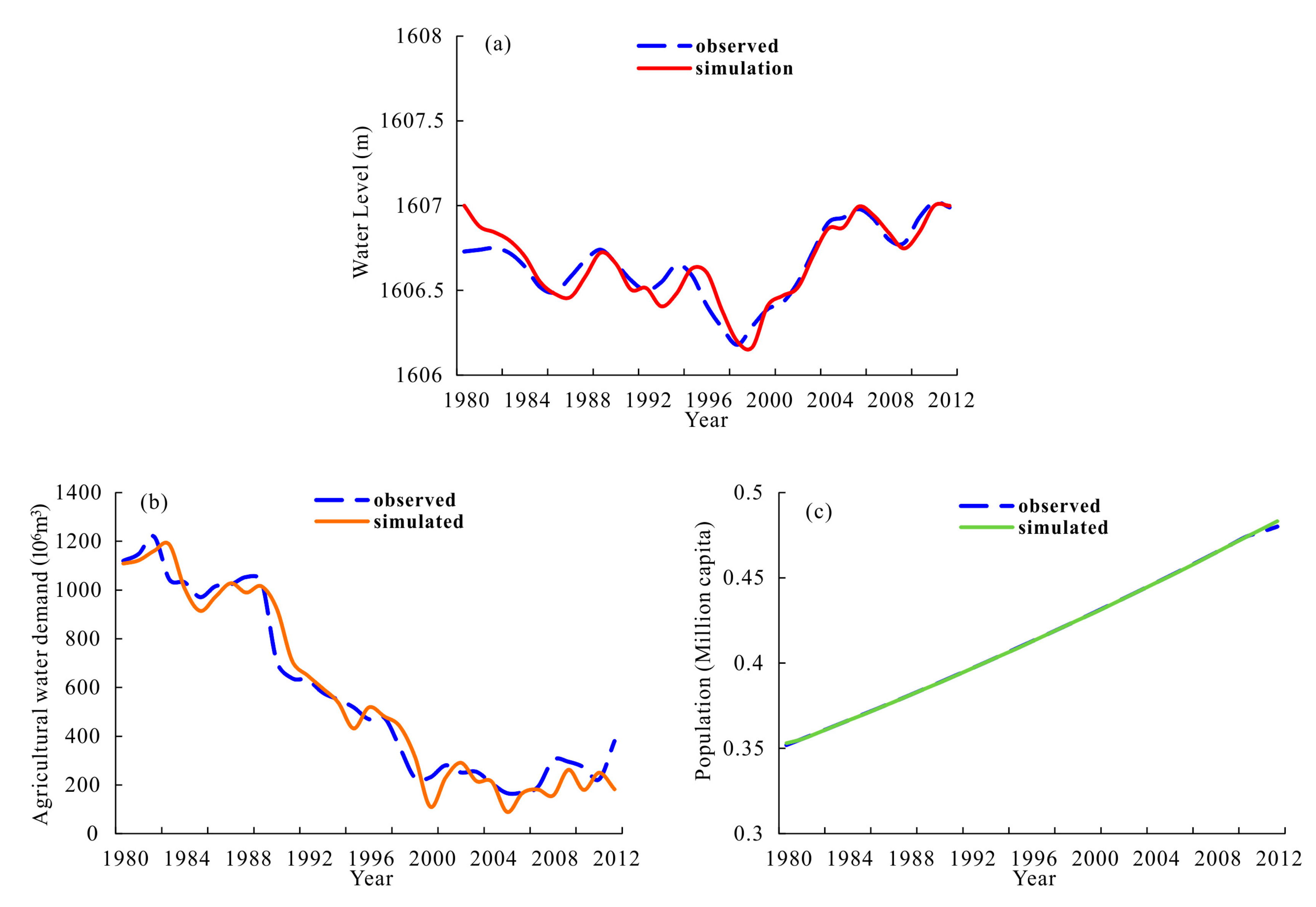
| Variables | CF | MAE | RMSE | MBias | NSE |
|---|---|---|---|---|---|
| Lake level | 0.928 | 0.0667 | 0.0906 | 1.000 | 0.9132 |
| Total population | 0.999 | 0.0002 | 0.0006 | 1.000 | 0.9998 |
| Agricultural water demand | 0.966 | 0.5816 | 0.7761 | 0.988 | 0.9327 |
| Parameter Change (%) | SW | GW | E | P | ||||||
| +10 | −10 | +10 | −10 | +10 | −10 | +10 | −10 | |||
| Lake Level | 1.47 | 1.09 | 0.57 | 0.63 | −1.02 | −0.53 | 0.41 | −0.08 | ||
| Parameter Change (%) | p | Awd | Iwd | Dwd | Lagr | |||||
| +10 | −10 | +10 | −10 | +10 | −10 | +10 | −10 | +10 | −10 | |
| Lake Level | 0.045 | −0.040 | 0.16 | 0.08 | 0.006 | 0.007 | 0.007 | −0.007 | 0.073 | 0.10 |
| Scenario | Description |
|---|---|
| Base run | Variables used the average values of the observation period after 2012 |
| River flow | Surface runoff assumed to close to maximum runoff and minimum runoff in past 33 years, respectively, after 2012 |
| Water cycle components | Based the evaporation data in 2012, assumed the evaporation will increase by 1.76 mm per year after 2012; Precipitation changes under RCP 4.5 and RCP 8.5 scenarios after 2012 |
| Decrease in water consumption | Assumed the water consumption decreased by 10% after 2012 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alifujiang, Y.; Abuduwaili, J.; Ma, L.; Samat, A.; Groll, M. System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan. Water 2017, 9, 989. https://doi.org/10.3390/w9120989
Alifujiang Y, Abuduwaili J, Ma L, Samat A, Groll M. System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan. Water. 2017; 9(12):989. https://doi.org/10.3390/w9120989
Chicago/Turabian StyleAlifujiang, Yilinuer, Jilili Abuduwaili, Long Ma, Alim Samat, and Michael Groll. 2017. "System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan" Water 9, no. 12: 989. https://doi.org/10.3390/w9120989
APA StyleAlifujiang, Y., Abuduwaili, J., Ma, L., Samat, A., & Groll, M. (2017). System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan. Water, 9(12), 989. https://doi.org/10.3390/w9120989






