1. Introduction
Over the past 40 years, numerical models of groundwater flow and solute transport have been widely used in studies of water resources management, migration of pollutants, sea water intrusion and many other applications [
1,
2,
3,
4]. However, because of the complexity of hydrogeological conditions and the limited budget and time, scientists often find it difficult to collect sufficient data to completely describe the hydrogeological systems in great details. Lack of hydrogeological data will inevitably affect the reliability of the model simulations and result in model uncertainty. Therefore, how to describe the uncertainty of model inputs and outputs and to improve the reliability of model predictions has become an important element of the numerical simulations used in studies of groundwater flow and solute transport [
5,
6,
7,
8,
9].
Stochastic method based on a certain statistical structure is one of the most important methods currently used to study the uncertainty of numerical models of groundwater flow [
2,
3,
4,
5,
6,
7,
8,
9]. Stochastic methods include a host of mathematical methods such as the traditional random methods [
7,
8] and the Bayesian statistical methods [
9]. The traditional random methods mainly include the Monte Carlo (MC) method, the moment equation method and Taylor expansion method or the perturbation expansion method. The Bayesian method is a widely used stochastic method in recent decades.
The MC method is first widely used to obtain the statistical characteristics of groundwater head or solute concentrations by random sampling after the probability density function (PDF) of the hydrogeological elements is known, where the hydrogeological elements refer to the aquifer parameters such as hydraulic conductivity or transmissivity, storativity, porosity, dispersivity, etc., boundary and initial conditions of flow and transport, and sinks and sources of flow and transport [
10,
11,
12,
13]. The moment equation method can be used to calculate the mean and variance of groundwater head or solute concentrations, provided that the mean and variance of known hydrogeological elements are given [
14,
15,
16,
17,
18]. The moment equation method is used to obtain the first and second moments of the hydraulic head (for flow problems) or the solute concentration (for transport problems) by the first and second moments of the stochastic governing equation. Many investigators have carried out the uncertainty analysis of numerical simulations based on the Taylor expansion method or the perturbation expansion method, which also requires the mean and variance of the hydrogeological elements [
19,
20]. The Taylor expansion method or the perturbation expansion method expands head or concentration around its mean value and tries to make a connection between the mean and variance of head and concentration with the mean and variance of the hydrogeological elements [
21,
22]. The Taylor expansion or perturbation expansion method often involves the inversion of a large coefficient matrix, which could be computationally expensive. In addition, several investigators have studied the random theory using other methods [
23,
24,
25,
26,
27,
28,
29].
Bayesian theory has also been widely used in the uncertainty analysis of numerical simulations of groundwater flow and solute transport. This theory involves three aspects including sampling methods, likelihood functions and convergence criteria [
1]. A crucial step of the Bayesian theory is the sampling algorithm. There are several commonly used sampling algorithms, such as the Metropolis-Hastings algorithm, the Gibbs algorithm and the adaptive Metropolis algorithm [
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40]. Bayesian theory can obtain the posterior probability density function of hydrogeological elements, but the premise is that the distribution of hydrogeological parameters is known a priori.
Based on the random statistical characteristics of the hydrogeological elements, the stochastic method obtains the statistical characteristics of the output (mainly, the head and concentration). Unfortunately, it is sometimes difficult to know the stochastic statistical characteristics of the hydrogeological elements a priori in actual applications.
However, although precise statistical characteristics of the hydrogeological elements may be difficult to obtain, it may be easier to determine the ranges of possible values for the hydrogeological elements, probably with the help hydrogeological surveys, which is conventionally conducted in nearly all the hydrogeological investigations. If this is true, now the question is: Can we quantitatively determine the ranges of system outputs, given the bounded but uncertain inputs of the hydrogeological elements? The method used to tackle this question is named the interval uncertainty method (IUM), and it is practically appealing in terms of managing groundwater resources and conducting risk assessment of contaminated aquifers. A minor point to note is that IUM has been successfully carried out in other disciplines such as structural engineering, interval optimization method, and irrigation water distribution, but has never been applied in subsurface hydrology [
41,
42,
43,
44,
45,
46,
47,
48,
49,
50].
This study is the first attempt to use IUM for dealing with a linear groundwater flow system in a confined aquifer. Comparison of the presented (analytic) IUM and numerical analysis of a few hypothetical examples shows that the computational efficiency and precision of this method are very well. The validity of IUM in nonlinear subsurface flow systems such as flow in variably saturated porous media or flow in an unconfined aquifer with considerable variation of water table with time is out of the scope of this study, and will be investigated in the future.
3. Interval Response Solution
3.1. Groundwater Head Interval Response Expression
When determining the interval solution of H in Equation (15), we will first obtain the average value H0 of H, and then calculate the variation ΔH, which is a key issue to deal with. The following discussion provides the solution to Equation (15).
The average
H0 of the groundwater head satisfies the following equation:
where
is the coefficient matrix when the hydrogeological parameters are set at their averages,
is the column vector when sources and sinks take their averages as well.
Meanwhile, using
,
and
, the following equation can be written:
where Δ
K and Δ
F are respectively the variations of
K and
F. Considering Equations (16) and (17), and ignoring the second order and higher order terms of Δ
K, Δ
H, and Δ
F, we can obtain an approximate expression of the first-order disturbance about the head [
51].
where
is the first-order approximation of Δ
H. That is, replacing Δ
H with
in Equation (18), where
H is
The second-order approximation of Δ
H and the corresponding
H is
According to the interval expansion from interval mathematics, substituting Equation (14) into Equation (18), the first order perturbation of Δ
H is approximately
and the component form of Equation (21) can be written as
where
and
are respectively the number of columns and rows of
ψ in Equation (22). That is, they indicate the number of nodes to be solved. When Equation (22) is substituted into Equation (21), the following can be obtained:
According to the interval algorithm [
51], the following can be obtained:
Therefore, one can obtain the first-order perturbation of
H, which is approximately expressed as
Equation (25) is obtained when and both are linear expressions. It can be seen from the solution of the interval head equation that one only needs to find the inverse of the coefficient matrix rather than the head derivative of the changing elements to calculate the interval value of H. In addition, when the interval value of H is obtained by this method, we find the extreme of H (i.e., the maximum and minimum values) in a certain interval, which is obviously different from the general perturbation method that only finds the variation of H within a certain interval rather than its extreme value. When applied in groundwater, the general perturbation method is a method of calculating the variation of groundwater head, which is based on the hydrogeological elements rate of change is known.
3.2. Algorithmic Details
The groundwater head interval response calculation is applied in the whole process of the number simulation of groundwater flow. Because the coefficient matrixes of the subdivision element sections are first obtained based on the subdivision elements coefficient matrixes superposition, the total coefficient matrix in the number simulation program of groundwater flow is obtained. The algorithmic description of the interval parameter perturbation method is listed in Algorithm 1.
| Algorithm 1. Interval Parameter Perturbation Method Algorithm. |
| After the head for a certain calculation period was obtained |
| 1. Solving , and for the section of each subdivision element; |
| 2. Solving , and then can be obtained; |
| 3. Traversing each subdivision element, can be obtained; |
| 4. Calculating , could be obtained; |
| Calculating above-described steps 1–4, the current time head can be obtained |
In the whole calculation, when the hydrogeological elements change within a certain interval, determining the head interval response is essentially a matter of interval optimization. In the following sections, numerical examples will be used to analyze the effectiveness of the proposed interval method.
4. Numerical Examples
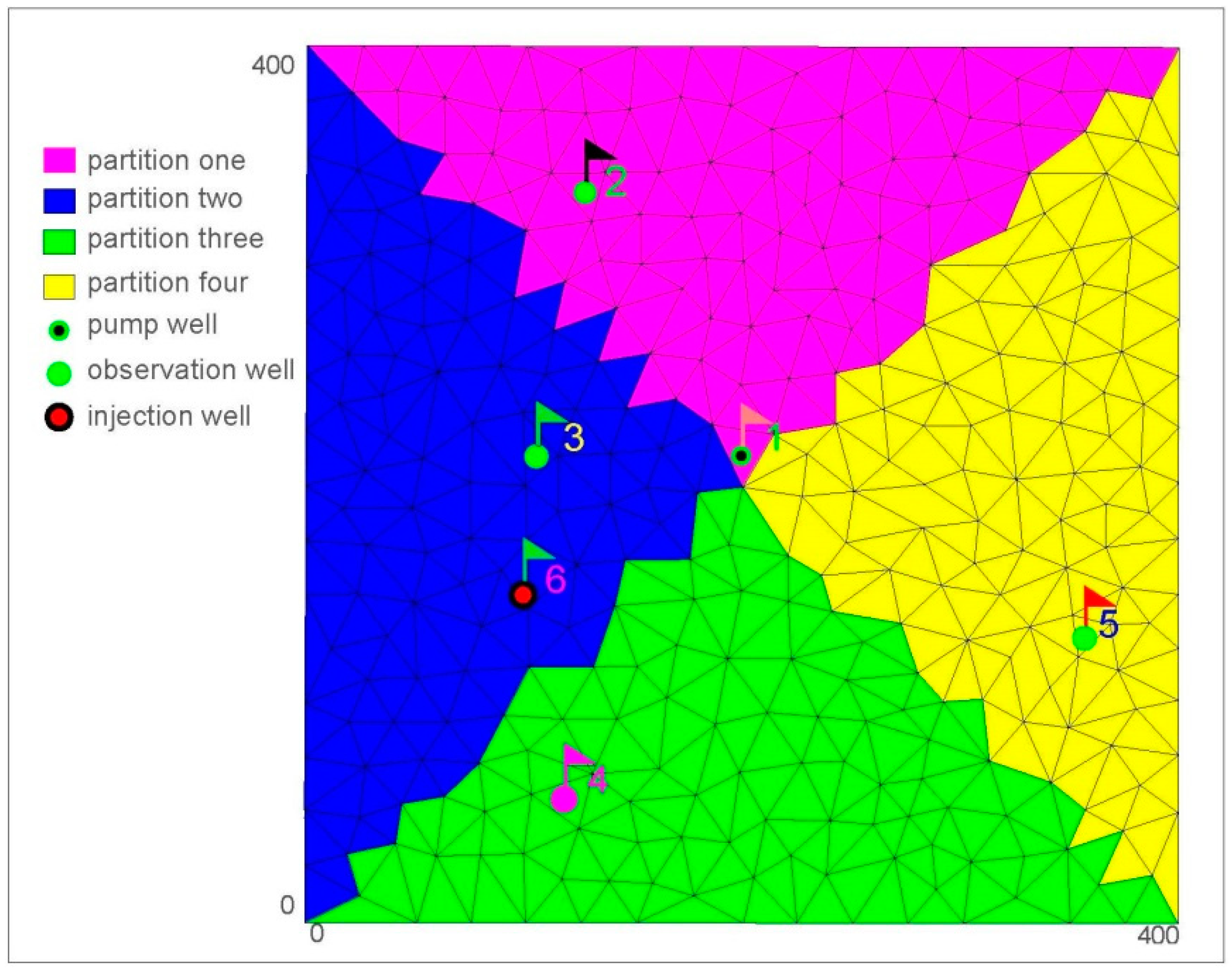
To verify the effectiveness of the method in solving the interval-based parametric groundwater head equation, we establish a synthetic two-dimensional confined aquifer flow model in this section. The confined aquifer has an extent of 400 m × 400 m in horizontal dimensions, and a thickness of 10 m. The total numbers of subdivision triangular elements are 620. Taking the aquifer base as the reference surface, the top elevation of the aquifer is 10 m. The initial water head of the aquifer is uniformly set at 100 m, the initial hydraulic gradient is zero, and the left boundary of the aquifer is defined as a constant-head boundary with a value of 100 m. The remaining three boundaries of the aquifer are set to be general-head boundaries (GHB) in which the head, the hydraulic conductivity and the reciprocal of the distance are 100 m, 1 m/day and 0.1 m−1, respectively. The aquifer is heterogeneous and isotropic. According to different hydraulic conductivity values chosen at different regions, the aquifer is divided into four sections.
A graphic representation of the aquifer associated with a sample discretization used in the numerical simulation is shown in
Figure 1. The values of the hydraulic conductivities of different zones are shown in
Table 1. From
Figure 1, one can see that the pumping well (well No. 1 in
Figure 1), which has coordinates of (200 m, 200 m), is located at the center of the aquifer. Meanwhile, each section contains an observation well. Considering steady-state flow, we will calculate and analyze three scenarios in the following sections. For Scenario One, the conductivities of the four sections are considered as the interval variable. On the basis of Scenario One, an injection well at coordinates of (100 m, 150 m) is added in Scenario Two. On the basis of Scenario Two, additional interval of boundary conditions is considered in Scenario Three. To verify the effectiveness of this proposed method, the degree of problem complexity increases from Scenario One to Scenario Three.
Where the numerical calculations are performed, we adopt the Groundwater Flow Model (GFModel) program which is based on an arbitrary polygon finite-difference method, developed by the first author (Guiming Dong) of China University of Mining and Technology [
52]. The domain of interest is discretized into polygons. Further refinement of the discretization mesh does not provide noticeable improvement of the simulation results. Adopting the method of superposition of the osmotic matrix of the triangular element to form the coefficient matrix, the GFModel is a newly developed program, which can deal with the common boundary conditions, sources and sinks, and time-dependent hydrogeological parameters and can also carry out three-dimensional groundwater flow MC calculation, the general perturbation calculation, and interval parameter perturbation calculation.
4.1. Scenario One
We set the flow of the pumping wells to be 1500 m
3/day. Increasing at 0.05 intervals, the rate of change in the hydraulic conductivity changes from 0.05 to 0.4 in four zones seen in
Figure 1, where the average value multiplied by the rate of change is equal to half of the variation of the parameter as referring to Equation (10). For example, the average hydraulic conductivity of the first partition is 1 m/day, when the rate of change is 0.2, then the interval of the hydraulic conductivity is [0.8, 1.2], and the variation of the parameter is 0.4 m/day. Moreover, we perform a comparative analysis of the MC method and the method proposed in this paper. The number of realizations used in the MC method is found to be 6.25 × 10
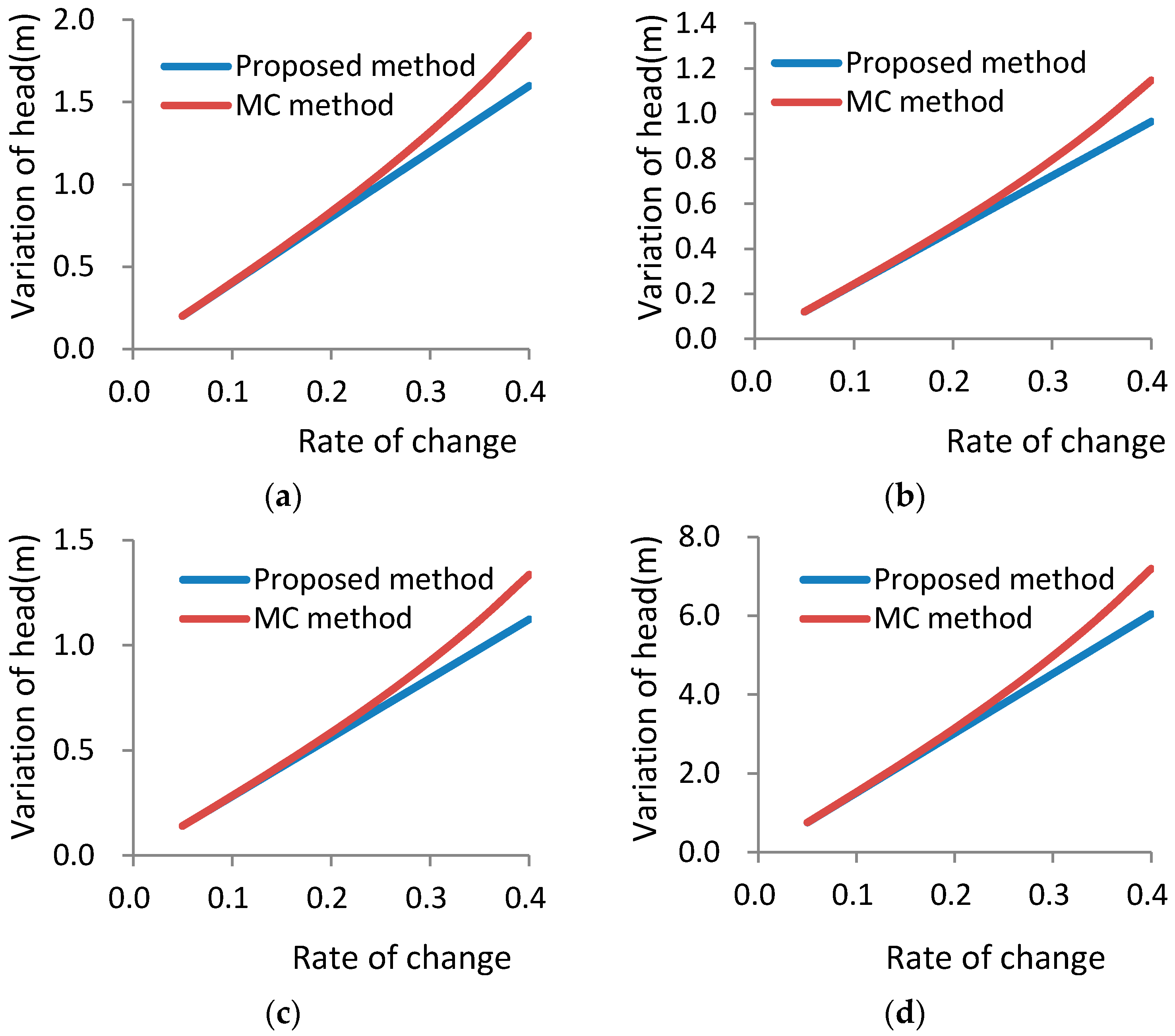
6 after some numerical exercises. The maximum, minimum and variation of the groundwater head obtained by the MC method are taken as theoretical values. Using a computer with 4 GB of memory and CPU frequency of 2.5 GHz, the calculation time of MC is 2.6 days, and the calculation time of the IUM is 4.2 s. The results are shown in
Figure 2,
Table 2 and
Table 3.
The smallest head and the largest head in each observation well decrease and increase respectively as the hydraulic conductivity rate of change increases, and the variations in head and the relative error increase correspondingly. The results of the proposed method show that when the rate of change is less than 0.2, the relative error of the head variation is generally limited to within 5%; while when the rate of change is less than 0.3, the relative error of the head variation is generally limited to within 10%, as seen in
Table 1.
The theoretical head variation obtained from the MC method in the observation wells displays somewhat nonlinear relationship with the rate of change in the hydraulic conductivity. Instead, the relationship is best described as piecewise-linear. As can be seen from
Figure 2, the theoretical head variation follows a nice linear relationship with the rate of change when the latter is less than 0.2. However, the theoretical variation starts to deviate from the linear trend when the rate of change is greater than 0.2.
For a given rate of change, when the hydraulic conductivities of four sections simultaneously take their minimum values, the head for the observation well is the same as the minimum theoretical head. Similarly, when the hydraulic conductivities of four sections simultaneously take their maximum values, the head for the observation well is also the same as the maximum theoretical head. The variations in the head calculated by the general perturbation method are the same as those calculated using the method proposed in this study. In the meantime, the corresponding values of ψ all must be positive in Equation (22), because only in this case, the general perturbation method calculated results will be the same with the computational result of Equation (25), which suggests that the general perturbation method has a close relationship with the proposed method.
4.2. Scenario Two
Based on Scenario One, we install a new injection well with a flow rate of 1500 m
3/day at the coordinates (100 m, 150 m). The hydraulic conductivity rate of change is also adjusted from 0.05 to 0.4. The number of realizations used in the MC method model is also 6.25 × 10
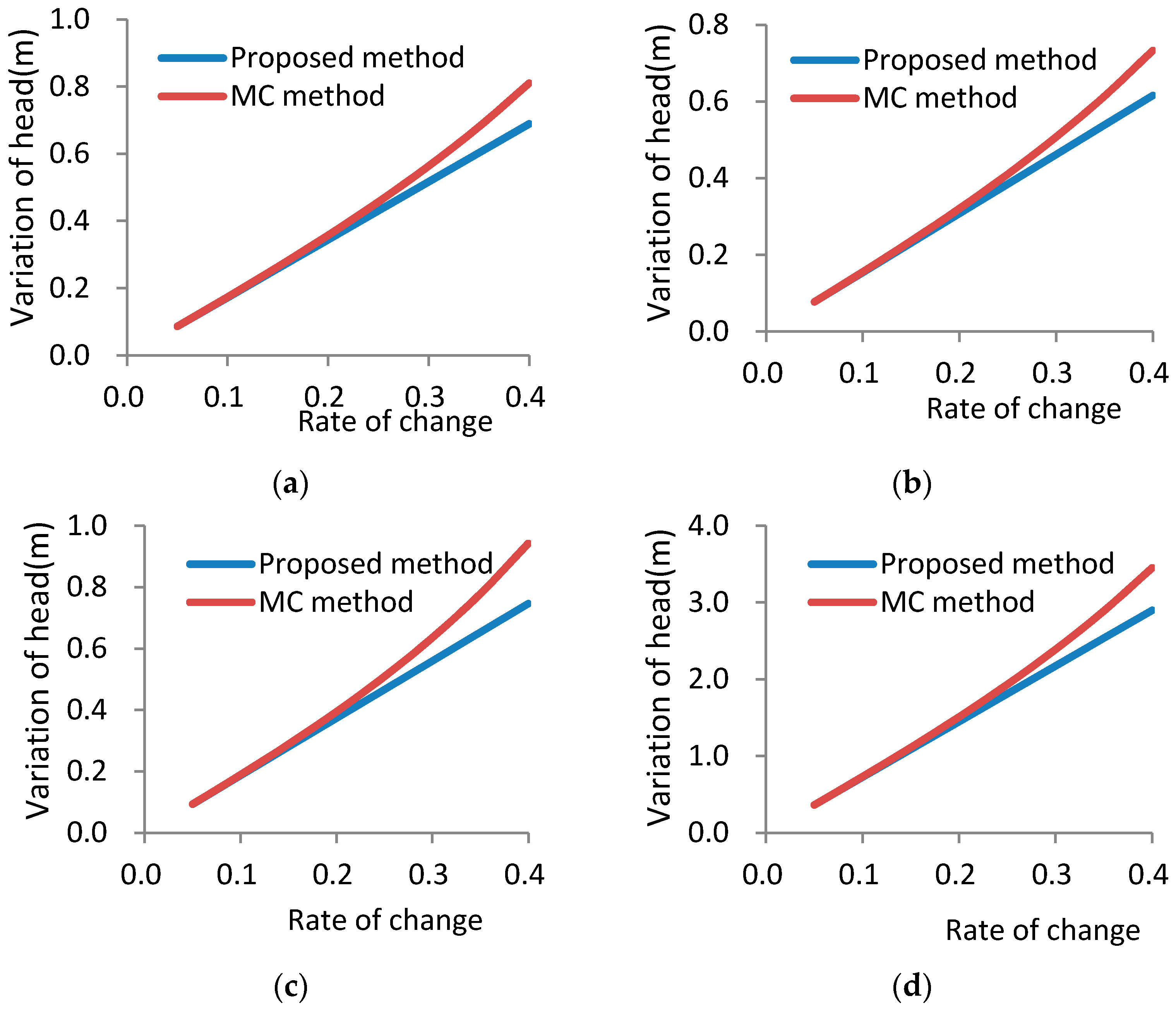
6. The calculation time of MC and the IUM is same as that on the scenario One. The results are shown in
Figure 3,
Table 4 and
Table 5.
The results of Scenario Two are consistent with their counterparts in Scenario One, with some slight discrepancies in terms of specific values shown in
Table 3 and
Figure 3. For the same rate of change in the hydraulic conductivity, the relative errors of observation well 3 and observation well 5 are basically the same in both scenarios; while the relative error of observation well 4 in Scenario Two is slightly larger than its corresponding value in Scenario One. Moreover, the relative error of the observation well 2 under Scenario Two is slightly less than its corresponding value under Scenario One. It is obvious that although Scenario Two is more complicated hydrogeologically (as it involves an additional injection well) than that of Scenario One, the accuracy of the proposed method does not show any noticeable decline. In addition, the results of the proposed method show that when the rate of change is less than 0.2, the relative error of the head variation is generally less than 5%; while when the rate of change is less than 0.3, the relative error of the head variation is generally less than 10%.
For a given rate of change of the hydraulic conductivity, further analysis shows that when the hydraulic conductivities of four sections simultaneously take their minimum values, the head for the observation well does not correspond to the minimum theoretical head calculated from the MC method. Similar conclusion can be drawn when the hydraulic conductivities of four sections simultaneously take their maximum values. This finding is certainly quite different from that of Scenario One. Taking the observation well 4 as an example, with a rate of change of 0.2, when the hydraulic conductivities of four sections are set at their minimum and maximum values simultaneously, the heads of observation well 4 are 100.62 and 100.41 m, respectively. These values are clearly different from the minimum (100.35 m) and the maximum (100.74 m) heads calculated using the MC method.
Based on above analysis, one can conclude that the result of the general perturbation method will differ from the method proposed in this paper. That implies that the corresponding value of ψ in Equation (22) is not always positive. Using observation well 4 as an example, when the hydraulic conductivity rate of change is all 0.2 in four sections, the head variation of the observation well is 0.20 m using the general perturbation method, which is obviously different from the head variation of 0.37 m calculated using the method of this study. It also shows that the method proposed in this study can calculate the extreme values of the head at any given node, whereas the general perturbation method only calculates the head variation of the node under a certain variation, which is obviously different.
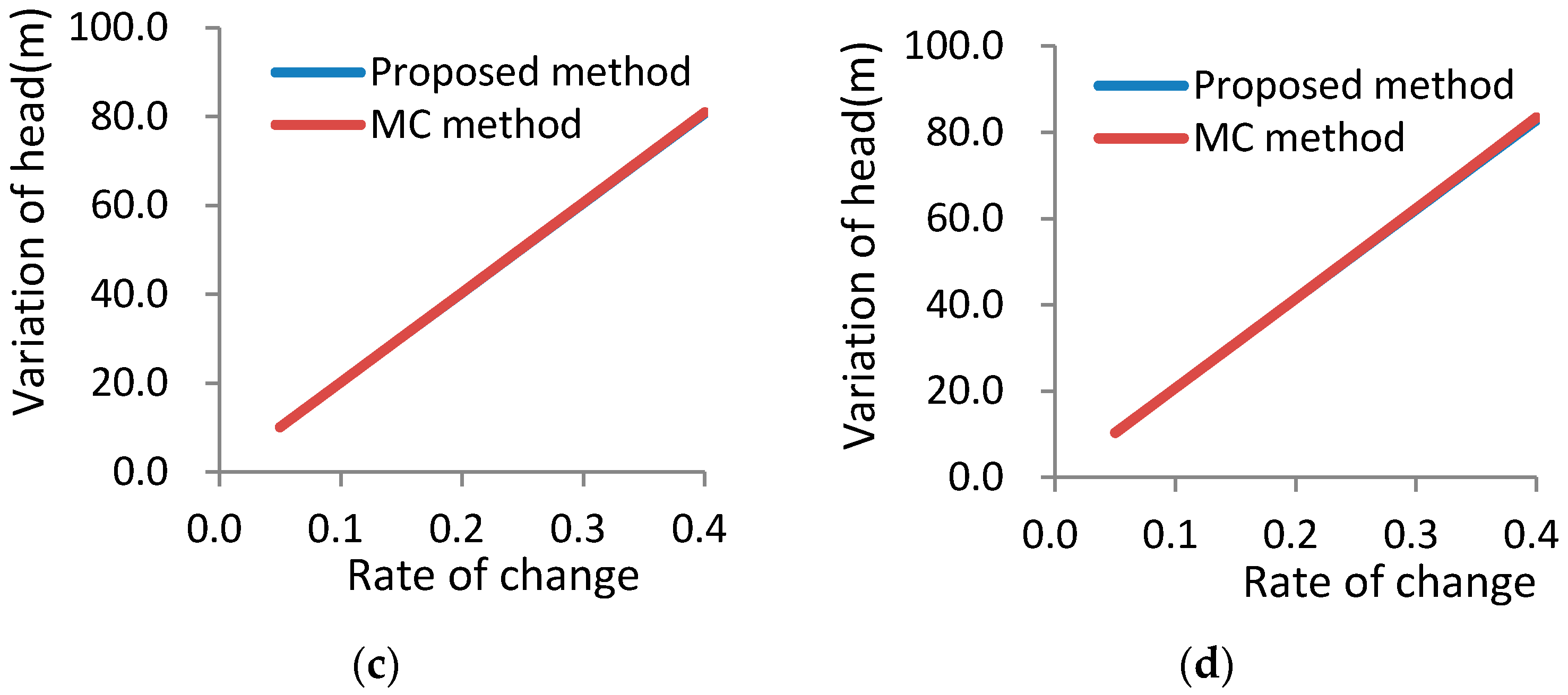
4.3. Scenario Three
The difference between Scenario Three and Scenario Two is that the number of hydrogeological elements with interval variations, and the hydrogeological elements with interval variations, include the hydraulic conductivities of four sections, the head at the head boundary, the hydraulic conductivity, and the head at GHB. The reciprocal of the distance at GHB is constant. The hydraulic conductivity rate of change also changes from 0.05 to 0.4 in four sections. The numbers of realizations used in the MC method model are also 6.25 × 10
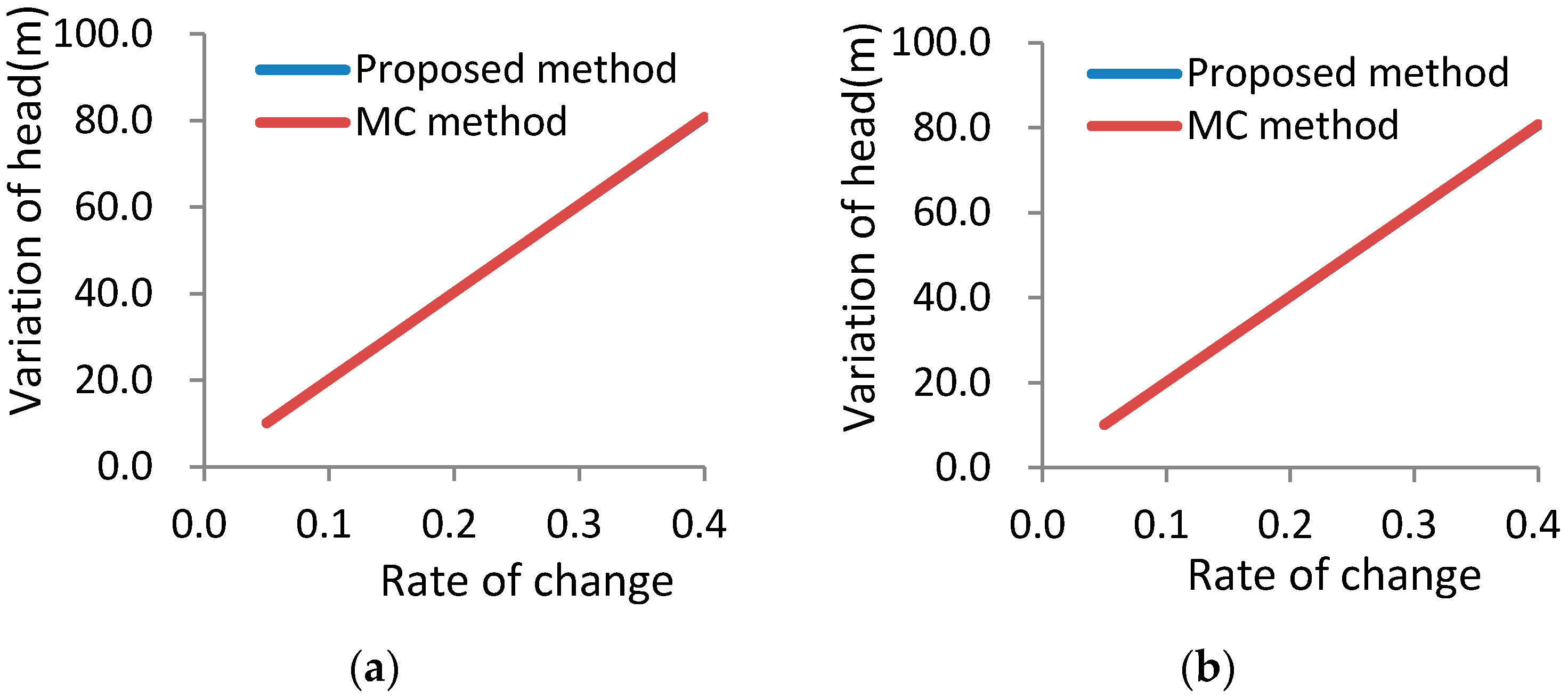
6 times. The calculation time of MC is 4.1 days, while the calculation time of the IUM is only 4.2 s. The results are shown in
Figure 4,
Table 6 and
Table 7.
The smallest head and the largest head for each observation well decrease and increase, respectively, as the hydraulic conductivity rate of change increases, and the variations in head and the relative error increase correspondingly. The results of the proposed method show that when the rate of change reaches 0.4, the maximum of the relative error is only 0.65%. This suggests that the relative error is generally limited to 1%.
There is a nice linear relationship between the theoretical head variation calculated from the MC method and the rate of change of the hydraulic conductivity, as can be seen from
Figure 4. Interestingly enough, the head variation calculated by the proposed method of this study shows almost the same linear relationship with the rate of change in the hydraulic conductivity. This explains why the two methods have relatively small relative errors. It is obvious that, although the number of hydrogeological elements that are allowed to change in Scenario Three is larger (Scenario Three includes seven changing hydrogeological elements), the linearity of the system interval response is improved, and the accuracy of the method is improved as well. Therefore, the number of intervals does not appear to be the primary factor determining the accuracy of the proposed method. Because the degree of linearity of Scenario Three is higher than that of Scenario Two, it is reasonable to infer that the degree of linearity should be the main factor affecting the accuracy of the proposed method.
As in Scenario Two, the head for the observation well is not always the same as the minimum (or maximum) theoretical head when all the hydrogeological elements take their minimum (or maximum) values. The result of the general perturbation method is also different from that obtained from the method of this study. Once again, using observation well 4 as an example, with a rate of change of 0.1, where the rate of change is for all the seven changing hydrogeological elements, the head variation of the observation well is 19.90 m using the general perturbation method. This result is obviously different from the head variation of 20.19 m calculated by the method of this study. It can be seen from the three scenarios of numerical examples when three conditions, including the aquifer are confined aquifer, and both are linear expressions and the interval of the changing elements is little change, are satisfied in the same time, the IUM can perform better, while any of the above three conditions are not satisfied, the IUM validity has not yet been checked. The inverse of matrix is the main factor that influences the calculation efficiency of the method. For the above problems, we will carry out research in the following study. In addition, the method can only obtain the changing interval of the head, while giving the statistical characteristics of the head.
5. Conclusions
In this study, in contrast to the stochastic methods used in many numerical simulations of groundwater flow and solute transport, a new concept involving interval mathematics is proposed to quantify the uncertainty analysis of groundwater flow and solute transport. This concept originates from the concept of interval uncertainty. The form of the interval-type groundwater flow governing equation is presented, and the interval parameter perturbation method is provided. Since this method only required matrix inversion to obtain the derivative of the head for the changing hydrogeological elements, the method is computationally much more efficient than the conventional MC method. Using this method, the interval response of the groundwater head can be obtained, which is different from the value obtained by the general perturbation method.
Three hypothetical scenarios with an increasing degree of hydrogeological complexity and uncertainty are used as examples to illustrate the performance of the proposed method, including its accuracy and robustness. It appears that the accuracy of the method depends on the linearity between the simulated head variation and the changing hydrogeological elements. In addressing practical problems, the proposed method is recommended when the rate of change for the changing hydrogeological elements is less than a certain value such as 0.2, as great linearity between the simulated head variation and the changing hydrogeological elements has been identified under such condition. Further research is needed to determine the upper limit of the rate of change for the changing hydrogeological elements when this method is used under a wide range of hydrogeological conditions.