Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations
Abstract
1. Introduction
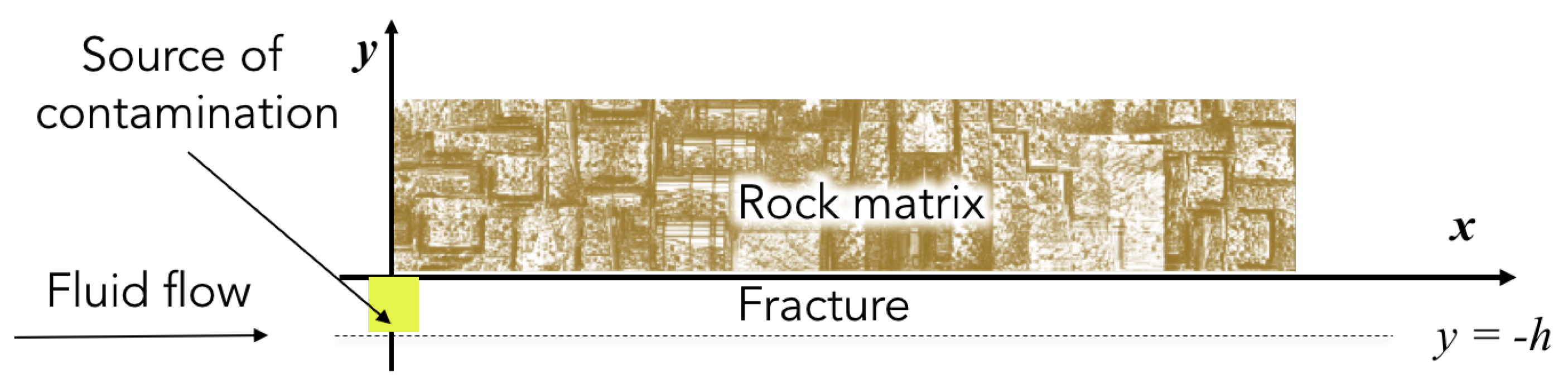
2. Model
2.1. Governing Equation
2.2. Analytical Solution
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Coats, K.; Smith, B.D. Dead-end pore volume and dispersion in porous media. Soc. Petrol. Eng. J. 1964, 4, 73–84. [Google Scholar] [CrossRef]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for network of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef]
- Sahimi, M. Flow phenomena in rocks: From continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 1993, 65, 1395–1534. [Google Scholar]
- Edery, Y.; Guadagnini, A.; Scher, H.; Berkowitz, B. Origins of anomalous transport in heterogeneous media: Structural and dynamic controls. Water Resour. Res. 2014, 50, 1490–1505. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N. Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resour. Res. 1998, 34, 1027–1033. [Google Scholar] [CrossRef]
- Haggerty, R.; Wondzell, S.M.; Johnson, M.A. Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream. Geophys. Res. Lett. 2002, 29, 1640. [Google Scholar] [CrossRef]
- Radilla, G.; Sausse, J.; Sanjuan, B.; Fourar, M. Interpreting tracer tests in the enhanced geothermal system (EGS) of Soultz-sous-Forêts using the equivalent stratified medium approach. Geothermics 2012, 44, 43–51. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Navier-Stokes flow and transport simulations using real fractures shows heavy tailing due to eddies. Geophys. Res. Lett. 2007, 34, L14404. [Google Scholar] [CrossRef]
- Hodgkinson, D.; Benabderrahmane, H.; Elert, M.; Hautojärvi, A.; Selroos, J.O.; Tanaka, Y.; Uchida, M. An overview of Task 6 of the Aspö Task Force: Modelling groundwater and solute transport: Improved understanding of radionuclide transport in fractured rock. Hydrogeol. J. 2009, 17, 1035–1049. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Interpreting tracer breakthrough tailing from different forced-gradient tracer experiment configurations in fractured bedrock. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Tsang, Y.W. Study of alternative tracer tests in characterizing transport in fractured rocks. Geophys. Res. Lett. 1995, 22, 1421–1424. [Google Scholar] [CrossRef]
- Tang, D.H.; Frind, E.O.; Sudicky, E.A. Contaminant transport in fractured porous media: Analytical solution for a single fracture. Water Resour. Res. 1981, 17, 555–564. [Google Scholar] [CrossRef]
- Sudicky, E.; Frind, E. Contaminant transport in fractured porous media: Analytical solutions for a system of parallel fractures. Water Resour. Res. 1982, 18, 1634–1642. [Google Scholar] [CrossRef]
- Neretnieks, I. A note on fracture flow dispersion mechanisms in the ground. Water Resour. Res. 1983, 19, 364–370. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef]
- Yates, S.R. An analytical solution for one-dimensional transport in heterogeneous porous media. Water Resour. Res. 1990, 26, 2331–2338. [Google Scholar]
- Haggerty, R.; Gorelick, S.M. Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Morales-Casique, E.; Neuman, S.P.; Guadagnini, A. Non-local and localized analyses of non-reactive solute transport in bounded randomly heterogeneous porous media: Theoretical framework. Adv. Water Resour. 2006, 29, 1238–1255. [Google Scholar] [CrossRef]
- Schumer, R.; Meerschaert, M.M.; Baeumer, B. Fractional advection-dispersion equations for modeling transport at the Earth surface. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.V.; Turner, I.; Zhuang, P. Time fractional advection-dispersion equation. J. Appl. Math. Comput. 2003, 13, 233–245. [Google Scholar] [CrossRef]
- Fomin, S.; Chugunov, V.; Hashida, T. The effect of non-Fickian diffusion into surrounding rocks on contaminant transport in a fractured porous aquifer. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2923–2939. [Google Scholar] [CrossRef]
- Suzuki, A.; Fomin, S.A.; Chugunov, V.A.; Niibori, Y.; Hashida, T. Fractional diffusion modeling of heat transfer in porous and fractured media. Int. J. Heat Mass Transf. 2016, 103, 611–618. [Google Scholar] [CrossRef]
- Zumofen, G.; Klafter, J. Scale-invariant motion in intermittent chaotic systems. Phys. Rev. E 1993, 47, 851–863. [Google Scholar] [CrossRef]
- Penttinen, L.; Siitari-kauppi, M.; Ikonen, J. Forsmark Site Investigation Determination of Porosity and Micro Fracturing Using the C-PMMA Technique in Samples Taken from Forsmark Area; Technical Report; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2006. [Google Scholar]
- Fomin, S.A.; Chugunov, V.A.; Hashida, T. Non-Fickian mass transport in fractured porous media. Adv. Water Resour. 2011, 34, 205–214. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar] [CrossRef]
- Grisak, G.; Pickens, J. An analytical solution for solute transport through fractured media with matrix diffusion. J. Hydrol. 1981, 52, 47–57. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations: Volume 2: Applications in Engineering and Physical Sciences; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, A.; Fomin, S.; Chugunov, V.; Hashida, T. Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water 2018, 10, 123. https://doi.org/10.3390/w10020123
Suzuki A, Fomin S, Chugunov V, Hashida T. Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water. 2018; 10(2):123. https://doi.org/10.3390/w10020123
Chicago/Turabian StyleSuzuki, Anna, Sergei Fomin, Vladimir Chugunov, and Toshiyuki Hashida. 2018. "Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations" Water 10, no. 2: 123. https://doi.org/10.3390/w10020123
APA StyleSuzuki, A., Fomin, S., Chugunov, V., & Hashida, T. (2018). Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water, 10(2), 123. https://doi.org/10.3390/w10020123



