Next Article in Journal
Water Experts’ Perception of Risk for New and Unfamiliar Water Projects
Previous Article in Journal
SPHysics Simulation of Experimental Spillway Hydraulics
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 12
10.3390/w9120936
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods

by
Elahe Akbari
1,2,
Seyed Kazem Alavipanah
1,*,
Mehrdad Jeihouni
1,
Mohammad Hajeb
1,3,
Dagmar Haase
4,5 and
Sadroddin Alavipanah
4
1
Department of Remote Sensing and GIS, Faculty of Geography, University of Tehran, Tehran 1417853933, Iran
2
Department of Climatology and Geomorphology, Faculty of Geography and Environmental Sciences, Hakim Sabzevari University, Sabzevar 9617976487, Iran
3
Department of Remote Sensing and GIS, Shahid Beheshti University, Tehran 1983963113, Iran
4
Department of Geography, Humboldt University of Berlin, Unter den Linden 6, 10099 Berlin, Germany
5
Department of Computational Landscape Ecology, Helmholtz Centre for Environmental Research UFZ, 04318 Leipzig, Germany
*
Author to whom correspondence should be addressed.
Water 2017, 9(12), 936; https://doi.org/10.3390/w9120936
Submission received: 3 October 2017 / Revised: 13 November 2017 / Accepted: 16 November 2017 / Published: 14 December 2017
Browse Figures
Versions Notes

Abstract

:
Oceans/Seas are important components of Earth that are affected by global warming and climate change. Recent studies have indicated that the deeper oceans are responsible for climate variability by changing the Earth’s ecosystem; therefore, assessing them has become more important. Remote sensing can provide sea surface data at high spatial/temporal resolution and with large spatial coverage, which allows for remarkable discoveries in the ocean sciences. The deep layers of the ocean/sea, however, cannot be directly detected by satellite remote sensors. Therefore, researchers have examined the relationships between salinity, height, and temperature of the oceans/Seas to estimate their subsurface water temperature using dynamical models and model-based data assimilation (numerical based and statistical) approaches, which simulate these parameters by employing remotely sensed data and in situ measurements. Due to the requirements of comprehensive perception and the importance of global warming in decision making and scientific studies, this review provides comprehensive information on the methods that are used to estimate ocean/sea subsurface water temperature from remotely and non-remotely sensed data. To clarify the subsurface processes, the challenges, limitations, and perspectives of the existing methods are also investigated.

1. Introduction

Further temperature increases and climate changes are projected for the future [1,2,3,4,5] due to the dominant positive forcing of increasing greenhouse gases [4,6]. Most threats under projected climate change are related to warming in many parts of the planet, droughts [7,8,9], floods [7,8,10,11,12], food production [5,13,14], negative economic effects on aircraft performance [15], sea level rise [4,10,12], economic assets, human lives, forcing of inland migration in coastal zones, and dust storms leading to aerosol pollution [7]. Additionally, climate change includes indirect threats to public health [5] through harmful changes in air quality, the spread of disease vectors, food insecurity and under-nutrition, mental illness [8], and death due to cardiovascular and respiratory diseases [16]. Since the current most serious challenge is global warming, the prediction of these possible changes in ecosystem function seems to be necessary [2].
Ocean surface water temperature has increased due to climate change [17], runoff from impervious surfaces [18] and thermal effluents from industrial processes [19]. Since 1990, deep oceans below 2000 m along several sections have warmed [20,21,22]. At the same time, several researchers have suggested the warming of the world oceans [23,24,25,26,27,28,29,30,31]. Additionally, Balmaseda et al. (2013) [30] claimed that “30% of the ocean warming over the past decade has occurred in the deeper oceans below 700 m”, which they note is unprecedented over at least the past half century.
Temperature is an important factor in coastal processes such as biological activity, heat momentum and exchange, interaction with the surrounding air, and climate change [32]. Another crucial issue in oceanography is assessing ecosystem changes by remotely sensed satellite data. Reliable global ocean coverage of environmental properties such as sea surface temperature, sea surface height, surface winds, and ocean color have been provided by satellite imagery with relatively high spatial/temporal resolutions. These properties of satellite-based oceanographic data can lead to their use in a variety of ecosystem studies [33]. For example, the investigation of chlorophyll-a pigment concentrations and oceanographic features such as fronts or eddies can be evaluated by temperature [34].
Visible light consists of various wavelengths of light ranging from violet to red. Violet light has the highest energy and penetrates deeper than other wavelengths. Penetration of the visible portion of the spectrum in the upper layers of the oceans plays a crucial role in sea surface temperature (SST) and heat transfer [35]. Violet light penetrates to deeper depths and is ultimately absorbed; this mechanism, along with more effective processes such as vertical motion, horizontal transport, and mixing, may impact the temperature of subsurface waters. Subsurface is defined as below the surface of the Earth, the oceans, etc. [36]. The oceans’ subsurface has been categorized into five main layers/zones by scientists. Their expansion is from the surface to the most extreme depths where light can no longer penetrate. As we come down into these unexplored zones of oceans, the temperature decreases and the pressure increases at an amazing rate. These large zones are: Epipelagic, Mesopelagic, Bathypelagic, Abyssopelagic and Hadalpelagic, respectively. The Epipelagic zone extends from the surface to 200 m, and is where most of the visible light penetrates and causes an increase in the temperature. In the Mesopelagic zone, which extends from 200 m to 1000 m, the light penetrating to this depth is extremely faint and temperature is changed rapidly. In the other zones, the only visible light is produced by the creatures themselves and with increasing depth there is no light at all. The water temperature decreases as the depth increases, and reaches to near/below freezing [37].
Satellite remote sensing acquires information about the surface, subsurface, and atmosphere of the Earth remotely using onboard satellite sensors, and is of great importance to climate system observations. The use of satellites allows for the observation of the states and processes of the atmosphere, land, and ocean at several spatiotemporal scales [38]. However, remote sensing data cannot directly provide information about ocean/sea subsurface water temperature [39]. Most of the studies about ocean/sea subsurface water temperature must rely on in situ measurements, model-based data assimilation (numerical-based and statistical), and dynamical modeling. Additionally, by assessing the in situ based methods, we conclude that they cannot provide suitable spatial coverage in near-real time. Therefore, researchers have tried to improve the accuracy of large-scale subsurface temperature estimates in near-real time using assimilation models. Alternatively, satellite measurements can be used to obtain subsurface information from assimilation models if special algorithms/techniques are developed [31,40].
Based on the development of sensors and simulation algorithms, it is possible to estimate and assess ocean/sea subsurface water temperature. To date, there have been no reviews on the methods used to estimate ocean/sea subsurface water temperature. This state-of-the-art review provides clear and comprehensive information on the methods used to estimate ocean/sea subsurface water temperature using remotely sensed surface temperature. We reviewed approximately 15,000 articles related to water temperature, and found 187 articles related to the estimation and measurement of ocean/sea subsurface water temperature. In the current study, we separated the remote sensing and non-remote sensing-based methods used for assimilating and measuring ocean/sea subsurface water temperature.
A literature search via Google Scholar (Google, Menlo Park, CA, USA), a large abstract and citation database of peer-reviewed literature, shows that the number of existing studies on remote sensing and non-remote sensing of ocean/sea subsurface water temperature is 110 and 77 articles, respectively. We followed all keywords about ocean/sea subsurface water temperature, including: subsurface, water, temperature, ocean, sea, remote sensing, thermal, heat, satellite, diurnal warming. In addition to the above single words, combinations of them were also considered. All related articles parts demonstrated below the title of each article in Google Scholar were also downloaded. After reading the articles, we saved those related to the objective of this review to the library section of Google Scholar. The literature review indicated that between 1975 and 1991, the number of publications on the remote sensing of ocean/sea subsurface water temperature increased, but most studies were performed using in situ measurements of Raman and Brillouin scattering (Figure 1). This greatly reflects the lack of suitable remote sensors for the detection and estimation of ocean/sea subsurface water temperature, undeveloped digital image processing techniques, and constrained computing power. Figure 1 shows the increasing rate of annual citations on the subject. In the 1990s, the average number of annual remote sensing and non-remote sensing citations (the number of citations per article per year) on ocean/sea subsurface water temperature were 101.8 and 147, respectively. At the same time, the publication citations increased, while the average number of annual citations in the 2000s were 238.3 and 359.4 for remote sensing and non-remote sensing studies, respectively. This comparison indicates that ocean/sea subsurface water temperature has become one of the more dynamic fields in remote sensing and non-remote sensing studies. In remote sensing, not only has the number of publications increased since the late 1990s, but the number of citations has also increased. However, the number of citations for the years 2015 and 2016 appears to be low, as shown in Figure 1b. This could be due to the pattern that literature is often cited several months or even years after it has been published. Therefore, the number of citations for the years of 2015 and 2016 was lower in comparison with the previous years. Furthermore, the remote sensing of ocean/sea subsurface water temperature using assimilation techniques along with in situ measurements rapidly gained interest at the turn of the 21st century.
Our review not only surveys the structure of the subsurface of the water but it also presents the key limitations and perspectives. We also intend to follow the categories of subsurface parameter estimation methods of Wu et al. [41], including dynamical modeling, model-based data assimilation, and in situ measurements. Model-based data assimilations are separated into two subtopics: numerical modeling and statistical approaches. Table 1 lists the relevant peer-refereed journals that published remote-sensing articles using at least one of the categorized methods. This list confirms the abundant literature related to ocean/sea subsurface water temperature from different journals and conference proceedings. In this table, we only list the journals and proceedings that published articles related to dynamical models and model-based data assimilation methods. The articles using in situ Raman and Brillouin scattering measurements (56 articles total) were published mostly in applied optics, optical engineering, nuclear technology, ocean remote sensing using lasers, proceedings, grants, and patents.

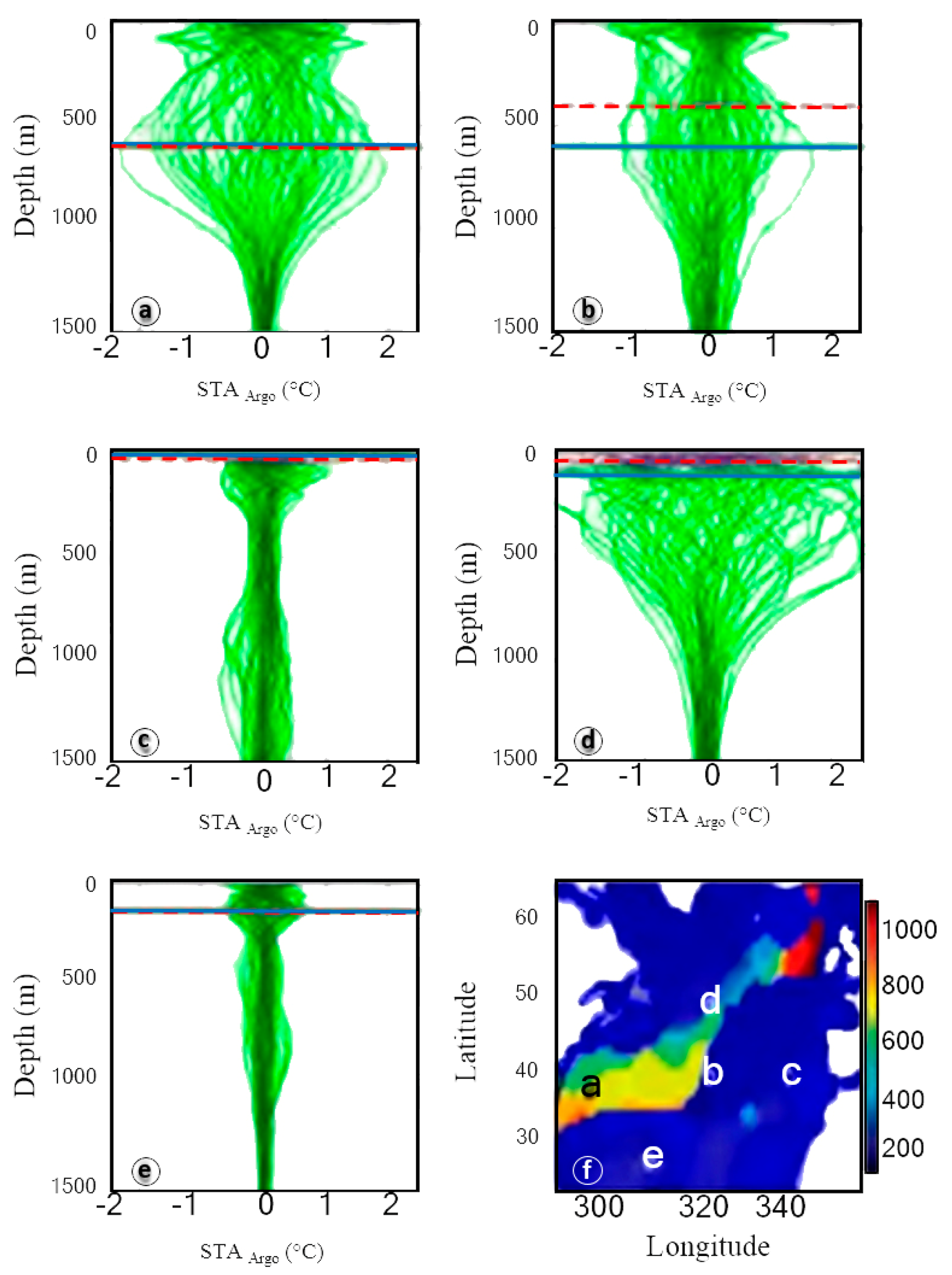
2. Vertical and Horizontal Ocean/Sea Subsurface Water Temperature Anomalies

Since widespread warming of the world’s deeper oceans has been proven by more evidence, [20,21,22,28,42,43], estimating the subsurface thermal structure of the global oceans accurately is important [28,30,31]. Hence, subsurface flow fields have been estimated by oceanographers, and horizontal and vertical advection have been computed in the ocean interior [40].
Comparisons of the vertical and horizontal anomalies between the Baltic and the North Sea are shown in Figure 2a,b, respectively. Karagali et al. [44] indicated that most anomalies could be seen at depths up to 200 m. This was also confirmed by Eastwood et al. [45]. They showed that diurnal warming events are mostly observed between depths of 20 m and 40 m. In addition, in the North Sea (blue color), most observations are recorded within the first 5 km from the coast, decreasing to zero observations 300 km from the shore. No anomalies are detected further than 120 km offshore in the Baltic Sea (red color); however, the first 10 km from the coast contains the most anomalies. In general, both figures demonstrate the conditions of the coastal and shallow seas, where 75% of the anomalies are at depths shallower than 90 m (80 m) in the North Sea (Baltic Sea) and within 125 km (45 km) from the coast.
Because global warming has accelerated, the roles of the oceans are crucial considerations, as they are huge heat and water reservoirs. Therefore, it is beneficial to understand what occurred in the global oceans over the last century. Levitus et al. [29] showed that more warming occurred at the surface in all basins. The largest total increase was exposed in the 0–100 m layer of the Pacific. At depths deeper than 100 m, the Atlantic presents the greatest increase of all ocean basins in all layers above 2000 m (Figure 3). Additionally, the authors showed the 700–2000 m layer is responsible for approximately one-third of the total warming of the 0–2000 m layer. Kawano et al. [46] estimated that approximately 5% of the heat in the Pacific Ocean was below 3000 m, and widely increased from 1999 to 2007.

3. Impacts of Different Dynamics on Ocean/Sea Subsurface Water Temperature Profiles

Ocean/sea subsurface water temperature is deeply affected by water turbulence. Both vertical motion and horizontal transport disturb some simple roles about changing their subsurface water temperature by depth. Accordingly, considering vertical motion and horizontal transport seem to be necessary for estimating ocean/sea subsurface water temperature, and simulating these movements may lead to more precise estimations of ocean/sea subsurface water temperature. It can be interestingly stated that ocean dynamics and subsurface water temperature have cause and effect relations, meaning that one affects the other and simultaneously is affected by it.
Halkides et al. [47] illustrated the turbulent vertical mixing along with surface heat flux contribution to the mixed-layer temperature (MLT) tendency in the Banda–Arafura Seas region. Halkides et al. [48] confirmed the horizontal advection and both subsurface processes and surface heat flux are generally more important controlling factors in the Equator and away from that, respectively.
The effect of Golf Stream on the monthly subsurface temperature anomaly (STA) and temperature profiles was investigated in Wu et al. [41]. For this purpose, Argo measurements and different dynamic mechanisms in five areas of the North Atlantic are used. The results showed that because of the powerful mixing and advection from the Gulf Stream in the western Atlantic, vast STA changes occurred and the seasonal thermocline could reach up to 1000 m (Figure 4a). Moreover, they mentioned that in the eastern part of the ocean, especially east of the mid-Atlantic Ridge (Figure 4c), the mixed layer occurred within less than 100 m from the surface because of an “undercurrent” of warm and high-salinity water outflowing from the Mediterranean Sea. Additionally, they illustrated that the variation in the eastern basin is approximately one-third to one-fourth that of the variation in the western basin.

4. Remote Sensing Capabilities for Estimating Ocean/Sea Subsurface Water Temperature

Notwithstanding the extensive subsurface in situ measurement projects, such as the Integrated Ocean Observing System (IOOS) and the Global Ocean Observing System (GOOS) with more than 8000 platforms containing Argo floats, drift buoys, moored buoys, gliders, and expendable bathythermographs (XBTs), the existing subsurface observations are spatially sporadic and temporally scarce in most parts of the ocean [28,41]. Therefore, the accurate estimation of the full depth steric height and the amount of ocean heat using exclusively available data is still impossible [28]. Hence, improvements in the accuracy of subsurface thermal structure measurements at large scales are needed for near-real time assimilation models [40]. Oceanography has been revolutionized in the last decade by satellite sensors because of their repetitive, synoptic temperature measurement capabilities over the sea surface [39] and satellite measurements over large-scale regions [31].
Despite the fact that since the 1970s, much of the high spatial and temporal resolution, large overall coverage, and long sea surface time series data have been provided by remote sensing, the data are confined to sea surface phenomena [41]. Knowledge of subsurface temperature seems to be necessary for understanding the mechanisms and processes in the ocean as well as the entire Earth climate system [49].
Diverse and useful ocean subsurface observations have been provided by satellite remote sensing [41,50]. The interior dynamic parameters of oceans can be derived from subsurface and deeper ocean remote sensing, which can help us implicate climate change and determine the processes of subsurface and deeper oceans [40].
Researchers have used the relationship between sea surface and subsurface parameters to estimate the subsurface temperature structure [31,41,50,51,52,53]. Specifically, they have used the relationships between salinity, height, and temperature, and have extended the methodology for assimilating the temperature of the subsurface of the water. Not only are sensors that are able to measure subsurface parameters under development, but the methods for estimating subsurface parameters from sea surface information are also improving. In addition to in situ measurement methods, there are two categories of methods used to estimate subsurface parameters, including dynamical models [52,54,55] and model-based data assimilation. Model-based data assimilation—either numerical model-based data assimilation or a statistical approach—has been used to estimate subsurface ocean parameters. The statistical approach has been used for decades; is relatively easy to establish and has reasonable accuracy, but is not constrained by the dynamical equations. At the same time, the predicted parameter may be limited to the range of the available data. However, numerical models based on data assimilation have become powerful methodologies for parameter estimation in the ocean, and have improved with the development of computational technology. Numerical methods have not only combined in situ measurements and dynamic principles, but they are also the most efficient, accurate, and realistic estimations of interest parameters, and have been accessed with several aspects of introduced uncertainty [41].
Table 2 shows the methods used to estimate ocean/sea subsurface water temperature. In this table, we illustrate the category and subcategory of each ocean/sea subsurface water temperature estimation method along with the types of sensors used. The studies have mostly been performed using statistical methods, and dynamic and numerical models need to be further developed to achieve more accurate results. In addition to the methods applied to estimate ocean/sea subsurface water temperature, in situ measurements of Raman and Brillouin scattering have also been used.
Figure 5 illustrates the methodologies used in relation to ocean/sea subsurface water temperature in the (a) remote sensing and (b) non-remote sensing scopes. This figure proves that statistical models have been used more in both scopes to achieve improved ocean/sea subsurface water temperature assimilation results, and the development of numerical models is the next logical step.
The types of sensors and satellites widely used to assimilate ocean/sea subsurface water temperature include Topex/Poseidon, Jason-1/2, ERS-1/2, ENVISAT, Nimbus-7-SMMR, AVHRR, and other AVISO products. At the same time, researchers have used other ancillary data such as XBT, conductivity-temperature-depth (CTD), Argo floats and ocean databases to assimilate of ocean/sea subsurface water temperature. They have used these data for combining and complementing satellite measurements to relate salinity, height, and temperature, and have extended the methodology for assimilating ocean/sea subsurface water temperature.
In this study, to illustrate most of these studies about modeling ocean/sea subsurface water temperature, we attempt to discuss their methodology, significant findings, and suggestions (Table 3).

5. Vertical Thermal Structure

For the sake of brevity, in this research, some of the parameters influencing ocean/sea subsurface water temperature have been assessed. These parameters include SST, sea surface height (SSH), mixed layer depth (MLD), and thermocline depth. These and other parameters have been used to estimate ocean/sea subsurface water temperature as training and testing data in statistical and numerical models or to construct the dynamical models. These data could be collected and used in the models by in situ measurements or remote sensing data assimilation.
The SSH variation mostly affects the movement of thermocline depth [62]; wind can also cause this movement [63,64,65,66]. So, there is a significant relationship between SSH variation and the subsurface temperature and salinity [24,62,67]. The MLD and thermocline bottom are two regions that affect the ocean’s interior vertical structure. The temperature does not change in MLD, but it changes rapidly until the thermocline bottom and then the temperature is almost constant. There are also complex relationships between all surface parameters (e.g., SST, wind, radiation flux, SSH, salinity) and subsurface parameters (e.g., MLD, thermocline depth) and the ocean/sea subsurface water temperature changes. Accordingly, the following subsections discuss these parameters in more detail.

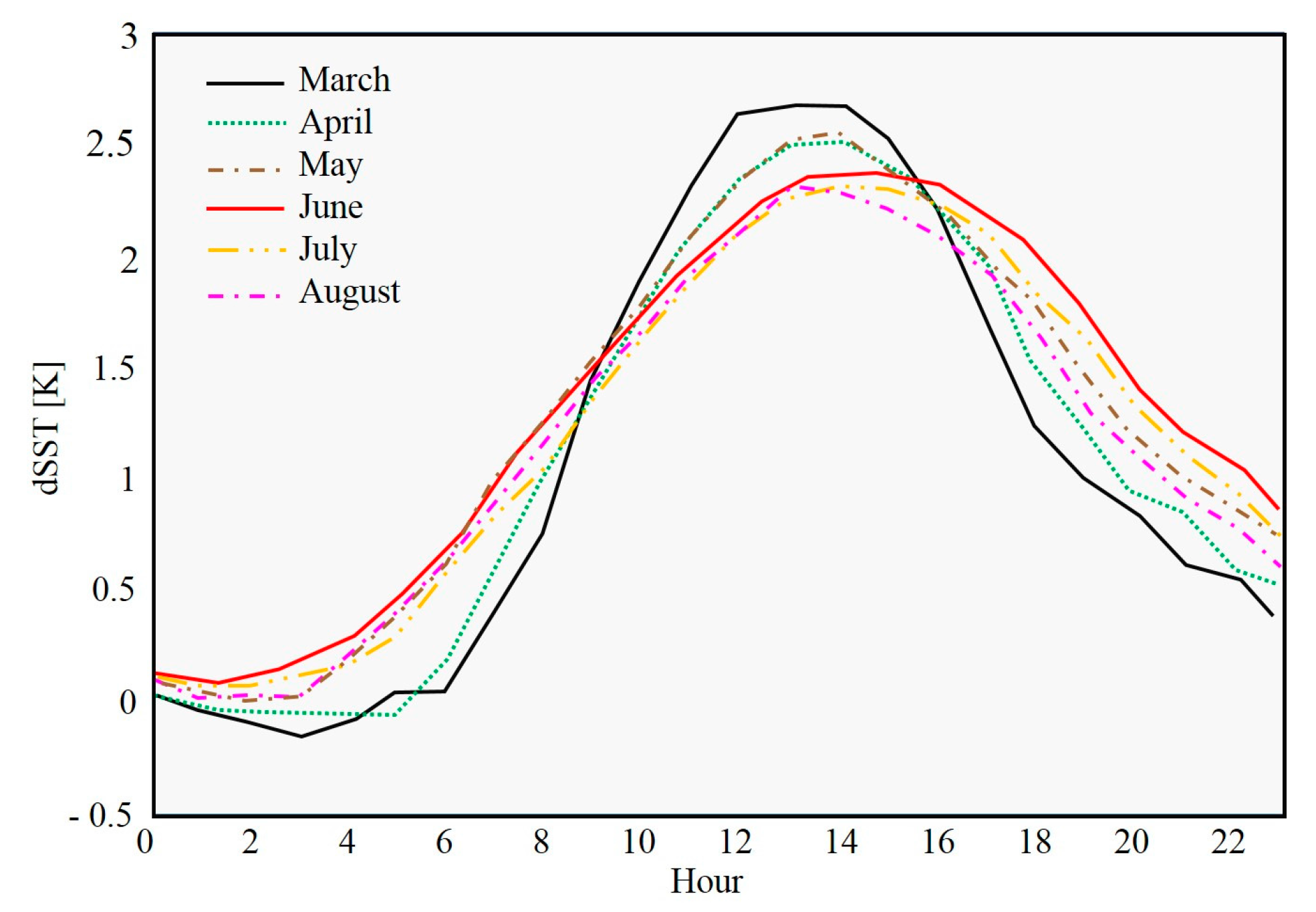
5.1. Sea Surface Temperature

The temperature of the sea surface is an important parameter in the upper ocean that governs biological activity, the exchange of gas, heat, and momentum with the atmosphere [44], ecological and biogeochemical processes; it controls water metabolism and specifies the habitat area for aquatic life [68]. Information about SST is required by scientific, commercial, and social interest activities [69], such as weather forecasting, air–sea interaction modeling, climate change studies, fisheries, and coastal zone management [44].
Figure 6 shows the monthly diurnal Sea Surface Temperature (dSST) from Karagali et al. [44] as the mean hourly difference from the night-time reference SST from March to August. In March, April, and May, the peak SST occurred between 10:00 and 15:00, while this time range was shifted to between 11:00 and 16:00 in June, July, and August. In all months, the minimum values were almost always observed between 02:00 and 04:00. The largest decrease was observed during the transition from late winter to summer. Moreover, the researchers mentioned that there was an approximately 0.5 K difference between sunrise and sunset. This demonstrates that diurnal warming was also related to the general warming that persisted to the following day.
The day–night difference between SST peaks may surpass 3 K [70,71] due to different locations and environmental conditions. Air–sea interactions may be temporarily affected by the changing heat and gas fluxes, atmospheric circulation, and the height of the atmospheric boundary layer [44].
SST has been modeled by single channel, split window, triple window, linear, regression coefficients, and non-linear algorithms. For example, Llewellyn-Jones et al. [72] used a split window and triple window regression relationship for SST determinations. Additionally, Francois et al. [73] used seven daytime algorithms: linear, nonlinear—including a first-guess temperature term, nonlinear complete including more secant-dependent terms, a water vapor first version algorithm, a water vapor special version algorithm including quadratic terms in W, a quadratic algorithm, and a quadratic alternate version algorithm including a developed form of the quadratic term (T11_T12), and seven nighttime algorithms including T37 nonlinear algorithms (including T37 and Ts clim), a triple-window algorithm (TRI), T37 algorithm version 0–3 and a multiple-window algorithm (triple-window algorithm) to estimate SST from NOAA-14 and compared the results of each algorithm. Hosoda et al. [74] investigated multiple SST algorithms for atmospheric correction: multi-channel SST (MCSST), water vapor SST (WVSST), quadratic SST (QDSST) and nonlinear SST (NLSST) algorithms. They showed that the NLSST method using high-resolution climatological SST as a first-guess had good quality and high efficiency. Petrenko et al. [75] applied non-linear regression (NLR) and optimal estimation (OE) as well as two novel methods—incremental regression (IncR) and corrected non-linear regression (CNLR)—to create the preparations for the GOES-R ABI mission. The results indicated that IncR delivered the highest overall SST precision. Peng et al. [76] used two algorithms to estimate SST from MODIS data—Qin Zhihao’s split-window algorithm and a general SST algorithm—and they found improved results using the Qin Zhihao’s split-window algorithm. To assess the effects of anomalous atmospheres, Szczodrak et al. [77] applied the MODIS SST retrieval split window algorithm versions 5 and 6 to obtain the SST and the retrieval errors. Furthermore, Kilpatrick et al. [78] described the evolution of, motivation for, and improvements to the MODIS SST global products using their split window NLSST and LWIR NLSST with different estimation coefficients for over a decade.

5.2. Sea Surface Height

SSH variability is caused by four categories of phenomena, including dynamical/non-dynamical responses to forcing mechanisms; buoyancy, tidal, wind forcing, and atmospheric pressure [79]. The integrated measurements of parameters need to correct the SSH variability. After correcting the effects of tidal and atmospheric pressure, the SSH is still affected by steric effects such as density changes from heating/cooling or salinity changes and wind forcing [80].
SSH variability is mostly used to infer about the subsurface thermal or density structure changes and often to reflect the relative motion of the thermocline. This variation can also be applied to estimate absolute variations in the surface layer depth [81,82]. The correlation between SSH and thermocline depth is decreased by dipper and more diffuse thermocline and powerful surface buoyancy fluxes. If temperature dominantly changes and causes fluctuations in surface density, MLD or thermocline depth can be inferred by SST data [83].
The SSH data can be retrieved by several solutions, such as localized direct measurements by tide gauges [79], the XBT profiles (e.g., [57,84]), and approximate calculation by modelling the relationship between SSH and temperature, salinity, and pressure measurements [79], and this data has been monitored by remote sensing satellites [56,60] since 1992 [31]. These available and valuable satellites’ altimetry data include the Topex/Poseidon, Jason products, ERS-1/2, Envisat altimeters, and all gridded sea level products from AVISO (e.g., [27,31,41,56,59,85], etc.) with extremely good coverage in space and time [56].

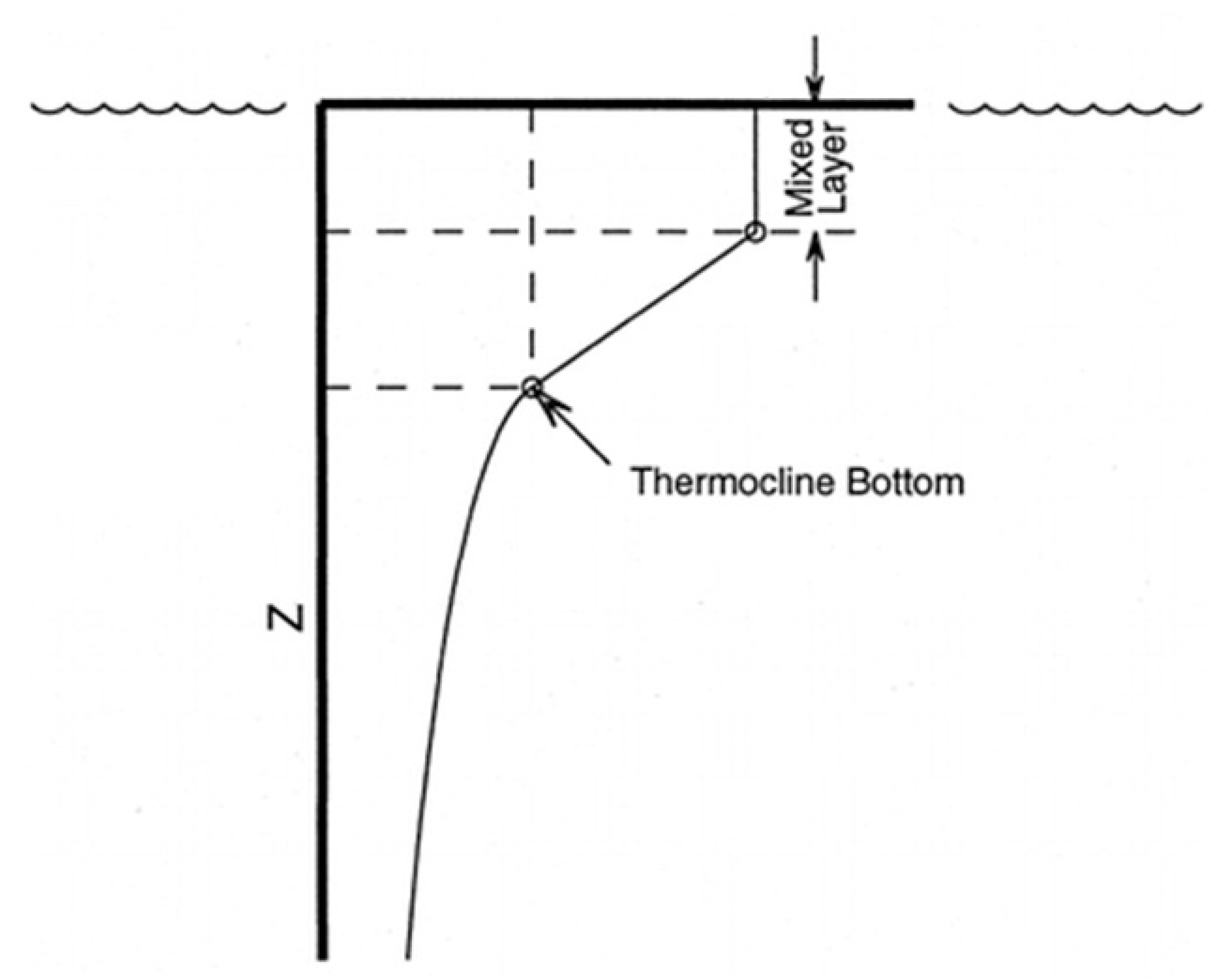
5.3. Mixed Layer Depth

The mixed layer depth (the surface zone with near-uniform temperature) [83] that links the atmosphere to the deep ocean and plays a critical role in climate variability [86] determines both the thermal and mechanical inertia of the layer in direct contact with the atmosphere [52,87]. Determining the MLD and its variability are crucial for understanding and interpreting the thermal and velocity fields of the upper ocean, parameterizing the mixed layer processes, and studying air–sea interactions [55,86], acoustic propagation [88], ocean biology [89], long-term climate change [90], carbon dioxide, fresh water, and other physical and biological activities [91]. At the same time, knowledge of MLD variability on a diurnal scale is important to the studies of fisheries and upper ocean dynamics [52]. Figure 7 shows the mixed layer depth and the depth of the thermocline.
The thermal inertia of the MLD represents the resistance of a water body to temperature change. Because a substance with a large heat capacity has a large thermal inertia and a small range of temperature change, the spatial and temporal changes in heat capacity and density of sea water are usually relatively small. Additionally, advective changes in temperature are small on a diurnal time scale. Sea water turbidity and surface albedo affect the amount of solar radiation absorbed by the surface layer. Strong surface wind stress also drives thermal energy down the water column. At the same time, when the heat flux is unchanged, the thermal inertia and the MLD are inversely proportional to the diurnal temperature range of the mixed layer [52]. This assessment has been done because the thermal inertia and mixed layer depth are highly correlated.
Traditionally, models of the upper ocean response to wind forcing and heat flux have relied more on in situ data than remotely sensed data [52,54,92]. The in-situ profiles are not only sparse because of the limited availability of measurements, but MLD estimations also involve the complex nature of physical, chemical, and biological processes. Therefore, researchers have used several numerical models to overcome these limitations [91]. Because thermodynamics and flow conditions in the upper ocean are directly altered by wind stress, albedo, and surface fluxes, they can potentially be directly assimilated by ocean remote sensing. Today, remotely sensed and in situ data are usually integrated to initialize, force, and evaluate the analytical and numerical models of mixed layer processes [52,54,91,92]. Hence, the development of quantitative techniques using satellite-derived surface characteristics to determine subsurface oceanic conditions is challenging.

5.4. Thermocline Depth

The thermocline is the region in thermally layered bodies of water that separates warmer surface water from cold deep water. A sudden temperature reduction with depth characterizes this region [93]. The depth of the thermocline is important in modeling the physics of the ocean because it affects the heat transfer between the ocean and the atmosphere more than the heat transfer between the ocean surface and the deeper layers [94,95]. The thermocline region exhibits the most rapid decrease in temperature with depth, is often highly variable, and depends on location and time [93]. Moreover, the variabilities in the MLD and the thermocline depth (TD; the depth of the maximum thermal gradient) are important to understand the interactions between the ocean and the atmosphere, ocean biology, and CO2 drawdown due to their effects on surface biology and air–sea CO2 fluxes [83].
Some researchers have assessed the seasonal changes in the MLD and the thermocline resulting from wind effects. Alvera-Azcárate et al. [95] showed that in open ocean areas that are predominantly oligotrophic, higher wind speeds increase the mixing of the surface layers, and therefore deepen the thermocline. However, increasing wind speeds induce an upwelling response in the water column inside the basin. Consequently, the rise of the thermocline brings nutrient-rich waters to the surface and increases the amount of chlorophyll-a.
Namias and Born [96,97] and Alexander and Deser [98] showed that thermal anomalies in the deep ocean mixed layer could remain intact in the seasonal thermocline (30–100 m) in the summer and revert to the surface layer during the fall and winter. At the same time, in the winter, the strong surface buoyancy losses increase the MLD, and the seasonal thermocline is not distinguishable in temperature profiles [99].

6. Limitations and Challenges

Remotely sensed data presents special advantages among other monitoring techniques by providing a timely, synoptic, and near-real-time overview of ocean/sea surface water temperature over large areas at multiple stages. Additionally, the data can be utilized in conjunction with models to improve the prediction of ocean/sea subsurface water temperature at a range of spatial scales. Thus, data assimilation—an approach that synthesizes field or other observations into models—can produce an accurate estimation of model input parameters and state variables. This approach has been broadly used for ocean/sea subsurface water temperature monitoring, with substantial success.
Some uncertainty is introduced by the model’s architecture and especially by uncertainties in the SST, SSH, MLD, thermocline bottom depth, and other influential input parameters, resulting in a biased simulation of ocean/sea subsurface water temperature. The impact of the spatial and temporal resolution of remote sensing images/data to re-initialize input parameters must also be evaluated. For reducing the uncertainties, researchers try to adjust the models to the site-specific characteristics by remote sensing data assimilation. In this way, they involve the simple statistics to dynamic algorithms to re-initialize the model parameters and minimize the difference between the in-situ measurement and simulation values. Each procedure has needed some parameters to solve the problem of estimating a variable, as the number of a model’s input parameters increases, the difference between the model and the reality of the phenomenon decreases and the accuracy is thus increased. By considering which parameters are available from the in-situ measurements and satellite data, the researchers could use the method that is suitable for their available data. Additionally, the simple/advanced statistics methods have been adjusted to that location and they are site-specific, data-specific, and model-specific. However, the dynamical/numerical-based model could be used around the world, comprehensively. In recent years, in order to decrease model biases, researchers have tried to use machine learning methods as optimization algorithms for adjusting the assimilation-based models by using remote sensing. The use this approach because machine learning optimization techniques are considerably fast and approximately find an optimal solution based on known properties learned from the training dataset.
Additionally, in most studies, the parameters involved in the retrieval of ocean/sea subsurface water temperature have been mostly limited to a few, such as SST, SSH, MLD, and thermocline bottom depth. However, Zhang et al. [100] illustrated the variations in the monthly diurnal temperature cycle under different average daytime wind speed conditions. When the wind speed increases to >3 ms−1 but <6 ms−1, the amplitudes of all months declined to 0.3–0.65 °C. A wind speed more than 6 ms−1 leads to a very weak diurnal cycle, and therefore reorganization becomes difficult.
Therefore, the wind shear, incoming solar radiation [101], heat exchange, ocean circulation, and turbulent mixing all dynamically affect the ocean surface [41]. Balmaseda et al. [30] showed that surface wind variability changes the vertical distribution of heat in the ocean. Additionally, Karagali et al. [44] showed that in some areas, high numbers of observed SST anomalies coincided with frequently low wind, but almost no warming was observed in other areas with low wind. They claimed that the diurnal variability of SST is not only affected by the wind as one of the requirements for warming but other parameters such as water turbidity, net heat flux, light penetration depth depending on solar elevation and cloud cover are also effective [44].
In this way, few researches have been investigated and involved these parameters in estimating and modelling the ocean/sea subsurface water temperature. Such as, Li et al. [102] estimated the subsurface temperature anomaly (STA) in the global ocean by employing satellite remote sensing observations of sea surface parameters by support vector regression (SVR) method. These parameters include sea surface height anomaly (SSHA), sea surface temperature anomaly (SSTA), sea surface salinity anomaly (SSSA), and sea surface wind anomaly (SSWA)) with in situ Argo data for training and testing at different depths. Their results showed that SSSA and SSWA, in addition to SSTA and SSHA, are useful parameters to estimate the subsurface thermal structure and improve the STA estimation accuracy. Ali et al. [50] have estimated the sea subsurface water temperature from SST, SSH, wind stress, net radiation, and net heat flux by neural network approach. They illustrated a proper relationship between the estimated temperature profiles and in situ observations. Yan et al. [52] used SST, albedo, and surface wind speed parameters by assimilating remotely sensed data in a dynamic mixed layer thermal inertia (MLTI) model in order to calculate the thermal inertia and predict changes in subsurface diurnal mixed layer depth.
At the same time, ocean subsurface temperatures can be estimated with preferable accuracy using more precise measurements of surface parameters such as wind speed, radiation/heat balance at the surface, SST, SSH/dynamic height, mixed layer depth, thermocline bottom depth, and sea surface salinity. Because the thermal dynamics of subsurface and deeper ocean waters play important roles in global warming, accurate and more successful estimation of the complex nature of SST and subsurface ocean temperature by considering the most effective parameters is currently challenging.

7. Accurate Sea Surface Temperature

Many factors are important in estimating ocean/sea subsurface water temperature such as SST, salinity, height, pressure, heat capacity, and density. In this study, the emphasis is on remotely sensed SST as a prerequisite parameter to estimating accurate ocean/sea subsurface water temperature. In the remote sensing approaches used to determine SST, water emissivity is an important constant in the SST equation [103]. When there is a slight spatial change in thermal inertia and the structure of the water, the emissivity is equal both vertically and horizontally, and is assumed to be 1 or near 1.
The radiation temperature (Trad) in the water is approximately equal to the actual kinetic temperature (Tkin). Of course, this approximation is applicable to the surface of the water and not the subsurface [104]. It is also not the case in all situations; the emissivity changes in areas with seawater foam [105], which can cause errors in the determination of SST.
In remote sensing studies of ocean/sea subsurface water temperature, the relationship between water temperature, salinity, and pressure has been used. Additionally, in numerical models, researchers have tried to improve the accuracy of ocean/sea subsurface water temperature estimation by considering physical parameters such as density, heat capacity, and pressure. Nayar et al. [106] reviewed and developed a correlation for physical seawater parameters such as Gibbs energy, enthalpy, and entropy based on salinity and temperature. The correlation is based on thermodynamic relationships, and is a function of temperature, salinity, and pressure. It is possible that enthalpy, Gibbs energy, and entropy correlations can help to accurately estimate SST in the near future. The accurate estimation of SST may improve the results of methods to reconstruct the ocean’s interior implemented by, for example, Wang et al. [107] and Liu et al. [62,108].

8. Perspective

Existing methods—especially model-based data assimilation and statistical methods—are mostly restricted to specific locations and a range of data. Numerical model-based data assimilation methods have not only been used with in situ measurement data, but have also used physical parameters. Access to these characteristics is leading to more accurate temperature estimates, and the results are not location-based. However, this method is limited to a few studies in a subcategory including gravest empirical mode-altimetry gravest empirical mode (GEM-AGEM), oceanic general circulation model (OGCM), 4D assimilation system, isopycnal empirical orthogonal function (EOF), and MODAS (Modular Ocean data Assimilation System). Furthermore, dynamical models are only found in a few studies. The development of model-based data assimilation for estimating subsurface temperature by considering optimization algorithms, heuristic optimization, and meta-heuristic optimization algorithms could lead to more accurate estimations.
Satellite measurements are constrained by the number of overpasses for a particular site, interference by clouds, and the spatial coverage limitations of ground measurements. Therefore, in addition to considering the heterogeneous conditions in the ocean, using more accurate and developed data from satellite images to measure the subsurface parameters seems necessary. The combined use of microwave, thermal, and optical remote sensing can obtain more parameters from the surface of water to model the subsurface temperature. The NASA soil moisture active and passive (SMAP) project uses low-frequency microwave radiometer and radar data to measure surface soil moisture, freeze–thaw state, and sea surface salinity (SSS). For example, the SSS data allows for the extension of the data record of the highly successful 3-year Aquarius salinity mission into the future for use as an input parameter in model-based data assimilation [109]. Additionally, the NASA hyperspectral infrared imager (HyspIRI) mission comprises two instruments—a visible to short-wavelength infrared (VSWIR) imaging spectrometer and a thermal infrared sensor (TIR) multispectral imager [35]. These new and future technologies may open a new horizon for the comprehensive and detailed analysis of subsurface land processes. At the same time, the HyspIRI satellite is well-suited for sea-surface temperature studies. The TIR hyperspectral sensors have more bands than multispectral sensors, are more relative to atmospheric parameters, and are used for the extraction of surface temperature. Here, we illustrated the state of ocean measurements from space in 2010, 2020, and 2025 (Table 4). Currently, the Topex/Poseidon, Jason-1/2, ERS-1/2, ENVISAT, Nimbus-7-SMMR, AVHRR, and the other AVISO product sensors are widely used to assimilate ocean/sea subsurface water temperature and the GOES, M-AERI, AMSR-E, GRACE, GEOSAT, SMOS, SMAP, Seasat, SeaSoar-JES, SeaWiFS, and MIRAS sensors have been used only one or two times. These sensors have proven their capabilities in assimilating ocean/sea subsurface water temperature. According to Freeman et al. [110], these capabilities will improve in both spatial and temporal resolution until 2020 and 2025.
HyspIRI was designed to assess the world’s terrestrial and aquatic ecosystems, as well as provide crucial information on natural disasters. Other hyperspectral satellite missions such as the Precursore IperSpettrale della Missione Applicativa (PRISMA), Environmental Mapping and Analysis Program (EnMAP), and thermal infrared satellite missions such as the ecosystem spaceborne thermal radiometer experiment on space station (ECOSTRESS) will not have the global observational capability of HyspIRI. Additionally, HyspIRI is the only planned mission that combines hyperspectral measurements from a visible to shortwave infrared (VSWIR: 380–2500 nm) sensor with eight-channel multispectral measurements from a mid to thermal infrared sensor (TIR: 4–13 μm). The nominal ground sample distances of the HyspIRI VSWIR and TIR sensors are 30 m and 60 m, respectively [111].
In addition, the European Commission’s Copernicus Program launched a series of four satellites, including the Sentinel-3A satellite. This satellite is the first one of this program, and was launched on the 16 February 2016. Sea-surface topography and sea/land-surface temperature have been measured by Sentinel-3 instruments. These instruments include the Sentinel-3 optical instruments—namely, the Ocean Land Color Imager (OLCI) and the Sea and Land Surface Temperature Radiometer (SLSTR) [112]. The SLSTR mission includes three product types: level-1B (radiance and brightness temperature), level-2 WST SST, and level-2 LST (land surface temperature). The Level-1B and Level-2 WST have produced 500 m and 1 km spatial resolutions of the solar reflectance and thermal infrared bands, respectively. The mean global coverage revisit times for the dual view SLSTR observations are between 1.9 days at the equator and 0.9 days (in constellation with a 180° in-plane separation between the two space-crafts) [113].

9. Conclusions

This study presents a comprehensive review of the methods used to estimate ocean/sea subsurface water temperature and assesses the current difficulties and challenges. To accurately estimate ocean subsurface temperature, the precise determination of some surface parameters is necessary. We conclude that the affecting parameters include wind speed, radiation/heat balance at the surface, heat exchange, water turbidity, net heat flux, light penetration depth, and cloud cover. To date, these parameters that affect ocean/sea subsurface water temperature have been considered in only a small number of studies. Along with these parameters, SST, SSH, and SSS have been more considered in estimating the ocean/sea subsurface water temperature. Because subsurface and deeper ocean thermal properties play an important role in global warming, it is necessary to develop methods for more precise estimation of the complex nature of SST and ocean subsurface temperature by considering the most effective parameters. To precisely estimate and consider the heterogeneous conditions in the ocean, studies should fully utilize new developments in satellite remote sensing. At the same time, optimization algorithms such as heuristic optimization and meta-heuristic optimization could lead to the more accurate estimation of these parameters.

Acknowledgments

The authors deeply thank the Iranian National Science Foundation and Iranian National Space Administration for their great support in conducting this research.

Author Contributions

Elahe Akbari reviewed the articles and wrote the manuscript. Seyed Kazem Alavipanah managed the review. Mehrdad Jeihouni, Mohammad Hajeb, Dagmar Haase and Sadroddin Alavipanah helped in edit and improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007: The physical science basis. In Fourth Assessment Report of the Intergovernmental Panel on Climate Change Cambridge; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Contribution of Working Group I; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  2. Mänd, P.; Hallik, L.; Peñuelas, J.; Nilson, T.; Duce, P.; Emmett, B.A.; Beier, C.; Estiarte, M.; Garadnai, J.; Kalapos, T.; et al. Responses of the reflectance indices PRI and NDVI to experimental warming and drought in European shrublands along a north–south climatic gradient. Remote Sens. Environ. 2010, 114, 626–636. [Google Scholar] [CrossRef]
  3. Intergovernmental Panel on Climate Change (IPCC). Summary for policymakers. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Midgley, P.M., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
  4. Nazarenko, L.; Schmidt, G.A.; Miller, R.L.; Tausnev, N.; Kelley, M.; Ruedy, R.; Russell, G.L.; Aleinov, I.; Bauer, M.; Bauer, S. Future climate change under RCP emission scenarios with GISS ModelE2. J. Adv. Model. Earth Syst. 2015, 7, 244–267. [Google Scholar] [CrossRef]
  5. Molua, E.L. Reappraisal of the climate change challenge in the congo basin and implications for the cost of adaptation. Environ. Nat. Resour. Res. 2015, 5, 80–97. [Google Scholar] [CrossRef]
  6. Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Blumenstock, T.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and quality assessment of near-surface-sensitive satellite-derived CO2 and CH4 global data sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
  7. Ghoneim, E. A remote sensing study of some impacts of global warming on the Arab Region. In Arab Environment: Climate Change; Report by at the Center for Remote Sensing; Boston University: Boston, MA, USA, 2009; Chapter 3; pp. 31–46. [Google Scholar]
  8. Watts, N.; Adger, W.N.; Agnolucci, P.; Blackstock, J.; Byass, P.; Cai, W.; Chaytor, S.; Colbourn, T.; Collins, M.; Cooper, A.; et al. Health and climate change: Policy responses to protect public health. Lancet 2015, 386, 1861–1914. [Google Scholar] [CrossRef]
  9. Cook, B.I.; Ault, T.R.; Smerdon, J.E. Unprecedented 21st-century drought risk in the American Southwest and Central Plains. Sci. Adv. 2015, 1, e1400082. [Google Scholar] [CrossRef] [PubMed]
  10. Bruno, M.F.; Molfetta, M.G.; Petrillo, A.F. The influence of interannual variability of mean sea level in the Adriatic Sea on extreme values. J. Coast. Res. 2014, 70, 241–246. [Google Scholar] [CrossRef]
  11. Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global warming increases the frequency of river floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef] [Green Version]
  12. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earth’s Future 2017, 5, 304–323. [Google Scholar] [CrossRef]
  13. Brown, M.E.; de Beurs, K.M.; Marshall, M. Global phenological response to climate change in crop areas using satellite remote sensing of vegetation, humidity and temperature over 26 years. Remote Sens. Environ. 2012, 126, 174–183. [Google Scholar] [CrossRef]
  14. Asseng, S.; Ewert, F.; Martre, P.; Rötter, R.P.; Lobell, D.B.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
  15. Coffel, E.; Horton, R. Climate change and the impact of extreme temperatures on aviation. Weather Clim. Soc. 2015, 7, 94–102. [Google Scholar] [CrossRef]
  16. Li, T.; Horton, R.M.; Bader, D.A.; Huang, G.; Sun, Q.; Kinney, P.L. Heat-related mortality projections for cardiovascular and respiratory disease under the changing climate in Beijing, China. Sci. Rep. 2015, 5, 11441. [Google Scholar] [CrossRef] [PubMed]
  17. Preston, B.L. Observed winter warming of the Chesapeake Bay Estuary (1949–2002): Implications for ecosystem management. Environ. Assess. 2004, 34, 125–139. [Google Scholar] [CrossRef] [PubMed]
  18. Tan, J.; Cherkauer, K.A. Assessing stream temperature variation in the Pacific Northwest using airborne thermal infrared remote sensing. J. Environ. Manag. 2013, 115, 206–216. [Google Scholar] [CrossRef] [PubMed]
  19. Fisher, J.I.; Mustard, J.F. High spatial resolution sea surface climatology from Landsat thermal infrared data. Remote Sens. Environ. 2004, 90, 293–307. [Google Scholar] [CrossRef]
  20. Johnson, G.C.; Mecking, B.; Sloyan, B.M.; Wijffels, S.E. Recent bottom water warming in the Pacific Ocean. J. Clim. 2007, 20, 5365–5375. [Google Scholar] [CrossRef]
  21. Johnson, G.C.; Purkey, S.G.; Bullister, J.L. Warming and freshening in the abyssal southeast Indian Ocean. J. Clim. 2008, 21, 5351–5363. [Google Scholar] [CrossRef]
  22. Johnson, G.C.; Purkey, S.G.; Toole, J.M. Reduced Antarctic meridional overturning circulation reaches the North Atlantic Ocean. Geophys. Res. Lett. 2008, 35, L22601. [Google Scholar] [CrossRef]
  23. Cazenave, A.; Nerem, R.S. Present-day sea level change: Observations and cause. Rev. Geophys. 2004, 42, RG3001. [Google Scholar] [CrossRef]
  24. Willis, J.K.; Roemmich, D.; Cornuelle, B. Interannual variability in upper ocean heat content, temperature and thermosteric expansion on global scales. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
  25. Levitus, S.; Antonov, J.I.; Boyer, T.P. Warming of the world ocean, 1955–2003. Geophys. Res. Lett. 2005, 32, L02604. [Google Scholar] [CrossRef]
  26. Antonov, J.I.; Levitus, S.; Boyer, T.P. Thermosteric sea level rise, 1955–2003. Geophys. Res. Lett. 2005, 32, L12602. [Google Scholar] [CrossRef]
  27. Ishii, M.; Kimoto, M.; Sakamoto, K.; Iwasaki, S.-I. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J. Oceanogr. 2006, 62, 155–170. [Google Scholar] [CrossRef]
  28. Song, Y.T.; Colberg, F. Deep Ocean warming assessed from altimeters, Gravity Recovery and Climate Experiment, In Situ measurements and a non-Boussinesq ocean general circulation model. J. Geophys. Res. 2011, 116, C02020. [Google Scholar] [CrossRef]
  29. Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39, L10603. [Google Scholar] [CrossRef]
  30. Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
  31. Su, H.; Wu, X.; Yan, X.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
  32. Alavipanah, S.K.; Akbari, E.; Jeihouni, M.; Hajeb, M. A comparison between surface and subsurface temperature of water body based on remotely sensed thermal infrared data in the coastal zone. In Proceedings of the International Conference on Coastal Zones, Osaka, Japan, 16–18 May 2016; Volume 4. [Google Scholar] [CrossRef]
  33. Laurs, R.M.; Polovina, J.J. Satellite remote sensing: An important tool in fisheries oceanography. In Fisheries Oceanography: An Integrative Approach to Fisheries Ecology and Management; Harrison, P.J., Parsons, T.R., Eds.; Fish and Aquatic Resources Series 4; Blackwell Science: Oxford, UK, 2000; pp. 146–157. [Google Scholar]
  34. Polovina, J.J.; Howell, E.A. Ecosystem indicators derived from satellite remotely sensed oceanographic data for the North Pacific. ICES J. Mar. Sci. 2005, 62, 319–327. [Google Scholar] [CrossRef]
  35. Lee, Z.; Du, K.; Arnone, R.; Liew, S.; Penta, B. Penetration of solar radiation in the upper ocean: A numerical model for oceanic and coastal waters. J. Geophys. Res. 2005, 110, C09019. [Google Scholar] [CrossRef]
  36. Subsurface. Webster’s New World College Dictionary, 4th ed.; Houghton Mifflin Harcourt: Boston, MA, USA; Available online: https://www.collinsdictionary.com/dictionary/english/subsurface (accessed on 30 October 2017).
  37. Creatures of the Deep Sea. Layers of the Ocean. Available online: http://www.seasky.org/deep-sea/ocean-layers.html (accessed on 30 October 2017).
  38. Yang, J.; Gong, P.; Fu, R.; Zhang, M.H.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
  39. Fiedler, P.C. Surface manifestations of subsurface thermal structure in the California Current. J. Geophys. Res. 1988, 93, 4975–4983. [Google Scholar] [CrossRef]
  40. Klemas, V.; Yan, X.-H. Subsurface and deeper ocean remote sensing from satellites: An overview and new results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
  41. Wu, X.; Yan, X.-H.; Jo, Y.-H.; Liu, W.T. Estimation of subsurface temperature anomaly in the North Atlantic using a self-organizing map neural network. J. Atmos. Ocean. Technol. 2012, 29, 1675–1688. [Google Scholar] [CrossRef]
  42. Meredith, M.P.; Garabato, A.C.; Gordon, A.L.; Johson, G.C. Evolution of the deep and bottom waters of the Scotia Sea, Southern Ocean, during 1995–2005. J. Clim. 2008, 21, 2237–3343. [Google Scholar] [CrossRef]
  43. Purkey, S.G.; Johnson, G.C. Warming of global abyssal and deep southern ocean waters between the 1990s and 2000s: Contributions to global heat and sea level rise. J. Clim. 2010, 23, 6336–6351. [Google Scholar] [CrossRef]
  44. Karagali, I.; Høyer, J.; Hasager, C. SST diurnal variability in the North Sea and the Baltic Sea. Remote Sens. Environ. 2012, 121, 159–170. [Google Scholar] [CrossRef]
  45. Eastwood, S.; LeBorgne, P.; Préré, S.; Poulter, D. Diurnal variability in sea surface in the Arctic. Remote Sens. Environ. 2011, 115, 2594–2602. [Google Scholar] [CrossRef]
  46. Kawano, T.; Doi, T.; Uchida, H.; Kouketsu, S.; Fukasawa, M.; Kawai, Y.; Katsumata, K. Heat content change in the Pacific Ocean between the 1990s and 2000s. Deep Sea Res. Part II 2010, 57, 1141–1151. [Google Scholar] [CrossRef]
  47. Halkides, D.; Lee, T.; Kida, S. Mechanisms controlling the seasonal mixed-layer temperature and salinity of the Indonesian seas. Ocean Dyn. 2011, 61, 481–495. [Google Scholar] [CrossRef]
  48. Halkides, D.J.; Waliser, D.E.; Lee, T.; Menemenlis, D.; Guan, B. Quantifying the processes controlling intraseasonal mixed-layer temperature variability in the tropical Indian Ocean. J. Geophys. Res. 2015, 120, 692–715. [Google Scholar] [CrossRef]
  49. Meehl, G.A.; Arblaster, J.M.; Fasullo, J.T.; Hu, A.; Trenberth, K.E. Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nat. Clim. Chang. 2011, 1, 360–364. [Google Scholar] [CrossRef]
  50. Ali, M.M.; Swain, D.; Weller, R.A. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004, 31, L20308. [Google Scholar] [CrossRef]
  51. Khedouri, E.; Szczechowski, C.; Cheney, R. Potential oceanographic applications of satellite altimetry for inferring subsurface thermal structure. In Proceedings of the OCEANS ‘83, San Francisco, CA, USA, 29 August–1 September 1983; Marine Technology Society: Washington, DC, USA, 1983; pp. 274–280. [Google Scholar]
  52. Yan, X.-H.; Schubel, J.R.; Pritchard, D.W. Oceanic upper mixed layer depth determination by the use of satellite data. Remote Sens. Environ. 1990, 32, 55–74. [Google Scholar] [CrossRef]
  53. Chu, P.C.; Fan, C.; Liu, W.T. Determination of vertical thermal structure from sea surface temperature. J. Atmos. Ocean. Technol. 2000, 17, 971–979. [Google Scholar] [CrossRef]
  54. Yan, X.-H.; Okubo, A.; Shubel, J.R.; Pritchard, D.W. An analytical model for remote sensing determination of the mixed layer depth. Deep Sea Res. Part A 1991, 38, 267–287. [Google Scholar] [CrossRef]
  55. Yan, X.-H.; Okubo, A. Three-dimensional analytical model for the mixed layer depth. J. Geophys. Res. 1992, 97, 20201–20226. [Google Scholar] [CrossRef]
  56. Fischer, M. Multivariate projection of ocean surface data onto subsurface sections. Geophys. Res. Lett. 2000, 27, 755–757. [Google Scholar] [CrossRef]
  57. Willis, J.K.; Roemmich, D.; Cornuelle, B. Combining altimetric height with broadscale profile data to estimate steric height, heat storage, subsurface temperature and sea-surface temperature variability. J. Geophys. Res. 2003, 108, 3292. [Google Scholar] [CrossRef]
  58. Guinehut, S.; Le Traon, P.Y.; Larnicol, G.; Philipps, S. Combining Argo and remote-sensing data to estimate the ocean three-dimensional temperature fields—A first approach based on simulated observations. J. Mar. Syst. 2004, 46, 85–98. [Google Scholar] [CrossRef]
  59. Swart, S.; Speich, S.; Ansorge, I.J.; Lutjeharms, J.R.E. An altimetry-based gravest empirical mode south of Africa: 1. Development and validation. J. Geophys. Res. 2010, 115, C03002. [Google Scholar] [CrossRef]
  60. Meijers, A.J.S.; Bindoff, N.L.; Rintoul, S.R. Estimating the four-dimensional structure of the southern ocean using satellite altimetry. J. Atmos. Ocean. Technol. 2011, 28, 548–568. [Google Scholar] [CrossRef]
  61. Guinehut, S.; Dhomps, A.-L.; Larnicol, G.; Le Traon, P.-Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef] [Green Version]
  62. Liu, L.; Peng, S.; Wang, J.; Huang, R.X. Retrieving density and velocity fields of the ocean’s interior from surface data. J. Geophys. Res. 2014, 119, 8512–8529. [Google Scholar] [CrossRef]
  63. Stammer, D. Steric and wind-induced changes in TOPEX/POSEIDON large-scale sea surface topography observations. J. Geophys. Res. 1997, 102, 20987–21009. [Google Scholar] [CrossRef]
  64. Fukumori, I.; Raghunath, R.; Fu, L.L. Nature of global large-scale sea level variability in relation to atmospheric forcing: A modeling study. J. Geophys. Res. 1998, 103, 5493–5512. [Google Scholar] [CrossRef]
  65. Ferry, N.; Reverdin, G.; Oschlies, A. Seasonal sea surface height variability in the North Atlantic Ocean. J. Geophys. Res. 2000, 105, 6307–6326. [Google Scholar] [CrossRef] [Green Version]
  66. Mayer, D.A.; Molinari, R.L.; Baringer, M.O.N.; Goni, G.J. Transition regions and their role in the relationship between sea surface height and subsurface temperature structure in the Atlantic Ocean. Geophys. Res. Lett. 2001, 28, 3943–3946. [Google Scholar] [CrossRef]
  67. Gilson, J.; Roemmich, D.; Cornuelle, B.; Fu, L.L. Relationship of TOPEX/Poseidon altimetric height to steric height and circulation in the North Pacific. J. Geophys. Res. 1998, 103, 27947–27965. [Google Scholar] [CrossRef]
  68. Ding, H.; Elmore, A.J. Spatio-temporal patterns in water surface temperature from Landsat time series data in the Chesapeake Bay, USA. Remote Sens. Environ. 2015, 168, 335–348. [Google Scholar] [CrossRef]
  69. Oke, P.R.; Larnicol, G.; Fujii, Y.; Smith, G.C.; Lea, D.J.; Guinehut, S.; Remy, E.; Alonso Balmaseda, M.; Rykova, T.; Surcel-Colan, D.; et al. Assessing the impact of observations on ocean forecasts and reanalyses: Part 1, Global studies. J. Oper. Oceanogr. 2015, 8, s49–s62. [Google Scholar] [CrossRef]
  70. Gentemann, C.L.; Minnett, P.J.; Le Borgne, P.; Merchant, C. Multi-satellite measurements of large diurnal warming events. Geophys. Res. Lett. 2008, 35, L22602. [Google Scholar] [CrossRef]
  71. Merchant, C.J.; Filipiak, M.J.; Le Borgne, P.; Roquet, H.; Autret, E.; Piollé, J.F.; Lavender, S. Diurnal warm-layer events in the western Mediterranean and European shelf seas. Geophys. Res. Lett. 2008, 35, L04601. [Google Scholar] [CrossRef]
  72. Llewellyn-Jones, D.T.; Minnett, P.J.; Saunders, R.W.; Zavody, A.M. Satellite multichannel infrared measurements of sea surface temperature of the N.E. Atlantic Ocean using AVHRR/2. Q. J. R. Meteorol. Soc. 1984, 110, 613–631. [Google Scholar] [CrossRef]
  73. Francois, C.; Brisson, A.; Le Borgne, P.; Marsouin, A. Definition of a radio sounding database for sea surface brightness temperature simulations Application to sea surface temperature retrieval algorithm determination. Remote Sens. Environ. 2002, 81, 309–326. [Google Scholar] [CrossRef]
  74. Hosoda, K.; Murakami, H.; Sakaida, F.; Kawamura, H. Algorithm and validation of sea surface temperature observation using MODIS sensors aboard terra and aqua in the Western North Pacific. J. Oceanogr. 2007, 63, 267–280. [Google Scholar] [CrossRef]
  75. Petrenko, B.; Ignatov, A.; Shabanov, N.; Kihai, Y. Development and evaluation of SST algorithms for GOES-R ABI using MSG SEVIRI as a proxy. Remote Sens. Environ. 2011, 115, 3647–3658. [Google Scholar] [CrossRef]
  76. Peng, H.; Li, H.; Gao, H. Study on methods of retrieval of sea surface temperature by using remote sensing data. In Advanced Materials Research; Trans Tech Publications: Zurich, Switzerland, 2013; Volumes 610–613, pp. 3742–3746. [Google Scholar] [CrossRef]
  77. Szczodrak, M.; Minnett, P.J.; Evans, R.H. The effects of anomalous atmospheres on the accuracy of infrared sea-surface temperature retrievals: Dry air layer intrusions over the tropical ocean. Remote Sens. Environ. 2014, 140, 450–465. [Google Scholar] [CrossRef]
  78. Kilpatrick, K.A.; Podestá, G.; Walsh, S.; William, E.; Halliwell, V.; Szczodrak, M.; Brown, O.B.; Minnett, P.J.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
  79. McCarthy, M.C.; Talley, L.D.; Roemmich, D. Seasonal to interannual variability from expendable bathythermograph and TOPEX/Poseidon altimeter data in the South Pacific subtropical gyre. J. Geophys. Res. 2000, 105, 19535–19550. [Google Scholar] [CrossRef]
  80. Fu, L.-L. Ocean circulation and variability from satellite altimetry. In Ocean Circulation and Climate Observing and Modelling the Global Ocean; Siedler, G., Church, J., Gould, J., Eds.; Elsevier: New York, NY, USA, 2001; pp. 141–172. [Google Scholar]
  81. Siegel, D.A.; McGillicuddy, D.J., Jr.; Fields, E. Mesoscale eddies, satellite altimetry and new production in the Sargasso Sea. J. Geophys. Res. 1999, 104, 359–379. [Google Scholar] [CrossRef]
  82. Tilburg, C.E.; Subrahmanyam, B.; O’Brien, J.J. Ocean color variability in the Tasman Sea. Geophys. Res. Lett. 2002, 29, 1487. [Google Scholar] [CrossRef]
  83. Wilson, C.; Coles, V.J. Global climatological relationships between satellite biological and physical observations and upper ocean properties. J. Geophys. Res. 2005, 110, 1–14. [Google Scholar] [CrossRef]
  84. Rintoul, S.R.; Donguy, J.R.; Roemmich, D.H. Seasonal evolution of upper ocean thermal structure between Tasmania and Antarctica. Deep Sea Res. Part I 1997, 44, 1185–1202. [Google Scholar] [CrossRef]
  85. Ji, M.; Reynolds, R.W.; Behringer, D.W. Use of TOPEX/Poseidon Sea level data for ocean analyses and ENSO prediction: Some early results. J. Clim. 2000, 13, 216–231. [Google Scholar] [CrossRef]
  86. Dong, S.; Sprintall, J.; Gille, S.T.; Talley, L. Southern Ocean mixed-layer depth from Argo float profiles. J. Geophys. Res. 2008, 113, C06013. [Google Scholar] [CrossRef]
  87. Yan, X.-H.; Bowman, A.; Schubel, J. Satellite observed spatial and temporal variability of the mixed layer depth in the Sargasso Sea. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience, Vancouver, BC, Canada, 10–14 July 1989; Volume I, pp. 323–329. [Google Scholar]
  88. Sutton, P.J.; Worcester, P.F.; Masters, G.; Cornuelle, B.D.; Lynch, J.F. Ocean mixed layers and acoustic pulse propagation in the Greenland Sea. J. Acoust. Soc. Am. 1993, 94, 1517–1526. [Google Scholar] [CrossRef]
  89. Fasham, M.J.R. Variations in the seasonal cycle of biological production in subarctic oceans: A model sensitivity analysis. Deep Sea Res. Part II 1995, 42, 1111–1149. [Google Scholar] [CrossRef]
  90. Thomson, R.E.; Fine, I.V. Estimating mixed layer depth from oceanic profile data. J. Atmos. Ocean. Technol. 2003, 20, 319–329. [Google Scholar] [CrossRef]
  91. Swain, D.; Ali, M.M.; Weller, R.A. Estimation of mixed-layer depth from surface parameters. J. Mar. Res. 2006, 64, 745–758. [Google Scholar] [CrossRef]
  92. Yan, X.-H.; Niller, P.P.; Stewart, R.H. Construction and accuracy analysis of images of the daily–mean mixed layer depth. Int. J. Remote Sens. 1991, 12, 2573–2584. [Google Scholar] [CrossRef]
  93. Petillo, S.; Balasuriya, A.; Schmidt, H. Autonomous Adaptive Environmental Assessment and Feature Tracking via Autonomous Underwater Vehicles. In Proceedings of the OCEANS 2010 IEEE, Sydney, Australia, 24–27 May 2010; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2010; pp. 1–9. [Google Scholar] [CrossRef]
  94. Alexander, M.; Scott, J.; Deser, C. Processes that influence sea surface temperature and ocean mixed layer depth variability in a coupled model. J. Geophys. Res. 2000, 105, 16823–16842. [Google Scholar] [CrossRef]
  95. Alvera-Azcárate, A.; Barth, A.; Weisberg, R.H.; Castañeda, J.J.; Vandenbulcke, L.; Beckers, J.-M. Thermocline characterization in the Cariaco basin: A modelling study of the thermocline annual variation and its relation with wind sand chlorophyll-a concentration. Cont. Shelf Res. 2011, 31, 73–84. [Google Scholar] [CrossRef]
  96. Namias, J.; Born, R.M. Temporal coherence in North Pacific sea-surface temperature patterns. J. Geophys. Res. 1970, 75, 5952–5955. [Google Scholar] [CrossRef]
  97. Namias, J.; Born, R.M. Further studies of temporal coherence in North Pacific Sea surface temperatures. J. Geophys. Res. 1974, 79, 797–798. [Google Scholar] [CrossRef]
  98. Alexander, M.A.; Deser, C. A mechanism for the recurrence of wintertime mid latitude SST anomalies. J. Phys. Oceanogr. 1995, 25, 122–137. [Google Scholar] [CrossRef]
  99. Houpert, L.; Testor, P.; Durrieu de Madron, X.; Somot, S.; D’Ortenzio, F.; Estournel, C.; Lavigne, H. Seasonal cycle of the mixed layer, the seasonal thermocline and the upper-ocean heat storage rate in the Mediterranean Sea derived from observations. Prog. Oceanogr. 2015, 132, 333–352. [Google Scholar] [CrossRef]
  100. Zhang, H.; Beggs, H.; Majewski, L.; Wang, X.H.; Kiss, A. Investigating sea surface temperature diurnal variation over the Tropical Warm Pool using MTSAT-1R data. Remote Sens. Environ. 2016, 183, 1–12. [Google Scholar] [CrossRef]
  101. Price, J.; Weller, R.; Pinkel, R. Diurnal cycling: Observations and models of the upper ocean response to diurnal heating, cooling and wind mixing. J. Geophys. Res. 1986, 91, 8411–8427. [Google Scholar] [CrossRef]
  102. Li, W.E.; Su, H.; Wang, X.Q.; Yan, X.H. Estimation of global subsurface temperature anomaly based on multisource satellite observations. J. Remote Sens. 2017, 21, 881–891. [Google Scholar] [CrossRef]
  103. Branch, R.; Chickadel, C.C.; Jessup, A.T. Thermal infrared multipath reflection from breaking waves observed at large incidence angles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 249–256. [Google Scholar] [CrossRef]
  104. Alavipanah, S.K. Thermal Remote Sensing and Its Application in the Earth Sciences, 3rd ed.; University of Tehran: Tehran, Iran, 2017. [Google Scholar]
  105. Branch, R.; Chickadel, C.C.; Jessup, A.T. Infrared emissivity of seawater and foam at large incidence angles in the 3–14 μm wavelength range. Remote Sens. Environ. 2016, 184, 15–24. [Google Scholar] [CrossRef]
  106. Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
  107. Wang, J.; Flierl, G.R.; LaCasce, J.H.; McClean, J.L.; Mahadevan, A. Reconstructing the ocean’s interior from surface data. J. Phys. Oceanogr. 2013, 43, 1611–1626. [Google Scholar] [CrossRef]
  108. Liu, L.; Peng, S.; Huang, R.X. Reconstruction of ocean’s interior from observed sea surface information. J. Geophys. Res. 2017, 122, 1042–1056. [Google Scholar] [CrossRef]
  109. Scott, J.; Meissner, T. Ocean Surface Salinity from SMAP: Continuing the Legacy of Aquarius; Remote Sensing Systems: Santa Rosa, CA, USA, 2015. [Google Scholar]
  110. Freeman, A.; Holt, B.; Siegel, D. Ocean Measurements from Space in 2025. Oceanography 2010, 23, 144–161. [Google Scholar] [CrossRef]
  111. Hochberg, E.J.; Roberts, D.A.; Dennison, P.E.; Hulley, G.C. Special issue on the Hyperspectral Infrared Imager (HyspIRI): Emerging science in terrestrial and aquatic ecology, radiation balance and hazards. Remote Sens. Environ. 2015, 167, 1–5. [Google Scholar] [CrossRef]
  112. Nieke, J.; Mavrocordatos, C.; Berruti, B. Sentinel-3A: First commissioning results of its optical payload. In Sensors, Systems and Next-Generation Satellites XX; International Society for Optics and Photonics: Bellingham, WA, USA, 2016. [Google Scholar] [CrossRef]
  113. European Space Agency (ESA). 2016. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-slstr (accessed on 30 December 2016).
Water 09 00936 g001a 550Water 09 00936 g001b 550
Figure 1. (a) Yearly literature count and (b) citation count related to ocean/sea subsurface water temperature, as indexed by Google Scholar since 1975. The search was conducted on 1 December 2016. Journal articles, conference proceedings, patents, and grants are included, and the total number of remote sensing and non-remote sensing citations is 4360 and 7127, respectively. The non-remote sensing scope includes all methods for estimating ocean/sea subsurface water temperature without satellite data. Since this article mainly focuses on the remote sensing scope, we illustrate these patterns later.
Figure 1. (a) Yearly literature count and (b) citation count related to ocean/sea subsurface water temperature, as indexed by Google Scholar since 1975. The search was conducted on 1 December 2016. Journal articles, conference proceedings, patents, and grants are included, and the total number of remote sensing and non-remote sensing citations is 4360 and 7127, respectively. The non-remote sensing scope includes all methods for estimating ocean/sea subsurface water temperature without satellite data. Since this article mainly focuses on the remote sensing scope, we illustrate these patterns later.
Water 09 00936 g001aWater 09 00936 g001b
Water 09 00936 g002 550
Figure 2. Distribution of anomalies larger than 2 K according to (a) depth and (b) distance to the nearest coast for the North Sea and the Baltic Sea [44]. Reprinted from [44] with permission from Elsevier.
Figure 2. Distribution of anomalies larger than 2 K according to (a) depth and (b) distance to the nearest coast for the North Sea and the Baltic Sea [44]. Reprinted from [44] with permission from Elsevier.
Water 09 00936 g002
Water 09 00936 g003 550
Figure 3. Linear trends and total increases of ocean basin heat content based on the linear trends of the global and individual basins as a function of depth (0–2000 m) at 100 m increments [29]. Reprinted from [29] with permission from Wiley (Copyright © 1999–2017 John Wiley & Sons, Inc).
Figure 3. Linear trends and total increases of ocean basin heat content based on the linear trends of the global and individual basins as a function of depth (0–2000 m) at 100 m increments [29]. Reprinted from [29] with permission from Wiley (Copyright © 1999–2017 John Wiley & Sons, Inc).
Water 09 00936 g003
Water 09 00936 g004 550
Figure 4. Argo subsurface temperature anomaly (STA) profiles from January 2005 to December 2010. (a–e) present STA profiles in areas labeled a, b, c, d, and e of subfigure (f). The geographic locations are: (a): western part of the North Atlantic subtropical gyre; (b): central part of the mid latitude North Atlantic; (c): eastern part of the mid latitude North Atlantic; (d): the sub polar gyre of the North Atlantic and (e): western part of the mid latitude North Atlantic [41]. ©American Meteorological Society. Used with permission.
Figure 4. Argo subsurface temperature anomaly (STA) profiles from January 2005 to December 2010. (a–e) present STA profiles in areas labeled a, b, c, d, and e of subfigure (f). The geographic locations are: (a): western part of the North Atlantic subtropical gyre; (b): central part of the mid latitude North Atlantic; (c): eastern part of the mid latitude North Atlantic; (d): the sub polar gyre of the North Atlantic and (e): western part of the mid latitude North Atlantic [41]. ©American Meteorological Society. Used with permission.
Water 09 00936 g004
Water 09 00936 g005 550
Figure 5. (a) A tag cloud of the literature methods related to ocean/sea subsurface water temperature in the remote sensing scope and (b) the non-remote sensing scope, where a larger font denotes a higher frequency.
Figure 5. (a) A tag cloud of the literature methods related to ocean/sea subsurface water temperature in the remote sensing scope and (b) the non-remote sensing scope, where a larger font denotes a higher frequency.
Water 09 00936 g005
Water 09 00936 g006 550
Figure 6. Monthly variation of the SST diurnal cycle from 00:00 to 23:00 for the spring and summer months. Only grid cells showing anomalies >2 K at least once a day are used. For those grid cells, all hourly values are used [44]. Reprinted from [44] with permission from Elsevier.
Figure 6. Monthly variation of the SST diurnal cycle from 00:00 to 23:00 for the spring and summer months. Only grid cells showing anomalies >2 K at least once a day are used. For those grid cells, all hourly values are used [44]. Reprinted from [44] with permission from Elsevier.
Water 09 00936 g006
Water 09 00936 g007 550
Figure 7. The mixed layer depth and thermocline bottom depth [53]. ©American Meteorological Society. Used with permission.
Figure 7. The mixed layer depth and thermocline bottom depth [53]. ©American Meteorological Society. Used with permission.
Water 09 00936 g007
Table
Table 1. Relevant journals and conference proceedings that have published studies related to ocean/sea subsurface water temperature in remote sensing scope. The search was conducted on 1 December 2016.
Table 1. Relevant journals and conference proceedings that have published studies related to ocean/sea subsurface water temperature in remote sensing scope. The search was conducted on 1 December 2016.
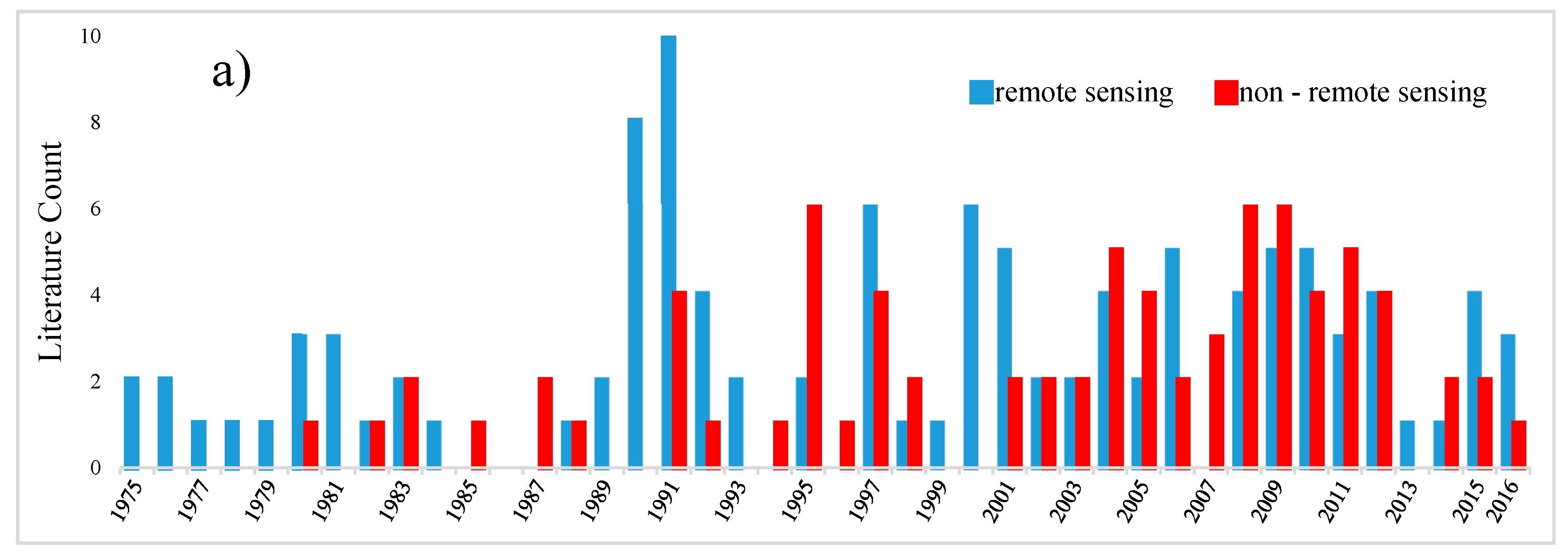
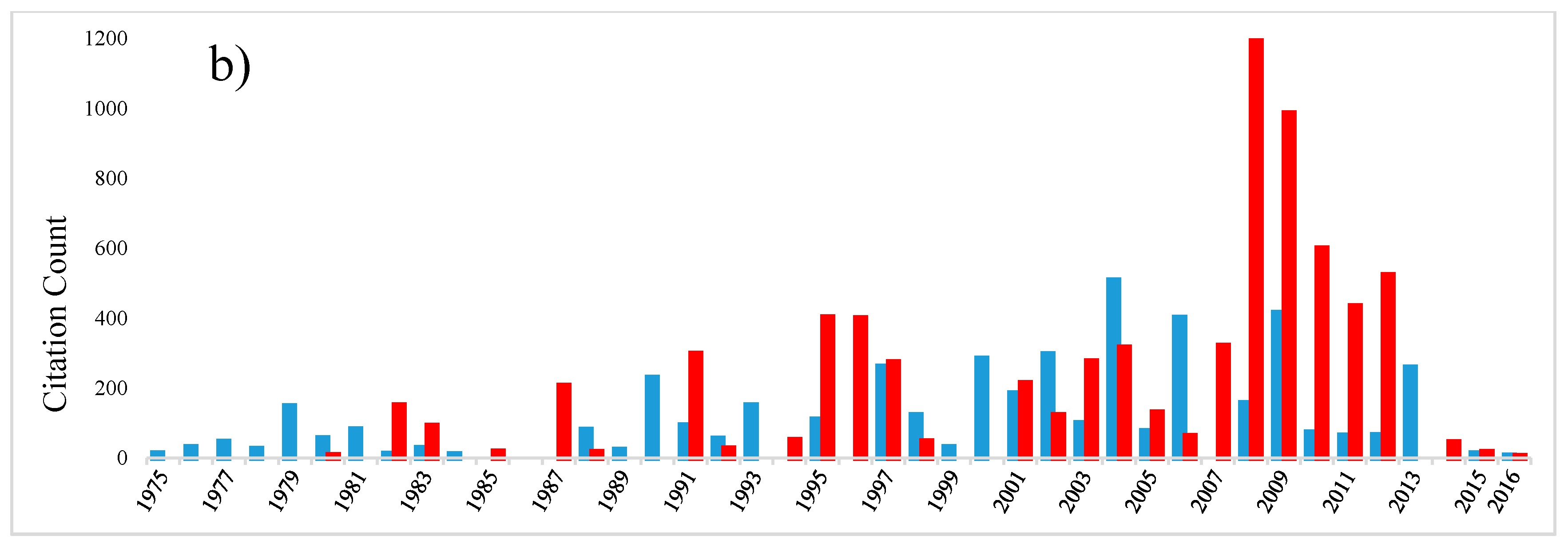
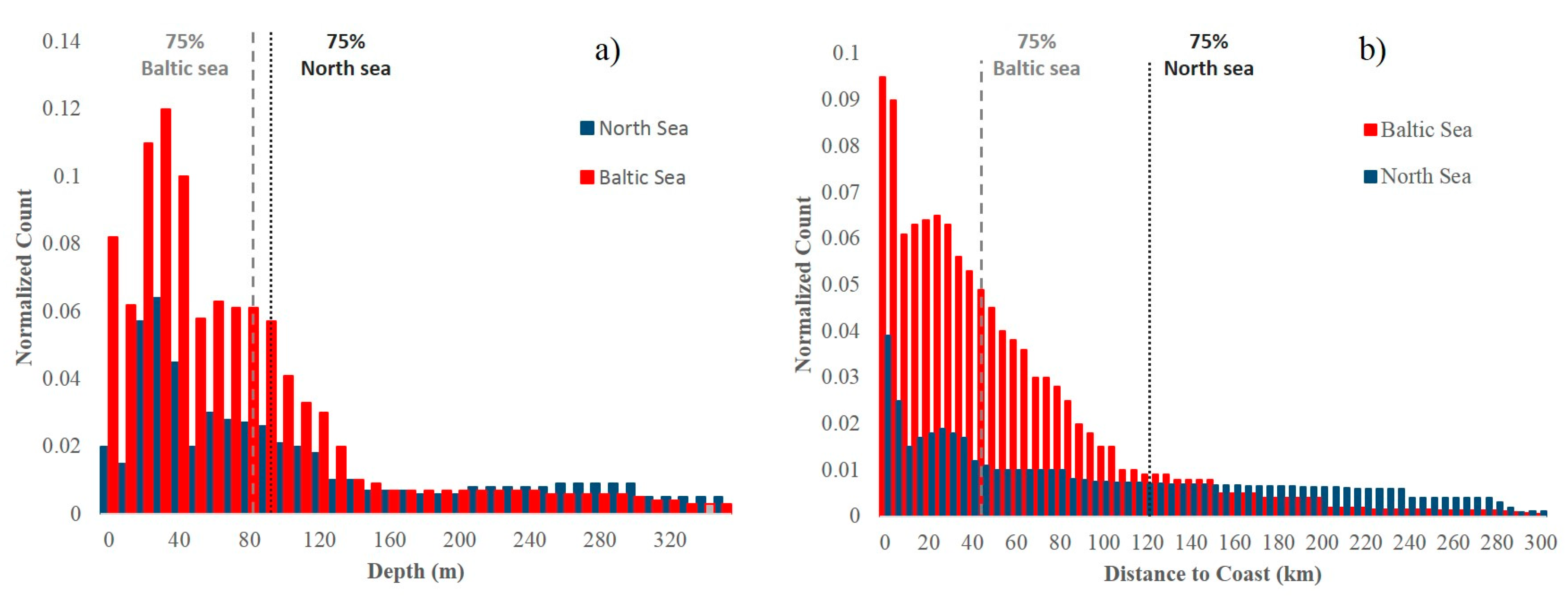
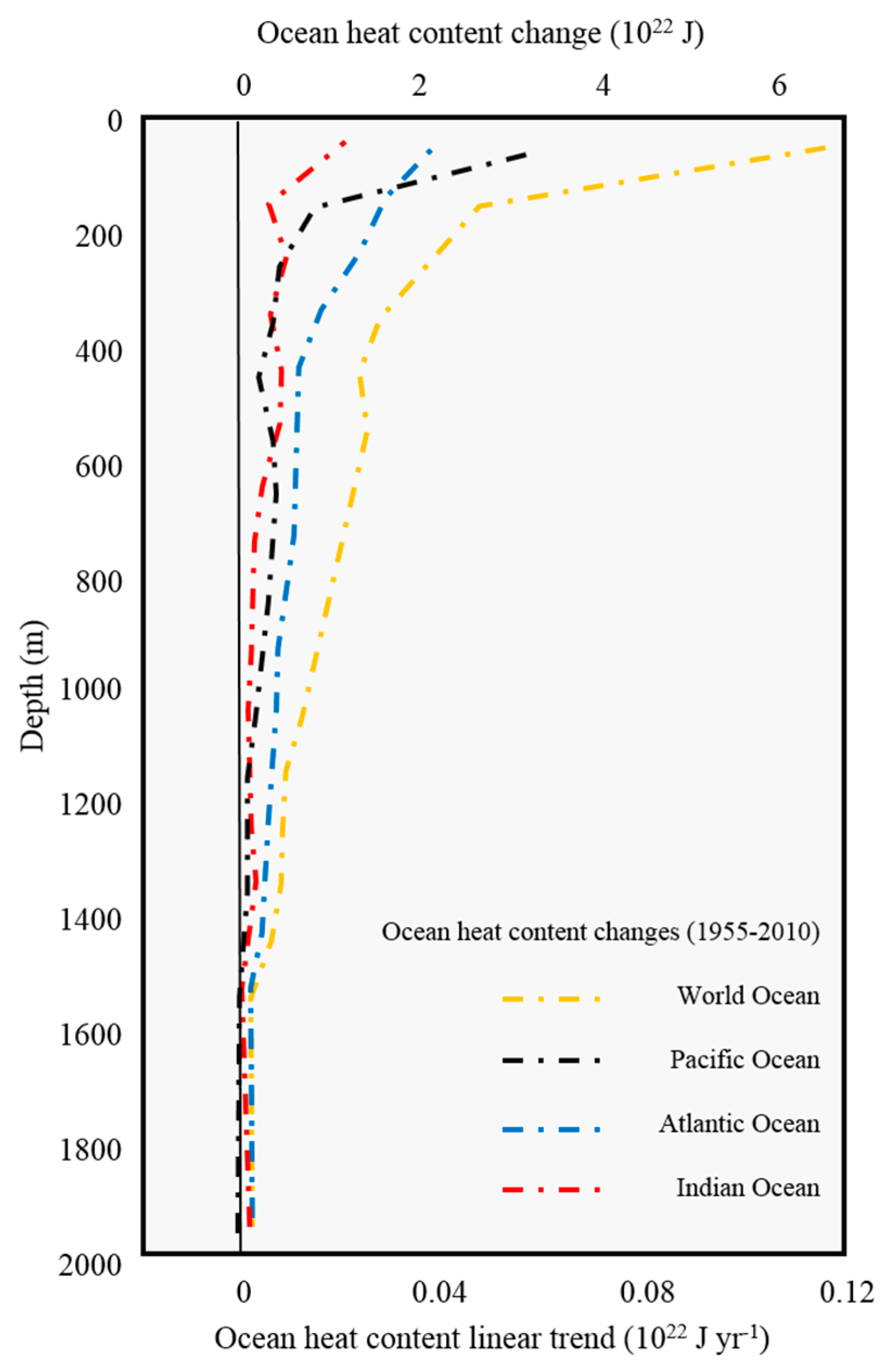
CategoryName of JournalNumber of Papers
Simple statisticsJournal of Geophysical Research: Oceans7
Geophysical Research Letters: Oceans5
Journal of Atmospheric and Oceanic Technology1
Journal of Climate1
Remote Sensing of Environment1
Ocean Science Journal1
Progress in Oceanography1
Journal of Oceanography1
Journal of Marine Systems1
Climate Dynamics1
Deep-sea research. Part I, Oceanographic research papers1
proceedings1
Advanced statisticsJournal of Atmospheric and Oceanic Technology2
Journal of Geophysical Research: Oceans2
Geophysical Research Letters: Oceans2
Remote Sensing of Environment1
IEEE Geoscience and Remote Sensing Letters1
Polish Maritime Research1
Journal of Climate1
Numerical modelJournal of Geophysical Research: Oceans9
Journal of Atmospheric and Oceanic Technology4
Geophysical Research Letters: Oceans3
Remote Sensing of Environment1
Journal of Climate1
Ocean Dynamics1
Dynamical modelRemote Sensing of Environment1
Deep-sea research. Part I, Oceanographic research papers1
International Journal of Remote Sensing1
Journal of Geophysical Research: Oceans1
Table
Table 2. Methods used to estimate ocean/sea subsurface water temperature along with the sensor types.
Table 2. Methods used to estimate ocean/sea subsurface water temperature along with the sensor types.
CategoryName of TechniquesSensor TypeYear
Simple statisticsRegressionTopex/Poseidon, ERS-1/21995, 2000, 2001, 2003
GOES1983
AVHRR, AMSR2012
M-AERI, NOAA-AVHRR2010
Jason-1/2, Topex/Poseidon, ERS-1/22004
Topex/Poseidon2001
AVHRR1997
Simple statistics, interpolation, comparisonJason-1, Topex/Poseidon, ERS-1/2, ENVISAT2006
Topex/Poseidon1998, 2000, 2001
AVISO product2009
Topex/Poseidon, ERS-1/22005
AMSR-E2012
Satellite based SST2003
Trend analysisAVISO product, NOAA2013
Topex/Poseidon2006
Jason-1, Topex/Poseidon, ERS-1/2, ENVISAT, NOAA2008
Topex/Poseidon, ERS-1/22000
Advanced statisticsEOFNOAA-AVHRR2005
GEOSAT1990
Topex/Poseidon2000
Fourier analysisNOAA-AVHRR2000, 2005
Artificial neural network (ANN)-back propagationAVISO product2015
the temperature sensor2004
Self-organization mapping (SOM)AVISO product, NOAA2012
Support vector machine (SVM)AMSR-E, MIRAS, SMOS, AVISO product2015
Principle component analysis (PCA)AVISO product2009
Simple ocean data assimilation (SODA)SMAP2016
Numerical modelDeveloped parametric modelAVHRR2000
One-dimensional mixed layer modelSeasat, Nimbis-7-SMMR1981
Net heat flux physical based modelM-AERI2009
Oceanic general circulation model (OGCM)NOAA, Topex/Poseidon2001
GRACE, Jason-1, Topex/Poseidon, ERS-1, ENVISAT2011
SeaWIFS2001
4D—Var assimilation systemTopex/Poseidon2006
empirical mode—dynamic parameterTopex/Poseidon, ERS-1/22004
Jason-1/2, Topex/Poseidon2006
AVISO product2009
Jason-1/2, Topex/Poseidon, ERS-1/2, ENVISAT2010
AGEM—GEMAVISO product2010, 2011, 2016, 2016
AVISO product, Jason-1, ERS-1/2, ENVISAT, NOAA2010
Isopycnal EOF by considering the dynamic parameterSatellite altimetry1990, 2002
Modular Ocean data Assimilation System (MODAS)Seasoar-JES2002
Dynamical models Nimbis-7-SMMR, NOAA-AVHRR1990, 1991
Nimbis-7-SMMR, NOAA-AVHRR, GOES1991
NOAA-AVHRR1992
Note: EOF: empirical orthogonal function; GEM: gravest empirical mode; AGEM: altimetry GEM.
Table
Table 3. Illustration of most studies used to estimate ocean/sea subsurface water temperature using model-based simulations.
Table 3. Illustration of most studies used to estimate ocean/sea subsurface water temperature using model-based simulations.
NamePurposeLocationMethodologySignificant FindingSuggestion
Khedouri et al. [51]Estimate subsurface temperature from satellite altimetry.Gulf Stream region (analyzed depth: upper 700 m)The least square linear between XBT measurement and GOES satellite data and inferring subsurface thermal structure from sea surface topography.There are high correlations between subsurface temperature measured by XBT and sea level height variability measured by GOES, and this relationship can be used to infer subsurface thermal structure.
Fiedler [39]Detect potential surface manifestations of subsurface thermal structure.Northern to Southern California Oceanic coastal (analyzed depth: upper 500 m)Correlation analysis between surface temperature and vertical structure parameters (thermocline strength and mixed layer depth) were applied by linear regression. Temperature correlation profiles (between surface temperature and subsurface temperature) at different regions and seasons. Improvement of the precision of vertical structure parameters by considering the sea surface winds from satellite scatterometers or ocean color from new color sensors.
Chu et al. [53]Determine the subsurface thermal structure from satellite SST observation.South of China sea (analyzed depth: upper 600 m)Parametric model (relationship between SST and subsurface parameters such as MLD, TBD, and TTG in multi time scales profiles).The parametric model is more accurate than the simple method of estimating subsurface temperature. After testing the validity of the multi time scale hypothesis between the mentioned parameters, had better globally apply the multi time scale inverse method.
Fischer [56]Estimating the vertical thermal structure.Tropical Pacific (analyzed depth: upper 300 m)Using the SSTA and SSHA data to compute regression matrices that were obtained from a forced integration of the Modular Ocean Model (MOM).He obtained significantly better results by the multivariate projection method than by the univariate method.For other regions, other surface observations such as salinity and pressure gradients seem to be necessary.
Willis et al. [57]Estimation of steric height, heat storage, subsurface temperature, and sea-surface temperature variability.Southwestern Pacific enclosing the Tasman Sea (analyzed depth: upper 800 m)Combining altimetry height (AH) and SST with in situ data to produce improved estimates of steric height (SH), heat content, and temperature variability by linear regression.Nine-year time series of heat storage and temperature variability are calculated. The RMSE of estimated approximately was 4.6 W/m2 in heat storage, 0.10 °C in subsurface temperature and 0.11 °C in surface temperature.
Ali et al. [50]Determination the subsurface thermal structure from surface parameters.Central Arabian Sea (analyzed depth: upper 300 m)Estimation of the subsurface temperature from SST, sea surface height, wind stress, net radiation, and net heat flux by neural network approach.There were proper relationships between the estimated temperature profiles and in situ observations, meanwhile, 50% and 90% of the estimations were a ±0.5 °C and ±1 °C error, respectively.
Guinehut et al. [58]Estimation of the ocean 3-D temperature fields by combining Argo and remote-sensing dataNorth Atlantic Ocean (analyzed depth: upper 500 m)Multiple linear regression was used to derive a synthetic 200-m temperature from simulated altimeter and SST data, then they are combined with individual Argo 200-m simulated temperature to correct the high-resolution synthetic T using an optimal interpolation method.Obtaining a large reduction of RMSE by combining both data types of the large-scale and low-frequency temperature fields at 200-m depth (by a factor of four in large mesoscale variability regions) as compared to the results obtained using only in situ profiles.(1) Providing a better estimation of the 3-D thermohaline structure of the ocean by this method.
(2) Using the dynamic height instead of sea surface height for reducing the errors due to the regression method.
(3) Extending the analyses to other depths and also to the salinity fields.
Swart et al. [59]Estimating GEM and AGEM sections of temperature, salinity, and density.South-western tip of South Africa and the Antarctic continent (analyzed depth: upper 2500 m) Using the CTD, satellite altimetry data (SLA, ADT), Argo float data of temperature and salinity and XBT data. 2-D GEM produced, and then dynamic topography data derived from satellite altimetry are combined with the gravest empirical mode (GEM) to obtain a 16-year time series of temperature and salinity fields. RMSE of assimilation for temperature, salinity, and density is 0.15 °C, 0.02, and 0.02 kg m−3, respectively. The accuracy of the AGEM to reproduce subsurface thermohaline conditions serves as a catalyst to further studies that utilize time series analysis.
Meijers et al. [60]Estimating the four-dimensional structure of the ocean using satellite altimetry.Southern Ocean (analyzed depth: upper 2000 m)By using the altimetry SSH values and Argo floats, a GEM projection of temperature and salinity fields is presented and is used to correlate with the AVISO data to produce gridded, full depth, time-evolving temperature, salinity, and velocity fields.Strongly correlated with in situ measurements and satellite data for estimating meaningful subsurface properties. The combination of altimetry with the GEM fields allows the resolution of the subsurface structure of the filamentary fronts and eddy features.Authors confronted the smooth frontal and eddy features due to the limitation of the spatial and temporal resolution of the satellite altimetry, so they suggested the satGEM requires that each dynamic height be associated with just one T–S profile at each longitude.
Guinehut et al. [61]Combining the main components of the global ocean observing system (in situ and satellite altimeter) using statistical methods and deriving high-resolution 3-D temperature and salinity fields.Atlantic, Pacific, and Indian Oceans (analyzed depth: upper 1500 m)Deriving synthetic temperature fields from altimeter and sea surface temperature observations and salinity fields from altimeter observations, through multiple/simple linear regression methods. Then combining the synthetic fields with in situ temperature and salinity profiles using an optimal interpolation method.Up to 50% of the variance of the temperature fields can be reconstructed from altimeter and sea surface temperature observations and a statistical method. Because of reconstructing only about 20 to 30% of the signal altimeter observations for salinity, making the in situ observing system essential for its estimates.In this study, only thermohaline fields are presented, but the Global Ocean Observation-based products also include 3-D geostrophic velocity estimates that are calculated using the thermal wind equation combined with absolute surface altimeter geostrophic currents and can be used towards integrating climate-relevant global ocean Datasets.
Wu et al. [41] Estimation of subsurface temperature anomaly by remote sensing data.North Atlantic Ocean (analyzed depth: upper 2000 m) Training self-organizing map (SOM) neural network method using anomalies of SST, SSH, and SSS data from Argo gridded monthly anomaly datasets in order to estimate a STA.Estimating STA time series for 1993–2004 from remote sensing SST. Obtaining good agreement between the STA estimations from the SOM algorithm and in situ measurements taken from the surface down to 700-m depth. SOM algorithm can only predict the STA that lies in the range of labeling data.
Su et al. [31]Determining the subsurface temperature anomaly by satellite measurements (AMSR-E, MIRAS, AVISO altimetry).Indian Ocean (analyzed depth: upper 1000 m)Estimation STA from a suite of satellite remote sensing measurements including SSTA, SSHA, and SSSA by the support vector machine.Detecting the SSTA, SSHA, and SSSA parameters had improved and describe the STA estimation accuracy.Providing a useful technique for studying subsurface and deeper ocean thermal which has played an important role in global warming.
Note: SST: sea surface temperature; XBT: expendable bathythermograph; MLD: mixed layer depth; TBD: thermocline bottom depth; TTG: thermocline temperature gradient; RMSE: Root Mean Square Error; STA: subsurface temperature anomaly; SSTA: sea surface temperature anomaly; SSHA: sea surface height anomaly; SSSA: sea surface salinity anomaly; SSH: sea surface height; SSS: sea surface salinity; SLA: sea level anomaly; CTD: conductivity, temperature, and depth; ADT: absolute dynamic topography; DHA: dynamic height anomaly; AGEM: altimetry GEM (the product of combining ADT data with the GEM empirical relationships); AVISO: archiving, validation, and interpretation of satellite oceanographic data; AMSR-E: Advanced Microwave Scanning Radiometer for EOS; MIRAS: Microwave Imaging Radiometer using Aperture Synthesis.
Table
Table 4. State of ocean/sea measurements from space in 2010, 2020, and 2025 [110].
Table 4. State of ocean/sea measurements from space in 2010, 2020, and 2025 [110].
Measurement from Space201020202025
Sea surface height (SSH)100-km spatial scales; 10-day revisit (Topex/Jason series)10-km spatial scales; 10-day revisit (SWOT)10-km spatial scales; 1-day revisit (multiple SWOT satellites)
Ocean vector winds (OVW)25-km spatial scales; 1–2 day revisit (QuikSCAT/ASCAT)3–25 km spatial scales; 6-h revisit (XOVWM/ASCAT/Oceansat 2)3-6 km spatial scales; 6-h revisit (XOVWM and follow-ons)
Ocean surface salinity (SSS)150–200 km spatial scales; 30-day time scale (SMOS in 2009; Aquarius in 2010)40-km spatial scales; 10–3-day time scale (SMAP)20-km spatial scales; 7-day time scale (Aquarius follow-ons)
Sea surface temperature (SST)1-2-km spatial scales; 1-day revisit; no visibility through clouds (MODIS)1–2 km spatial scales; <1-day revisit; no visibility through clouds (VIIRS)1–2 km spatial scales; <1-day revisit; no visibility through clouds (VIIRS)
40-km spatial scales; 1-day revisit; all-weather (AMSR-E)40-km spatial scales; 1-day revisit; all-weather (AMSR-E)1–2 km spatial scales; 1-day revisit; all-weather (next-generation micro-wave radiometers)
Note: AMSR-E: Advanced Microwave Scanning Radiometer-Earth Observing System; ASCAT: Advanced Scatterometer; MODIS: Moderate Resolution Imaging Spectroradiometer; SMAP: Soil Moisture Active-Passive; SMOS: Soil Moisture Ocean Salinity; SWOT: Surface Water and Ocean Topography; VIIRS: Visible/Infrared Imager Radiometer Suite; XOVWM: Extended Ocean Vector Winds Mission.

Share and Cite

MDPI and ACS Style

Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods. Water 2017, 9, 936. https://doi.org/10.3390/w9120936

AMA Style

Akbari E, Alavipanah SK, Jeihouni M, Hajeb M, Haase D, Alavipanah S. A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods. Water. 2017; 9(12):936. https://doi.org/10.3390/w9120936

Chicago/Turabian Style

Akbari, Elahe, Seyed Kazem Alavipanah, Mehrdad Jeihouni, Mohammad Hajeb, Dagmar Haase, and Sadroddin Alavipanah. 2017. "A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods" Water 9, no. 12: 936. https://doi.org/10.3390/w9120936

APA Style

Akbari, E., Alavipanah, S. K., Jeihouni, M., Hajeb, M., Haase, D., & Alavipanah, S. (2017). A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods. Water, 9(12), 936. https://doi.org/10.3390/w9120936

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop