1. Introduction
Integrated Catchment Modelling (ICM) is a key tool in the assessment of environmental impacts of urban water drainage on river ecosystems [
1]. ICM aims to represent the link between the relevant sub-systems affecting receiving water quality dynamics. This is often done by jointly simulating urban drainage systems, Wastewater Treatment Plants (WWTP), rural hydrology and river processes [
2,
3]. The simulation of Dissolved Oxygen (DO) in urbanised rivers is of interest to guide in the decision-making process of environmental management studies. Those simulators allow estimating the effect of corrective measures prior to their adoption. However, the complexity of water quality dynamics and the systematic deficit of observed data result in predictions from such modelling studies presenting a significant degree of uncertainty [
4,
5].
Rainfall is one of the main driving forces for water pollution dynamics in urbanised catchments. Large urban water systems often produce discharges from partially treated WWTP effluents and combined sewer overflow structures (CSO) under severe storm events. These discharges impact on the chemical and ecological status of the receiving surface waters. When modelling water quality processes, it is necessary to represent the urban pollution load, which is heavily linked to rainfall–runoff dynamics. Several studies have addressed the effect of rainfall input errors in the behaviour of individual urban drainage systems and detailed hydrodynamic modelling. It has been reported that the uncertainties of rainfall input data contribute less to the total uncertainty in urban runoff estimation for a small urban drainage system (~180 ha), compared with flow measurement errors [
6]. A comprehensive sensitivity analysis of modelled flow in individual urban drainage systems (200–800 ha) for varying rainfall spatiotemporal resolutions was presented in [
7]. This study showed that the impact of rainfall errors rapidly decreases with catchment area size, and discussed the strong link between temporal and spatial effects. The impact of rainfall dataset selection in the calibration of hydrodynamic models is recognised as significant [
8].
Nevertheless, when modelling receiving water quality dynamics, urban drainage simulators are often conceptualised through spatially lumped model structures [
9,
10]. Lumped urban rainfall–runoff models reduce significantly the simulator’s computational cost. Accuracy of modelled outflow variables is expected to be sufficient for the application at large-scale water quality modelling and real time control of drainage systems [
11]. These lumped model structures further distort the effect of uncertainties in rainfall measurement data, especially those associated with the in-catchment micro spatial and temporal scales. Also, urban wastewater systems are often composed by several connected sewer networks across municipal areas (e.g., centralised wastewater treatment layouts), and the distances between those connected catchments are often beyond the de-correlation length of convective storm events [
12]. This means that spatial and temporal scales of rainfall processes can affect in different manner the individual and the total catchment system [
13].
Little research has been conducted on the effect of rainfall input characteristics at integrated catchment scale and their impact on water quality dynamic simulations. The total contribution of rainfall errors to water quality modelling uncertainties is expected to be moderate [
14]; however, it is important to characterise the desired properties of rainfall input datasets when modelling water quality processes of large-scale urban systems.
The present work investigates the effect of the spatiotemporal variability of selected rainfall inputs on the prediction of dissolved oxygen dynamics in an urbanised river catchment. It aims to ascertain whether uncertainties induced by the miss-representation of the rainfall field at the municipal scale are transferred to the simulation of dissolved oxygen dynamics at a sensitive river section. This paper describes the process to characterise the urban drainage and river time-space scales and a procedure to generate rainfall estimations at catchment-area spatial support with increasing spatial and temporal resolutions. The performance of a large-scale conceptual integrated catchment model was compared against monitoring data. This provided insights on the optimal selection of rainfall data sources in large lowland urban water systems for dissolved oxygen assessment.
The effects of the rainfall input selection are discussed by contrasting model output with observed patterns at CSO and dissolved oxygen concentrations in the river.
2. Materials and Methods
2.1. System and Data Description
The Dommel River is a relatively small river (4–30 m
3/s) representative of a lowland water system located in the south of The Netherlands. Several municipalities are connected to this water system (~4500 ha) emitting their excess water through ~200 CSO structures into the receiving water body. Also, a WWTP with a capacity of 750,000 PE is discharging its effluent into the river. The river suffers from acute oxygen depletion events under severe storm conditions, which impacts its ecological status.
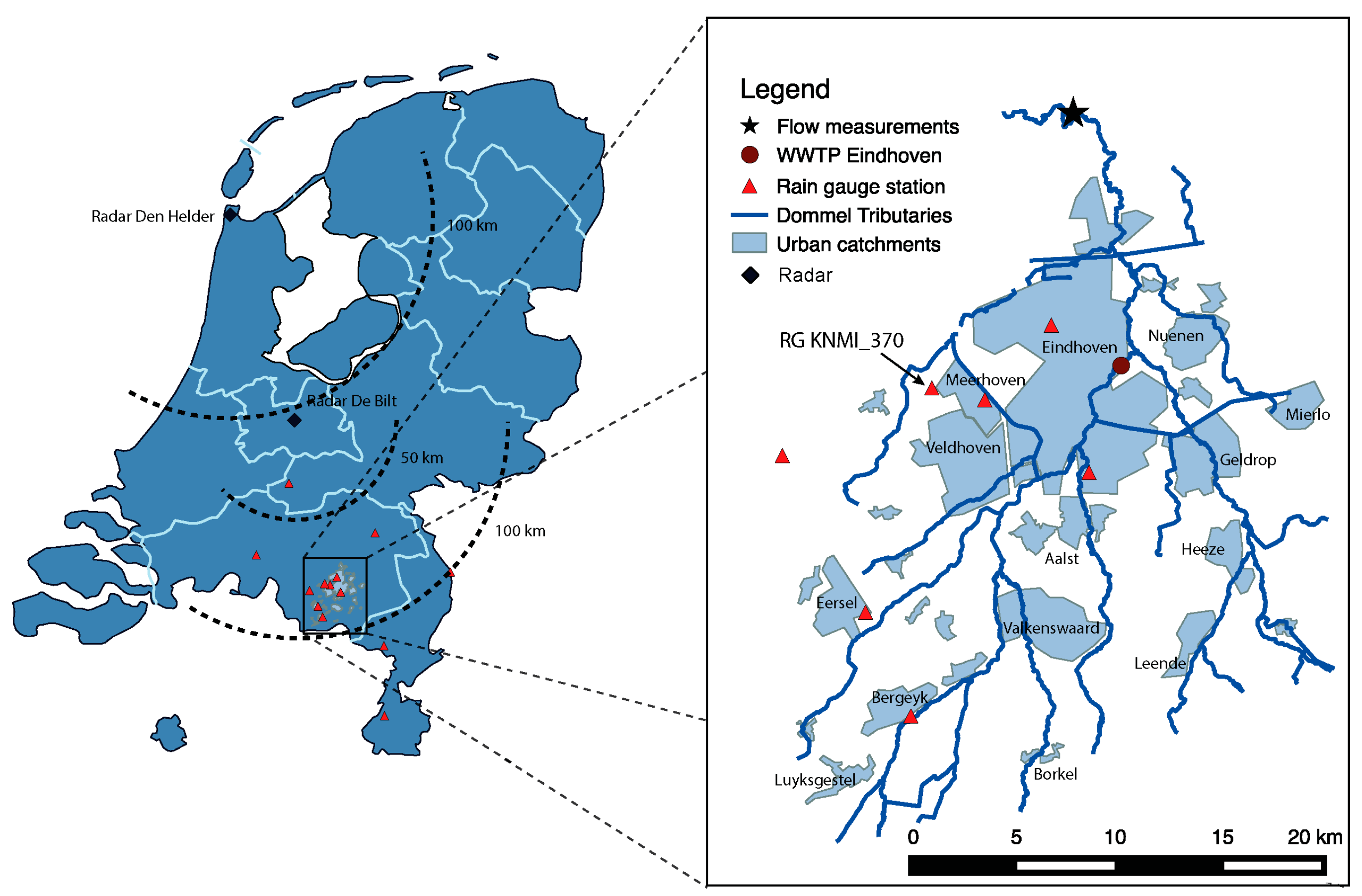
Figure 1 depicts the physical layout of the Dommel water system, along with the rain gauge network, the Dutch weather C-Band Radar network and the geographical layout of connected draining urban areas.
River data were obtained at a monitoring station (black star in
Figure 1) located roughly 17 km downstream of the WWTP (water-depth, velocity and Dissolved Oxygen (DO) concentration). DO measurements were taken by an online probe located in the river, with a sampling frequency of 10 min. The measuring station is periodically maintained and calibrated. Manual data inspection was performed to validate time series by the water authority of the river. Time series for Combined Sewer Overflow (CSO) discharges were estimated from water depth monitoring data at the main structures (although those estimations can contain significant level of uncertainties). The WWTP operator provided water quantity and quality data of the influent-effluent. More information about the data set can be found at [
9]. In total, three years of data were obtained (2011–2013).
Measured rainfall data were obtained from three sources: (1) An automatic rain gauge network from the Dutch Meteorological agency (KNMI). One station was deployed close to the civil airport of the city of Eindhoven (KNMI_370 in
Figure 1) and six more were found within a radius of 70 km from the centre of catchment (those rain gauges add very limited information since most rainfall processes have shorter decorrelation lengths, but were used to constrain the interpolation process in drainage areas located in the limits of the catchment). KNMI automatic rain gauges use a floating device and an electronic register, providing a high accuracy, measuring frequency and resolution (1% of the rainfall rate-1 min-0.02 mm/h). These stations are calibrated and maintained regularly; (2) A local network of tipping bucket rain gauges (resolution 0.15 mm). This network is composed of six stations managed by the Water Board de Dommel (the public company responsible for the water quality in this river) and the municipality of Eindhoven. Rain gauge stations are located within the urban area of several municipalities (
Figure 1); (3) Single polarisation C-Band radar rainfall estimations from the composite of the KNMI. These rainfall estimates are provided at a resolution of 1 km
2 and 5-min accumulation. The estimated radar rainfall is further bias-corrected by the KNMI (from 3-h and 1-day rain gauge data) in order to eliminate the systematic errors present in the raw radar data [
15] (
Figure 1, provides distances to the two KNMI radars).
The urban system connected to the studied section of the river Dommel is composed of approximately 29 contributing urbanised areas (
Figure 1), which are characteristics of a low land area with high in-sewer storage and low slopes. Catchment areas were extracted manually from a land-use GIS database. This catchment comprises a rural area of ~800 km
2, which contributes to the base-flow of the river. The rural catchment is mainly composed of forestry and low intensity agricultural areas. The system is characterised by mild slopes and it is naturally drained.
Section 2.5 contains further description of the system under study, attending in detail to the relevant characteristic spatiotemporal scales.
2.2. Description of the Model Structure
An integrated catchment model (ICM) was developed with the purpose to simulate water quality dynamics (dissolved oxygen and ammonium) in the river Dommel. A previous version can be found at [
9] along with a detailed description of the monitoring data needed for its development and the calibration process (in a dataset from 2001 to 2010). The ICM consists of: An urban drainage routine, which was conceptualised as a set of lumped rainfall–runoff models representing the 29 urban systems of the Dommel area. A tank-in-series scheme served to simplify the hydraulic routing network to the WWTP. A total of ~200 CSO structures were reduced to 35 clusters representing the spatial locations of the most relevant discharge structures. The WWTP model’s characteristics and calibration are described in detail in [
9]. This model represents three biological lines and a storm-bypass section. The link of state variables at the boundary urban drainage—WWTP were produced using an stochastic generator [
13]. A river sub-model, which is composed of a flow propagation scheme, was modelled through a hydrological storage–discharge model (tank-in-series scheme). This was calibrated based on river flow and depth measurements over one year (2012) using CSO and WWTP discharge measured data and hydrologically derived base-flow as inputs. The calibration scheme produced a Nash–Sutcliffe efficiency at calibration/validation of 0.92/0.84. Further description of this scheme can be found in [
16]. The water quality routine was conceptualised, assuming completely stirred reactor-like river sections (with section lengths between 800–3000 m).
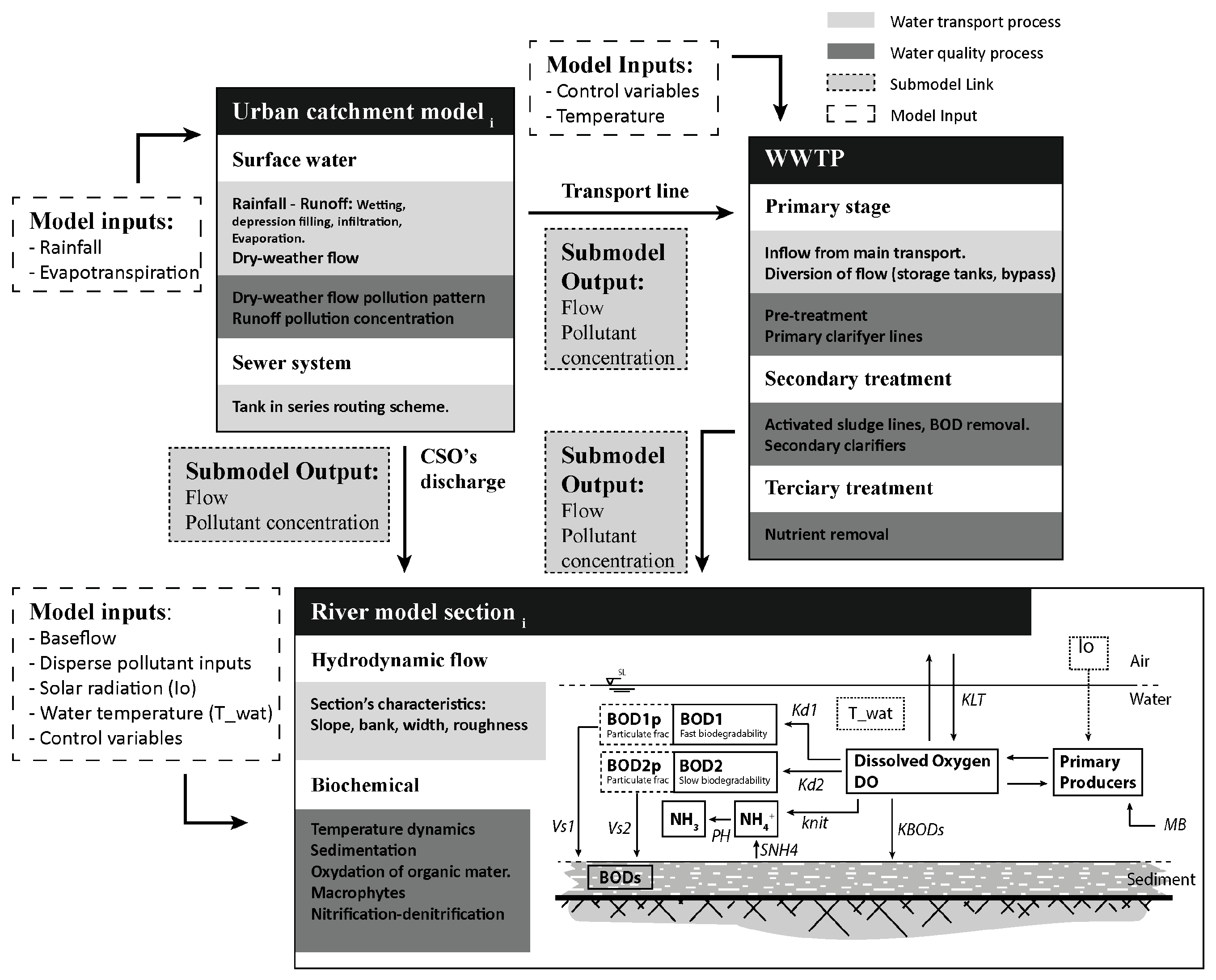
Figure 2 provides a scheme of the link between subsystems and the processes accounted for in the water quantity and quality routines. Within the river model section a graphical scheme summarises the water quality processes used to simulate dissolved oxygen dynamics. This included the balance between a three-phase layout (atmosphere, water volume and sediment), fractionation of biological oxygen demand (BOD) in dissolved/particulate and fast/slow biodegradability, respiration from macrophyte biomass (primary producers) and nitrification–denitrification. The main source term in the DO dynamic balance is the reaeration process (
KLT), which depends on water turbulence, depth and temperature. Meanwhile, consumption is generated by oxidation of fast and slow biodegradable matter in the sediment/suspended fraction (
kd1,
kd2 and kBODs) and from the nitrification process (
knit). The sedimentation of organic matter was also considered (
Vs1 and
Vs2).
2.3. Storm Selection
Three periods of summer were selected for a continuous modelling time window: period (1) 10 August 2011–31 August 2011 (21 days), period (2) 5 July 2012–4 August 2012 (30 days) and period (3) 25 July 2013–19 August 2013 (25 days). Summer storm impacts are considered critical for the dissolved oxygen content in urban rivers. These events often couple several critical factors: Firstly, high temperatures lead to a lower oxygen saturation point at the water mass (which consequently produces a lower initial DO concentration during the event). High temperatures also lead to faster biodegradability rates at the sediment bed in the river. Secondly a low base-flow level reduces the buffering capacity of the river.
As water quality-related processes exhibit a significant inertia (e.g., biological masses at the waste water treatment works can take stabilisation times up to weeks-months), the initial conditions for each simulated period were extracted from one-year of previous continuous simulation (using the rain gauge KNMI_370 as input).
A total of seven rainfall events were selected within the three periods (which induced oxygen levels at the river monitoring station lower than 3 mg/L). A summary of the storm characteristics can be found in
Table 1. Rainfall maximum intensity and accumulated depth were calculated using 5 rain gauge stations located within the boundaries of the Dommel system (maximum distance-to-centre 18 km). Rainfall variability and measuring errors induced dispersion in the chosen parameters, thus the mean value and one standard deviation are provided as
. Visual and quantitative assessment of rain gauge time series did not show systematic deviations.
2.4. Generation of Rainfall Estimations
Rain gauge/disdrometer networks are usually considered the most reliable data source for rainfall measurements at urban scale. However, these networks present low spatial densities, thus the significance of punctual measurements decreases when extrapolating measurements to ungauged locations. On the other hand, weather radar rainfall estimations can represent the spatial structure of storm processes (at the cost of lower accuracy). When possible, both data sources should be merged to provide rainfall measurements respecting both punctual rain gauge measurements and radar spatial structure [
17,
18].
The allocation of rainfall inputs from measured locations to the model of an individual draining area is generally done based on the modeller’s expertise. This defines a time-accumulation scale in which the rainfall estimations will be generated. This time step definition is constrained by data technical specifications (lower limit) and by the dynamics of the modelled process (upper limit). Manual/automatic quality checks are performed to assign reliable time-windows to each dataset. Then a selection of these measured points is used to generalise values to the rest of the catchment. This is often done by simple spatial association as using Thiessen polygons, distance-averaging schemes or through geostatistical methods. A geostatistical interpolation scheme was used in this work since it allows accounting for the spatial structure of the rainfall process and it facilitates the merging process of different data sources.
When generating rainfall predictions, an often-neglected factor is the spatial support of the estimation. In this case, the studied ICM was composed of several individual lumped rainfall-runoff model structures. These models spatially aggregate the internal connected areas. Thus, the rainfall input should be representative for the full domain and not only of an arbitrary internal location. Although measurements provided by rain gauge networks are of point values, rainfall predictions should be performed over a certain area. This is often referred to as change of block spatial support [
19].
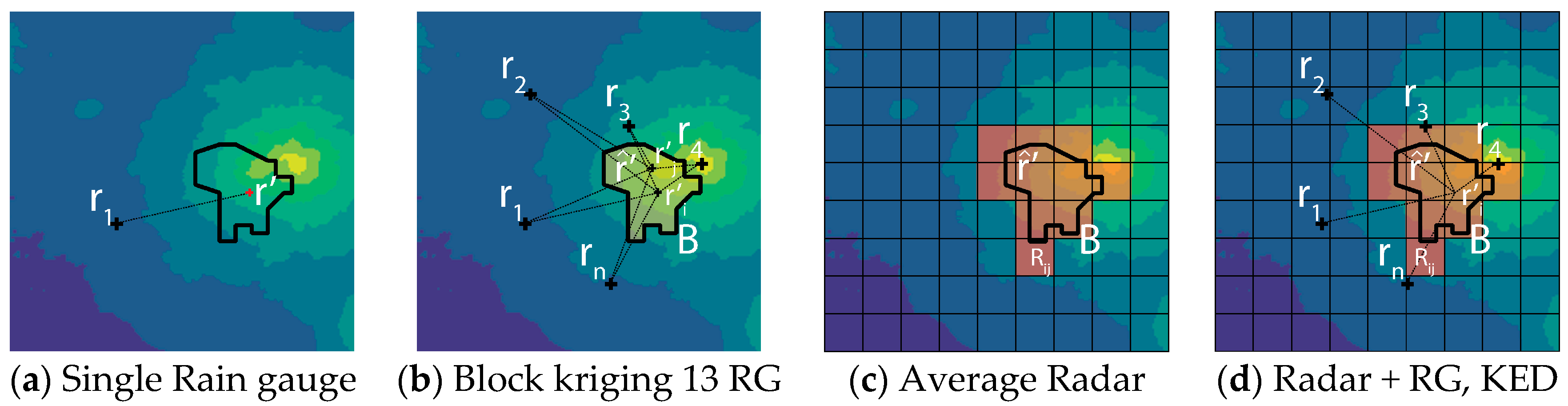
Figure 3 depicts the strategies followed to generate predictions by interpolating a set of sampled points from the rainfall map. In
Figure 3a a direct use of the measurements of a single rain gauge to all catchments
Figure 3b rainfall estimations at catchment’s area (B) are rendered from a block kriging scheme from n point samples (
Section 2.4.1) in
Figure 3c the estimated rainfall is extracted from a weighted average of the radar pixels covered by the catchment
Figure 3d presents the case in which radar measurements are used as an external covariate within the area support to refine an interpolation from n rain gauges (point-to-block kriging with external drift,
Section 2.4.2). The simplification of spatial rainfall description through point or block estimates will not always contribute significantly to the rainfall predictive accuracy. Its influence depends on the spatial variability of the observed field and the size of the support area. In other words, a highly correlated spatial field would be well approximated by a point estimate. However, spatial variability of rainfall may become increasingly relevant at large draining areas subjected to highly convective storm conditions.
Rainfall input time series were generated using four data sources:
Rainfall input time series were generated by varying the accumulated time step T (10, 30 and 60 min), for each of the four data sources, thus rendering 12 different products for each of the 29 individual rainfall–runoff model catchments.
2.4.1. Ordinary Kriging with Change of Spatial Support
Kriging is a well-known geostatistical technique [
20] which is widely used to generate estimations of continuously spatially distributed variables at non-sampled locations, taking into account the spatial structure exhibited by the variable.
Let
be the rainfall intensity at a certain non-sampled location
. This can be approximated by a linear combination of,
observed values at nearby locations,
:
where
denotes a set of local weights. Ordinary Kriging stems from the assumption that the process is Gaussian and has a constant and unknown mean value or
. Forcing the estimation to be unbiased;
and minimising the prediction’s variance leads to the derivation of the kriging system, which in matrix form is:
in which
refers to the Lagrange multiplier (used on the minimisation of the variance),
to the covariance matrix between data points,
covariance vector between each of the measured points at the estimation’s location and
a vector of ones.
Block kriging usually denotes a variation of the kriging system in which the target is not a point estimate but a spatial averaged prediction within a certain area domain,
. This is computed as:
in this case, the covariance structure changes to the point-to-block covariance, or:
which represents the average covariance between the location
i and all the possible locations within the block
. Thus the kriging system accounting for the estimation at block level is:
by solving
and using it as the weights for the Equation (1), it is possible to generate estimations at the target support area.
2.4.2. Kriging with External Drift (KED) with Change of Spatial Support
Ordinary kriging is analogous to a Gaussian process model with an unknown but constant mean field. However, additional variables that are correlated to the targeted process (and extensively measured) can be used to further refine the spatial model. Regression kriging and Kriging with external drift cover this problem. This involves assuming a spatial model, which has a deterministic mean
and a stochastic component
:
and in which the mean field is linearly related to a set of
external variables
through a set of weights
(also referred as regression coefficients). In Regression Kriging, the mean field is first fitted, and the field of stochastic residuals
is interpolated though Simple or Ordinary Kriging. On the other hand, Kriging with External Drift (KED) includes the regression process within the solution of kriging system. Thus, predictions on KED are also performed as a linear combination of the values at observed locations:
in which the weight values are obtained by solving the KED equation system
:
Radar-reflectivity derived rainfall maps were the only covariate used in this study. Therefore, the solution of the KED system in matrix notation with radar as an extra covariate could be expressed as:
in which
and
are the Lagrange multipliers,
a row vector of the radar values associated to the observed locations,
the covariance matrix between sampled points and
the covariance vector between each of the measured points and the targeted location.
As discussed in the case of Ordinary Kriging, the objective estimation should be done at an area block support. Thus the equations were adapted in an analogous manner:
the covariance matrix should represent the point-to-block covariance (
). The radar covariate was averaged within the block area:
this step facilitates the implementation of the kriging system, and it is consistent since the deterministic mean (in Equation (7)) is calculated through a linear application. Thus, averaging the covariate beforehand is equivalent to performing predictions at each location and later spatially averaging them.
2.4.3. Rainfall Spatial Correlation
The covariance used in Equations (5) and (11) represents the spatial structure exhibited by the measured process. This was expressed in terms of a semivariogram structure, which in this case is related to the covariance as:
where
(total variance). An empirical semivariogram was computed from the rain gauge dataset. This should ideally be computed independently at each time step (as temporal autocorrelation was neglected). However, in most cases, the urban scale rain gauge network does not present enough spatial density to compute a reliable semivariogram structure per time step. Therefore the rain field was assumed to be stationary of second order, isotropic and was computed as time-lumped, obtaining an averaged structure for each storm process in the form:
for which
is the number of sampled pairs located at distance
(Euclidean distance). The semivariogram was time-averaged over each selected independent storm process and normalised by the variance of the rainfall variable at each time step
.
The empirical semivariogram is a cloud of discrete points relating space lag (
) and semivariance. In order to generate a continuous spatial correlation map, a valid functional representation (experimental semivariogram) was fitted. An exponential structure was used in this case:
where
c is the partial sill,
is the nugget effect and
φ the effective range or de-correlation distance (distance at which the semivariogram value reaches the 95% of the total sill). No relevant nugget was found in a preliminary study and therefore it was excluded from the semivariogram model (this is in agreement with the findings of [
21]).
2.5. Characterisation of the Water System
This section attends exclusively to the definition of the spatial and temporal scales characterising the water system under study. This is directed to improve the generalisation potential of the results (by allowing comparison with other systems).
2.5.1. Spatial Scales
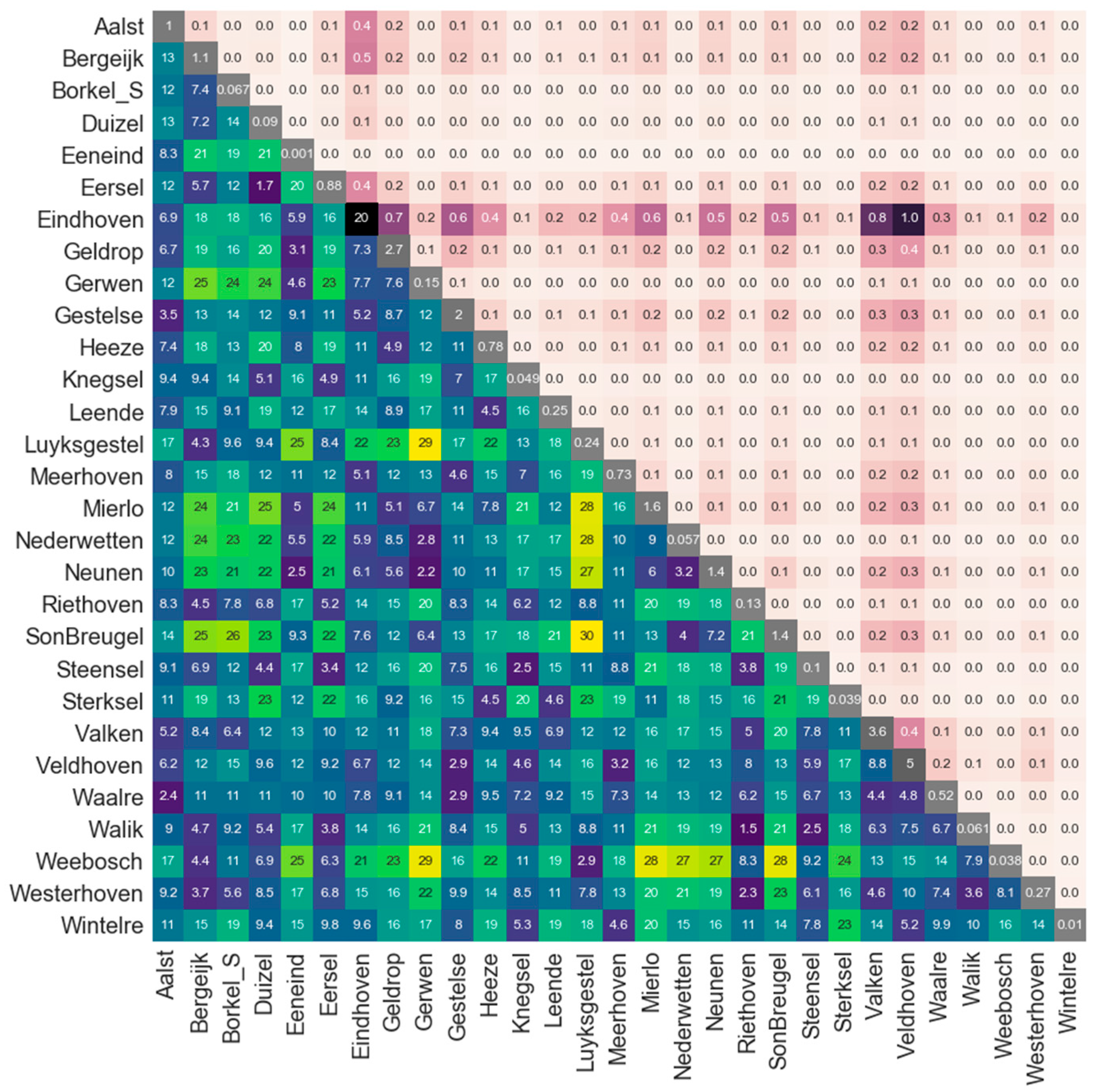
Figure 1 shows the geographical location of the different municipalities connected to the Dommel catchment. The system is composed by 29 individual drainage areas, which are scattered over an area of roughly 25 × 30 km. The distance from the different urban drainage systems along with their drained area morphology plays a role on the sensitivity to rainfall spatial scales (e.g., a highly clustered system could be sufficiently represented with a few sampled locations, while a sparse one may require a more detailed spatial description).
Figure 4 introduces the main spatial dimensions of this system. The lower triangular matrix displays the distance between centroids of the catchment areas, the area
Ai in km
2 is shown in the diagonal, while the upper triangular matrix introduces a ranking metric of importance between area couples (normalized
). This ranking metric shows the clustering effect exerted by the biggest municipal area (Eindhoven).
A global characteristic spatial scale was computed as a weighted average of the centroid-to-centroid distances plus the average area length scale, expressed as:
where
is the area of the
ith catchment and
is the distance between the centroids
i and
j. This metric aims at accounting for the distances between connected areas, giving an increased importance to larger area couples. This provides an estimated catchment characteristic scale that can be used to diagnose the system’s behaviour against rainfall processes with different correlation scales.
2.5.2. Temporal Scales
A characterisation of the system’s reaction time was extracted from observed datasets at the rain gauge network, CSO structures, WWTP and river.
Table 2 provides a summary for the characteristic temporal scales. Additionally, the accumulated discharged volume from the CSO structures and the minimum DO level in the river linked to each storm process are shown. This provides an insight on the impact mechanism of each event and on the reaction patterns of the system.
3. Results
3.1. Urban Drainage Dynamics
The effect of rainfall input source (space–time variability) in the urban drainage dynamics is illustrated by the comparison of the four most relevant internal variables: (1) Maximum estimated rainfall intensity in the catchment; (2) accumulated rainfall depth; (3) maximum discharge at the CSO and (4) accumulated discharged volume. The estimated rainfall intensity and accumulated depth describes differences in the rainfall input at each catchment. Each of those inputs were propagated through the urban drainage sub-model, and subsequently rendered the pollutant load in the river system. The urban drainage response is characterised by the CSO dynamics, described by the maximum flow peak and the accumulated discharged volume.
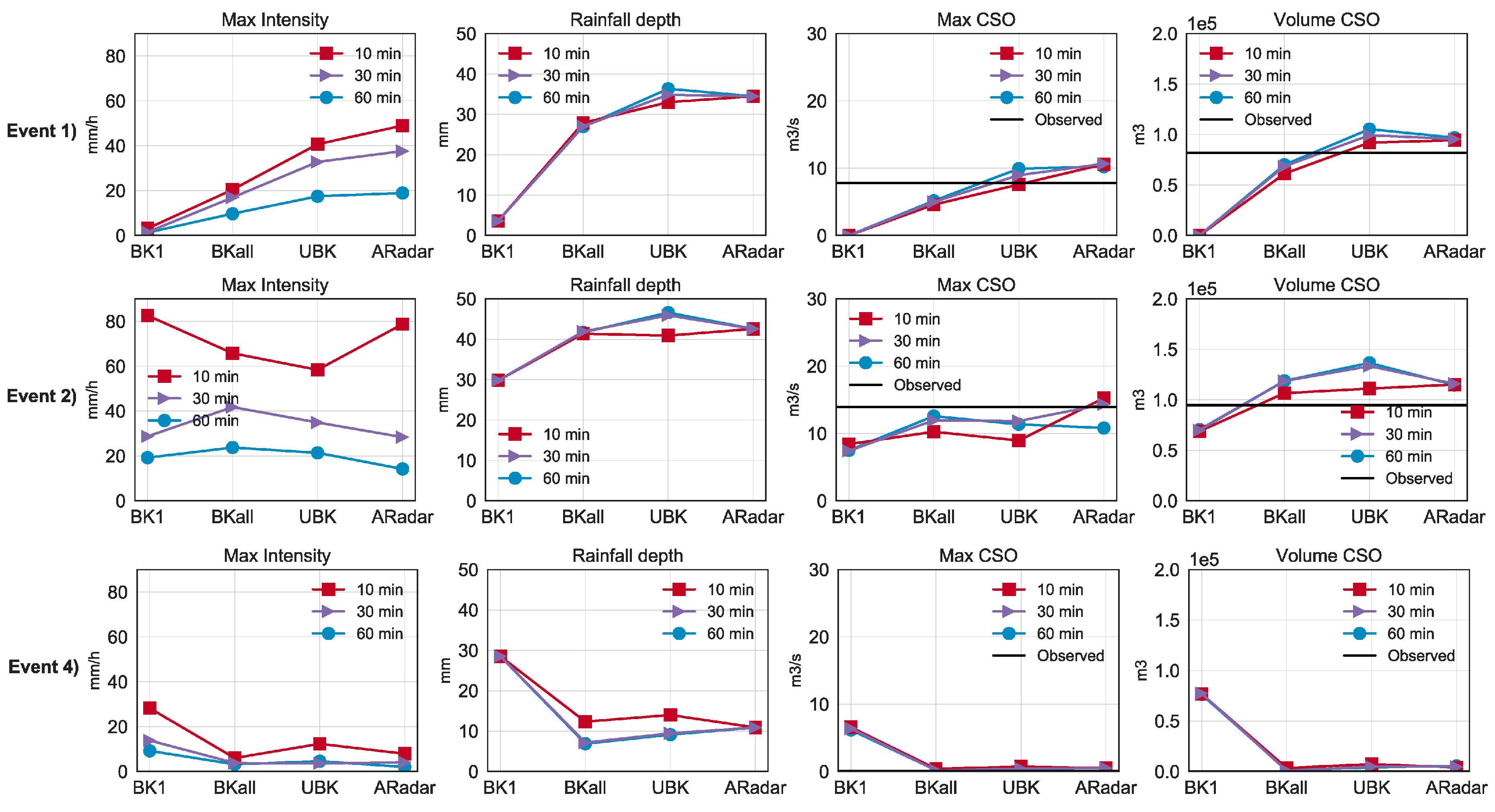
Figure 5 shows the effect of rainfall input on the urban drainage system of Valkenswaard (
Figure 1). This municipality is an especially illustrative example since it is located ~12 km from the rain gauge KNMI_370 (the source of the BK1 product) and represents a relevant contribution to the total discharged volume (2nd largest connected area). This example allows the observation of the joint effect of time and space variability. The selected time aggregation influences the estimated maximum rainfall intensity, which however does not propagate to the estimation of total rainfall volume and to the CSO simulation. A certain effect of time-aggregation at the interpolated rainfall products (BKall and UBK) can be observed. However, this difference is relatively small compared with the exhibited by the selected spatial data sources. The use of a single rain gauge input, BK1 creates an appreciable deviation in the computation of CSO dynamics in most of the rainfall processes studied when compared with monitoring data (
Figure A1). Differences between the other three products (BKall, UBK and ARadar) are less apparent.
The time–space rainfall input variations were decoupled to display the effect in all urban drainage catchments connected to the water system.
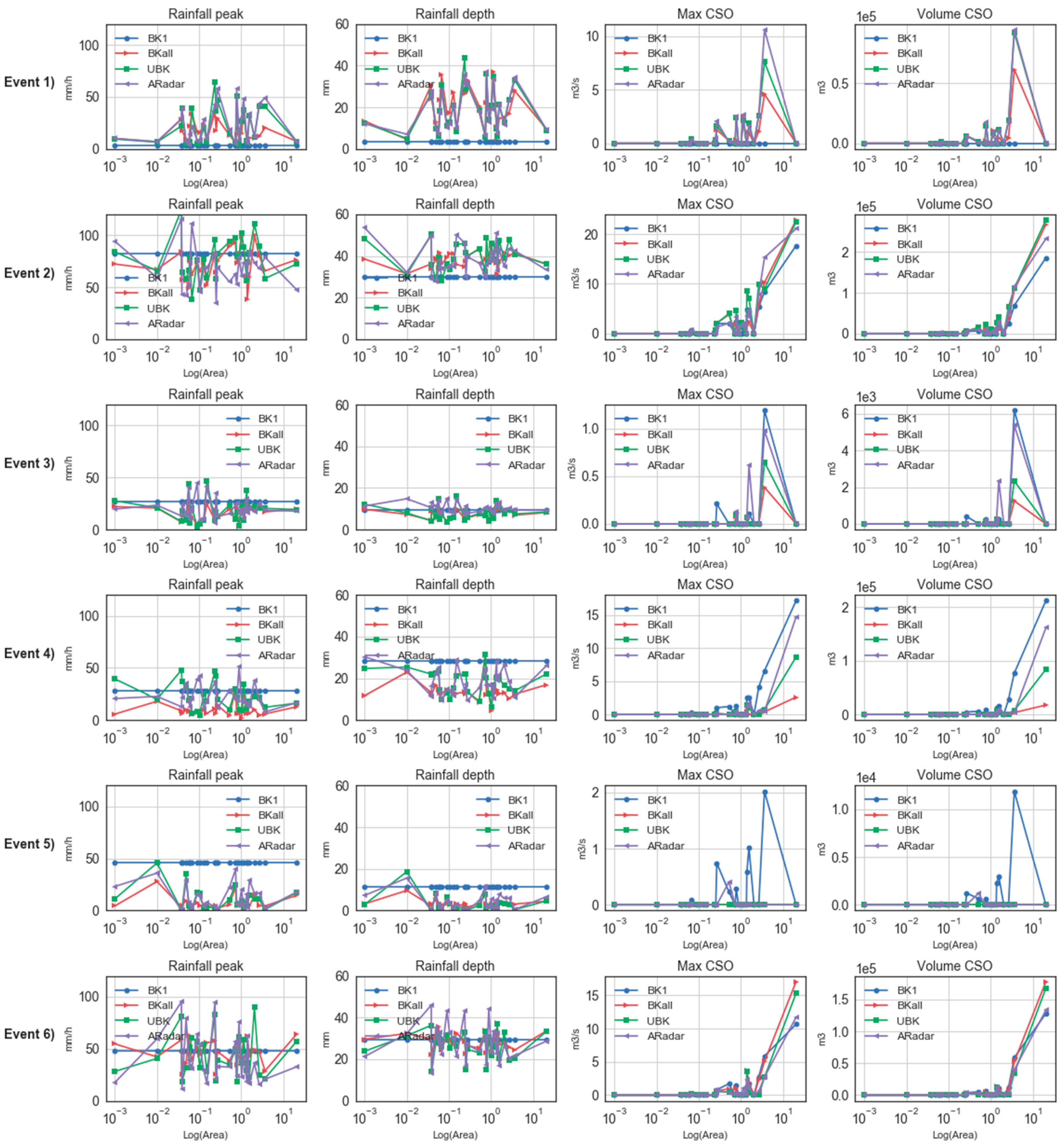
Figure 6 shows the effect of variations of the spatial product (at fixed 60 min time aggregation) for each catchment (represented by their connected areas in abscises). The rainfall intensity and depth provided by the product BK1 produces a distortion of the rainfall map, which can be appreciated in events 1, 2 and 5 (
Figure 6). Although in some cases like in Storm 6 or Storm 7, BK1 can be representative of the mean of the process, it generally induces a deviation into the rainfall input description with respect to the rest of the products shown in this work. This error is not systematic and it is linked to the homogeneity of the rainfall process (if the central rain gauge is representative for the overall spatial domain or not). In consequence, these differences in the rainfall quantification due to spatial data variation affects the CSO simulated dynamics, Event 1 and 4 in
Figure 5 are a good example of this phenomenon in which BK1 underestimates first and overestimates later the total rain volume and this is consequently transferred to the accumulated CSO volume.
Figure 7 shows the effect of the selection of time-aggregation level at each urban drainage system (using the ARadar spatial data source as fixed input). Here it can be seen how the selection of a certain time aggregation (10–60 min) impacts on the estimation of the maximum rainfall intensity. However those differences do not propagate to the computation of accumulated rainfall volume and in consequence to the simulation of CSO discharges.
3.2. Rainfall Estimation Variability
The spatial characteristics of the observed rainfall processes under study were estimated by the use of a time-averaged empirical semivariogram (as described in the methods section).
Table 3 shows the fitted range and sill parameters for each storm process depending on the time-aggregation level. This describes the correlation structure present in the rainfall process. A large range indicates a spatially homogeneous rainfall process. This was used in order to relate the rainfall input influence with its spatial correlation and the characteristic scale of the catchment. The increase in accumulation time of the rainfall input produced a more spatially correlated map (seen by the increase in range). This was to be expected since aggregating on time acts as smoothing of the process. Additionally,
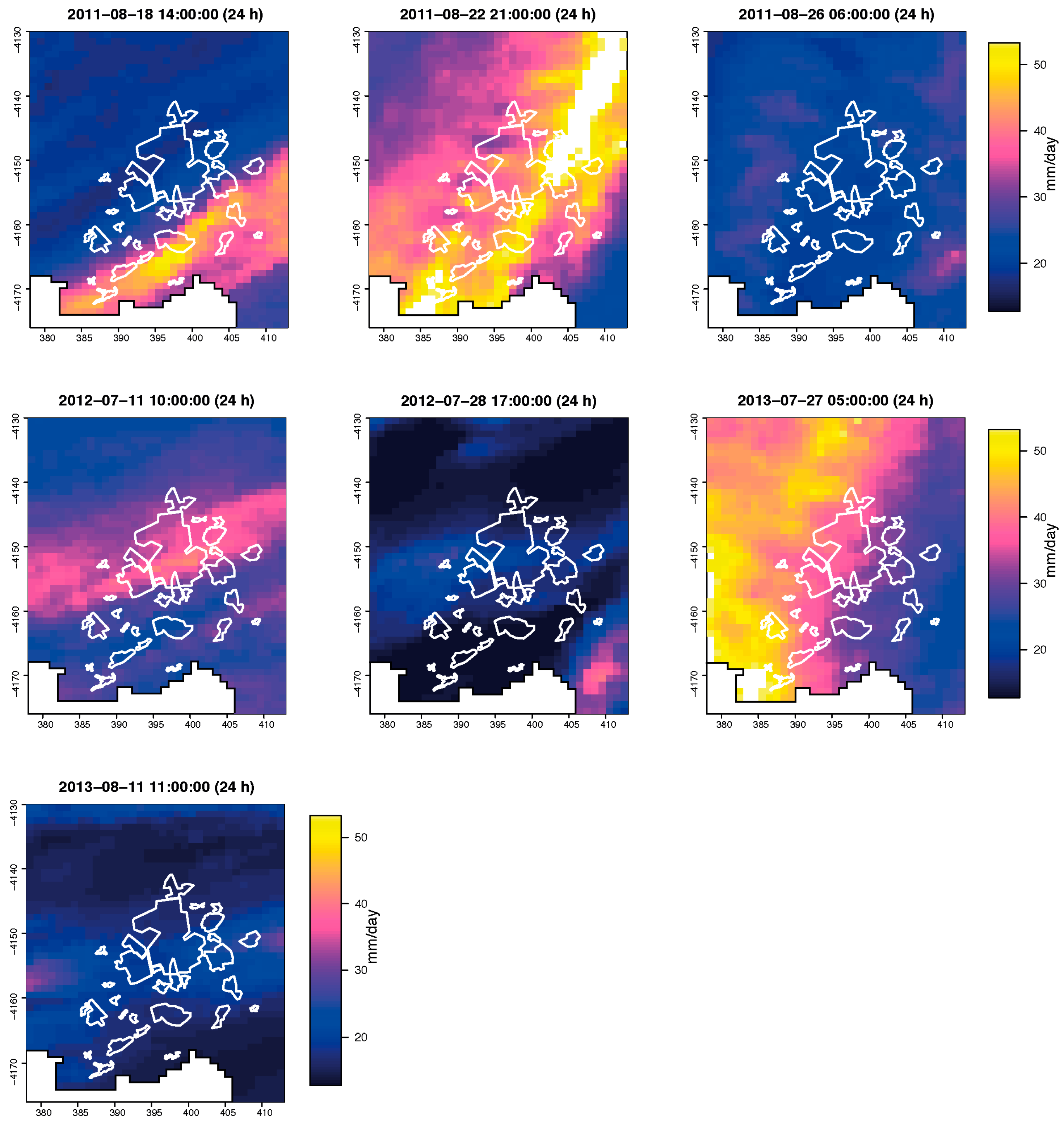
Figure 8 shows the accumulated rainfall depth map at 24 h from the start of each storm. This represents the storm main path, which describes the total rainfall volume spatial distribution.
3.3. Rainfall Input Effect on Dissolved Oxygen Dynamics
In order to assess the effect of rainfall input in dissolved oxygen simulations, modelled time-series were compared against existing monitoring data.
Table 4 presents the residuals between the minimum oxygen level observed and modelled at all storm-input combinations. Minimum oxygen simulated level is highly relevant in practice since it captures the magnitude of impact at the receiving water body and is directly related to the pollution load in the system (which is driven by the rainfall process).
Table 5 shows the root-mean-squared-error (rmse) between simulated-observed time series from the beginning of the storm event until 5 days later when the DO concentration is recovered (except in the case of Event 2, which overlapped partially with Event 3). The performance indicators for dissolved oxygen show that the effect of time-accumulation of the rainfall input is negligible.
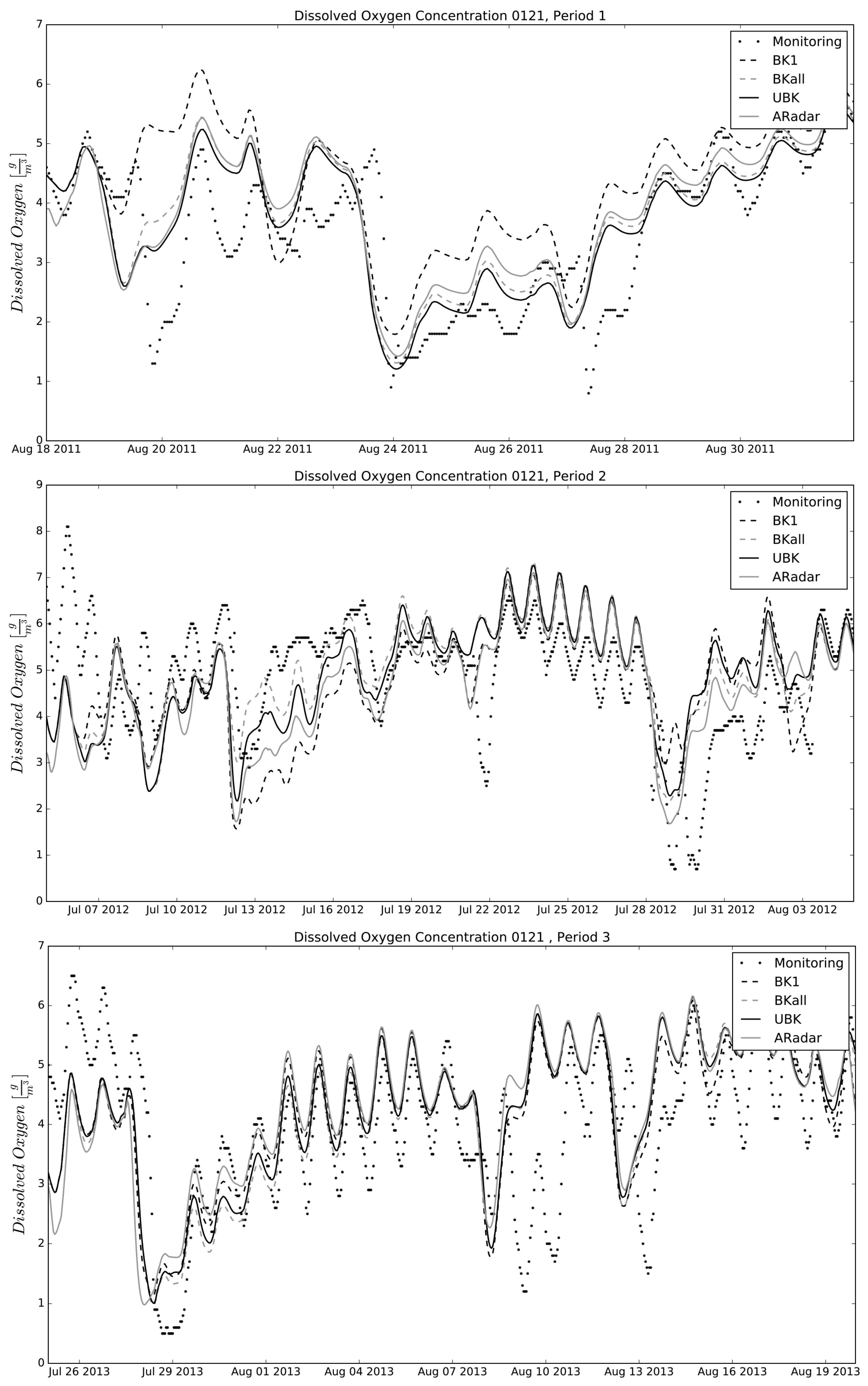
Figure 9 presents a graphical comparison between dissolved oxygen (DO) river observations and modelled series at each spatial data source selection (fixed 60-min time accumulation). The graph considers the three time period simulations, as described at
Table 1.
It can be seen how the effect of rainfall selection had a varying impact depending on the storm process. This is linked to the mechanism of DO depletion of each event and on the characteristics of the rainfall process. For instance, storms from period (1) and (2) exhibit differences due to the spatial data selection in both the DO depletion depth and recovery duration. However, the events occurring in period (3) show very little sensitivity to the selected rainfall input. In the case of Event 7 this can be explained by the fact that CSO volumes were low (see
Table 2). Thus the DO depletion was likely not due to CSOs but rather to the discharge from the WWTP (which filters the effect of time-space) or by unaccounted processes not included in the model structure. Event 6, on the other hand, presented a rainfall event for which the rain gauge KNMI370 was a good representation of the main contributing urban areas (as appreciated in
Figure 6).
4. Discussion
Figure 5 and
Figure 6 show the deviation generated by the homogenous rainfall source (BK1) for the rainfall estimation (depth and intensity), which was consequently transferred to the CSO discharge patterns. There is a clear difference between predictions rendered by a homogenous rainfall data source (BK1) and the results stemming from the use of extra spatial information either the extended rain gauge network (BKall), radar spatial predictions (ARadar) or a merged product rain gauge-radar (UBK). Varying the time aggregation of rainfall products (at 10, 30 or 60 min) influenced the maximum estimated rainfall peak. However, this difference was not transferred to the estimated total rainfall volume (depth) and to the CSO-DO dynamics.
Figure 7 shows that the influence of time aggregation on CSO patterns is almost negligible when modelling discharged volumes and that this is generalizable to all catchments under study. This is explained by the nature of the urban drainage system, which as described, is characterised by low slopes and large in-sewer storage. Thus, the behaviour of CSO spills is dominated by the rainfall volume and not by its dynamic component. A direct link between the rainfall characteristics (maximum intensity, total volume, average correlation range) and the sensitivity of dissolved oxygen to rainfall events could not be established. Therefore, the characterisation of the spatial scales at the measured rainfall intensity maps (through the semivariogram calculation) is insufficient to ascertain their effect on the integrated model DO output variability (since this is sensitive to rainfall volume and not to intensity).
Figure 8 shows the accumulated rainfall volume spatial distribution of the rainfall events. It can be appreciated how the storm cell “path” can play an important role in the process since its variability occurs within the spatial scale of the catchment system. Thus, the spatial distribution of storm processes should be included in synthetic rain generators used for design and test purposes (as described in [
22]). A slightly higher influence of the time-step is observed at both kriging inputs BKall and UBK (for modelling CSO discharge). This was due to the nature of the interpolation process: the performance is known to decrease at short time scales [
17] (lower than 30′).
The effect of time aggregation of the rainfall field in DO dynamics is negligible. This is shown in
Table 4 in which the variation of the modelled-observed minimum oxygen level residual is practically insensitive to the variation in time. This effect is explained by the fact that DO dynamics in the system are mainly affected by the WWTP effluent and by the total CSO discharged volume. Both of them seem to be relatively insensitive to rainfall input time accumulation (between 10–60 min). Additionally, DO processes present a significant inertia with respect to the rainfall process (15–28 h, as shown in
Table 2), which acts like a high-frequency filter of the CSO dynamics.
This study intends to describe the interaction of a large-scale integrated urban catchment model and the rainfall input characteristics. It is relevant to mention that such integrated modelling studies are subjected to several sources of uncertainties (which are not independent). The water quality model applied has not been calibrated for the studied time series, due to the fact that the main goal of this study is the observation of changes due to input data source. Therefore several errors can be observed in the simulated time series. First, there is a systematic underestimation of DO depletion processes of 1–0.5 mg/L (which could be indicative of a wrong description of the urban-WWTP pollutant concentration load). Additionally the DO simulations reacted slightly faster (1–8 h) than observed in the measured data, which can be indicative of a wrong timing effect in CSO-WWTP effluent simulation (since the hydraulics in the system were calibrated). Those errors however are not expected to have an influence on the conclusions of this study.
Examples of similar studies are scarce as of yet due to the complexity of creating a fully integrated catchment study and the lack of sufficient monitoring data in those systems. However, partial studies on the effect of input errors in similar systems can be found in [
23], which described the sensitivity of a river model to several sources of uncertainties, indicating that 60% of DO simulation variability is explained by the input data. However, this considered variations in pollution load inputs from urban systems and not directly on rainfall. A full uncertainty quantification scheme was proposed for a small integrated system in [
4], but only accounting for urban drainage and WWTP outputs (not receiving water), and reported that rainfall uncertainties had a contribution of 15–20% to uncertainties in BOD loads from a sewer and WWTP effluents. Freni et al. [
24] reported in a fully integrated example for a small-scale river system that DO river concentration is highly sensitive to the upstream subsystem outputs (in this case urban drainage discharges). Those studies report a relative sensitivity of DO or related variables to the input description. Thus, reducing the errors in the rainfall input data set could influence the ability to simulate DO patterns. The findings of this study aim to describe the relevant characteristics that the input data source should have when modelling DO in a large urban integrated water system, which can be used to direct further monitoring and modelling efforts in this system or in similar ones.
5. Conclusions
This work addresses the influence of rainfall input spatial and temporal characteristics in the modelling of dissolved oxygen patterns in a large lowland integrated urban water system. The effect of varying the rainfall process description by using different accumulation time scales and different rainfall measurement sources was investigated. A total of 12 rainfall input products were tested for seven storm events, which generated significant oxygen depletion events in the receiving water body. Rainfall inputs were generated at three time-accumulation levels (10, 30 and 60 min) and using four different rainfall sources: (1) A single rain gauge (BK1), (2) a block kriging interpolation from 13 rain gauges (BKall), (3) radar-derived rainfall composites from the KNMI (ARadar) and (4) the results of kriging with external drift merging of rain gauges and radar (UBK). All estimations were generated at the spatial support of the individual connected urban drainage networks.
The tested rainfall time-accumulation level did not influence the modelled dissolved oxygen patterns in the river. Although it influenced the maximum estimated rainfall intensity, the effect on rainfall-accumulated volumes was very limited (with the exception of kriging based products, which exhibited a minor influence of time accumulation). This effect was not propagated to simulated CSO dynamics at the urban system in most cases and therefore the effect on DO dynamics was negligible. It was found that the use of a single rainfall point measurement generates a non-systematic deviation in the simulated CSO series (although the measurement was located 5 km from the main contributing urban catchment). This misrepresentation has the potential to affect DO dynamics. No relevant difference was found in the use of radar estimations or a network of rain gauges in the system.
The results obtained in this study can only be generalised to similar systems with an equivalent mechanistic relationship urban, WWTP and river. Nevertheless, we present a detailed description of the process followed to: (1) Characterise the rainfall process and the system’s response patterns; (2) generate rainfall inputs at the spatial support of the target catchment and (3) assess the sensitivity of the model to the characteristics of rainfall input. This process can be followed in other integrated catchment studies in order to identify the desired characteristics of rainfall input datasets for each selected system variable.
Acknowledgments
This research was done as part of the Marie Curie ITN—Quantifying Uncertainty in Integrated Catchment Studies (QUICS) project. This project received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement No. 607000. The authors would like to thank Lorenzo Benedetti (Waterways) and Filip Claeys (MIKE DHI) for their support with the simulation software WEST. Thanks to MIKE DHI for a free-of-charge academic agreement for the use of their software. Also to the three anonymous reviewers, who contributed to improving this manuscript.
Author Contributions
Antonio Moreno-Rodenas conceived the experimental design, sorted the theoretical background of the methods and performed all the simulations, analysed the data and wrote most of the manuscript. Francesca Cecinati gathered the necessary rainfall data, performed the data quality analysis and implemented the methods for rainfall interpolation; Jeroen Langeveld and François H. L. R. Clemens provided guidance and supervision during all the process and contributed to the interpretation of results.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A
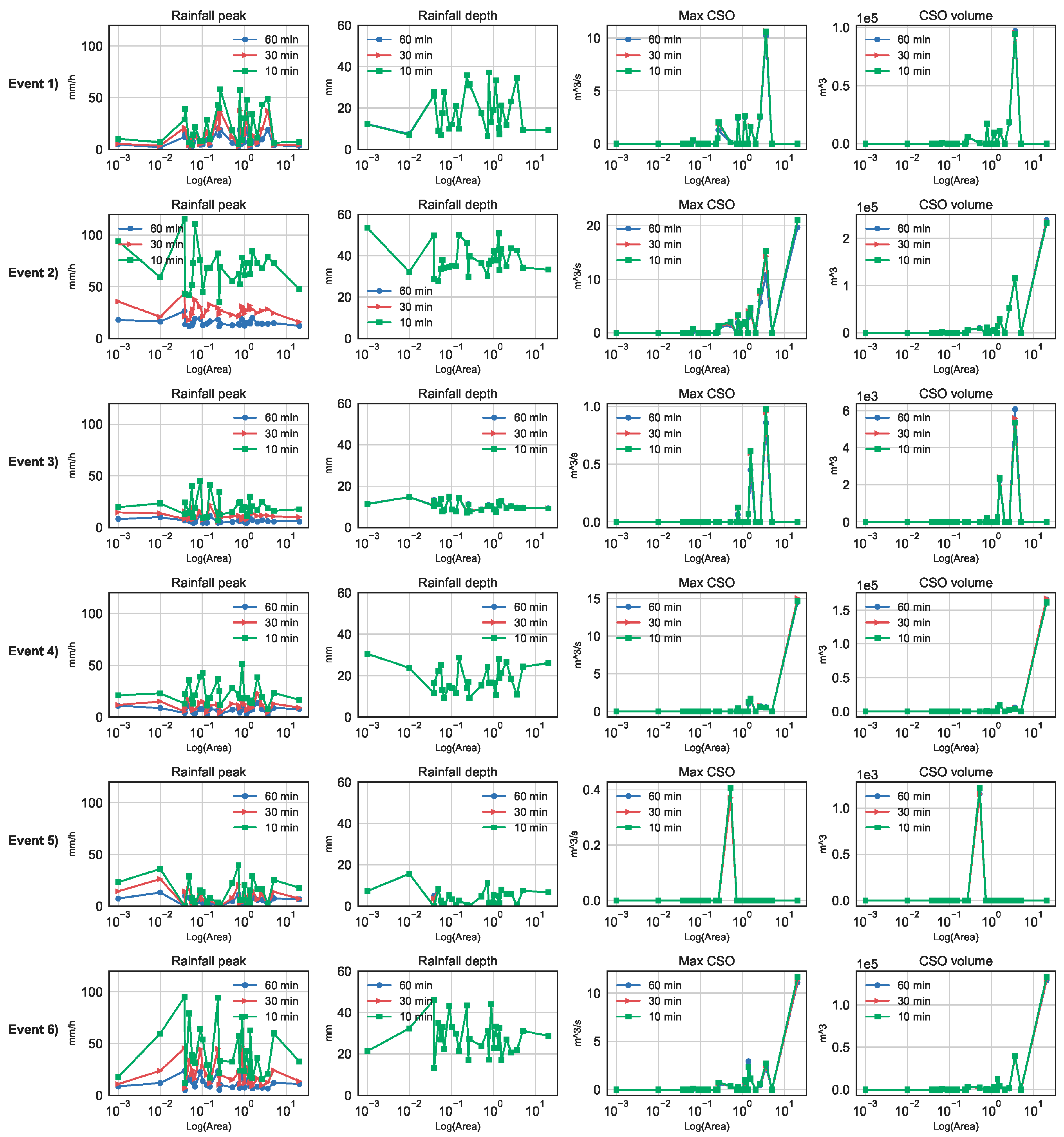
Effect of rainfall input in the urban drainage system of Valkenswaard compared with monitoring data. All cases.
Figure A1.
Rainfall input and urban drainage response of the municipality of Valkenswaard during three of the selected storm events. Each graph depicts the effect of the four rainfall products, rendered at different time accumulation steps. From left to right: maximum rainfall intensity, accumulated rainfall depth, maximum CSO flow and accumulated CSO volume.
Figure A1.
Rainfall input and urban drainage response of the municipality of Valkenswaard during three of the selected storm events. Each graph depicts the effect of the four rainfall products, rendered at different time accumulation steps. From left to right: maximum rainfall intensity, accumulated rainfall depth, maximum CSO flow and accumulated CSO volume.
References
- The Foundation for Water Research (FWR). Urban Pollution Management Manual, 3rd ed.; FWR: Buckinghamshire, UK, 2012. [Google Scholar]
- Muschalla, D.; Schutze, M.; Schroeder, K.; Bach, M.; Blumensaat, F.; Gruber, G.; Klepiszewski, K.; Pabst, M.; Pressl, A.; Schindler, N.; et al. The hsg procedure for modelling integrated urban wastewater systems. Water Sci. Technol. 2009, 60, 2065–2075. [Google Scholar] [CrossRef] [PubMed]
- Rauch, W.; Bertrand-Krajewski, J.; Krebs, P.; Mark, O.; Schilling, W.; Schutze, M.; Vanrolleghem, P. Deterministic modelling of integrated urban drainage systems. Water Sci. Technol. 2002, 45, 81–94. [Google Scholar] [PubMed]
- Willems, P. Quantification and relative comparison of different types of uncertainties in sewer water quality modeling. Water Res. 2008, 42, 3539–3551. [Google Scholar] [CrossRef] [PubMed]
- Schellart, A.N.; Tait, S.J.; Ashley, R.M. Towards quantification of uncertainty in predicting water quality failures in integrated catchment model studies. Water Res. 2010, 44, 3893–3904. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Bertrand-Krajewski, J.-L. Separately accounting for uncertainties in rainfall and runoff: Calibration of event-based conceptual hydrological models in small urban catchments using bayesian method. Water Resour. Res. 2013, 49, 5381–5394. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Zeisl, P.; Kinzel, C.; Leimgruber, J.; Ertl, T.; Rauch, W.; Kleidorfer, M. Lost in calibration: Why people still do not calibrate their models, and why they still should—A case study from urban drainage modelling. Water Sci. Technol. 2016, 74, 2337–2348. [Google Scholar] [CrossRef] [PubMed]
- Langeveld, J.G.; Benedetti, L.; de Klein, J.J.M.; Nopens, I.; Amerlinck, Y.; van Nieuwenhuijzen, A.; Flameling, T.; van Zanten, O.; Weijers, S. Impact-based integrated real-time control for improvement of the dommel river water quality. Urban Water J. 2013, 10, 312–329. [Google Scholar] [CrossRef]
- Vezzaro, L.; Benedetti, L.; Gevaert, V.; De Keyser, W.; Verdonck, F.; De Baets, B.; Nopens, I.; Cloutier, F.; Vanrolleghem, P.A.; Mikkelsen, P.S. A model library for dynamic transport and fate of micropollutants in integrated urban wastewater and stormwater systems. Environ. Model. Softw. 2014, 53, 98–111. [Google Scholar] [CrossRef]
- Van Daal-Rombouts, P.; Sun, S.; Langeveld, J.; Bertrand-Krajewski, J.-L.; Clemens, F. Design and performance evaluation of a simplified dynamic model for combined sewer overflows in pumped sewer systems. J. Hydrol. 2016, 538, 609–624. [Google Scholar] [CrossRef]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modelling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef]
- Langeveld, J.; Van Daal, P.; Schilperoort, R.; Nopens, I.; Flameling, T.; Weijers, S. Empirical sewer water quality model for generating influent data for WWTP modelling. Water 2017, 9. [Google Scholar] [CrossRef]
- Willems, P. Model uncertainty analysis by variance decomposition. Phys. Chem. Earth Parts A/B/C 2012, 42–44, 21–30. [Google Scholar] [CrossRef]
- Overeem, A.; Holleman, I.; Buishand, A. Derivation of a 10-year radar-based climatology of rainfall. J. Appl. Meteorol. Climatol. 2009, 48, 1448–1463. [Google Scholar] [CrossRef]
- Moreno-Rodenas, A.; Bellos, V.; Langeveld, J.; Clemens, F.H.L.R. Influence of river routing methods on integrated catchment water quality modelling. In Proceedings of the 10th World Congress of EWRA on Water Resources and Environment “Panta Rhei”, Athens, Greece, 5–9 July 2017; pp. 293–298. [Google Scholar]
- Nanding, N.; Rico-Ramirez, M.A.; Han, D. Comparison of different radar-raingauge rainfall merging techniques. J. Hydroinform. 2015, 17, 422–445. [Google Scholar] [CrossRef]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Jaime Gómez-Hernández, J. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar] [CrossRef]
- Heuvelink, G.B.; Pebesma, E.J. Spatial aggregation and soil process modelling. Geoderma 1999, 89, 47–65. [Google Scholar] [CrossRef]
- Matheron, G. The Theory of Regionalized Variables and Its Applications; Ecole Nationale Supérieure des Mines de Paris: Paris, France, 1971; Volume 5. [Google Scholar]
- Van de Beek, C.Z.; Leijnse, H.; Torfs, P.J.J.F.; Uijlenhoet, R. Seasonal semi-variance of dutch rainfall at hourly to daily scales. Adv. Water Resour. 2012, 45, 76–85. [Google Scholar] [CrossRef]
- Willems, P. A spatial rainfall generator for small spatial scales. J. Hydrol. 2001, 252, 126–144. [Google Scholar] [CrossRef]
- Radwan, M.; Willems, P.; Berlamont, J. Sensitivity and uncertainty analysis for river quality modelling. J. Hydroinform. 2004, 6, 83–99. [Google Scholar]
- Freni, G.; Mannina, G. Uncertainty in water quality modelling: The applicability of variance decomposition approach. J. Hydrol. 2010, 394, 324–333. [Google Scholar] [CrossRef]
Figure 1.
The Dommel water system and the distribution of the main urban contributing areas. Location of rain gauges, C-Band radar stations and river monitoring stations.
Figure 1.
The Dommel water system and the distribution of the main urban contributing areas. Location of rain gauges, C-Band radar stations and river monitoring stations.
Figure 2.
Scheme of sub-model links and processes.
Figure 2.
Scheme of sub-model links and processes.
Figure 3.
Rainfall estimations under change of spatial support from different data sources: (a) Single rain gauge data source (direct application); (b) Kriging estimation from n point measurements with change of block support for the area B, areal estimation ; (c) Weighted average of radar map (R) for the area B; (d) Merged product between n rain gauges and the radar map through a kriging with external drift estimation under change of spatial support.
Figure 3.
Rainfall estimations under change of spatial support from different data sources: (a) Single rain gauge data source (direct application); (b) Kriging estimation from n point measurements with change of block support for the area B, areal estimation ; (c) Weighted average of radar map (R) for the area B; (d) Merged product between n rain gauges and the radar map through a kriging with external drift estimation under change of spatial support.
Figure 4.
Length scales for each municipal urban drainage system. Distance between area centroids (km) is shown in the lower triangular. The diagonal displays the area size (km2). The upper triangular shows a ranking of the relative importance between areas.
Figure 4.
Length scales for each municipal urban drainage system. Distance between area centroids (km) is shown in the lower triangular. The diagonal displays the area size (km2). The upper triangular shows a ranking of the relative importance between areas.
Figure 5.
Rainfall input and urban drainage response for the municipality of Valkenswaard. Each graph depicts the effect of the four rainfall products rendered at different time accumulation steps. From left to right; maximum rainfall intensity, accumulated rainfall depth, maximum CSO flow and accumulated CSO volume.
Figure 5.
Rainfall input and urban drainage response for the municipality of Valkenswaard. Each graph depicts the effect of the four rainfall products rendered at different time accumulation steps. From left to right; maximum rainfall intensity, accumulated rainfall depth, maximum CSO flow and accumulated CSO volume.
Figure 6.
By-catchment response to rainfall spatial information for the 10-min temporal-accumulated product (catchments are represented on the x axis by their connected area in km2).
Figure 6.
By-catchment response to rainfall spatial information for the 10-min temporal-accumulated product (catchments are represented on the x axis by their connected area in km2).
Figure 7.
By-catchment response to rainfall temporal accumulation for the ARadar spatial product (catchments are represented on the x axis by their connected area in km2).
Figure 7.
By-catchment response to rainfall temporal accumulation for the ARadar spatial product (catchments are represented on the x axis by their connected area in km2).
Figure 8.
Spatial distribution of 24 h-accumulated rainfall (over the urban areas of the Dommel system) covering the seven storm events (extracted from the radar product).
Figure 8.
Spatial distribution of 24 h-accumulated rainfall (over the urban areas of the Dommel system) covering the seven storm events (extracted from the radar product).
Figure 9.
Graphical comparison of dissolved oxygen dynamics measured vs. modelled by the different spatial products (60 min time-accumulated).
Figure 9.
Graphical comparison of dissolved oxygen dynamics measured vs. modelled by the different spatial products (60 min time-accumulated).
Table 1.
Storm characteristics. Rainfall volume and maximum intensity computed from five rain gauges within the Eindhoven catchment. ADWP stands for antecedent dry weather period length. D refers to the duration of the rainfall in minutes. All variables were calculated from the 10-min accumulated time series.
Table 1.
Storm characteristics. Rainfall volume and maximum intensity computed from five rain gauges within the Eindhoven catchment. ADWP stands for antecedent dry weather period length. D refers to the duration of the rainfall in minutes. All variables were calculated from the 10-min accumulated time series.
| Event Code | Period | Storm Time Window | Rainfall Depth (mm) | Max Intensity (mm/h) | D (min) | ADWP (days) |
|---|
| 1 | 1 | 18 August 2011 14:00–18 August 2011 21:00 | 7.9 (±5.4) | 3.1 (±2.1) | 170 | 4 |
| 2 | 1 | 22 August 2011 21:00–23 August 2011 14:00 | 30.8 (±10.1) | 17.8 (±6.9) | 270 | 3 |
| 3 | 1 | 26 August 2011 06:00–26 August 2011 14:00 | 7.1 (±2.2) | 5.8 (±2.1) | 100 | 2.5 |
| 4 | 2 | 11 July 2012 10:00–11 July 2012 22:00 | 24.7 (±12.3) | 7.6 (±3.8) | 320 | 2 |
| 5 | 2 | 28 July 2012 17:00–28 July 2012 20:00 | 9.6 (±3.0) | 7.9 (±2.0) | 30 | 3.5 |
| 6 | 3 | 27 July 2013 05:00–28 July 2013 03:00 | 33.5 (±6.4) | 17.6 (±5.4) | 220 | 2 |
| 7 | 3 | 11 August 2013 11:00–11 August 2013 23:00 | 11.4 (±1.9) | 6.5 (±0.8) | 150 | 4 |
Table 2.
Characteristic time scales. Calculated as the delay time between the main rainfall peak and the maximum discharge for; (1) the sum of combined sewer overflows (CSO); (2) the time to reach maximum flow capacity at the treatment works (WWTP) and (3) the time of stabilisation of the dissolved oxygen minimum river level (DO, measured ~17 km downstream of the WWTP).
Table 2.
Characteristic time scales. Calculated as the delay time between the main rainfall peak and the maximum discharge for; (1) the sum of combined sewer overflows (CSO); (2) the time to reach maximum flow capacity at the treatment works (WWTP) and (3) the time of stabilisation of the dissolved oxygen minimum river level (DO, measured ~17 km downstream of the WWTP).
| | Delay from Rainfall Maximum Intensity (h) | |
|---|
| Event Code | Storm Time Window | CSO | WWTP | DO | CSO Volume (m3) | Min DO Level (g/m3) |
|---|
| 1 | 18 August 2011 14:00–18 August 2011 21:00 | 2 h | 5 h | 28 h | 119.6 × 103 | 1.3 |
| 2 | 22 August 2011 21:00–23 August 2011 14:00 | 1 h | 2 h | 13 h | 573.1 × 103 | 0.7 |
| 3 | 26 August 2011 06:00–26 August 2011 14:00 | - | 4 h | 23 h | 3.7 × 103 | 0.8 * |
| 4 | 11 July 2012 10:00–11 July 2012 22:00 | 3 h | 3 h | 23 h | 157.4 × 103 | 2.8 |
| 5 | 28 July 2012 17:00–28 July 2012 20:00 | 1 h | 1 h | 25 h | 20.8 × 103 | 0.8 |
| 6 | 27 July 2013 05:00–28 July 2013 03:00 | 2 h | 3 h | 18 h | 103.3 × 103 | 0.6 |
| 7 | 11 August 2013 11:00–11 August 2013 23:00 | - | 3 h | 14 h | 0.45 × 103 | 1.6 |
Table 3.
Fitted parameters sill and range (φ, in km) for an averaged exponential semivariogram model.
Table 3.
Fitted parameters sill and range (φ, in km) for an averaged exponential semivariogram model.
| T | Event 1 | Event 2 | Event 3 | Event 4 | Event 5 | Event 6 | Event 7 |
|---|
| (min) | Sill | φ | Sill | φ | Sill | φ | Sill | φ | Sill | φ | Sill | φ | Sill | φ |
|---|
| 10′ | 0.87 | 17.6 | 0.69 | 15.8 | 0.93 | 18.8 | 0.87 | 13.6 | 0.4 | 5.3 | 0.31 | 26.7 | 0.64 | 12.7 |
| 30′ | 0.86 | 24.7 | 0.88 | 24.5 | 0.87 | 25.2 | 0.87 | 25.0 | 0.83 | 23.4 | 0.90 | 26.4 | 0.91 | 26.4 |
| 60′ | 1.13 | 43.6 | 1.16 | 45.5 | 1.09 | 40.8 | 1.15 | 45.3 | 1.14 | 44.4 | 1.08 | 40.1 | 1.07 | 39.4 |
Table 4.
Observed–modelled residual for the minimum dissolved oxygen concentration (g/m3).
Table 4.
Observed–modelled residual for the minimum dissolved oxygen concentration (g/m3).
| Rainfall Input | Event 1 | Event 2 | Event 3 | Event 4 | Event 5 | Event 6 | Event 7 |
|---|
| BK1_10′ | −3.9 | −1 | −1.4 | 1.2 | −2.15 | −0.49 | −1.1 |
| BK1_30′ | −3.9 | −1 | −1.4 | 1.2 | −2.15 | −0.49 | −1.2 |
| BK1_60′ | −3.9 | −1 | −1.4 | 1.2 | −2.15 | −0.49 | −1 |
| BKall_10′ | −1.25 | −0.76 | −1.3 | −0.05 | −1.8 | −0.38 | −1.15 |
| Bkall_30′ | −1.25 | −0.67 | −1.21 | −0.2 | −1.5 | −0.38 | −1.1 |
| Bkall_60′ | −1.25 | −0.58 | −1.1 | −0.2 | −1.35 | −0.38 | −1.05 |
| UBK_10′ | −1.3 | −0.49 | −1.09 | 0.55 | −1.74 | −0.4 | −1.2 |
| UBK_30′ | −1.28 | −0.52 | −1.09 | 0.65 | −1.5 | −0.4 | −1.25 |
| UBK_60′ | −1.28 | −0.51 | −1.09 | 0.65 | −1.4 | −0.4 | −1.2 |
| ARadar_10′ | −1.26 | −0.71 | −1.2 | 1.05 | −0.9 | −0.37 | −1.4 |
| ARadar_30′ | −1.26 | −0.72 | −1.2 | 1.06 | −0.9 | −0.37 | −1.4 |
| ARadar_60′ | −1.26 | −0.72 | −1.2 | 1.06 | −0.9 | −0.37 | −1.3 |
Table 5.
Observed–modelled RMSE for dissolved oxygen concentration (five days).
Table 5.
Observed–modelled RMSE for dissolved oxygen concentration (five days).
| Rainfall Input | Event 1 | Event 2 | Event 3 | Event 4 | Event 5 | Event 6 | Event 7 |
|---|
| BK1_10′ | 1.58 | 1.27 | 1.2 | 1.9 | 1.85 | 0.98 | 1.15 |
| BK1_30′ | 1.58 | 1.27 | 1.2 | 1.92 | 1.87 | 0.99 | 1.15 |
| BK1_60′ | 1.57 | 1.26 | 1.18 | 1.94 | 1.86 | 1 | 1.14 |
| BKall_10v | 1.16 | 0.99 | 0.54 | 0.88 | 1.76 | 0.96 | 1.2 |
| Bkall_30′ | 1.12 | 0.95 | 0.44 | 0.87 | 1.58 | 0.98 | 1.18 |
| Bkall_60′ | 1.12 | 0.91 | 0.31 | 0.89 | 1.51 | 0.98 | 1.17 |
| UBK_10′ | 0.99 | 0.88 | 0.2 | 1.1 | 1.61 | 0.96 | 1.07 |
| UBK_30′ | 1 | 0.87 | 0.15 | 1.15 | 1.81 | 0.95 | 1.1 |
| UBK_60′ | 0.99 | 0.88 | 0.17 | 1.14 | 1.69 | 0.95 | 1.14 |
| ARadar_10′ | 1.07 | 0.98 | 0.64 | 1.47 | 1.28 | 1.26 | 1.16 |
| ARadar_30′ | 1.07 | 0.97 | 0.6 | 1.51 | 1.28 | 1.25 | 1.16 |
| ARadar_60′ | 1.1 | 0.97 | 0.57 | 1.51 | 1.28 | 1.26 | 1.16 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).