Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment
Abstract
1. Introduction
2. Interpolation Methods
2.1. Deterministic Methods
2.1.1. Nearest-Neighbor Interpolation
2.1.2. Polynomial Interpolation
2.1.3. Methods Based on Distance Weighting
2.1.4. Methods Based on Fourier’s Theory: Use of Signal Analysis Methods
2.1.5. Other Deterministic Interpolation Method
2.2. Stochastic Methods
2.2.1. Regression Methods
2.2.2. AutoRegressive Methods
2.2.3. Machine Learning Methods
Artificial Neural Networks (ANN)
Kernel Methods
Tree Approaches
Meta-Algorithms of Machine Learning Methods
2.2.4. Methods Based on Data Dynamics
k-Nearest Neighbors (kNN)
Box-Jenkins Models
Method of Moment Fitting
Other Methods Based on Data Dynamic
2.2.5. Methods Based on Kriging
2.2.6. Other Stochastic Methods
3. Criteria Used to Compare Interpolation
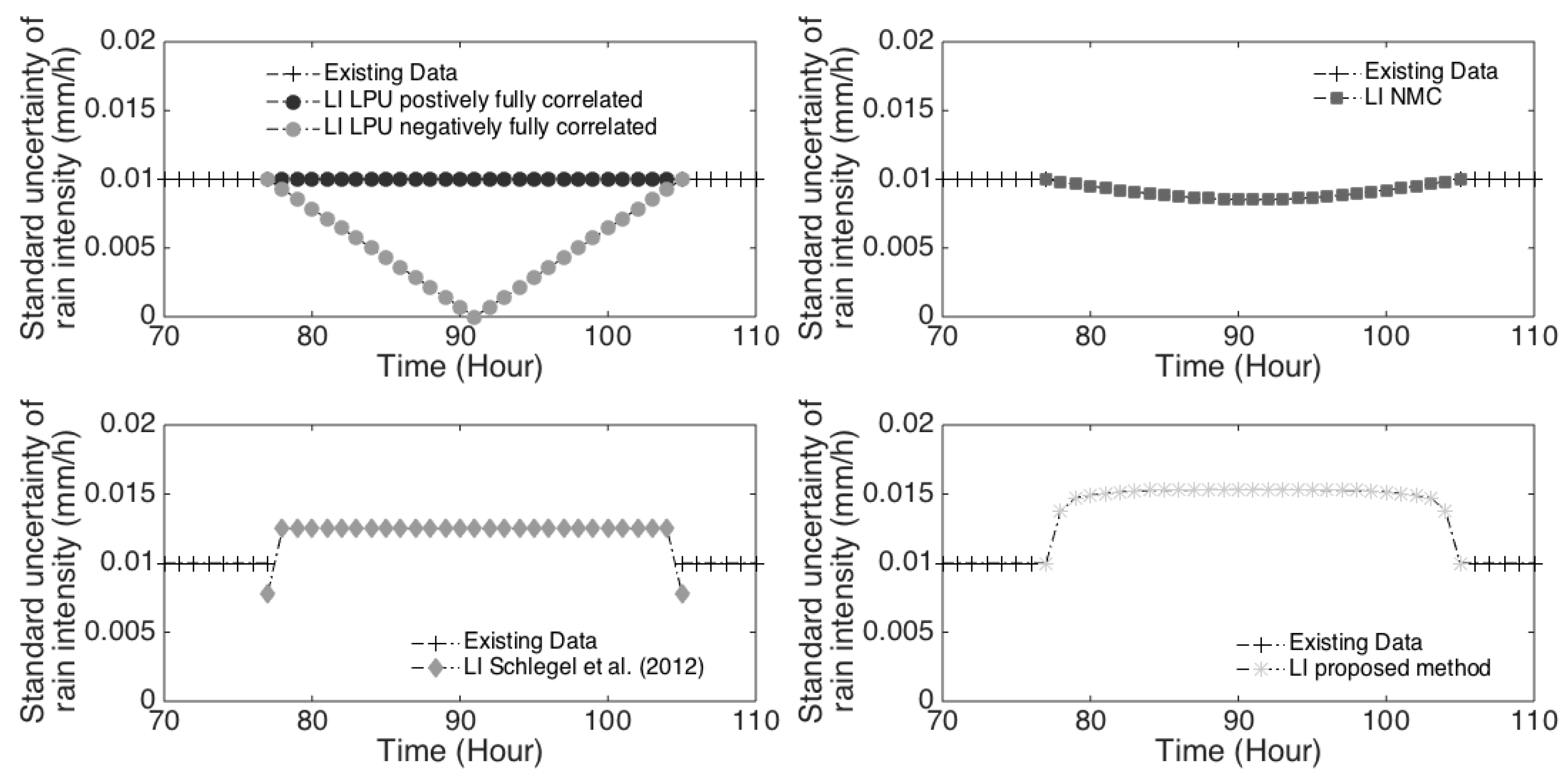
4. Evaluation of Uncertainties
4.1. Law of Propagation of Uncertainties
4.2. Monte-Carlo Simulation
5. Discussion: From Literature Outcomes to a New Method
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beveridge, S. Least squares estimation of missing values in time series. Commun. Stat. Theory Methods 1992, 21, 3479–3496. [Google Scholar] [CrossRef]
- Brubacher, S.R.; Tunnicliffe Wilson, G. Interpolating time series with application to the estimation of holiday effects on electricity demand. J. R. Stat. Soc. Ser. C 1976, 25, 107–116. [Google Scholar] [CrossRef]
- Singh, S.K.; McMillan, H.; Bardossy, A. Use of the data depth function to differentiate between case of interpolation and extrapolation in hydrological model prediction. J. Hydrol. 2013, 477, 213–228. [Google Scholar] [CrossRef]
- Wong, W.K.; Xia, M.; Chu, W.C. Adaptive neural networks models for time-series forecasting. Eur. J. Oper. Res. 2010, 207, 807–816. [Google Scholar] [CrossRef]
- JCGM 109. Uncertainty of Measurement–Part 1: Introduction to Expression of Uncertainty in Measurement. In ISO/EIC Guide 98-1; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- ISO. ISO/IEC Guide 98-3/Suppl. 1: Uncertainty of Measurement—Part #: Guide to the Expression of Uncertainty in Measurement (GUM: 1995) Supplement 1: Propagation of Distributions Using a Monte Carlo Method; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Ramirez-Cobo, P.; Marzo, X.; Olivares-Nadal, A.V.; Francoso, J.A.; Carrizosa, E.; Pita, M.F. The Markovian arrival process, a statistical model for daily precipitation amounts. J. Hydrol. 2014, 510, 459–471. [Google Scholar] [CrossRef]
- Van Steenbergen, N.; Ronsyn, J.; Willems, P. A non-parametric data-based approach for probabilistic flood forecasting in support of uncertainty communication. Environ. Model. Softw. 2012, 33, 92–105. [Google Scholar] [CrossRef]
- Musial, J.P.; Verstraete, M.M.; Gobron, N. Technical Note: Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. 2011, 11, 7905–7923. [Google Scholar] [CrossRef]
- Thévenaz, P.; Blu, T.; Unser, M. Interpolation revisited. IEEE Trans. Med. Imaging 2000, 19, 739–758. [Google Scholar] [CrossRef] [PubMed]
- Hocke, K.; Kämpfer, N. Gap filling and noise reduction of unevenly sampled data by means of the Lomb-Scargle periodigram. Atmos. Chem. Phys. 2009, 9, 4197–4206. [Google Scholar] [CrossRef]
- Gómez, V.; Maravall, A.; Peña, D. Missing observations in ARIMA models: Skipping approach versus additive outlier approach. J. Econom. 1999, 88, 341–363. [Google Scholar] [CrossRef]
- Carrizosa, E.; Olivares-Nadal, N.V.; Ramirez-Cobo, P. Times series interpolation via global optimization of moments fitting. Eur. J. Oper. Res. 2014, 230, 97–112. [Google Scholar] [CrossRef]
- Sibson, R. A brief description of natural neighbor interpolation. In Proceedings of the Interpreting Multivariate Data, Sheffield, UK, 24–27 March 1980. [Google Scholar]
- Athawale, T.; Entezari, A. Uncertainty quantification in linear interpolation for isosurface extraction. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2723–2732. [Google Scholar] [CrossRef] [PubMed]
- Gnauck, A. Interpolation and approximation of water quality time series and process identification. Anal. Bioanal. Chem. 2004, 380, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Schlegel, S.; Korn, N.; Scheuermann, G. On the interpolation of data with normally distributed uncertainty for visualization. Vis. Comput. Graph. 2012, 18, 2305–2314. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-Y.; Fan, Z.-P.; Sun, M. A hierarchical multiple kernel support vector machine for customer churn prediction using longitudinal behavioural data. Eur. J. Oper. Res. 2012, 223, 461–472. [Google Scholar] [CrossRef]
- Bates, R.; Maruri-Aguilar, H.; Wynn, H. Smooth Supersaturated Models; Technical Report; London School of Economics: London, UK, 2008; Available online: http://www.mucm.ac.uk/Pages/Downloads/Other_Papers_Reports/HMA%20Smooth%20supersaturated%20models.pdf (accessed on 16 October 2017).
- Knotters, M.; Heuvelink, G.B.M.; Hoogland, T.; Walvoort, D.J.J. A Disposition of Interpolation Techniques. 2010. Available online: https://www.wageningenur.nl/upload_mm/e/c/f/43715ea1-e62a-441e-a7a1-df4e0443c05a_WOt-werkdocument%20190%20webversie.pdf (accessed on 16 October 2017).
- Attore, F.; Alfo, M.; De Sanctis, M.; Fransceconi, F.; Bruno, F. Comparison of interpolation methods for mapping climatic and bioclimatic variables at regional scale. Environ. Ecol. Stat. 2007, 14, 1825–1843. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily European climate data. J. Geophys. Res. Atmos. 2008, 113, D21110. [Google Scholar] [CrossRef]
- Roy, S.C.D.; Minocha, S. On the phase interpolation problem—A brief review and some news results. Sãdhanã 1991, 16, 225–239. [Google Scholar] [CrossRef]
- Chen, Y.; Kopp, G.A.; Surry, D. Interpolation of wind-induced pressure time series with an artificial network. J. Wind Eng. Ind. Aerodyn. 2002, 90, 589–615. [Google Scholar] [CrossRef]
- Bienkiewicz, B.; Ham, H.J. Wavelet study of approach-wind velocity and building pressure. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 671–683. [Google Scholar] [CrossRef]
- Thornhill, N.F.; Naim, M.M. An exploratory study to identify rogue seasonality in a steel company’s supply network using spectral component analysis. Eur. J. Oper. Res. 2006, 172, 146–162. [Google Scholar] [CrossRef]
- Plazas-Nossa, L.; Torres, A. Comparison of discrete Fourier transform (DFT) and principal components analysis/DFT as forecasting tools of absorbance time series received by UV-visible probes installed in urban sewer systems. Water Sci. Technol. 2014, 69, 1101–1107. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef]
- Pettit, C.L.; Jones, N.P.; Ghanem, R. Detection and simulation of roof-corner pressure transients. J. Wind Eng. Ind. Aerodyn. 2002, 90, 171–200. [Google Scholar] [CrossRef]
- Gurley, K.; Kareem, A. Analysis interpretation modelling and simulation of unsteady wind and pressure data. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 657–669. [Google Scholar] [CrossRef]
- Paulson, K.S. Fractal interpolation of rain rate time series. J. Geophys. Res. 2004, 109, D22102. [Google Scholar] [CrossRef]
- Tripathi, S.; Govindajaru, R.S. On selection of kernel parameters in relevance vector machines for hydrologic applications. Stoch. Environ. Res. Risk Assess. 2007, 21, 747–764. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Pourahmadi, M. Estimation and interpolation of missing values of a stationary time series. J. Time Ser. Anal. 1989, 10, 149–169. [Google Scholar] [CrossRef]
- Jones, R.H. Maximum likelihood fitting of ARMA models to time series with missing observations. Technometrics 1980, 22, 389–395. [Google Scholar] [CrossRef]
- Ljung, G.M. A note on the estimation of missing values in time series. Commun. Stat. Simul. Comput. 1989, 18, 459–465. [Google Scholar] [CrossRef]
- Dunsmuir, W.T.M.; Murtagh, B.A. Least absolute deviation estimation of stationary time series models. Eur. J. Oper. Res. 1993, 67, 272–277. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. Am. Soc. Mech. Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Alonso, A.M.; Sipols, A.E. A time series bootstrap procedure for interpolation intervals. Comput. Stat. Data Anal. 2008, 52, 1792–1805. [Google Scholar] [CrossRef]
- Peña, D.; Tiao, G.C. A note on likelihood estimation of missing values in time series. Am. Stat. 1991, 45, 212–213. [Google Scholar] [CrossRef]
- Lu, Z.; Hui, Y.V. L-1 linear interpolator for missing values in time series. Ann. Inst. Stat. Math. 2003, 55, 197–216. [Google Scholar] [CrossRef]
- Dijkema, K.S.; Van Duin, W.E.; Meesters, H.W.G.; Zuur, A.F.; Ieno, E.N.; Smith, G.M. Sea level change and salt marshes in the Waaden Sea: A time series analysis. In Analysing Ecological Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Visser, H. The significance of climate change in the Netherlands. An Analysis of Historical and Future Trends (1901–2020) in Weather Conditions, Weather Extremes and Temperature Related Impacts. In Technical Report RIVM Report 550002007/2005; National Institute of Public Health and Environmental Protection RIVM: Bilthoven, The Netherlands, 2005. [Google Scholar]
- Sliwa, P.; Schmid, W. Monitoring cross-covariances of a multivariate time series. Metrika 2005, 61, 89–115. [Google Scholar] [CrossRef]
- Gould, P.G.; Koehler, A.B.; Ord, J.K.; Snyder, R.D.; Hyndman, R.J.; Vahid-Araghi, F. Forecasting time series with multiple seasonal patterns. Eur. J. Oper. Res. 2008, 191, 207–222. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superposition of a sigmoïdal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Masters, T. Advanced Algorithms for Neural Networks: A C++ Sourcebook; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Liu, M.C.; Kuo, W.; Stastri, T. An exploratory study of a neural approach for reliability data analysis. Q. Reliab. Eng. 1995, 11, 107–112. [Google Scholar] [CrossRef]
- Zhang, P.; Qi, G.M. Neural network forecasting for seasonal trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistic Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Sonnenburg, S.; Rätsch, G.; Schäfer, C.; Schölkopf, B. Large scale multiple kernel learning. J. Mach. Learn. Res. 2006, 1, 1–18. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Amato, A.; Calabrese, M.; Di Lecce, V. Decision trees in time series reconstruction problems. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Victoria, Vancouver Island, BC, Canada, 12–15 May 2008. [Google Scholar]
- Kulesh, M.; Holschneider, M.; Kurennaya, K. Adaptive metrics in the nearest neighbor’s method. Physica D 2008, 237, 283–291. [Google Scholar] [CrossRef]
- Chen, B.; Andrews, S.H. An Empirical Review of methods for Temporal Distribution and Interpolation in the National Accounts. Surv. Curr. Bus. 2008, 31–37. Available online: https://www.bea.gov/scb/pdf/2008/05%20May/0508_methods.pdf (accessed on 16 October 2017).
- Cholette, P.A.; Dagum, E.B. Benchmarking, temporal distribution and reconciliation methods of time series. In Lecture Notes in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for environmental scientists. In Statistic in Practice; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Heidelberg/Berlin, Germany, 2005. [Google Scholar]
- Matheron, G. Principles of Geostatistics. Ecomony Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Jamshidi, R.; Dragovich, D.; Webb, A.A. Catchment scale geostatistical simulation and uncertainty of soil erodibility using sequential Gaussian simulation. Environ. Earth Sci. 2014, 71, 4965–4976. [Google Scholar] [CrossRef]
- Juang, K.W.; Chen, Y.S.; Lee, D.Y. Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils. Environ. Pollut. 2004, 127, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists. In Technical Report GeoCat #68229; Australian Government: Canberra, Australia, 2008. [Google Scholar]
- Journel, A.G.; Huijbergts, C.J. Mining Geostatistics; Academic Press: London, UK, 1998. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Goovaerts, P.; Gebreab, S. How does the Poisson kriging compare to the popular BYM model for mapping disease risks? Int. J. Health Geogr. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Raty, L.; Gilbert, M. Large-scale versus small-scale variation decomposition, followed by kriging based on a relative variogram, in presence of a non-stationary residual variance. J. Geogr. Inf. Decis. Anal. 1998, 2, 91–115. [Google Scholar]
- Allard, D. Geostatistical classification and class kriging. J. Geogr. Inf. Decis. Anal. 1998, 2, 77–90. [Google Scholar]
- Biggeri, A.; Dreassi, E.; Catelan, D.; Rinaldi, L.; Lagazio, C.; Cringoli, G. Disease mapping in vetenary epidemiology: A Bayesian geostatistical approach. Stat. Methods Med. Res. 2006, 15, 337–352. [Google Scholar] [CrossRef] [PubMed]
- Fournier, B.; Furrer, R. Automatic mapping in the presence of substitutive errors: A robust kriging approach. Appl. GIS 2005, 1. [Google Scholar] [CrossRef]
- Genton, M.G.; Furrer, R. Analysis of rainfall data by robust spatial statistic using S+SPATIALSTATS. J. Geogr. Inf. Decis. Anal. 1998, 2, 116–126. [Google Scholar]
- Demyanov, V.; Kanevsky, S.; Chernov, E.; Savelieva, E.; Timonin, V. Neural network residual kriging application for climatic data. J. Geogr. Inf. Decis. Anal. 1998, 2, 215–232. [Google Scholar]
- Erxleben, J.; Elder, K.; Davis, R. Comparison of spatial interpolation methods for snow distribution in the Colorado Rocky Mountains. Hydrol. Process. 2002, 16, 3627–3649. [Google Scholar] [CrossRef]
- Walvoort, D.J.J.; De Gruitjer, J.J. Compositional kriging: A spatial interpolation method for compositional data. Math. Geol. 2001, 33, 951–966. [Google Scholar] [CrossRef]
- Verbake, W.; Dejaeger, K.; Martens, D.; Hur, J.; Baesens, B. New insights into churn prediction in the telecommunication sector: A profit driven data mining approach. Eur. J. Oper. Res. 2012, 218, 211–229. [Google Scholar] [CrossRef]
- Žukovič, M.; Hristopulos, D.T. Environmental time series interpolation based on spartan random processes. Atmos. Environ. 2008, 42, 7669–7678. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Webster, R. Modelling soil variation: Past, present and future. Geoderma 2001, 100, 269–301. [Google Scholar] [CrossRef]
- Von Asmuth, J.R.; Knotters, M. Characterising groundwater dynamics based on a system identification approach. J. Hydrol. 2004, 296, 118–134. [Google Scholar] [CrossRef]
- Varouchakis, E.A.; Hristopulos, D.T. Improvement of groundwater level prediction is sparsely gauged basins using physical laws and local geographic features as auxiliary variables. Adv. Water Resour. 2013, 52, 34–49. [Google Scholar] [CrossRef]
- Woodley, E.J.; Loader, N.J.; McCarroll, D.; Young, G.H.F.; Robertson, I.; Hetqon, T.H.E.; Gagen, M.H. Estimating uncertainty in pooled stable isotope time-series from tree-rings. Chem. Geol. 2012, 294–295, 243–248. [Google Scholar] [CrossRef]
- Chen, Y.; Kopp, G.A.; Surry, D. Prediction of pressure coefficients on roofs of low buildings using artificial neural networks. J. Wind Eng. Ind. Aerodyn. 2003, 91, 423–441. [Google Scholar] [CrossRef]
- Mühlenstädt, T.; Kuhnt, S. Kernel interpolation. Comput. Stat. Data Anal. 2011, 55, 2962–2974. [Google Scholar] [CrossRef]
- Schilperoort, T. Statistical aspects in design aspects of hydrological networks. In Proceedings and Information No. 35 of the TNO Committee on Hydrological Research CHO; TNO: The Hague, The Netherlands, 1986; pp. 35–55. [Google Scholar]
| Equations | Names | References |
|---|---|---|
| Coefficient of correlation (r) | [80] | |
| Squared coefficient of correlation (r2) | [16] | |
| Mean of autocorrelation function r(l) | [9] 1 | |
| Mean Bias Error (MBE) | [9] | |
| Bias | [80] | |
| Mean Error (ME) | [12] | |
| Absolute differences | [13] | |
| Mean Absolute Error (MAE) | [9,77,80] | |
| Mean Relative Error (MRE) | [77,80] | |
| Mean Absolute Relative Error (MARE) | [77,80] | |
| Mean Absolute Percentage Error (MAPE) | [4,54] | |
| Sum of Squared Errors (SSE) | [45] | |
| Quadratic differences | [13] | |
| Standard errors | [16] | |
| Prediction risk—leave one out MSE (RLOO) | [32] | |
| Mean Square Error (MSE) | [32,39] | |
| nc | [1,81] | |
| [82] | ||
| Root Mean Squares (RMS) | ||
| [24] | ||
| Root Mean Square Errors of Prediction (RMSEP) | [54] | |
| Mean Squares Error (NMSE) | [4] | |
| Reduction of Error (RE) | [81] | |
| Nash-Sutcliffe coefficient (NS) | [3] | |
| Mean Squared Forecast Error (MFSE(h)) | [45] 2 | |
| Root Mean Squares Deviations (RMSD) | [9] | |
| Root Mean Squares Errors (RMSE) | [12,77,80,83] | |
| Normalized Root Mean Square Deviation | [27] | |
| Root Mean Square Standardized error (RMSS) | [80] | |
| Absolute Percent Error (APE) | [13] 3 | |
| Chi-Square (X2) | [9] 4 | |
| Coverage | [39] | |
| Left Mis-coverage | [39] | |
| Right Mis-coverage | [39] | |
| Various equations | 95% confidence interval | [39] |
| Percentage of Correctly Classified observations (PCC) | [18] | |
| Percentage of correctly classified observations in the positive class (Sensitivity) | [18] | |
| Percentage of correctly classified observations in the negative class (Specificity) | [18] | |
| Top 10% lift (Lift) | [18] | |
| H-measure (H) | [18] | |
| No equation | Time of computation | [10,12,18,84] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lepot, M.; Aubin, J.-B.; Clemens, F.H.L.R. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. https://doi.org/10.3390/w9100796
Lepot M, Aubin J-B, Clemens FHLR. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water. 2017; 9(10):796. https://doi.org/10.3390/w9100796
Chicago/Turabian StyleLepot, Mathieu, Jean-Baptiste Aubin, and François H.L.R. Clemens. 2017. "Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment" Water 9, no. 10: 796. https://doi.org/10.3390/w9100796
APA StyleLepot, M., Aubin, J.-B., & Clemens, F. H. L. R. (2017). Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water, 9(10), 796. https://doi.org/10.3390/w9100796






