Optimal Allocation Method of Irrigation Water from River and Lake by Considering the Field Water Cycle Process
Abstract
:1. Introduction
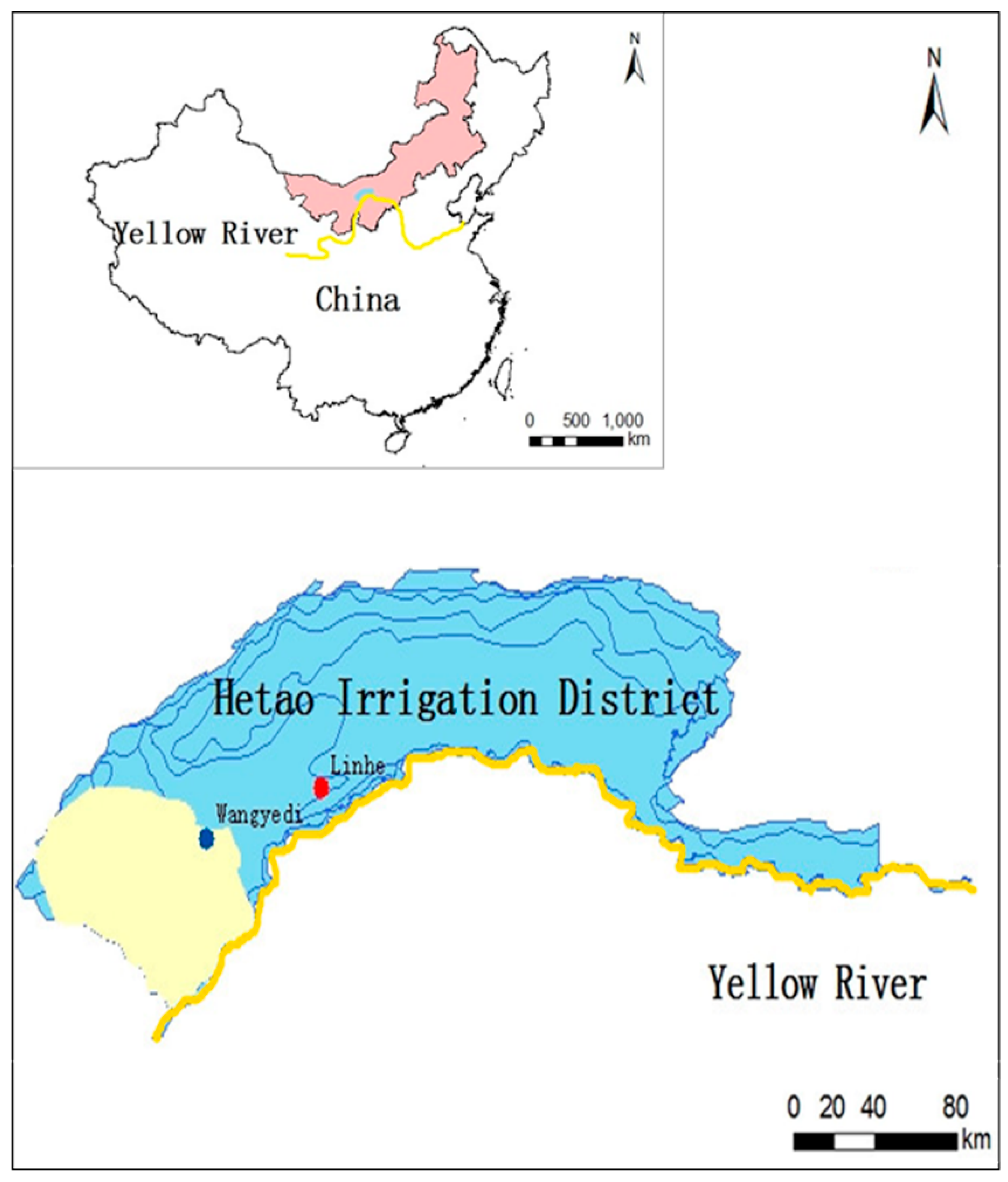
2. Study Area
2.1. Description of the Study Area
2.2. Data Collection
3. Methodology
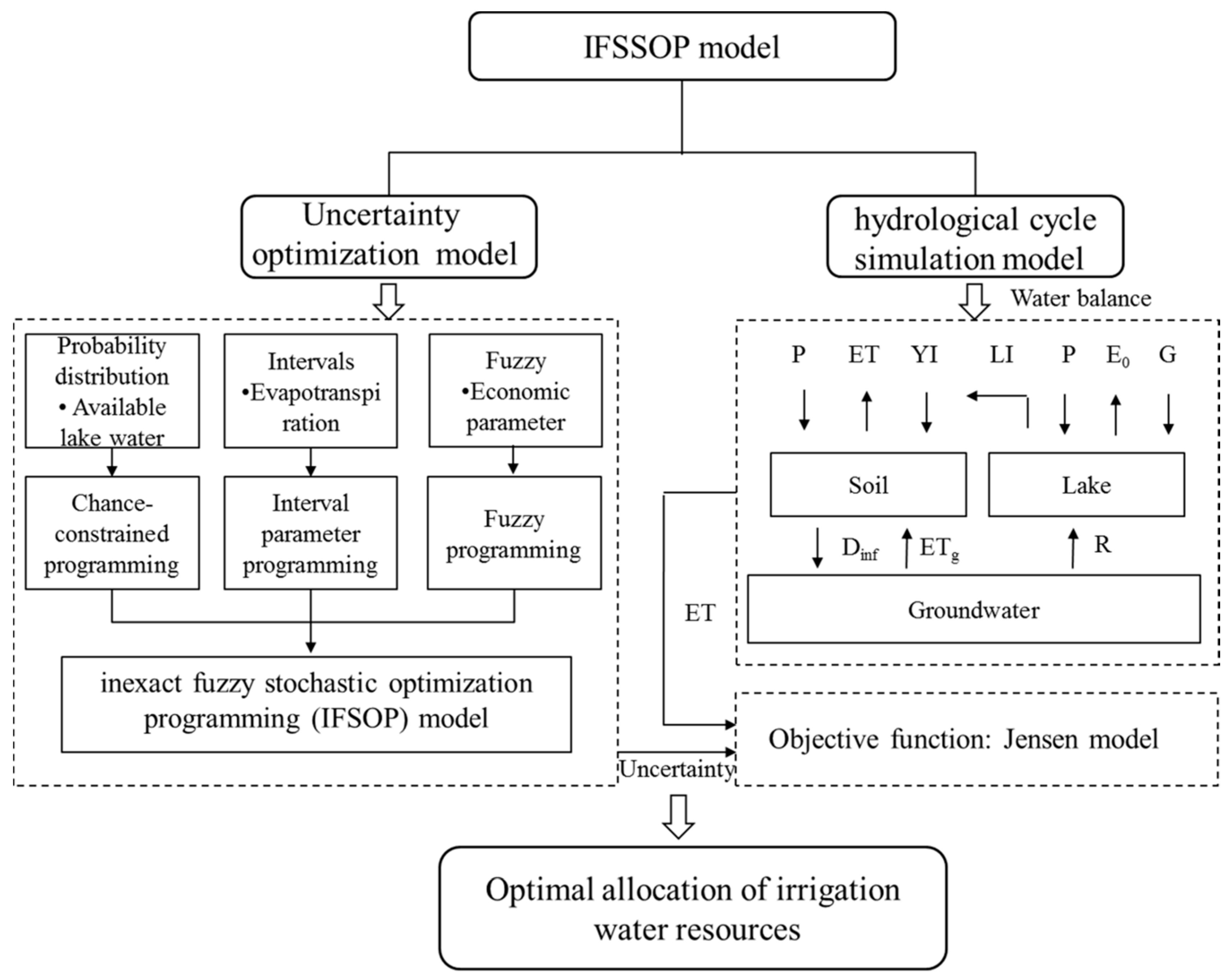
3.1. The Hydrological Cycle Simulation Model
3.1.1. Water Balance Model
3.1.2. Actual Evapotranspiration Model
3.1.3. Jensen Model
3.2. Uncertainty Optimization Model of Irrigation Schedule with Multi-Water Resources
4. Results and Discussion
4.1. Evaluation of the Inexact Fuzzy Stochastic Simulation-Optimization Programming (IFSSOP) Model
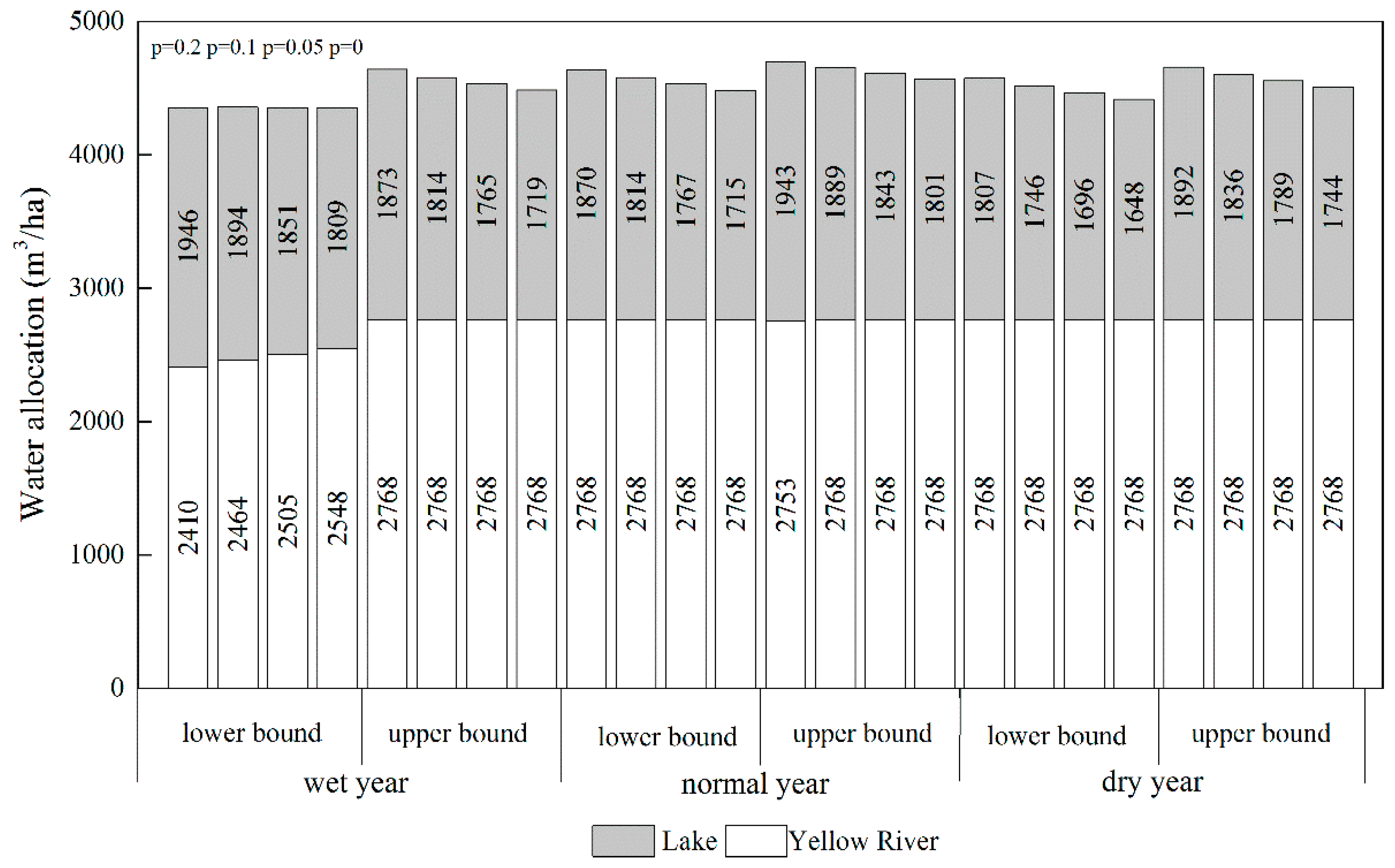
4.1.1. Water Amount Allocation under Different P in Different Hydrological Years
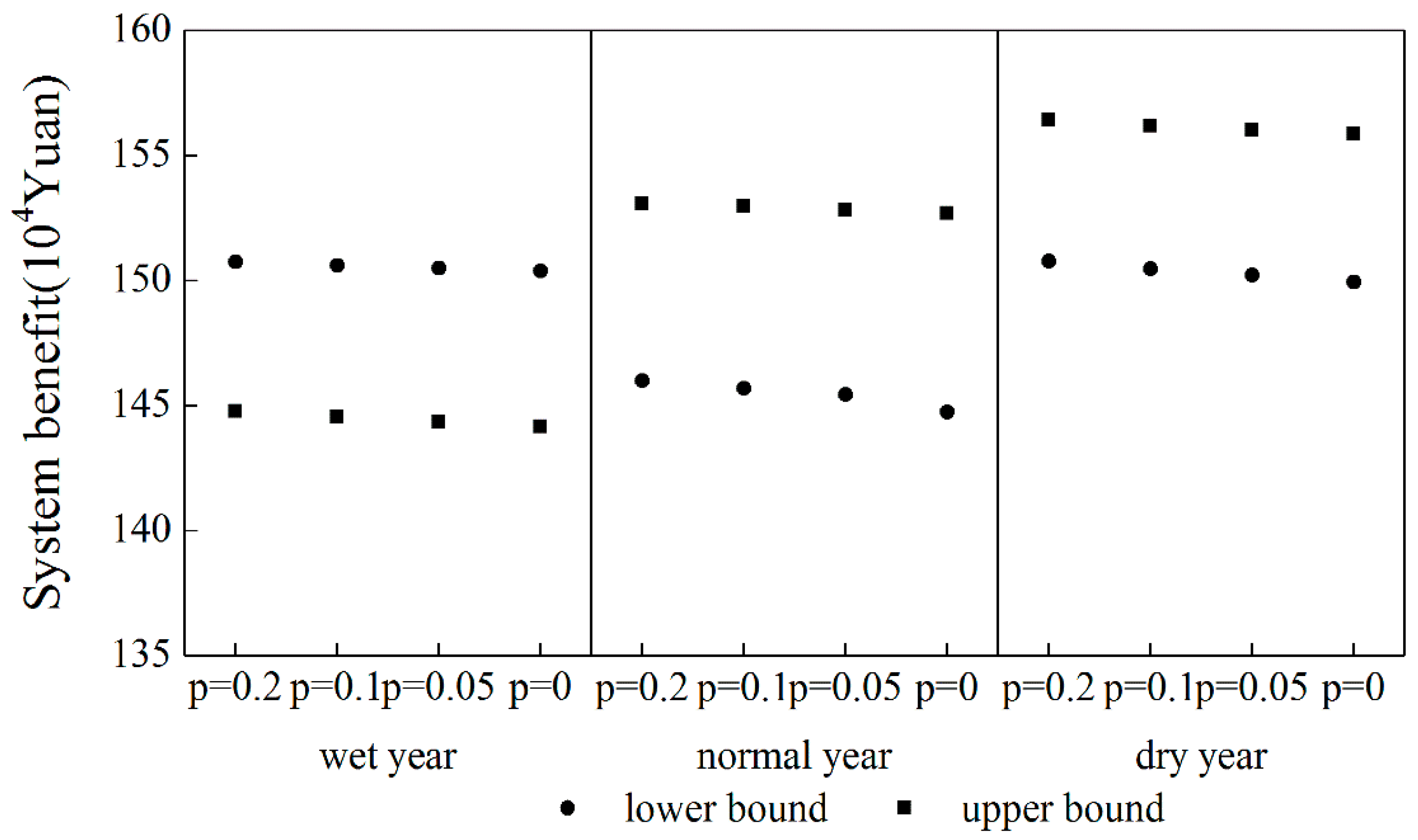
4.1.2. System Economic Benefit under Different P in Different Hydrological Years
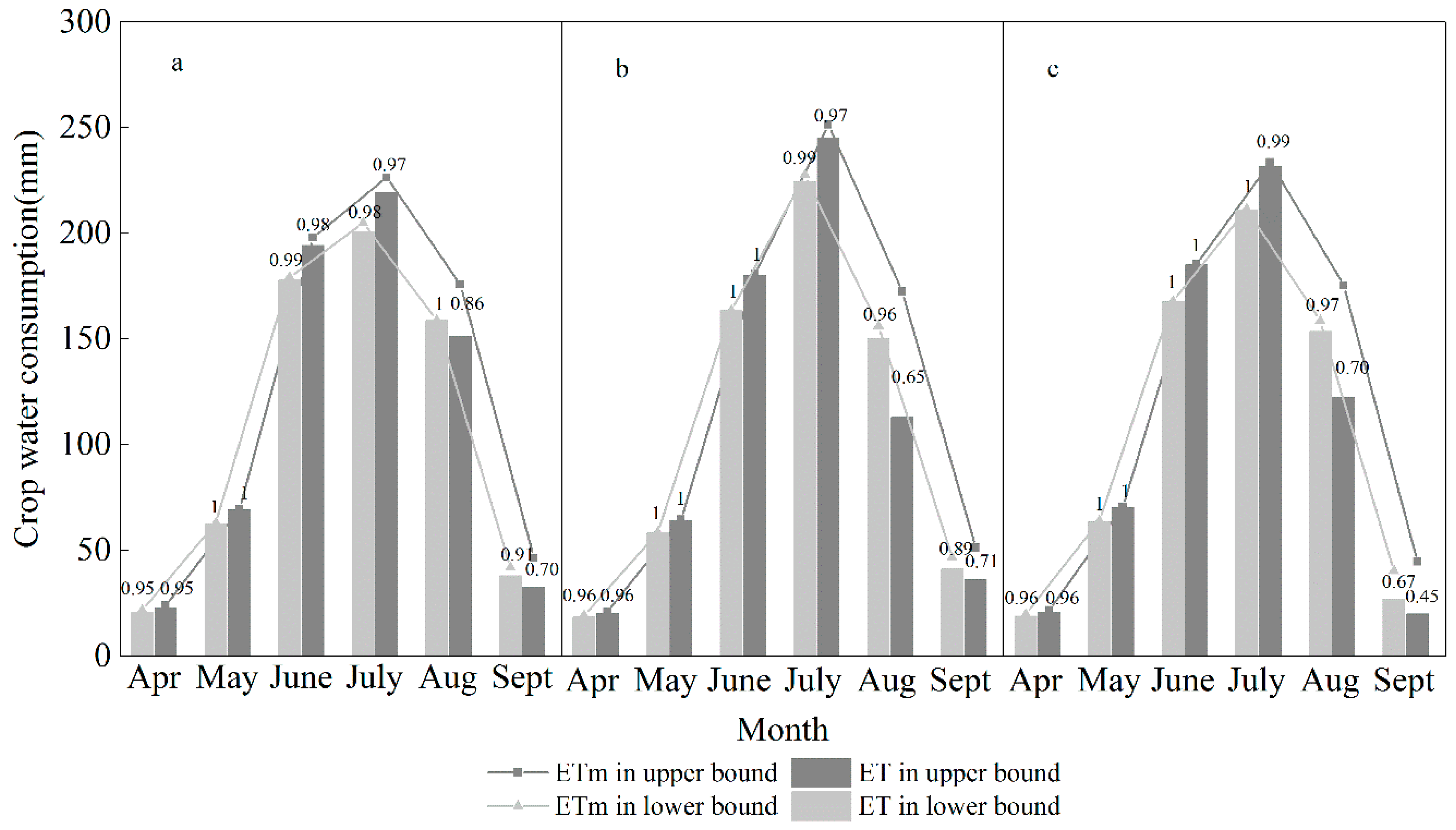
4.1.3. Water Consumption of Maize in Different Months of Different Hydrological Years
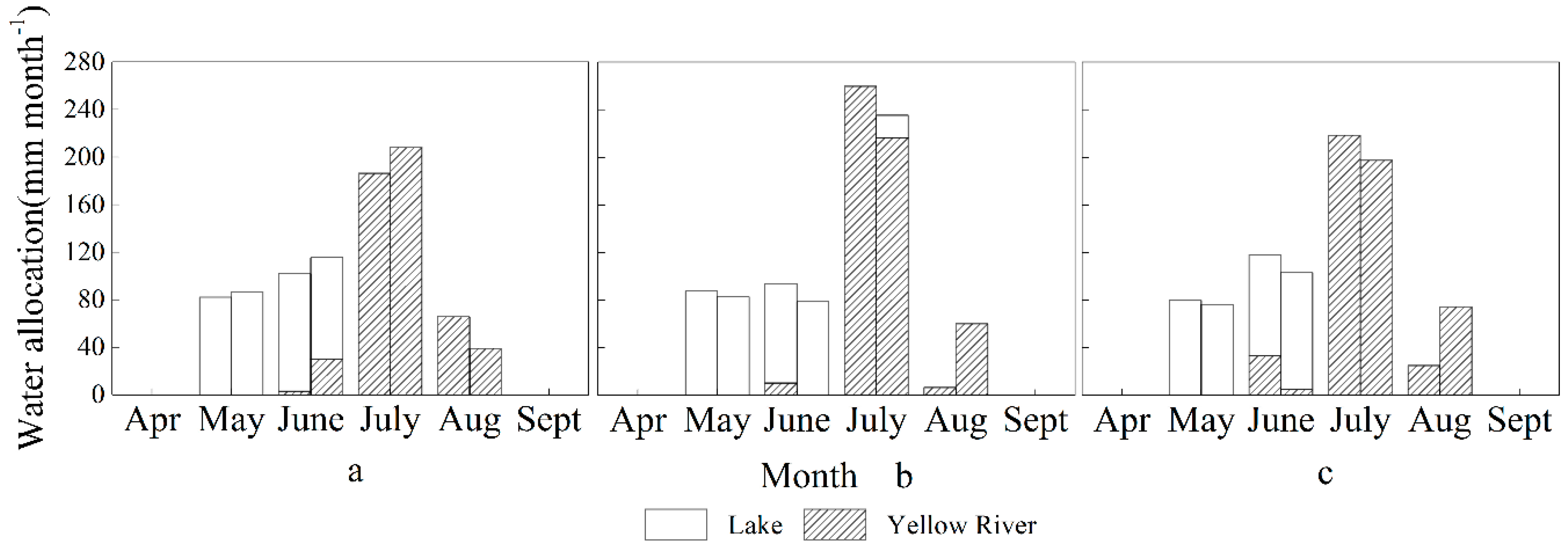
4.1.4. Irrigation Water Allocation in Different Months of Different Hydrological Years
4.2. Comparison between the IFSSOP Model and the IFSSOP-NG Model
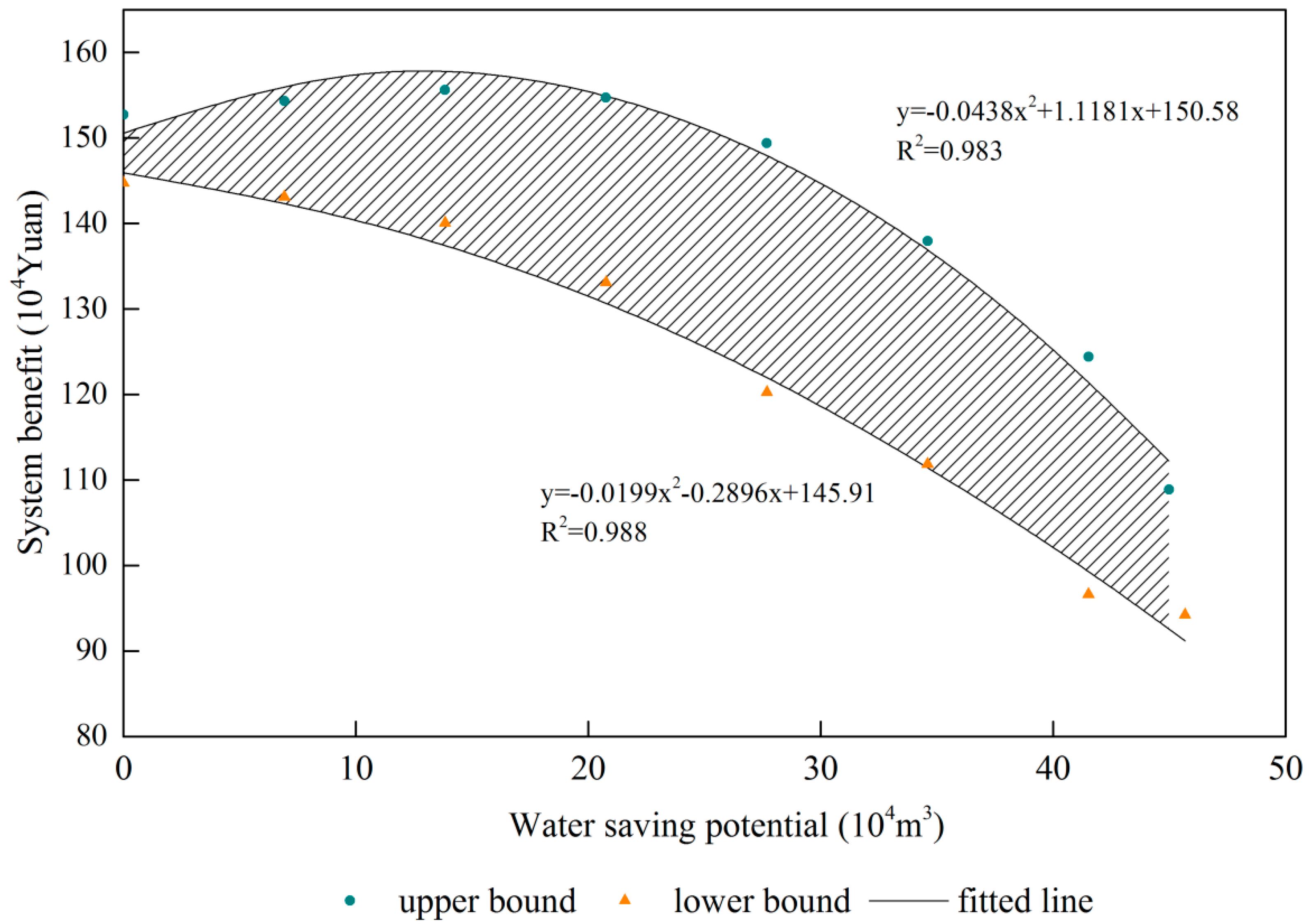
4.3. Analysis of Agriculture Water Saving Potential with IFSSOP Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, S.K.; Wang, Y.B.; Wang, F.F.; Liu, J.; Luan, X.B.; Li, X.L.; Zhou, T.W.; Wu, P.T. Alleviating Pressure on Water Resources: A new approach could be attempted. Sci. Rep. 2015, 5, 14006. [Google Scholar] [CrossRef] [PubMed]
- United Nations Environment Programme (UNEP). Food Security Report; UNEP: Stockholm, Sweden, 2012. [Google Scholar]
- Akhtar, F.; Tischbein, B.; Awan, U.K. Optimizing deficit irrigation scheduling under shallow groundwater conditions in lower reaches of Amu Darya River Basin. Water Resour. Manag. 2013, 27, 3165–3178. [Google Scholar] [CrossRef]
- Flinn, J.C.; Musgrave, W.F. Development and analysis of input-output relations for irrigation water. Aust. J. Agric. Econ. 1967, 11, 127–137. [Google Scholar] [CrossRef]
- Rao, N.H.; Sarma, P.B.S. Optimal multicrop allocation of seasonal and intraseasonal irrigation water. Water Resour. Res. 1990, 26, 551–559. [Google Scholar] [CrossRef]
- Vedula, S.; Kumar, D.N. An integrated model for optimal reservoir operation for irrigation of multiple crops. Water Resour. Res. 1996, 32, 1101–1108. [Google Scholar] [CrossRef]
- Wong, H.S.; Sun, N.Z.; Yeh, W.W.-G. A Two-Step Nonlinear Programming Approach to the Optimization of Conjunctive Use of Surface Water and Ground Water; University of California Water Resources Center: Davis, CA, USA, 1997. [Google Scholar]
- Shangguan, Z.P.; Shao, M.G.; Horton, R.; Lei, T.W.; Qin, L.; Ma, J.Q. A model for regional optimal allocation of irrigation water resources under deficit irrigation and its applications. Agric. Water Manag. 2002, 52, 139–154. [Google Scholar] [CrossRef]
- Bijan, G.; Ali-Reza, S. Linear and Non-Linear optimization models for allocation of a limited water supply. Irrig. Drain. 2004, 53, 39–54. [Google Scholar] [CrossRef]
- Regulwar, D.G.; Gurav, J.B. Irrigation planning under uncertainty—A multi objective fuzzy linear programming approach. Water Resour. Manag. 2011, 25, 1387–1416. [Google Scholar] [CrossRef]
- Zhang, X.D.; Huang, G.H.; Nie, X.H.; Lin, Q.G. Model-based decision support system for water quality management under hybrid uncertainty. Expert Syst. Appl. 2011, 38, 2809–2816. [Google Scholar] [CrossRef]
- Sethi, L.N.; Panda, S.N.; Nayak, M.K. Optimal crop planning and water resources allocation in a coastal groundwater basin, Orissa, India. Agric. Water Manag. 2006, 83, 209–220. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; He, L. An inexact rough-interval fuzzy linear programming method for generating conjunctive water-allocation strategies to agricultural irrigation systems. Appl. Math. Model. 2011, 35, 4330–4340. [Google Scholar] [CrossRef]
- Mahmood, S.S.; Mostafa, M. Application of Robust Optimization Approach for Agricultural Water Resource Management under Uncertainty. J. Irrig. Drain. 2013, 139, 571–581. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties. Appl. Math. Model. 2014, 38, 4897–4911. [Google Scholar] [CrossRef]
- Li, W.; Wang, B.; Xie, L.Y.; Huang, G.H.; Liu, L. An inexact mixed risk-aversion two-stage stochastic programming model for water resources management under uncertainty. Environ. Sci. Pollut. Res. 2015, 22, 2964–2975. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.Q.; Guo, P.; Li, M.; Fang, S.Q.; Zhang, L.D. An improved solving approach for interval-parameter programming and application to an optimal allocation of irrigation water problem. Water Resour. Manag. 2016, 30, 701–729. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Yeomans, J.S. An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Han, Y.; Huang, Y.F.; Wang, G.Q. Interval-parameter linear optimization model with stochastic vertices for land and water resources allocation under dual uncertainty. Environ. Eng. Sci. 2011, 28, 197–205. [Google Scholar] [CrossRef]
- Nevill, C.J. Managing cumulative impacts: Groundwater reform in the Murray-Darling Basin, Australia. Water Resour. Manag. 2009, 23, 2605–2631. [Google Scholar] [CrossRef]
- Harmancioglu, N.B.; Barbaros, F.; Cetinkaya, C.P. Sustainability issues in water management. Water Resour. Manag. 2013, 27, 1867–1891. [Google Scholar] [CrossRef]
- Cosgrove, D.M.; Johnson, G.S. Aquifer management zones based on simulated surface-water response functions. J. Water Resour. Plan. Manag. 2005, 131, 89–100. [Google Scholar] [CrossRef]
- Safavi, H.R.; Alijanian, M.A. Optimal crop planning and conjunctive use of surface water and groundwater resources using fuzzy dynamic programming. J. Irrig. Drain. Eng. 2011, 137, 383–397. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; Zhang, Y.M.; He, L. Strategic agricultural land-use planning in response to water-supplier variation in a China’s rural region. Agric. Syst. 2012, 108, 19–28. [Google Scholar] [CrossRef]
- Shi, B.; Lu, H.W.; Ren, L.X.; He, L. A fuzzy inexact two-phase programming approach to solving optimal allocation problems in water resources management. Appl. Math. Model. 2014, 38, 5502–5514. [Google Scholar] [CrossRef]
- Guo, P.; Chen, X.H.; Tong, L.; Li, J.B.; Li, M. An optimization model for a crop deficit irrigation system under uncertainty. Eng. Opt. 2014, 46, 1–14. [Google Scholar] [CrossRef]
- Ren, D.Y.; Xu, X.; Hao, Y.Y.; Huang, G.H. Modeling and assessing field irrigation water use in a canal system of Hetao, upper Yellow River basin: Application to maize, sunflower and watermelon. J. Hydrol. 2016, 532, 122–139. [Google Scholar] [CrossRef]
- Gao, X.Y.; Huo, Z.L.; Bai, Y.N.; Feng, S.Y.; Huang, G.H.; Shi, H.B.; Qu, Z.Y. Soil salt and groundwater change in flood irrigation field and uncultivated land: A case study based on 4-year field observations. Environ. Earth Sci. 2015, 73, 2127–2139. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.H.; Qu, Z.Y.; Pereira, L.S. Assessing the groundwater dynamics and impacts of water saving in the Hetao Irrigation District, Yellow River basin. Agric. Water Manag. 2010, 98, 301–313. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Yang, S.Q.; Shi, H.B.; Ma, J.H.; Li, R.P.; Han, W.G.; Zhang, W.J. Irrigation infiltration and recharge coefficient in Hetao irrigation district in Inner Mongolia. Trans. CSAE 2011, 27, 6–66. [Google Scholar]
- Hu, S.J.; Zhao, R.F.; Tian, C.Y.; Song, Y.D. Empirical models of calculating phreatic evaporation from bare soil in Tarim river basin, Xinjiang. Environ. Earth Sci. 2009, 59, 663–668. [Google Scholar] [CrossRef]
- Chen, D.L.; Gao, G.; Xu, C.Y.; Guo, J.; Ren, G.Y. Comparison of the Thornthwaite method and pan data with the standard Penman-Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Hao, F.H.; Ou, Y.W.; Yue, W. Analysis of water cycle characteristics and soil water movement in the agricultural irrigation area in Inner Mongolia. Acta Sci. Circumst. 2008, 5, 825–831. [Google Scholar]
- Ren, Z.H.; Li, M.Q.; Zhang, W.M. Conversion Coefficient of SMAII Evaporation PAN into E-601B PAN in China. J. Appl. Meteorol. Sci. 2002, 4, 508–514. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Gudelines for Computing Crop Water Requirements, Irrigation and Drainage 56; United Nations (FAO): Rome, Italia, 1998. [Google Scholar]
- Tsakiris, G.P. A method for applying crop sensitivity factors in irrigation scheduling. Agric. Water Manag. 1982, 5, 335–343. [Google Scholar] [CrossRef]
- Wang, Y.R.; Lei, Z.D.; Yang, S.X. Cumulative function of sensitive index for winter wheat. J. Hydraul. Eng. 1997, 5, 29–36. [Google Scholar]
- Zhang, X.Y.; Chen, S.Y.; Sun, H.Y.; Shao, L.W.; Wang, Y.Z. Changes in evapotranspiration over irrigated winter wheat and maize in North China Plain over three decades. Agric. Water Manag. 2011, 98, 1097–1104. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P. An efficient irrigation water allocation model under uncertainty. Agric. Syst. 2016, 144, 46–57. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications, 3rd ed.; Kluwer Academic Publishers: Boston, MA, USA, 1996; ISBN 9780792396246. [Google Scholar]
- Li, Y.P.; Huang, G.H.; Wang, G.Q.; Huang, Y.F. FSWM: A hybrid fuzzy-stochastic water management model for agricultural sustainability under uncertainty. Agric. Water Manag. 2009, 96, 1807–1818. [Google Scholar] [CrossRef]
- Guo, P.; Huang, H.G.; He, L.; Li, H.L. Interval-parameter Fuzzy-stochastic Semi-infinite Mixed-integer Linear Programming for Waste Management under Uncertainty. Environ. Model. Assess. 2009, 14, 521–537. [Google Scholar] [CrossRef]
- Hanson, B.R.; Kite, S.W. Irrigation scheduling under saline high water tables. Trans. ASABE 1984, 27, 1430–1434. [Google Scholar] [CrossRef]
- Ayars, J.E.; Hutmacher, R.B. Crop coefficients for irrigating cotton in the presence of groundwater. Irrig. Sci. 1994, 15, 45–52. [Google Scholar] [CrossRef]
- Zhang, D.M.; Guo, P. Integrated agriculture water management optimization model for water saving potential analysis. Agric. Water Manag. 2016, 170, 5–19. [Google Scholar] [CrossRef]
- Gohari, A.; Eslamian, S.; Mirchi, A.; Abedi-Koupaei, J.; Bavani, A.M.; Madani, K. Water transfer as a solution to water shortage: A fix that can Backfire. J. Hydrol. 2013, 491, 23–39. [Google Scholar] [CrossRef]
- Wang, L.M.; Li, Y. The overall planning of the Yellow River water rights conversion in Inner Mongolia. Inn. Mong. Water Conserv. 2005, 1, 55–56. [Google Scholar]
- Wallender, W.W.; Grimes, D.W.; Henderson, D.W.; Stromberg, L.K. Estimating the Contribution of a Perched Water Table to the Seasonal Evapotranspiration of Cotton. Agron. J. 1979, 71, 1056–1060. [Google Scholar] [CrossRef]
- Qtaishat, T. Impact of Water Reallocation on the Economy in the Fertile Crescent. Water Res. Manag. 2013, 27, 3765–3774. [Google Scholar] [CrossRef]

| Hydrological Year | Month | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| λ | 0.01 | 0.05 | 0.14 | 1.31 | 0.03 | 0.01 | |
| Wet year | ETm (mm) | [21.54, 23.80] | [62.84, 69.45] | [179.03, 197.87] | [204.78, 226.34] | [158.79, 175.51] | [41.81, 46.21] |
| Normal year | ETm (mm) | [19.79, 21.08] | [60.53, 64.46] | [169.51, 80.58] | [236.02, 251.35] | [161.86, 172.39] | [48.07, 51.20] |
| Dry year | ETm (mm) | [19.60, 21.67] | [63.92, 70.65] | [167.69, 185.34] | [211.30, 233.55] | [158.49, 175.18] | [40.21, 44.44] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huo, Z.; Xu, B. Optimal Allocation Method of Irrigation Water from River and Lake by Considering the Field Water Cycle Process. Water 2017, 9, 911. https://doi.org/10.3390/w9120911
Li X, Huo Z, Xu B. Optimal Allocation Method of Irrigation Water from River and Lake by Considering the Field Water Cycle Process. Water. 2017; 9(12):911. https://doi.org/10.3390/w9120911
Chicago/Turabian StyleLi, Xuemin, Zailin Huo, and Bing Xu. 2017. "Optimal Allocation Method of Irrigation Water from River and Lake by Considering the Field Water Cycle Process" Water 9, no. 12: 911. https://doi.org/10.3390/w9120911
APA StyleLi, X., Huo, Z., & Xu, B. (2017). Optimal Allocation Method of Irrigation Water from River and Lake by Considering the Field Water Cycle Process. Water, 9(12), 911. https://doi.org/10.3390/w9120911





