Lateral Saturated Hydraulic Conductivity of Soil Horizons Evaluated in Large-Volume Soil Monoliths
Abstract
1. Introduction
2. Material and Methods
2.1. Location
2.2. Soil Monolith Preparation
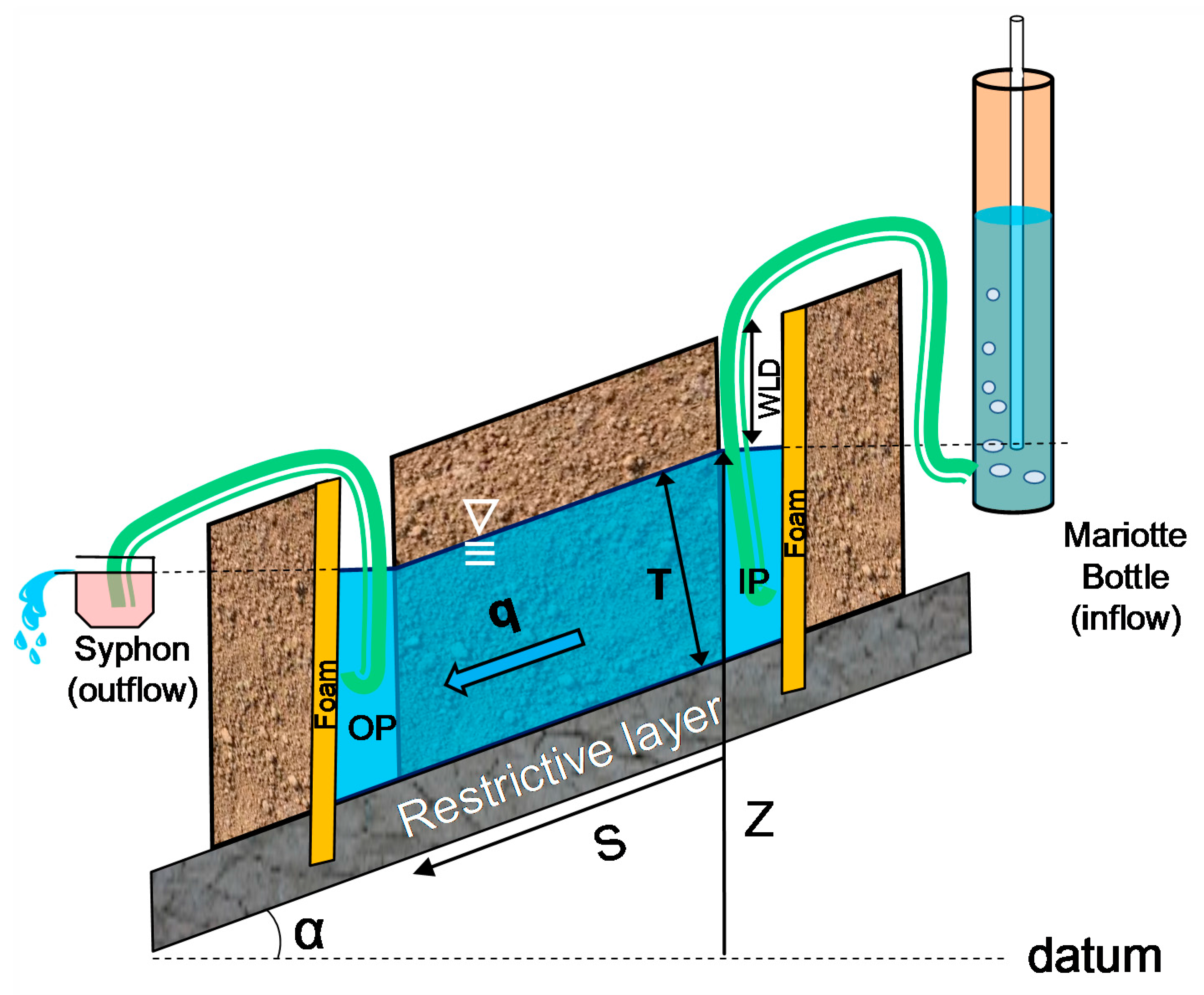
2.3. Instrumentation
2.4. Drainage Experiments
2.5. Ks,l Calculation
3. Results
3.1. Observed Inflow and Outflow Rates
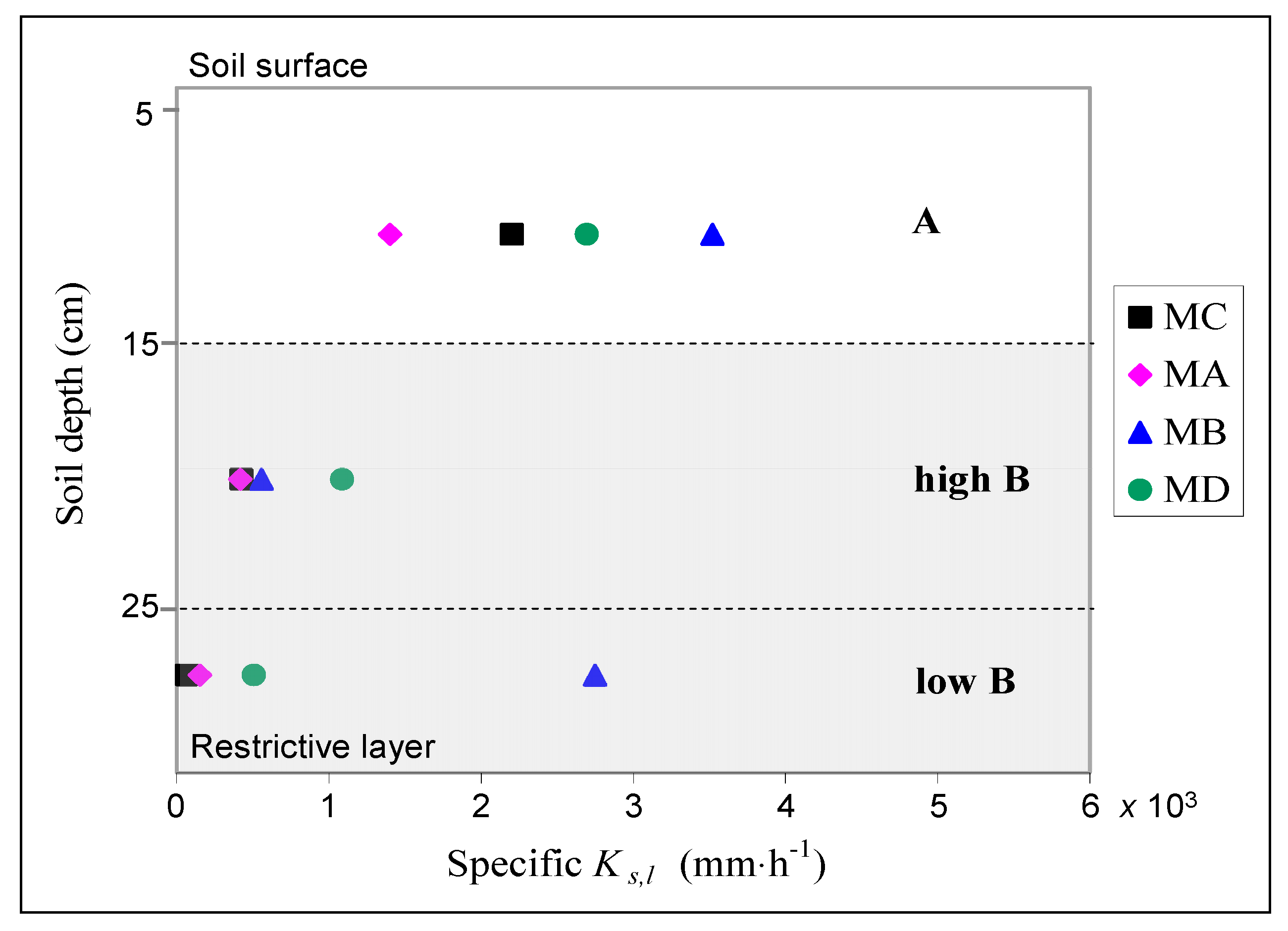
3.2. Lateral Saturated Soil Hydraulic Conductivities
4. Discussion
4.1. Benefits of the Proposed Field Soil Ks,l Assessment Tool
4.2. Ks,l Values of Individual Soil Horizons
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McDaniel, P.A.; Regan, M.P.; Brooks, E.; Boll, J.; Barndt, S.; Falen, A.; Young, S.K.; Hammel, J.E. Linking fragipans, perched water tables, and catchment-scale hydrological processes. CATENA 2008, 73, 166–173. [Google Scholar] [CrossRef]
- Du, E.; Rhett Jackson, C.; Klaus, J.; McDonnell, J.J.; Griffiths, N.A.; Williamson, M.F.; Greco, J.L.; Bitew, M. Interflow dynamics on a low relief forested hillslope: Lots of fill, little spill. J. Hydrol. 2016, 534, 648–658. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T.; Dohnal, M.; Gerke, H.H. Combining dual-continuum approach with diffusion wave model to include a preferential flow component in hillslope scale modeling of shallow subsurface runoff. Adv. Water Resour. 2012, 44, 113–125. [Google Scholar] [CrossRef]
- Alaoui, A.; Caduff, U.; Gerke, H.H.; Weingartner, R. A Preferential Flow Effects on Infiltration and Runoff in Grassland and Forest Soils. Vadose Zone J. 2011, 10, 367. [Google Scholar] [CrossRef]
- Van Schaik, N.L.M.B.; Schnabel, S.; Jetten, V.G. The influence of preferential flow on hillslope hydrology in a semi-arid watershed (in the Spanish Dehesas). Hydrol. Process. 2008, 22, 3844–3855. [Google Scholar] [CrossRef]
- Wienhöfer, J.; Zehe, E. Predicting subsurface stormflow response of a forested hillslope—The role of connected flow paths. Hydrol. Earth Syst. Sci. 2014, 18, 121–138. [Google Scholar] [CrossRef]
- Schmocker-Fackel, P.; Naef, F.; Scherrer, S. Identifying runoff processes on the plot and catchment scale. Hydrol. Earth Syst. Sci. 2007, 11, 891–906. [Google Scholar] [CrossRef]
- Weiler, M.; McDonnell, J.J.; Tromp-van Meerveld, I.; Uchida, T. Subsurface Stormflow. In Encyclopedia of Hydrological Sciences; Anderson, M.G., McDonnell, J.J., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2006; ISBN 0471491039, 9780471491033, 0470848944, 9780470848944. [Google Scholar]
- Brooks, E.S.; Boll, J.; McDaniel, P.A. A hillslope-scale experiment to measure lateral saturated hydraulic conductivity. Water Resour. Res. 2004, 40, W04208. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. Hydrologic Processes in a Low-Gradient Source Area. Water Resour. Res. 1995, 31, 1–10. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. Hydrological connectivity of hillslopes and streams: Characteristic time scales and nonlinearities. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Starr, J.L.; Sadeghi, A.M.; Pachepsky, Y.A. Monitoring and Modeling Lateral Transport through a Large In Situ Chamber. Soil Sci. Soc. Am. J. 2005, 69, 1871. [Google Scholar] [CrossRef]
- Stutter, M.I.; Deeks, L.K.; Billett, M.F. Transport of conservative and reactive tracers through a naturally structured upland podzol field lysimeter. J. Hydrol. 2005, 300, 1–19. [Google Scholar] [CrossRef]
- Van Verseveld, W.J.; McDonnell, J.J.; Lajtha, K. The role of hillslope hydrology in controlling nutrient loss. J. Hydrol. 2009, 367, 177–187. [Google Scholar] [CrossRef]
- Ambroise, B.; Beven, K.; Freer, J. Toward a Generalization of the TOPMODEL Concepts: Topographic Indices of Hydrological Similarity. Water Resour. Res. 1996, 32, 2135–2145. [Google Scholar] [CrossRef]
- Ameli, A.A.; Amvrosiadi, N.; Grabs, T.; Laudon, H.; Creed, I.F.; McDonnell, J.J.; Bishop, K. Hillslope permeability architecture controls on subsurface transit time distribution and flow paths. J. Hydrol. 2016, 543, 17–30. [Google Scholar] [CrossRef]
- Matonse, A.H.; Kroll, C.N. Applying hillslope-storage models to improve low flow estimates with limited streamflow data at a watershed scale. J. Hydrol. 2013, 494, 20–31. [Google Scholar] [CrossRef]
- Maneta, M.; Schnabel, S.; Jetten, V. Continuous spatially distributed simulation of surface and subsurface hydrological processes in a small semiarid catchment. Hydrol. Process. 2008, 22, 2196–2214. [Google Scholar] [CrossRef]
- Van Schaik, N.L.M.B.; Bronstert, A.; De Jong, S.M.; Jetten, V.G.; Van Dam, J.C.; Ritsema, C.J.; Schnabel, S. Process-based modelling of a headwater catchment in a semi-arid area: The influence of macropore flow: Process-based modelling of a headwater catchment. Hydrol. Process. 2014, 28, 5805–5816. [Google Scholar] [CrossRef]
- Bathke, G.R.; Cassel, D.K. Anisotropic Variation of Profile Characteristics and Saturated Hydraulic Conductivity in an Ultisol Landscape. Soil Sci. Soc. Am. J. 1991, 55, 333. [Google Scholar] [CrossRef]
- Beckwith, C.W.; Baird, A.J.; Heathwaite, A.L. Anisotropy and depth-related heterogeneity of hydraulic conductivity in a bog peat. I: Laboratory measurements. Hydrol. Process. 2003, 17, 89–101. [Google Scholar] [CrossRef]
- Vepraskas, M.J.; Williams, J.P. Hydraulic Conductivity of Saprolite as a Function of Sample Dimensions and Measurement Technique. Soil Sci. Soc. Am. J. 1995, 59, 975. [Google Scholar] [CrossRef]
- Mendoza, G.; Steenhuis, T.S. Determination of hydraulic behavior of hillsides with a hillslope infiltrometer. Soil Sci. Soc. Am. J. 2002, 66, 1501. [Google Scholar] [CrossRef]
- Blanco-Canqui, H.; Gantzer, C.J.; Anderson, S.H.; Alberts, E.E.; Ghidey, F. Saturated Hydraulic Conductivity and Its Impact on Simulated Runoff for Claypan Soils. Soil Sci. Soc. Am. J. 2002, 66, 1596. [Google Scholar] [CrossRef]
- Brye, K.R.; Morris, T.L.; Miller, D.M.; Formica, S.J.; Van Eps, M.A. Estimating Bulk Density in Vertically Exposed Stoney Alluvium Using a Modified Excavation Method. J. Environ. Qual. 2004, 33, 1937. [Google Scholar] [CrossRef] [PubMed]
- Muller, R.N.; Hamilton, M.E. A simple, effective method for determining the bulk density of stony soils. Commun. Soil Sci. Plant Anal. 1992, 23, 313–319. [Google Scholar] [CrossRef]
- Page-Dumroese, D.S.; Brown, R.E.; Jurgensen, M.F.; Mroz, G.D. Comparison of Methods for Determining Bulk Densities of Rocky Forest Soils. Soil Sci. Soc. Am. J. 1999, 63, 379. [Google Scholar] [CrossRef]
- Bagarello, V.; Sgroi, A. Testing Soil Encasing Materials for Measuring Hydraulic Conductivity of a Sandy-Loam Soil by the Cube Methods. Soil Sci. Soc. Am. J. 2008, 72, 1048. [Google Scholar] [CrossRef]
- Bagarello, V.; Sferlazza, S.; Sgroi, A. Testing laboratory methods to determine the anisotropy of saturated hydraulic conductivity in a sandy–loam soil. Geoderma 2009, 154, 52–58. [Google Scholar] [CrossRef]
- Germer, K.; Braun, J. Determination of Anisotropic Saturated Hydraulic Conductivity of a Macroporous Slope Soil. Soil Sci. Soc. Am. J. 2015, 79, 1528. [Google Scholar] [CrossRef]
- Castellini, M.; Iovino, M.; Pirastru, M.; Niedda, M.; Bagarello, V. Use of BEST Procedure to Assess Soil Physical Quality in the Baratz Lake Catchment (Sardinia, Italy). Soil Sci. Soc. Am. J. 2016, 80, 742. [Google Scholar] [CrossRef]
- Pirastru, M.; Niedda, M.; Castellini, M. Effects of maquis clearing on the properties of the soil and on the near-surface hydrological processes in a semi-arid Mediterranean environment. J. Agric. Eng. 2014, 45, 176. [Google Scholar] [CrossRef]
- Giadrossich, F.; Niedda, M.; Cohen, D.; Pirastru, M. Evaporation in a Mediterranean environment by energy budget and Penman methods, Lake Baratz, Sardinia, Italy. Hydrol. Earth Syst. Sci. 2015, 19, 2451–2468. [Google Scholar] [CrossRef]
- Day, R.L.; Calmon, M.A.; Stiteler, J.M.; Jabro, J.D.; Cunningham, R.L. Water balance and flow patterns in a fragipan using in situ soil block. Soil Sci. 1998, 163, 517–528. [Google Scholar] [CrossRef]
- Alagna, V.; Bagarello, V.; Di Prima, S.; Giordano, G.; Iovino, M. Testing infiltration run effects on the estimated water transmission properties of a sandy-loam soil. Geoderma 2016, 267, 24–33. [Google Scholar] [CrossRef]
- Dikinya, O.; Hinz, C.; Aylmore, G. Decrease in hydraulic conductivity and particle release associated with self-filtration in saturated soil columns. Geoderma 2008, 146, 192–200. [Google Scholar] [CrossRef]
- Appels, W.M.; Graham, C.B.; Freer, J.E.; McDonnell, J.J. Factors affecting the spatial pattern of bedrock groundwater recharge at the hillslope scale: Spatial Patterns of Bedrock Groundwater Recharge. Hydrol. Process. 2015, 29, 4594–4610. [Google Scholar] [CrossRef]
- Pirastru, M.; Bagarello, V.; Iovino, M.; Marrosu, R.; Castellini, M.; Giadrossich, F.; Niedda, M. Subsurface flow and large-scale lateral saturated soil hydraulic conductivity in a Mediterranean hillslope with contrasting land uses. J. Hydrol. Hydromech. 2017, 65. [Google Scholar] [CrossRef]
- Chappell, N.A.; Lancaster, J.W. Comparison of methodological uncertainties within permeability measurements. Hydrol. Process. 2007, 21, 2504–2514. [Google Scholar] [CrossRef]
- Niedda, M.; Pirastru, M.; Castellini, M.; Giadrossich, F. Simulating the hydrological response of a closed catchment-lake system to recent climate and land-use changes in semi-arid Mediterranean environment. J. Hydrol. 2014, 517, 732–745. [Google Scholar] [CrossRef]


| Monolith | Length (cm) | Width (cm) | Soil Depth (cm) | Soil Volume (m3) | Surface Slope |
|---|---|---|---|---|---|
| MA | 80 | 52.5 | 31 | 0.13 | 0.27 |
| MB | 69 | 50.0 | 29 | 0.10 | 0.35 |
| MC | 68 | 50.0 | 30 | 0.10 | 0.42 |
| MD | 85 | 54.0 | 35 | 0.16 | 0.36 |
| Monolith | Water-Level Depth (WLD) | ||
|---|---|---|---|
| 5 cm | 15 cm | 25 cm | |
| MA | 810 (838) | 218 (236) | 42 (47) |
| MB | 2660 (2671) | 851 (864) | 565 (565) |
| MC | 1581 (1595) | 273 (272) | 21 (15) |
| MD | 307 (2308) | 98 (867) | 23 (286) |
| Monolith | Water-Level Depth | ||
|---|---|---|---|
| 5 cm | 15 cm | 25 cm | |
| MA | 724 | 313 | 153 |
| MB | 2157 | 1184 | 2750 |
| MC | 1066 | 307 | 70 |
| MD | 1416 | 791 | 509 |
| Median | 1241 | 552 | 331 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirastru, M.; Marrosu, R.; Di Prima, S.; Keesstra, S.; Giadrossich, F.; Niedda, M. Lateral Saturated Hydraulic Conductivity of Soil Horizons Evaluated in Large-Volume Soil Monoliths. Water 2017, 9, 862. https://doi.org/10.3390/w9110862
Pirastru M, Marrosu R, Di Prima S, Keesstra S, Giadrossich F, Niedda M. Lateral Saturated Hydraulic Conductivity of Soil Horizons Evaluated in Large-Volume Soil Monoliths. Water. 2017; 9(11):862. https://doi.org/10.3390/w9110862
Chicago/Turabian StylePirastru, Mario, Roberto Marrosu, Simone Di Prima, Saskia Keesstra, Filippo Giadrossich, and Marcello Niedda. 2017. "Lateral Saturated Hydraulic Conductivity of Soil Horizons Evaluated in Large-Volume Soil Monoliths" Water 9, no. 11: 862. https://doi.org/10.3390/w9110862
APA StylePirastru, M., Marrosu, R., Di Prima, S., Keesstra, S., Giadrossich, F., & Niedda, M. (2017). Lateral Saturated Hydraulic Conductivity of Soil Horizons Evaluated in Large-Volume Soil Monoliths. Water, 9(11), 862. https://doi.org/10.3390/w9110862








