Incorporating Temporal and Spatial Variations of Groundwater into the Construction of a Water-Based Ecological Network: A Case Study in Denko County
Abstract
1. Introduction
2. Materials
2.1. Site Description and Data Sources
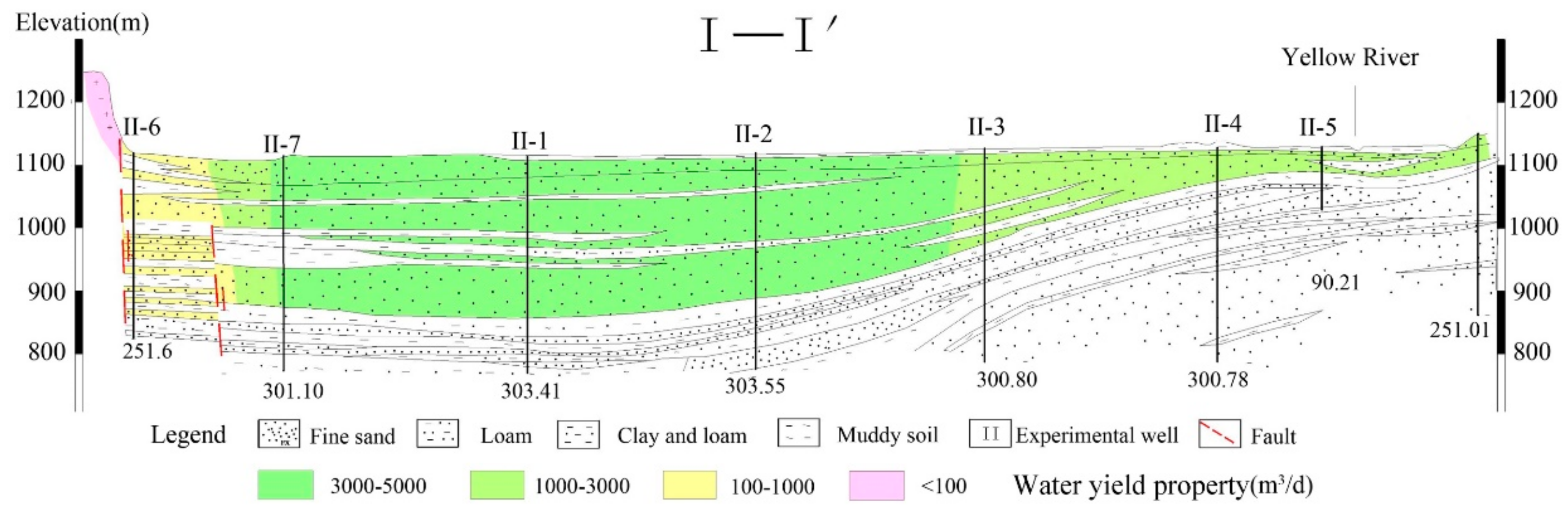
2.2. Physiography and Hydrogeological Conditions
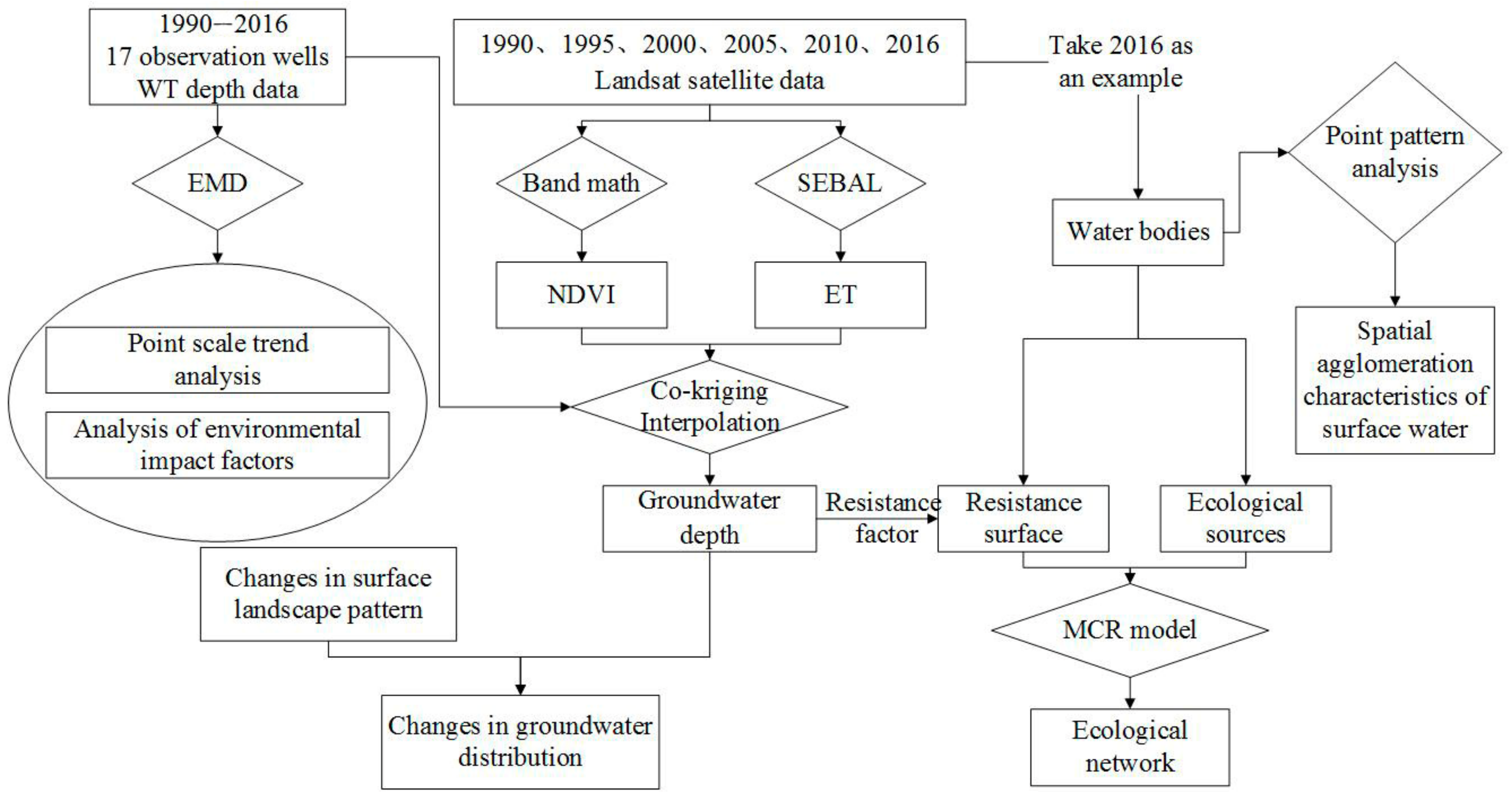
3. Methodology
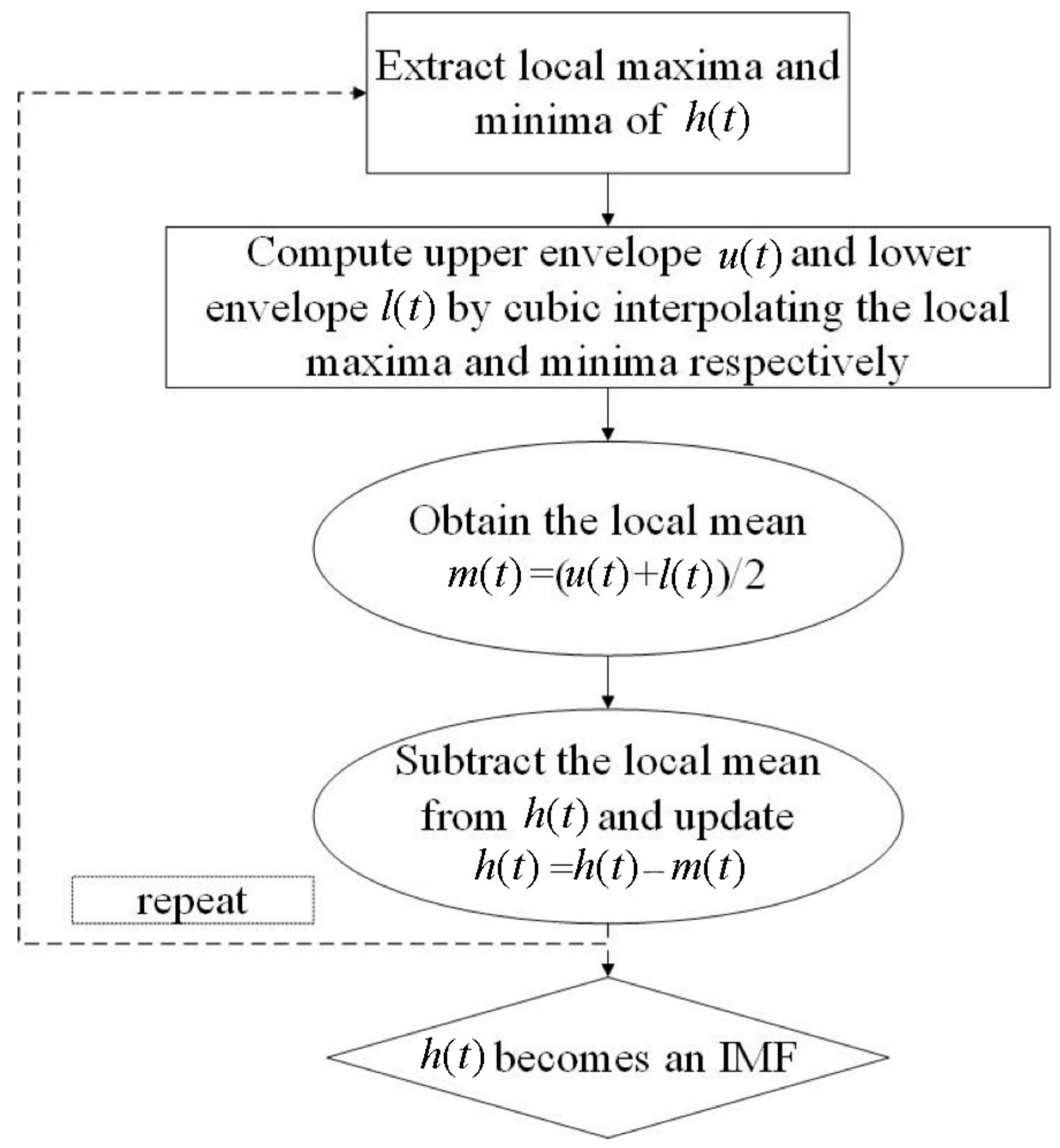
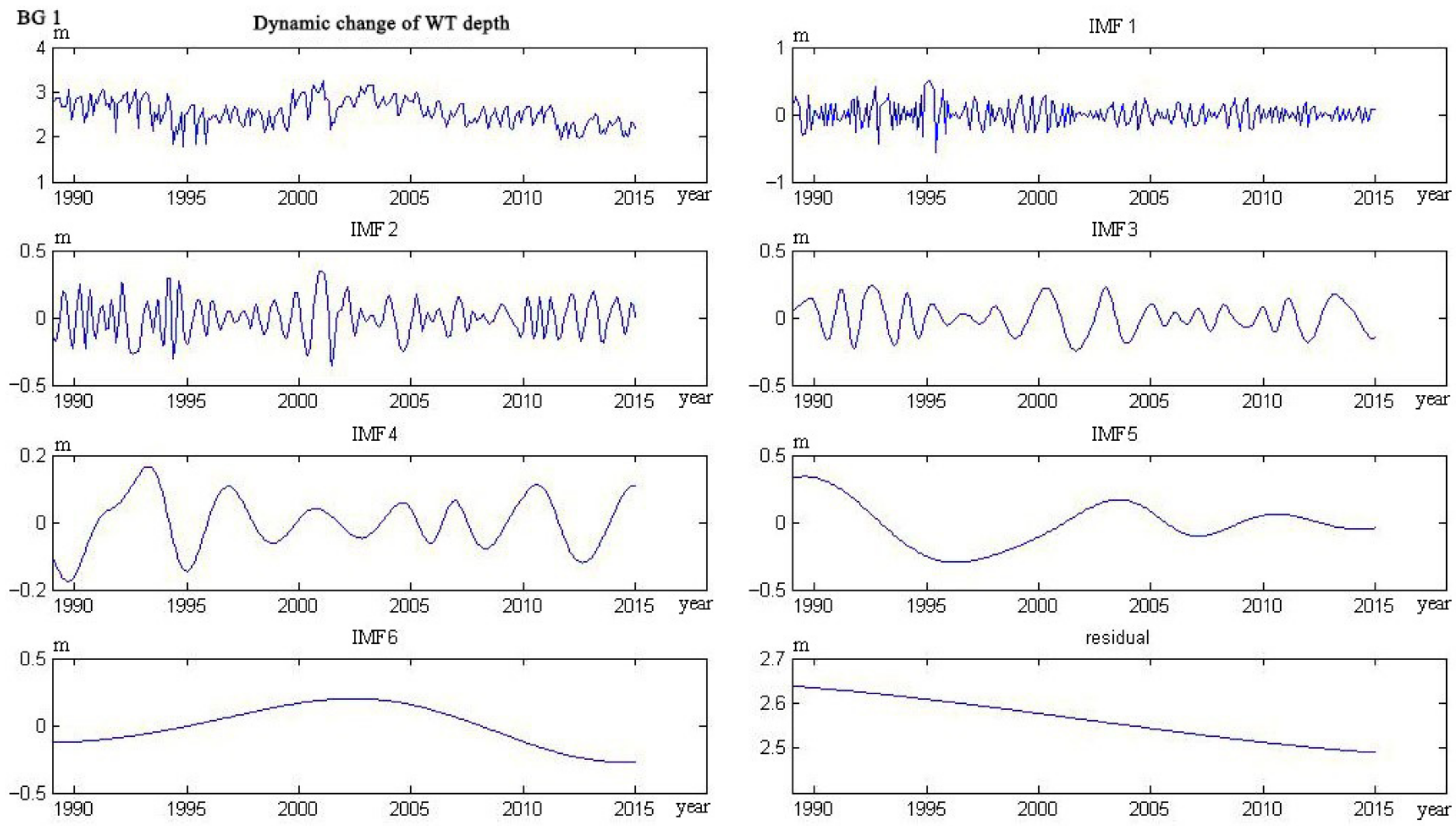
3.1. Empirical Modal Decomposition Model
- (1)
- Find the local maxima in the original sequence . To better preserve the characteristics of the original sequence, the local maximum was defined as the value of a point in the time series, which is not larger than the previous or subsequent moment.
- (2)
- Next, the cubic spline function was used to interpolate, and the upper envelope sequence of the original sequence was obtained.
- (3)
- Similarly, the lower envelope was obtained.
- (4)
- The maximum envelope and the minimum envelope were averaged, and the instantaneous average value obtained:
- (5)
- The class normal value sequence was obtained by subtracting the instantaneous mean sequence from the original sequence :
3.2. Co-Kriging Interpolation Algorithm
3.3. Point Pattern Analysis Algorithm
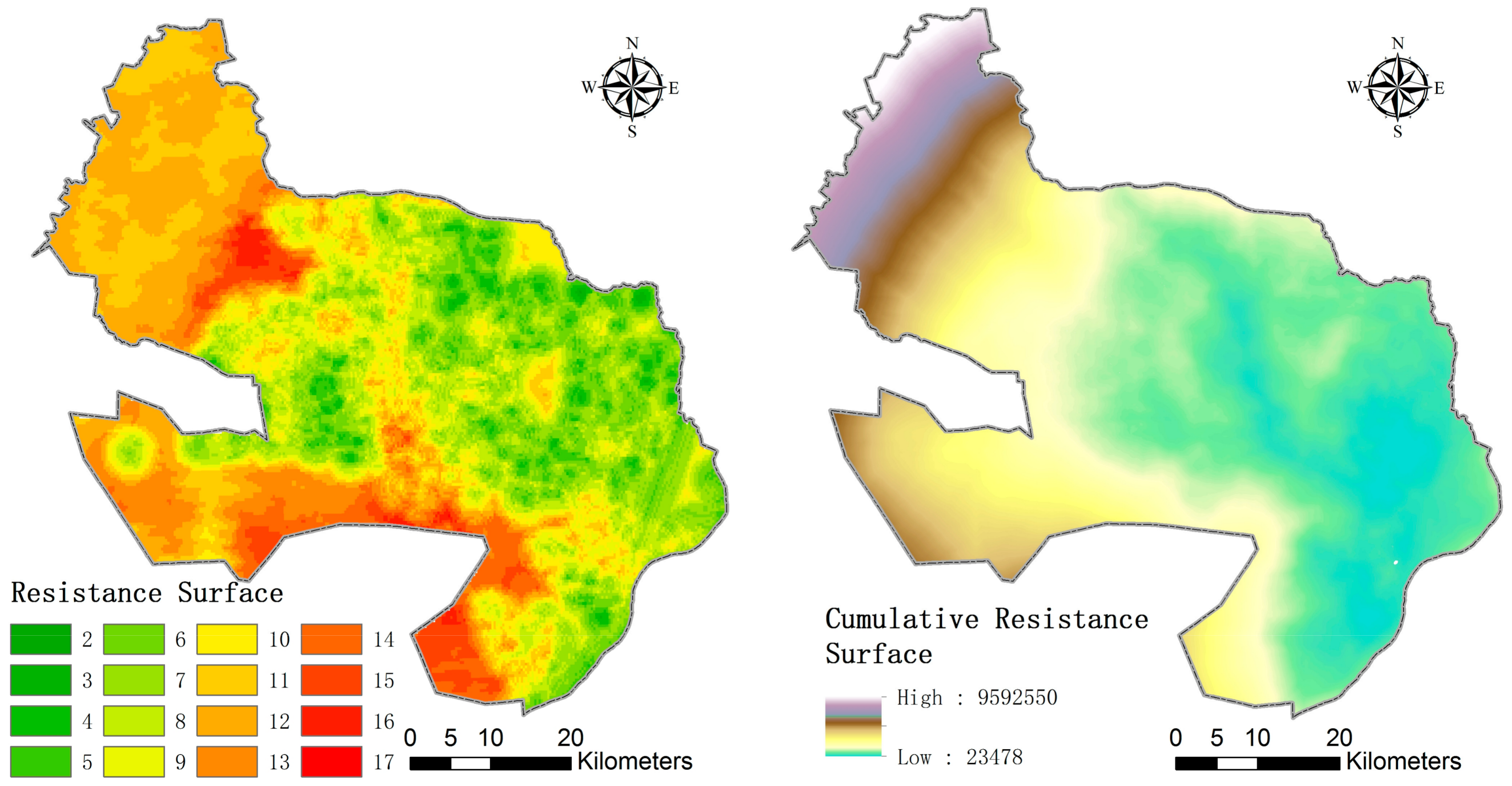
3.4. Minimum Cumulative Resistance Surface Model
4. Results and Discussions
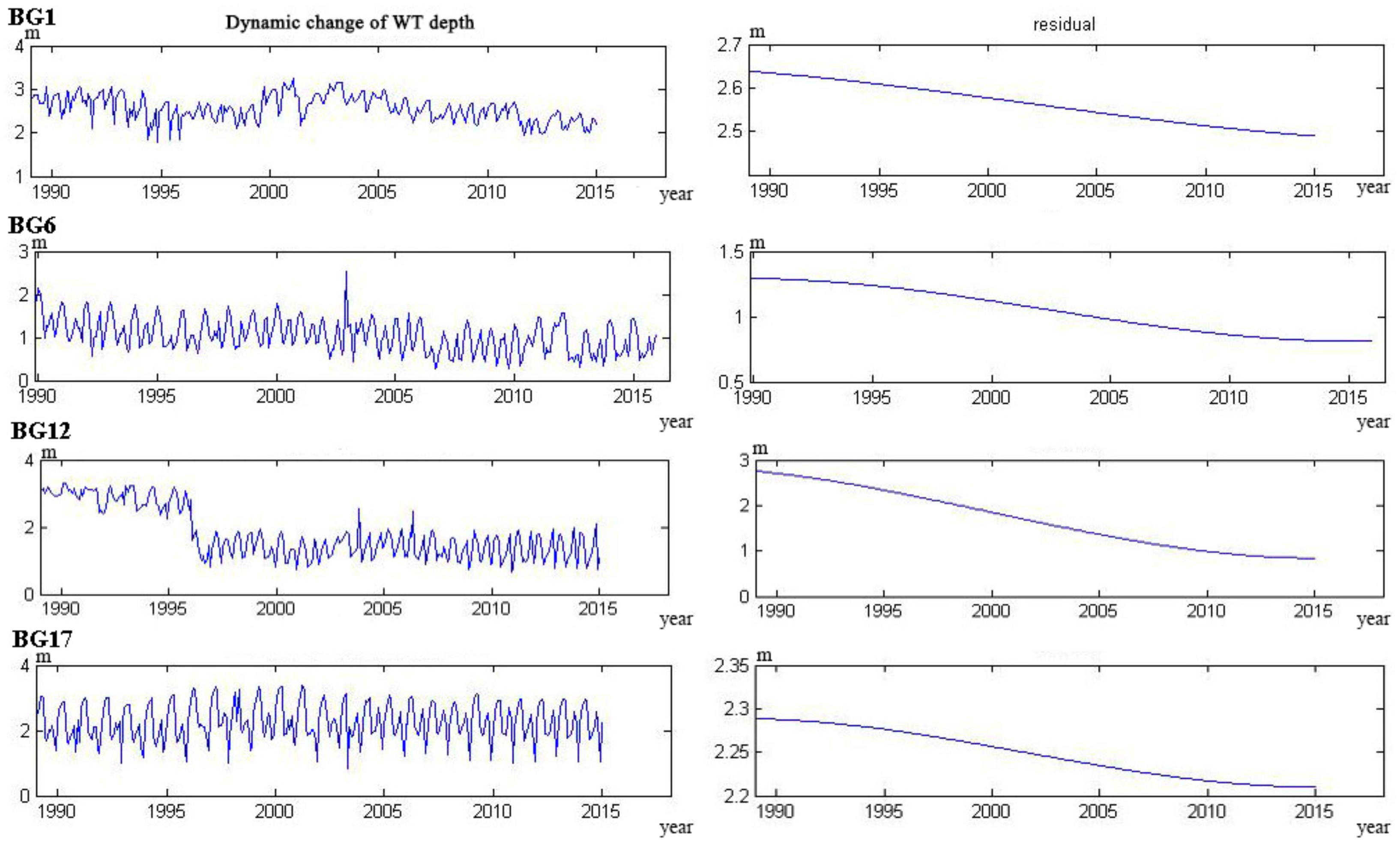
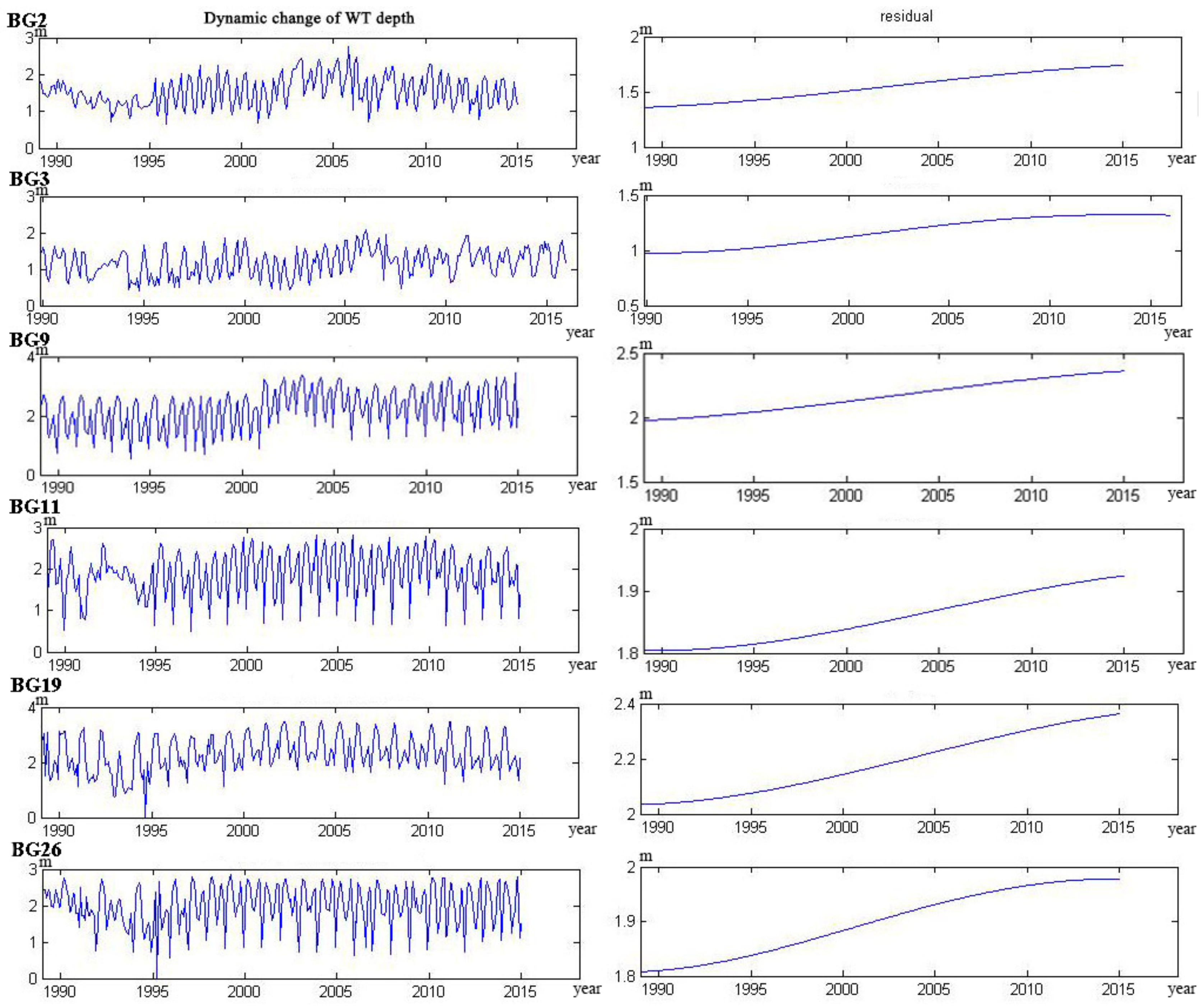
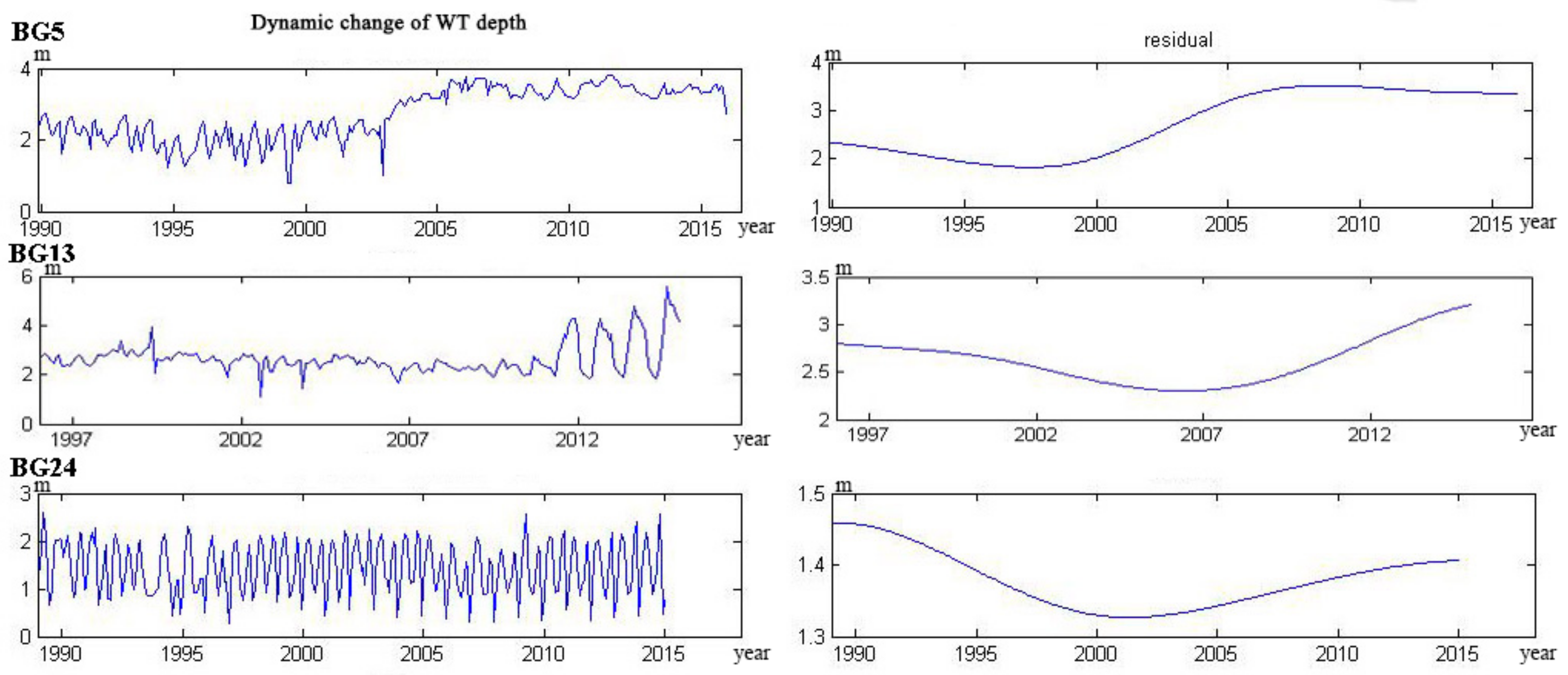
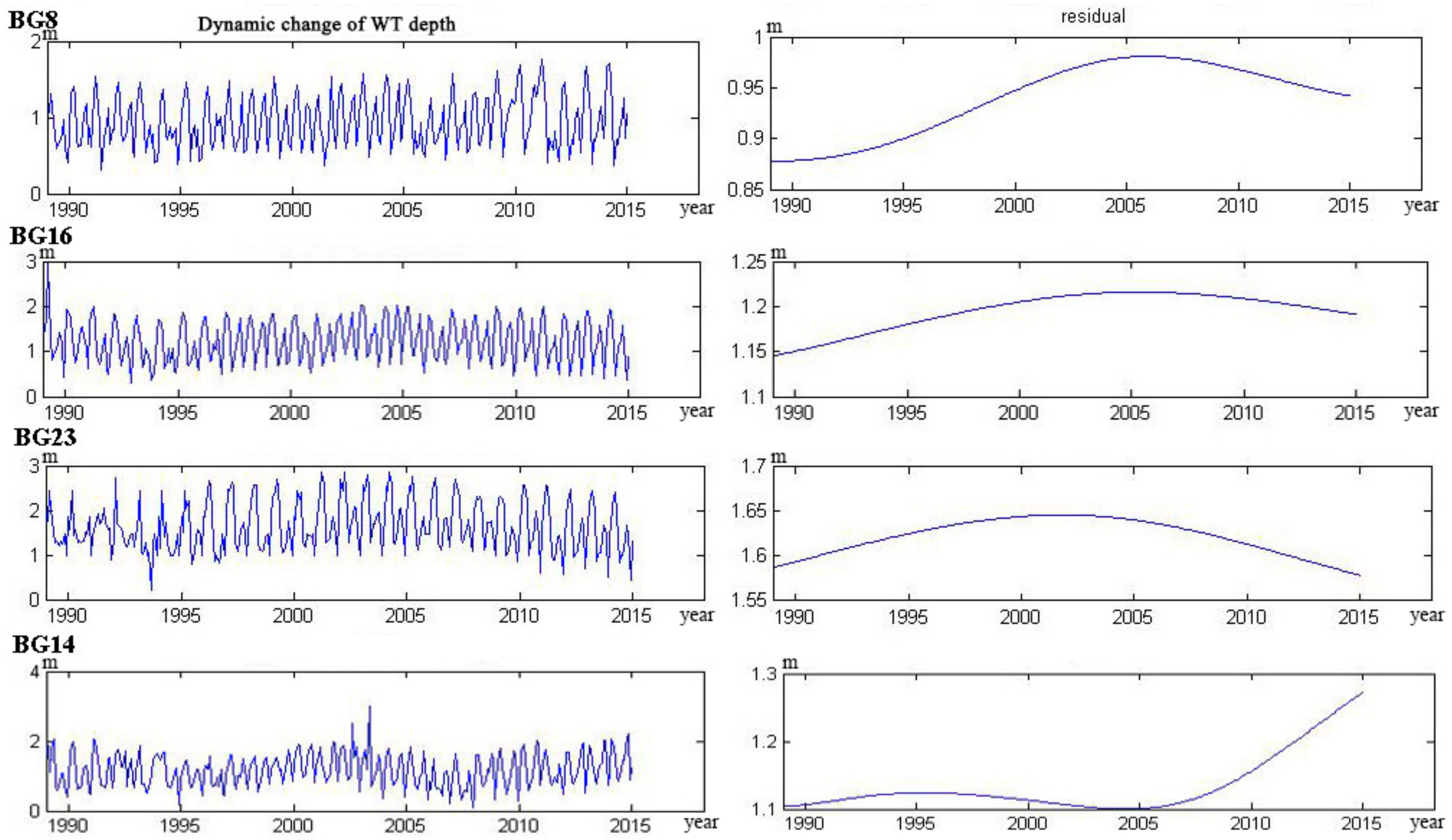
4.1. Water Table Dynamics
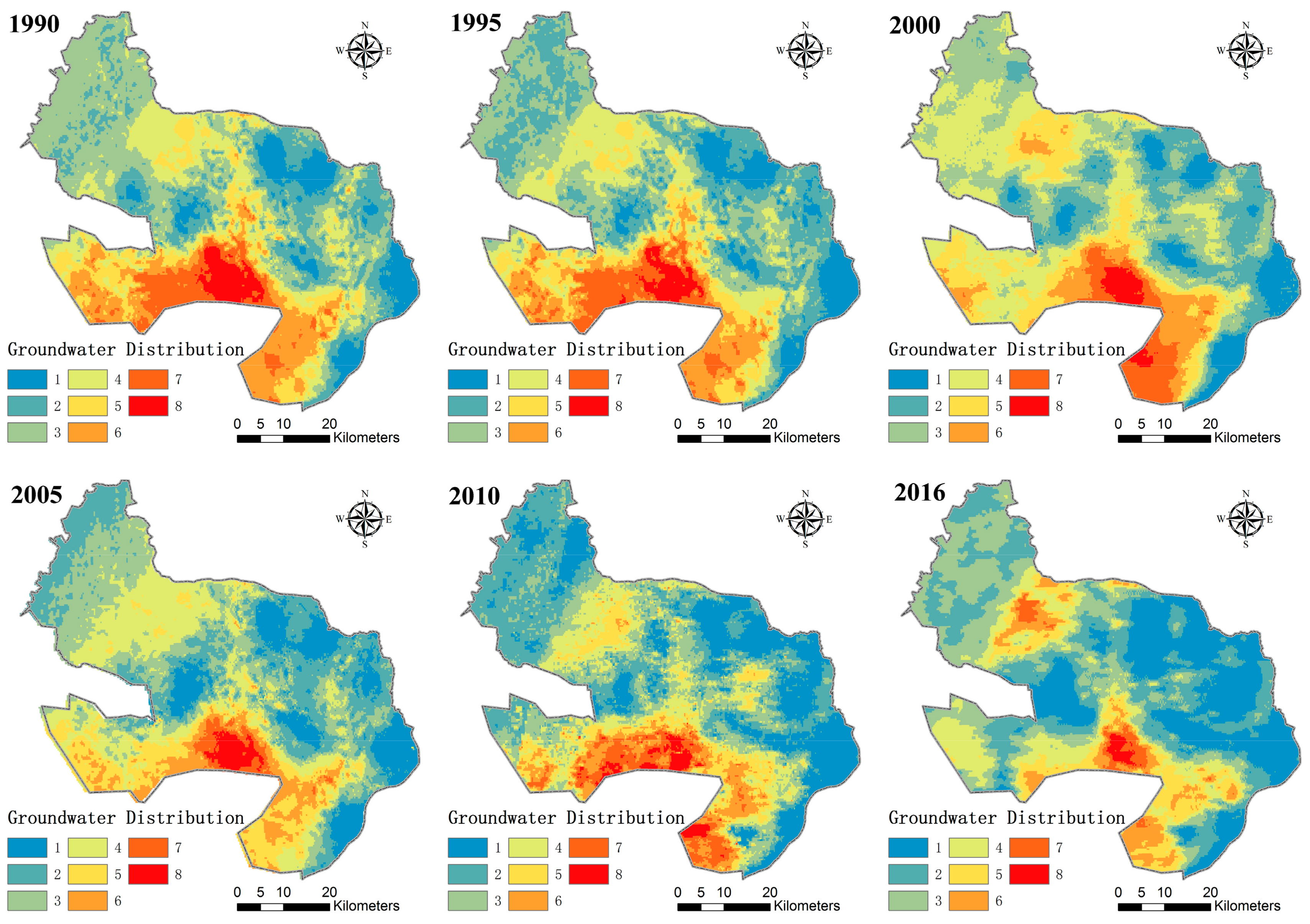
4.2. Spatial Distribution of Groundwater
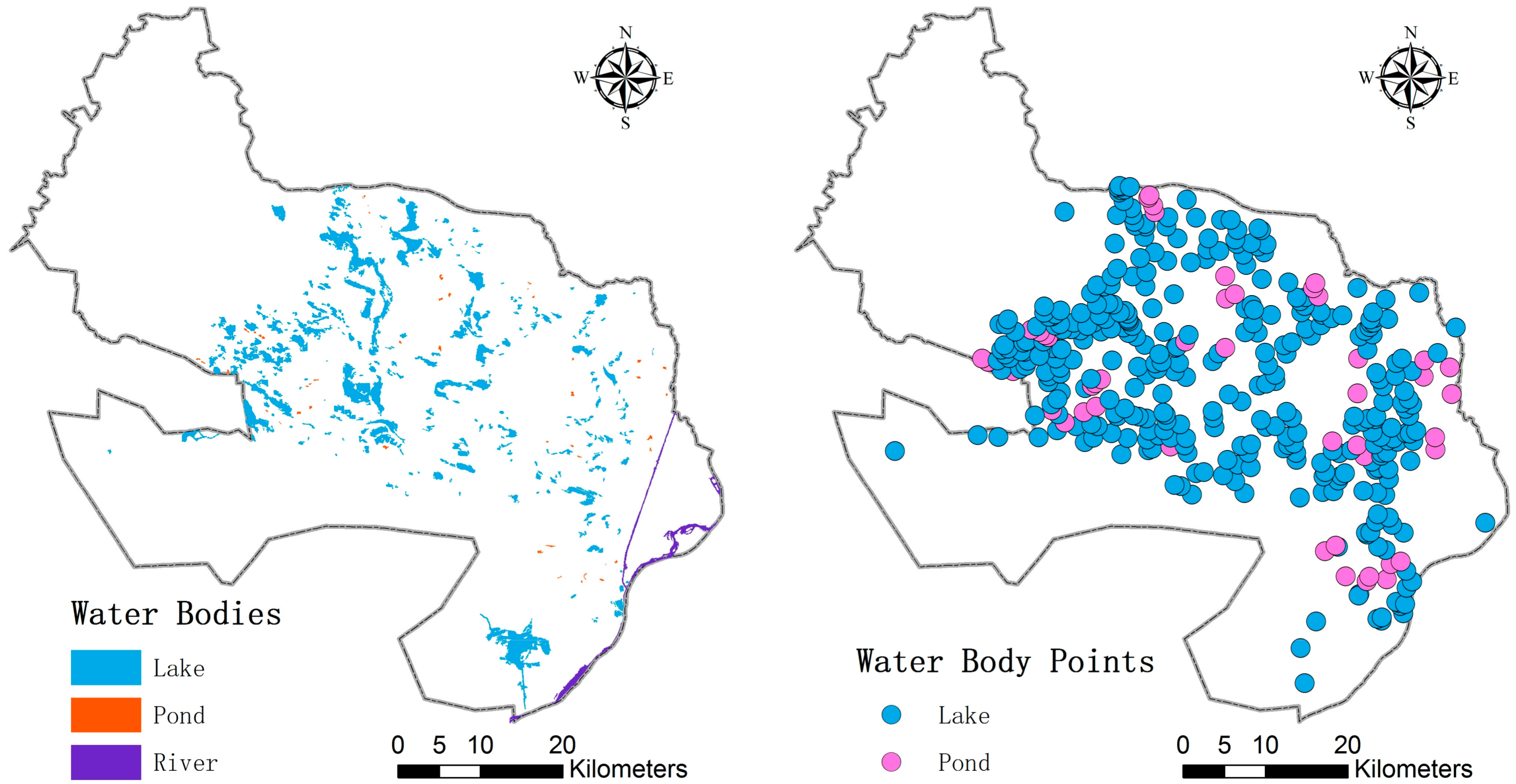
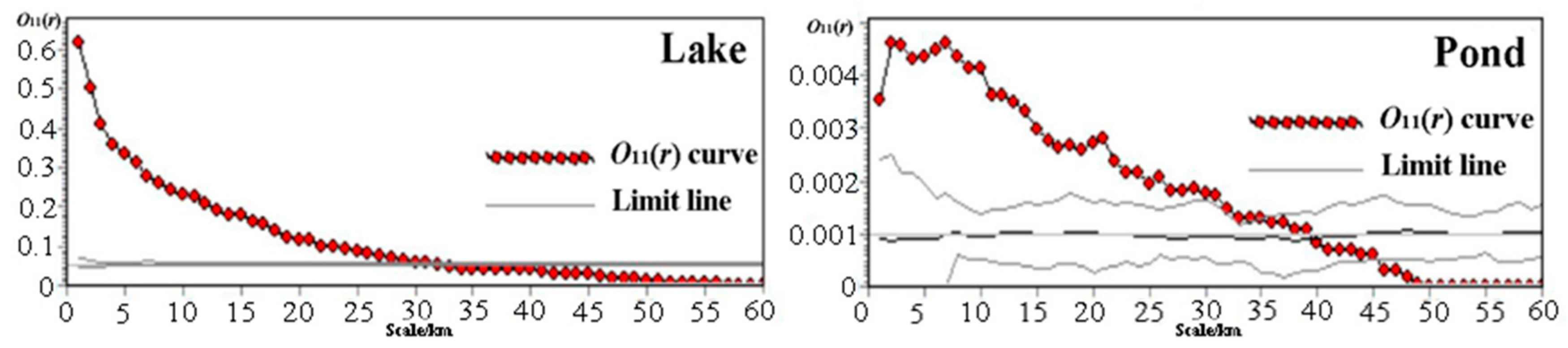
4.3. Point Pattern Analysis of Surface Water
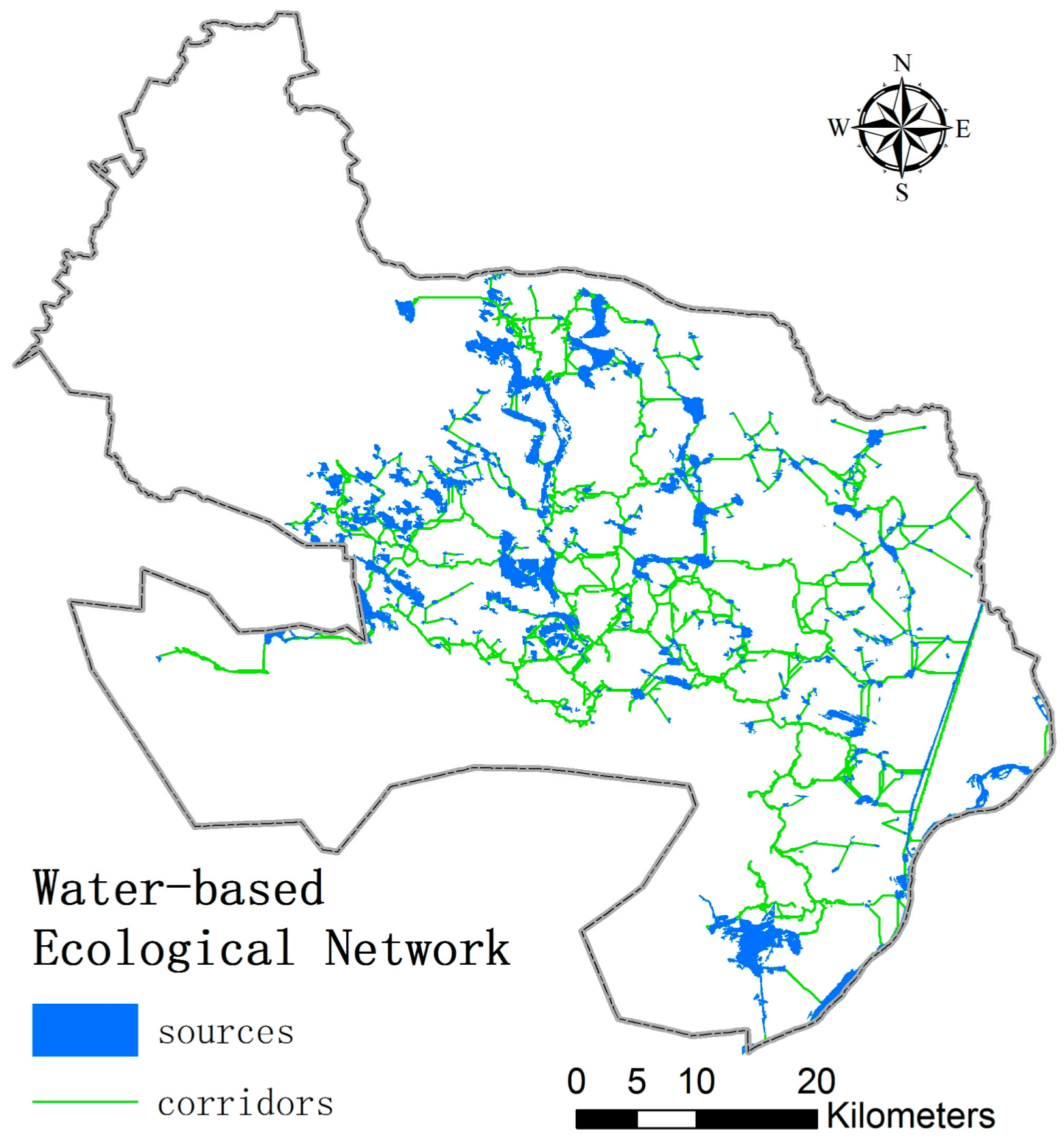
4.4. Construction of a Water-Based Ecological Network
4.5. Discussions on the Reliability of the Main Results
5. Conclusions
- The trend lines of 17 wells could be categorized into five types. The curve of four wells monotonically decreased, and six wells monotonically rose. The curve of three wells showed a trend from decline to rise, and the other three wells showed a trend from rise to decline. Only one well showed a rise–decline–rise trend.
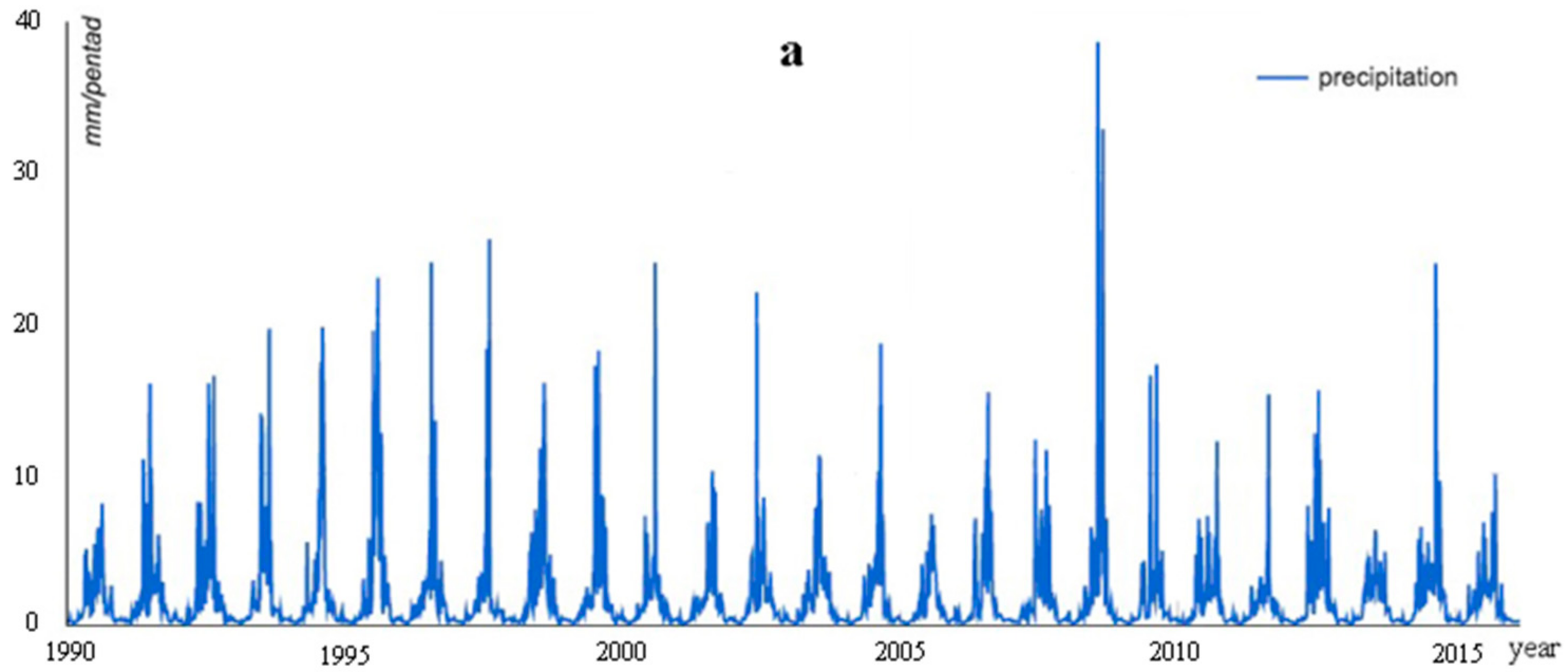
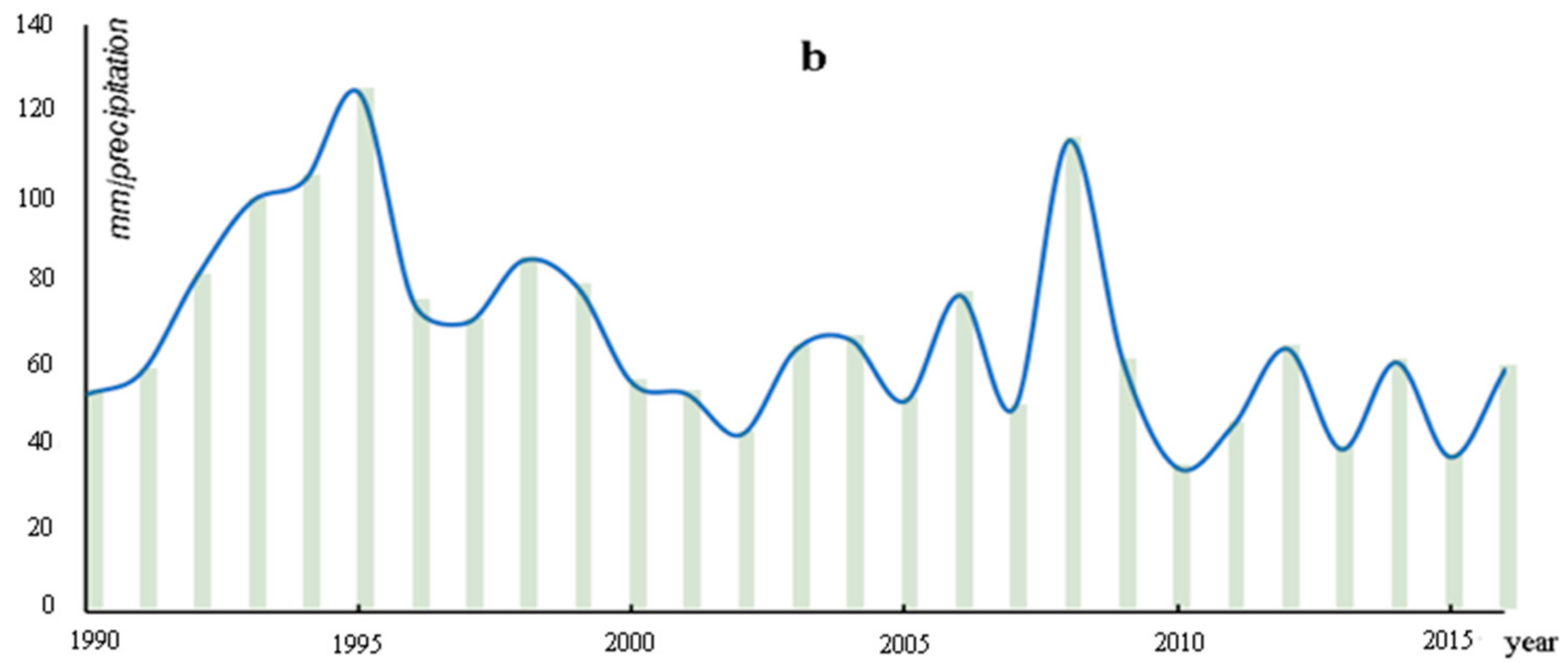
- There were three representative areas where the groundwater level changed dramatically. Among them, the landscape type changed from a desert landscape to an oasis landscape in the first and second representative areas. The changes in the landscape pattern of these two regions had a positive effect on the spatial distribution of groundwater. However, the urbanization of the third representative area had a negative impact on the spatial distribution of groundwater. In summary, appropriate human interventions (such as the construction of an artificial oasis) are of great significance to the stability of arid and semi-arid ecological environments. Furthermore, the precipitation trends were related to the spatial distribution of groundwater depth.
- The spatial pattern of water nodes was characterized by a small-scale highly aggregated distribution and a large-scale uniform distribution. This pattern stabilized the surface water bodies and the regional environment. A more stable ecological network was constructed based on surface water bodies.
- Lakes, ponds, and major rivers were identified as ecological sources, and the ecological source was divided into four grades. Spatial data of WT depth, multiple buffering data of surface water bodies, and spatial density data of surface water bodies were used to construct resistance surfaces. The 2016 water-based ecological network in Denko County consisted of 391 ecological sites and 7360 ecological corridors.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
// Load the CHIRPS data
var CHIRPS = ee.ImageCollection(‘UCSB-CHG/CHIRPS/PENTAD’);
//Identify Denko County
var GLTP = ee.FeatureCollection(‘ft:14UUynJScUtra5vI9cZ-iPWwZgcZOmbnpgX7qLQl_’);
Map.addLayer(GLTP);
//Identify region of interest
var ROI
// Select dates: the CHIRPS data is from 1981-01-01 to 2016-02-27
var precip = CHIRPS.filterDate(‘1990-01-01’, ‘2016-02-27’);
var TS5 = Chart.image.series(precip, GLTP, ee.Reducer.mean(),1000, ‘system:time_start’).setOptions({
title: ‘Precipitation Full Time Series’,
vAxis: {title: ‘mm/pentad’},
});
print(TS5);
// Charts One Year
var precip1year = CHIRPS.filterDate(‘2016-01-01’, ‘2016-12-31’);
var TS1 = Chart.image.series(precip1year, GLTP, ee.Reducer.mean(),1000, ‘system:time_start’).setOptions({
title: ‘Precipitation 1-Year Time Series’,
vAxis: {title: ‘mm/pentad’},
});
print(TS1);
var Precip1 = precip1year.mean().clip(GLTP);
var Precip=precip.mean().clip(GLTP);
Map.addLayer(Precip1, {‘min’: 0, ‘max’: 70, ‘palette’:"CCFFCC,00CC66,006600"},’Precip 2015’);
Map.addLayer(Precip, {‘min’: 0, ‘max’: 70, ‘palette’:"CCFFCC,00CC66,006600"},’Precip 2000-2015’);
var path = Precip.getDownloadURL({
‘scale’:250,
‘crs’: ‘EPSG:4326’,
‘region’: ‘[[21.4453125,-18.1249706393865], [33.310546875,-18.35452552912664], [34.27734375,-8.015715997869059], [21.59912109375,-7.776308503776192], [21.4453125,-18.1249706393865]]’
});
print (path);
Appendix B
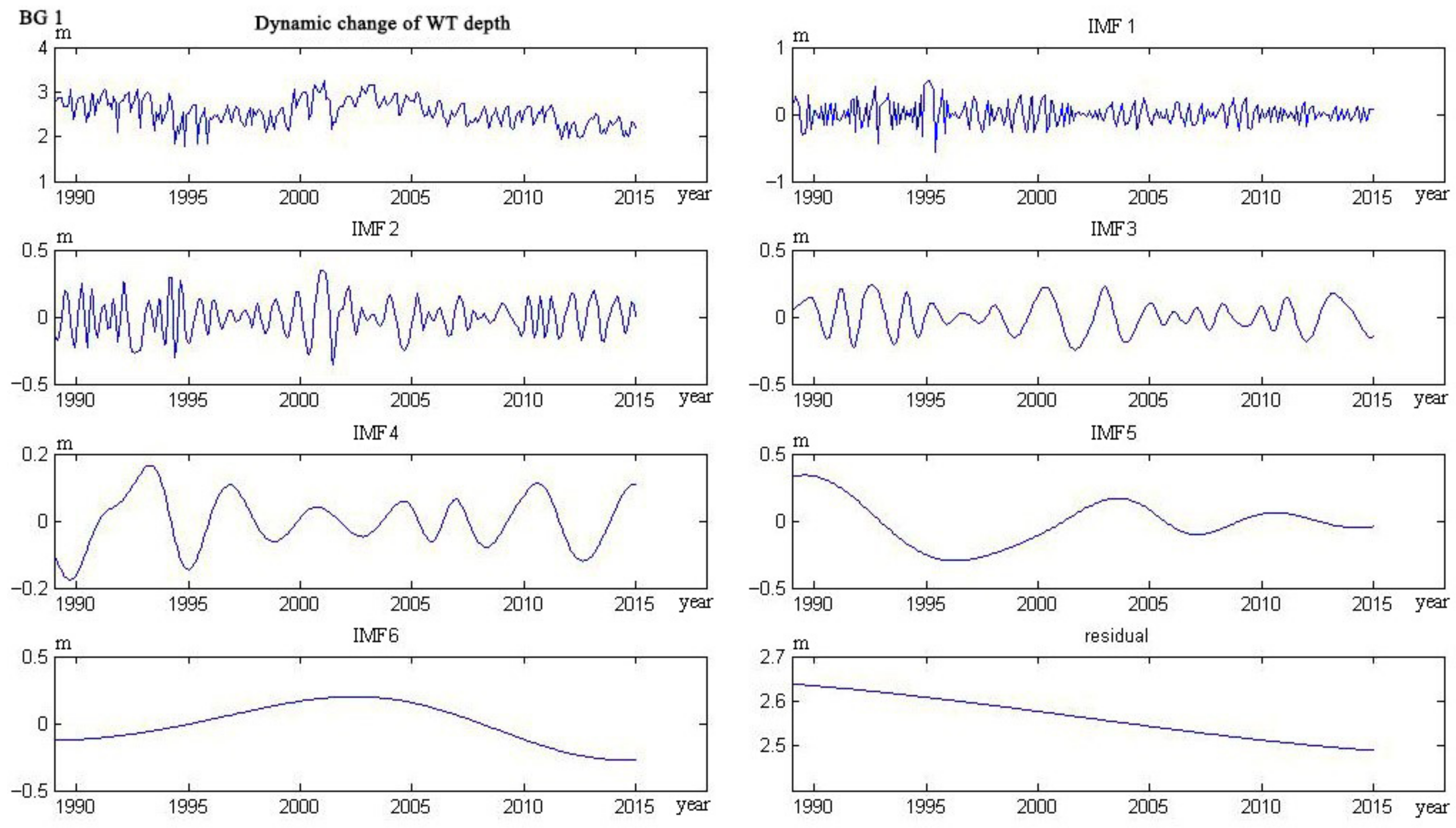

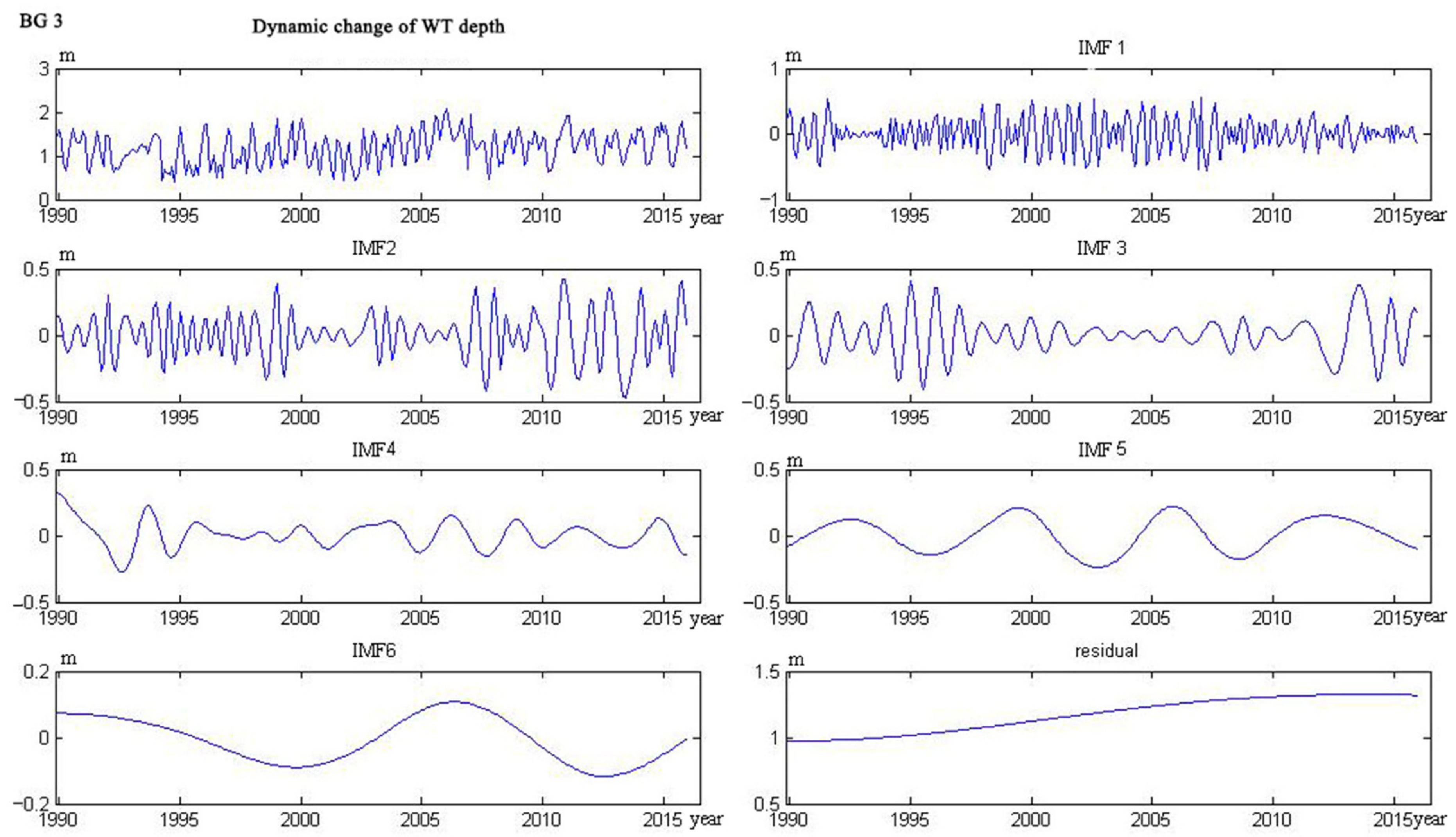

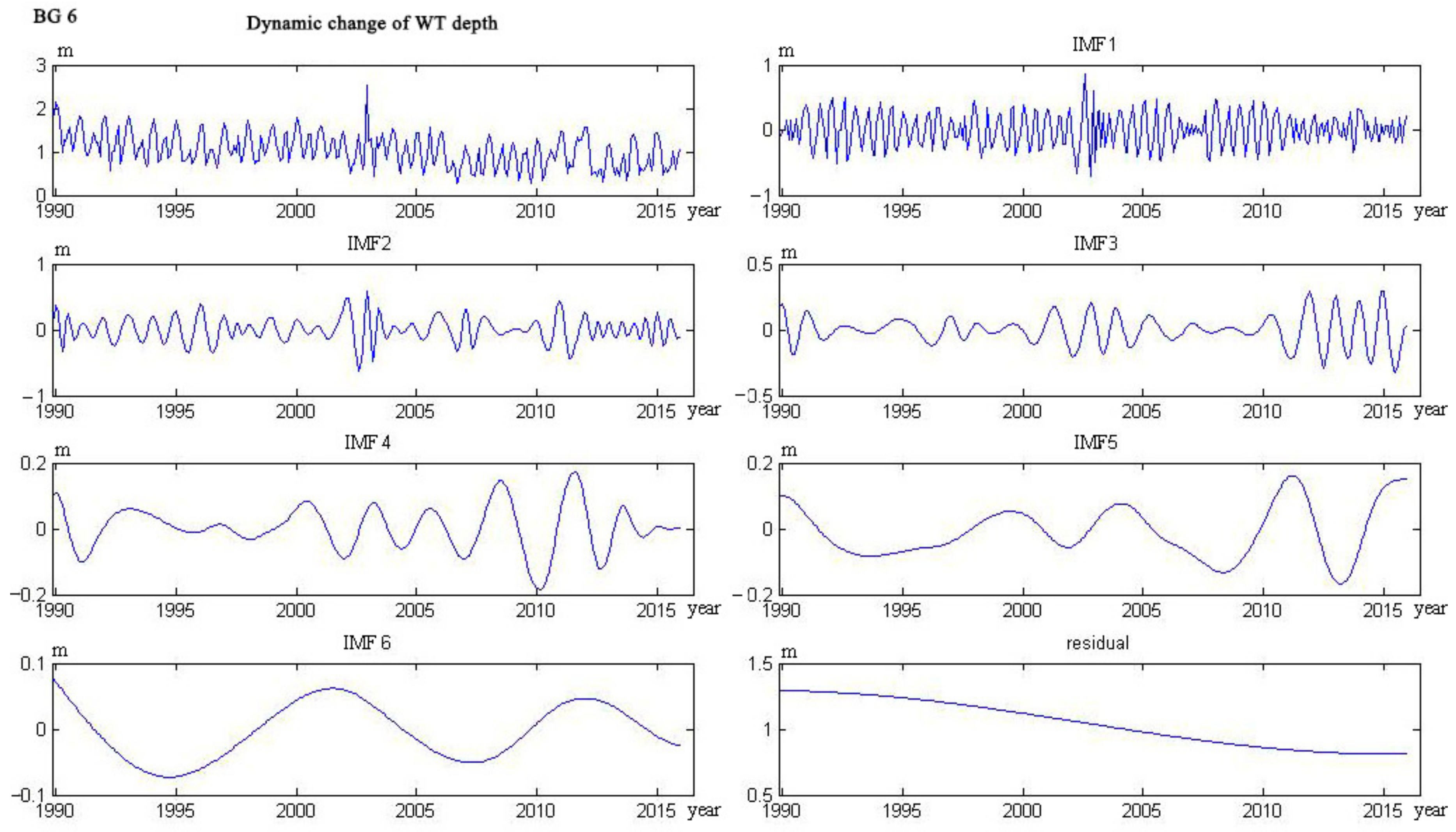

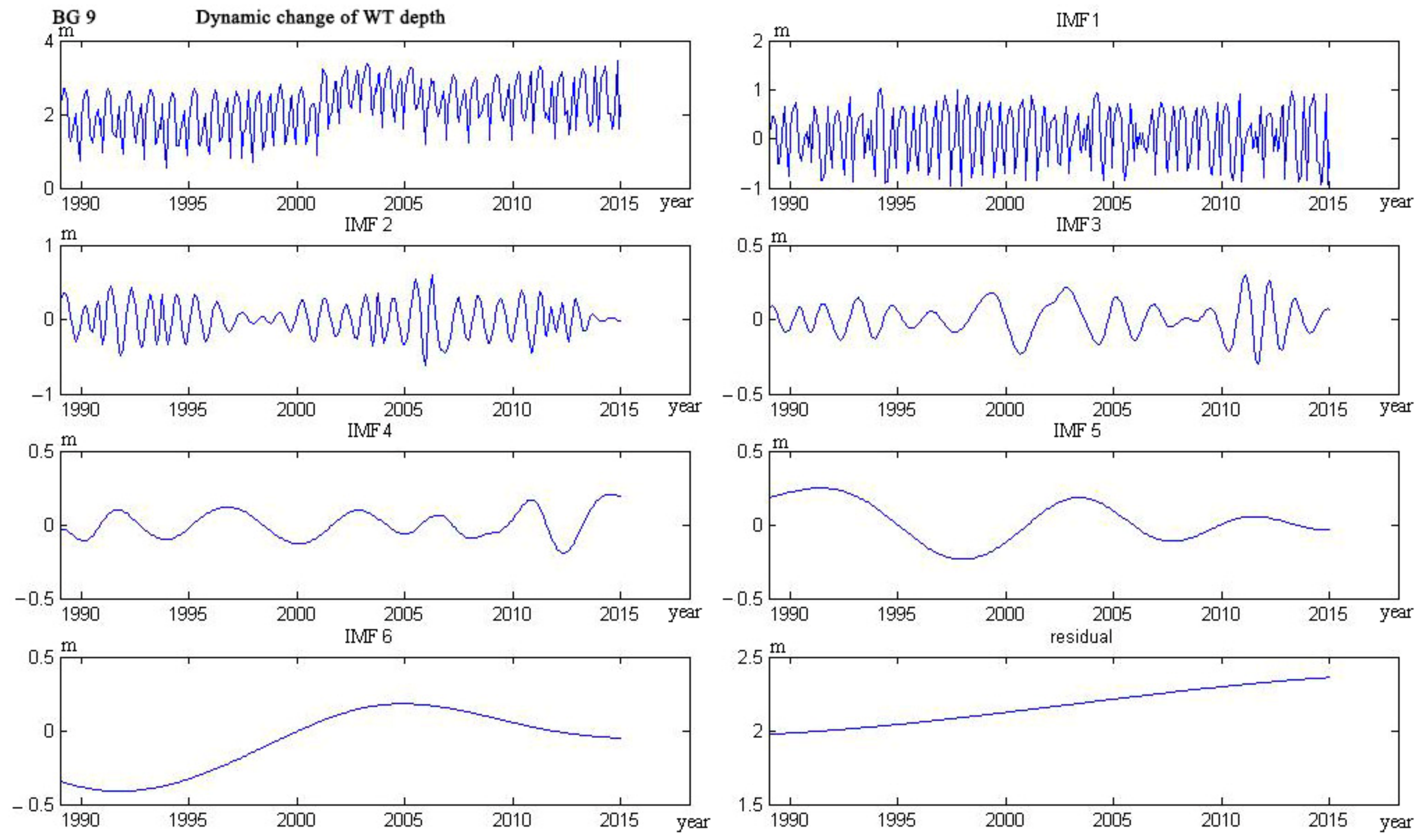
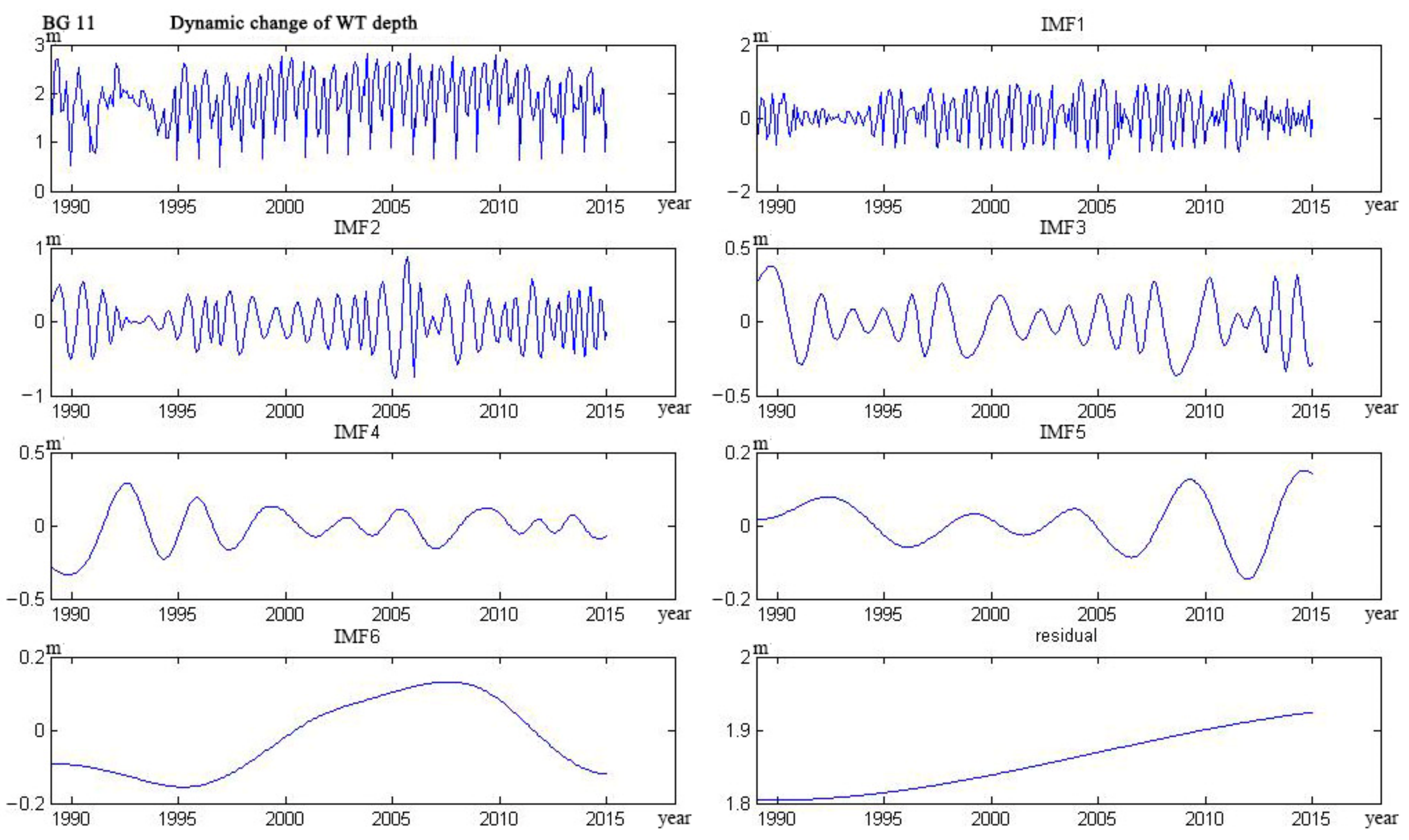
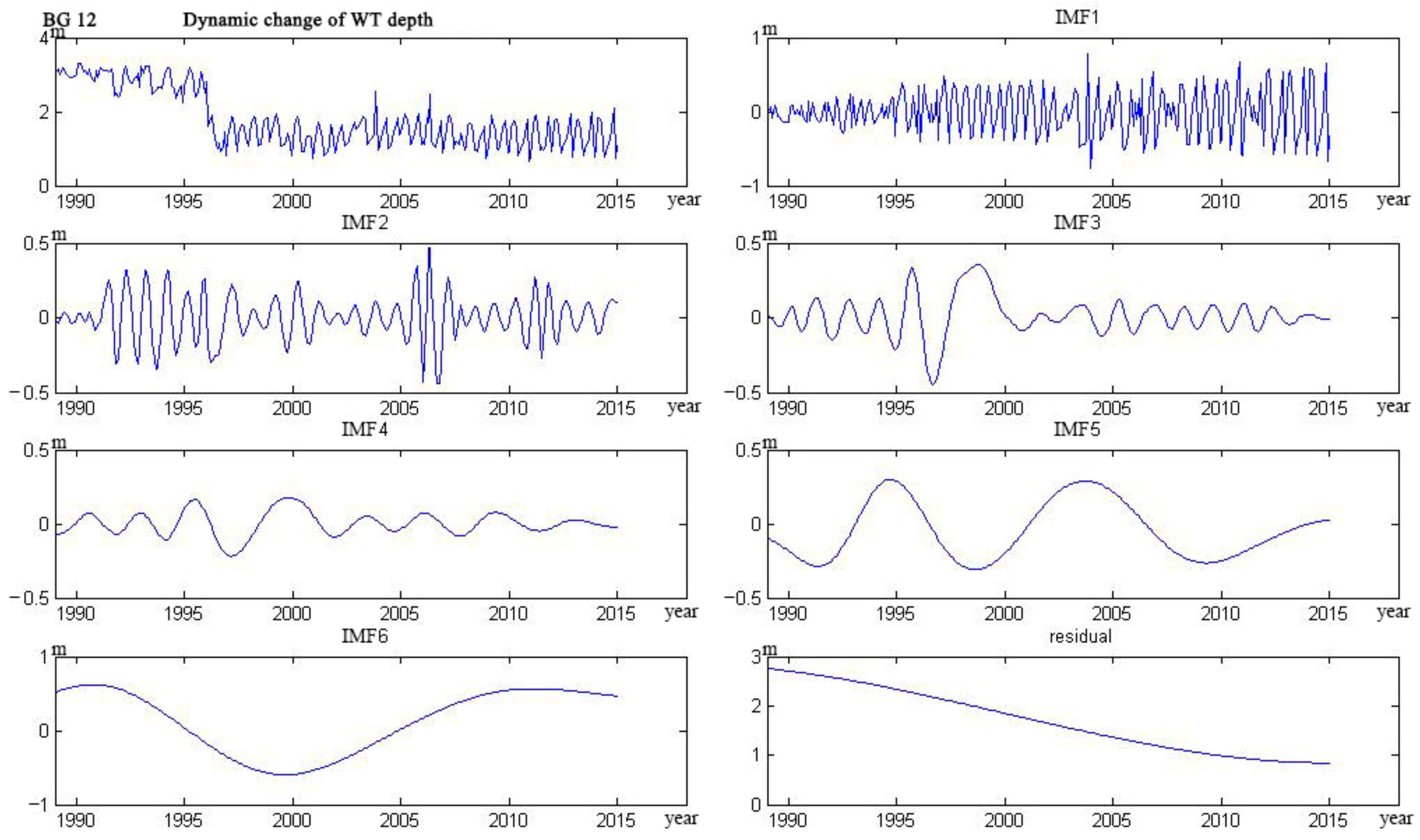
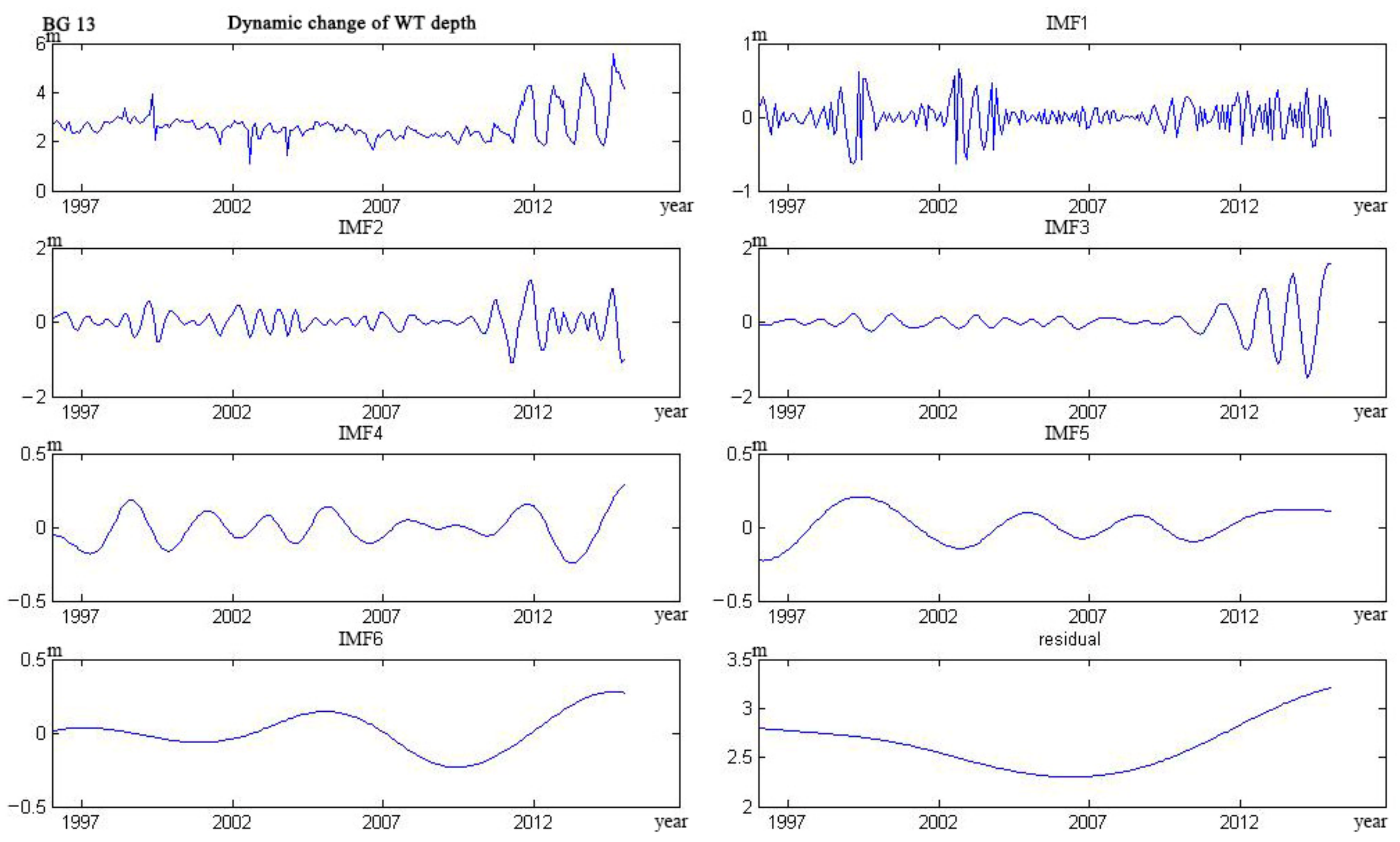
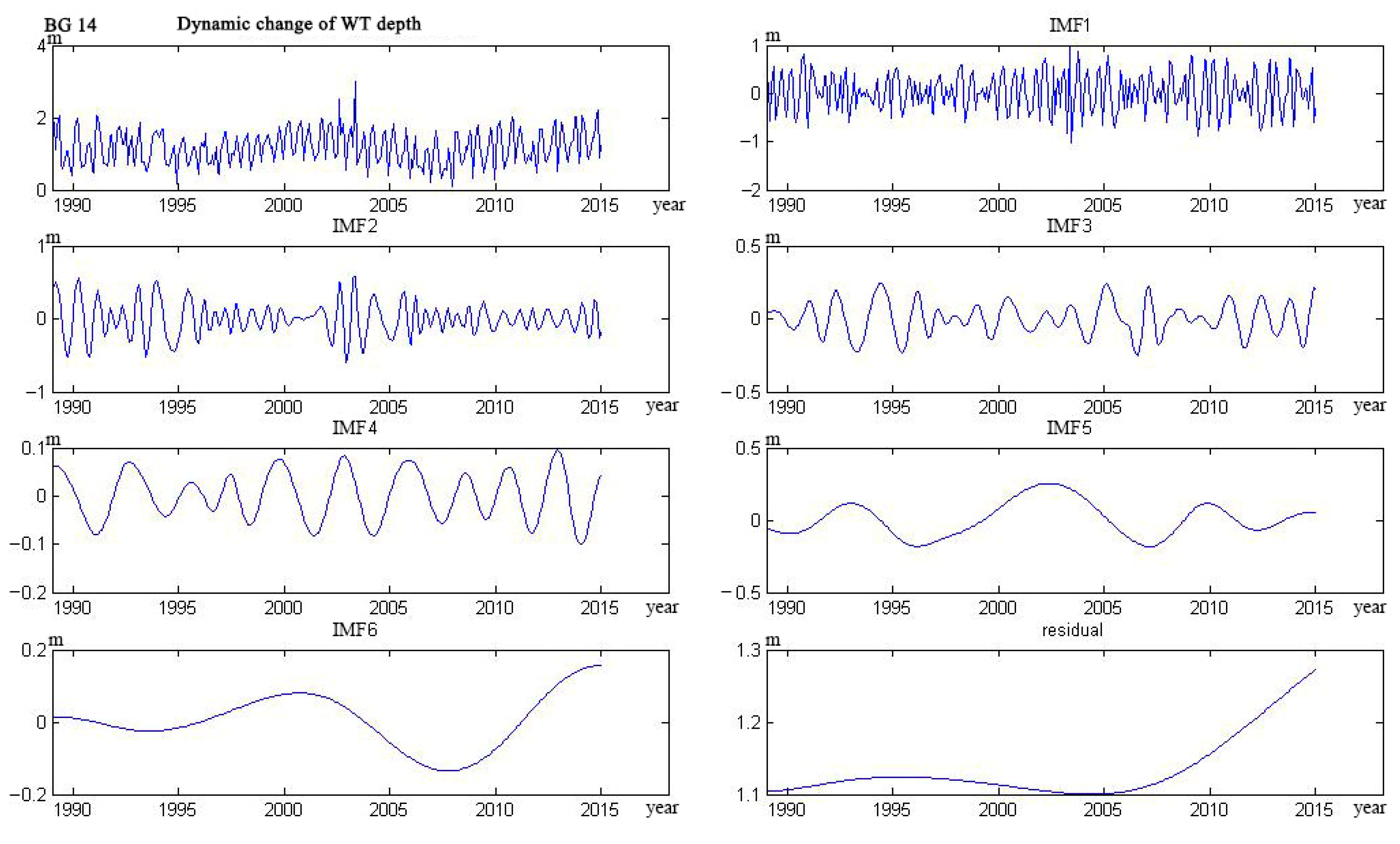
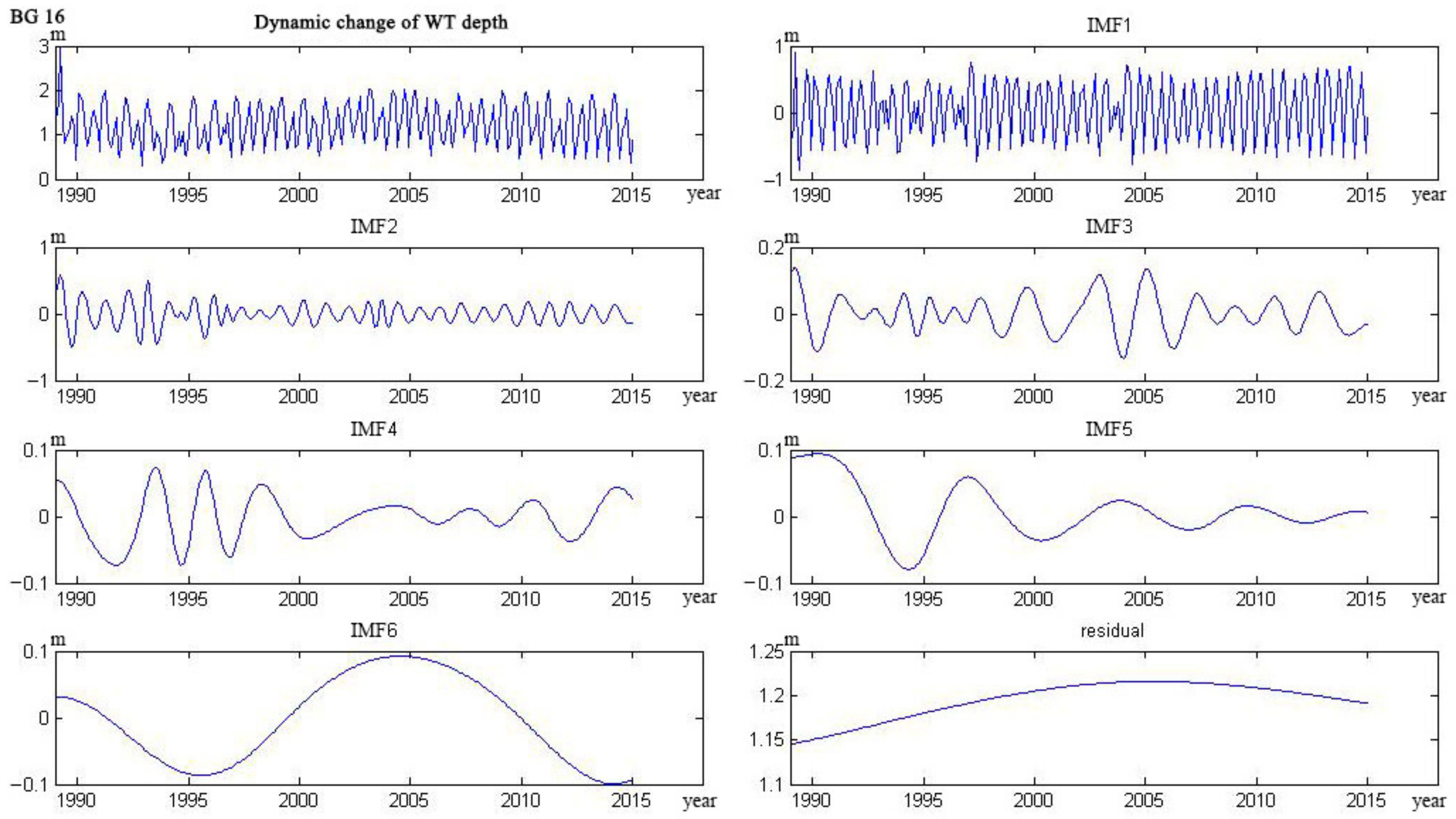
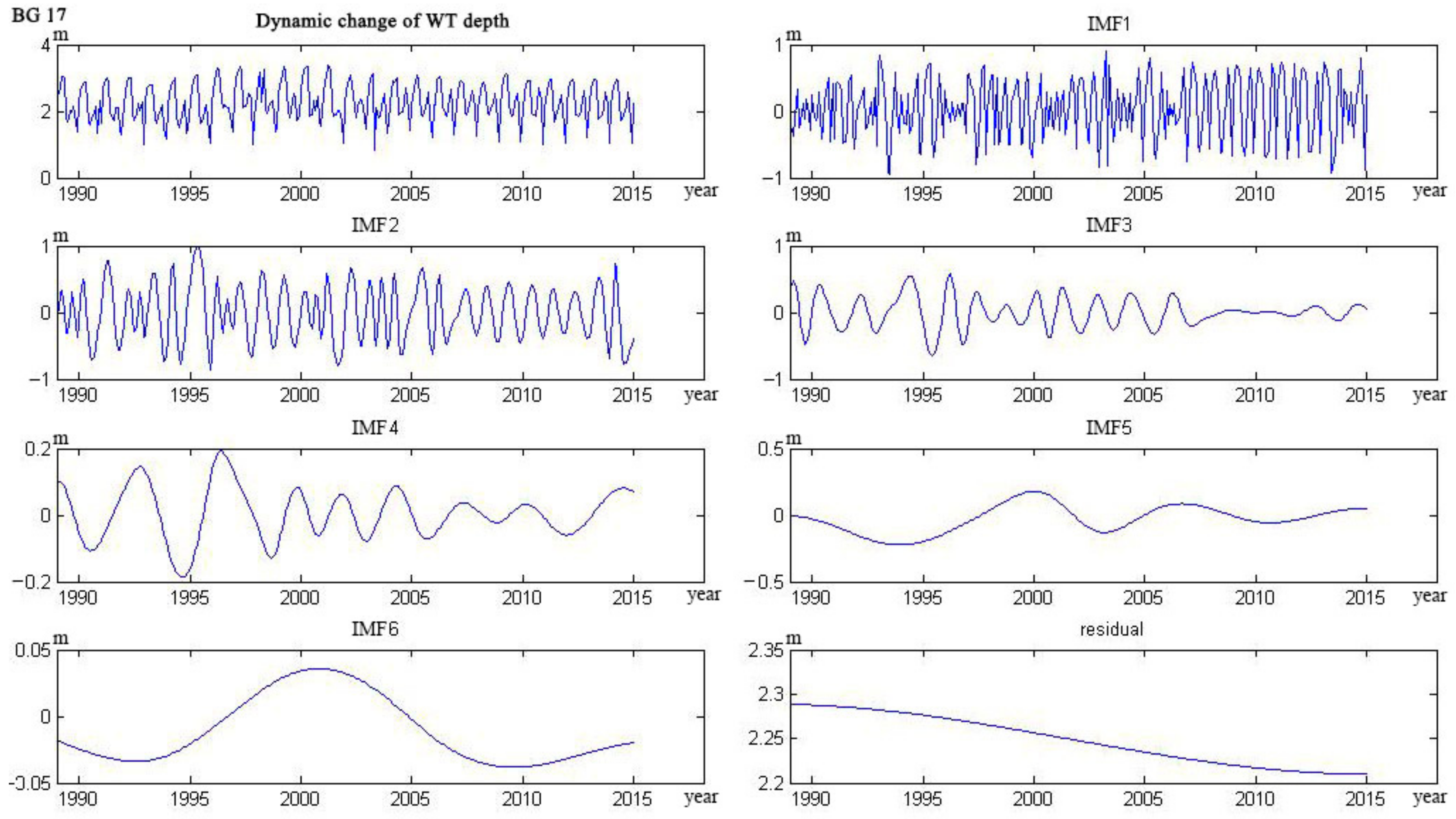
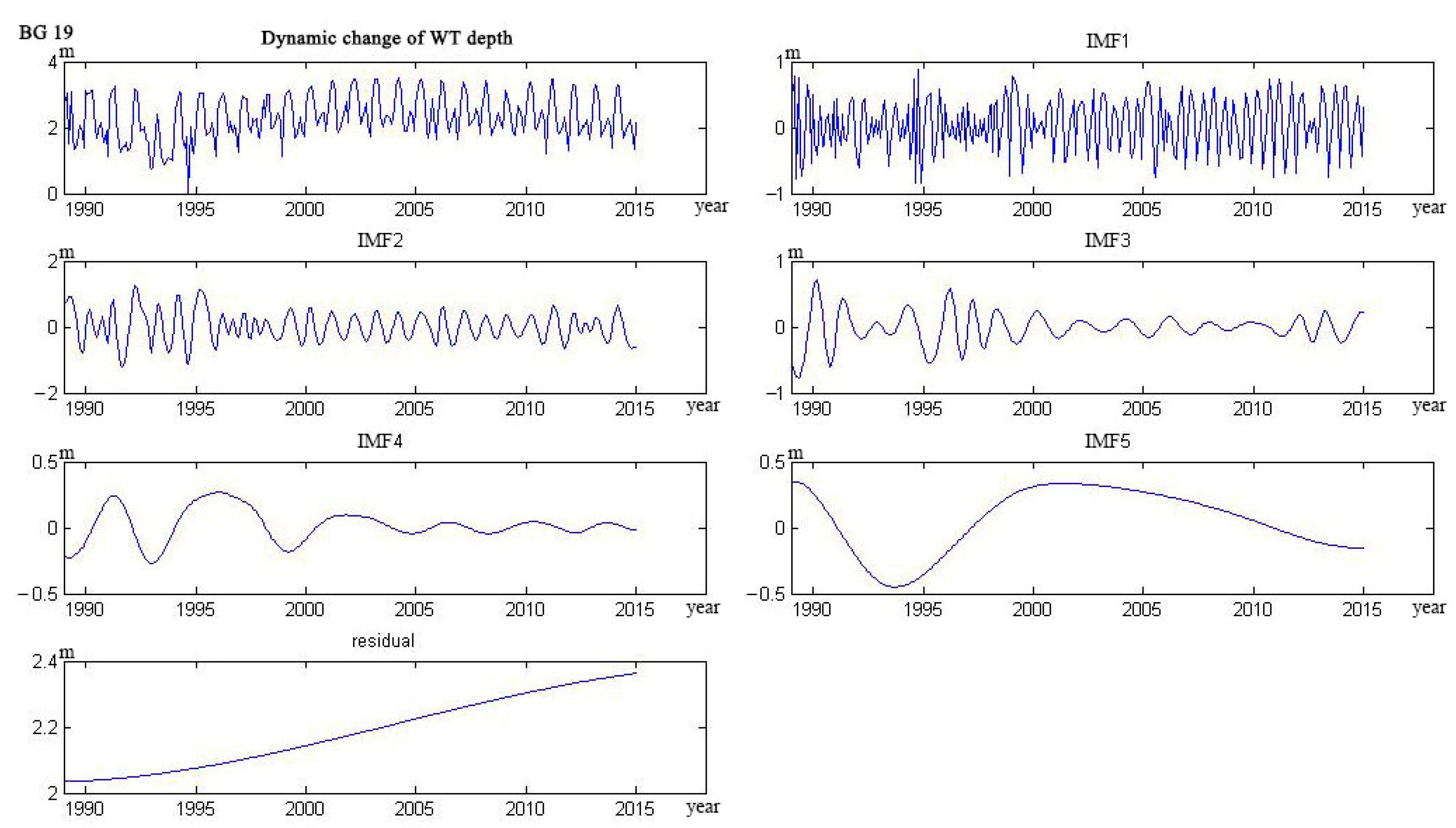
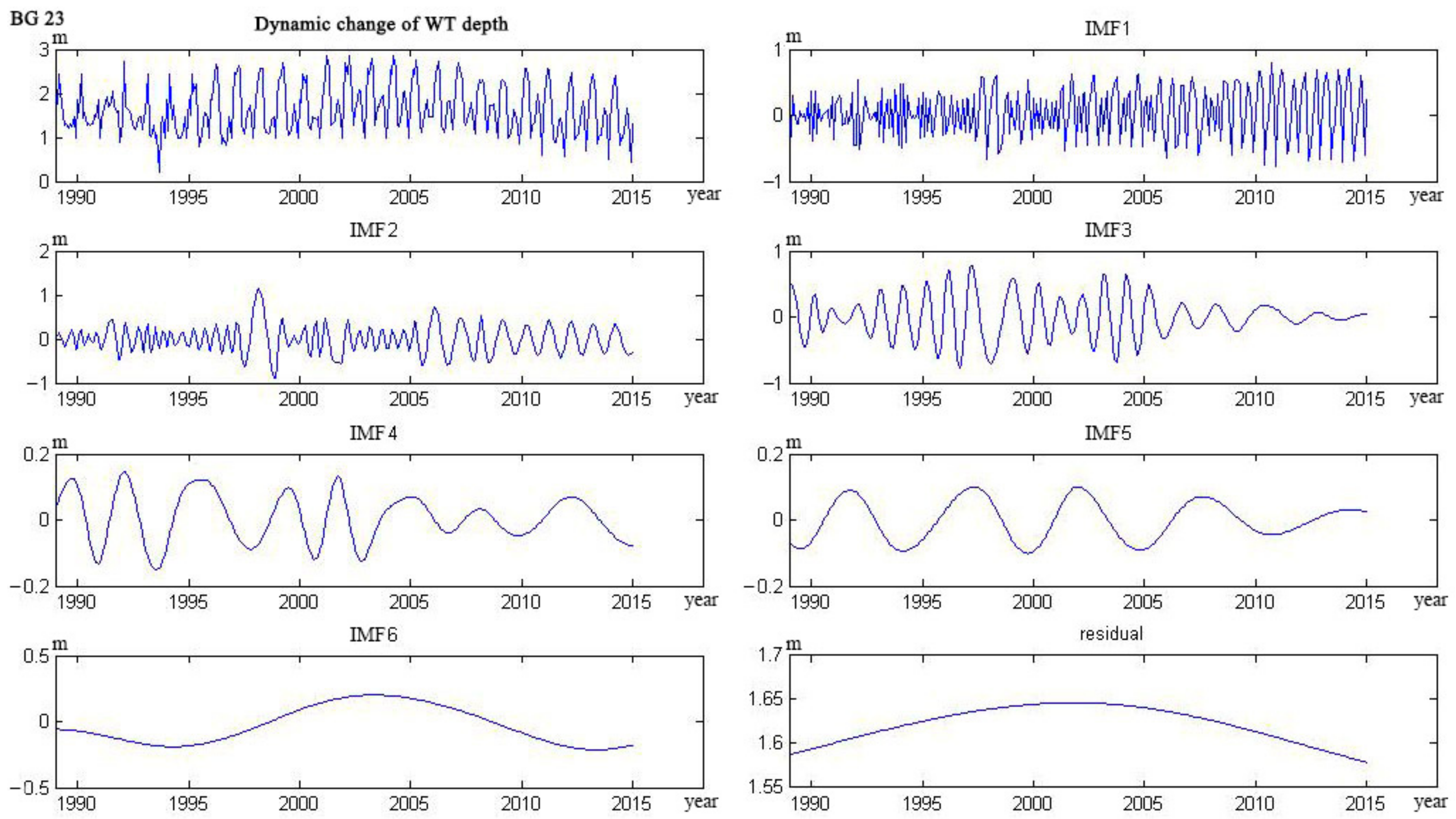

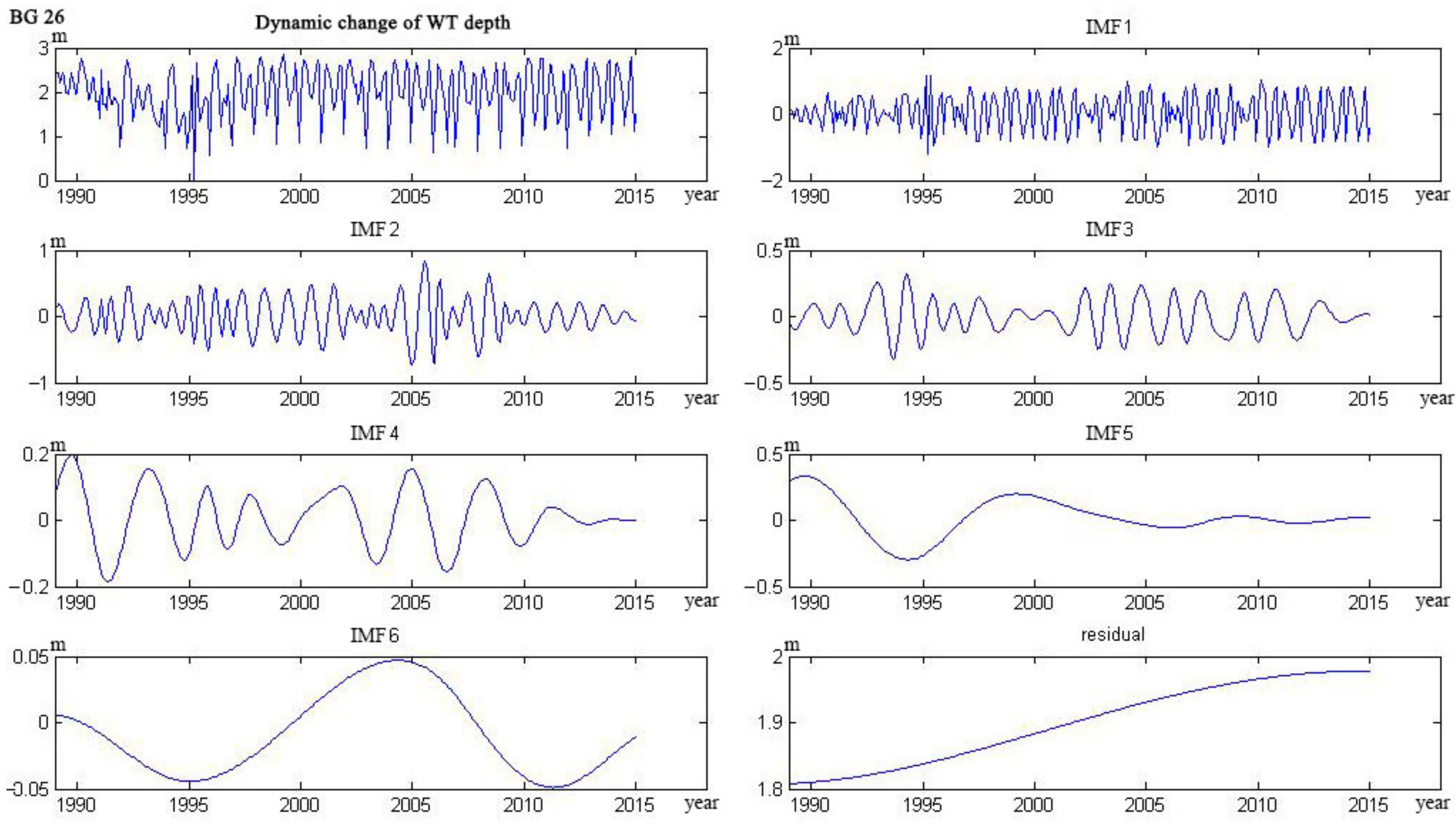
Appendix C

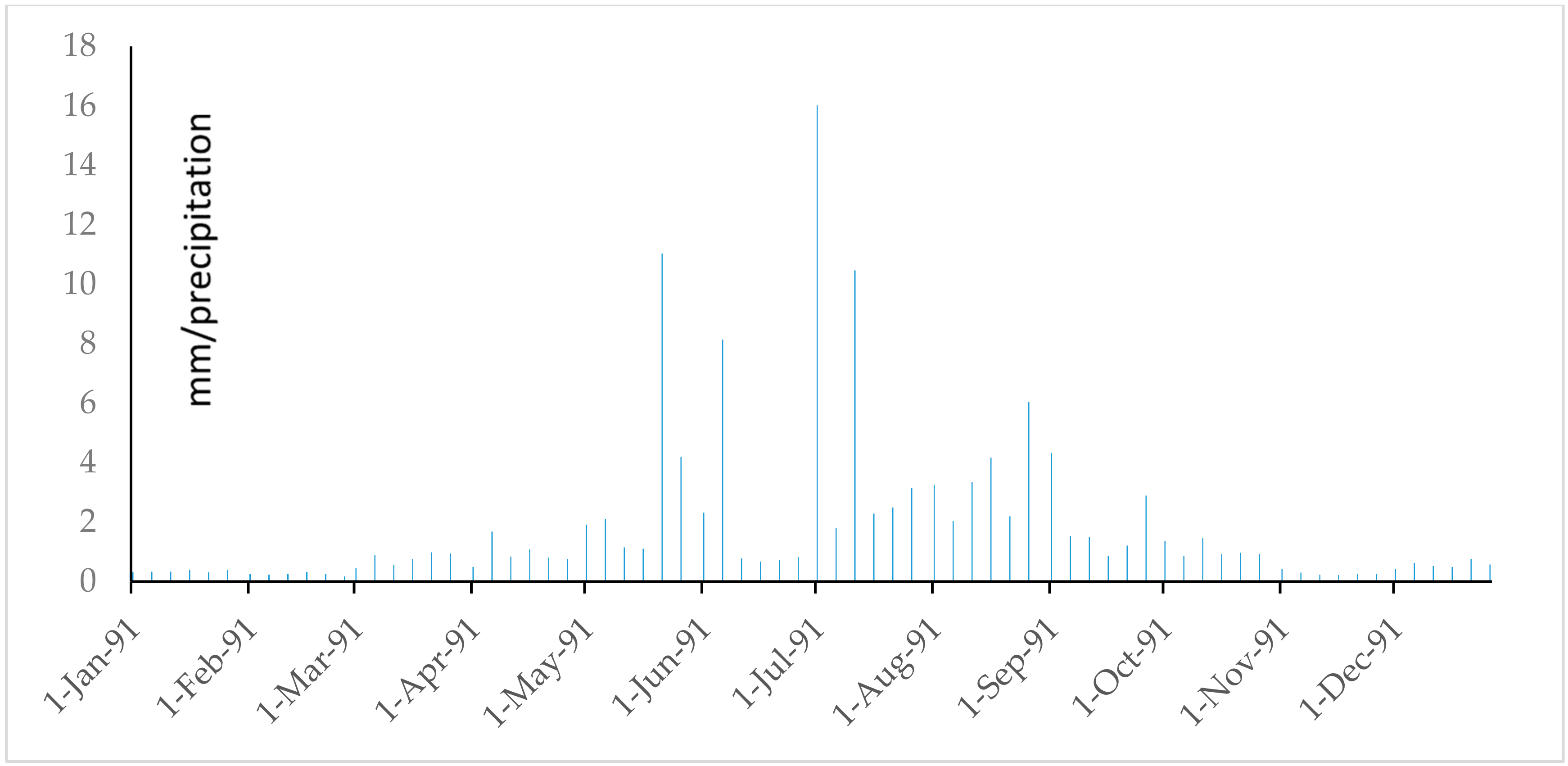
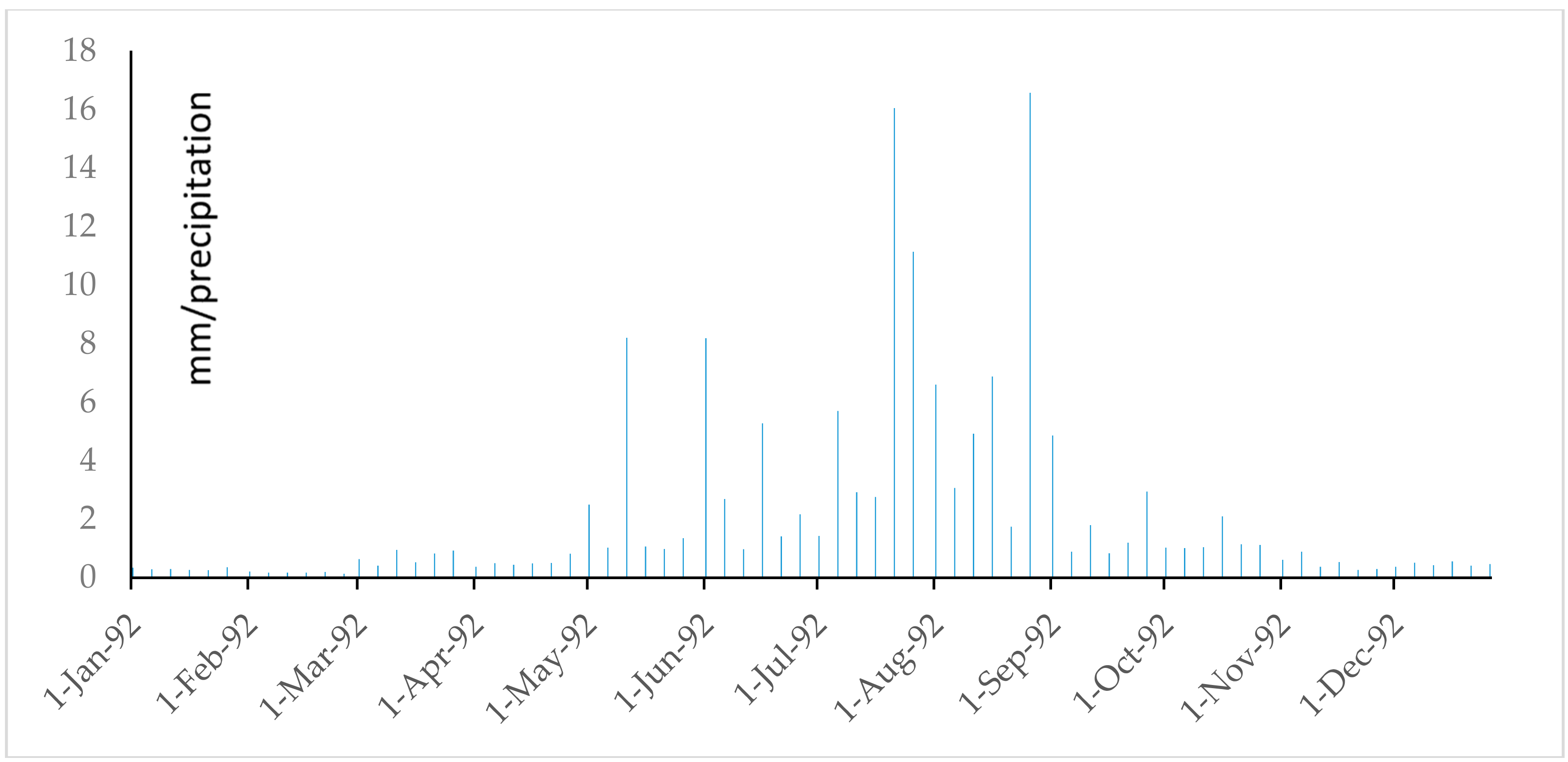
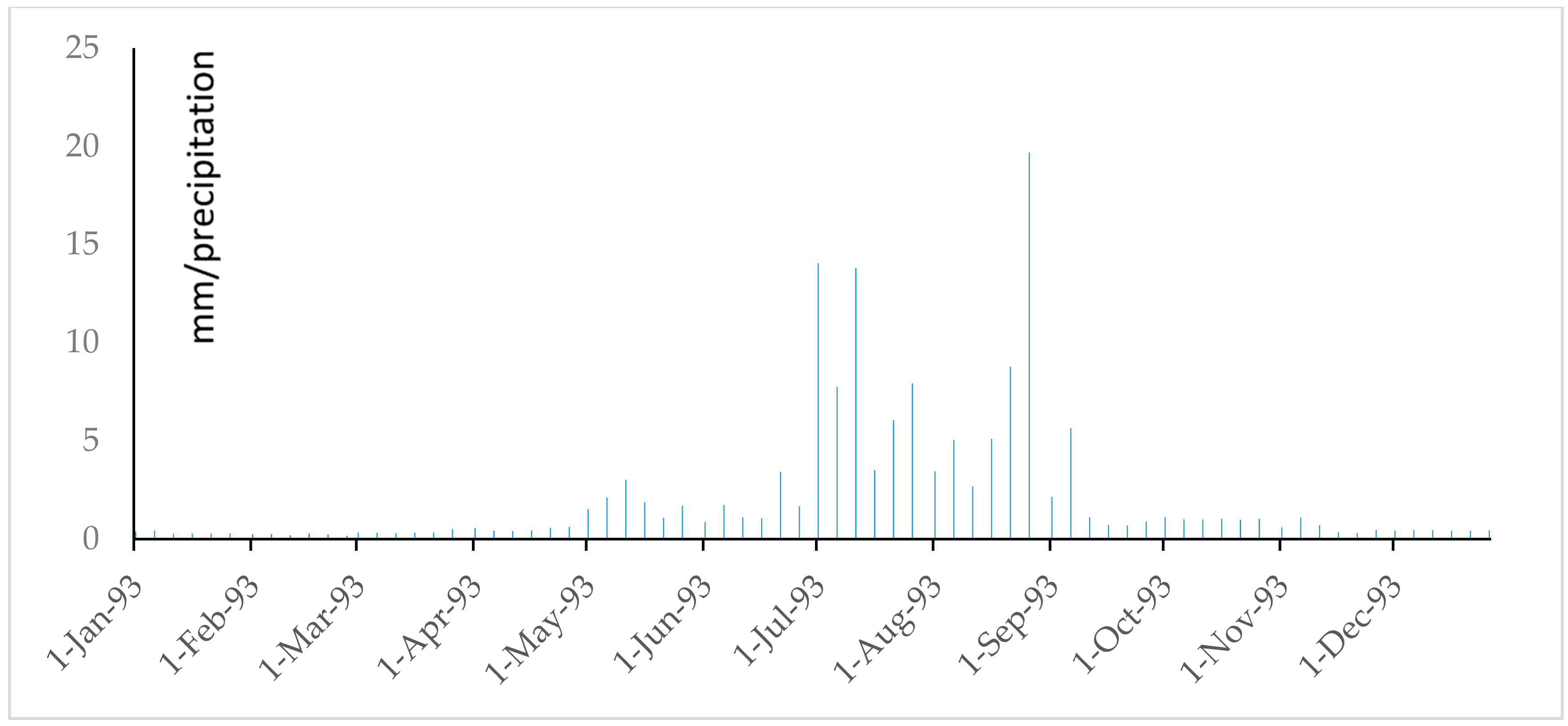
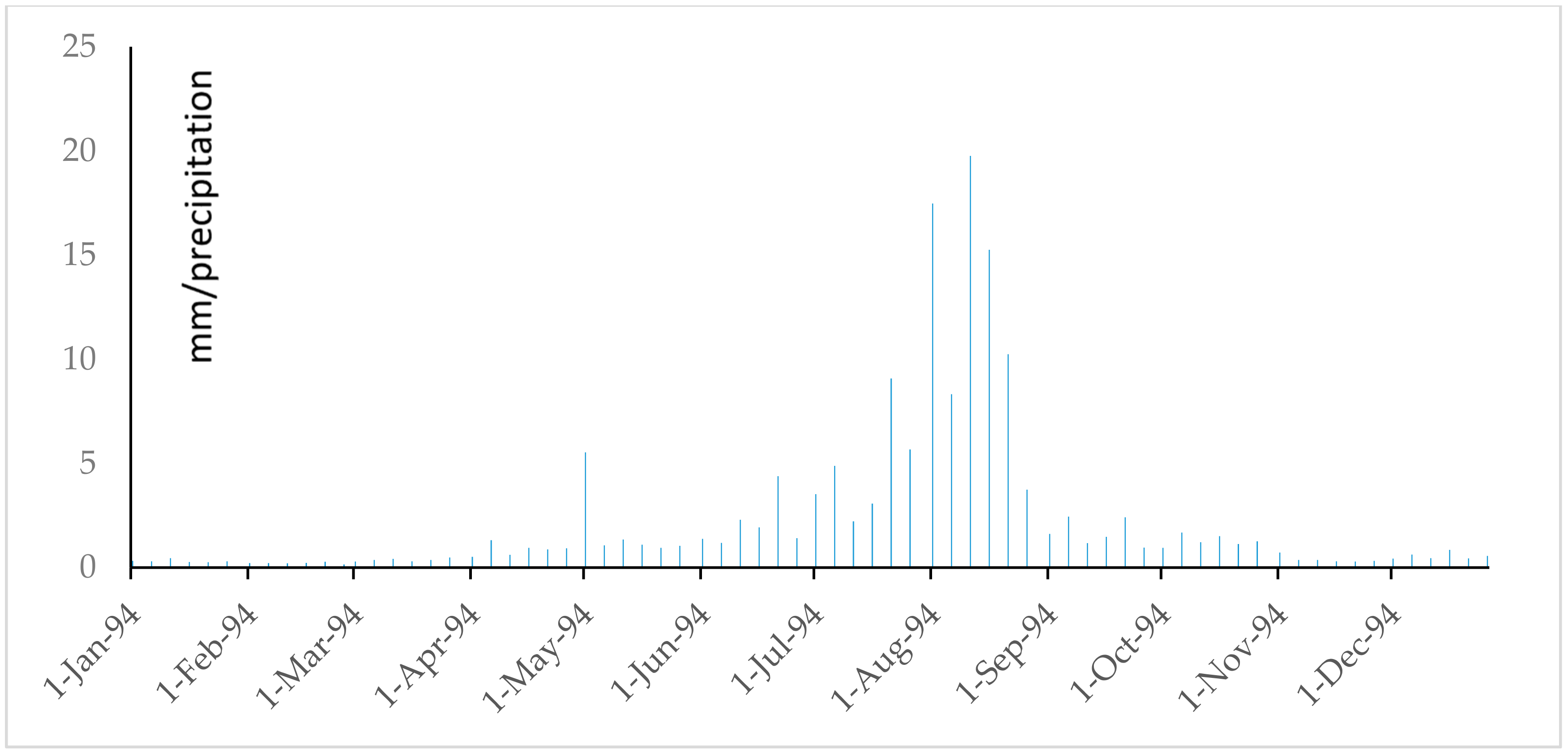

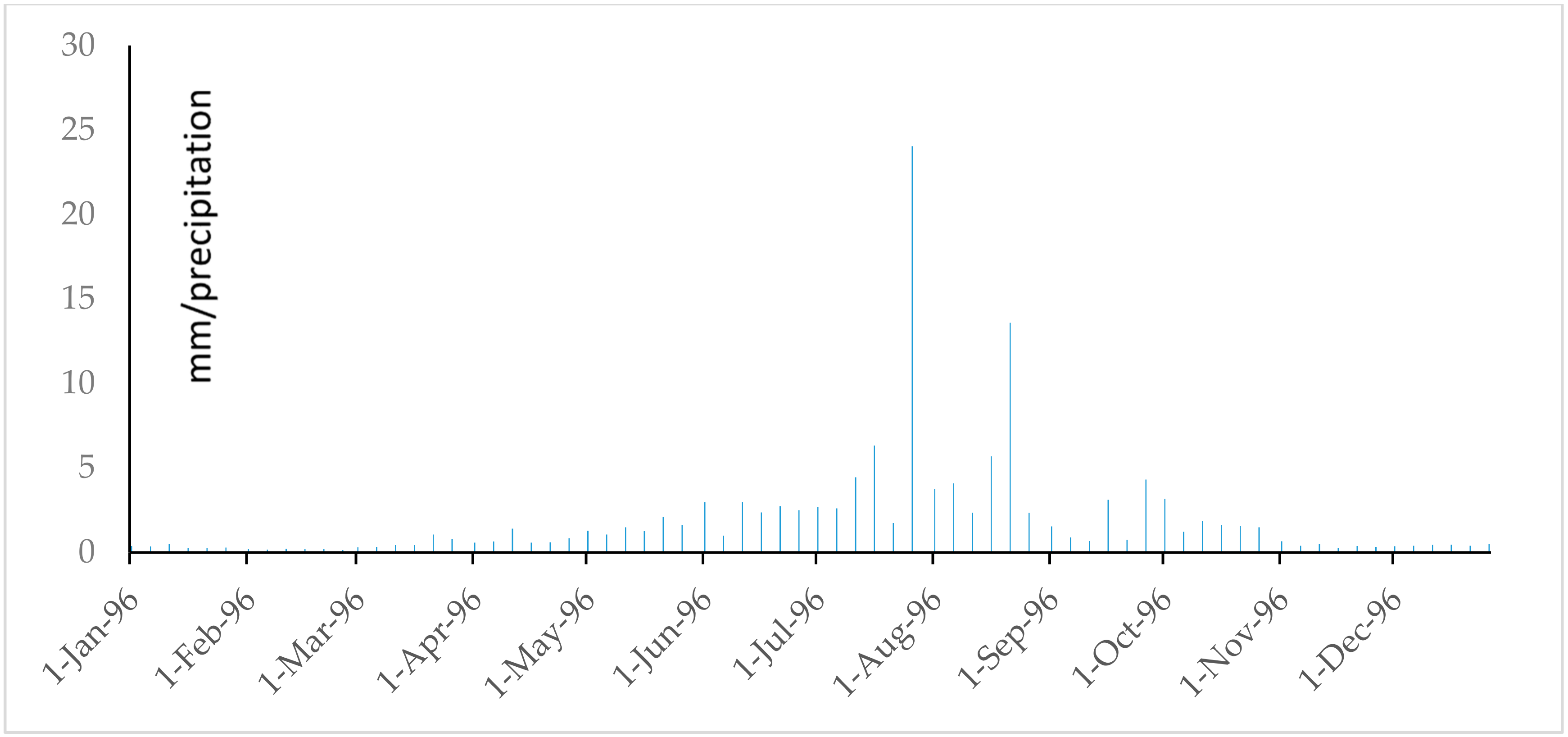
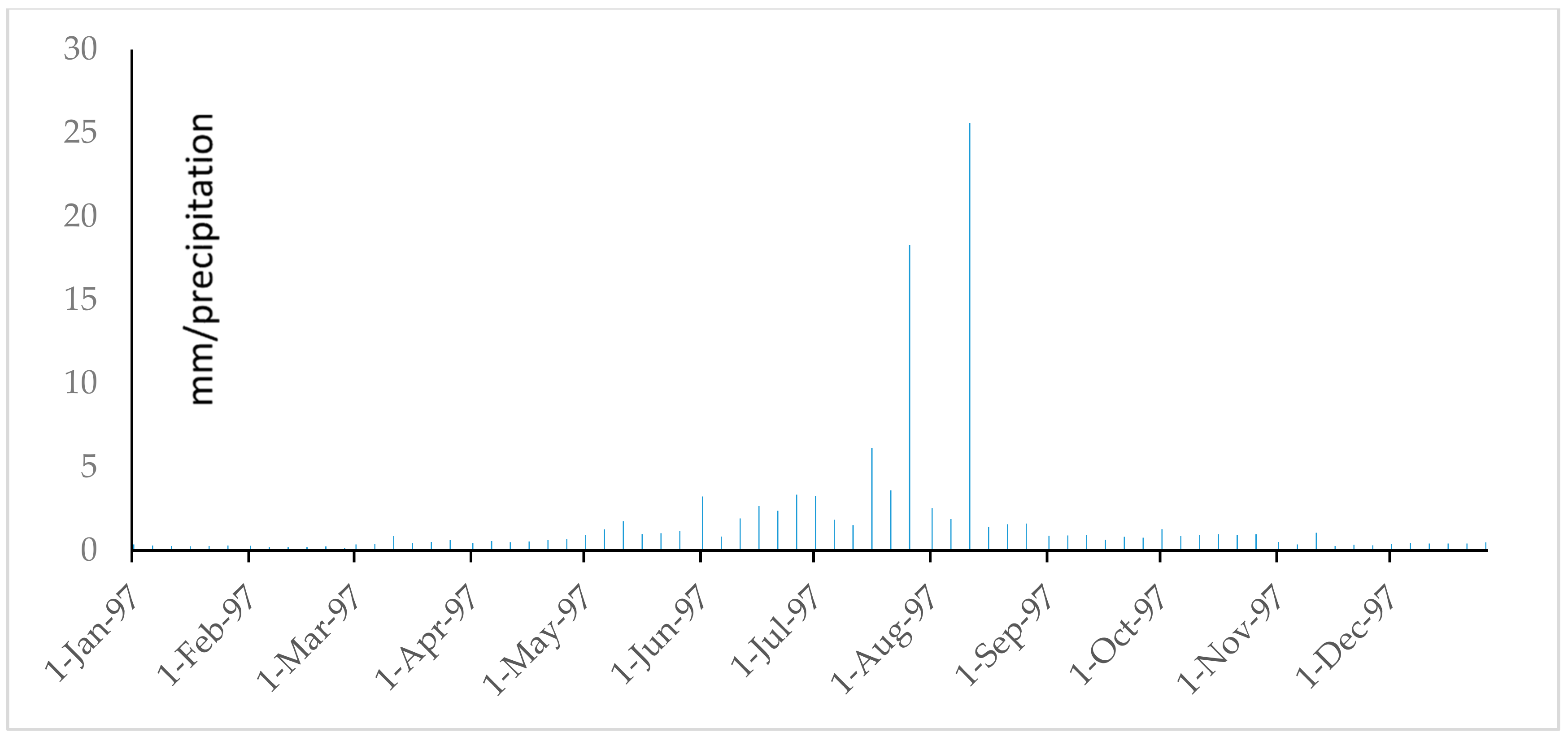
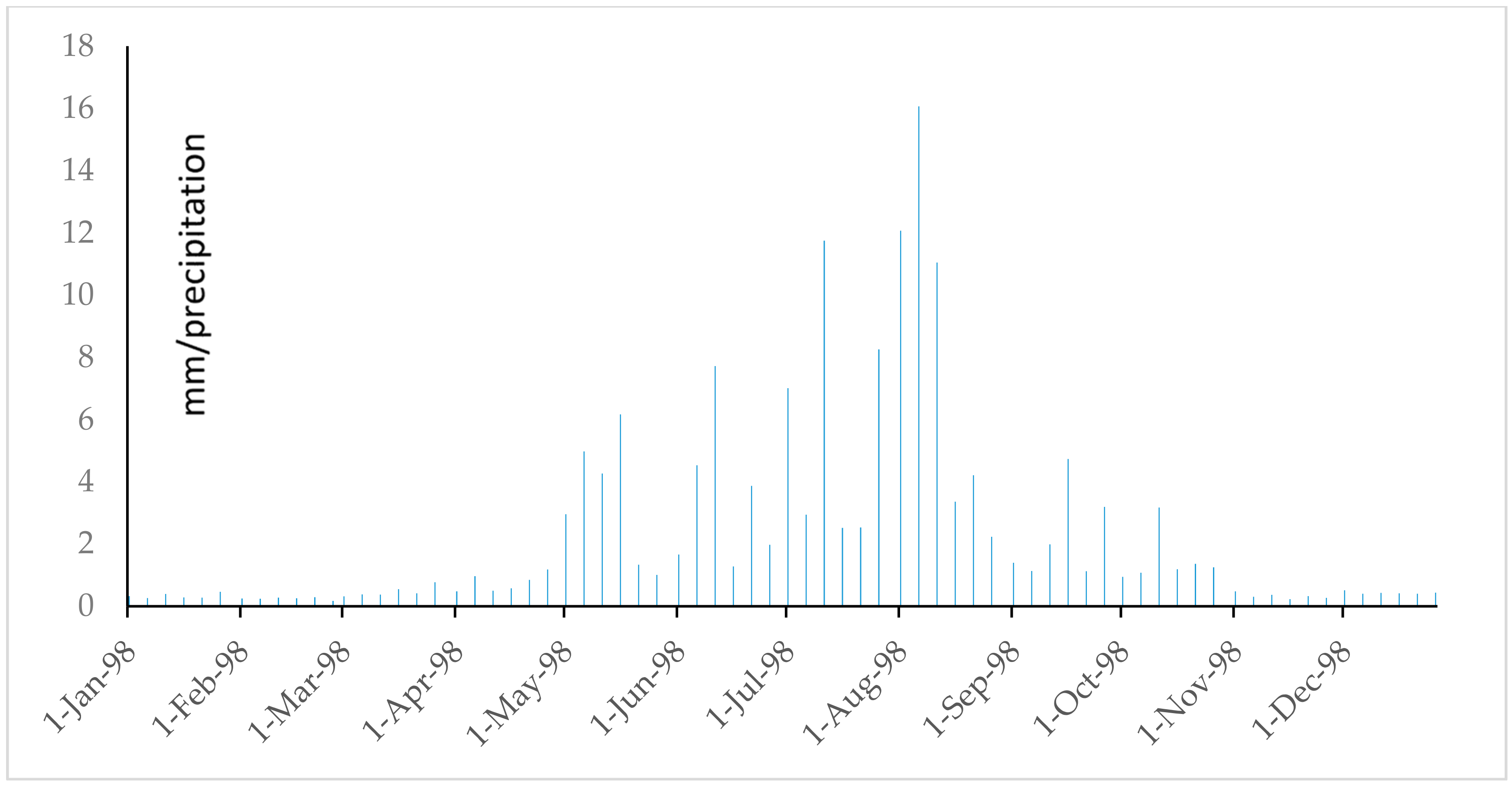

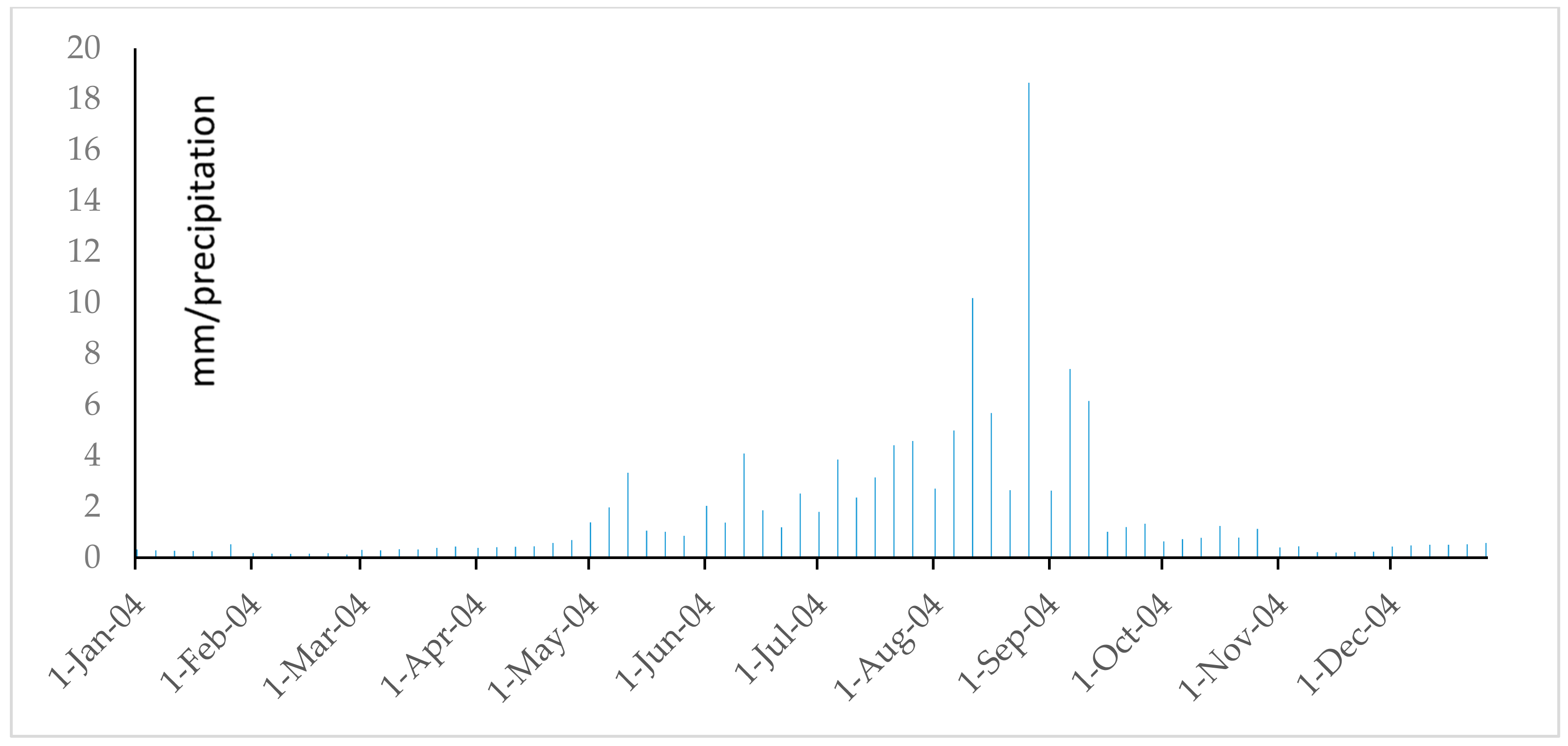
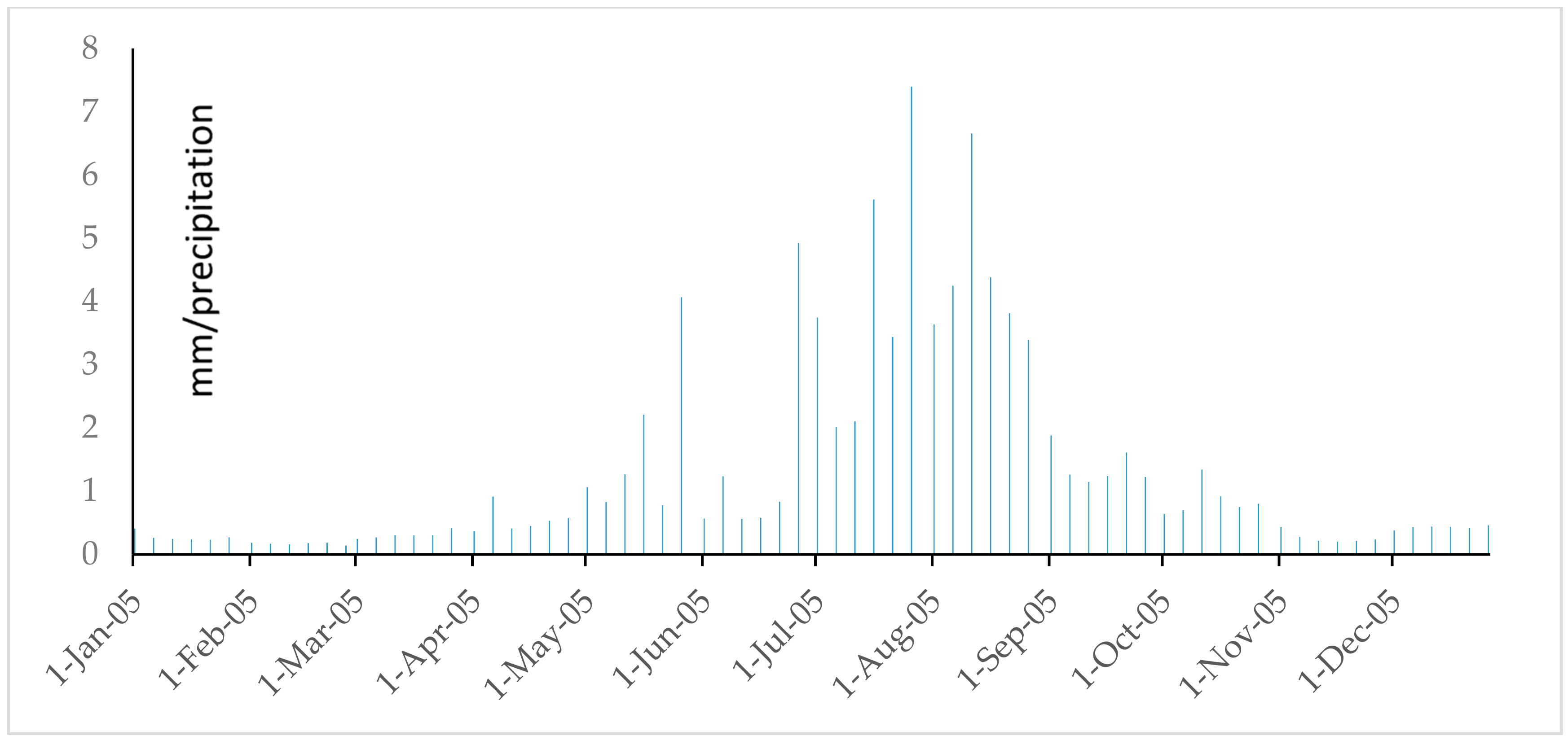
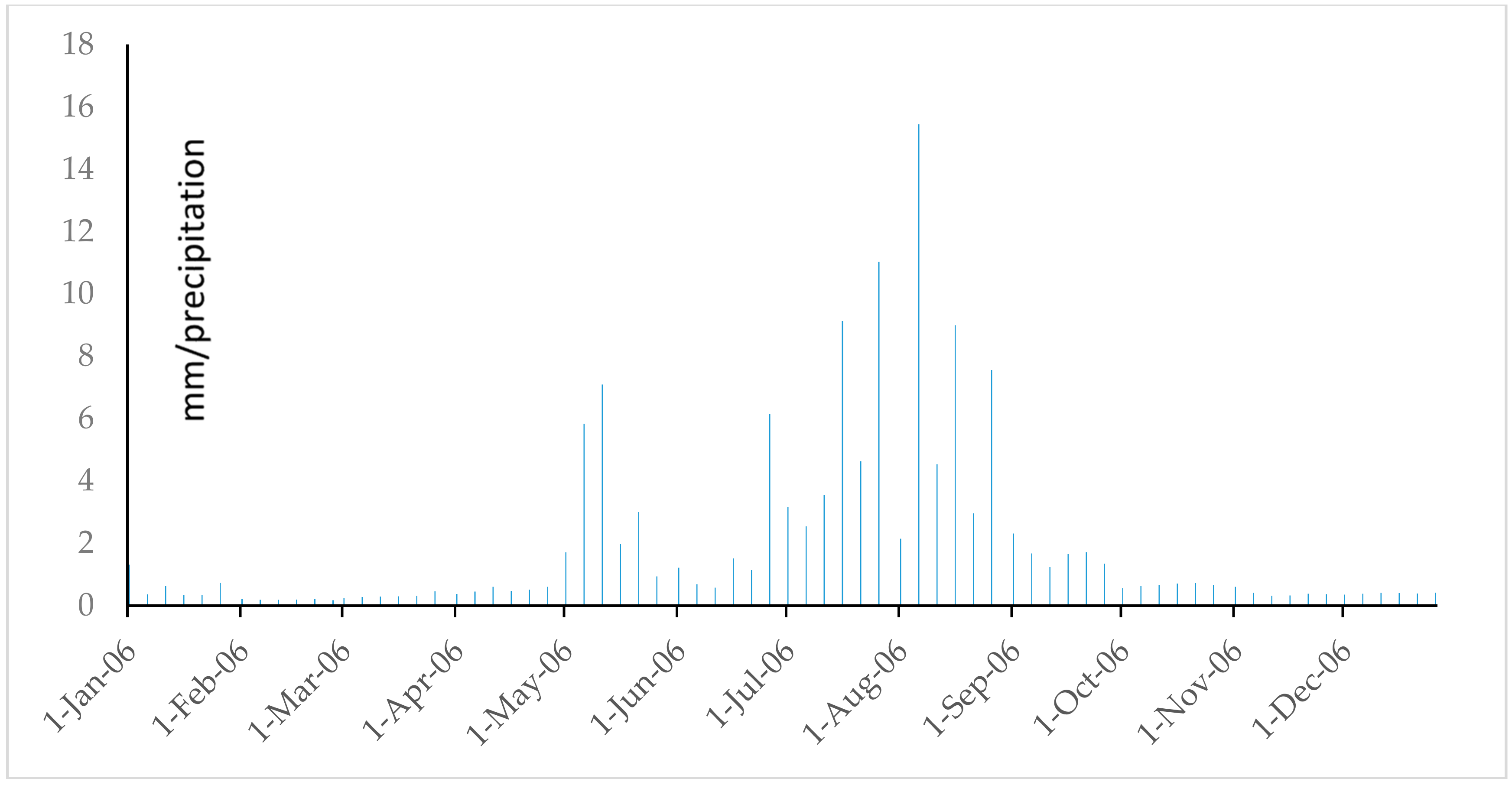
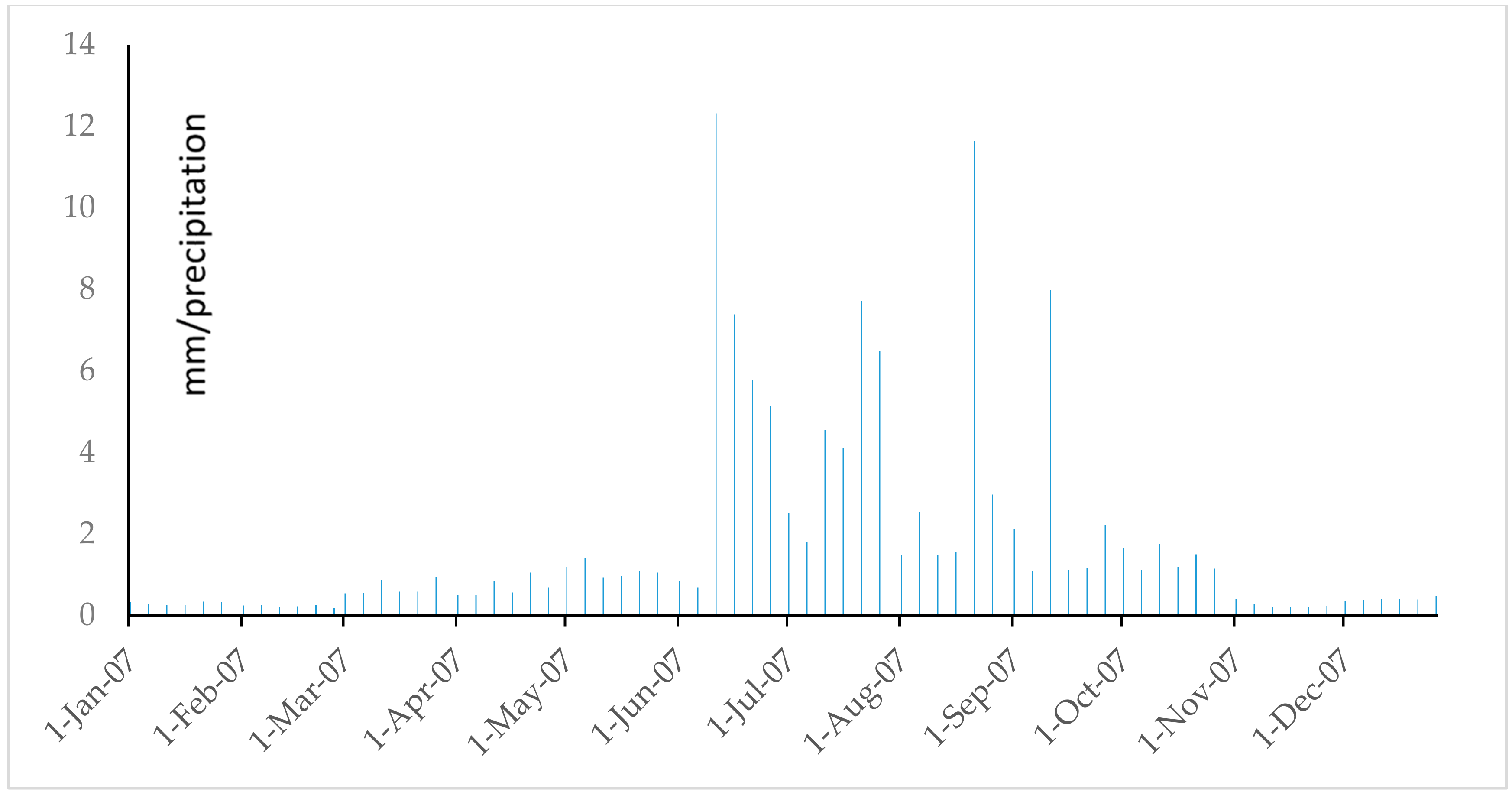
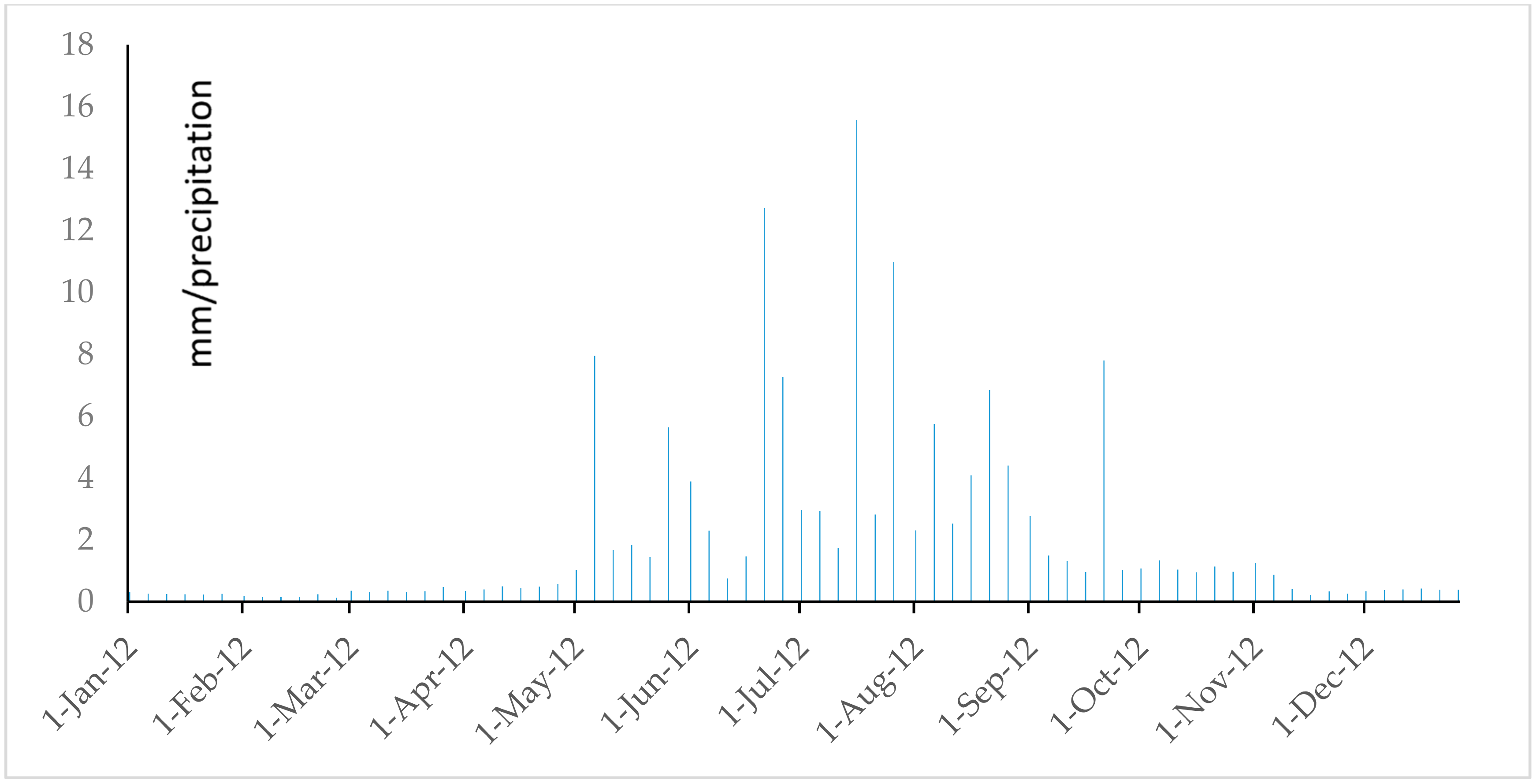
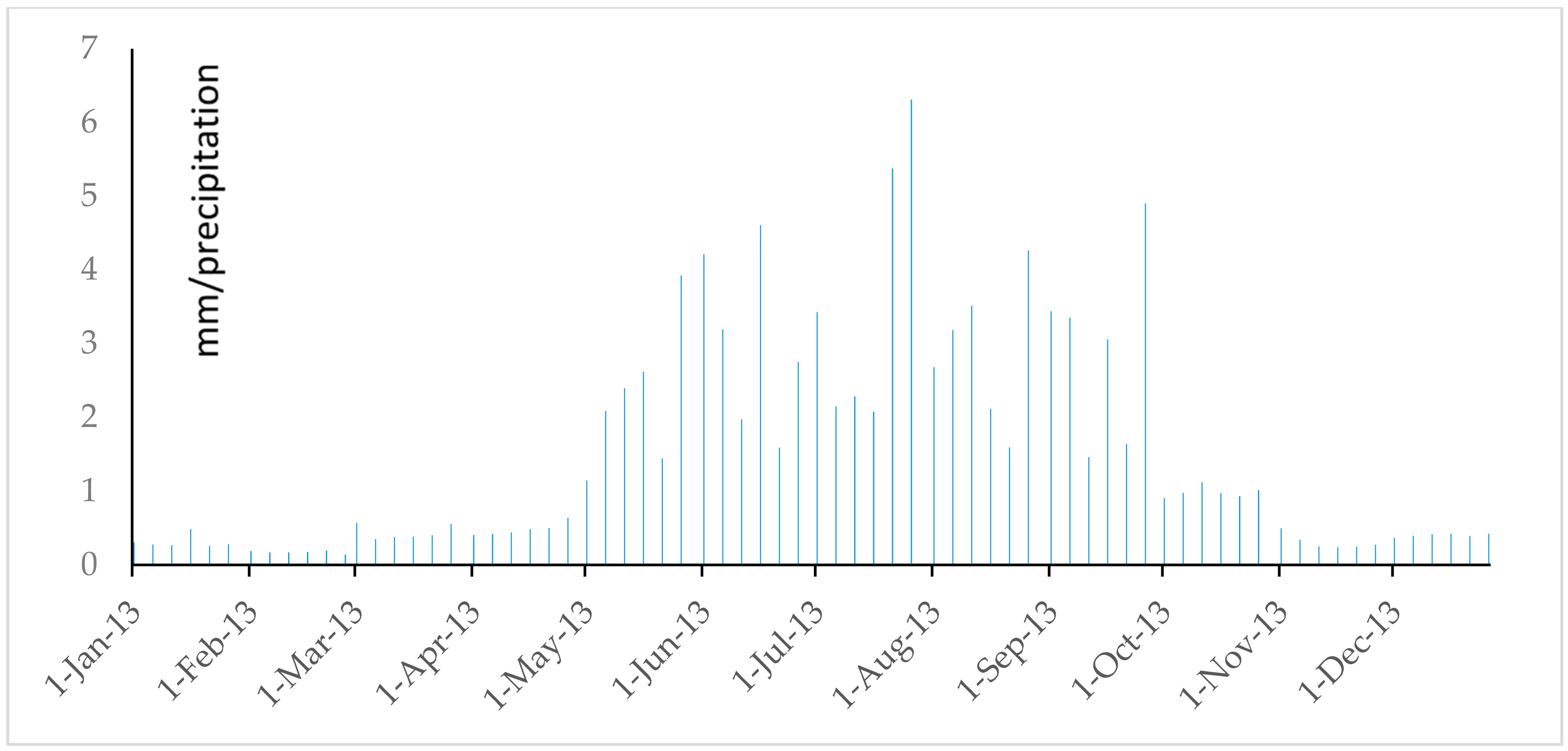
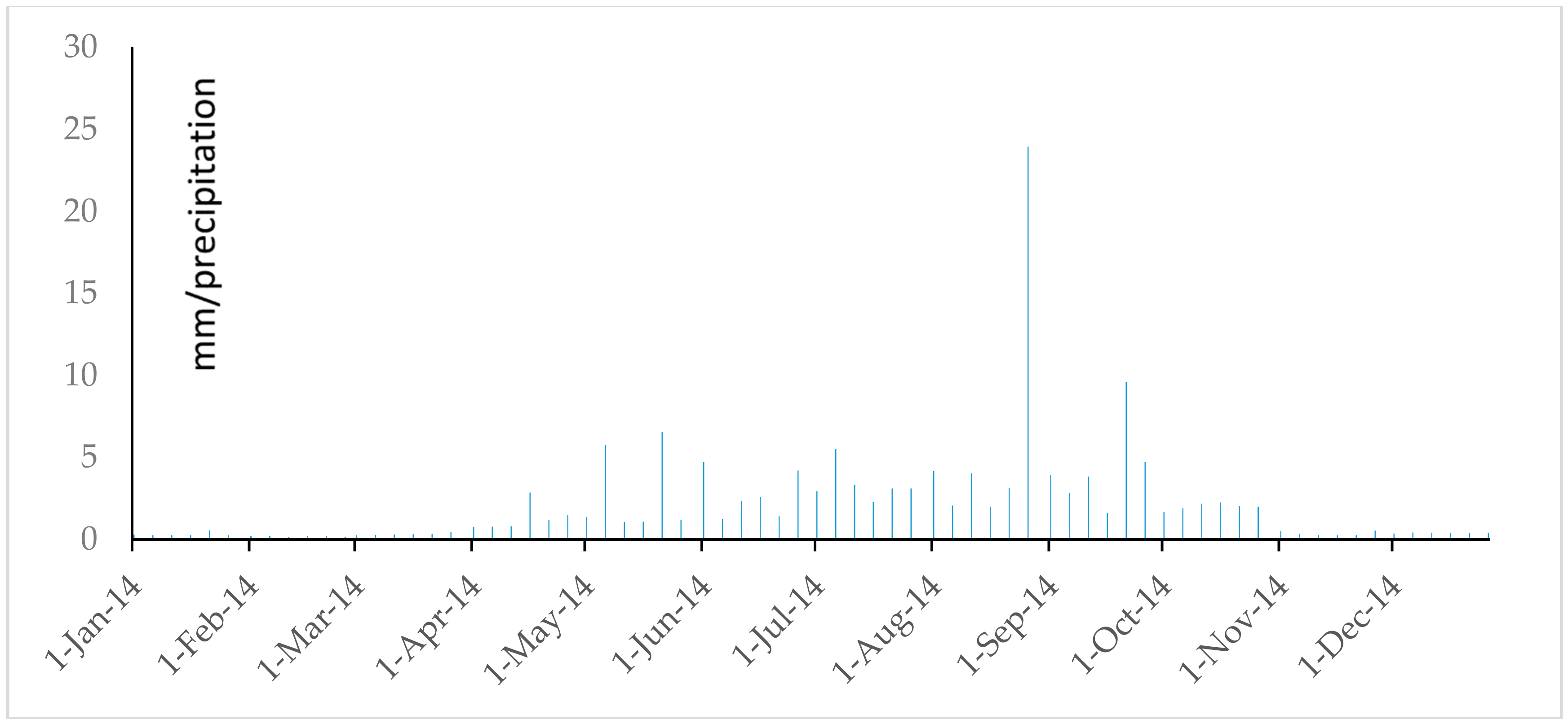

References
- Bestelmeyer, B.T.; Okin, G.S.; Duniway, M.C. Desertification, land use, and the transformation of global drylands. Front. Ecol. Environ. 2016, 13, 28–36. [Google Scholar] [CrossRef]
- Liu, A.; Wang, J.; Liu, Z.; Wang, J. Monitoring desertification in arid and semi-arid areas of China with NOAA-AVHRR and MODIS data. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’05, Seoul, Korea, 25–29 July 2005; pp. 2362–2364. [Google Scholar]
- Varghese, N.; Singh, N.P. Linkages between land use changes, desertification and human development in the Thar Desert Region of India. Land Use Policy 2016, 51, 18–25. [Google Scholar] [CrossRef]
- Yuan, J.; Cohen, M.J.; Kaplan, D.A. Linking metrics of landscape pattern to hydrological process in a lotic wetland. Landsc. Ecol. 2015, 30, 1893–1912. [Google Scholar] [CrossRef]
- Fu, B.J.; Zhao, W.W.; Chen, L.D. Eco-hydrological effects of landscape pattern change. Landsc. Ecol. Eng. 2005, 1, 25–32. [Google Scholar] [CrossRef]
- Han, M.; Zhao, C.; Feng, G. An eco-hydrological approach to predicting regional vegetation and groundwater response to ecological water conveyance in dryland riparian ecosystems. Quat. Int. 2015, 380, 224–236. [Google Scholar] [CrossRef]
- Chen, S.; Chen, B. Urban energy consumption: Different insights from energy flow analysis, input-output analysis and ecological network analysis. Appl. Energy 2015, 138, 99–107. [Google Scholar] [CrossRef]
- Mossman, H.L.; Panter, C.J.; Dolman, P.M. Modelling biodiversity distribution in agricultural landscapes to support ecological network planning. Landsc. Urban Plan. 2015, 141, 59–67. [Google Scholar] [CrossRef]
- Kati, V.; Hovardas, T.; Dieterich, M.; Ibisch, P.L.; Mihok, B.; Selva, N. The challenge of implementing the European network of protected areas Natura 2000. Conserv. Biol. 2015, 29, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Schaubroeck, T.; Staelens, J.; Verheyen, K. Improved ecological network analysis for environmental sustainability assessment; a case study on a forest ecosystem. Ecol. Model. 2012, 247, 144–156. [Google Scholar] [CrossRef]
- Fu, Q.; Song, J.; Mao, F. Evaluation and construction of wetland ecological network in Qingdao City. Acta Ecol. Sin. 2012, 32, 3670–3680. [Google Scholar]
- Kyushik, O.; Dongwoo, L.; Changsug, P. Urban ecological network planning for sustainable landscape management. J. Urban Technol. 2011, 18, 39–59. [Google Scholar]
- Matthew, S.D.; Travis, B.R.; Gregory, H.A.; Jocelyn, L.A. The world’s largest wilderness protection network after 50 years: An assessment of ecological system representation in the U.S. National Wilderness Preservation System. Biol. Conserv. 2015, 184, 431–438. [Google Scholar]
- Zhang, L.; Zhao, M.; Gao, Y. Estimation of vegetation ecological water requirement in arid areas based on neural network. In Proceedings of the International Symposium on Computational Intelligence and Design, Hangzhou, China, 29–31 October 2010; pp. 28–30. [Google Scholar]
- Liu, H.L.; Willems, P.; Bao, A.M.; Wang, L.; Chen, X. Effect of climate change on the vulnerability of a socio-ecological system in an arid area. Glob. Planet. Chang. 2016, 137, 1–9. [Google Scholar] [CrossRef]
- Mo, W.B.; Wang, Y.; Zhang, Y.X.; Zhuang, D.F. Impacts of road network expansion on landscape ecological risk in a megacity, China: A case study of Beijing. Sci. Total Environ. 2017, 574, 1000–1011. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Bojie, F.U.; Zhao, W. Source-sink landscape theory and its ecological significance. Acta Ecol. Sin. 2008, 3, 131–136. [Google Scholar] [CrossRef]
- Olagunju, T.E. Drought, desertification and the Nigerian environment: A review. J. Ecol. Natl. Environ. 2015, 7, 196–209. [Google Scholar] [CrossRef]
- Mahamane, M.; Volker, H.; Alfred, S.; Jude, N.K. Fragmentation rate and landscape structure of the Tillabry landscape (Sahel region) with reference to desertification. J. Geogr. Reg. Plan. 2016, 9, 77–86. [Google Scholar] [CrossRef]
- Blanco-Libreros, J.F.; Estrada-Urrea, E.A. Mangroves on the edge: Anthrome-dependent fragmentation influences ecological condition (Turbo, Colombia, Southern Caribbean). Diversity 2015, 7, 206–228. [Google Scholar] [CrossRef]
- Haddad, N.M.; Brudvig, L.A.; Clobert, J.; Davies, K.F.; Gonzalez, A.; Holt, R.D.; Lovejoy, T.E.; Sexton, J.O.; Austin, M.P.; Collins, C.D.; et al. Habitat fragmentation and its lasting impact on earth’s ecosystems. Sci. Adv. 2015, 1. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Ma, L.; Liu, J.; Zhuang, Z.; Huang, Q.; Li, M. Constructing ecological networks based on habitat quality assessment: A case study of Changzhou, China. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Liu, Y. Connecting regional landscapes by ecological networks in the greater Pearl River Delta. Landsc. Ecol. Eng. 2016, 13, 265–278. [Google Scholar] [CrossRef]
- Ding, W.; Tan, X.; Yuan, L. Construction of ecological network for urban green space system from the perspective of landscape ecology: A case study of Wanzhou District, Chongqing Municipality. J. Landsc. Res. 2016, 8, 41–48. [Google Scholar]
- Chen, J.Y.; Yin, H.W.; Kong, F.H.; Yao, G.P. The complex eco-network development around Taihu Lake, China. Acta Ecol. Sin. 2015, 35, 3113–3123. [Google Scholar]
- Zhang, X.; Guo, X.; Jing, G.; Xie, H. Research of improved shortest path algorithm in campus GIS. Open Cybern. Syst. J. 2015, 9, 1060–1063. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using Landsat TM to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar] [CrossRef]
- Panzacchi, M.; Van, M.B.; Strand, O.; Saerens, M.; Kivimäki, I.; St Clair, C.C.; Herfindal, I.; Boitani, L. Predicting the continuum between corridors and barriers to animal movements using step selection functions and randomized shortest paths. J. Anim. Ecol. 2015, 85, 32–42. [Google Scholar] [CrossRef] [PubMed]
- Soininen, J. Spatial structure in ecological communities—A quantitative analysis. Oikos 2015, 8, 51–60. [Google Scholar] [CrossRef]
- Pierik, M.E.; Dell’Acqua, M.; Confalonieri, R.; Bocchi, S.; Gomarasca, S. Designing ecological corridors in a fragmented landscape: A fuzzy approach to circuit connectivity analysis. Ecol. Indic. 2016, 67, 807–820. [Google Scholar] [CrossRef]
- Li, F.; Ye, Y.P.; Song, B.; Wang, R.S. Evaluation of urban suitable ecological land based on the minimum cumulative resistance model: A case study from Changzhou, China. Ecol. Model. 2015, 318, 194–203. [Google Scholar] [CrossRef]
- Fath, B.D.; Scharler, U.M.; Ulanowicz, R.E. Ecological network analysis: Network construction. Ecol. Model. 2007, 208, 49–55. [Google Scholar] [CrossRef]
- Yuyao, Y.E.; Yongxian, S.U.; Zhang, H.O. Construction of an ecological resistance surface model and its application in urban expansion simulations. J. Geogr. Sci. 2015, 25, 211–224. [Google Scholar]
- Meng, J.; Wang, X.; Zhen, Z. Integrated landscape pattern optimization in arid region: A case study of middle reaches of Heihe River. Acta Sci. Nat. Univ. Pekin. 2017, 53, 451–461. [Google Scholar]
- D’Alelio, D.; Libralato, S.; Wyatt, T.; Ribera, D.M. Ecological-network models link diversity, structure and function in the plankton food-web. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.F.; Yin, L.K.; Cao, Q.M.; Wang, Q. Vegetation information extraction and analysis of Xinjiang Altay two-river source nature reserve. Arid Land Geogr. 2016, 39, 843–850. [Google Scholar]
- Ling, H.; Jia, Q.; Chao, L.; Li, Z.; Hao, X. Land use pattern simulation based on ecosystem service value and ecological security pattern. Trans. Chin. Soc. Agric. Eng. 2016, 32, 275–584. [Google Scholar]
- Sun, D.; Yu, X.; Liu, X.; Li, B. A new artificial oasis landscape dynamics in semi-arid Hongsipu region with decadal agricultural irrigation development in Ning Xia, China. Earth Sci. Inform. 2016, 9, 21–33. [Google Scholar] [CrossRef]
- Echeverría, J.C.; Crowe, J.A.; Woolfson, M.S.; Hayes-Gill, B.R. Application of empirical mode decomposition to heart rate variability analysis. Med. Biol. Eng. Comput. 2001, 39, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, Z.; Mo, W. A time varying filter approach for empirical mode decomposition. Signal Process. 2017, 138, 146–158. [Google Scholar] [CrossRef]
- Gatrell, A.C.; Bailey, T.C.; Diggle, P.J.; Rowlingson, B.S. Spatial point pattern analysis and its application in geographical epidemiology. Trans. Inst. Br. Geogr. 1996, 21, 256–274. [Google Scholar] [CrossRef]
- Lancaster, J.; Downes, B.J. Spatial point pattern analysis of available and exploited resources. Ecography 2004, 27, 94–102. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D. A Quasi-Global Precipitation Time Series for Drought Monitoring Data Series 832; USGS Professional Paper; Data Series (832); U.S. Geological Survey: Reston, VA, USA, 2014.
- Rilling, G.; Flandrin, P. One or two frequencies? The empirical mode decomposition answers. IEEE Trans. Signal Process. 2008, 56, 85–95. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Washington-Allen, R.A. High-resolution prediction of soil available water content within the crop root zone. J. Hydrol. 2015, 530, 167–179. [Google Scholar] [CrossRef]
- Ma, H.; Yue, D.P.; Yang, D.; Yu, Q.; Zhang, Q.B.; Huang, Y. Interpolation of groundwater depth based on data assimilation. Trans. Chin. Soc. Agric. Mach. 2017, 48, 206–214. [Google Scholar]
- Birtwistle, A.N.; Laituri, M.; Bledsoe, B.; Friedman, J.M. Using NDVI to measure precipitation in semi-arid landscapes. J. Arid Environ. 2016, 131, 15–24. [Google Scholar] [CrossRef]
- Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G.; Bastiaanssen, W.G.M.; Noordman, E.J.M. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar]
- Li, Z.; Liu, X.; Ma, T. Retrieval of the surface evapotranspiration patterns in the alpine grassland-wetland ecosystem applying SEBAL model in the source region of the Yellow River, China. Ecol. Model. 2013, 270, 64–75. [Google Scholar] [CrossRef]
- Tang, W.; Feng, W.; Jia, M. Massively parallel spatial point pattern analysis: Ripley’s K function accelerated using graphics processing units. Int. J. Geogr. Inf. Sci. 2015, 29, 412–439. [Google Scholar] [CrossRef]
- Yu, Q.; Yue, D.P.; Wang, J.P.; Zhang, Q.B.; Li, Y.T.; Yu, Y.; Chen, J.X.; Li, N. The optimization of urban ecological infrastructure network based on the changes of county landscape patterns: A typical case study of ecological fragile zone located at Dengkou (Inner Mongolia). J. Clean. Prod. 2017, 163, S54–S67. [Google Scholar] [CrossRef]
- Knaapen, J.P.; Scheffer, M.; Harms, B. Estimating habitat isolation in landscape planning. Landsc. Urban Plan. 1992, 23, 10–16. [Google Scholar] [CrossRef]
- Shi, P.Z.; Yu, B.J.; Yang, X.Y. Research on bitter and salt water irrigation on cotton in a desert oasis area. J. Exp. Bot. 2003, 54, 54–55. [Google Scholar]
- Nguyen, H.; Wiegand, K.; Getzin, S. Spatial patterns and demographics of Streblus macrophyllus trees in a tropical evergreen forest, Vietnam. J. Trop. For. Sci. 2014, 26, 309–319. [Google Scholar]
- Kathleen, L.S.; Amatangelo, K.L.; Behrensmeyer, A.K. Holocene shifts in the assembly of plant and animal communities implicate human impacts. Nature 2015, 529, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Matt, M.E.; Vladimir, R.; Wei, Z. Improved particle counting and size distribution determination of aggregated virus populations by asymmetric flow field-flow fractionation and multiangle light scattering techniques. Biotechnol. Prog. 2011, 27, 547–554. [Google Scholar]
- Cook, E.A. Landscape structure indices for assessing urban ecological networks. Landsc. Urban Plan. 2002, 58, 269–280. [Google Scholar] [CrossRef]
- Dong, J.; Dai, W.; Shao, G. Ecological network construction based on minimum cumulative resistance for the city of Nanjing, China. ISPRS Int. J. Geo-Inf. 2015, 4, 2045–2060. [Google Scholar] [CrossRef]
- Hasanuzzaman, M.; Song, X.; Han, D.; Zhang, Y.; Hussain, S. Prediction of groundwater dynamics for sustainable water resource management in Bogra District, Northwest Bangladesh. Water 2017, 9, 238. [Google Scholar] [CrossRef]
- Blazquez-Cabrera, S.; Gastón, A.; Beier, P. Influence of separating home range and dispersal movements on characterizing corridors and effective distances. Landsc. Ecol. 2016, 31, 2355–2366. [Google Scholar] [CrossRef]
| No. | Sub-Administrative District | Well No. | Elevation (m) | Longitude (°) | Latitude (°) |
|---|---|---|---|---|---|
| 1 | Bayan Gaole | BG13 | 1040 | 106.98 | 40.33 |
| BG14 | 1047 | 106.96 | 40.28 | ||
| 2 | Bu Longnao | BG16 | 1030 | 107.05 | 40.55 |
| BG17 | 1041 | 107.08 | 40.52 | ||
| BG19 | 1045 | 107.08 | 40.48 | ||
| BG23 | 1040 | 107.05 | 40.42 | ||
| 3 | Du Kou | BG24 | 1042 | 107.08 | 40.42 |
| BG26 | 1038 | 107.07 | 40.37 | ||
| 4 | Long Shenghe | BG8 | 1027 | 106.92 | 40.63 |
| 5 | Shajin Taohai Sumu | BG1 | 1029 | 106.73 | 40.70 |
| BG2 | 1019 | 106.53 | 40.52 | ||
| BG3 | 1029 | 106.57 | 40.55 | ||
| BG5 | 1036 | 106.67 | 40.50 | ||
| BG6 | 1028 | 106.80 | 40.67 | ||
| BG9 | 1034 | 106.98 | 40.62 | ||
| BG11 | 1039 | 106.80 | 40.57 | ||
| BG12 | 1032 | 106.85 | 40.47 |
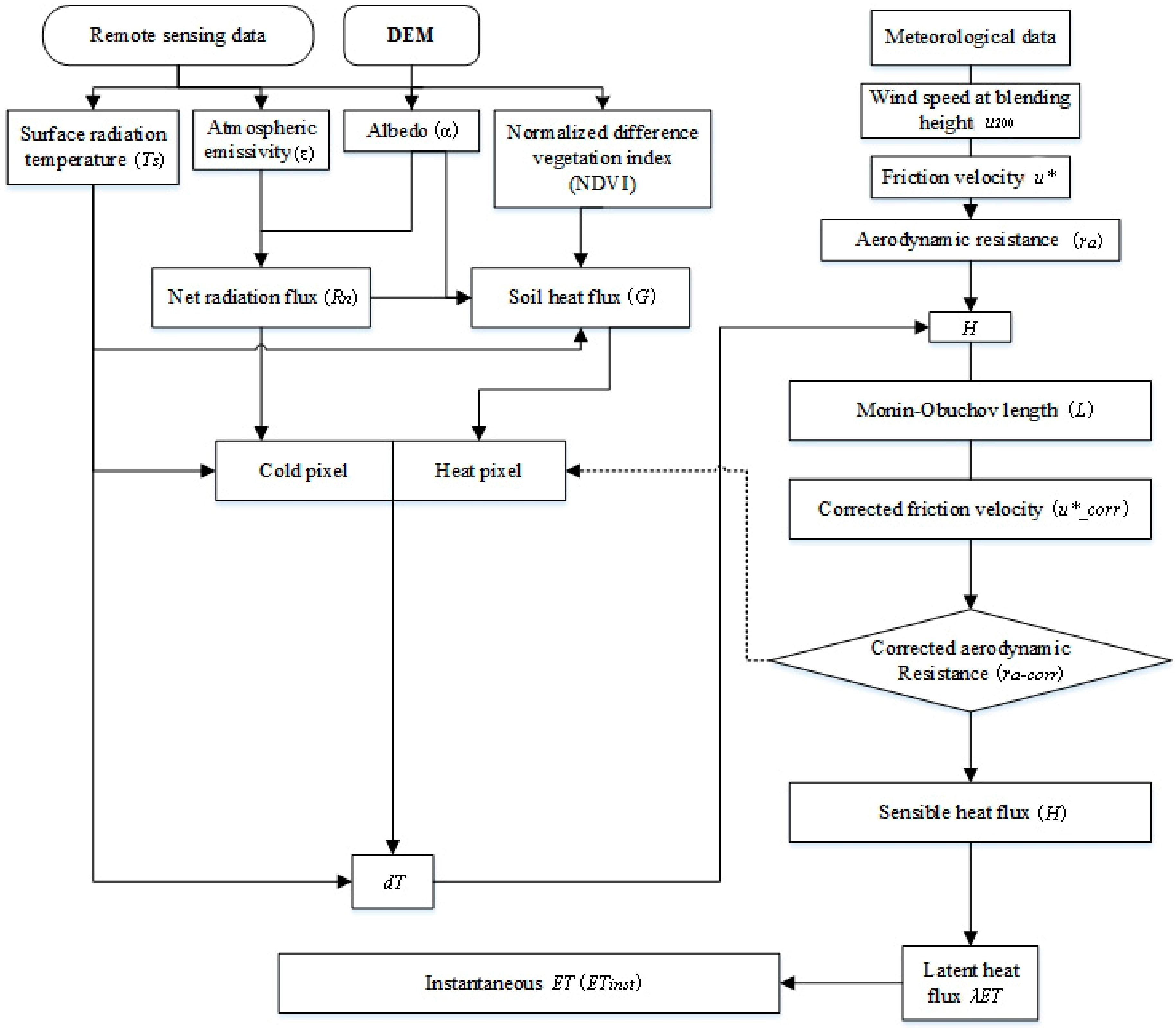
| Key Variables | Formulas | Basic Variables |
|---|---|---|
| Normalized difference vegetation index | NDVI = ()/() | and : reflectivities for bands 4 and band 3 |
| Atmospheric emissivity (ε) | ε = 1.009 + 0.047 ln(NDVI) | – |
| The surface radiation temperature (K) | Ts = K2/ln (K1·ε/L6 + 1) | : constant for Landsat images, 607.76 mW/cm2/sr/m |
| : constant for Landsat images, 1260.56 mW/cm2/sr/m | ||
| : the spectral radiance of band 6 | ||
| Albedo | α = Rs-reflected/Rs | : the reflected radiation (W/m2) |
| : the total incident shortwave radiation (W/m2) | ||
| Net radiation flux (W/m2) | Rn = Kin − α·Kin + Lin − Lout | : incoming shortwave radiation (W/m2) |
| : reflected shortwave radiation (W/m2) | ||
| : incoming longwave radiation (W/m2) | ||
| : outgoing longwave radiation (W/m2) | ||
| Soil heat flux (W/m2) | G = Ts·Rn/[·(0.0038 + 0.0074) (1 − 0.98NDVI4)] | – |
| Sensible heat fluxes (W/m2) | H = ··Cp/ra | : temperature difference between the two certain heights (K) |
| : air density, 1.293 × 103 kg/m3 | ||
| Cp: air specific heat, 1004 J/kg/K | ||
| ra: aerodynamic resistance to heat transport (s/m) | ||
| Latent heat fluxes (W/m2) | ET = Rn − G − H | – |
| Instantaneous ET (mm/h) | ETinst = 3600(Rn − G − H)/ | : latent heat of vaporization (J/kg) |
| Wind speed at the blending height (m/s) | u200 = u*·ln(z200/z0)/k | u*: the friction velocity at the weather station (m/s) |
| z200: the blending height, 200 m | ||
| z0: the measure of the land surface friction, 0.36 m in this case study | ||
| k: the von Karman’s constant, 0.41 | ||
| Friction velocity at each pixel (m/s) | u* = k·u200/ln(z200/z0) | – |
| Aerodynamic resistance to heat transport (s/m) | ra = ln(z2/z1)/(u*·k) | z1 and z2: the heights in meters above zero displacement of the vegetation |
| Groundwater Depth | 1990 | 1995 | 2000 | 2005 | 2010 | 2016 |
|---|---|---|---|---|---|---|
| Max | 20.54 | 19.43 | 19.91 | 22.36 | 20.71 | 20.83 |
| Min | 0.21 | 0.23 | 0.50 | 0.18 | 0.20 | 0.57 |
| Grade | Weight | |
|---|---|---|
| WT depth (m) | <2 | 1 |
| 2–4 | 2 | |
| 4–6 | 3 | |
| 6–8 | 4 | |
| 8–10 | 5 | |
| 10–12 | 6 | |
| 12–14 | 7 | |
| > 14 | 8 | |
| Distance from water bodies (m) | <500 | 1 |
| 500–1000 | 2 | |
| 1000–1500 | 3 | |
| 1500–2000 | 4 | |
| 2000–2500 | 5 | |
| 2500–3000 | 6 | |
| 3500–4000 | 7 | |
| >4000 | 8 | |
| Density of surface water bodies | 0.9–1 | 1 |
| 0.75–0.9 | 2 | |
| 0.6–0.75 | 3 | |
| 0.45–0.6 | 4 | |
| 0.3–0.45 | 5 | |
| 0.15–0.3 | 6 | |
| 0–0.15 | 7 | |
| 0 | 8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Jiang, Q.; Yang, D.; Yue, D.; Ma, H.; Huang, Y.; Zhang, Q.; Fang, M. Incorporating Temporal and Spatial Variations of Groundwater into the Construction of a Water-Based Ecological Network: A Case Study in Denko County. Water 2017, 9, 864. https://doi.org/10.3390/w9110864
Yu Q, Jiang Q, Yang D, Yue D, Ma H, Huang Y, Zhang Q, Fang M. Incorporating Temporal and Spatial Variations of Groundwater into the Construction of a Water-Based Ecological Network: A Case Study in Denko County. Water. 2017; 9(11):864. https://doi.org/10.3390/w9110864
Chicago/Turabian StyleYu, Qiang, Qun’ou Jiang, Di Yang, Depeng Yue, Huan Ma, Yuan Huang, Qibin Zhang, and Minzhe Fang. 2017. "Incorporating Temporal and Spatial Variations of Groundwater into the Construction of a Water-Based Ecological Network: A Case Study in Denko County" Water 9, no. 11: 864. https://doi.org/10.3390/w9110864
APA StyleYu, Q., Jiang, Q., Yang, D., Yue, D., Ma, H., Huang, Y., Zhang, Q., & Fang, M. (2017). Incorporating Temporal and Spatial Variations of Groundwater into the Construction of a Water-Based Ecological Network: A Case Study in Denko County. Water, 9(11), 864. https://doi.org/10.3390/w9110864







