Abstract
The soil particle movement under seepage flow is one of the predominant mechanisms responsible for incidents and failures of dams and streambanks. However, little attention has been paid to the critical hydraulic gradient under two-dimensional (2-D) seepage flow. In this study, a theoretical model was established under 2-D seepage flow to predict the critical hydraulic gradients for soil particle movement. In this model, the sediment particle rolling theory was used, while taking into account the relative exposure degree of the soil grains and the seepage direction. The model was validated through qualitative analysis and comparison with previous data, and showed considerable superiority over Terzaghi's model. In addition, the effect of the soil internal instability, implying that the critical hydraulic gradient of unstable soil is lower than that of stable soil, was discussed. Various parameters of the model were also analyzed. The results showed that the seepage direction angle was positively related to the critical gradient, whereas the void and the mean diameter of the soil were negatively related to it. Finally, the model proposes a calculation method for the particle movement initiation probability, which is regarded as a key parameter in the sediment transport model.
1. Introduction
Seepage flow could result in erosion and bank instability through several mechanisms. The soil-water pressure, seepage gradient forces, and the soil particle movement in relation to seepage erosion were the focus of previous studies [1,2]. Among these factors, seepage erosion is the predominant failure mechanism causing incidents in dams and streambanks [3,4], being responsible for approximately 50% of the failures [5,6].
The initiation of seepage erosion in soils has been assessed on the basis of hydraulic criteria, particularly in relation to the critical hydraulic gradient ic. This parameter is usually defined as the critical condition at which the effective stress of the soil becomes negligible [7]. Apparently, a large number of theoretical and experimental approaches have been used to obtain critical hydraulic gradients in water-retaining structures [8,9,10,11,12]. The critical gradient is generally calculated as the ratio of the buoyant unit weight of soil to the unit weight of water, as established by Terzaghi [8] according to the following Equation (1):
In this equation, γs is the specific weight of soil, γw is the specific weight of water, and n is the porosity. Terzaghi suggested that the critical gradient depends only on the void ratio and on the specific gravity of the solids. However, both in the field and in the laboratory, it has been observed that seepage erosion can initiate at gradients much lower than those determined with Terzaghi’s classical approach [6,9,10]. For example, Skempton and Brogan [9] carried out tests with upward flow for unstable soils. They found gradient values from one-third to one-fifth smaller than the theoretical values established by Terzaghi. Critical hydraulic gradients lower than 0.1 have also been observed in the field, for example in the failures of the Herbert Hoover Dike and of the A. V. Watkins Dam [10]. Other parameters have been proposed, for instance if, defined by Samani [11] as the critical hydraulic gradient of seepage failure. In addition, Wan and Fell [12] introduced istart and iboil to represent the critical hydraulic gradients for the starting of internal erosion and soil boiling, respectively. However, the critical hydraulic gradients described above are generally used for the conventional one-dimensional upward seepage flow; moreover, the resulting estimates are usually not accurate [6,9,10].
The upward seepage parameters described above can only be used to determine the hydraulic criteria in simple cases. In other circumstances, such as the seepage in streambanks and dams, they are invalid, as the seepage includes both a horizontal and a vertical water flow. The criteria for the seepage in both the vertical and the horizontal directions are still not well understood, although several recent studies have quantified soil properties associated with seepage erosion and piping [1,13,14,15]. There are few equations that accurately estimate the hydraulic criteria. Howard and McLane [16] introduced a critical shear stress equation based on the balance of forces’ moments. The forces on the soil grains comprise the tractive force of cumulative surface flow, the seepage force, and gravity. Another theory was developed by Dune [17], whose equation considered the seepage flow direction [2]. Lobkovsky et al. defined a criterion related to the critical slope [18], which was determined by the critical generalized Shields number for overland flow and the density contrast between the granular material and water. Other criteria, such as the initiation iini and the failure if of landslide dams under different geometrical and hydraulic conditions, were determined by Okeke and Wang [7]. The influences of several factors on the gradients were discussed in their research. The critical hydraulic gradients were studied by Adel et al. [19] through tests with stable and unstable soils (based on the Kenney and Lau's criterion [20]). Wan and Fell found that smaller critical hydraulic gradients apply tendentially to soils in a loose state, rather than to soils in a dense state [21]. Similar conclusions were obtained by Ahlinhan et al. in their experimental investigations [22]. Five soil specimens were examined in their experiments to determine the gradient for vertical and horizontal seepages. The internal stability of the soil was proved to be a decisive factor for the critical gradient. However, only few criteria for the soil particle movement in 2-D seepage have been studied so far; in addition, the influence of various parameters on these criteria also requires further study.
According to the previous studies, the hydraulic criteria are influenced by many soil properties. The soil unit weight [8,10], the friction angle [10], the soil particle size [10,23], the soil grain size distribution [7,21], the coefficient of uniformity [10,24], the stress state [25], and the void ratio [21,22,26] were all shown to influence the critical hydraulic conditions. Despite the wealth of research done so far, few studies have thoroughly examined the influence of the relative position of the soil particles and of the seepage direction on the seepage erosion. The locations of soil particles are completely random, which results in different initiation conditions for different particles. As shown in Figure 1, particle C on the far right of the figure is the particle that will be taken away by the flow most easily. On the other hand, the 2-D seepage flow is inhomogeneous in a seepage field with different flow directions. The seepage forces acting on movable particles are different, causing differences in the initiation of soil particles in a 2-D seepage field. Therefore, a deeper understanding of these two aspects of particle movement is absolutely essential.
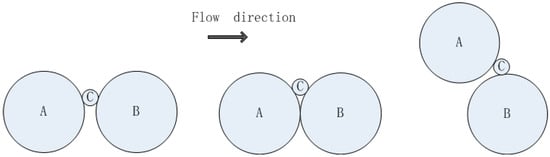
Figure 1.
The randomness of particle position.
In this study, a theoretical model was established based on the soil particle rolling theory. In the model, the particles' relative positions and the seepage directions were considered. A calculation formula was derived to predict the hydraulic critical gradients. A qualitative analysis and experimental results demonstrated the formula's validity. The effects of various parameters were discussed, and the particle initiation probability was determined based on the theoretical model.
2. Methods
2.1. Particle Movement Process
The initiation of sediment particles caused by the surface flow can be classified into three different modes: rolling, sliding, and lifting [27]. A previous study showed that the rolling threshold corresponds to the minimum values of the dimensionless critical shear stresses [27]. Particles in the rolling mode present the lowest critical velocity when compared to particles in the other modes. However, in the seepage field, the velocity is generally so small that the rolling condition is relatively easy to achieve. Therefore, in this paper, the rolling mode was assumed to be the initiation process and it was purposely simplified in order to facilitate the ensuing considerations.
2.2. Forces on the Movable Particles
As shown in Figure 2, when the water flows through the soil void, the water force acting on the movable particles (A) is defined as the seepage force (F). The seepage force includes two parts: the drag force and the hydraulic pressure force, resulting from the seepage velocity and the hydraulic gradient, respectively [28]. The seepage force F is determined through the Equation (2) by Wu [29]. The other forces include lift FL, contact force of motionless particle (B) Fn, friction Fτ, and gravity G. The forces G and FL are described in Equations (3) and (4).
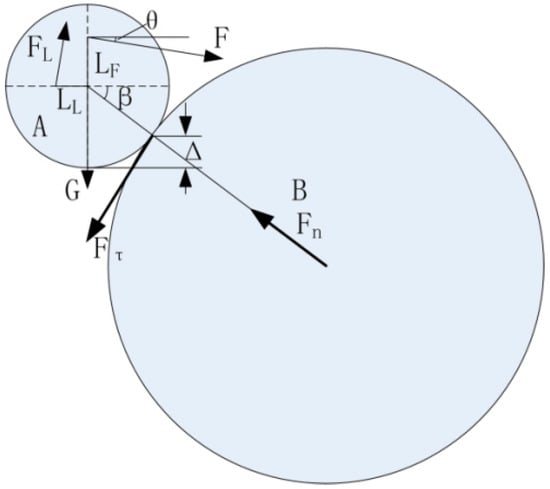
Figure 2.
Forces on the movable particles.
In the above equations, D is the movable particle diameter, ρW and ρS are the densities of the water and the soil particles, respectively, g is the gravity acceleration, i is the hydraulic gradient, e is the void ratio of the soil, dθk is the equivalent diameter (defined by 1/Σ(pi/di), where pi is the percent of grains with the diameter of di), CL is the lift coefficient, and Vb is the seepage velocity in the void. The forces Fn and Fτ have no computational method, and they are obtained from the mechanical equilibrium of a movable particle.
2.3. Equilibrium Equations
The critical rolling condition of particle A is a moment equilibrium state. The forces on the movable particles are shown in Figure 2 and represented by Equation (5), in which the moments of Fn and Fτ are equal to zero.
2.4. Analysis of the Relative Exposure Degree
The exposure degree Δ, shown in Figure 2, was proposed by Han [30]. It is the vertical distance between the lowest point of the movable particle and the contact point of particle A with the fixed particle B. Δ′ = Δ/R is the relative exposure degree. In this paper, Δ′ was considered to have a uniform distribution from 0 to 1 [31]. The relationships between Δ′ and β, shown in Figure 2, are described by the following equations:
2.5. Equation for the Critical Hydraulic Gradient
The flow velocity in the seepage field, which is much smaller than in the surface flow, is of the same order of magnitude as the diameters of the sediment particles. Therefore, according to Equations (2)–(4), the magnitude order of the lift force FL is much lower than that of the seepage force F and of the gravity force G. Thus, the lift force FL will be ignored in the following sections. The critical hydraulic gradient ic can be obtained from Equation (5) as follows:
where ρ′ = ρS − ρW is the particle density in water. In Equation (8), the critical hydraulic gradient is influenced by the soil particle density, the movable particle size, the seepage direction, the soil void ratio, the soil gradation, and the particle relative positions. When the soil parameters are constant, the critical hydraulic gradient varies only with Δ′ and θ. Equation (8) can be expressed in a simpler form, as Equation (9)
where Θ is dependent on the seepage field and the relative exposure degree, as shown in Equation (10), and Π is dependent on the soil parameters, as is shown in Equation (11).
3. Results
3.1. Qualitative Analysis
The seepage inside a slope is not uniform. Generally, the seepage velocity of the slope toe is larger and more prone to seepage erosion. To better characterize it, the critical gradient of the seepage in a slope was analyzed. The distribution of critical hydraulic gradients was calculated through Equation (8). The soil E2 [22] was taken as an example. The specimen in exam can be defined as grit sand, and the hydraulic conductivity can be calculated according to Alyamani and Zekâi [32] as 1.0 × 10−4 m/s, which is consistent with the empirical value in Table 1. The seepage field of a vertical slope model (1 m × 0.5 m), with water levels of 0.5 m upstream and 0 m downstream, respectively, is shown in Figure 3. The seepage direction θ can be obtained from the seepage field.

Table 1.
Empirical values of hydraulic conductivity.
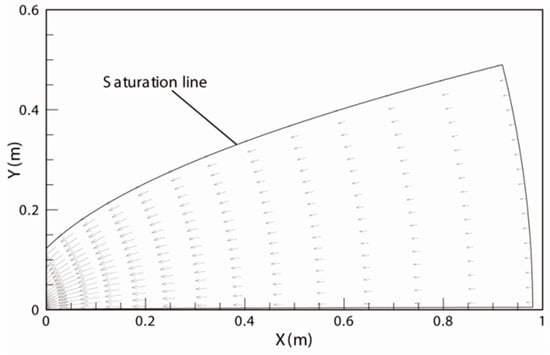
Figure 3.
Seepage field of a vertical slope model.
On the basis of previous studies [33], the ratio dc,15/df,85 was used to determine the stability of the soils, with dc,15 = grain diameter with 15% w/w of the grains of the coarse soil being finer, and df,85 = grain diameter with 85% w/w of the grains of the fine soil being finer. The finer particles can be removed by the flow easily. As suggested by Kezdi [33], d15 is assumed to be the largest movable particle in Equation (8), and, thus, D = d15. Figure 4 shows the distribution of the critical hydraulic gradients that were predicted under different relative exposure degrees (Δ′ = 0.05, 0.1, 0.2) and different porosities (e = 0.43, 0.67, 1).
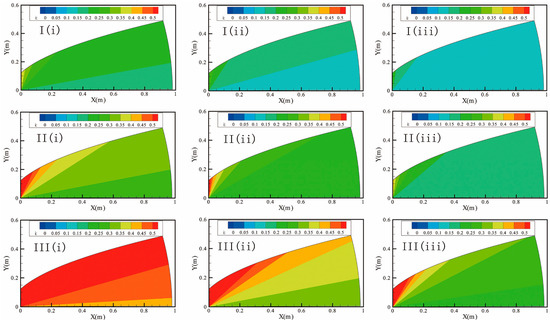
Figure 4.
The distribution of the critical hydraulic gradients. In I, II, and III Δ′ are 0.05, 0.1. and 0.2, respectively; in (i), (ii), and (iii) e are 0.3, 0.4, and 0.5, respectively.
For the vertical slope shown in Figure 4, the critical hydraulic gradient in the slope toe, where seepage erosion and seepage undercutting in the sand are most likely to happen, as demonstrated by Chu-Agor et al. [1,34], is small. From the toe, up to the top, the critical hydraulic gradient gradually becomes larger. With different Δ′ and e, the distributions of the critical hydraulic gradients in the slope are obviously different. More specifically, as Δ′ increases, the critical hydraulic gradient will increase and the seepage erosion will occur less likely. On the other hand, as the void ratio increases and the soil becomes less compact, the critical hydraulic gradient will decrease and the seepage erosion will occur more likely.
3.2. Experimental Validation
Experimental data were collected and compared with those predicted by the theoretical model. The predicted i is calculated through Equation (8). In the prediction, the relative exposure degree of d15 was set at 0.1 because a few movements of particles can lead to seepage failure. The value of the soil particle density was 2.65 g/cm3. According to the analyses above, Equation (8) can be reduced to Equation (12).
The experimental data were obtained from Ahlinhan et al. [22]. In the examined experiment, five different non-cohesive soils were tested in specially developed test devices, under horizontal seepage flow. The void ratio of the soils varied in the tests. The predicted and experimentally measured data, depicted in Figure 5, matched very well (R2 = 0.98).
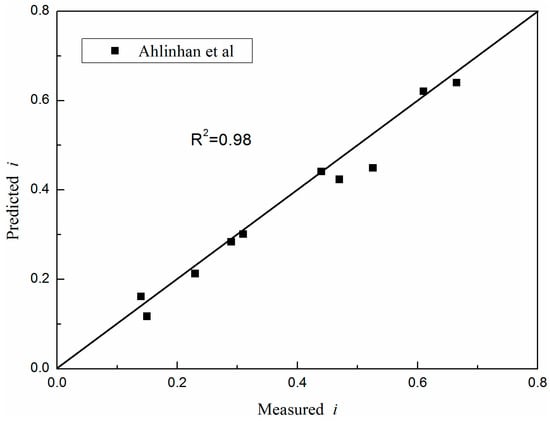
Figure 5.
Comparison between predicted and measured data (Ahlinhan’s test).
Another set of experimental data was obtained from Liang et al. [35]. These researchers carried out a series of non-cohesive soil tests, with varying angle model slots. The angles were set as 96°, 100°, 104°, 108°, 112°, and 116° (with the direction of gravity). The critical hydraulic gradients of four groups of particles were measured in the test. The comparison between the predicted data and the measured data is shown in Figure 6.
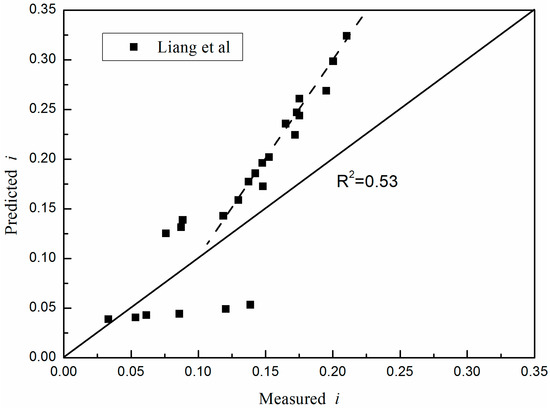
Figure 6.
Comparison between predicted and measured data (Liang’s test).
As can be seen from Figure 6, the predicted values did not match with the measured values (R2 = 0.53). The data-points above the solid line indicate that the predicted values were greater than the measured values. This is because the gradients of the soil specimens gradually increased during the test. In smaller gradients, fine particles were removed by the flow, which made the soil much looser. In a looser soil, the measured gradients are smaller than the real gradients. The points below the line indicate that the predicted i were underestimated. This may result from the obstruction caused by the finer particles, which affects the other particles of the group when the hydraulic gradient is small.
Equation (8) can also be applied to the case of an upward vertical seepage flow. In the vertical seepage flow, the seepage angle θ is equal to −90°, and the parameter Θ is 1. Equation (8) can be simplified to Equation (13).
Many studies examined the critical gradient under an upward seepage. The results of three experiments were collected to be compared with the predicted results [9,22,36,37] (Figure 7). Overall, the predicted results and the measured data matched very well (R2 = 0.91), though there was some discrepancies between them. The results from these experiments are presented in Table 2. For the experiment of Ahlinhan et al., the predicted results were more accurate than for the other two experiments. In the Fleshman and Rice’s test, the critical hydraulic gradient was overestimated.
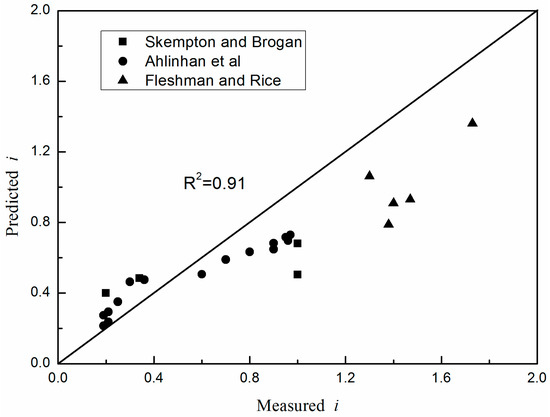
Figure 7.
Comparison between predicted and measured data for an upward seepage.

Table 2.
Predicted and measured i in the analyzed experiments.
4. Discussion
4.1. Effect of the Soil Internal Instability
The internal instability of the soil is the main factor affecting the critical hydraulic gradient [9]. The theoretical model described in this paper can explain this effect effectively. For the unstable soil, dθk is much larger than d15, which leads to a smaller Π. Therefore, the calculated critical hydraulic gradient was significantly smaller than that of the stable soil. Our theoretical model also agrees with experimental data found in the literature. In the horizontal seepage, Adel [19] demonstrated that the critical hydraulic gradient for unstable soils should be around 0.2, while in Ahlinhan’s test [22], the gradients were between 0.14 and 0.29. In our study, the gradients calculated for unstable soils were between 0.16 and 0.28. For stable soils, Adel [19] showed that the critical hydraulic gradient was about 0.7, while in Ahlinhan’s test, it was shown to be between 0.52 and 0.66. Our calculated gradients were between 0.42 and 0.64, and, thus, they were similar to those determined experimentally, with only some deviations. In the vertical seepage, the critical hydraulic gradients were between 0.2 and 0.34 for the unstable soil [9]; in Ahlinhan’s test [22], they were between 0.19 and 0.25. According to our calculations, the gradients were between 0.21 and 0.48, and, thus, slightly different from the experimental results, but consistent on the whole. For stable soils, Skempton’s [9] experimental critical hydraulic gradient was 1.0, while the values determined by Ahlinhan’s [22] were between 0.7 and 0.97, and those found by Fleshman’s [36,37] were between 1.3 and 1.73. In our study, the gradients varied from 0.51 to 1.36, thus showing that the range of values for the critical hydraulic gradients is relatively large in this case for different soils. In any case, the gradients’ values determined in our study were more accurate than Terzaghi’s, which were reported to be higher than the real ones [6]. In our analysis, we could also determine the influence of soil instability on the critical hydraulic gradients. We concluded that the critical hydraulic gradients of unstable soil were lower than those of stable soil.
4.2. Effects of Other Parameters
Other parameters including both hydraulic parameters (seepage angle) and soil parameters (void ratio, gradation) affect the critical hydraulic gradient to different extents. In Liang’s test [35], the effect of seepage angle on critical hydraulic gradients has been demonstrated. In our study, the relationship between the seepage angle and the predicted i is shown in Figure 8.
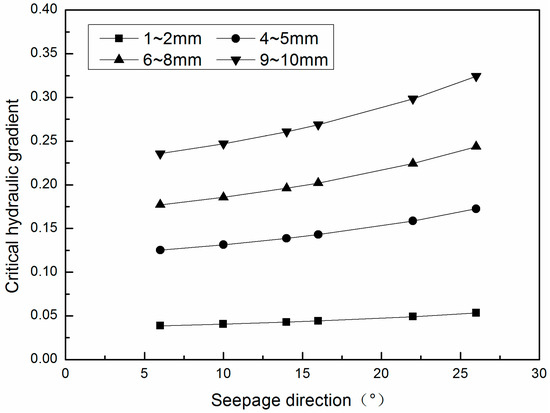
Figure 8.
Effects of seepage direction on the critical gradients.
It can be seen that at the same seepage direction angle, the hydraulic gradient at the initiation of the particle increased as the particle size increased. For particles in the same size range, the critical hydraulic gradient was positively correlated with the seepage direction angle, as observed for the experimental results reported in the test. Thus, the critical gradient of the vertical seepage is greater than that of the horizontal flow, as observed by Ahlinhan [22]. The vertical and the horizontal seepages were also studied by Skempton and Adel [9,19], respectively, and similar results were reported. The force analysis of soil particles described above can explain this phenomenon. In the vertical seepage flow, the particles’ movements need to overcome the gravity, while, in the horizontal flow, the particles can roll around large particles, moving downstream. In this situation the seepage force does not need to be greater than the gravity, but it has to overcome the gravity’s moment. In the case of a small seepage force, the seepage force’s moment may be greater than the gravity’s moment, as shown by the analysis of the particles’ exposure degree. Therefore, soil particles are very easily taken away by the horizontal seepage flow.
The soil parameters are also important for the critical gradients [7,21,22]. The effects of the void ratio e and the mean grain diameter dθk on the critical gradients are shown in Figure 9. In this figure, the experimental data were obtained from Ahlinhan’s vertical seepage test [22].
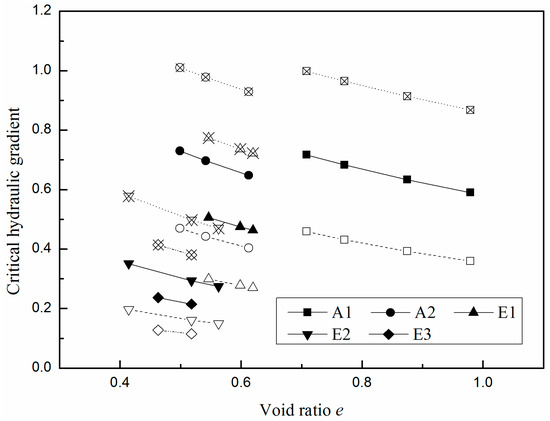
Figure 9.
Effects of the soil parameters on the critical gradients.
The dashed lines in Figure 9 denote the relationship between the critical hydraulic gradients and the void ratio after doubling or halving the mean grain diameter of the soil particles. The negative effects of the void ratio on the critical hydraulic gradient are evident, in agreement with Wan and Zhou results [20,38]. Small voids lead to poor mobility of the water flow, which will reduce the removal of soil particles by the water. The values of dθk are inversely correlated to those of the critical gradients. Larger dθk values indicate that the soil particles are relatively coarse, and the soil is more inhomogeneous and more unstable. This effect is consistent with Skempton and Ahlinhan’s results [9,22].
4.3. Exposure Degree and Particle Initiation Probability
Equation (8) also contains the parameter Δ′. This parameter is a random variable, considered to obey a random distribution, such as a uniform distribution, a normal distribution, a partial normal distribution, etc. [39]. Regardless of the distribution type, the exposure can be obtained through Equation (9), when the particles D can move away in certain hydraulic conditions:
The initiation probability of particles D is:
where f (Δ′) is the probability density function of Δ′. In Ahlinhan’s test [22], for hydraulic gradients of 0.2, 0.4 and 0.6 in a horizontal seepage, the initiation probabilities of soil samples A1 and E1 are shown in Figure 10, assuming that Δ′ is uniformly distributed between 0 and 1.
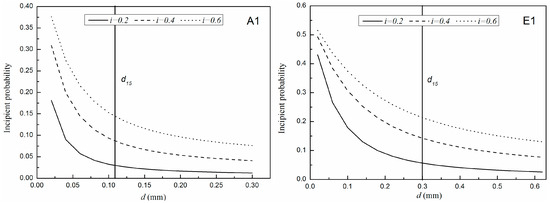
Figure 10.
Initiation probability of different particles.
As shown in Figure 10, with the increase of particle size, the initiation probability is gradually reduced, and the decreasing trend gradually becomes smaller. In addition, when the particle size is less than d15, the initiation probability of the particles is large, and the variation is drastic. This suggests that the movable particles are mostly smaller than d15, which, reasonably, represents the largest possible diameter for movable particles. In addition, the initiation probability of the particles is an important factor in the sediment transport studies regarding river dynamics. In the seepage erosion, also the effects of sediment transport need to be determined. Hence, the theoretical model needs to be further developed. The initiation probability determined in this study will allow to develop the theoretical model.
5. Conclusions
The initiation of soil particles is a complex dynamic process influenced by the seepage flow, especially the 2-D seepage flow. Among the multiple factors influencing it, the randomness of sediment particle position and the seepage direction were examined in this study. An equation was established to appraise the critical hydraulic gradient under 2-D seepage flow, based on the basic theory of single-grain rolling movement. By qualitative analysis and comparison with experimental data, our method was demonstrated to be highly accurate in predicting the critical gradient of the 2-D seepage flow.
The results we obtained are considerably more reliable than Terzaghi’s. The effects of various parameters on the critical gradients were also discussed. Our results showed that the critical hydraulic gradients of unstable soil were lower than those of stable soil, and that the seepage direction angle was positively related to the critical gradient, whereas the void and the mean diameter of soil were negatively related to it.
This theoretical model was used to determine the initiation probability of particles with an assumed exposure degree distribution. Through the analysis of the initiation probability, the diameter of the movable particles appeared to be, in general, smaller than d15. The initiation probability is a factor contributing to the development of sediment transport under seepage flow.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 41576093, No.51279124, No. 51621092), the Natural Science Foundation of Tianjin (No. 14JCZDJC39800) and State Key Laboratory of Hydraulic Engineering Simulation and Safety Fundation (No. HESS-1513).
Author Contributions
Zhe Huang and Haijue Xu conceived the idea and approach for the study. Zhe Huang and Yuchuan Bai analyzed the data. Yufen Cao and Xiao Hu contributed to the language translation. Zhe Huang wrote the paper. All the authors were involved in the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| β | Angle referred to the position of the movable particle |
| LL | Arm of lift force |
| LF | Arm of seepage force |
| Fn | Contact force |
| ic | Critical hydraulic gradient |
| ρS | Densities of the soil particles |
| ρW | Densities of the water |
| dθk | Equivalent diameter |
| Δ | Exposure degree |
| Fτ | Friction force |
| d15 | Grain diameter for which 15% of the grains by weight are finer |
| dc,15 | Grain diameter for which 15% of the grains by weight of the coarse soil are finer |
| df,85 | Grain diameter for which 85% of the grains by weight of the fine soil are finer |
| G | Gravity |
| g | Gravity acceleration |
| K | Hydraulic conductivity |
| i | Hydraulic gradient |
| if | Hydraulic gradient at slopes or dams failure |
| iboil | Hydraulic gradient at soil boil |
| istart | Hydraulic gradient at soil starting movement |
| iini | Hydraulic gradient at initiation of landslide dams |
| P | Initiation probability of particles |
| CL | Lift coefficient |
| FL | Lift force |
| D | Movable particle diameter |
| Θ | Parameter refered to the seepage field and the relative exposure degree |
| Π | Parameter refered to the soil parameters |
| ρ′ | Particle density in water |
| n | Porosity of the soil |
| f (Δ′) | Probability density function of Δ′ |
| R | Radius of the movable particle |
| Δ′ | Relative exposure degree |
| θ | Seepage direction |
| F | Seepage force |
| Vb | Seepage velocity |
| γs | Specific weight of soil |
| γw | Specific weight of the water |
| e | Void ratio of the soil |
References
- Chu-Agor, M.L.; Fox, G.A.; Cancienne, R.M.; Wilson, G.V. Seepage caused tension failures and erosion undercutting of hillslopes. J. Hydrol. 2008, 359, 247–259. [Google Scholar] [CrossRef]
- Fox, G.A.; Wilson, G.V. The role of subsurface flow in hillslope and stream bank erosion: A review. Soil Sci. Soc. Am. J. 2010, 74, 717–733. [Google Scholar] [CrossRef]
- Hagerty, D.J. Piping/sapping erosion I: Basic considerations. J. Hydraul. Eng. 1991, 117, 991–1008. [Google Scholar] [CrossRef]
- WöRman, A. Seepage-induced mass wasting in coarse soil slopes. J. Hydraul. Eng. 1993, 119, 1155–1168. [Google Scholar] [CrossRef]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2011, 37, 1000–1024. [Google Scholar] [CrossRef]
- Richards, K.S.; Reddy, K.R. Critical appraisal of piping phenomena in earth dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- Okeke, C.U.; Wang, F. Critical hydraulic gradients for seepage-induced failure of landslide dams. Geoenviron. Disasters 2016, 3, 1–22. [Google Scholar] [CrossRef]
- Terzaghi, K. Der Grundbruch an Stauwerken und Seine Verhütung. Wasserkraft 1922, 17, 445–449. [Google Scholar]
- Skempton, A.W.; Brogan, J.M. Experiments on piping in sandy gravels. Géotechnique 1994, 44, 449–460. [Google Scholar] [CrossRef]
- Fleshman, M.S.; Rice, J.D. Constant gradient piping test apparatus for evaluation of critical hydraulic conditions for the initiation of piping. Geotech. Test. J. 2013, 36, 834–846. [Google Scholar] [CrossRef]
- Samani, Z.A. Soil hydraulic stability in a subsurface drainage system. Trans. ASAE 1981, 24, 666–669. [Google Scholar] [CrossRef]
- Wan, C.F. Experimental Investigations of Piping Erosion and Suffusion of Soils in Embankment Dams and Their Foundations; The University of New South Wales: Sydney, Australia, 2006. [Google Scholar]
- Wilson, G.V.; Periketi, R.K.; Fox, G.A.; Cullum, R.F. Seepage erosion properties contributing to streambank failure. Earth Surf. Process. Landf. 2007, 32, 447–459. [Google Scholar] [CrossRef]
- Fox, G.A.; Wilson, G.V.; Simon, A.; Langendoen, E.J.; Akay, O.; Fuchs, J.W. Measuring streambank erosion due to ground water seepage: Correlation to bank pore water pressure, precipitation and stream stage. Earth Surf. Process. Landf. 2007, 32, 1558–1573. [Google Scholar] [CrossRef]
- Chu-Agor, M.L.; Wilson, G.V.; Fox, G.A. Numerical modeling of bank instability by seepage erosion undercutting of layered streambanks. J. Hydrol. Eng. 2008, 13, 1133–1145. [Google Scholar] [CrossRef]
- Howard, A.D.; Mclane, C.F. Erosion of cohesionless sediment by groundwater seepage. Water Resources Res. 1988, 24, 1659–1674. [Google Scholar] [CrossRef]
- Dunne, T. Hydrology, mechanics, and geomorphic implications of erosion by subsurface flow. Spec. Pap. Geol. Soc. Am. 1990, 252, 1–28. [Google Scholar] [CrossRef]
- Lobkovsky, A.E.; Jensen, B.; Kudrolli, A.; Rothman, D.H. Threshold phenomena in erosion driven by subsurface flow. J. Geophys. Res. Earth Surf. 2005, 109, 357–370. [Google Scholar] [CrossRef]
- Adel, H.D.; Bakker, K.J.; Breteler, M.K. Internal stability of minestone. In Proceedings of International Symposium of Modelling Soil–Water-Structure Interaction; Balkema: Rotterdam, The Netherlands, 1988; pp. 225–231. [Google Scholar]
- Kenney, T.C.; Lau, D. Internal stability of granular filters. Can. Geotech. J. 1985, 23, 420–423. [Google Scholar] [CrossRef]
- Wan, C.F.; Fell, R. Assessing the potential of internal instability and suffusion in embankment dams and their foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 401–407. [Google Scholar] [CrossRef]
- Ahlinhan, M.F.; Achmus, M.; Burns, S.E.; Bhatia, S.K.; Avila, C.M.C. Experimental investigation of critical hydraulic gradients for unstable soils. Geotech. Spec. Publ. 2010, 599–608. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.D. Determination of critical head in piping. J. Hydraul. Eng. 2003, 129, 511–518. [Google Scholar] [CrossRef]
- Schmertmann, J.H. The no-filter factor of safety against piping through sands. Geotech. Spec. Publ. 2000, 65–105. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Critical hydraulic gradients of internal erosion under complex stress states. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.D. Influence of porosity on piping models of levee failure. J. Geotech. Geoenviron. Eng. 2001, 127, 1071–1074. [Google Scholar] [CrossRef]
- Choi, S.U.; Kwak, S. Theoretical and probabilistic analyses of incipient motion of sediment particles. KSCE J. Civ. Eng. 2001, 5, 59–65. [Google Scholar] [CrossRef]
- Marot, D.; Rochim, A.; Nguyen, H.H.; Bendahmane, F.; Sibille, L. Assessing the susceptibility of gap-graded soils to internal erosion: Proposition of a new experimental methodology. Nat. Hazards 2016, 29, 1–24. [Google Scholar] [CrossRef]
- Wu, L. Computation of the critical hydraulic gradient for piping of non-cohesive soil. Hydro-Sci. Eng. 1980, 4, 90–95. (In Chinese) [Google Scholar] [CrossRef]
- Han, Q.W.; He, M.M. Statistical Theory of Sediment Movement; Science Press: Beijing, China, 1984. (In Chinese) [Google Scholar]
- Xu, H.; Shen, Y.; Bai, Y. Statistical analysis on motion characteristics of bedload rolling. J. Hydraul. Eng. 2014, 110, 1184–1192. (In Chinese) [Google Scholar] [CrossRef]
- Alyamani, M.S.; Zekâi, S. Determination of hydraulic conductivity from complete grain-size distribution curves. Ground Water 1993, 31, 551–555. [Google Scholar] [CrossRef]
- Kezdi, A. Soil Physics; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Chu-Agor, M.L.; Fox, G.A.; Wilson, G.V. Empirical sediment transport function predicting seepage erosion undercutting for cohesive bank failure prediction. J. Hydrol. 2009, 377, 155–164. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, Q.; Zeng, C.; Liu, Z. Non-Cohesive Particles Starting Mechanism under the Changing Seepage Direction. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2016, 35, 89–93. (In Chinese) [Google Scholar]
- Rice, J.D.; Fleshman, M.S. Laboratory Modeling of Critical Hydraulic Conditions for the Initiation of Piping. In Proceedings of the Geo-Congress 2013, San Diego, CA, USA, 3–7 March 2013; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2013; pp. 1044–1055. [Google Scholar]
- Fleshman, M.S.; Rice, J.D. Laboratory Modeling of the Mechanisms of Piping Erosion Initiation. J. Geotech. Geoenviron. Eng. 2014, 140, 04014017. [Google Scholar] [CrossRef]
- Zhou, J.; Bai, Y.F.; Yao, Z.X. A mathematical model for determination of the critical hydraulic gradient in soil piping. In Proceedings of the GeoShanghai International Conference 2010, Shanghai, China, 3–5 June 2010; American Society of Civil Engineers (ASCE): Reston, VA, USA; pp. 239–244. [Google Scholar] [CrossRef]
- Xing, R.; Zhang, G.; Liang, Z.; Wu, Z. Study on the location characteristics of bed surface particle. J. Sediment. Res. 2016, 4, 28–33. (In Chinese) [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).