Abstract
A thorough review has been performed on interpolation methods to fill gaps in time-series, efficiency criteria, and uncertainty quantifications. On one hand, there are numerous available methods: interpolation, regression, autoregressive, machine learning methods, etc. On the other hand, there are many methods and criteria to estimate efficiencies of these methods, but uncertainties on the interpolated values are rarely calculated. Furthermore, while they are estimated according to standard methods, the prediction uncertainty is not taken into account: a discussion is thus presented on the uncertainty estimation of interpolated/extrapolated data. Finally, some suggestions for further research and a new method are proposed.
1. Introduction
For numerous purposes, different time series are recorded and analyzed to understand phenomena or/and behaviors of variables, to try to predict future values, etc. Unfortunately, and for several reasons, there are gaps in data, irregular time steps of recordings, or removed data points that often need to be filled for data analysis, calibration of models, or for data with a regular time step. Generally in practice, incomplete series are the rule [1]. In order to fill gaps in time series, numerous methods are available, and the choice of the method(s) to apply is not easy for non-mathematicians among data users. This paper presents a general overview, as a general and non-detailed introduction to such methods, especially written for readers without an introduction on interpolation methods.
First to all, a distinction should be clearly stated: the difference between interpolation and extrapolation. A first approach can be defined as the following. To fill gaps and, respectively, to predict future values, often require similar methods [2], named as interpolation and extrapolation methods respectively. A second approach distinguishes between both cases, while comparing the range of existing and missing data. If there is a model to fill the gaps in a time series, if predictions are similar in content, and there is variability to observations, model errors should be equivalent for the existing and the missing data set (interpolation). Otherwise an extrapolation (i.e., predictions are outside of the observation range) has been performed, and expected errors would be greater for the predictions. An algorithm based on the data depth theory has been coded to make the distinction between interpolation and extrapolation [3]. Differences between existing and missing data in those methods could cause significant errors [4]. This paper deals with the interpolation method, in the sense of a first approach without consideration of the potential differences between the ranges of existing and missing data.
Secondly, there are many different kinds of data. Economical, financial, chemical, physical and environmental variables do not have the same characteristics: they can range from random to polycyclic processes. This wide range of characteristics requires a wide range of methods to fill gaps, and poses problems to researchers and practitioners when they choose one of the available methods. One thing is clear: a straightforward calculation of prediction uncertainty does not yield satisfactory results.
Finally, an increasing proportion of data contains values and their uncertainties (standard uncertainties, 95% confidence intervals, etc.), and requires specific methods to properly assess the uncertainties of the interpolated data. Two normalized methods are recommended and presented in a fourth section to assess uncertainties: the law of propagation of uncertainties [5] and Monte-Carlo simulations [6]. The estimation of prediction uncertainties can be easily performed with combined procedures. Assessment of the uncertainties of interpolated data is reported only seldomly: a brief review of the literature is presented in Section 4. Two articles are already mentioned here, due to the relevance of their data and ideas: [7], where the application of a Markovian arrival process to interpolate daily rainfall amount applied on a wide range of existing distributions is presented, and [8], where an overview of methods and questions/consequences related to the evaluation of uncertainties in missing data is presented.
According to [1], a useful interpolation technique should meet four criteria: (i) not a lot of data is required to fill missing values; (ii) estimation of parameters of the model and missing values are permitted at the same time; (iii) computation of large series must be efficient and fast, and (iv) the technique should be applicable to stationary and non-stationary time series. The selected method should also be accurate and robust. Prior to the application of interpolation methods, [9] mentioned two preliminary steps to apply prior to the determination of a model: (i) to separate the signal (trends of interest, i.e., relevant and dependent on subsequent use of the data) from the noise (variability without interest) as in [10], or (ii) to understand the past or existing data to better forecast the future, or to fill gaps in missing data. Despite the fact that smoothing algorithms, which may be used to distinguish signals while removing their noise, and interpolation methods are sometimes similar, this article does not deal with smoothing methods.
The following example aims at presenting pending scientific questions on this topic. Suppose rainfall intensity is measured at an hourly basis. The value at 1 p.m. is equal to 10 mm/h with a standard uncertainty of ±1 mm/h at 1 p.m. The instrument produced an error signal at 2 p.m. Finally, at 3 p.m., the instrument again logged 10 ± 1 mm/h. Under the assumption of randomness of the series (covariances and correlation coefficients are equal to 0, direct calculation by law of propagation of uncertainties (an average between 1 p.m. and 3 p.m. values) of the missing value at 2 p.m. yields 10 ± 0.7 mm/h. The standard uncertainty is marked off by calculations that are applied with the minimal (equal to −1) and the maximal (equal to +1) correlation coefficient values. These calculations lead to a standard uncertainty range between ± 0.0 and ± 1 mm/h, which is always smaller or equal to the measurement uncertainties. The smaller uncertainty value, due to the averaging process, reflects the uncertainty of a 2 h averaging period, whereas we are interested in a 1 h averaging period around 2 p.m., similar to the measurement points at 1 p.m. and 3 p.m. It is concluded that the prediction uncertainty cannot be estimated from the law of propagation of uncertainties [5].
This review paper is structured as follows. Numerous methods (see Section 2) have been published about filling gaps in data. This paper gives an accessible overview of those methods in Section 2. In spite of the recommended comparisons [11] between existing methods, only a few studies have compared methods (e.g., [11,12,13]); these are detailed in the second section. In the third section of this article, criteria applied and published in past studies for comparison of methods are given. Due to the numerous methods and criteria available, a comparison between different studies with numerical values is often impossible. To improve the readability of the present article, a common notation has been applied to present methods: xi are observed data, Xi are the interpolated value(s) of missing data, i is an index, and are the residuals. Each of them apply only for univariate time-series. This paper does not deal with multivariate time series.
2. Interpolation Methods
Existing methods are detailed in the following Sections: Section 2.1 for deterministic methods, and Section 2.2 for stochastic methods. This distinction, based on the existence or non-existence of residuals (differences between predictions at known locations and observations) in the interpolation function, also deals with uncertainty.
2.1. Deterministic Methods
This first group includes methods that perform basic interpolation between the last known point before the gap (xB), and the first one known after the gap (xA).
2.1.1. Nearest-Neighbor Interpolation
The nearest neighbor or proximal interpolation, introduced by [14], is the easiest method [13,15]: the value of the closest known (existing) neighbor is assigned to the missing value (such as Equation (1)). Interpolated data by this method are discontinuous [16]. This method often yields the worst results [13,16], and should not be confused with the k-nearest-neighbors methods.
where a and b are the indexes of xA and xB.
2.1.2. Polynomial Interpolation
Another basic method is linear interpolation [16]. This method searches for a straight line that passes through the end points xA and xB. Various equivalent equations exist for this method, such as (2a) given in [16], and (2b) given in [17].
where is the interpolation factor and varies from 0 to 1. This method has been considered to be useful and easy to use [18]. By construction and according to [9], interpolated data are bound between xA and xB, and true values are, in average, underestimated: this affirmation is strongly dependent on the distribution of data (on which side the distribution is tailed—left or right) and should be verified for each data set. [16] demonstrated that this method is efficient, and most of the time it is better than non-linear interpolations for predicting missing values in environmental phenomena with constant rates.
The linear interpolation could be extended to higher degrees (Equation (3)). Polynomial, piecewise polynomials, Lagrange form polynomials [9], cubic interpolations such as Cubic Hermite [16] or spline interpolations are different terms for the same technique. Data are exactly fitted with a local polynomial function. These methods differ with the degrees of the polynomial and the continuity of derivatives function. For polynomial or piecewise polynomial interpolation, known and interpolated data are continuous. For the cubic Hermite interpolation, the first derivative function is continuous [16]. For spline techniques, the second derivative function is also continuous [16].
where NMAX is the maximum degree of the polynomial function, cij are coefficients and xi are existing data. As an interpolation method, the amount of data used to estimate the coefficients is equal to K, in order to force the model to match the original records [9]: this is too strong a constraint for when data are uncertain. Sometimes these methods interpolate outside of the observed range of data, contrary to nearest-neighbor and linear interpolations [9], or with spurious oscillations due to too high a degree of polynomials. Bates et al. [19] proposed to penalize the second derivative function of the polynomial to avoid oscillations. Many types of splines are very popular for interpolation. B-splines and their derivative functions could be summed and weighted in MOMS (Maximal Order and Minimal Support) functions [10].
2.1.3. Methods Based on Distance Weighting
These methods are quite similar to the autoregressive methods, and use nearest values weighted by a p power of the distance di to the interpolated point (see Equation (4)).
where n is the number of points used for the interpolation.
These methods can be named inverse distance weighting (if p = 1) of inverse squared distance weighting (if p = 2). Equation (4) shows that the methods are not very different from a moving average. In the review by [20], Taylor’s adjustments of these methods for specific applications (e.g., in [21]) have been proposed for detrended inverse distance weighting, [22] for angular distance weighting, etc.).
2.1.4. Methods Based on Fourier’s Theory: Use of Signal Analysis Methods
In some studies, interpolation methods based on the Fourier’s Transform (FT) are presented. Basically, a Fourier’s transform converts a signal from time or spatial domain to frequency domain: the signal becomes a sum of complex magnitudes. Fourier was the first researcher who used function superpositions to describe physical phenomena: this method assumes that a signal is a sum of different periodic signals (with different periods and magnitudes). If the signal contains aperiodic variations, the FT needs a lot of frequencies. There are many kinds of partial transforms for phase alone, magnitude alone, or signed magnitude [23]. Authors have pointed out the advantages of FT. Chen et al. [24] considered that FT is a good technique, especially for autocorrelation and power spectrum simulations. Musial et al. [9] qualified this method as suitable and efficient for predicting future values, especially if the behavior of the missing values was similar to the existing values. However, some disadvantages have been listed: FT requires Gaussian distribution as autoregressive methods [24], and a similar behavior between observations and predictions [9]. FT is only suitable for stationary data, and without aperiodic extreme behaviors [25].
To avoid a high number of frequencies for aperiodic signals, [9] have used different basic functions as Legendre or Tchebicheff polynomials, and Empirical Orthogonal Functions (EOFs), such as an extension of Principal Component Analysis (PCA) for time-series, also called Spectral PCA (SPCA) by [26]. In this last study, methods have been presented: data pre-processing and filtering of spectra. According to [26], SPCA is more efficient than a basic PCA, due to the fact that the power spectrum is invariant to delays and phase shifts, and that SPCA is less sensitive to the range of missing data (by comparison the range of existing ones) than PCA. Plazas-Nossa and Torres [27] have compared two methods: one based on Discrete FT (DFT), and one mixed with PCA (PCA/DFT). According to the NRMSD criteria (Table 1), efficiencies of these methods are strongly dependent on data and the time of extrapolation. No generalizable conclusions have been found.

Table 1.
Criteria used to evaluate performance of interpolation methods found in literature.
Musial et al. [9] have compared two methods based on FT. The first one is called the Long-Scargle method and retrieves the periodogram of time-series with non-constant time steps. This method could be used with two moving windows: the Hamming or the Kaiser-Bessel [11]. The second window appears to be less sensitive to periodic gaps, and offers better estimations close to the start or the end of the series than the first one. The second one is Singular Spectrum Analysis (SSA) presented by [28] based on EOFs, and where functions are chosen by the data itself [9]. The time series is a sum of trends, oscillations, and noise functions. This method possesses a good theoretical background, and is suitable for a large variety of series (with non-linear trend and non-harmonic oscillations). However, SSA requires a lot of computational effort, and shows a poor performance for long and continuous gaps.
Bienkiewicz et al. [25] have reminded that the Short-Time FT (STFT)—a FT with a fixed size and moving window—is suitable for non-stationary data, but strongly limited by fixed size window and frequency resolution.
The Wavelet Transforms (WTs) are a generalization of the STFT: the size of the window varies with the frequency [25]. Two types of WT exist: the Continuous (CWT, Equation (5)) and the Discrete (DWT).
where is a localized and oscillatory function called a wavelet [29], and CD and CT are the wavelet coefficients of dilatation and translation [30]. These coefficients can be used to understand phenomena. A lot of wavelet functions are available. WT seems to be useful for data with sudden changes [25].
Each of these transforms based on Fourier’s theory (FT, DFT, CFT, STFT, DWT, CWT) can be reversed to assess X(t) and fill in gaps: see e.g., [29] for CWT or [27] for DFT.
A final method has been found in the literature, called Fractal Interpolation [31].
2.1.5. Other Deterministic Interpolation Method
Polynomial interpolations could be extended to any other kind of function if there is a model with a theoretical (e.g., chemical, physical) process description: to predict a discharge with a water level, or to predict a tension with a current, etc. All of those models need to be defined by a user with expertise in the concerned topic. Logistic regressions can be used to predict the missing values of a binary variable [13].
2.2. Stochastic Methods
2.2.1. Regression Methods
Regression methods differ from real interpolation methods in several aspects. The number of data used to calibrate parameters of the regression function is higher than the number of parameters (risk of overfitting). Splines become smoothing splines and the function does not fit each observation as exponential functions (Equation (6)—[16]).
where x0 is the initial value, k is the rate of change, and E(i) represents the stochastic part.
Gnauck [16] designated a part of these methods (and Auto-Regressive methods—Section 2.2.2) as approximation methods: residuals occur and may be a source of uncertainties in interpolated or predicted values. Apart from the nearest-neighbor method and a reformulation of linear interpolations (Equation (2) to Equation (3) with NMAX = 1), both methods presented in Section 2.1 are specific cases of regression methods.
An important advantage of these methods is that no assumptions need to be formulated about the nature of the phenomena [9]. Several authors have pointed out two disadvantages: (i) polynomial interpolations, polynomial or logistic regressions, and splines are tedious [24], inefficient and inapplicable methods [32], and (ii) management of oscillations. Chen et al. [24] pointed out that these methods could miss some variations if a phenomenon is shorter than the size of the gap. NMAX can be chosen according to variables and gaps: [16] preferred non-linear interpolations if gaps lasted more than 28 days for water quality time series. The trade-off between significant and noise variability requires the expertise of the physical processes that underline the data regarding the missing data to be interpolated, and probably to check a posteriori the predictions (interpolated values).
2.2.2. AutoRegressive Methods
These methods are statistical parametric models [13,33] based on a Markovian process. Schlegel et al. [16] explained the basic idea of those methods: a stochastic signal X(t) can be extracted from white noise (, with an average equal to 0) through smoothing processes.
Autoregressive models (AR(p), see Equation (7)), have been mostly used for extrapolation [16].
where p is the order of the autoregressive part, and are coefficients. AR(1) is the Markov process. According to [20], the method combining a state-space approach and the Kalman filter [33] is similar to AR(1).
Moving Average models (MA(q), see Equation (8)) have been considered to be as efficient as linear interpolation for filling gaps [16].
where q is the order of the moving average part and are coefficients. q could be extended to infinity: , as presented in [34].
ARMA(p,q) models are combinations [35] of the two last models (Equation (9)), sometimes called general or mixed ARMA processes [36]. This model can be used only for stationary series [35], and is efficient if the series has Gaussian fluctuations [24].
Other equivalent equations are available to describe ARMA(p,q) models: e.g., in [37]. Ref. [33,35] presents a good introduction to these techniques. Box and Jenkins [33] gave two recommendations: if q < p, the observational errors increase with p, and if q < p − 1, modeling observational errors directly may yield a more parsimonious representation [35]. The introduction of [12] was a good update until the late 1990s.
For interpolation through ARMA(p,q) methods, [12] advised the following four steps: (i) application of the Kalman filter [38]; (ii) skipping the missing values; (iii) estimation of parameters ( and ), and (iv) application of a smoothing algorithm (as Fixed Point Smoothing) to fill gaps [39]. Three methods are available for estimating parameters at the third step. The most popular is the Maximum Likelihood Estimator (MLE), and this has been used by [35]. A second option is the use of the linear least squares interpolator to estimate parameters, as in [2]. Despite the fact that estimation of parameters is equivalent through both methods [36], Ref. [40] considered that this method (linear least square interpolator) to be conceptually and statistically superior to the MLE. Ref. [1,37] extended the use of the Least Absolute Deviation (LAD) to estimate parameters as a third option. A fourth method developed by [41], called Minimum Mean Absolute Error Linear Interpolator (MMAELI) seemed to be less sensitive to outliers or non-usual values, according to [20].
ARMA models have been used on residuals (after a linear regression) for interpolation by [42]: this model, called the Additive Mixed Model is, according to [20], similar to the structural time-series model presented in [43]. Ref. [16] has mentioned ARMAX(p,q) by adding a measurable input signal (called X, external and used as control signal) to ARMA(p,q) model.
There is a last method, based on ARMA(p,q) which is available for non-stationary series: ARIMA(p,d,q) models (Auto-Regressive Integrated Moving Average, Equation (10)). Algorithms are similar than for ARMA(p,q) models. According to [12], the attention of users should be focused on starting conditions of the Kalman filter [38] and a proper definition of the likelihood.
where d is the order of the integrated part. The ARIMA (0,1,1) is also called the simple smoothing exponential [4], or the Exponentially Weighted Moving Average (EWMA, in [44]), and is presented in Equations (11a) and (11b).
where is the smoothing factor and varies from 0 to 1. Gomez et al. [12] proposed three approaches and compared with the RMSE criteria (see Table 1) to estimate missing values: one based on the SKipping approach (SK), one based on the Additive Outlier approach without determinant correction (AON), and a last approach with determinant correction (AOC). Comparisons have been done for pure AR, pure MA, and mixed models. The approaches yielded the same results if there was less than 5% missing data. When more data were missing (20%), the SK approach was clearly faster than the others, but the AOC sometimes gave very precise estimations compared to values given by SK or AON approaches. Differences are explained by convergence properties of reverse filters, and are not negligible for mixed models. Alonso and Sipols [39] demonstrated that a sieve bootstrap procedure is better than methods proposed by [12] for estimating missing values according to the coverage criteria (see Table 1).
Other methods [45] are based on this recursive principle: (i) Holt-Winter exponential or double seasonal exponential (see Equations (12) and (13)), (ii) triple exponential (Equations (14)), and the SARIMA (Seasonal ARIMA) presented in [20].
where is the smoothing factor, is the trend smoothing factor, and is the seasonal change-smoothing factor. Each of them vary from 0 to 1.
2.2.3. Machine Learning Methods
Artificial Neural Networks (ANN)
ANN have been applied since late 1990s for interpolation purposes as a promising method [24] to model and predict missing data. This method is able to approximate universal functions [46]. Neurons are disposed in many layers: an input layer where input variables are added (here existing records), an output layer (here the estimation of the missing values), and between them, one or a few hidden layers. Neurons, also called nodes or ‘perceptrons’, are connected with weighted links and contain basic functions from vectors (input of the neuron) to scalar (output). This is a data-driven method, and a number of hypotheses have to be set a priori for the number of hidden layers and underlying models.
ANNs have precious advantages. They are able to learn underlying behaviors under widely varying circumstances [24] such as non-linear or complex relationships, and to work with noisy data [47]. Of course there are some disadvantages as well. ANN can suffer from over-fitting and under-fitting, mainly due to the number of hidden layers [4]. To avoid over-fitting, two solutions can be applied: (i) application of a smoothing method to reduce the noise of predictions, or (ii) application of an Adaptative Neural Network, as presented by [4]. There is no theoretical background to choose the optimal shape of the model, special skills are needed, and this requires a lot of computation time [24]. Training is necessary to calibrate the networks with observations [4]: parameters of the pattern (connection weights and nodes biases) can iteratively change to decrease prediction errors [48]. Data for the learning process should be similar to the missing data, in order to provide accuracy and robust predictions. Some studies have been published to improve the efficiency of training in ANN [3]. Chen et al. [24] used ANN for churn predictions.
The structure or shape of the network is strongly correlated to data characteristics [4]. Zhang and Qi [49] suggested that a single hidden layer, where neurons are connected with acyclic links, is the most used shape of network for modeling and forecasting in time series. Many hidden layers are required to catch non-linear relationships between variables [4].
Wong et al. [4] gave an explicit relationship (Equation (15)) to predict a missing value (Xi+1).
where and are parameters of the model, il is the number of neurons of the input layer, r is the number of hidden neurons, and g is the hidden-layer transfer function from hidden layer. The logistic function is often used.
To avoid over-fitting problems, [4] developed the ADNN method, based on ANN with adaptive metrics input (a solution to take local trends and amplitude in considerations and based on the Adaptive K-nearest neighbors method—AKN) and an admixture mechanism for output data. They demonstrated that this method gives better results than usual techniques (ANN, AKN, AR, especially for chaotic and real time series).
Kernel Methods
Kernel methods have been used since the 1990s: Support Vector Machines (SVMs), kernel Fisher discriminant, and kernel principal component analysis [32]. SVMs generally offer better performances than ANN methods, are adapted to high dimensional data, and have been used for interpolation purposes despite the required computation time. SVM builds a hyperplane (Equation (16)) in a high dimensional data set.
where is the hyperplane, is a non-linear function from a high to a higher dimensional area, and is the weighted vector. A kernel function is needed to estimate coefficients in the model. Kernel functions perform pairwise comparison: linear and algebraic functions, polynomials, and trigonometric polynomials functions can be used [32], but Gaussian (also called Radial Basis) functions are the most popular [18]. The accuracy of prediction with SVM is strongly dependent on the choice of the kernel function and its parameters. Tripathi and Govindajaru [32] underlined that there is no general consensus to calibrate parameters of the kernel function. More details about basics of SVM are presented in [50,51].
Multiple Kernel SVMs (MK-SVMs) use a combination of kernel functions [52] to find an optimal kernel [18]. Two kinds of algorithms can solve this formulation: (i) in one step that contains classic reformulations, and (ii) in two steps designed to decrease computational times [18].
Based on those techniques, [18] have implemented a Hierarchical-MK-SVM (H-MK-SVM) divided in three steps to learn coefficients for static or longitudinal behavioral data. According to the result of this study, H-MK-SVM is more efficient than most existing methods for churn prediction.
Relevance Vectors Machines (RVMs) are based on SVM and Bayesian theory [53]. RVMs have the same advantages and disadvantages as SVM and are able to predict uncertainty. Tripathi and Govindajaru [32] provided a four-step method based on RVMs to estimate the parameters of a kernel according to prediction risk (based on Leave-one-out cross validation). This method showed promising results for hydrologic data sets.
Tree Approaches
Decision trees have been used for decades to solve classification problems in the various sciences. Only a few studies have reported [18] or used [54] decision trees to fill gap(s): for churn prediction or for air quality data. Decision trees are used for too short a time to have a step back. Amato et al. [54] have demonstrated that the advantage of this method (by comparison to mean value and polynomial interpolation method) without detailing how many variables or the number of used acquired samples have been used for prediction. Many trees could be used through the random forest method.
Meta-Algorithms of Machine Learning Methods
Several meta-algorithms can also be used to fill gaps in data: boosting, adaboosting, bagging, etc. [18]. These meta-algorithms are used depending on the problem (classification, regression, etc.), to improve the performance (accuracy and robustness) of methods presented in this section.
2.2.4. Methods Based on Data Dynamics
In this section, methods based on the behavior of observations are briefly presented.
k-Nearest Neighbors (kNN)
The kNN method [55] is probably the simplest to understand of these methods, is well adapted to pseudo-periodic signals, and should not be confused with the nearest neighbor approach. This method is based on the understanding of the evolution of the k-nearest neighbors. In observations, N windows of size T are compared to the windows of interest (where data are missing) with different metrics. Local and global methods should be distinguished [55]: the global one takes the whole data into account: the global one is less sensitive to new behaviors. According to [55], the value of T is often chosen by sight (according to the period of the signal), and many metrics (cityblock, Euclidean, Chebychev, etc.) are available to choose the k-nearest neighbors. Kulesh et al. [55] presented an adaptation of the nearest neighbors based on flexible metrics that reduce problems of amplitude changing and trend determination. Missing values are estimated, with a function in which selected nearest-neighbors are the variables. The function could be a weighted average of the k nearest neighbors for any integer k > 1. In that case, this method is very similar to MA methods, especially EWMA.
Box-Jenkins Models
Brubacher and Tunnicliffe Wilson [2] have reported works on Box-Jenkins models. These models are mainly based on autoregressive methods (see Section 2.2.2) while including some seasonality. That is why they are considered to be useful for polycyclic data (with various frequencies i.e., in predicting data related to human behavior—like electricity or tap water demand—or natural data presenting some strong seasonal patterns—like water level in river or in water table).
Method of Moment Fitting
Carrizosa et al. [13] have proposed a method based on the preservation of moments and autocorrelation between observations and predictions: this method requires a smooth non-convex optimization problem to be solved. Authors have compared this method to other existing ones. According to absolute percent error, absolute and quadratic differences, the method outperformed linear, nearest neighbor, cubic interpolation, and spline methods for a single gap of 30% of the time series.
Other Methods Based on Data Dynamic
Chen and Andrew [56] listed a serial of other available methods, based on data behavior and applied to economical interpolations: Denton additive, Denton proportional, Growth rate preservation, and first and second difference smoothing. More details are presented in [57]. Another method, considered as a refinement of inverse distance weighting method by [20], is the natural neighbor interpolation [58]: this method requires additional data (such as topology and by extension, other univariate series) to interpolate the missing value(s).
2.2.5. Methods Based on Kriging
Despite the fact that kriging methods are mostly used for multi-dimensional (i.e., spatial) data interpolation, they can be used for time series. Kriging groups a wide range of geostatistical methods, often used for spatial interpolation and for multivariate [59] or sometimes univariate series [60]. A detailed review of these methods would require another review paper, but a brief introduction and list of the most relevant studies is given hereafter. As a common factor for all these methods, the interpolated value is estimated by a linear weighted combination of near values where weights and number of used values are dependent on the correlation between existing values [61]. Combinations of kriging methods with Sequential Gaussian Simulation (SGS, [62]) or Sequential Indicator Simulation (SIS, [63]) allows estimation of uncertainty, and the distribution of the predictions.
The most common version of kriging is Simple Kriging (SK, Equations (17), e.g., in [64]).
where i is the location of existing values (single or multiple), m is the known stationary average, R(i) is the stochastic portion at i location(s) with a zero mean, constant variance, and a non-constant covariance (that varies with a distance between the i location(s) and the location of observations used for the calculation), n is the number of existing values used for the calculation, j is the location of the interpolated value, and are the weights of the existing value(s) (at location i) to estimate the missing value(s) at the location j.
Other versions of kriging have been developed and published: Ordinary Kriging (OK) where the sum of the weights is equal to 1, and m is constant and unknown, Kriging with a Trend (KT) model [61], also called kriging in a presence of trend or drift [58] where m (Equation (17a)) is not constant, block kriging, which can be used to estimate a value for a defined block (in term of distance, duration, e.g., an average daily water table). Some other kriging methods allow the estimation of the conditional cumulative distribution function of Xi, such as indicator kriging, disjunctive kriging [65], and Multi-Gaussian kriging.
Knotters et al. [20] have listed numerous other kriging methods that are used for spatial (multivariate) and time (univariate) interpolation: log-normal kriging [65], trans-Gaussian kriging [66], factorial kriging, [67] and variability decomposition in combination with kriging with a relative variogram and non-stationary residual variance [68]—similar methods such as [20], class kriging [69], Poisson krigring [70], Bayesian kriging [70], robust kriging [71], de-trending combined with kriging [72], neural network residual kriging [73], modified residual kriging [74] and compositional kriging [75].
2.2.6. Other Stochastic Methods
A collection of other methods has been cited and listed in [18] and [76]: methods based on classification (rule based classifier), statistical methods (logistic regression, Bayesian Networks, hazard proportional model also Cox’s regression) or a combination (Naïve Bayes). Two methods based on stochastic processes have been used for interpolation purposes: Spartan random processes [77] and Markovian arrival processes [7]. Transfer function-noise (TFN) modeling is another interpolation method initially developed by [33], e.g., with application in [78]. A continuous-time transfer function noise model (PIRFICT) is described and has been used by [79] to characterize the dynamics of slow processes.
3. Criteria Used to Compare Interpolation
A brief overview of applied criteria is given in Table 1. Most of them use variance between observed n values (xi) and predicted n values (Xi). Their averages ( or ), and standard deviation of observed values have been also been used. Equations in Table 1 have been extracted from articles and, sometimes, from personal conversations with authors. More than 30 criteria have been used in previous studies. Sometimes the same equation has different names in the studies. In [1], the applied criterion (MSE) has not been explicitly given.
Gnauck [16] then considered that r2 criteria cannot be used, due to non-normally distributed data and non-linear effects in some phenomena, such as water quality processes. Some criteria could be used only for a specific method, such as AUC or MP, as proposed by [76], or APE [13]. Chen et al. [18] used criteria based on the confusion matrix for binary classification [76] where TP are the True Positive, FP the False Positive, FN the False Negative, and TN the True Negative values. Those criteria/methods can only be applied if variables have been divided in classes. Alonso and Sipols [39] introduced criteria about coverage interval of interpolated values: LL for Lower Limit, and UL for Upper Limit of the 95% confidence interval. These values can be calculated with various equations (by the law of propagation of uncertainties) or with numerical methods. This is why no equation has been given for those values. The time of computation has been used in some studies. This is a useful measure for future users, but the characteristics of the computer are not always given: relative comparisons between different studies becomes more complicated with regard to this criterion. Any trade-off between quality and the cost of methods needs to be performed by each user [10].
4. Evaluation of Uncertainties
Among all the existing methods, there are normalized methods to assess uncertainties that are most likely used by practitioners and end-users. These standards are briefly presented in this section.
4.1. Law of Propagation of Uncertainties
The law of propagation of uncertainties [5] is an analytical method: standard uncertainty (u(y)) of the output y of a model f calculated is with N variables; here, the observed data, (xi) is calculated through Equation (18).
Confidence intervals can be estimated with enlargement factors. This method requires that distributions of uncertain parameters and variables are known and symmetrical, and that an explicit and differentiable model f exists. This method always leads to underestimation of the prediction uncertainty due to the averaging effect, as illustrated in the example in the introduction.
4.2. Monte-Carlo Simulation
Monte-Carlo simulations can be used for uncertainty estimation [6]: the probability distributions of parameters and variables (generated with the respect of covariance between them) are propagated through NMC simulations (NMC is the number of Mont-Carlo simulations), to ascertain the probability distribution of the output y. This technique requires long computation times, but it can be used without an explicit model (as f in Section 4.1) and for every kind of distribution (symmetrical, asymmetrical, etc.). Any statistical property of y can be computed from the Monte Carlo realization of y. For example, the 95% confidence interval of y is calculated in four steps: (i) calculation of NMC values of y; (ii) ranking of values; (iii) calculation of the width of multiple 95% confidence intervals from the cumulative distribution function [; ] to [; ], and finally (iv) the smallest interval is retained as the final 95% confidence interval [6].
5. Discussion: From Literature Outcomes to a New Method
As this literature review has pointed out, there are numerous available methods to interpolate time series (Tables 5.1, 5.2 and 5.3 presented in [20] and other references in this study), and numerous criteria to assess the efficiencies of those methods. A second conclusion from the review is that uncertainties of the interpolated variables are generally not integrated in the interpolation methods, despite the fact that most of the methods can assess the uncertainty. End users of basic interpolation methods (real interpolation, regression methods, (k-) nearest neighbors, etc.) need some guidance for selecting the most appropriate method for their own purposes and data sets. Unfortunately, no study has presented quite an exhaustive comparison between a broad selection of methods, for a number of reasons, which are discussed in the paragraphs hereafter.
The first reason relates to the choice and the nomenclature of performance criteria of interpolation methods. As demonstrated in Table 1, there are quite a few non-conformities between formulas, names, and authors. In most of the published articles and communications, details of criteria are not given: this makes comparisons between studies more difficult, due to the lack of a common reference.
A second reason, already discussed by [12,16], is the typology of gaps that have to be filled. The ranking of desirable methods (obtained through a trade-off of criteria) could be strongly dependent on the size of the gaps, and the nature of recorded phenomena and data. The typologies of gaps should be specified and tested in future studies, to allow a critical review from partial comparisons (only few methods tested).
A third and a last reason is the evaluation of prediction uncertainties, which is the starting point and main question of this present study. During the review process presented, no satisfactory estimation (according to our standards and expected values of uncertainties) has been found to fit the following reflection.
In a given time series x and its standard uncertainty u(x) associated with the vector x, a few values of x (called hereafter xREMOVED) and their standard uncertainties u(xREMOVED) have been intentionally removed to simulate artificial gaps. Interpolation methods have then been applied to estimate the missing values xCALCULATED. Standard uncertainties (u(xCALCULATED)) associated to those estimated values should be equal or higher than u(xREMOVED), to take into account the added uncertainties due to the interpolation itself. Listed methods in this paper are at least numerical and often deterministic (i.e., derivatives could be calculated, under differentiability assumptions). Consequently, the law of propagation of uncertainties or Monte Carlo simulations could be applied to assess uncertainties of the interpolation method itself. As shown in the introduction for the law of propagation of uncertainties, those methods are not enough to properly assess prediction uncertainties.
Uncertainty has been estimated in a few studies only. Paulson [31] calculated uncertainties of predictions with linear interpolation: uncertainties of observations, correlation between them and residuals of the interpolation model have been taken into account in that study. Alonso and Sipols [39] developed a bootstrap procedure to calculate the lower and upper limit of the confidence interval of the predictions with ARMA models. Athawale and Entezari [15] presented a method for assessing the probability density function to cross a value between two existing points. Ref. [7] published a relevant study and review of experimental distribution of daily rain amounts.
To enhance the research on this topic, we propose to explicitly account for the process variance and autocorrelation in the evaluation of the process uncertainty. The following method is proposed here (based on [84]). Suppose the process state x represented in a equidistant time series (e.g., water level, discharge, flow velocity) (ti,xi), with i = 1, …, N and ti = i*dt at t = (with (i − 1)*dt < < i*dt) is obtained from a simple linear interpolation (Equation (19)):
where is the interpolated value, and are existing (measured) values, α and β are weighing factors in the interpolation. The process has a known process variance σP, a mean value of μp, and an autocorrelation function ρ(τ). The mean squared error (MSE, see Table 1) of the interpolation is calculated (Equation (20)).
The last term in the Equation (20) is the bias term, which vanishes when α + β = 1. Minimizing the MSE for α and β results in optimal values for the latter parameters. Assuming that α + β = 1 and imposing the following condition (Equation (21)):
Then, α and β can be derived (Equation (22)):
Which leads to (Equation (23)):
A simple case is obtained when the interpolation is done exactly halfway between the two adjacent samples, in this case, ρ (ti−1, τ) = ρ (ti, τ), resulting in (Equation (24)):
Assuming that the measuring error σm is independent from the process monitored (i.e., the sensor has a measuring error that is not depending on the measuring scale), the total uncertainty at the interpolated point is (Equation (25)):
It can be seen that in a process with an autocorrelation function, |ρ(t)| = 1, the error in the interpolation is equal to the measurement error. For every process with an autocorrelation −1 < ρ(t) < 1 the prediction uncertainty is larger than the measuring error.
The reasoning outlined (incorporating the process variability as well as the measuring uncertainty when interpolating) here can also be applied to more complicated interpolation techniques, as described in the literature review section of this article.
Future research will focus on the differences between several interpolations techniques in terms of prediction uncertainty, taking into account the characteristics of the (physical) process involved.
Figure 1 shows the uncertainties of interpolated values asset by: (i) the law of propagation of uncertainties (top left); (ii) the Monte-Carlo method (top right); (iii) the method proposed in [17] (bottom left), and (iv) the method proposed above (bottom right). The rain time series recorded in Rotterdam (The Netherlands) has been used for this comparison. On the top left, the law of propagation of uncertainties gave uncertainties lower than, and respectively equal to standard observation uncertainties (0.01 mm/h) under the hypothesis that data are fully negatively (ρ(t) = −1) and positively (ρ(t) = 1) correlated, respectively. Any additional calculation to estimate partial correlation in the time series will lead to estimations between these two dashed dot lines. The application of this first normalized method always leads to an underestimation of uncertainties, despite calculations of partial autocorrelation in the time series. On the top right, Monte Carlo method results have been plotted with a correlation coefficient of 0.051 (corresponding to the partial correlation of the time series, with a lag of 29 time steps—the lag between the last and the next values known around the gap): the resulting curve is in the area delimited by the law of propagation of uncertainties. The method proposed by [17] gave standard uncertainties (bottom left) mostly higher than the observation standard uncertainties except at the boundaries: standard uncertainties are lower here. The proposed method (bottom right) seems to give more logical estimations of standard uncertainties, with continuity at the gap boundaries, and the highest value in the middle of the interpolated values (the farthest position from the known data).
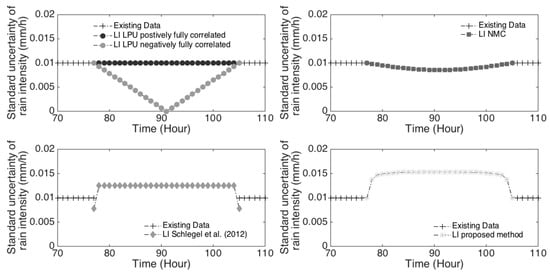
Figure 1.
Different methods to asset prediction uncertainties.
6. Conclusions
There are numerous methods and criteria for assessing the quality of interpolation methods. In the literature, many redundancies, discrepancies, or subtleties have been found: different names for the same method or criteria, different equations for the same criteria, etc. Future research should be very explicit and detailed, in order to avoid potential misunderstanding due to lexical discrepancies. No comprehensive comparative studies have been published so far: this lack of exhaustive feedback might be problematic for researchers, engineers, and practitioners who need to decide upon choosing interpolation methods for their purposes and data. To the authors’ knowledge, no comparative study published so far has dealt with methods to quantify prediction uncertainties. This can explain why prediction uncertainties are, in practice, only rarely calculated. The combination of the easiest interpolation methods and uncertainty calculation standards leads to mistakes in uncertainty assessments (as demonstrated in the discussion part), and methods that perform both interpolation and uncertainty calculation have not been exhaustively compared.
According to these conclusions, future work should focus on those topics to fill in the gaps in literature, and to give the tools for researchers to decide between the many available methods. In this respect, two kinds of studies could be useful: (i) exhaustive and comparative studies with a special attention for lexical issues, to standardize names of methods and criteria (used as a new reference), and (ii) development of new methods to assess prediction uncertainties.
Acknowledgments
This work has been completed as part of the Marie Curie Initial Training Network QUICS. This project has received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement No. 607000.
Author Contributions
Mathieu Lepot performed the bibliographic review and writing of the draft. François H.L.R. Clemens developed the proposed method. Jean-Baptiste Aubin gave his expertise on the overall review of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beveridge, S. Least squares estimation of missing values in time series. Commun. Stat. Theory Methods 1992, 21, 3479–3496. [Google Scholar] [CrossRef]
- Brubacher, S.R.; Tunnicliffe Wilson, G. Interpolating time series with application to the estimation of holiday effects on electricity demand. J. R. Stat. Soc. Ser. C 1976, 25, 107–116. [Google Scholar] [CrossRef]
- Singh, S.K.; McMillan, H.; Bardossy, A. Use of the data depth function to differentiate between case of interpolation and extrapolation in hydrological model prediction. J. Hydrol. 2013, 477, 213–228. [Google Scholar] [CrossRef]
- Wong, W.K.; Xia, M.; Chu, W.C. Adaptive neural networks models for time-series forecasting. Eur. J. Oper. Res. 2010, 207, 807–816. [Google Scholar] [CrossRef]
- JCGM 109. Uncertainty of Measurement–Part 1: Introduction to Expression of Uncertainty in Measurement. In ISO/EIC Guide 98-1; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- ISO. ISO/IEC Guide 98-3/Suppl. 1: Uncertainty of Measurement—Part #: Guide to the Expression of Uncertainty in Measurement (GUM: 1995) Supplement 1: Propagation of Distributions Using a Monte Carlo Method; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Ramirez-Cobo, P.; Marzo, X.; Olivares-Nadal, A.V.; Francoso, J.A.; Carrizosa, E.; Pita, M.F. The Markovian arrival process, a statistical model for daily precipitation amounts. J. Hydrol. 2014, 510, 459–471. [Google Scholar] [CrossRef]
- Van Steenbergen, N.; Ronsyn, J.; Willems, P. A non-parametric data-based approach for probabilistic flood forecasting in support of uncertainty communication. Environ. Model. Softw. 2012, 33, 92–105. [Google Scholar] [CrossRef]
- Musial, J.P.; Verstraete, M.M.; Gobron, N. Technical Note: Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. 2011, 11, 7905–7923. [Google Scholar] [CrossRef]
- Thévenaz, P.; Blu, T.; Unser, M. Interpolation revisited. IEEE Trans. Med. Imaging 2000, 19, 739–758. [Google Scholar] [CrossRef] [PubMed]
- Hocke, K.; Kämpfer, N. Gap filling and noise reduction of unevenly sampled data by means of the Lomb-Scargle periodigram. Atmos. Chem. Phys. 2009, 9, 4197–4206. [Google Scholar] [CrossRef]
- Gómez, V.; Maravall, A.; Peña, D. Missing observations in ARIMA models: Skipping approach versus additive outlier approach. J. Econom. 1999, 88, 341–363. [Google Scholar] [CrossRef]
- Carrizosa, E.; Olivares-Nadal, N.V.; Ramirez-Cobo, P. Times series interpolation via global optimization of moments fitting. Eur. J. Oper. Res. 2014, 230, 97–112. [Google Scholar] [CrossRef]
- Sibson, R. A brief description of natural neighbor interpolation. In Proceedings of the Interpreting Multivariate Data, Sheffield, UK, 24–27 March 1980. [Google Scholar]
- Athawale, T.; Entezari, A. Uncertainty quantification in linear interpolation for isosurface extraction. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2723–2732. [Google Scholar] [CrossRef] [PubMed]
- Gnauck, A. Interpolation and approximation of water quality time series and process identification. Anal. Bioanal. Chem. 2004, 380, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Schlegel, S.; Korn, N.; Scheuermann, G. On the interpolation of data with normally distributed uncertainty for visualization. Vis. Comput. Graph. 2012, 18, 2305–2314. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-Y.; Fan, Z.-P.; Sun, M. A hierarchical multiple kernel support vector machine for customer churn prediction using longitudinal behavioural data. Eur. J. Oper. Res. 2012, 223, 461–472. [Google Scholar] [CrossRef]
- Bates, R.; Maruri-Aguilar, H.; Wynn, H. Smooth Supersaturated Models; Technical Report; London School of Economics: London, UK, 2008; Available online: http://www.mucm.ac.uk/Pages/Downloads/Other_Papers_Reports/HMA%20Smooth%20supersaturated%20models.pdf (accessed on 16 October 2017).
- Knotters, M.; Heuvelink, G.B.M.; Hoogland, T.; Walvoort, D.J.J. A Disposition of Interpolation Techniques. 2010. Available online: https://www.wageningenur.nl/upload_mm/e/c/f/43715ea1-e62a-441e-a7a1-df4e0443c05a_WOt-werkdocument%20190%20webversie.pdf (accessed on 16 October 2017).
- Attore, F.; Alfo, M.; De Sanctis, M.; Fransceconi, F.; Bruno, F. Comparison of interpolation methods for mapping climatic and bioclimatic variables at regional scale. Environ. Ecol. Stat. 2007, 14, 1825–1843. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily European climate data. J. Geophys. Res. Atmos. 2008, 113, D21110. [Google Scholar] [CrossRef]
- Roy, S.C.D.; Minocha, S. On the phase interpolation problem—A brief review and some news results. Sãdhanã 1991, 16, 225–239. [Google Scholar] [CrossRef]
- Chen, Y.; Kopp, G.A.; Surry, D. Interpolation of wind-induced pressure time series with an artificial network. J. Wind Eng. Ind. Aerodyn. 2002, 90, 589–615. [Google Scholar] [CrossRef]
- Bienkiewicz, B.; Ham, H.J. Wavelet study of approach-wind velocity and building pressure. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 671–683. [Google Scholar] [CrossRef]
- Thornhill, N.F.; Naim, M.M. An exploratory study to identify rogue seasonality in a steel company’s supply network using spectral component analysis. Eur. J. Oper. Res. 2006, 172, 146–162. [Google Scholar] [CrossRef]
- Plazas-Nossa, L.; Torres, A. Comparison of discrete Fourier transform (DFT) and principal components analysis/DFT as forecasting tools of absorbance time series received by UV-visible probes installed in urban sewer systems. Water Sci. Technol. 2014, 69, 1101–1107. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef]
- Pettit, C.L.; Jones, N.P.; Ghanem, R. Detection and simulation of roof-corner pressure transients. J. Wind Eng. Ind. Aerodyn. 2002, 90, 171–200. [Google Scholar] [CrossRef]
- Gurley, K.; Kareem, A. Analysis interpretation modelling and simulation of unsteady wind and pressure data. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 657–669. [Google Scholar] [CrossRef]
- Paulson, K.S. Fractal interpolation of rain rate time series. J. Geophys. Res. 2004, 109, D22102. [Google Scholar] [CrossRef]
- Tripathi, S.; Govindajaru, R.S. On selection of kernel parameters in relevance vector machines for hydrologic applications. Stoch. Environ. Res. Risk Assess. 2007, 21, 747–764. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Pourahmadi, M. Estimation and interpolation of missing values of a stationary time series. J. Time Ser. Anal. 1989, 10, 149–169. [Google Scholar] [CrossRef]
- Jones, R.H. Maximum likelihood fitting of ARMA models to time series with missing observations. Technometrics 1980, 22, 389–395. [Google Scholar] [CrossRef]
- Ljung, G.M. A note on the estimation of missing values in time series. Commun. Stat. Simul. Comput. 1989, 18, 459–465. [Google Scholar] [CrossRef]
- Dunsmuir, W.T.M.; Murtagh, B.A. Least absolute deviation estimation of stationary time series models. Eur. J. Oper. Res. 1993, 67, 272–277. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. Am. Soc. Mech. Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Alonso, A.M.; Sipols, A.E. A time series bootstrap procedure for interpolation intervals. Comput. Stat. Data Anal. 2008, 52, 1792–1805. [Google Scholar] [CrossRef]
- Peña, D.; Tiao, G.C. A note on likelihood estimation of missing values in time series. Am. Stat. 1991, 45, 212–213. [Google Scholar] [CrossRef]
- Lu, Z.; Hui, Y.V. L-1 linear interpolator for missing values in time series. Ann. Inst. Stat. Math. 2003, 55, 197–216. [Google Scholar] [CrossRef]
- Dijkema, K.S.; Van Duin, W.E.; Meesters, H.W.G.; Zuur, A.F.; Ieno, E.N.; Smith, G.M. Sea level change and salt marshes in the Waaden Sea: A time series analysis. In Analysing Ecological Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Visser, H. The significance of climate change in the Netherlands. An Analysis of Historical and Future Trends (1901–2020) in Weather Conditions, Weather Extremes and Temperature Related Impacts. In Technical Report RIVM Report 550002007/2005; National Institute of Public Health and Environmental Protection RIVM: Bilthoven, The Netherlands, 2005. [Google Scholar]
- Sliwa, P.; Schmid, W. Monitoring cross-covariances of a multivariate time series. Metrika 2005, 61, 89–115. [Google Scholar] [CrossRef]
- Gould, P.G.; Koehler, A.B.; Ord, J.K.; Snyder, R.D.; Hyndman, R.J.; Vahid-Araghi, F. Forecasting time series with multiple seasonal patterns. Eur. J. Oper. Res. 2008, 191, 207–222. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superposition of a sigmoïdal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Masters, T. Advanced Algorithms for Neural Networks: A C++ Sourcebook; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Liu, M.C.; Kuo, W.; Stastri, T. An exploratory study of a neural approach for reliability data analysis. Q. Reliab. Eng. 1995, 11, 107–112. [Google Scholar] [CrossRef]
- Zhang, P.; Qi, G.M. Neural network forecasting for seasonal trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistic Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Sonnenburg, S.; Rätsch, G.; Schäfer, C.; Schölkopf, B. Large scale multiple kernel learning. J. Mach. Learn. Res. 2006, 1, 1–18. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Amato, A.; Calabrese, M.; Di Lecce, V. Decision trees in time series reconstruction problems. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Victoria, Vancouver Island, BC, Canada, 12–15 May 2008. [Google Scholar]
- Kulesh, M.; Holschneider, M.; Kurennaya, K. Adaptive metrics in the nearest neighbor’s method. Physica D 2008, 237, 283–291. [Google Scholar] [CrossRef]
- Chen, B.; Andrews, S.H. An Empirical Review of methods for Temporal Distribution and Interpolation in the National Accounts. Surv. Curr. Bus. 2008, 31–37. Available online: https://www.bea.gov/scb/pdf/2008/05%20May/0508_methods.pdf (accessed on 16 October 2017).
- Cholette, P.A.; Dagum, E.B. Benchmarking, temporal distribution and reconciliation methods of time series. In Lecture Notes in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for environmental scientists. In Statistic in Practice; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Heidelberg/Berlin, Germany, 2005. [Google Scholar]
- Matheron, G. Principles of Geostatistics. Ecomony Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Jamshidi, R.; Dragovich, D.; Webb, A.A. Catchment scale geostatistical simulation and uncertainty of soil erodibility using sequential Gaussian simulation. Environ. Earth Sci. 2014, 71, 4965–4976. [Google Scholar] [CrossRef]
- Juang, K.W.; Chen, Y.S.; Lee, D.Y. Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils. Environ. Pollut. 2004, 127, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists. In Technical Report GeoCat #68229; Australian Government: Canberra, Australia, 2008. [Google Scholar]
- Journel, A.G.; Huijbergts, C.J. Mining Geostatistics; Academic Press: London, UK, 1998. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Goovaerts, P.; Gebreab, S. How does the Poisson kriging compare to the popular BYM model for mapping disease risks? Int. J. Health Geogr. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Raty, L.; Gilbert, M. Large-scale versus small-scale variation decomposition, followed by kriging based on a relative variogram, in presence of a non-stationary residual variance. J. Geogr. Inf. Decis. Anal. 1998, 2, 91–115. [Google Scholar]
- Allard, D. Geostatistical classification and class kriging. J. Geogr. Inf. Decis. Anal. 1998, 2, 77–90. [Google Scholar]
- Biggeri, A.; Dreassi, E.; Catelan, D.; Rinaldi, L.; Lagazio, C.; Cringoli, G. Disease mapping in vetenary epidemiology: A Bayesian geostatistical approach. Stat. Methods Med. Res. 2006, 15, 337–352. [Google Scholar] [CrossRef] [PubMed]
- Fournier, B.; Furrer, R. Automatic mapping in the presence of substitutive errors: A robust kriging approach. Appl. GIS 2005, 1. [Google Scholar] [CrossRef]
- Genton, M.G.; Furrer, R. Analysis of rainfall data by robust spatial statistic using S+SPATIALSTATS. J. Geogr. Inf. Decis. Anal. 1998, 2, 116–126. [Google Scholar]
- Demyanov, V.; Kanevsky, S.; Chernov, E.; Savelieva, E.; Timonin, V. Neural network residual kriging application for climatic data. J. Geogr. Inf. Decis. Anal. 1998, 2, 215–232. [Google Scholar]
- Erxleben, J.; Elder, K.; Davis, R. Comparison of spatial interpolation methods for snow distribution in the Colorado Rocky Mountains. Hydrol. Process. 2002, 16, 3627–3649. [Google Scholar] [CrossRef]
- Walvoort, D.J.J.; De Gruitjer, J.J. Compositional kriging: A spatial interpolation method for compositional data. Math. Geol. 2001, 33, 951–966. [Google Scholar] [CrossRef]
- Verbake, W.; Dejaeger, K.; Martens, D.; Hur, J.; Baesens, B. New insights into churn prediction in the telecommunication sector: A profit driven data mining approach. Eur. J. Oper. Res. 2012, 218, 211–229. [Google Scholar] [CrossRef]
- Žukovič, M.; Hristopulos, D.T. Environmental time series interpolation based on spartan random processes. Atmos. Environ. 2008, 42, 7669–7678. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Webster, R. Modelling soil variation: Past, present and future. Geoderma 2001, 100, 269–301. [Google Scholar] [CrossRef]
- Von Asmuth, J.R.; Knotters, M. Characterising groundwater dynamics based on a system identification approach. J. Hydrol. 2004, 296, 118–134. [Google Scholar] [CrossRef]
- Varouchakis, E.A.; Hristopulos, D.T. Improvement of groundwater level prediction is sparsely gauged basins using physical laws and local geographic features as auxiliary variables. Adv. Water Resour. 2013, 52, 34–49. [Google Scholar] [CrossRef]
- Woodley, E.J.; Loader, N.J.; McCarroll, D.; Young, G.H.F.; Robertson, I.; Hetqon, T.H.E.; Gagen, M.H. Estimating uncertainty in pooled stable isotope time-series from tree-rings. Chem. Geol. 2012, 294–295, 243–248. [Google Scholar] [CrossRef]
- Chen, Y.; Kopp, G.A.; Surry, D. Prediction of pressure coefficients on roofs of low buildings using artificial neural networks. J. Wind Eng. Ind. Aerodyn. 2003, 91, 423–441. [Google Scholar] [CrossRef]
- Mühlenstädt, T.; Kuhnt, S. Kernel interpolation. Comput. Stat. Data Anal. 2011, 55, 2962–2974. [Google Scholar] [CrossRef]
- Schilperoort, T. Statistical aspects in design aspects of hydrological networks. In Proceedings and Information No. 35 of the TNO Committee on Hydrological Research CHO; TNO: The Hague, The Netherlands, 1986; pp. 35–55. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).