3.1. Box-Behnken Design
In this work, the response surface methodology (RSM) approach is applied to the evaluation and optimization of the piping stability in the bimsoils. In this work, the RSM approach is applied to evaluatean index of critical hydraulic gradient (which is defined as the value of piping initiation) for bimsoil during piping. Based on the least squares criterion, RSM is utilized to approximate a response over a range of variability of input factors, in terms of the maximum critical hydraulic gradient. The RSM model can offer a cost-effective and efficient way to deal with the uncertain factors for piping seepage, the form of it can be linear or fully quadratic. More detailed statistical and mathematical theories of RSM can refer to studies of Myers and Montgomery [
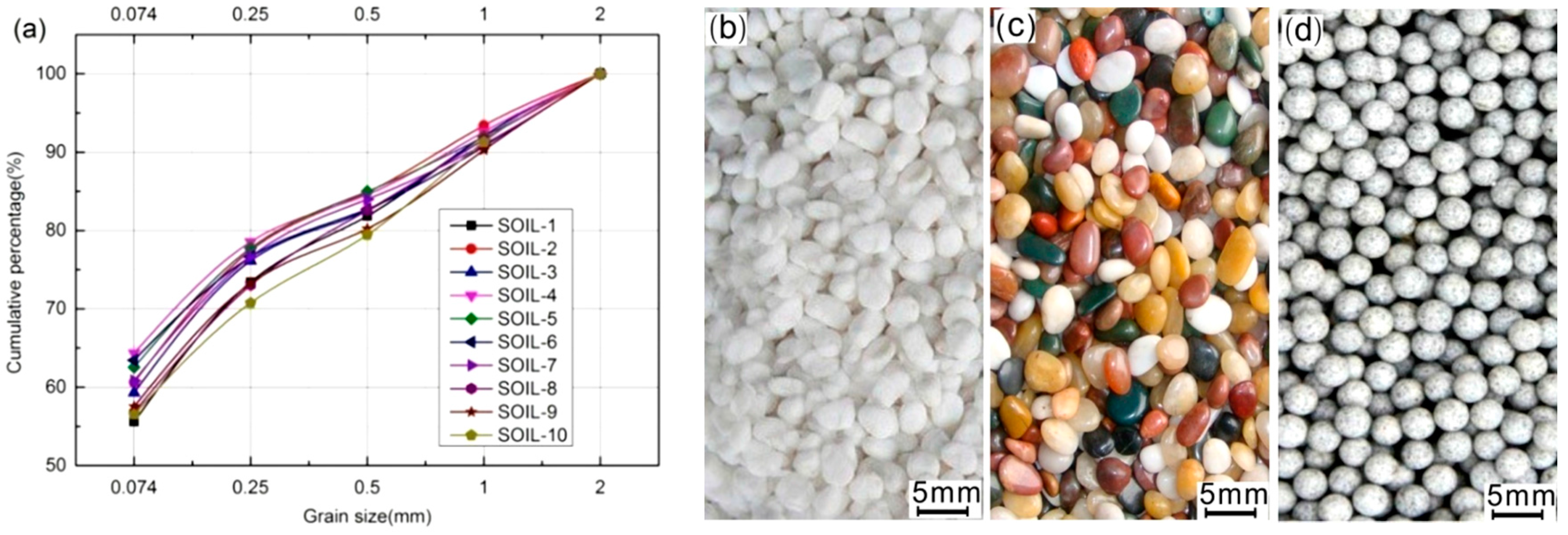
33]. Four uncertain parameters, such as rock block percentage (RBP), soil matrix density (SMD), confining pressure (CP), and block morphology (BM)are given a reasonable range with the actual minimum and maximum values or coded symbol of “−1” and “+1”, respectively, as listed in
Table 3. According the principle of the RSM method, for the four variables, a total of 27 cases were required based on the approach of Box-Behnken Design, which originated from the optimal design theory [
34,
35,
36].
Table 4 lists the 27 combinations of these uncertain parameters generated by the Box-Behnken Design. After the piping experiment of each case, the results of critical hydraulic gradient are listed in column 8 in
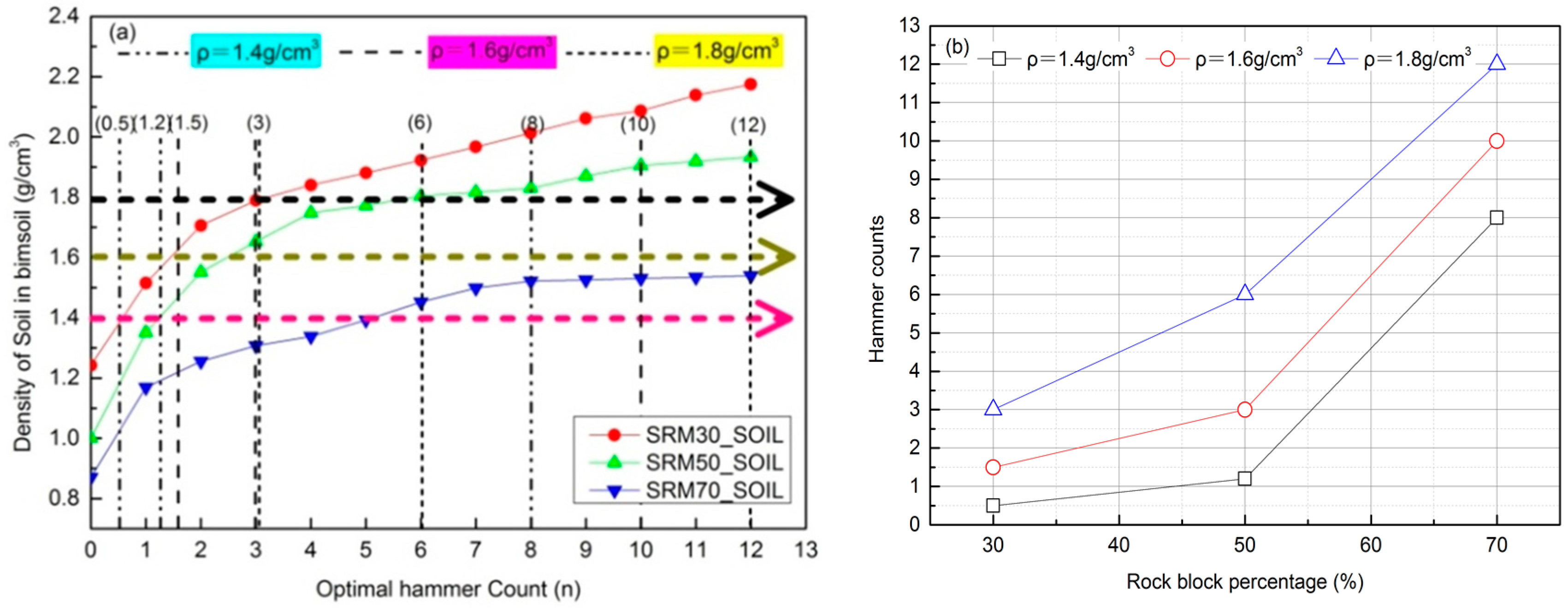
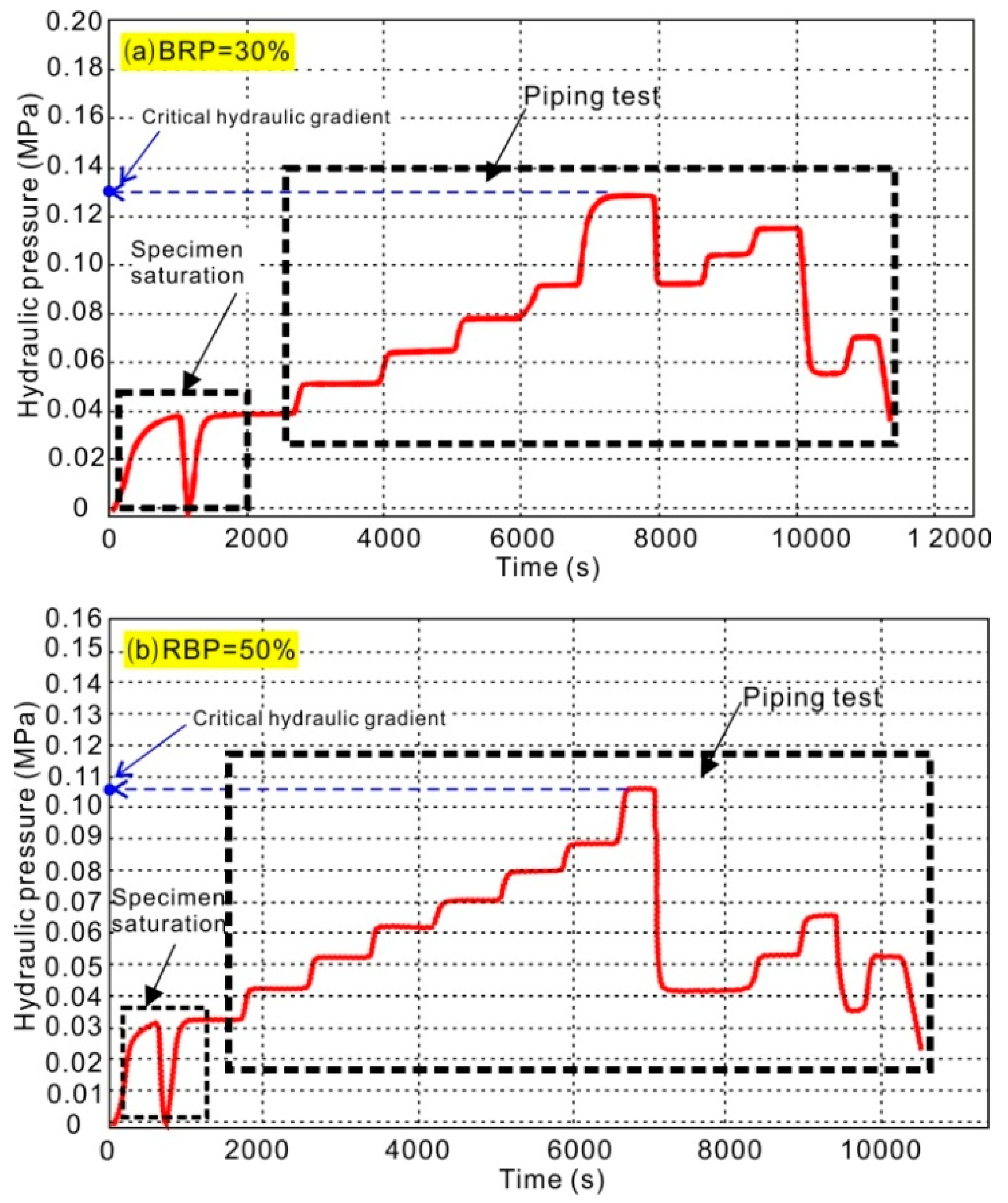
Table 4, as the response value. The critical hydraulic gradient is determined from the curves of hydraulic gradient against time. Taking the specimen with RBP of 30% and 50% for example (
Figure 9), hydraulic gradient increases with the increase of flow time. When it reaches a critical value, the curve suddenly drops and fluctuates with time. The inflection point is determined as the critical hydraulic gradient. Some significant results can be drawn from
Figure 9, as below:
- (1)
The curves presents fluctuation trend after the critical hydraulic pressure, however, the value cannot exceed the critical peak value. This result implies that irreversible damage occurs in bimsoil during piping. During process of piping, the erosion, and movement of soil particles result in the change of permeability. When the fine soil particles during movement are clogged in the pores, leading to the increment of hydraulic gradient, seepage velocity, and the associated permeability coefficient; and when the clogged pores are break through again, these values suddenly decrease. This non-linear multiple fluctuation always existsin the piping process.
- (2)
From the curves of flow water, it can also be seen that the slope of the curve in not constant, but variational during the whole test. The non-linear fluctuation behavior of the curves shows that the evolution of piping includes a series of complex movement behaviors, such as the erosion, migration of fine soil particles; contact erosion of rock-soil interface; forming of pore channel; blocking of flow channel by fine soil particles; breakdown of the blocked flow channel; and, re-block of the flow channel, etc. The characteristics of piping in bimsoilare progressive and repeated. The blocked flow channel can be attributed to two factors, one is the fine soil particles; the other is the movement of rock blocks, as the structure of bimsoil sample changes, the blocks would sink along the direction of water flow.
3.2. RSM Model Analysis
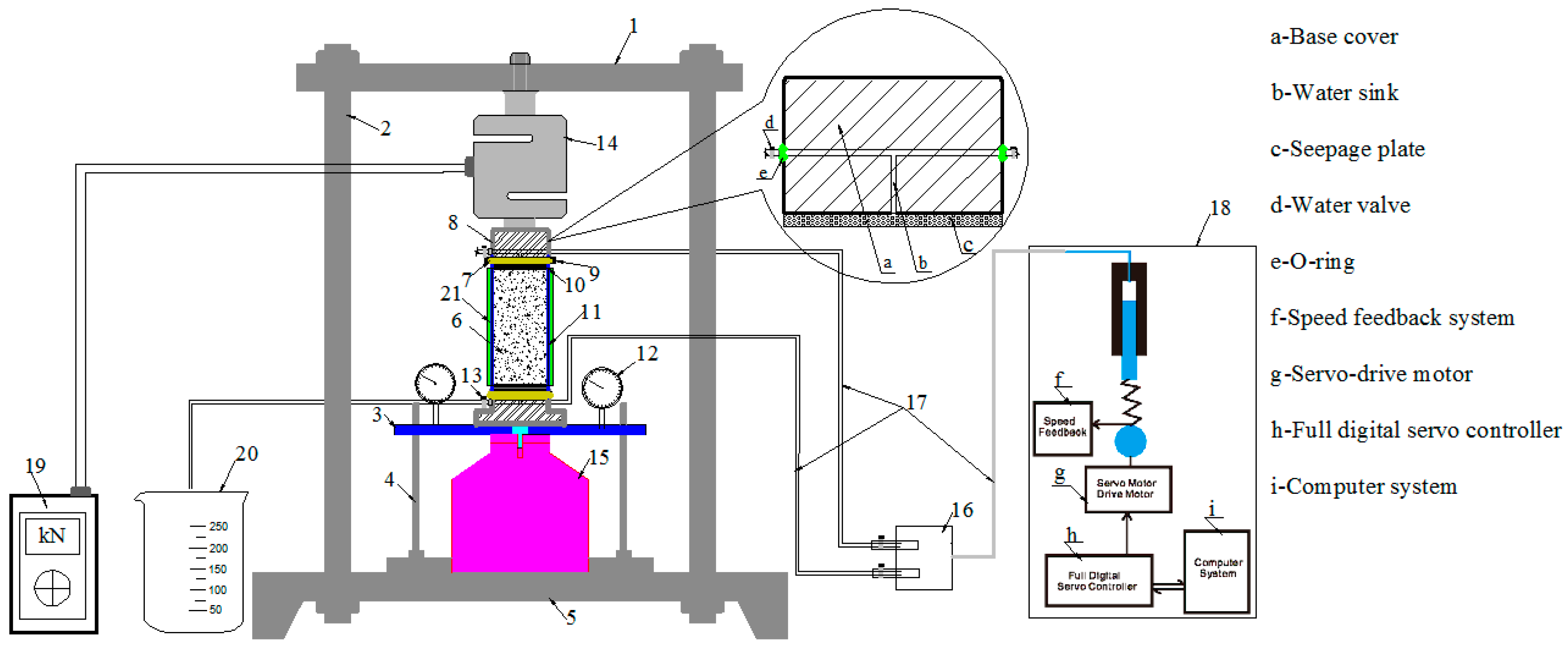
From
Figure 8, the onset of the steep drop in the hydraulic pressure-flow time curves was assumed to estimate the critical hydraulic gradient. Beyond this point, the seepage velocity, hydraulic gradient, and permeability fluctuate repeatedly. This method to determine the critical hydraulic gradient has also been used by other researchers, such as Das et al. [
37] and Das and Viswanadham [
38] during piping tests. When the critical hydraulic gradient was obtained, the RSM method is used to analyze the relationship between the response value and the four uncertain factors. In order to select the appropriate RSM model, a linear model, two factor model interaction model (2FI), quadratic model, and cubic model are selected to judge, which polynomial fits the equation based on the statistical approach, as shown in
Table 5.
Table 5 lists the response surface model for the critical hydraulic gradient. If the model has the highest polynomial, and the other additional terms are significant, and the model is not aliased [
12,
39], we choose it as the appropriate model. We would not select the cubic model, if it is aliased. Aliasing phenomenon decreases the number of experimental runs. When this appears, several groups of effects are combined into one group and the most significant effect in the group is used to represent the effect of the group. Essentially, it is important to note that the selected model should not be aliased. In addition, the model has the maximum “Predicted R-Squared” and “Adjusted R-Squared” is also important criteria to be considered [
39]. From the results of
Table 5, the fully quadratic model is finally selected to build the critical hydraulic gradient (CHG) response surface in the subsequent optimization process.
The anova for the response surface quadratic model of CHG is shown in
Table 6. From the result, the model F-value of 24.01 implies the model is very significant, the change is less than 0.1% that a “Model F-Value” this large could occur due to noise. Values of “Prob > F” less than 0.05 indicates that the model variations are significant. In this case, the model
p-value prob of the studied factors is <0.0001, 0.0020, 0.013, and 0.0325; this result indicates that the factors of A, B, C, and D are all significant model terms. The smaller the
p-value pro, the more sensitive of the factor is to the response surface. The influential order of these four factors is: A-rock block percentage > C-confining pressure > B-soil matrix density > D-block morphology. The equations fitted to the critical hydraulic gradient response surface in terms of actual factors are:
where A is the rock block percentage; B is the soil matrix density; C is the confining pressure; and, D is the block morphology.
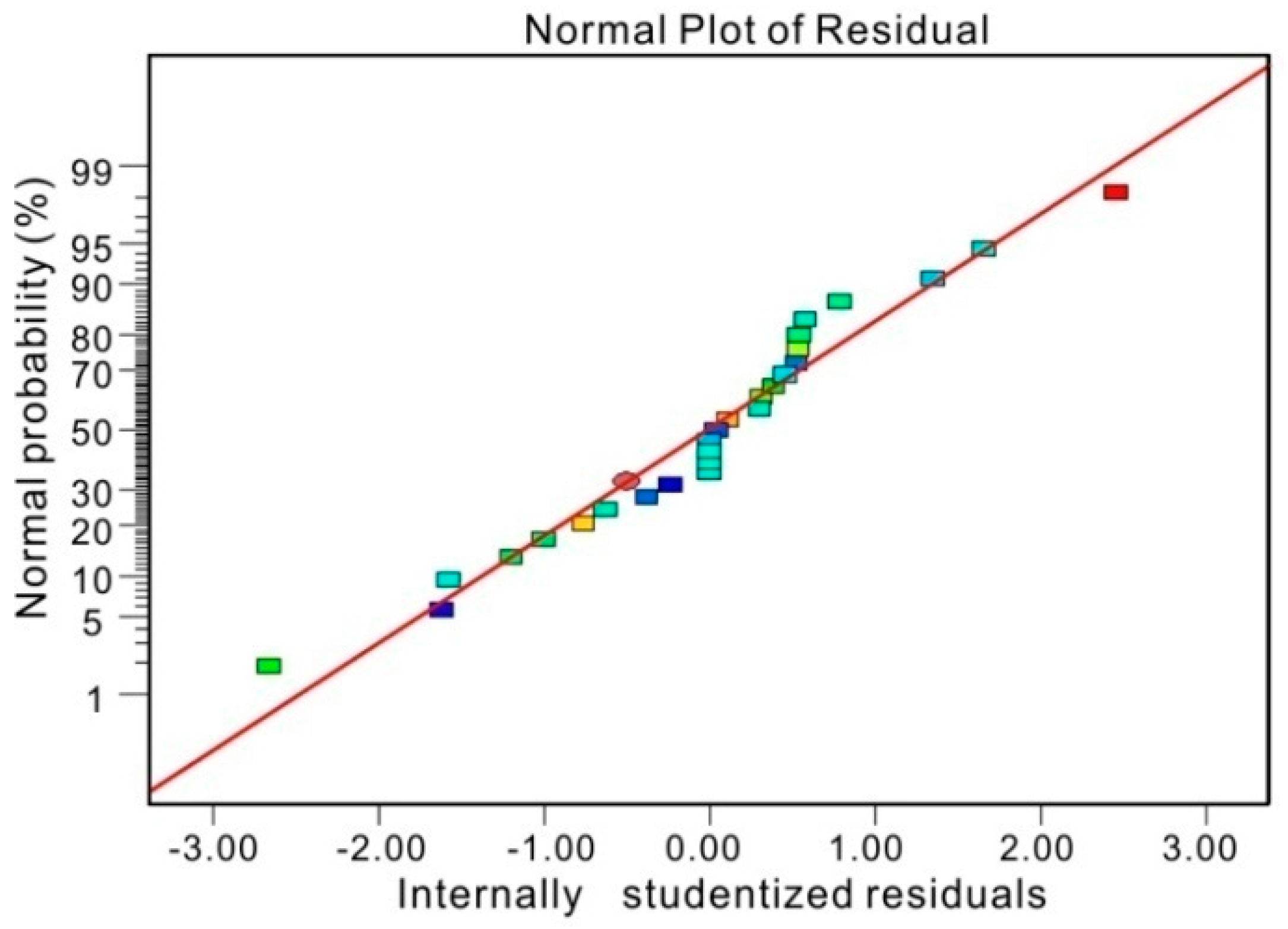
Figure 10 shows the normal plots of residuals, which can reflect the distribution of the residuals for the response value of the critical hydraulic gradient. All of the test points in the “Normal Plot of Residuals” fall on the straight line, implying that the residuals are normally distributed, and the model is significant.
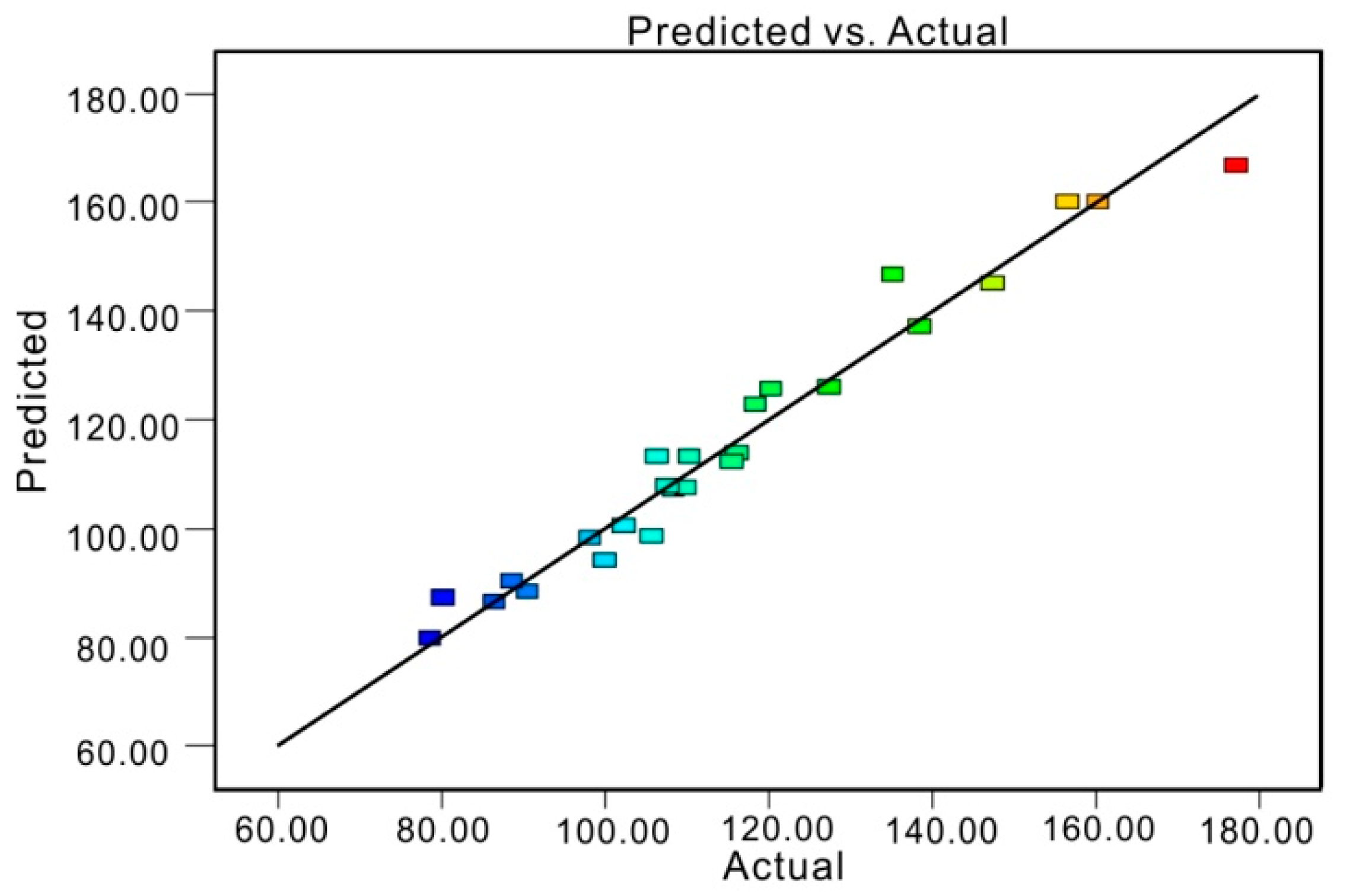
Figure 11 shows the “Predicted versus Actual” for critical hydraulic gradient, illustrating whether the generated equation of gradient response surface accurately predicts the actual values. It can be seen that generated hydraulic gradient response surface models provide such reliable predicted values for hydraulic gradient, as compared to the actual values of the hydraulic gradient.
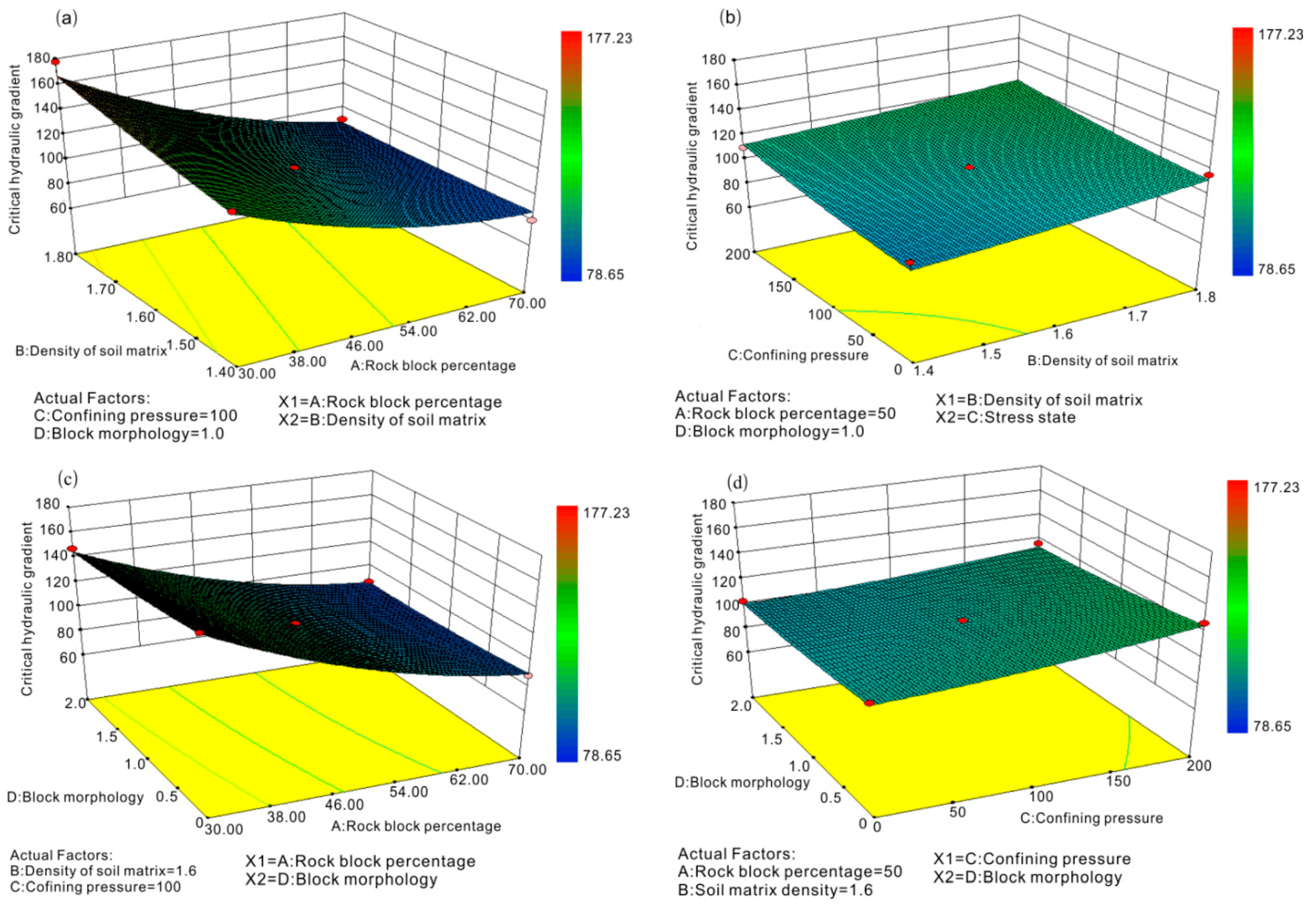
Figure 12 plots the three-dimensional (3D) response surface of the four studied factors, the response surface represents all the 27 run case. It shows the influential tread of the four factors to CHG.
Figure 12a plots the influence of factor rock block percentage and soil matrix density on the CHG response. It can be clearly seen that CHG decreases with the increasing rock block percentage;
Figure 12b plots the influence of soil matrix density and confining pressure on CHG response, the CHG increases with the increase of confining pressure and soil matrix density;
Figure 12c plots the influence of rock block percentage and block morphology on the CHG response, the CHG increases with the increase of block angularity, this result implies the incremental compactness of soil particles and contact between soil matrix and rock blocks. The coupling degree of rock block and soil matrix improves as the confining pressure and soil density increase. Content of rock blocks increases the number of rock-soil interface, the sudden drop of seepage force at these interfaces causes the occurrence of contact erosion, and the associated seepage failure, which leads to the decrement of flow stability of bimsoil specimen.
3.4. Discussions
Based on the experimental data of the piping test, we used the response surface method to conduct the sensitive analysis. The rock block percentage is the most sensitive factor influenced the seepage erosion failure. The role of rock blocks in bimsoil is always considered to be the important factor influencing the mechanical and physical properties. Xu et al. [
40], Liao [
41], Dan et al. [
15], and Wang et al. [
10] have conducted a series of permeable test forbimsoil, they found that rock blocks in bimsoil have obvious effect on permeability coefficient. In our study, it was also found that rock blocks have an obvious influence on the critical hydraulic gradient. Although the rock blocks play a role of an impervious effect, this effect may improve the permeability in some ways, however, the contact erosion at rock-soil interface is always the decisive factor controlling the seepage failure of bimsoil. Along the seepage direction, the hydraulic pressure drops sharply at rock-soil interfaces, resulting in the formation of a great seepage force at the interfaces, flow channel of erosion first forms at these parts. Therefore, the characteristics of rock blocks (e.g., size, shape, distribution, content, etc.) control the flow life of specimens, and the critical hydraulic gradient decreases with an increasing rock block content. The factor of confining pressure reflects the in-situ stress state of bimsoil, some scholars clearly point out that when studying the permeable characteristics of bimsoil, confining pressure should not be ignored [
29,
42]; otherwise, most of the testsdo not consider the actual stress state. Soil matrix density is also a crucial factor to the permeable characteristics of bimsoil, Zhou et al. [
28] conducted orthogonal tests on the permeability of bimsoil. They found that soil density is more sensitive to other factors. Tickell and Hiatt [
43] discussed the influence of granular angularity and roundness on the permeability coefficient, found that with the increasing of angularity, the permeability coefficient increases. The result implies that angularity has different degree of resistance on water flow. Our test results further prove this phenomenon and reveal some new insights on the seepage failure of bimsoils.