Variation of Aridity Index and the Role of Climate Variables in the Southwest China
Abstract
:1. Introduction
2. Study Area and Data
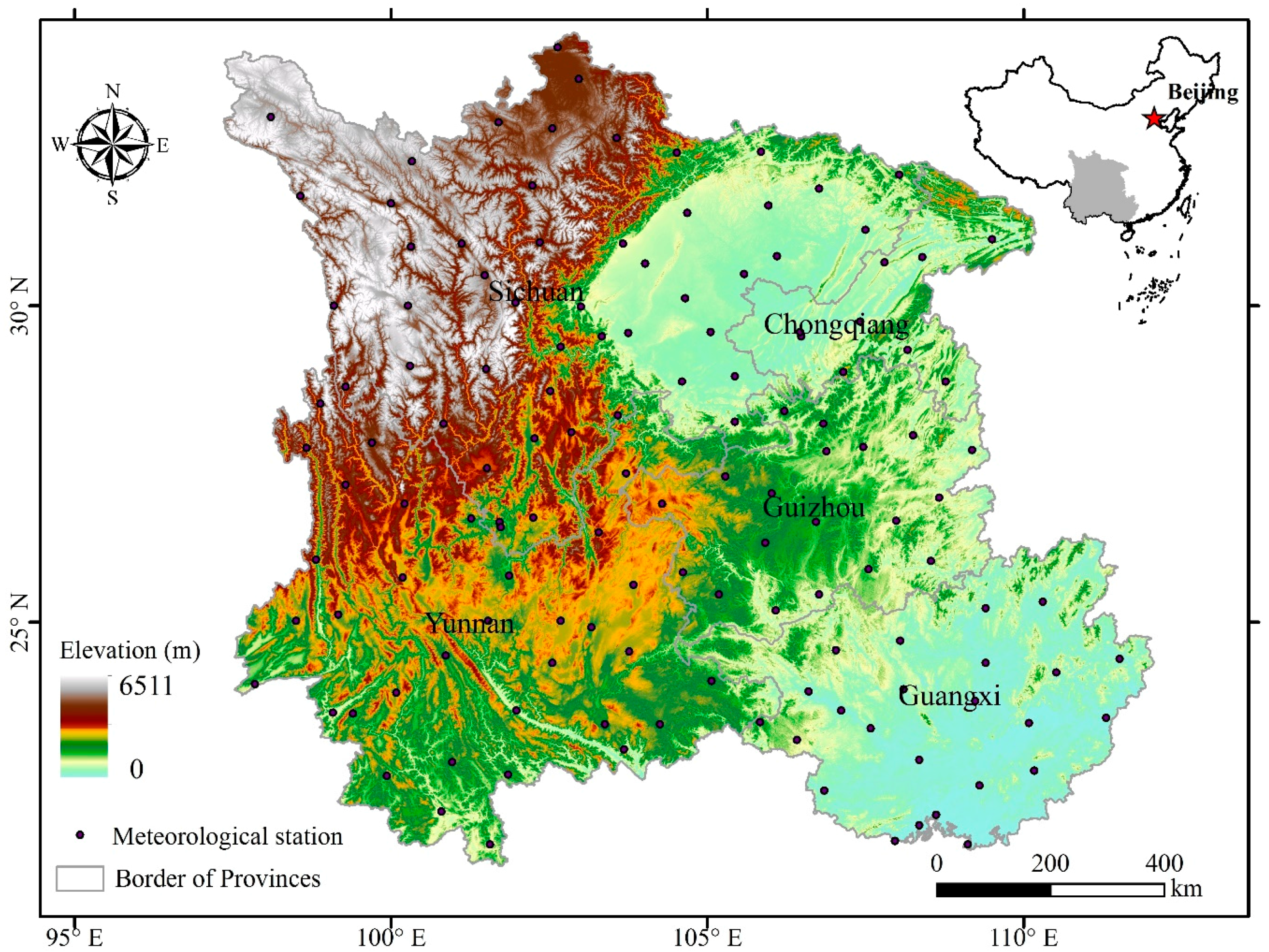
2.1. Study Area
2.2. Data
3. Methods
3.1. Calculation of Aridity Index
3.2. Attribution Analysis
3.3. Statistical Analysis
4. Results
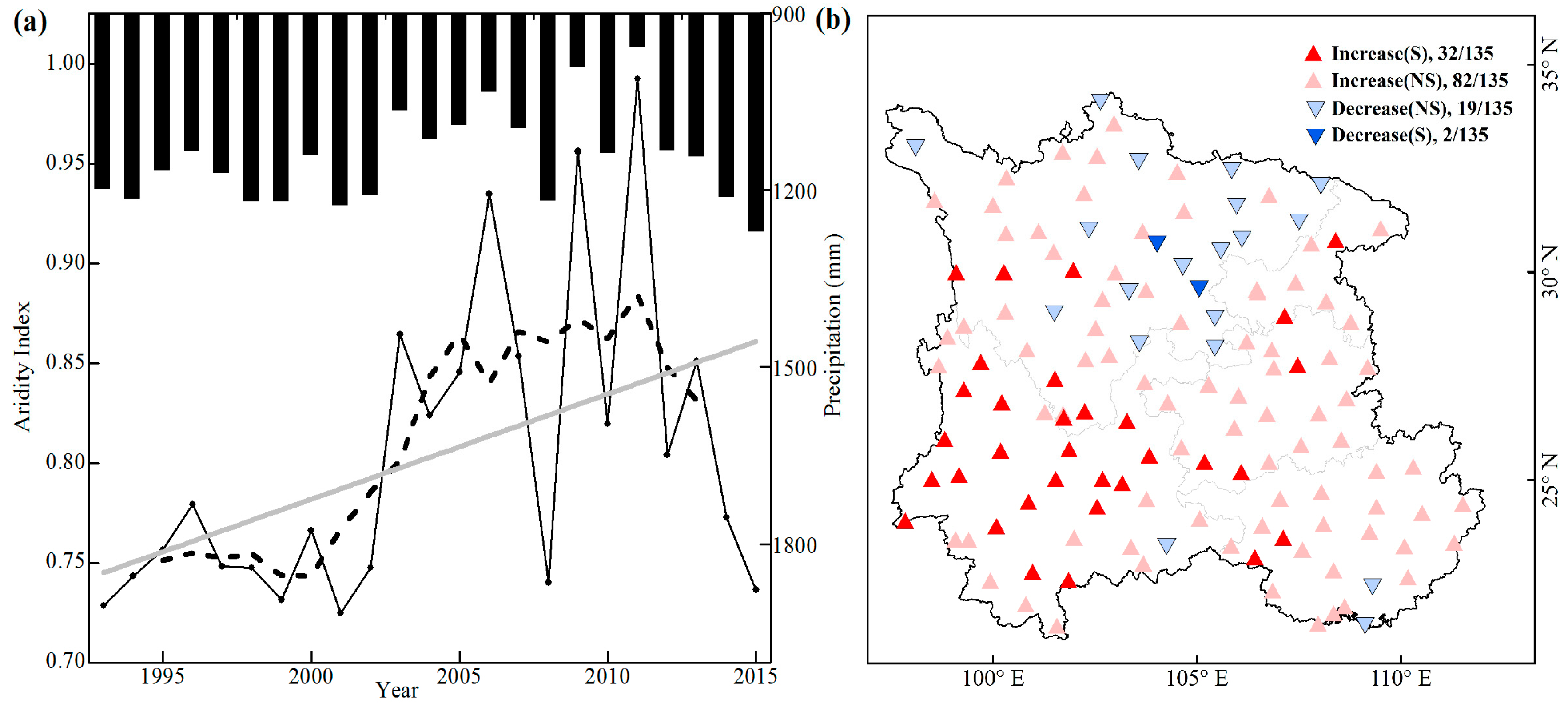
4.1. Variation of AI
4.2. Sensitivity of AI to Climate Variables
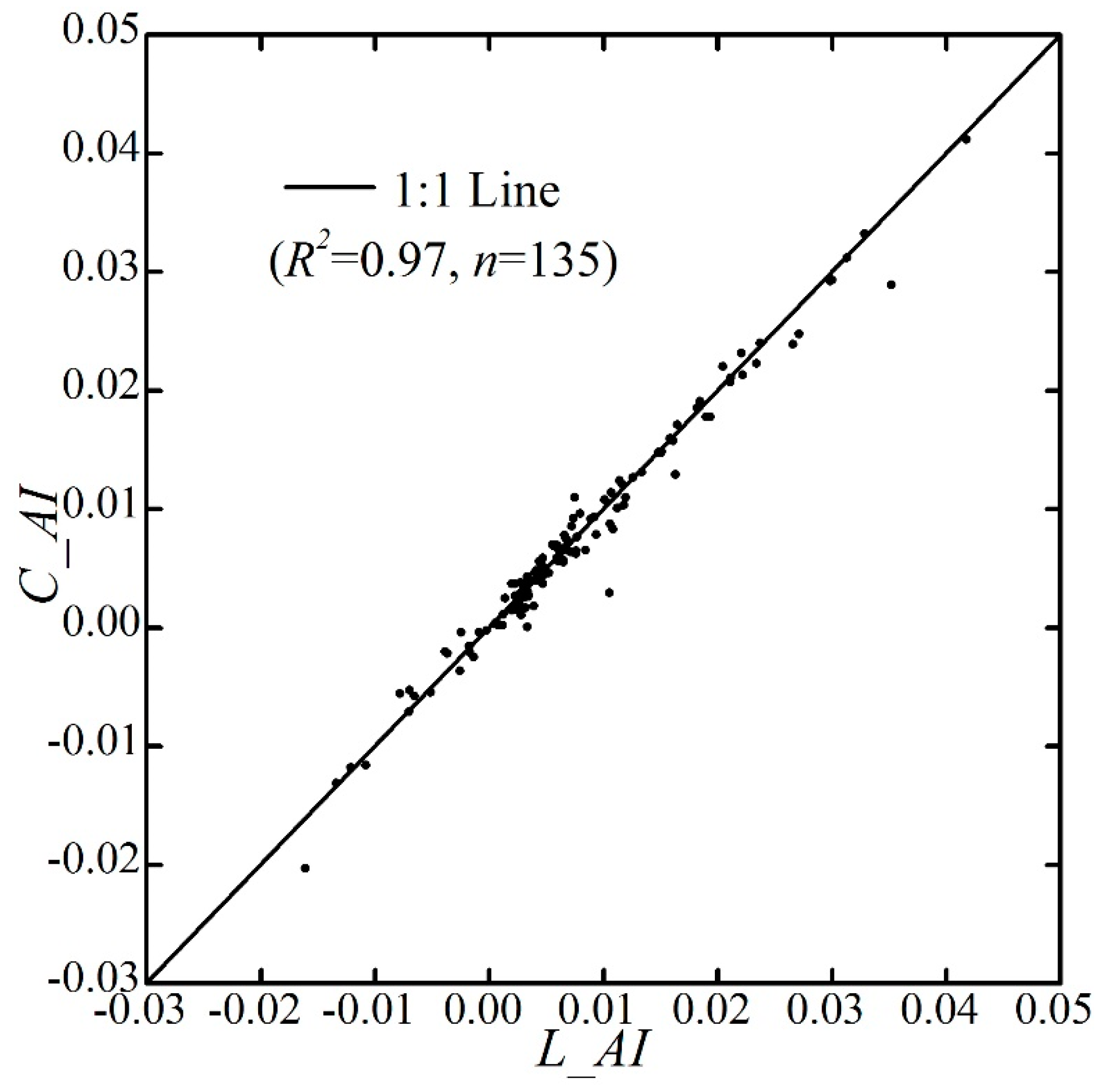
4.3. Attribution of the Variation in Aridity Index
5. Discussion
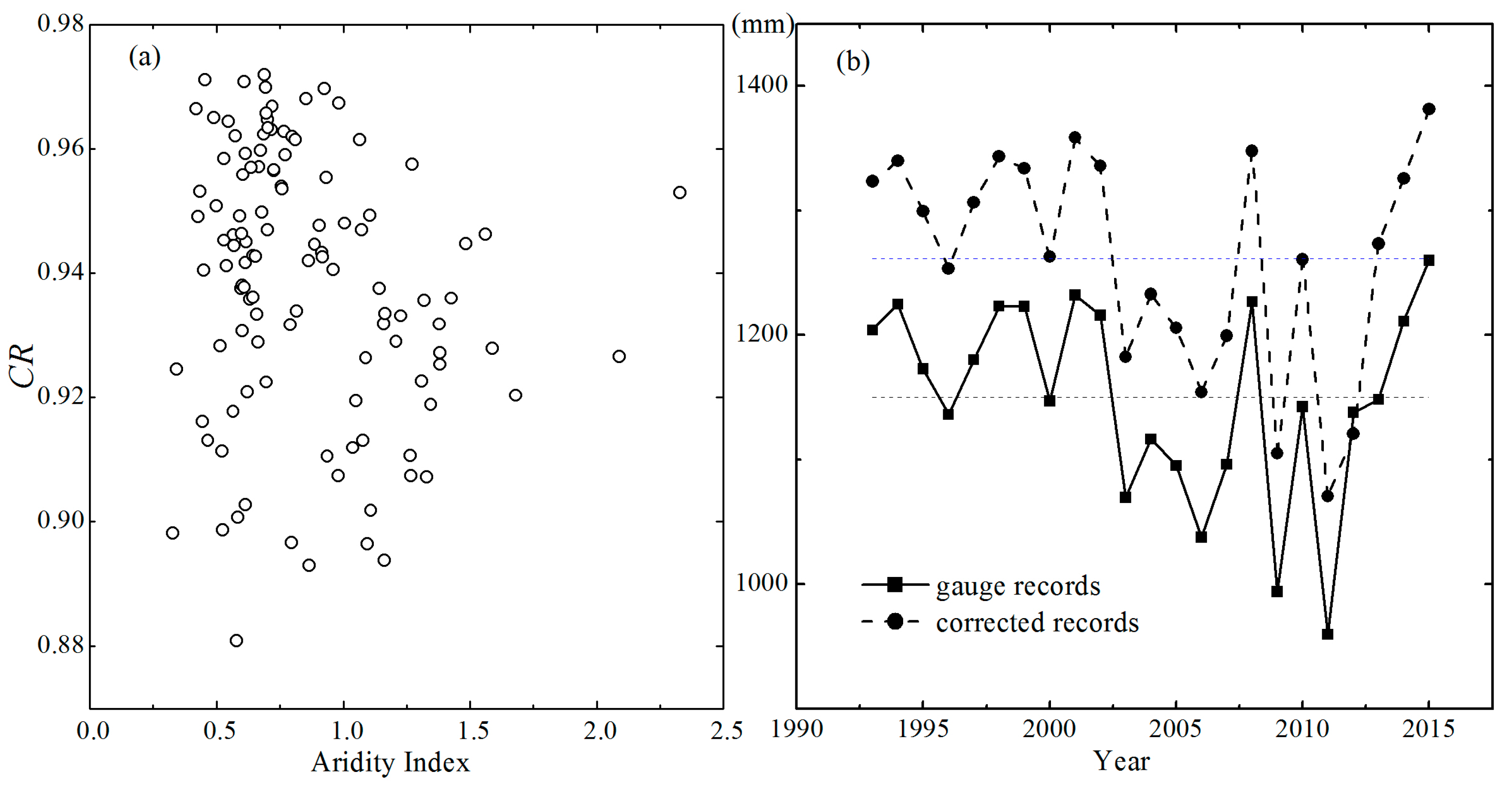
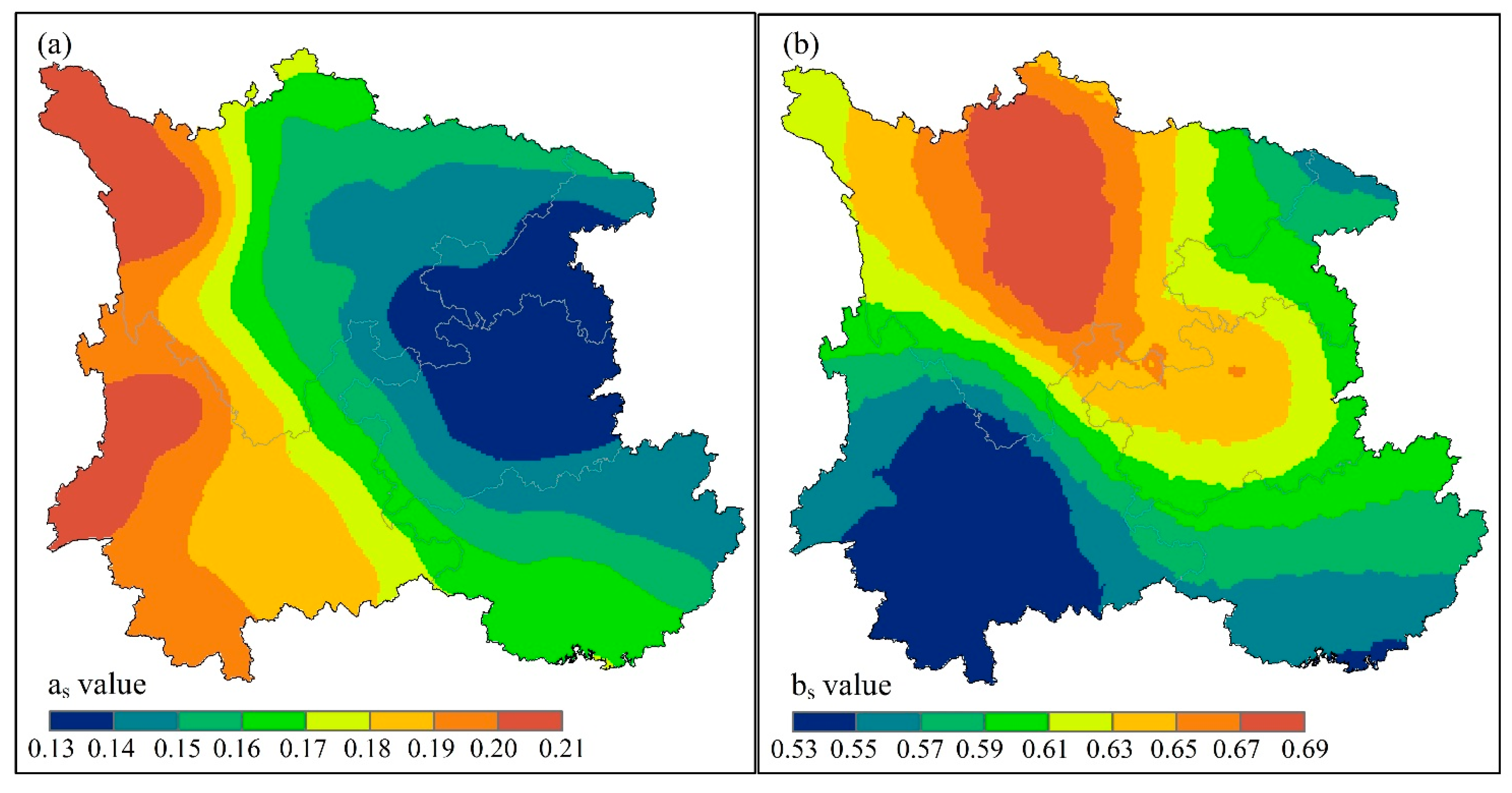
5.1. Uncertainties
5.2. Impacts of Change in Aridity Index on Drought
5.3. Impact of Change in Aridity Index on Water Resource
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notations
| AI | aridity index. |
| ET0 | potential evapotranspiration(mm). |
| Pre | precipitation (mm). |
| ETpan | pan evaporation (mm). |
| Tmax, Tmin, Ta | daily maximum, minimum and air temperature (°C). |
| Tmax,k, Tmin,k | daily maximum, minimum in kelvin temperature (°C). |
| es, ea | saturation and actual vapor pressure (kPa). |
| U2 | wind speed at 2 m (m s−1). |
| Pc | corrected precipitation. |
| Pg | precipitation measured from the gauge station. |
| ΔPw | wetting loss. |
| CR | ratio of gauge measured precipitation to the true precipitation. |
| G | soil heat flux density (MJ m−2 d−1). |
| Rs | incoming solar radiation (MJ m−2 d−1). |
| Rn | net radiation (MJ m−2 d−1). |
| Rns | net shortwave radiation (MJ m−2day−1). |
| Rnl | net long-wave radiation (MJ m−2day−1). |
| ∆ | slope of saturated vapor pressure (kPa °C−1). |
| γ | psychrometric constant (kPa °C−1). |
| α | albedo (α = 0.23). |
| n | actual duration of sunshine. |
| N | maximum possible duration of sunshine. |
| as, bs | parameters in calculating Rs (as = 0.25, bs = 0.50). |
| S(x) | sensitivity coefficient of AI to x variable. |
| L_AI | detected aridity index trend by linear regression. |
| C_AI | total contribution of variables. |
| ε | error between C_AI and L_AI. |
| RC(xi) | relative contribution of each climate variable. |
| Cr(xi) | contribution of each climate variable. |
| ETa | actual evapotranspiration. |
| R | streamflow. |
References
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakes: The Physical Science Basis, Contribution of Working Group I to the IPCC Fifth Assessment Report Climate Change; IPCC: Geneva, Switzerland, 2013. [Google Scholar]
- Taufik, M.; Torfs, P.J.J.; Uijlenhoet, R.; Jones, P.D.; Murdiyarso, D.; van Lanen, H.A.J. Amplification of wildfire area burnt by hydrological drought in the humid tropics. Nat. Clim. Chang. 2017, 7, 428–431. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2017, 7, 154–158. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed]
- Schwalm, C.R.; Anderegg, W.R.L.; Michalak, A.M.; Fisher, J.B.; Biondi, F.; Koch, G.; Litvak, M.; Ogle, K.; Shaw, J.D.; Wolf, A.; et al. Global patterns of drought recovery. Nature 2017, 548, 202–205. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Chen, H.; Ju, W.; Wang, G.; Sun, G.; Huang, J.; Ma, H.; Gao, C.; Hua, W.; Yan, G. On the coupling between precipitation and potential evapotranspiration: Contributions to decadal drought anomalies in the Southwest China. Clim. Dyn. 2016, 11–12, 1–19. [Google Scholar] [CrossRef]
- Cook, B.I.; Ault, T.R.; Smerdon, J.E. Unprecedented 21st century drought risk in the American Southwest and Central Plains. Sci. Adv. 2015, 1, e1400082. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Su, H.; Chen, F.; Wu, J.; Qi, J. The changing characteristics of drought in China from 1982 to 2005. Nat. Hazards 2013, 68, 723–743. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Yang, T.; Liang, K.; Zhang, M.; Liu, C. Investigation of the probability of concurrent drought events between the water source and destination regions of China’s water diversion project. Geophys. Res. Lett. 2015, 42, 8424–8431. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, F.-F.; Zhao, J.-X.; Qi, L.; Ren, H.-L. The Possible Influence of a Nonconventional El Niño on the Severe Autumn Drought of 2009 in Southwest China. J. Clim. 2013, 26, 8392–8405. [Google Scholar] [CrossRef]
- United Nations Educational, Scientific and Cultural Organization (UNESCO). Map of the World Distribution of Arid Regions: Explanatory Note; MAB Technical Notes; UNESCO: Paris, France, 1979. [Google Scholar]
- Food and Agriculture Organization (FAO). Arid Zone Forestry: A Guide for Field Technicians; FAO: Rome, Italy, 1989. [Google Scholar]
- Maliva, R.; Missimer, T. Arid Lands Water Evaluation and Management; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Tang, Y.; Yang, Y. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. J. Geophys. Res. Atmos. 2007, 112, 113–120. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Türkeş, M. Spatial and temporal variations in precipitation and aridity index series of Turkey. In Mediterranean Climate; Springer: Berlin/Heidelberg, Germany, 2003; pp. 181–213. [Google Scholar]
- Nastos, P.T.; Politi, N.; Kapsomenakis, J. Spatial and temporal variability of the Aridity Index in Greece. Atmos. Res. 2013, 119, 140–152. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.-B. Temporal pattern of aridity index in Iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D.; Luo, Y.; Liu, C. Spatial and temporal changes in aridity index in northwest China: 1960 to 2010. Theor. Appl. Climatol. 2013, 112, 307–316. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Zhang, Z. Observed changes of drought/wetness episodes in the Pearl River basin, China, using the standardized precipitation index and aridity index. Theor. Appl. Climatol. 2009, 98, 89–99. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; van der Schrier, G.; Beguería, S.; Azorin-Molina, C.; Lopez-Moreno, J.-I. Contribution of precipitation and reference evapotranspiration to drought indices under different climates. J. Hydrol. 2015, 526, 42–54. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Zhang, D.; Zhang, M.; Liu, C. Recent changes in pan-evaporation dynamics in China. Geophys. Res. Lett. 2011, 38, 142–154. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416, 182–205. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, D.; Liu, X.; Zhao, C. Spatial and temporal change in the potential evapotranspiration sensitivity to meteorological factors in China (1960–2007). J. Geogr. Sci. 2012, 22, 3–14. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. Trend analysis of reference evapotranspiration in Northwest China: The roles of changing wind speed and surface air temperature. Hydrol. Process. 2013, 27, 3941–3948. [Google Scholar] [CrossRef]
- Li, Y.; Liang, K.; Bai, P.; Feng, A.; Liu, L.; Dong, G. The spatiotemporal variation of reference evapotranspiration and the contribution of its climatic factors in the Loess Plateau, China. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are droughts becoming more frequent or severe in China based on the Standardized Precipitation Evapotranspiration Index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Yao, F.; Xu, Y.; Lin, E.; Yokozawa, M.; Zhang, J. Assessing the impacts of climate change on rice yields in the main rice areas of China. Clim. Chang. 2007, 80, 395–409. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guide to Meteorological Instruments and Methods of Observation, 6th ed.; World Meteorological Organization: Geneva, Switzerland, 1996. [Google Scholar]
- Liu, X.; Liu, C.; Brutsaert, W. Regional evaporation estimates in the eastern monsoon region of China: Assessment of a nonlinear formulation of the complementary principle. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- Goodison, B.; Sevruk, B.; Klemm, S. WMO solid precipitation measurement intercomparison: Objectives, methodology, analysis. Atmos. Depos. 1989, 179, 57–64. [Google Scholar]
- Yang, D.; Goodison, B.E.; Metcalfe, J.R.; Louie, P.; Leavesley, G.; Emerson, D.; Hanson, C.L.; Golubev, V.S.; Elomaa, E.; Gunther, T.; et al. Quantification of precipitation measurement discontinuity induced by wind shields on national gauges. Water Resour. Res. 1999, 35, 491–508. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef]
- Sevruk, B.; Hamon, W. International Comparison of National Precipitation Gauges with a Reference Pit Gauge; Instruments and Observing Methods Report; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1984. [Google Scholar]
- Wang, T.; Zhang, J.; Sun, F.; Liu, W. Pan evaporation paradox and evaporative demand from the past to the future over China: A review. Wiley Interdiscip. Rev. Water 2017, 4, e1207. [Google Scholar] [CrossRef]
- McCuen, R.H. A Sensitivity and Error Analysis Cf Procedures Used For Estimating Evaporation1. JAWRA J. Am. Water Resour. Assoc. 1974, 10, 486–497. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1948. [Google Scholar]
- Zheng, H.; Liu, X.; Liu, C.; Dai, X.; Zhu, R. Assessing contributions to panevaporation trends in Haihe River Basin, China. J. Geophys. Res. Atmos. 2009, 114, D24105. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Hong, H. Assessing the effect of climate change on reference evapotranspiration in China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1871–1881. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Zhang, D.; Liang, K.; Li, X.; Dong, G. Reduced Runoff Due to Anthropogenic Intervention in the Loess Plateau, China. Water 2016, 8, 458. [Google Scholar] [CrossRef]
- Li, Y.; Liang, K.; Liu, C.; Liu, W.; Bai, P. Evaluation of different evapotranspiration products in the middle Yellow River Basin, China. Hydrol. Res. 2016, 47. [Google Scholar] [CrossRef]
- Budyko, M.I. Evaporation under Natural Conditions; Gidrometeoizdat: Leningrad, Russia, 1963. [Google Scholar]
- Huang, S.; Huang, Q.; Leng, G.; Zhao, M.; Meng, E. Variations in annual water-energy balance and their correlations with vegetation and soil moisture dynamics: A case study in the Wei River Basin, China. J. Hydrol. 2017, 546, 515–525. [Google Scholar] [CrossRef]
- Baw-Puh, F. On the calculation of the evaporation from land surface. Chin. J. Atmos. Sci. 1981, 5, 23–31. [Google Scholar]
- Zhang, Y.; Chiew, F.H.S.; Peña-Arancibia, J.; Sun, F.; Li, H.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res. Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1982; Volume 1. [Google Scholar]
- Tan, L.; Cai, Y.; An, Z.; Cheng, H.; Shen, C.; Gao, Y.; Edwards, R.L. Decreasing monsoon precipitation in southwest China during the last 240 years associated with the warming of tropical ocean. Clim. Dyn. 2017, 48, 1769–1778. [Google Scholar] [CrossRef]
- Qiu, J. China Drought Highlights Future Climate Threats; Nature Publishing Group: London, UK, 2010. [Google Scholar]
- Zhang, L.; Xiao, J.; Li, J.; Wang, K.; Lei, L.; Guo, H. The 2010 spring drought reduced primary productivity in southwestern China. Environ. Res. Lett. 2012, 7, 045706. [Google Scholar] [CrossRef]
- Hou, W.; Gao, J.; Wu, S.; Dai, E. Interannual Variations in Growing-Season NDVI and Its Correlation with Climate Variables in the Southwestern Karst Region of China. Remote Sens. 2015, 7, 11105–11124. [Google Scholar] [CrossRef]
- Henley, B.J.; King, A.D. Trajectories toward the 1.5 °C Paris target: Modulation by the Interdecadal Pacific Oscillation. Geophys. Res. Lett. 2017, 44, 4256–4262. [Google Scholar] [CrossRef]
- King, A.D.; Karoly, D.J.; Henley, B.J. Australian climate extremes at 1.5[thinsp][deg]C and 2[thinsp][deg]C of global warming. Nat. Clim. Chang. 2017, 7, 412–416. [Google Scholar] [CrossRef]
- Mitchell, D.; James, R.; Forster, P.M.; Betts, R.A.; Shiogama, H.; Allen, M. Realizing the impacts of a 1.5 [deg]C warmer world. Nat. Clim. Chang. 2016, 6, 735–737. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Hobbins, M.T.; Ramírez, J.A.; Brown, T.C. The complementary relationship in estimation of regional evapotranspiration: An enhanced advection-aridity model. Water Resour. Res. 2001, 37, 1389–1403. [Google Scholar] [CrossRef]
- Liu, X.; Liu, W.; Xia, J. Comparison of the streamflow sensitivity to aridity index between the Danjiangkou Reservoir basin and Miyun Reservoir basin, China. Theor. Appl. Climatol. 2013, 111, 683–691. [Google Scholar] [CrossRef]
- Choudhury, B. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
| Differential Items | Formula |
|---|---|
| Pre | Tmax | Tmin | ea | U2 | Rs | ET0 | AI | ρ(ε)% | |
|---|---|---|---|---|---|---|---|---|---|
| Trend | −2.9474 | 0.0460 ** | 0.0346 ** | −0.0004 | 0.0039 | 0.0127 | 3.3135 | 0.0053 * | - |
| −0.0007 | 0.0416 | 0.0129 | −0.2769 | 0.0656 | 0.0211 | 0.0009 | - | - | |
| S(xi) | −1.00 | 1.11 | 0.19 | −0.56 | 0.10 | 0.33 | 1.00 | ||
| Cr(xi) | 0.0021 | 0.0019 | 0.0004 | 0.0001 | 0.0003 | 0.0003 | 0.0029 | - | −6.12 |
| RC(xi) | 38.98 | 36.26 | 8.49 | 2.27 | 4.83 | 5.10 | 56.95 | 95.93 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Feng, A.; Liu, W.; Ma, X.; Dong, G. Variation of Aridity Index and the Role of Climate Variables in the Southwest China. Water 2017, 9, 743. https://doi.org/10.3390/w9100743
Li Y, Feng A, Liu W, Ma X, Dong G. Variation of Aridity Index and the Role of Climate Variables in the Southwest China. Water. 2017; 9(10):743. https://doi.org/10.3390/w9100743
Chicago/Turabian StyleLi, Yanzhong, Aiqing Feng, Wenbin Liu, Xieyao Ma, and Guotao Dong. 2017. "Variation of Aridity Index and the Role of Climate Variables in the Southwest China" Water 9, no. 10: 743. https://doi.org/10.3390/w9100743
APA StyleLi, Y., Feng, A., Liu, W., Ma, X., & Dong, G. (2017). Variation of Aridity Index and the Role of Climate Variables in the Southwest China. Water, 9(10), 743. https://doi.org/10.3390/w9100743




