Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements
Abstract
:1. Introduction
2. Dataset
2.1. Study Areas
2.2. Satellite Data
2.3. Field Data
3. Description of the Backscattering Models
3.1. The Semi-Empirical Dubois Model
3.2. The Semi-Empirical Oh Model
3.3. The Physical Integral Equation Model (IEM)
3.4. IEM Modified by Baghdadi (IEM_B)
3.5. The Advanced Integral Equation Model
4. Results and Discussion
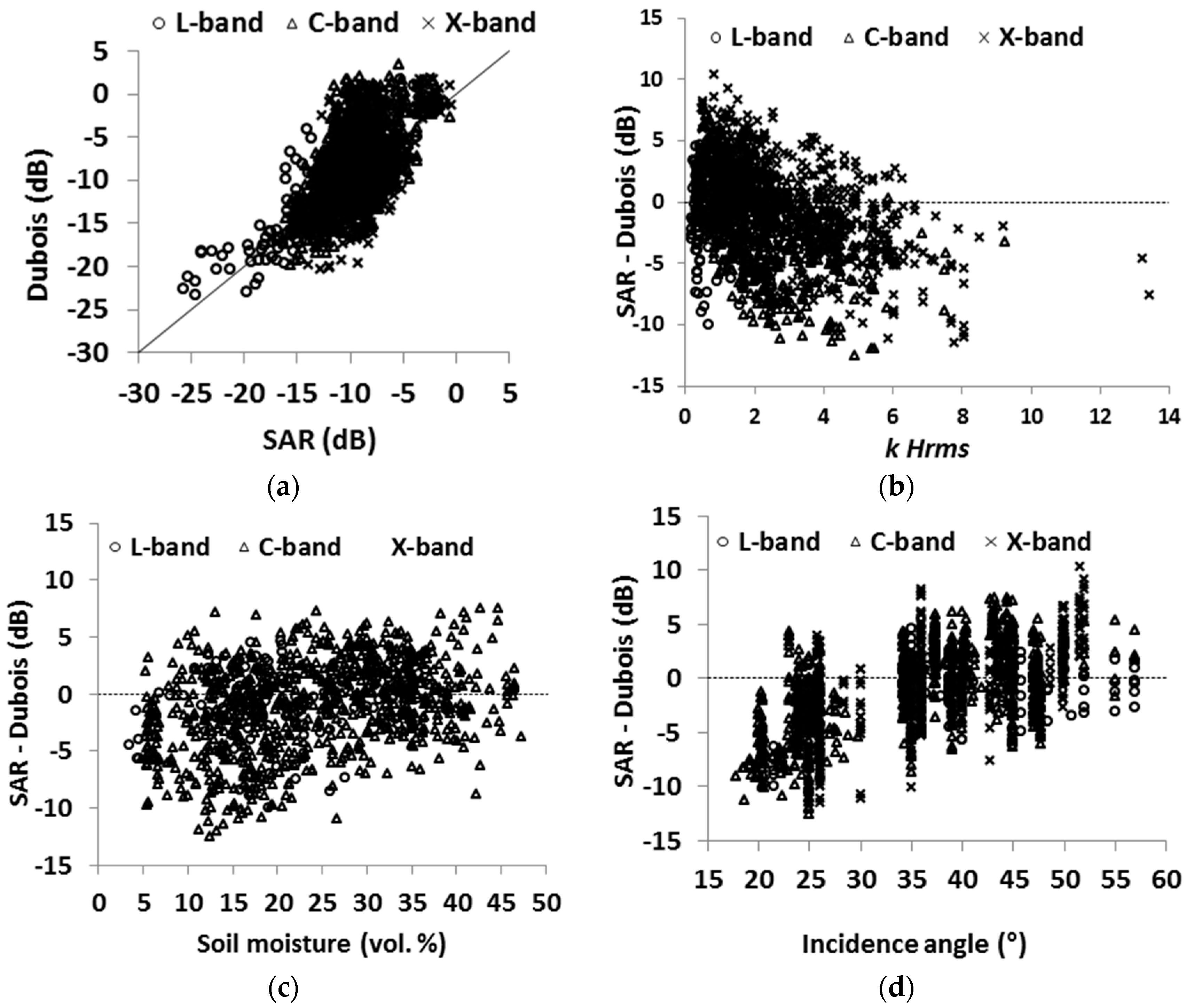
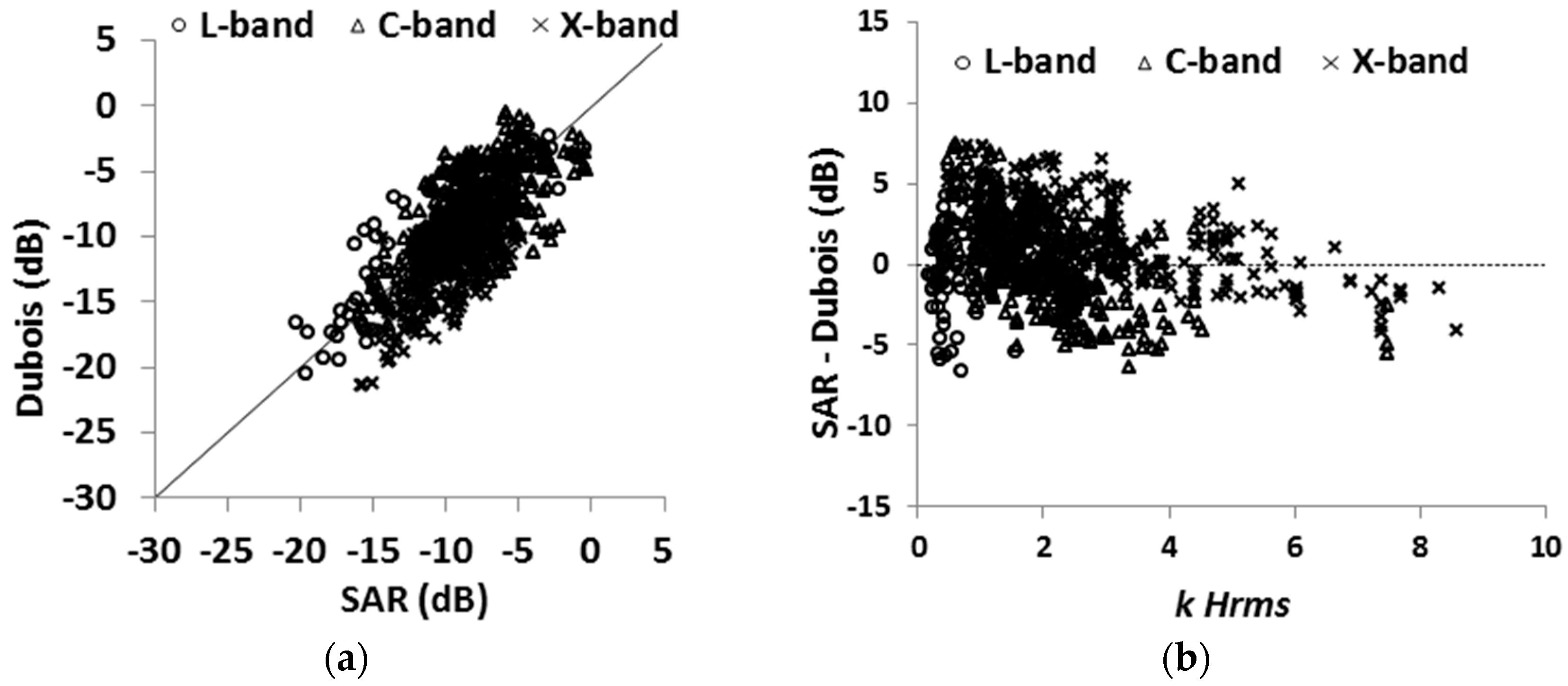
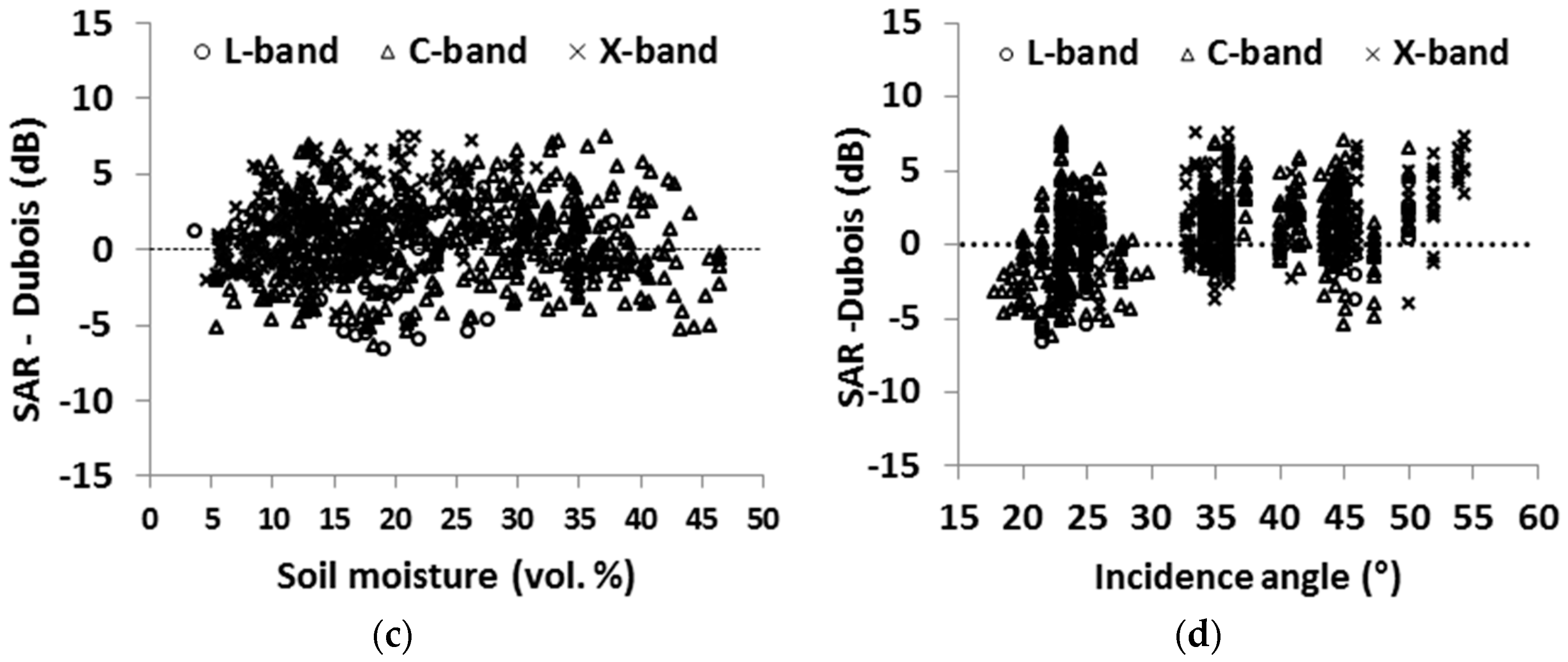
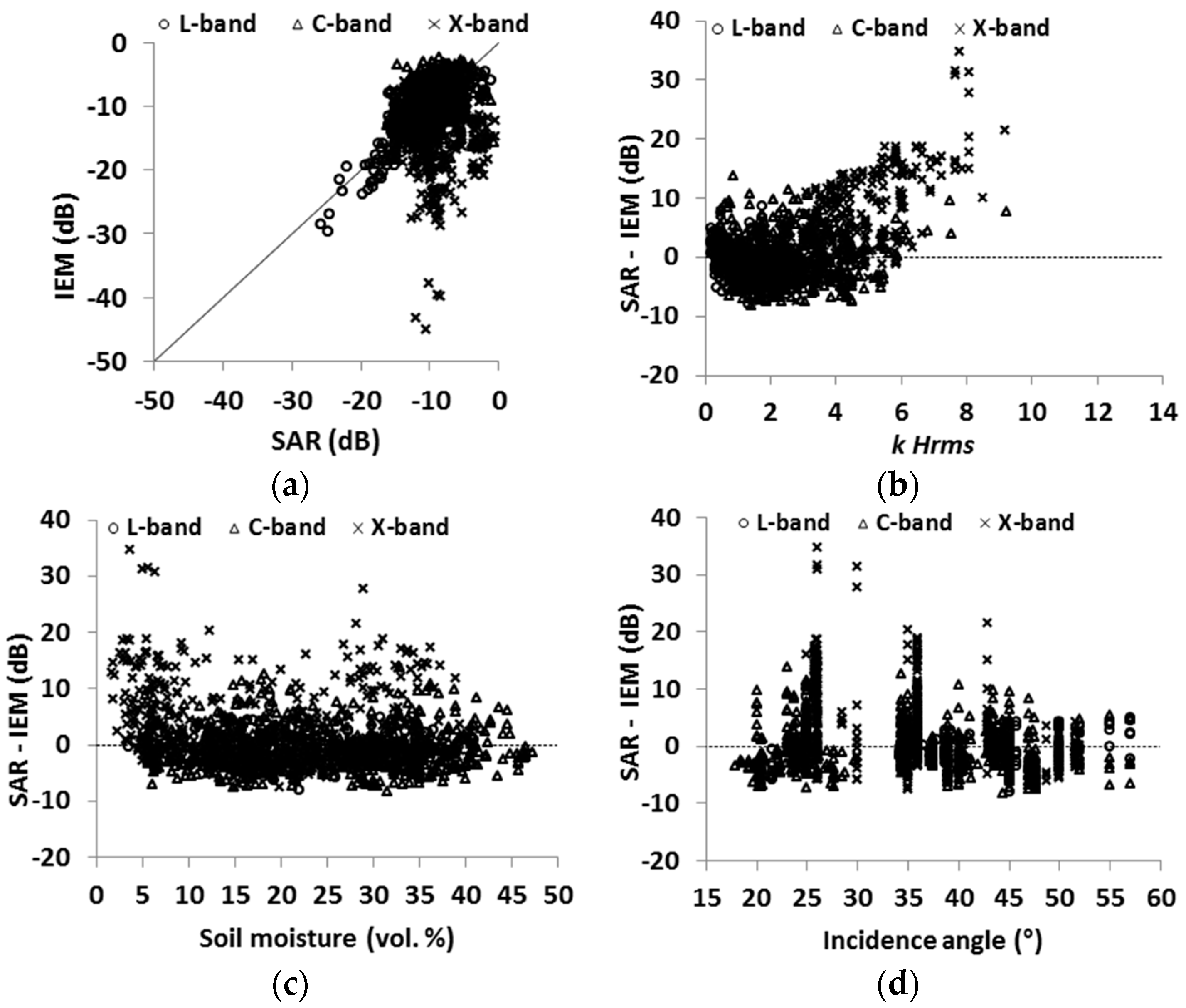
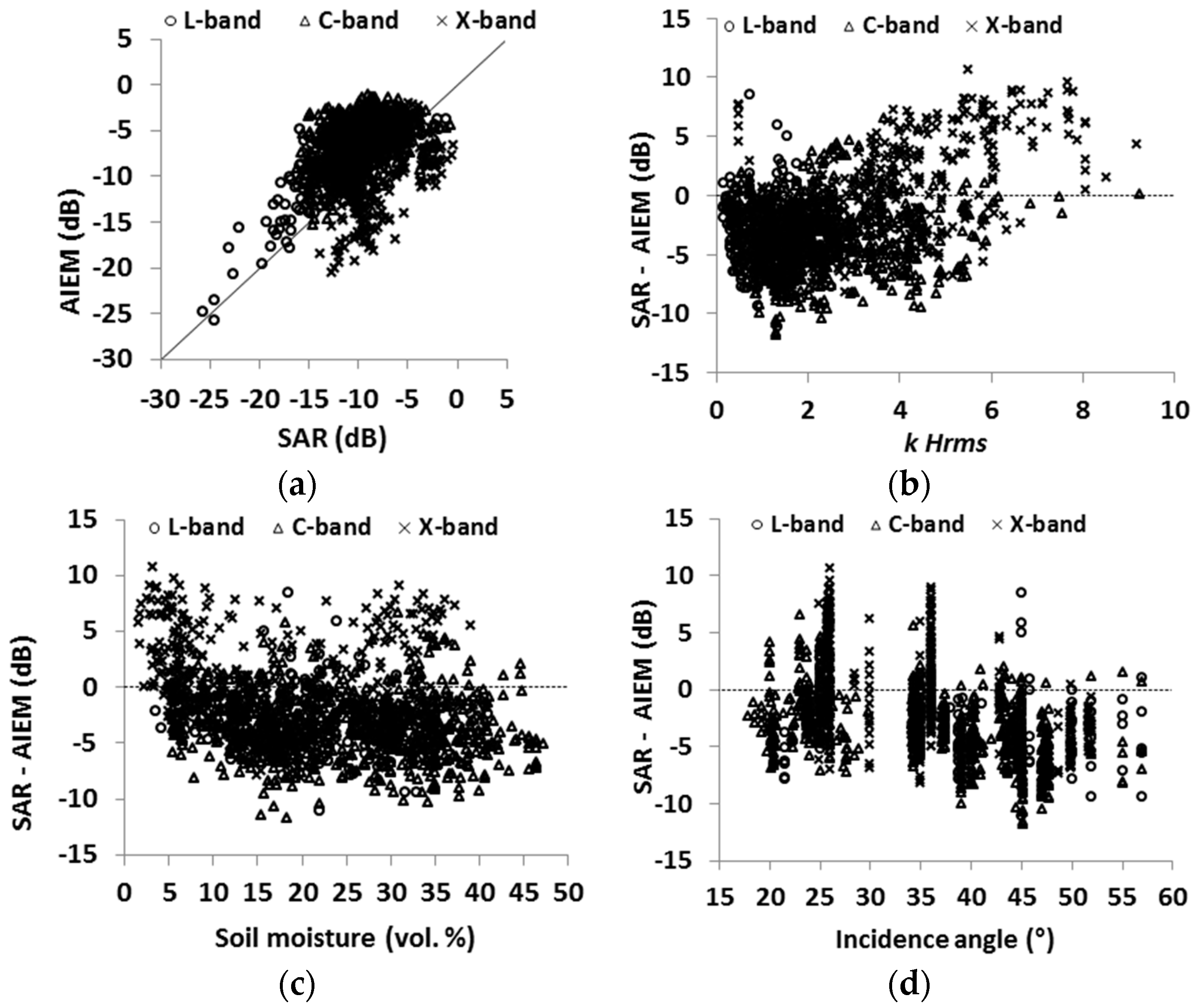
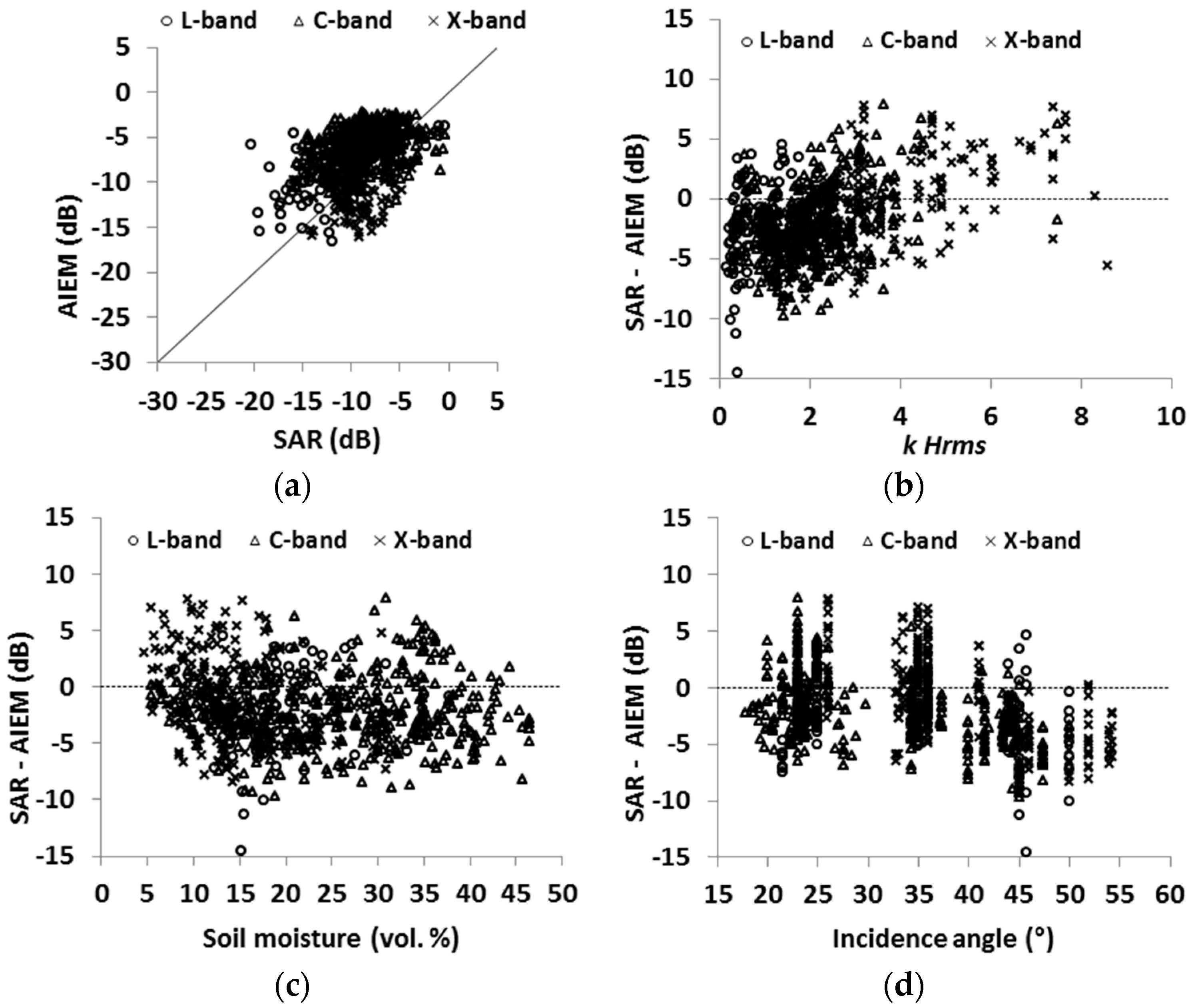
4.1. Evaluation of the Dubois Model
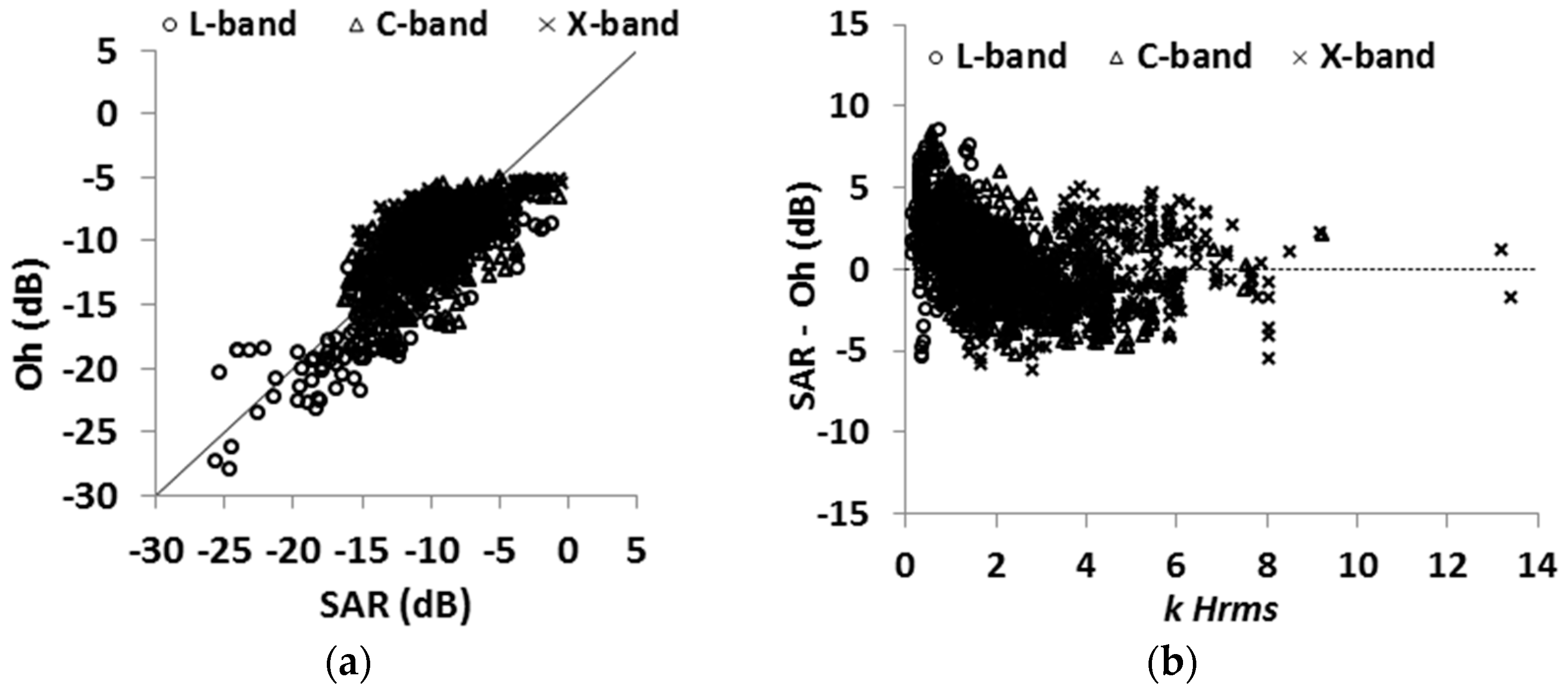
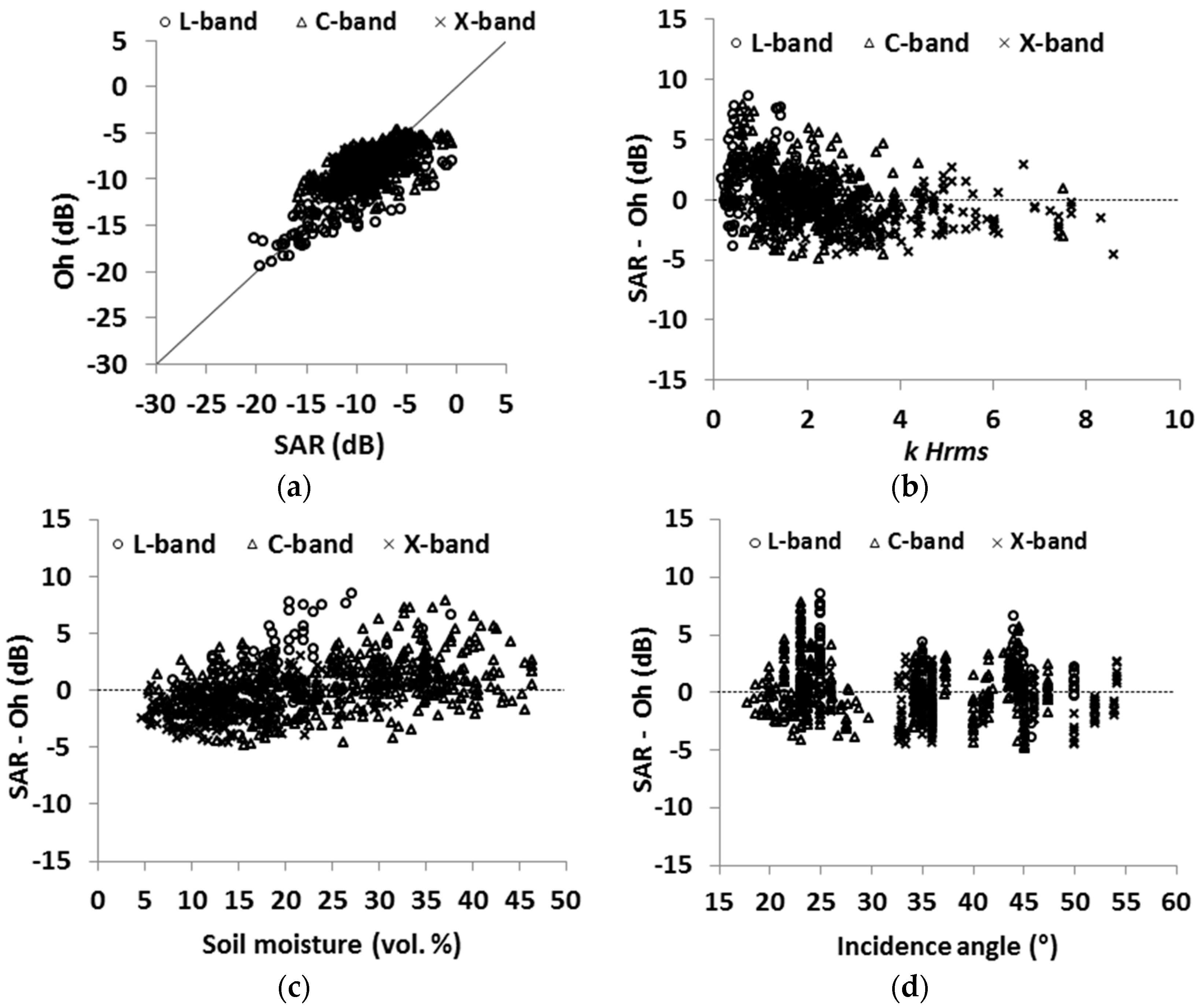
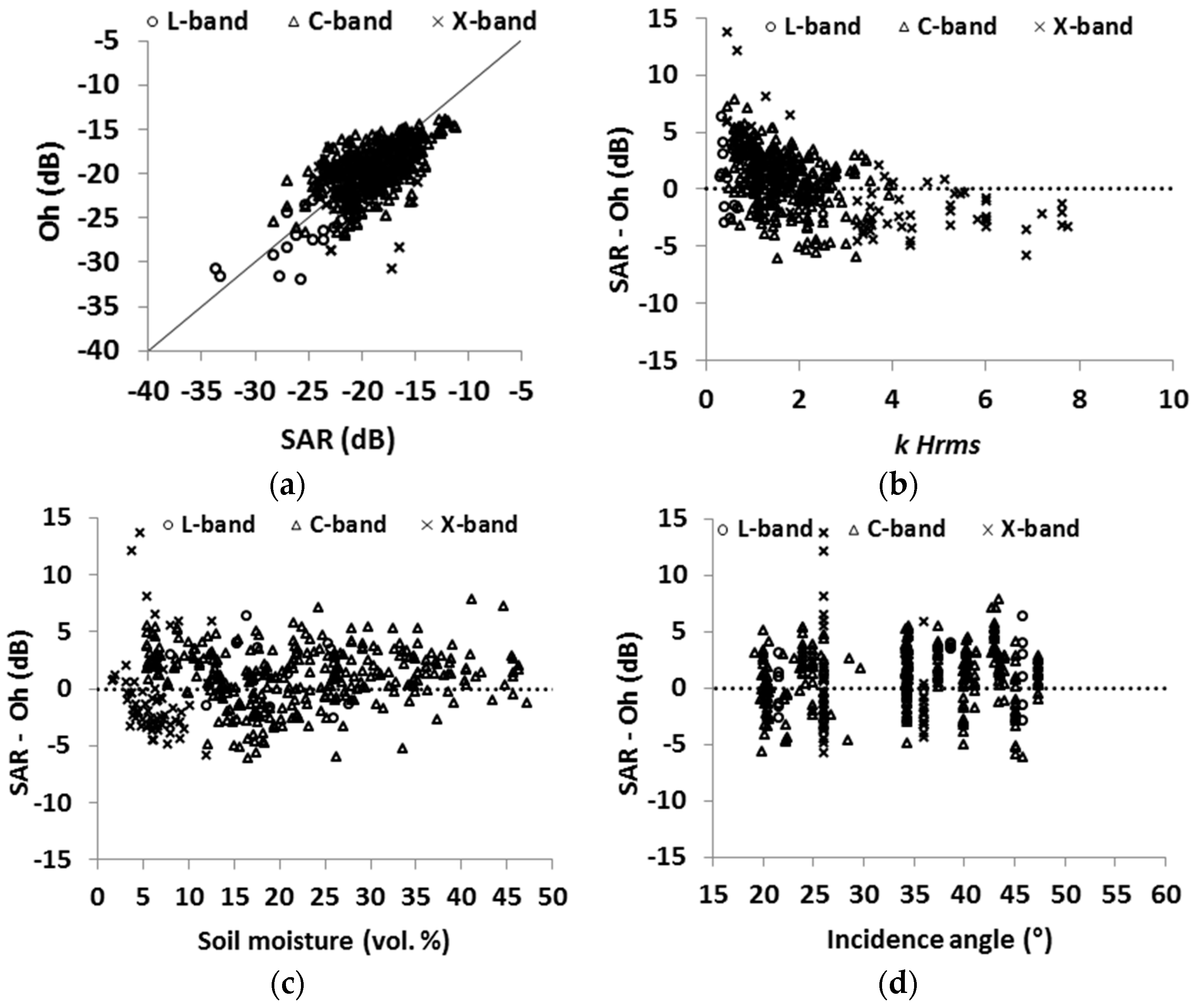
4.2. Evaluation of the Oh Model
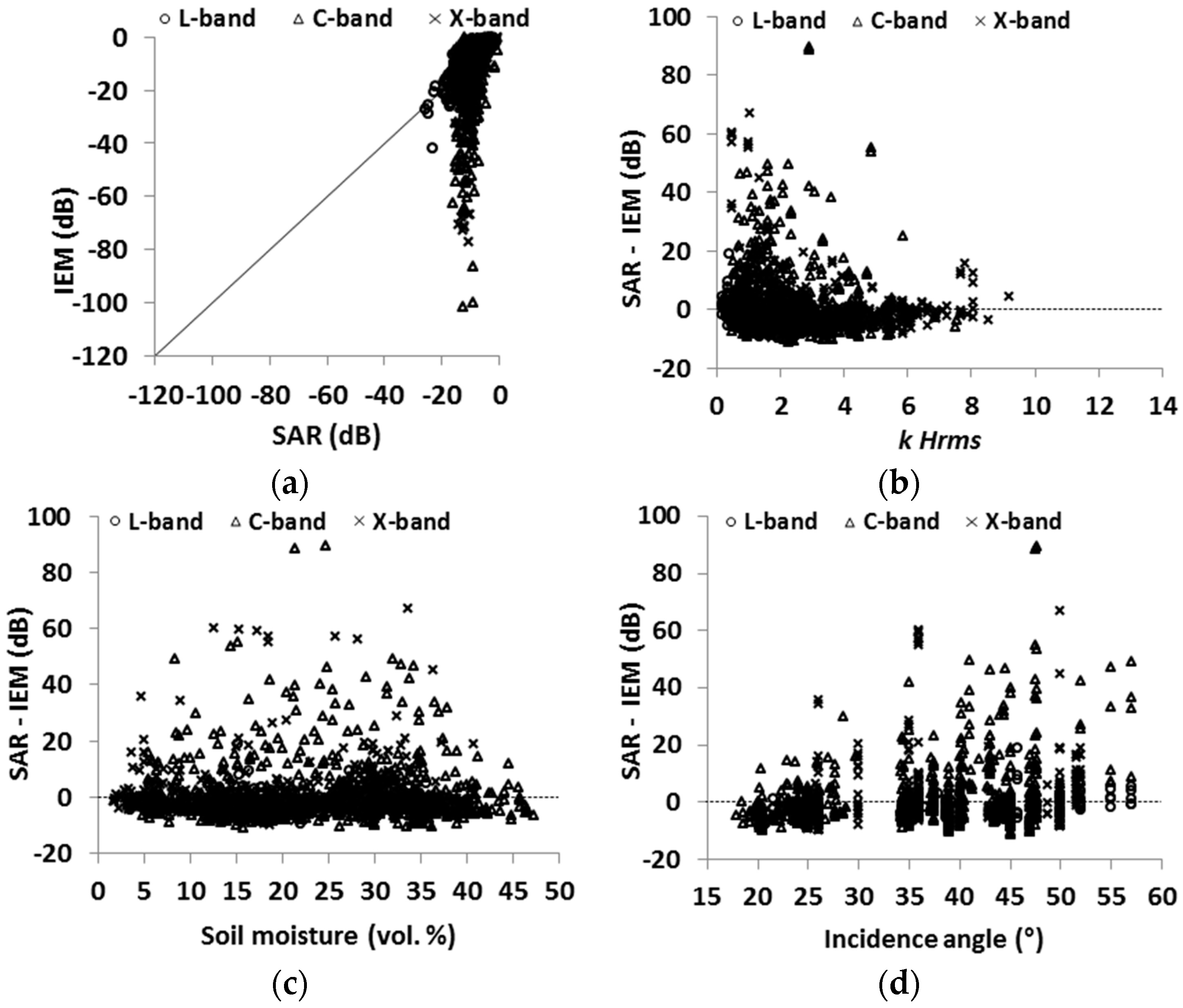
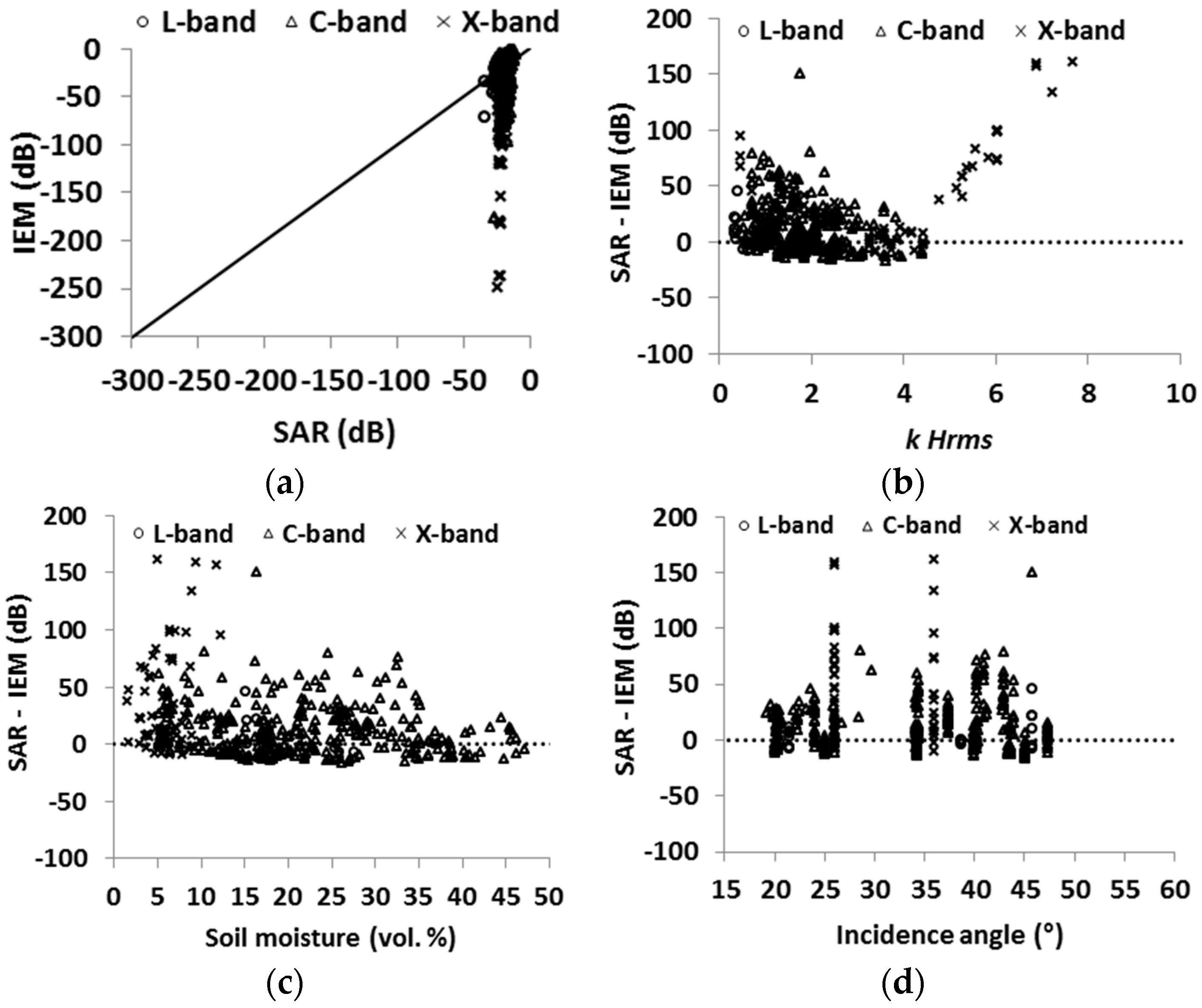
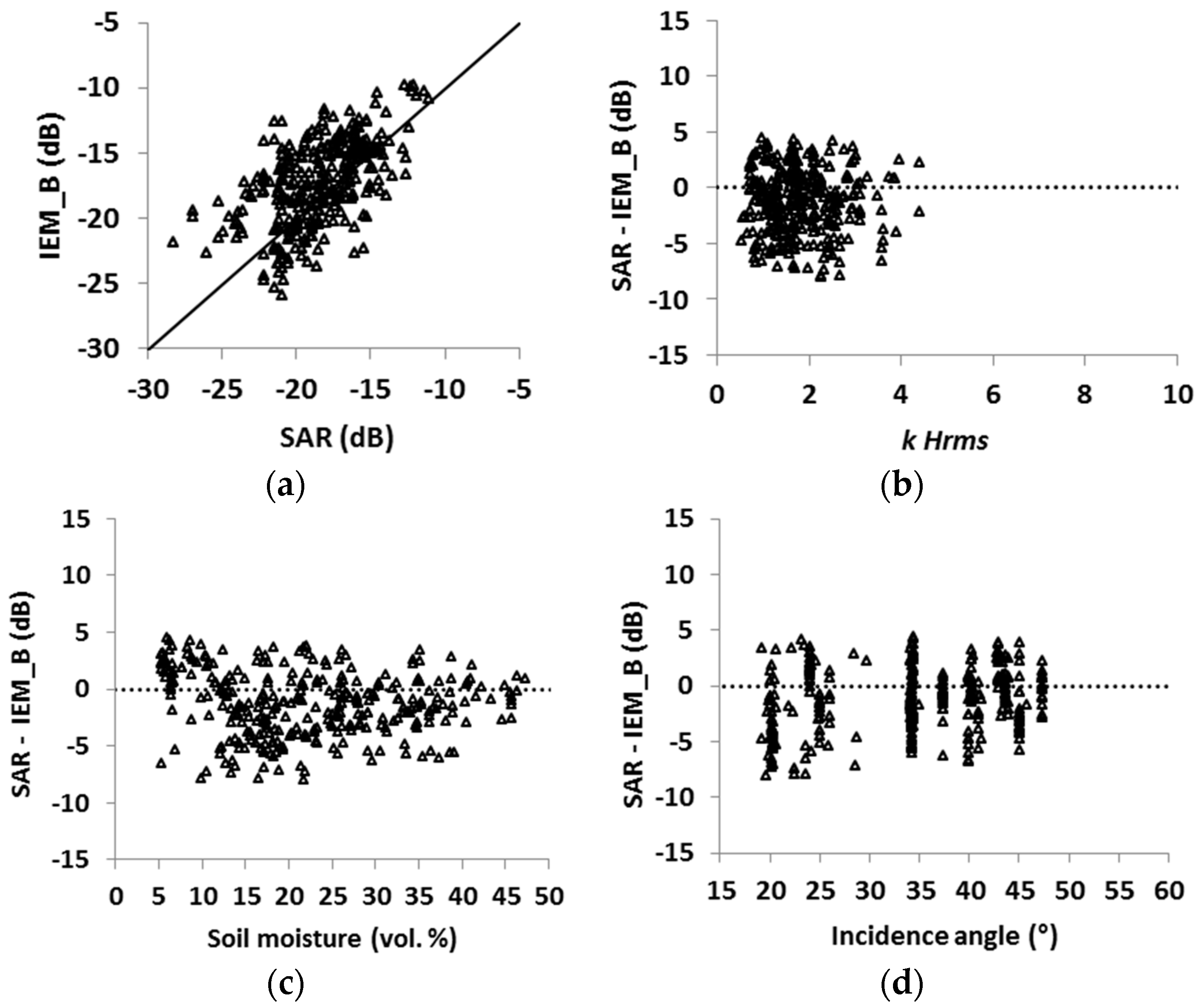
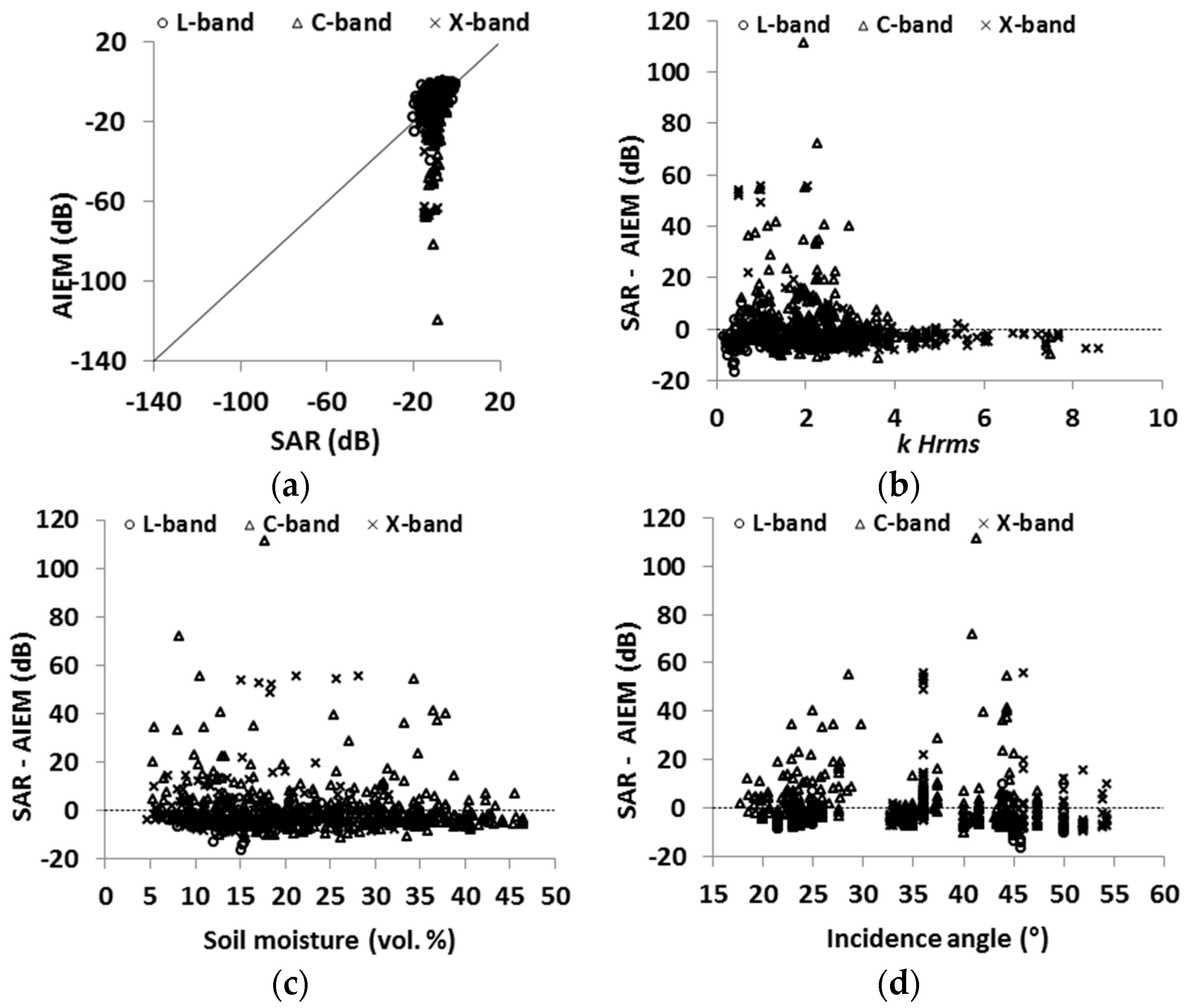
4.3. Evaluation of the IEM
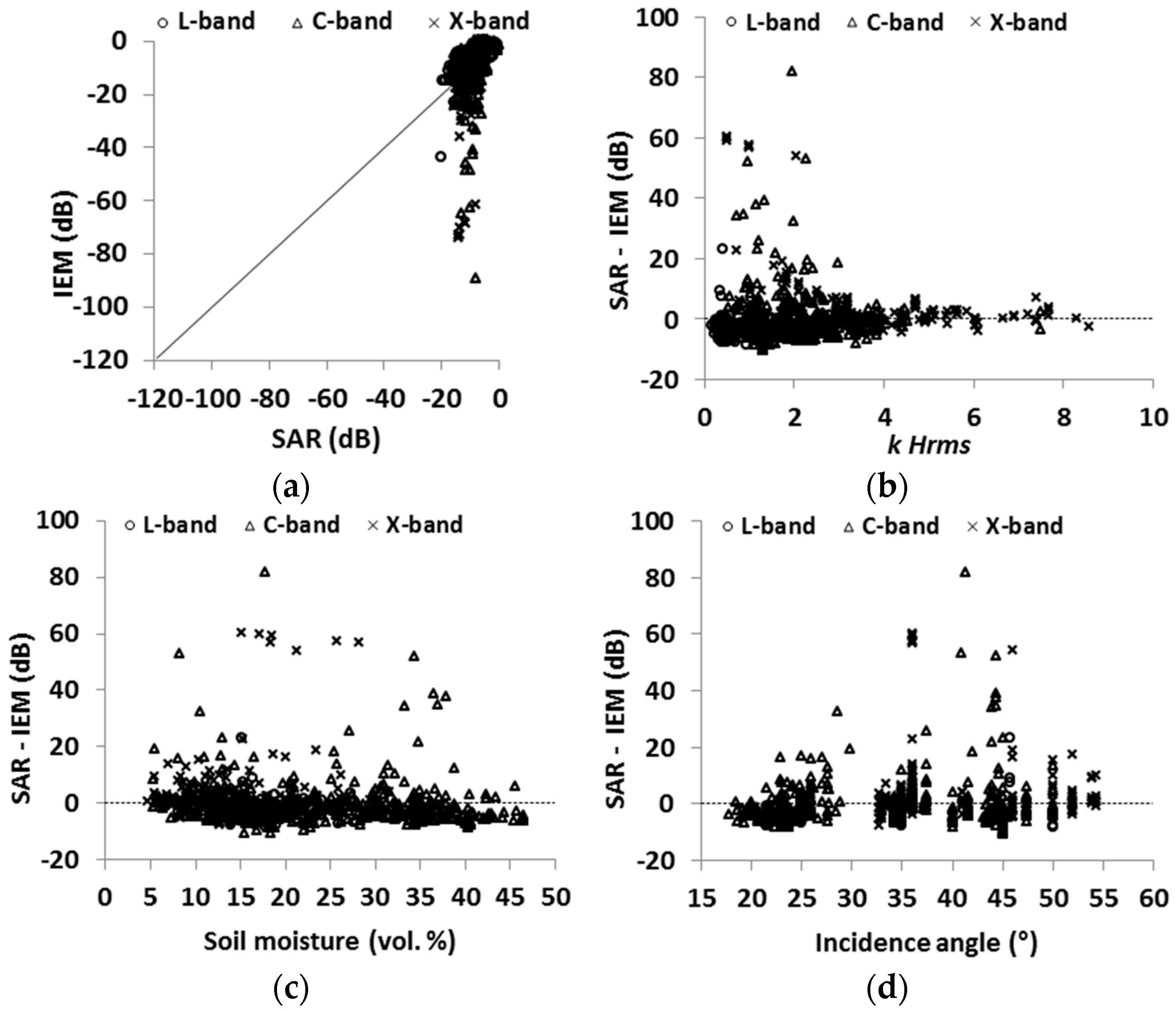
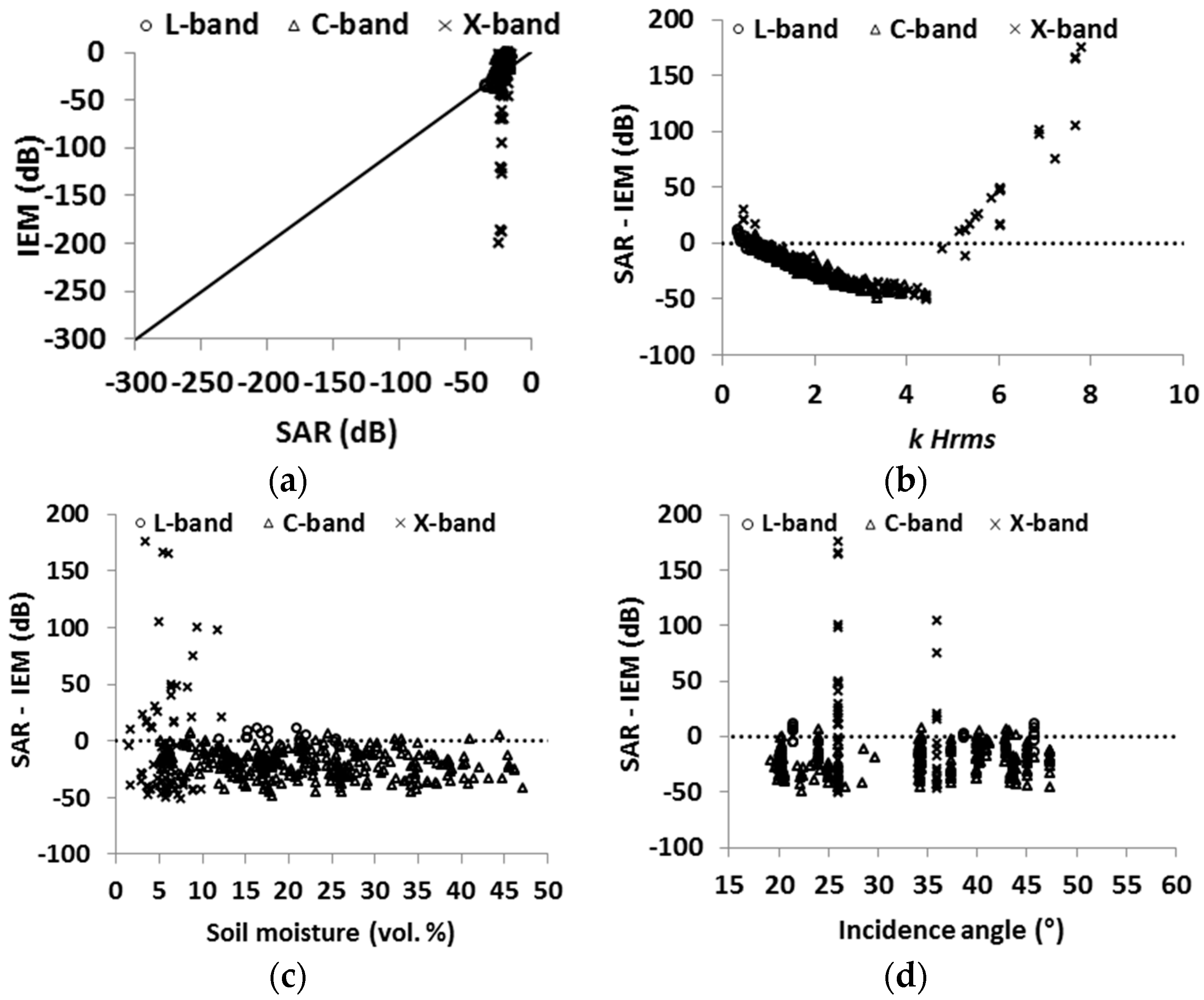
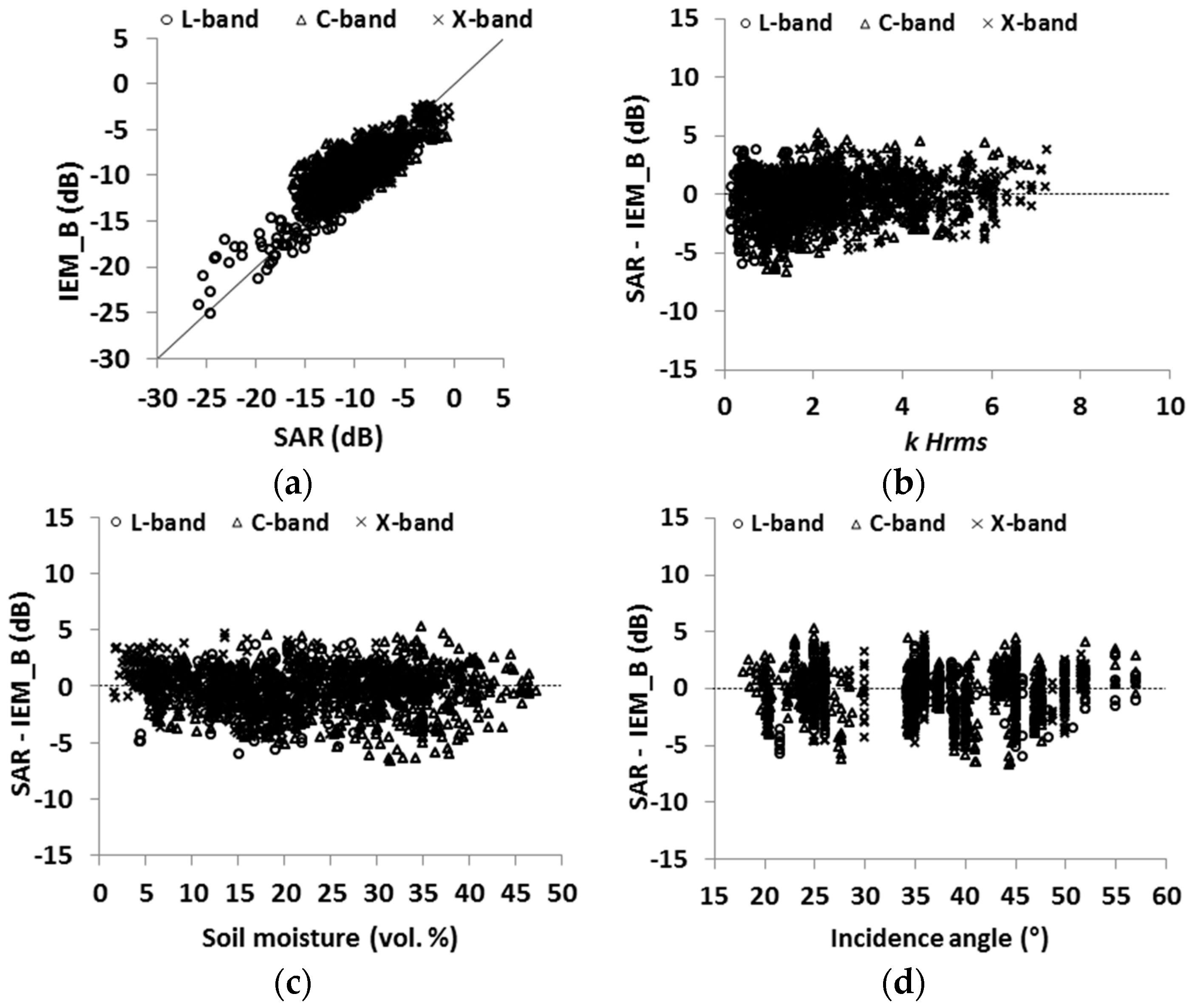
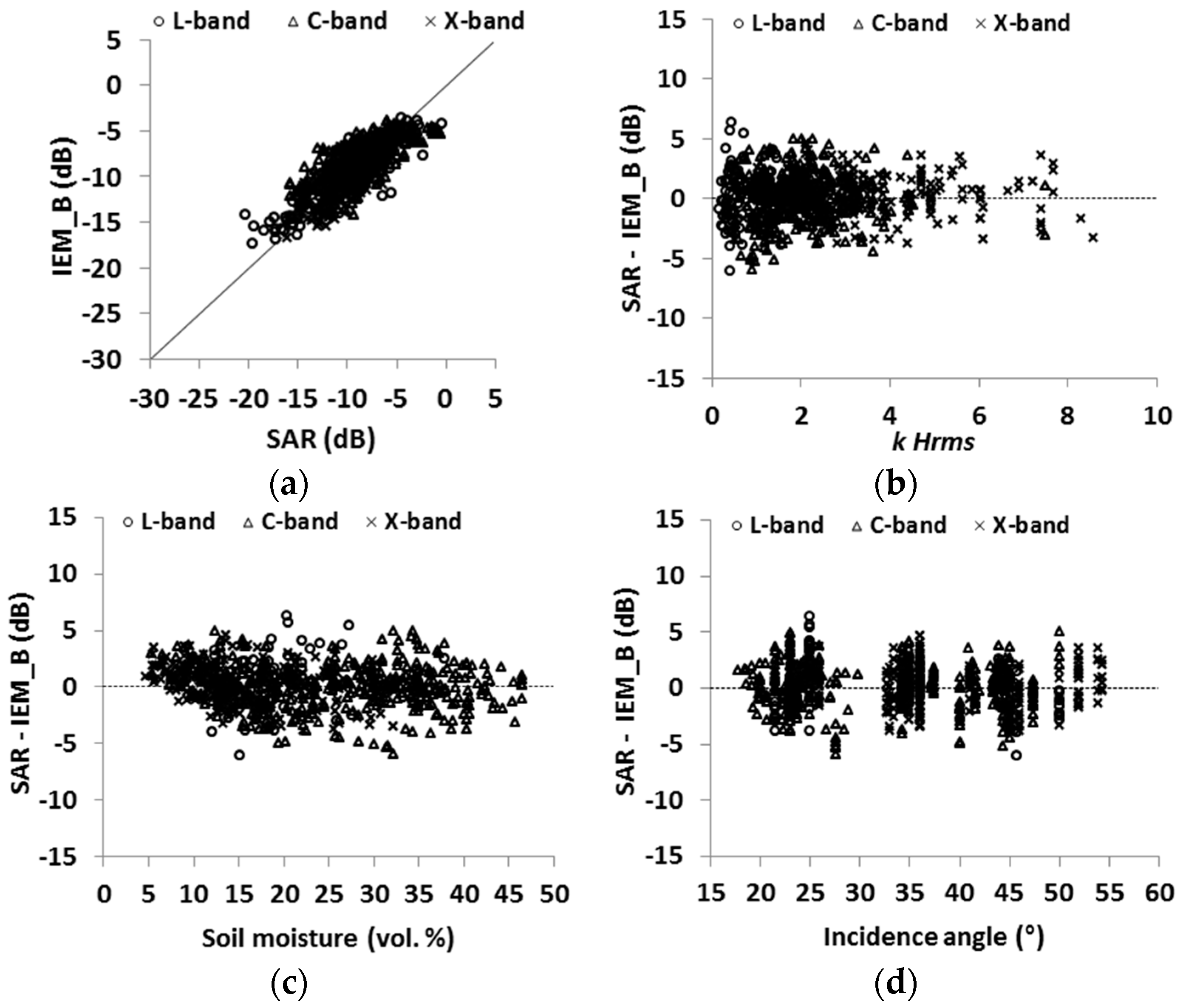
4.4. Evaluation of IEM Modified by Baghdadi (IEM_B)
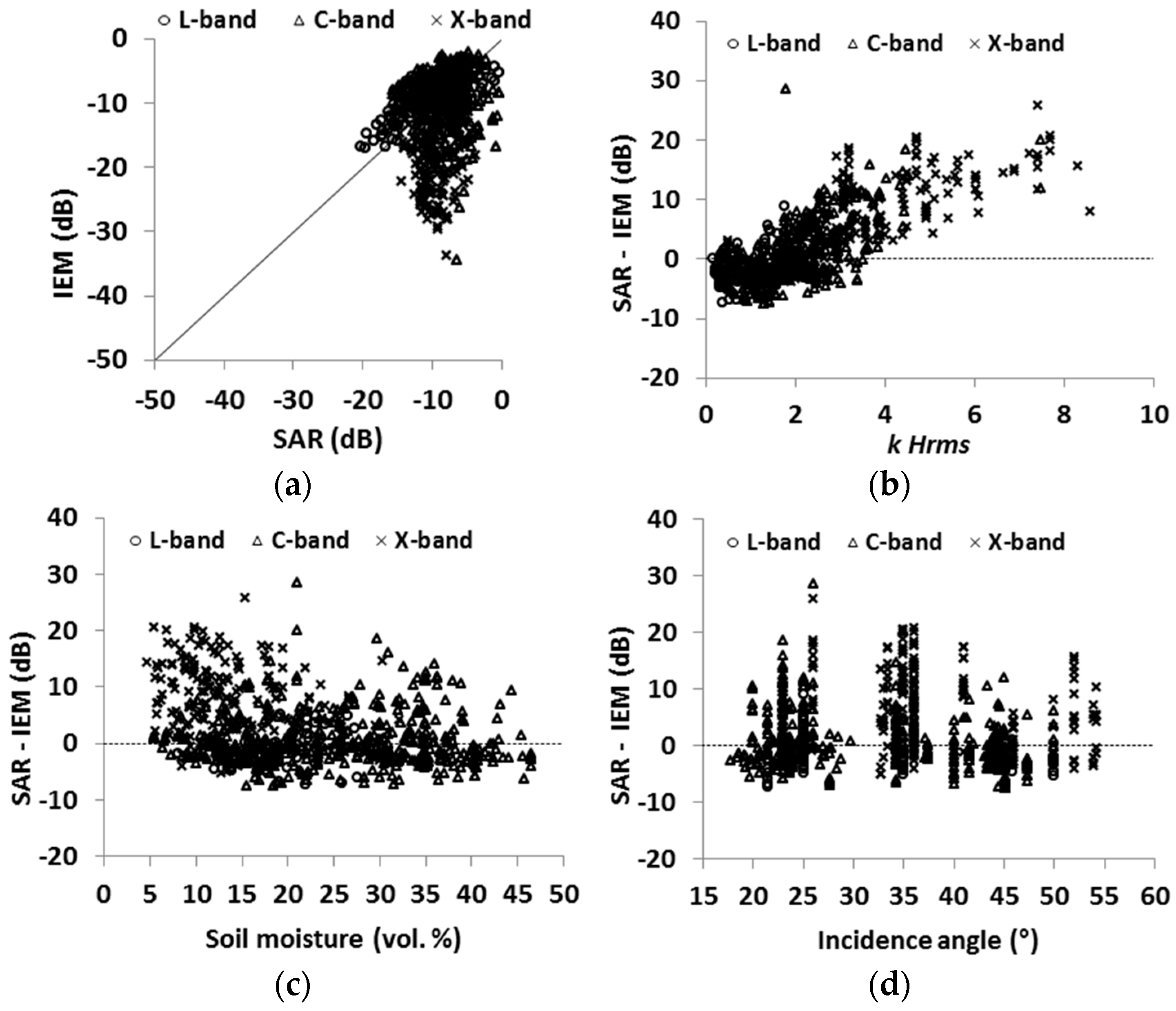
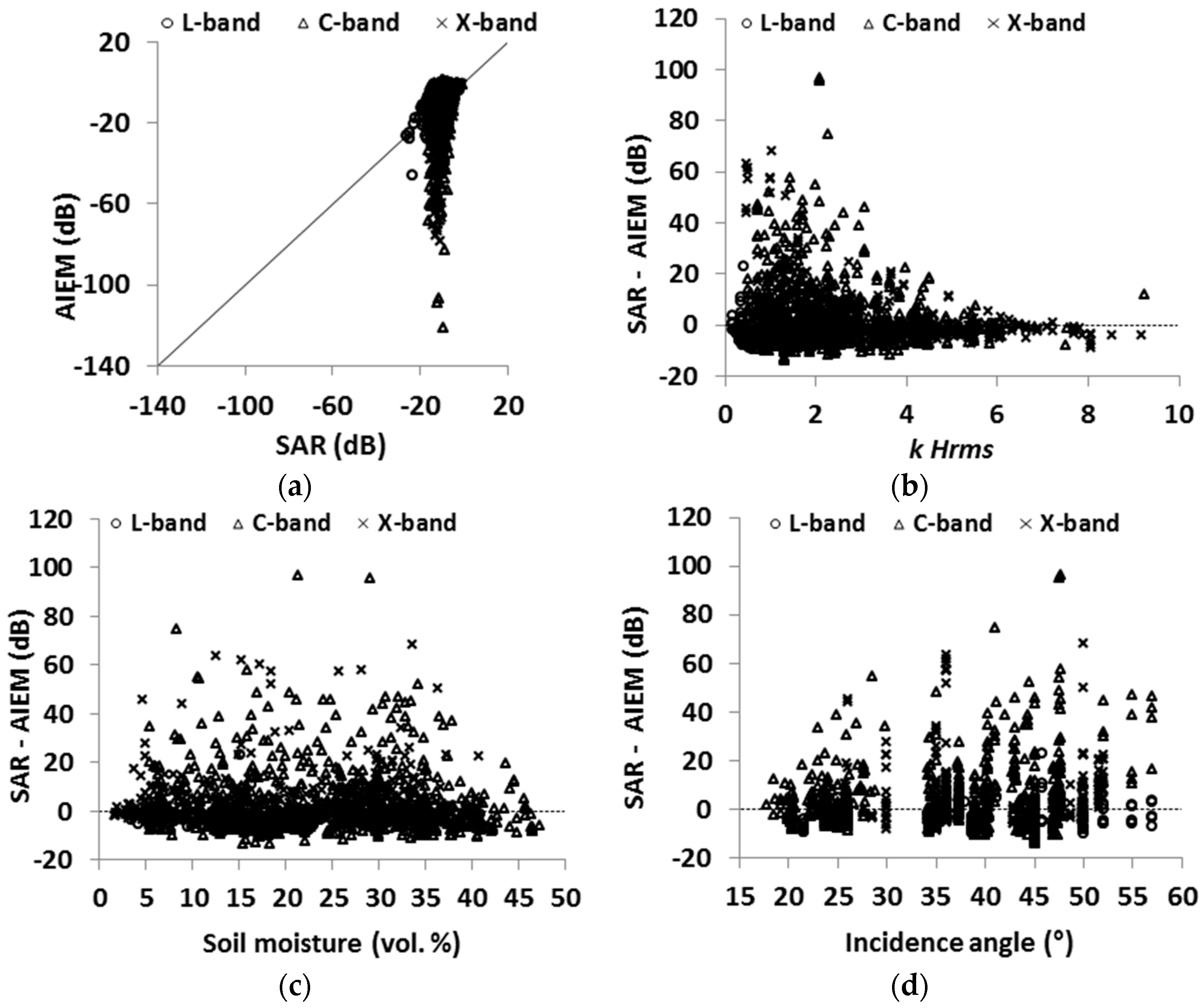
4.5. Evaluation of the Advanced Integral Equation Model (AIEM)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Condrea, P.; Bostan, I. Environmental issues from an economic perspective. Environ. Eng. Manag. J. 2008, 7, 843–849. [Google Scholar]
- Costantini, E.A. Soil indicators to assess the effectiveness of restoration strategies in dryland ecosystems. Solid Earth 2016, 7, 397. [Google Scholar] [CrossRef]
- Lakshmi, V. Remote sensing of soil moisture. ISRN Soil Sci. 2013, 21, 336–344. [Google Scholar] [CrossRef]
- Aubert, M.; Baghdadi, N.; Zribi, M.; Douaoui, A.; Loumagne, C.; Baup, F.; El Hajj, M.; Garrigues, S. Analysis of TerraSAR-X data sensitivity to bare soil moisture, roughness, composition and soil crust. Remote Sens. Environ. 2011, 115, 1801–1810. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of estimating soil moisture under vegetation cover by means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P.; Pettinato, S.; Santi, E. A comparison of algorithms for retrieving soil moisture from ENVISAT/ASAR images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3274–3284. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An inversion algorithm for retrieving soil moisture and surface roughness from polarimetric radar observation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’94)—Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation, Pasadena, CA, USA, 8–12 August 1994; Volume 3, pp. 1582–1584.
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1348–1355. [Google Scholar] [CrossRef]
- Dubois, P.C.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.-S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J.P. An empirical calibration of the integral equation model based on SAR data, soil moisture and surface roughness measurement over bare soils. Int. J. Remote Sens. 2002, 23, 4325–4340. [Google Scholar] [CrossRef]
- Baghdadi, N.; Gherboudj, I.; Zribi, M.; Sahebi, M.; King, C.; Bonn, F. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. Int. J. Remote Sens. 2004, 25, 3593–3623. [Google Scholar] [CrossRef]
- Baghdadi, N.; Holah, N.; Zribi, M. Calibration of the Integral Equation Model for SAR data in C-band and HH and VV polarizations. Int. J. Remote Sens. 2006, 27, 805–816. [Google Scholar] [CrossRef]
- Baghdadi, N.; Chaaya, J.A.; Zribi, M. Semiempirical calibration of the integral equation model for SAR data in C-band and cross polarization using radar images and field measurements. IEEE Geosci. Remote Sens. Lett. 2011, 8, 14–18. [Google Scholar] [CrossRef]
- Baghdadi, N.; Saba, E.; Aubert, M.; Zribi, M.; Baup, F. Evaluation of radar backscattering models IEM, Oh, and Dubois for SAR data in X-band over bare soils. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1160–1164. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Baup, F.; Mattia, F. Semi-empirical calibration of the integral equation model for co-polarized L-band backscattering. Remote Sens. 2015, 7, 13626–13640. [Google Scholar] [CrossRef]
- Chen, K.-S.; Wu, T.-D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, OH and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Mattia, F.; Le Toan, T.; Souyris, J.-C.; De Carolis, C.; Floury, N.; Posa, F.; Pasquariello, N.G. The effect of surface roughness on multifrequency polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 954–966. [Google Scholar] [CrossRef]
- Zribi, M.; Taconet, O.; Le Hégarat-Mascle, S.; Vidal-Madjar, D.; Emblanch, C.; Loumagne, C.; Normand, M. Backscattering behavior and simulation comparison over bare soils using SIR-C/X-SAR and ERASME 1994 data over Orgeval. Remote Sens. Environ. 1997, 59, 256–266. [Google Scholar] [CrossRef]
- Mattia, F.; Davidson, M.W.; Le Toan, T.; D’Haese, C.M.; Verhoest, N.E.; Gatti, A.M.; Borgeaud, M. A comparison between soil roughness statistics used in surface scattering models derived from mechanical and laser profilers. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1659–1671. [Google Scholar] [CrossRef]
- Verhoest, N.E.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed]
- Ulaby, F.T.; Dubois, P.C.; Van Zyl, J. Radar mapping of surface soil moisture. J. Hydrol. 1996, 184, 57–84. [Google Scholar] [CrossRef]
- Baghdadi, N.; Paillou, P.; Grandjean, G.; Dubois, P.; Davidson, M. Relationship between profile length and roughness variables for natural surfaces. Int. J. Remote Sens. 2000, 21, 3375–3381. [Google Scholar] [CrossRef]
- Davidson, M.W.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar] [CrossRef]
- Le Toan, T.; Davidson, M.; Mattia, F.; Borderies, P.; Chenerie, I.; Manninen, T.; Borgeaud, M. Improved observation and modelling of bare soil surfaces for soil moisture retrieval. Earth Obs. Q. 1999, 62, 20–24. [Google Scholar]
- Lievens, H.; Verhoest, N.E.C.; Keyser, E.D.; Vernieuwe, H.; Matgen, P.; Alvarez-Mozos, J.; Baets, B.D. Effective roughness modelling as a tool for soil moisture retrieval from C-and L-band SAR. Hydrol. Earth Syst. Sci. 2011, 15, 151–162. [Google Scholar] [CrossRef]
- De Keyser, E.; Vernieuwe, H.; Lievens, H.; Alvarez-Mozos, J.; De Baets, B.; Verhoest, N.E. Assessment of SAR-retrieved soil moisture uncertainty induced by uncertainty on modeled soil surface roughness. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 176–182. [Google Scholar] [CrossRef]
- Verhoest, N.E.C.; De Baets, B.; Mattia, F.; Satalino, G.; Lucau, C.; Defourny, P. A possibilistic approach to soil moisture retrieval from ERS synthetic aperture radar backscattering under soil roughness uncertainty. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E. Spatial and temporal soil moisture estimation from RADARSAT-2 imagery over Flevoland, The Netherlands. J. Hydrol. 2012, 456, 44–56. [Google Scholar] [CrossRef]
- Rahman, M.M.; Moran, M.S.; Thoma, D.P.; Bryant, R.; Sano, E.E.; Holifield Collins, C.D.; Skirvin, S.; Kershner, C.; Orr, B.J. A derivation of roughness correlation length for parameterizing radar backscatter models. Int. J. Remote Sens. 2007, 28, 3995–4012. [Google Scholar] [CrossRef]
- Panciera, R.; Tanase, M.A.; Lowell, K.; Walker, J.P. Evaluation of IEM, Dubois, and Oh radar backscatter models using airborne L-band SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4966–4979. [Google Scholar] [CrossRef]
- Dong, L.; Baghdadi, N.; Ludwig, R. Validation of the AIEM through correlation length parameterization at field scale using radar imagery in a semi-arid environment. IEEE Geosci. Remote Sens. Lett. 2013, 10, 461–465. [Google Scholar] [CrossRef]
- McNairn, H.; Merzouki, A.; Pacheco, A. Estimating surface soil moisture using Radarsat-2. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 576–579. [Google Scholar]
- Baghdadi, N.; Dubois-Fernandez, P.; Dupuis, X.; Zribi, M. Sensitivity of main polarimetric parameters of multifrequency polarimetric SAR data to soil moisture and surface roughness over bare agricultural soils. IEEE Geosci. Remote Sens. Lett. 2013, 10, 731–735. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M.; Loumagne, C.; Ansart, P.; Anguela, T.P. Analysis of TerraSAR-X data and their sensitivity to soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2008, 112, 4370–4379. [Google Scholar] [CrossRef]
- Baghdadi, N.; Aubert, M.; Zribi, M. Use of TerraSAR-X data to retrieve soil moisture over bare soil agricultural fields. IEEE Geosci. Remote Sens. Lett. 2012, 9, 512–516. [Google Scholar] [CrossRef]
- Baghdadi, N.; King, C.; Bourguignon, A.; Remond, A. Potential of ERS and RADARSAT data for surface roughness monitoring over bare agricultural fields: Application to catchments in Northern France. Int. J. Remote Sens. 2002, 23, 3427–3442. [Google Scholar] [CrossRef]
- Baghdadi, N.; Holah, N.; Zribi, M. Soil moisture estimation using multi-incidence and multi-polarization ASAR data. Int. J. Remote Sens. 2006, 27, 1907–1920. [Google Scholar] [CrossRef]
- Baghdadi, N.; Saba, E.; Aubert, M.; Zribi, M.; Baup, F. Comparison between backscattered TerraSAR signals and simulations from the radar backscattering models IEM, Oh, and Dubois. IEEE Geosci. Remote Sens. Lett. 2011, 6, 1160–1164. [Google Scholar] [CrossRef]
- Baghdadi, N.; Aubert, M.; Cerdan, O.; Franchistéguy, L.; Viel, C.; Eric, M.; Zribi, M.; Desprats, J.F. Operational mapping of soil moisture using synthetic aperture radar data: Application to the Touch basin (France). Sensors 2007, 7, 2458–2483. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N.; Lili-Chabaane, Z.; Mougenot, B. Influence of radar frequency on the relationship between bare surface soil moisture vertical profile and radar backscatter. IEEE Geosci. Remote Sens. Lett. 2014, 11, 848–852. [Google Scholar] [CrossRef]
- Gorrab, A.; Zribi, M.; Baghdadi, N.; Mougenot, B.; Fanise, P.; Chabaane, Z.L. Retrieval of both soil moisture and texture using TerraSAR-X images. Remote Sens. 2015, 7, 10098–10116. [Google Scholar] [CrossRef]
- Aubert, M.; Baghdadi, N.N.; Zribi, M.; Ose, K.; El Hajj, M.; Vaudour, E.; Gonzalez-Sosa, E. Toward an operational bare soil moisture mapping using TerraSAR-X data acquired over agricultural areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 900–916. [Google Scholar] [CrossRef]
- Baronti, S.; Del Frate, F.; Ferrazzoli, P.; Paloscia, S.; Pampaloni, P.; Schiavon, G. SAR polarimetric features of agricultural areas. Int. J. Remote Sens. 1995, 16, 2639–2656. [Google Scholar] [CrossRef]
- Macelloni, G.; Paloscia, S.; Pampaloni, P.; Sigismondi, S.; De Matthaeis, P.; Ferrazzoli, P.; Schiavon, G.; Solimini, D. The SIR-C/X-SAR experiment on Montespertoli: Sensitivity to hydrological parameters. Int. J. Remote Sens. 1999, 20, 2597–2612. [Google Scholar] [CrossRef]
- Paloscia, S.; Macelloni, G.; Pampaloni, P.; Sigismondi, S. The potential of C-and L-band SAR in estimating vegetation biomass: The ERS-1 and JERS-1 experiments. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2107–2110. [Google Scholar] [CrossRef]
- Oh, Y.; Kay, Y.C. Condition for precise measurement of soil surface roughness. IEEE Trans. Geosci. Remote Sens. 1998, 36, 691–695. [Google Scholar]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.-K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]
- Rakotoarivony, L.; Taconet, O.; Vidal-Madjar, D.; Bellemain, P.; Benallegue, M. Radar backscattering over agricultural bare soils. J. Electromagn. Waves Appl. 1996, 10, 187–209. [Google Scholar] [CrossRef]
- Remond, A. Image SAR: Potentialités D’extraction d’un Paramètre Physique du Ruissellement, la Rugosité (Modélisation et Expérimentation). Ph.D. Thesis, Université de Bourgogne, Dijon, France, 1997. [Google Scholar]
- Rakotoarivony, L. Validation de Modèles de Diffusion Electromagnétique: Comparaison Entre Simulations et Mesures Radar Héliporté sur des Surfaces Agricoles de sol nu. Ph.D. Thesis, Université de Caen, Caen, France, 1995. [Google Scholar]
- Boisvert, J.B.; Gwyn, Q.H.J.; Chanzy, A.; Major, D.J.; Brisco, B.; Brown, R.J. Effect of surface soil moisture gradients on modelling radar backscattering from bare fields. Int. J. Remote Sens. 1997, 18, 153–170. [Google Scholar] [CrossRef]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House, Incorporated: Norwood, UK, 1994. [Google Scholar]
- Wu, T.-D.; Chen, K.-S.; Shi, J.; Fung, A.K. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar]
- Altese, E.; Bolognani, O.; Mancini, M.; Troch, P.A. Retrieving soil moisture over bare soil from ERS 1 synthetic aperture radar data: Sensitivity analysis based on a theoretical surface scattering model and field data. Water Resour. Res. 1996, 32, 653–661. [Google Scholar] [CrossRef]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sens. Environ. 2005, 96, 485–496. [Google Scholar] [CrossRef]
- Callens, M.; Verhoest, N.E.; Davidson, M.W. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 878–888. [Google Scholar] [CrossRef]

| Site | SAR Sensor | Spatial Resolution | Freq | Year | Number of Data |
|---|---|---|---|---|---|
| Orgeval (Fr) [23] | SIR-C | 30 m × 30 m | L | 1994 | HH: 1262 measurements 66 in L-band 766 in C-band 430 in X-band VV: 790 measurements 159 in L-band 411 in C-band 220 in X-band HV: 390 measurements 13 in L-band 313 in C-band 64 in X-band |
| Orgeval (Fr) [23,38,39] | SIR-C, ERS, ASAR | 30 m × 30 m | C | 1994; 1995; 2008; 2009; 2010 | |
| Orgeval (Fr) [39] | PALSAR-1 | 30 m × 30 m | L | 2009 | |
| Orgeval (Fr) [40] | TerraSAR-X | 1 m × 1 m | X | 2008, 2009, 2010 | |
| Pays de Caux (Fr) [15,41] | ERS; RADARSAT | 30 m × 30 m | C | 1998; 1999 | |
| Villamblain (Fr) [6,16,42] Villamblain (Fr) [39,43] | ASAR TerraSAR-X | 30 m × 30 m | C X | 2003; 2004; 2006 2008; 2009 | |
| Thau (Fr) [44] | RADARSAT TerraSAR-X | 30 m × 30 m 1 m × 1 m | C X | 2010; 2011 2010 | |
| Touch (Fr) [6,44] | ERS-2; ASAR | 30 m × 30 m | C | 2004; 2006; 2007 | |
| Mauzac (Fr) [43] | TerraSAR-X | 1 m × 1 m | X | 2009 | |
| Garons (Fr) [43] | TerraSAR-X | 1 m × 1 m | X | 2009 | |
| Kairouan (Tu) [45] Kairouan (Tu) [43,45,46] | ASAR TerraSAR-X | 30 m × 30 m | C X | 2012 2010; 2012; 2013; 2014 | |
| Yzerons (Fr) [47] | TerraSAR-X | 1 m × 1 m | X | 2009 | |
| Versailles (Fr) [43] | TerraSAR-X | 1 m × 1 m | X | 2010 | |
| Seysses (Fr) [43] | TerraSAR-X | 1 m × 1 m | X | 2010 | |
| Chateauguay (Ca) [15] | RADARSAT | 30 m × 30 m | C | 1999 | |
| Brochet (Ca) [15] | RADARSAT | 30 m × 30 m | C | 1999 | |
| Alpilles (Fr) [15] | ERS; RADARSAT | 30 m × 30 m | C | 1996; 1997 | |
| Sardaigne (It) [36] | ASAR; RADARSAT | 30 m × 30 m | C | 2008; 2009 | |
| Matera (It) [22] | SIR-C | 30 m × 30 m | L | 1994 | |
| Alzette (Lu) [30,34] | PALSAR-1 | 30 m × 30 m | L | 2008 | |
| Dijle (Be) [30] | PALSAR-1 | 30 m × 30 m | L | 2008; 2009 | |
| Zwalm (Be) [30] | PALSAR-1 | 30 m × 30 m | L | 2007 | |
| Demmin (Ge) [30] | ESAR | 2 m × 2 m | L | 2006 | |
| Montespertoli (It) [35,48] Montespertoli (It) [49] Montespertoli (It) [50] | AIRSAR SIR-C JERS-1 | 30 m × 30 m | L L; C L | 1991 1994 1994 |
| Model | Statistics | All Data | L-Band | C-Band | X-Band | kHrms < 2.5 | kHrms > 2.5 | mv < 20 vol.% | mv > 20 vol. % | θ < 30° | θ > 30° |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dubois for HH pol. | Bias (dB) | −1.0 | −1.0 | −1.1 | −0.9 | +0.4 | −2.9 | −2.6 | +0.3 | −4.2 | +0.3 |
| RMSE (dB) | 4.0 | 3.0 | 4.1 | 4.1 | 3.6 | 4.6 | 4.6 | 3.4 | 5.5 | 3.2 | |
| Dubois for VV pol. | Bias (dB) | +0.7 | −0.2 | +0.4 | +1.8 | +1.2 | −0.2 | +0.5 | +1.0 | −0.6 | +1.5 |
| RMSE (dB) | 2.9 | 2.5 | 2.8 | 3.1 | 3.0 | 2.5 | 2.8 | 3.0 | 2.9 | 2.9 |
| Model | Pol. | Statistics | All Data | L-Band | C-Band | X-Band | kHrms < 2.0 | kHrms > 2.0 | mv < 29.1 vol. % | mv > 29.1 vol. % |
|---|---|---|---|---|---|---|---|---|---|---|
| Oh et al. (1992) [9] | HH | Bias (dB) | +0.4 | +2.5 | +0.1 | 0.0 | +1.3 | −0.5 | −0.3 | +1.9 |
| RMSE (dB) | 2.6 | 3.7 | 2.4 | 2.5 | 2.9 | 2.3 | 2.3 | 3.1 | ||
| VV | Bias (dB) | +0.1 | +2.1 | +0.4 | −1.2 | +1.0 | −0.7 | −0.4 | +1.5 | |
| RMSE (dB) | 2.4 | 3.4 | 2.3 | 2.1 | 2.7 | 2.0 | 2.3 | 2.7 | ||
| Oh et al. (1994) [10] | HH | Bias (dB) | −0.9 | +1.3 | −1.2 | −1.2 | −0.05 | −1.7 | −1.6 | +0.5 |
| RMSE (dB) | 2.8 | 2.8 | 2.7 | 2.8 | 2.6 | 2.9 | 2.9 | 2.5 | ||
| VV | Bias (dB) | −1.3 | +0.7 | −1.3 | −2.1 | −0.5 | −2.1 | −1.7 | −0.4 | |
| RMSE (dB) | 2.6 | 2.6 | 2.6 | 2.7 | 2.4 | 2.9 | 2.8 | 2.2 | ||
| Oh et al. (2002) [11] | HH | Bias (dB) | −0.3 | +2.1 | −0.9 | −1.0 | +0.3 | −0.9 | −0.7 | +0.4 |
| RMSE (dB) | 2.7 | 3.2 | 2.7 | 2.8 | 2.7 | 2.6 | 2.7 | 2.5 | ||
| HV | Bias (dB) | +0.7 | +1.5 | +1.0 | −0.9 | +1.8 | −0.7 | +0.5 | +0.8 | |
| RMSE (dB) | 2.9 | 3.1 | 2.7 | 3.8 | 3.2 | 2.5 | 3.0 | 2.6 | ||
| VV | Bias (dB) | −0.6 | +1.8 | −1.2 | +0.4 | −0.2 | −1.0 | −0.7 | −0.5 | |
| RMSE (dB) | 2.5 | 2.9 | 2.7 | 2.0 | 2.5 | 2.6 | 2.6 | 2.5 | ||
| Oh (2004) [8] | HH | Bias (dB) | −0.5 | +2.1 | −1.0 | −0.6 | 0.6 | +1.5 | −0.9 | +0.4 |
| RMSE (dB) | 2.6 | 3.3 | 2.7 | 2.3 | 2.6 | 2.6 | 2.7 | 2.6 | ||
| VV | Bias (dB) | −1.1 | +1.4 | −1.5 | −1.4 | −0.2 | −2.0 | −1.3 | −0.8 | |
| RMSE (dB) | 2.6 | 2.8 | 2.8 | 2.1 | 2.4 | 2.8 | 2.6 | 2.6 |
| Model | Pol. | Statistics | All Data | L-Band | C-Band | X-Band | Inside the Validity Domain | Outside the Validity Domain |
|---|---|---|---|---|---|---|---|---|
| IEM using GCF | HH | Bias (dB) | +0.8 | −0.9 | +0.7 | +1.5 | +2.6 | −1.8 |
| RMSE (dB) | 10.5 | 3.6 | 11.2 | 10.6 | 12.4 | 6.7 | ||
| HV | Bias (dB) | +17.2 | +5.2 | +11.8 | +46.3 | +18.0 | +14.1 | |
| RMSE (dB) | 38.4 | 14.5 | 26.7 | 74.0 | 28.5 | 50.1 | ||
| VV | Bias (dB) | +0.4 | −2.5 | +0.7 | +3.5 | +1.2 | −0.9 | |
| RMSE (dB) | 9.2 | 5.0 | 8.6 | 11.3 | 11.5 | 3.1 | ||
| IEM using ECF | HH | Bias (dB) | +0.8 | +0.6 | −1.0 | +4.2 | −1.2 | +3.8 |
| RMSE (dB) | 5.6 | 2.9 | 4.1 | 8.3 | 3.2 | 7.8 | ||
| HV | Bias (dB) | −15.8 | +1.2 | −19.9 | 0.0 | −15.8 | −17.1 | |
| RMSE (dB) | 31.4 | 6.8 | 25.1 | 54.4 | 20.1 | 44.3 | ||
| VV | Bias (dB) | +2.2 | −1.3 | +0.5 | +6.7 | −0.9 | +7.1 | |
| RMSE (dB) | 6.5 | 3.5 | 4.9 | 9.4 | 3.7 | 9.4 | ||
| IEM_B with Lopt using GCF | HH | Bias (dB) | −0.3 | −0.1 | −0.6 | +0.3 | ||
| RMSE (dB) | 2.0 | 2.3 | 2.1 | 1.8 | ||||
| HV | Bias (dB) | −1.3 | ||||||
| RMSE (dB) | 3.1 | |||||||
| VV | Bias (dB) | +0.1 | +0.2 | 0 | +0.3 | |||
| RMSE (dB) | 1.9 | 2.3 | 1.9 | 1.8 | ||||
| AIEM using GCF | HH | Bias (dB) | +2.3 | −3.2 | +2.9 | +3.1 | ||
| RMSE (dB) | 12.2 | 5.4 | 13.4 | 11.7 | ||||
| VV | Bias (dB) | 0.0 | −4.1 | +0.5 | +0.5 | |||
| RMSE (dB) | 10.8 | 5.9 | 11.4 | 11.0 | ||||
| AIEM using ECF | HH | Bias (dB) | −2.3 | −3.0 | −3.6 | +0.2 | ||
| RMSE (dB) | 4.4 | 4.4 | 4.6 | 4.2 | ||||
| VV | Bias (dB) | −1.8 | −2.4 | −2.3 | -0.7 | |||
| RMSE (dB) | 3.8 | 4.4 | 3.8 | 3.7 | ||||
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Mattia, F. Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements. Water 2017, 9, 38. https://doi.org/10.3390/w9010038
Choker M, Baghdadi N, Zribi M, El Hajj M, Paloscia S, Verhoest NEC, Lievens H, Mattia F. Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements. Water. 2017; 9(1):38. https://doi.org/10.3390/w9010038
Chicago/Turabian StyleChoker, Mohammad, Nicolas Baghdadi, Mehrez Zribi, Mohammad El Hajj, Simonetta Paloscia, Niko E. C. Verhoest, Hans Lievens, and Francesco Mattia. 2017. "Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements" Water 9, no. 1: 38. https://doi.org/10.3390/w9010038
APA StyleChoker, M., Baghdadi, N., Zribi, M., El Hajj, M., Paloscia, S., Verhoest, N. E. C., Lievens, H., & Mattia, F. (2017). Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements. Water, 9(1), 38. https://doi.org/10.3390/w9010038








