Water Footprint Calculation on the Basis of Input–Output Analysis and a Biproportional Algorithm: A Case Study for the Yellow River Basin, China
Abstract
:1. Introduction
2. Study Area and Method
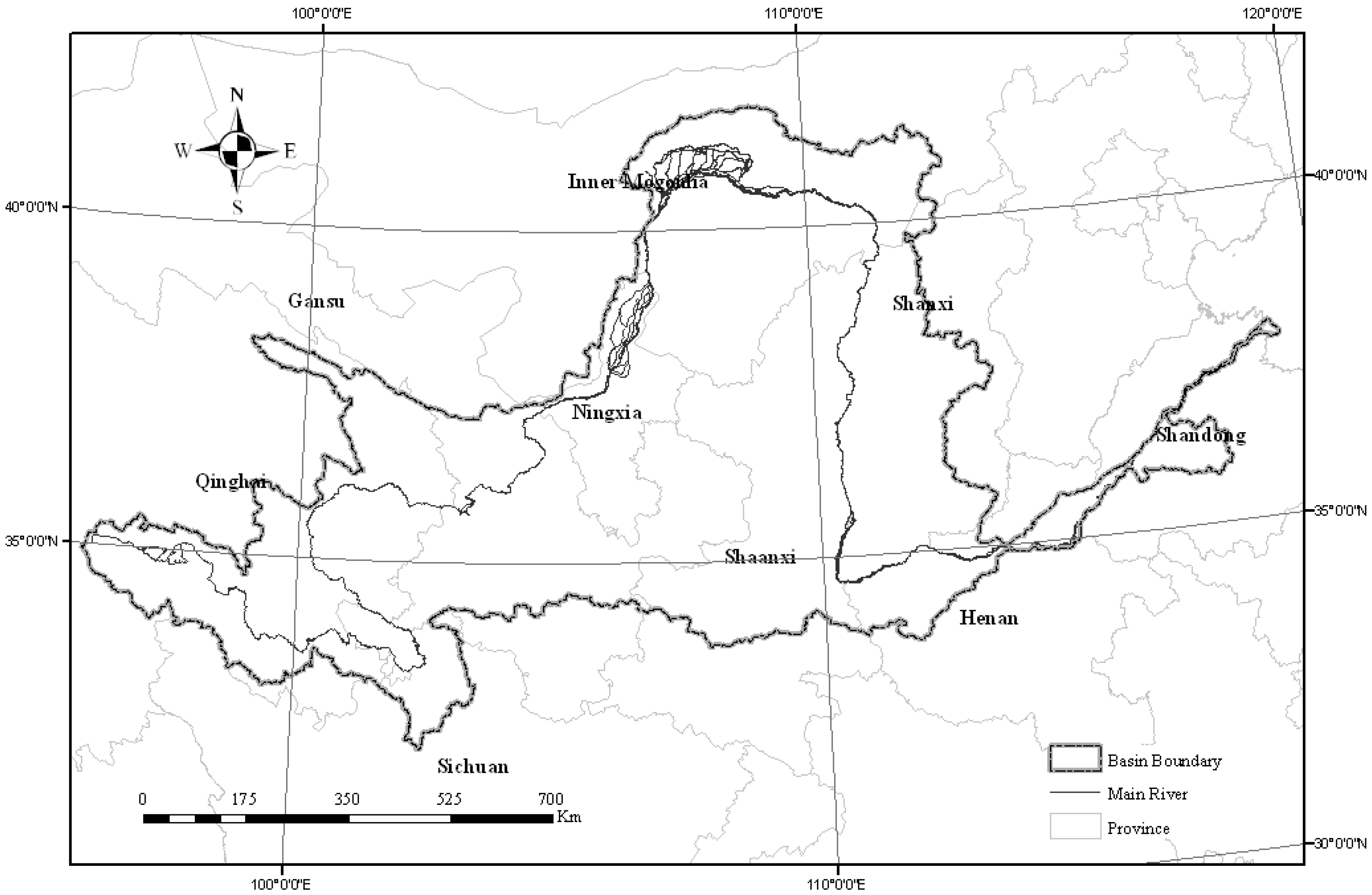
2.1. Study Area
2.2. Data
2.3. Method
2.3.1. Water Footprint (WF) Calculation
2.3.2. Water Footprint (WF) Dynamic Analysis
3. Results
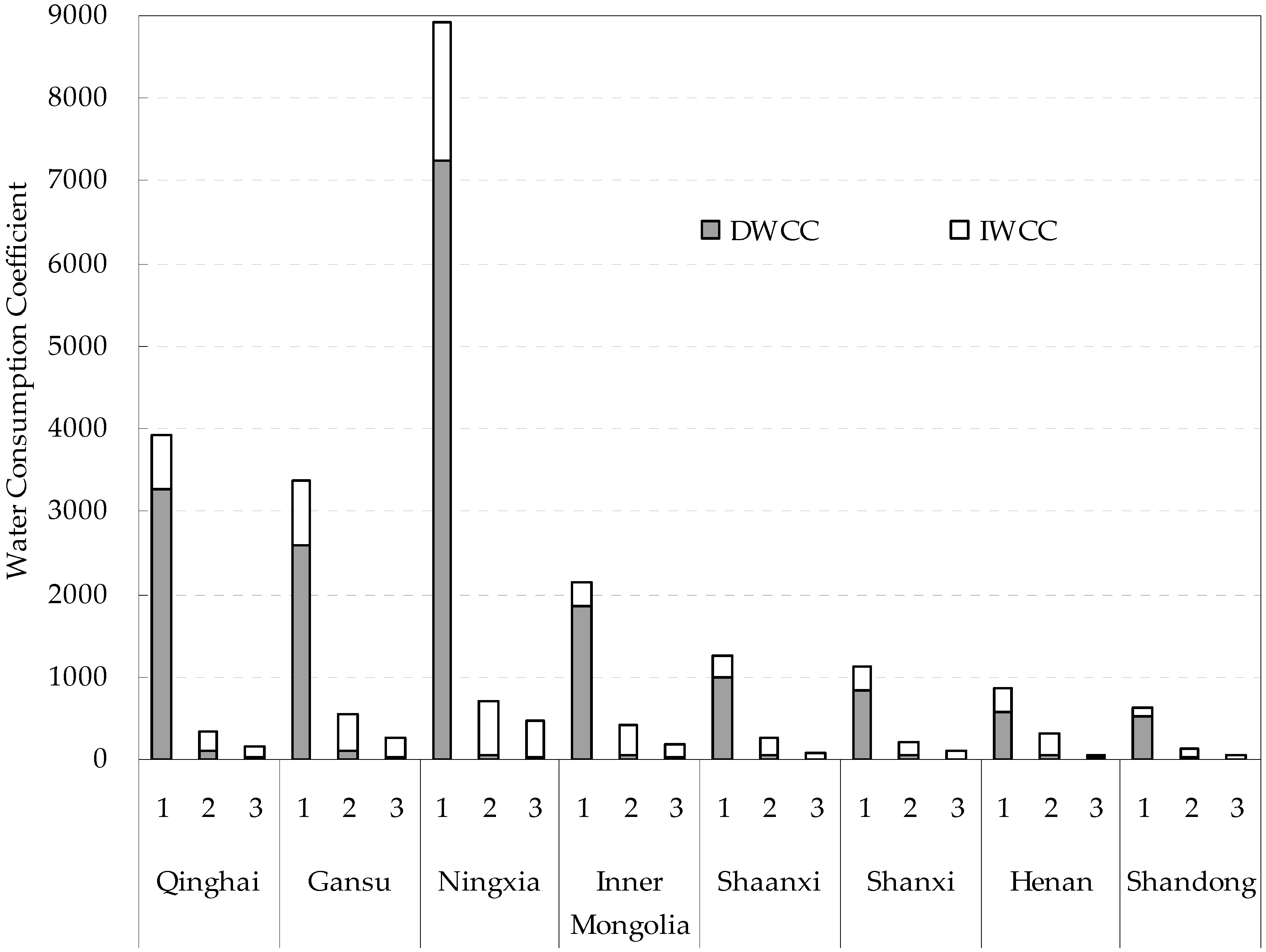
3.1. Water Consumption Coefficient
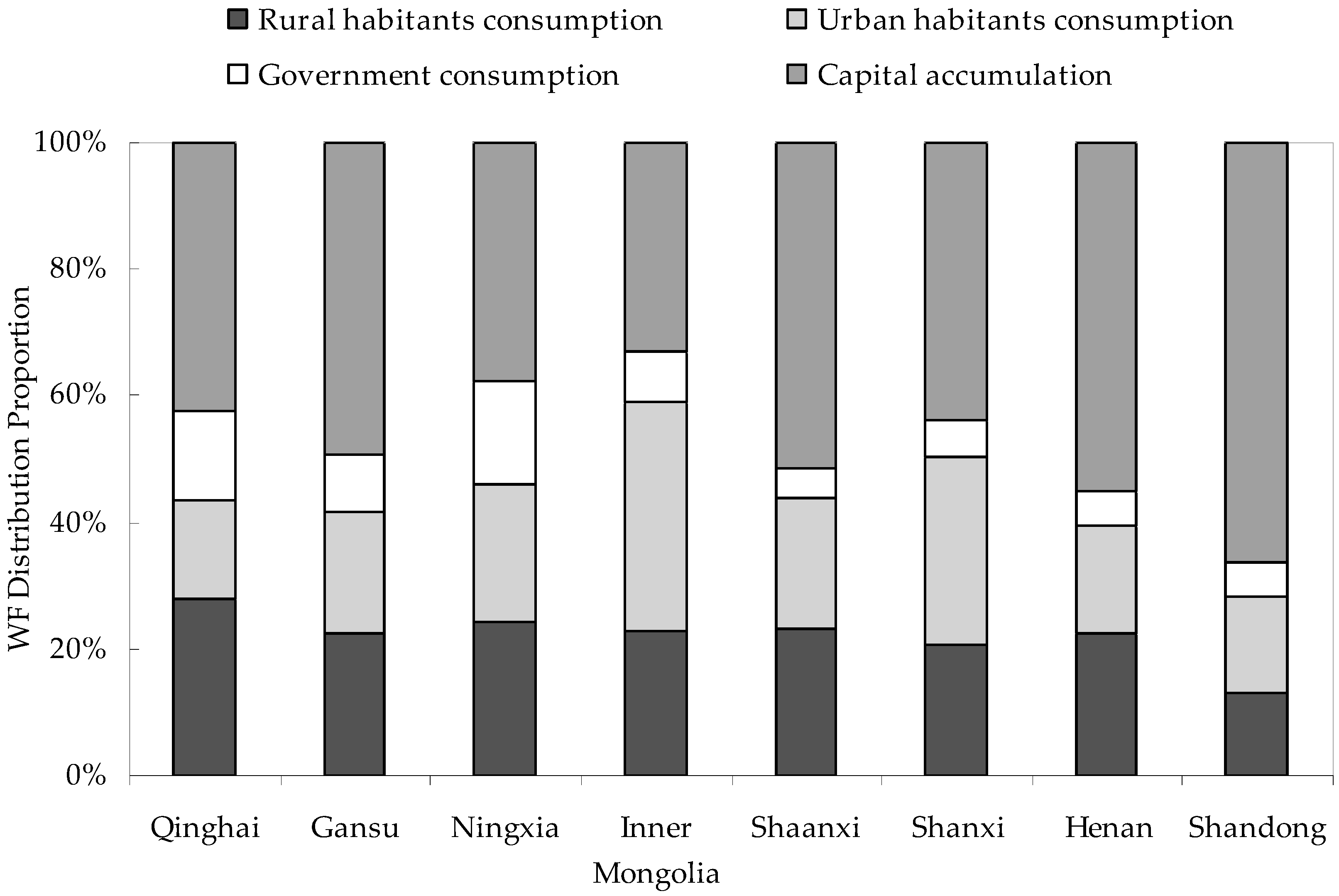
3.2. Distribution of Water Footprint (WF)
3.3. Total Water Footprint (WF)
3.4. Net External Water Footprint (WF)
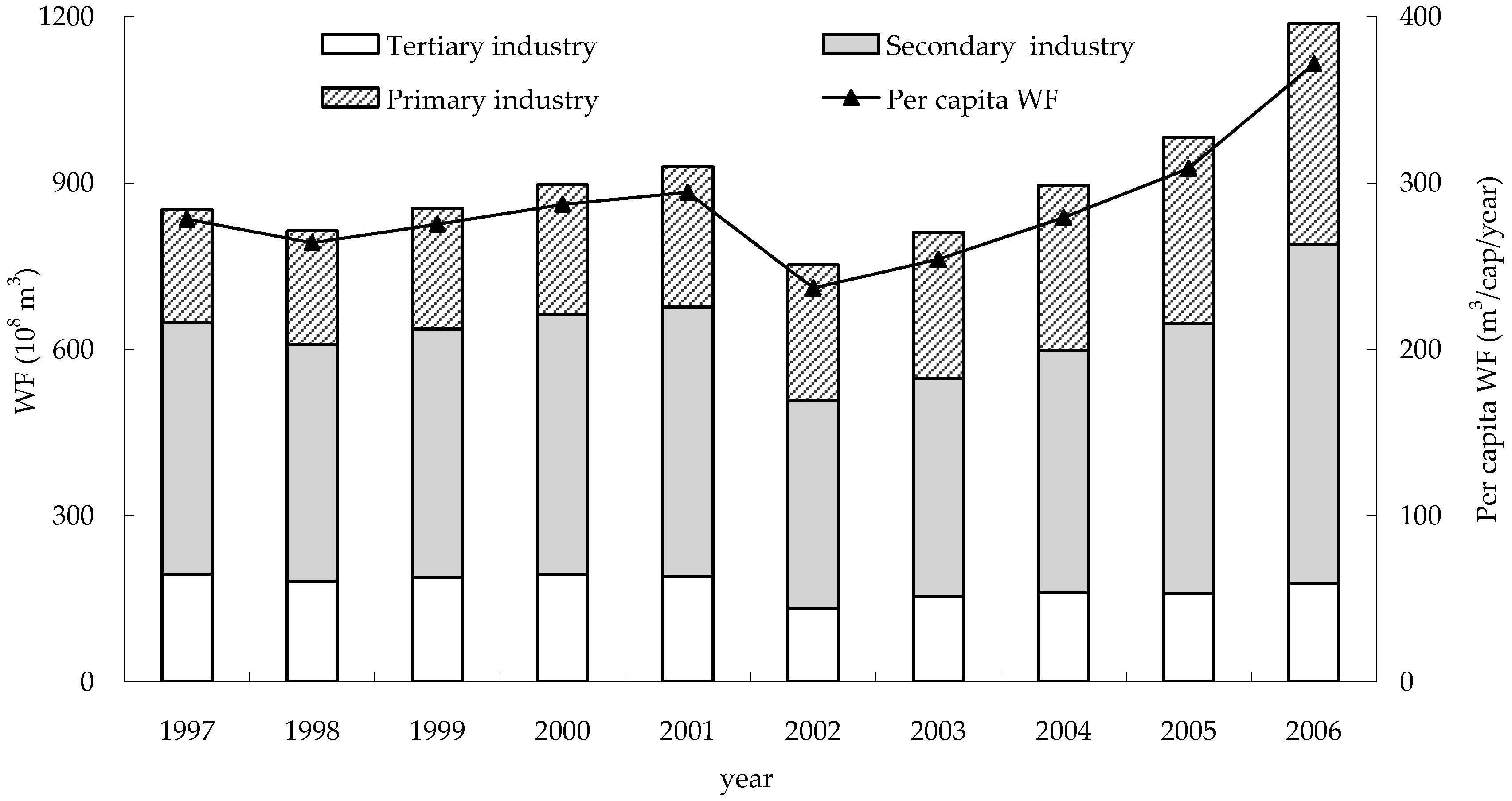
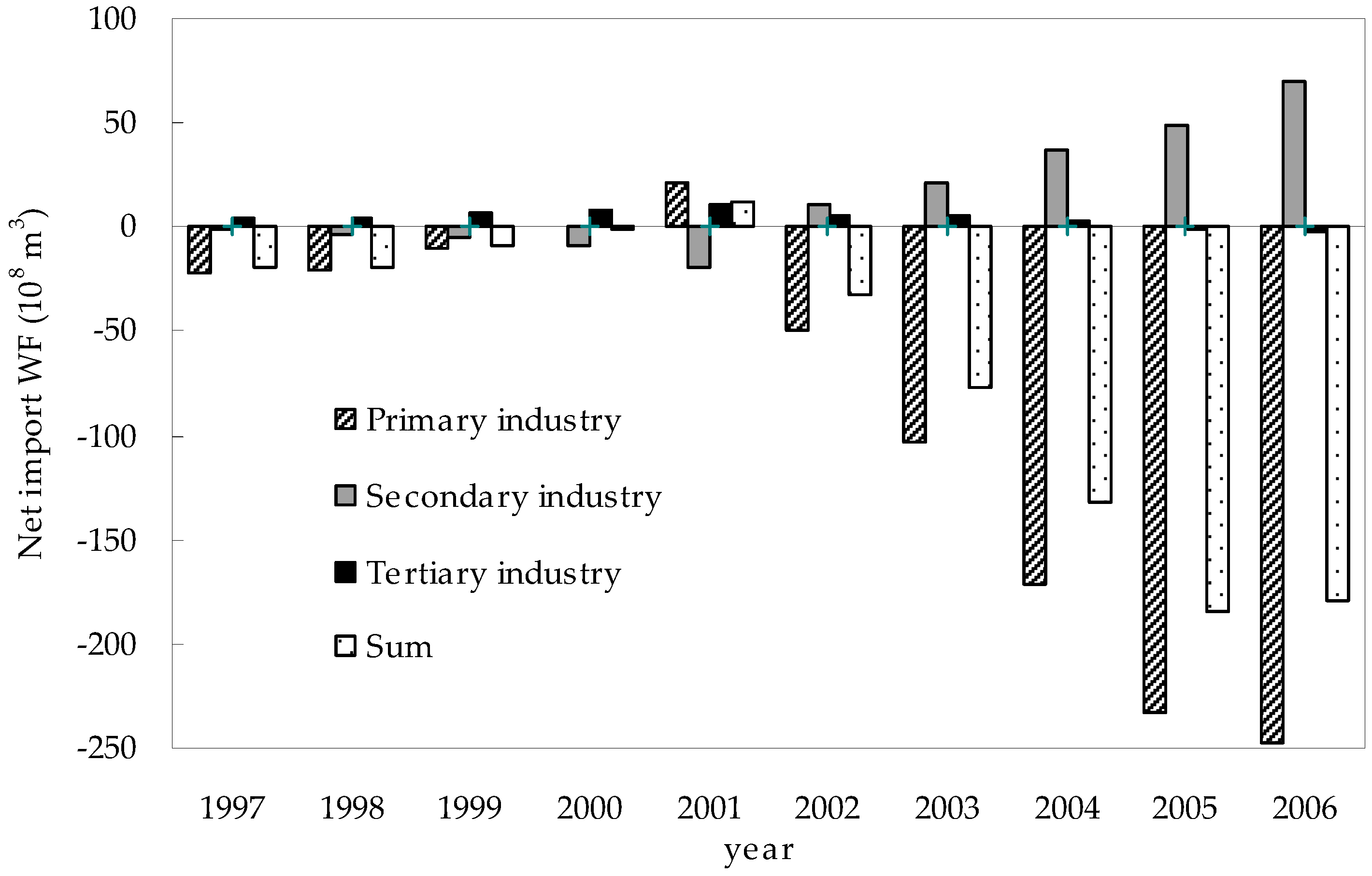
3.5. Annual Variation of Water Footprint (WF)
3.6. Driving Factors of Water Footprint (WF)
3.6.1. Index Selection
3.6.2. Factor Analysis and Linear Regression
4. Discussion and Implications
4.1. Discussion
4.2. Implications
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hoekstra, A.Y. Sustainable, efficient and equitable water use: The three pillars under wise freshwater allocation. Wiley Interdiscip. Rev. Water 2014, 1, 31–40. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Mekonnen, M.M. The water footprint of humanity. Proc. Natl. Acad. Sci. USA 2012, 109, 3232–3237. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Finkbeiner, M. Water Footprinting: How to address water use in life cycle assessment? Sustainability 2010, 2, 919–944. [Google Scholar] [CrossRef]
- Hoekstra, A.Y. A critique on the water-scarcity weighted water footprint in LCA. Ecol. Indic. 2016, 66, 564–573. [Google Scholar] [CrossRef]
- Chapagain, A.K.; Hoekstra, A.Y.; Savenije, H.H.G.; Gautam, R. The water footprint of cotton consumption: An assessment of the impact of worldwide consumption of cotton products on the water resources in the cotton producing countries. Ecol. Econ. 2006, 60, 186–203. [Google Scholar] [CrossRef]
- Duan, P.; Qin, L.; Wang, Y.; He, H. Spatiotemporal correlations between water footprint and agricultural inputs: A case study of maize production in northeast China. Water 2015, 7, 4026–4040. [Google Scholar] [CrossRef]
- Guan, D.B.; Hubacek, K. Assessment of regional trade and virtual water flows in China. Ecol. Econ. 2007, 61, 159–170. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K.; Aldaya, M.M.; Mekonnen, M.M. The Water Footprint Assessment Manual: Setting the Global Standard; Earthscan: London, UK, 2011. [Google Scholar]
- Okadera, T.; Okamoto, N. Regional water footprints of the Yangtze River: An interregional input-output approach. Econ. Syst. Res. 2014, 26, 444–462. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Shi, M. Analyses of water footprint of Beijing in an interregional input-output framework. Ecol. Econ. 2011, 70, 2494–2502. [Google Scholar] [CrossRef]
- Ercin, A.; Hoekstra, A. European water footprint scenarios for 2050. Water 2016, 8. [Google Scholar] [CrossRef]
- Gheewala, S.H.; Silalertruksa, T.; Nilsalab, P.; Mungkung, R.; Perret, S.; Chaiyawannakarn, N. Water footprint and impact of water consumption for food, feed, fuel Crops production in Thailand. Water 2014, 6, 1698–1718. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K. Water footprints of nations: Water use by people as a function of their consumption pattern. Water Resour. Manag. 2007, 21, 35–48. [Google Scholar] [CrossRef]
- Allan, J.A. Virtual water: A strategic resource. Ground Water 1998, 36, 545–546. [Google Scholar] [CrossRef]
- Debaere, P. The global economics of water: Is water a source of comparative advantage? Am. Econ. J. Appl. Econ. 2012, 6, 32–48. [Google Scholar] [CrossRef]
- Zhuo, L.; Mekonnen, M.M.; Hoekstra, A.Y.; Wada, Y. Inter- and intra-annual variation of water footprint of crops and blue water scarcity in the Yellow River basin (1961–2009). Adv. Water Resour. 2016, 87, 29–41. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K. Globalization of Water: Sharing the Planet’s Freshwater Resources; Blackwell: Oxford, UK, 2008. [Google Scholar]
- Hoekstra, A.Y. Human appropriation of natural capital: A comparison of ecological footprint and water footprint analysis. Ecol. Econ. 2009, 68, 1963–1974. [Google Scholar] [CrossRef]
- Williams, E.D.; Weber, C.L.; Hawkins, T.R. Hybrid framework for managing uncertainty in life cycle inventories. J. Ind. Ecol. 2009, 13, 928–944. [Google Scholar] [CrossRef]
- Cai, Z.; Shen, L.; Liu, J.; Zhao, X. Applying input-output analysis method for calculation of water footprint and virtual water trade in Gansu Province. Acta Ecol. Sin. 2012, 32, 6481–6488. (In Chinese) [Google Scholar]
- Leontief, W. Environmental repercussions and the economic structure: An input-output approach. Rev. Econ. Stat. 1970, 52, 262–271. [Google Scholar] [CrossRef]
- Lenzen, M.; Murray, S.A. A modified ecological footprint and its application to Australia. Ecol. Econ. 2001, 37, 229–255. [Google Scholar] [CrossRef]
- Ferng, J.J. Local sustainable yield and embodied resources in ecological footprint analysis—A case study on the required paddy field in Taiwan. Ecol. Econ. 2005, 53, 415–430. [Google Scholar] [CrossRef]
- Singh, S.; Bakshi, B.R. Footprints of carbon and nitrogen: Revisiting the paradigm and exploring their nexus for decision making. Ecol. Indic. 2015, 53, 49–60. [Google Scholar] [CrossRef]
- Mubako, S.; Lahiri, S.; Lant, C. Input-output analysis of virtual water transfers: Case study of California and Illinois. Ecol. Econ. 2013, 93, 230–238. [Google Scholar] [CrossRef]
- Feng, K.; Hubacek, K.; Minx, J.; Siu, Y.L.; Chapagain, A.; Yu, Y.; Guan, D.; Barrett, J. Spatially explicit analysis of water footprints in the UK. Water 2011, 3, 47–63. [Google Scholar] [CrossRef]
- Guan, D.B.; Hubacek, K. A Hydro-Economic accounting and analytical framework for water resources: A case study for North China. J. Environ. Manag. 2008, 88, 1300–1324. [Google Scholar] [CrossRef] [PubMed]
- Hubacek, K.; Sun, L.X. Economic and societal changes in China and their effects on water use: A scenario analysis. J. Ind. Ecol. 2005, 9, 187–200. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, B.; Yang, Z.F. National water footprint in an input-output framework—A case study of China 2002. Ecol. Model. 2009, 220, 245–253. [Google Scholar] [CrossRef]
- Feng, K.; Siu, Y.L.; Guan, D.; Hubacek, K. Assessing regional virtual water flows and water footprints in the Yellow River Basin, China: A consumption based approach. Appl. Geogr. 2011, 32, 691–701. [Google Scholar] [CrossRef]
- Deng, G.; Ma, Y.; Li, X. Regional water footprint evaluation and trend analysis of China—Based on interregional input-output model. J. Clean. Prod. 2016, 112, 4674–4682. [Google Scholar] [CrossRef]
- Leontief, W. Quantitative input and output relations in the economic system of the United States. Rev. Econ. Stat. 1936, 18, 105–125. [Google Scholar] [CrossRef]
- Lahr, M.L.; de Mesnard, L. Biproportional techniques in input-output analysis: Table updating and structural analysis. Econ. Syst. Res. 2004, 16, 115–134. [Google Scholar] [CrossRef]
- Jalili, A.R. Impacts of aggregation on relative performances of nonsurvey updating techniques and inter temporal stability of input-output coefficients. Econ. Chang. Restruct. 2005, 38, 147–165. [Google Scholar] [CrossRef]
- Dobrescu, E.; Gaftea, V. On the accuracy of RAS method in an emergent economy. Amfiteatru Econ. J. 2012, 14, 502–521. [Google Scholar]
- Dobrescu, E. Restatement of the I-O coefficient stability problem. J. Econ. Struct. 2013, 2, 1–67. [Google Scholar] [CrossRef]
- Yamada, M. Construction of a multi-regional input-output table for Nagoya metropolitan area, Japan. J. Econ. Struct. 2015, 4, 1–18. [Google Scholar] [CrossRef]
- Liu, J.G.; Williams, J.R.; Zehnder, A.J.B.; Yang, H. GEPIC—Modelling wheat yield and crop water productivity with high resolution on a global scale. Agric. Syst. 2007, 94, 478–493. [Google Scholar] [CrossRef]
- National Economy Accounting Department of National Bureau of Statistics. Regional Input–Output Tables of China 2002; Chinese Statistics Press: Beijing, China, 2008.
- Yellow River Conservancy Commission. Bulletin of Yellow River Water Resources; Yellow River Water Resources Press: Zhengzhou, China, 2007. [Google Scholar]
- Zhang, Q.; Peng, J.; Singh, V.P.; Li, J.; Chen, Y.D. Spatio-temporal variations of precipitation in arid and semiarid regions of China: The Yellow River basin as a case study. Glob. Planet. Chang. 2014, 114, 38–49. [Google Scholar] [CrossRef]
- Stone, J.M. Input-Output Relationships 1954–1966; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Härdle, W.; Simar, L. Applied Multivariate Statistical Analysis; Springer: Berlin, Germany, 2003. [Google Scholar]
- Draper, R.N.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Siddik, K.; Irfan, D.; Askin, K. Factor Analysis Scores in a Multiple Linear Regression Model for the Prediction of Carcass Weight in Akkeci Kids. J. Appl. Anim. Res. 2007, 31, 201–204. [Google Scholar]
- Thayer, J.D. Interpretation of Standardized Regression Coefficients in Multiple Regression. In Proceedings of the Annual Meeting of the American Educational Research Association, Chicago, IL, USA, 3–7 April 1991.
- Zhuo, L.; Mekonnen, M.M.; Hoekstra, A.Y. Sensitivity and uncertainty in crop water footprint accounting: A case study for the Yellow River basin. Hydrol. Earth Syst. Sci. 2014, 18, 2219–2234. [Google Scholar] [CrossRef]
- Dong, H.; Geng, Y.; Fujita, T.; Fujii, M.; Hao, D.; Yu, X. Uncovering regional disparity of China’s water footprint and inter-provincial virtual water flows. Sci. Total Environ. 2014, 500–501, 120–130. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization (ISO). ISO 14046: Environmental Management–Water Footprint–Principles, Requirements and Guidelines; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Boulay, A.M.; Hoekstra, A.Y.; Vionnet, S. Complementarities of water-focused life cycle assessment and water footprint assessment. Environ. Sci. Technol. 2013, 47, 11926–11927. [Google Scholar] [CrossRef] [PubMed]
- He, J.P.; He, Z. Spatio-temporal characteristics of extreme precipitation event in Yellow River basin in recent 53 years. Ecol. Environ. Sci. 2014, 23, 95–100. [Google Scholar]
- Jia, S.; Zhang, S.; Wang, H. Reasons of high irrigation quota and potential of water-saving in Ning-Meng Irrigation Area. Resour. Sci. 2003, 25, 29–34. [Google Scholar]


| Output | Intermediate Product | Final Use | Exports | Imports | Gross Output | |
|---|---|---|---|---|---|---|
| Input | ||||||
| Intermediate input | xij | fi | ei | mi | xi | |
| Value added | cj | - | - | - | - | |
| Total inputs | xj | - | - | - | - | |
| Water consumption | wj | - | - | - | - | |
| City | Per Capita WFrural | Per Capita WFurban | Per Capita WFwhole |
|---|---|---|---|
| Qinghai | 256.0 | 205.4 | 538.9 |
| Gansu | 146.7 | 383.4 | 490.2 |
| Ningxia | 396.6 | 918.0 | 1177.4 |
| Inner Mongolia | 158.2 | 918.8 | 541.7 |
| Shaanxi | 53.2 | 132.8 | 169.0 |
| Shanxi | 53.4 | 126.9 | 161.5 |
| Henan | 47.7 | 148.8 | 170.0 |
| Shandong | 36.7 | 132.9 | 168.7 |
| Sum | 71.2 | 225.3 | 247.1 |
| City | Primary Industry | Secondary Industry | Tertiary Industry | Sum |
|---|---|---|---|---|
| Qinghai | 0.18 | −0.06 | 0.22 | 0.35 |
| Gansu | −0.21 | 1.58 | −0.07 | 1.30 |
| Ningxia | −1.41 | 0.71 | 0.36 | −0.34 |
| Inner Mongolia | −5.39 | 1.91 | −0.17 | −3.65 |
| Shaanxi | −1.09 | 0.72 | −0.02 | −0.39 |
| Shanxi | 0.17 | 0.15 | 0.00 | 0.33 |
| Henan | 0.41 | −0.96 | 0.03 | −0.52 |
| Shandong | −1.01 | −0.55 | −0.03 | −1.58 |
| Sum | −8.35 | 3.51 | 0.34 | −4.51 |
| Indexes | Correlation Coefficient |
|---|---|
| Population | 0.635 * |
| GDP | 0.778 ** |
| Food output | 0.407 |
| Industrial added value | 0.807 ** |
| Proportion of the secondary industry | 0.772 ** |
| Water consumption per unit grain | −0.658 * |
| Water consumption per 10,000 Yuan of incremental industrial value | −0.588 |
| Capital formation | 0.821 ** |
| Meat consumption per capita | 0.650 ** |
| Food consumption per capita | 0.751 * |
| Irrigation area | 0.670 * |
| Indexes | Main Factor 1 | Main Factor 2 |
|---|---|---|
| Population | 0.971 | −0.077 |
| GDP | 0.896 | 0.436 |
| Food output | 0.847 | 0.518 |
| Industrial added value | 0.886 | 0.425 |
| Proportion of the secondary industry | 0.614 | 0.713 |
| Water consumption per unit grain | 0.974 | 0.209 |
| Water consumption per 10,000 Yuan of incremental industrial value | 0.829 | 0.545 |
| Capital formation | 0.864 | 0.418 |
| Meat consumption per capita | 0.844 | 0.513 |
| Food consumption per capita | 0.914 | 0.145 |
| Irrigation area | 0.971 | −0.077 |
| Indexes | Non-Standardized Regression Coefficient | Standardized Regression Coefficient |
|---|---|---|
| Population | 0.147 | 0.628 |
| GDP | 0.007 | 1.461 |
| Proportion of the secondary industry | 46.190 | 1.053 |
| Water consumption per 10,000 Yuan of incremental industrial value | 8.148 | 3.933 |
| Meat consumption per capita | 1.000 | 0.664 |
| Irrigation area | 0.213 | 1.008 |
| Constant | −11,986.274 | --- |
| Correlation Coefficient (R2) | 0.999 | |
| Value of F-test | 398.113 | |
| p-value | 0.0002 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Wang, H.; Cai, Y. Water Footprint Calculation on the Basis of Input–Output Analysis and a Biproportional Algorithm: A Case Study for the Yellow River Basin, China. Water 2016, 8, 363. https://doi.org/10.3390/w8090363
Yin J, Wang H, Cai Y. Water Footprint Calculation on the Basis of Input–Output Analysis and a Biproportional Algorithm: A Case Study for the Yellow River Basin, China. Water. 2016; 8(9):363. https://doi.org/10.3390/w8090363
Chicago/Turabian StyleYin, Jian, Huixiao Wang, and Yan Cai. 2016. "Water Footprint Calculation on the Basis of Input–Output Analysis and a Biproportional Algorithm: A Case Study for the Yellow River Basin, China" Water 8, no. 9: 363. https://doi.org/10.3390/w8090363
APA StyleYin, J., Wang, H., & Cai, Y. (2016). Water Footprint Calculation on the Basis of Input–Output Analysis and a Biproportional Algorithm: A Case Study for the Yellow River Basin, China. Water, 8(9), 363. https://doi.org/10.3390/w8090363





