2.1. Sector Definition Algorithm
Graphs are virtual structures topologically formed by nodes (or vertices) and links (or edges) that can be used to represent any kind of network, either physical or virtual. Graph theory is a branch of mathematics devoted to the study of these structures. WSNs can be represented as graphs, and over them, it is possible to implement algorithms of the graph theory domain. Two concepts of major importance from this theory are the “shortest path” between nodes and “community detection”. The first one allows finding the most efficient way to reach one node from any other, and the second one allows finding modules with a high level of cohesion that are separated from other modules by a minimized number of edges.
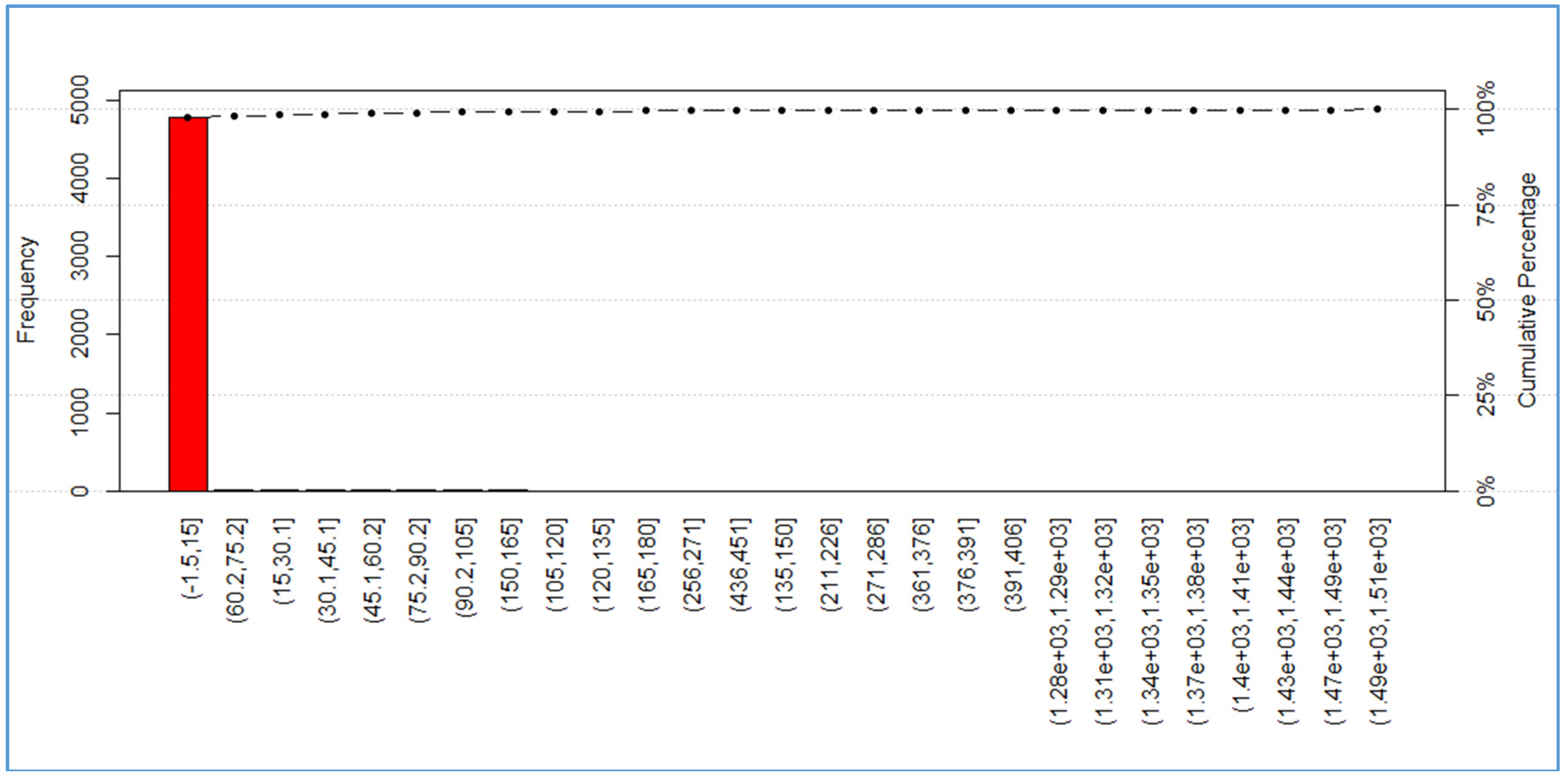
As previously mentioned, in this paper, the shortest path concept is used to define and segregate the trunk network from the distribution network; in this process, a ranking of pipes is generated. Such a ranking is based on the pipe’s role in the supply of the entire network. To assess the role of each pipe in the supply, a hydraulic simulation is conducted with EPANET for the most critical scenario (the instant of highest demand). Then, the direction of the flow in each pipe is retrieved and stored in a squared matrix. This matrix allows calculating the number of nodes/pipes that can be reached from every node, this being the Accumulated Shortest Path Value (ASPV). Then, the flow in each pipe is multiplied by its corresponding ASPV (the result is represented by AVSP*). The trunk network is expected to be formed by pipes with high and less frequent AVSP* values, whereas the pipes in the distribution network are expected to have low and highly frequent AVSP* values. This can be more clearly seen in
Figure 1, where the tallest red bar represents almost 97% of the pipes having values of ASPV* in the same range (0–15).
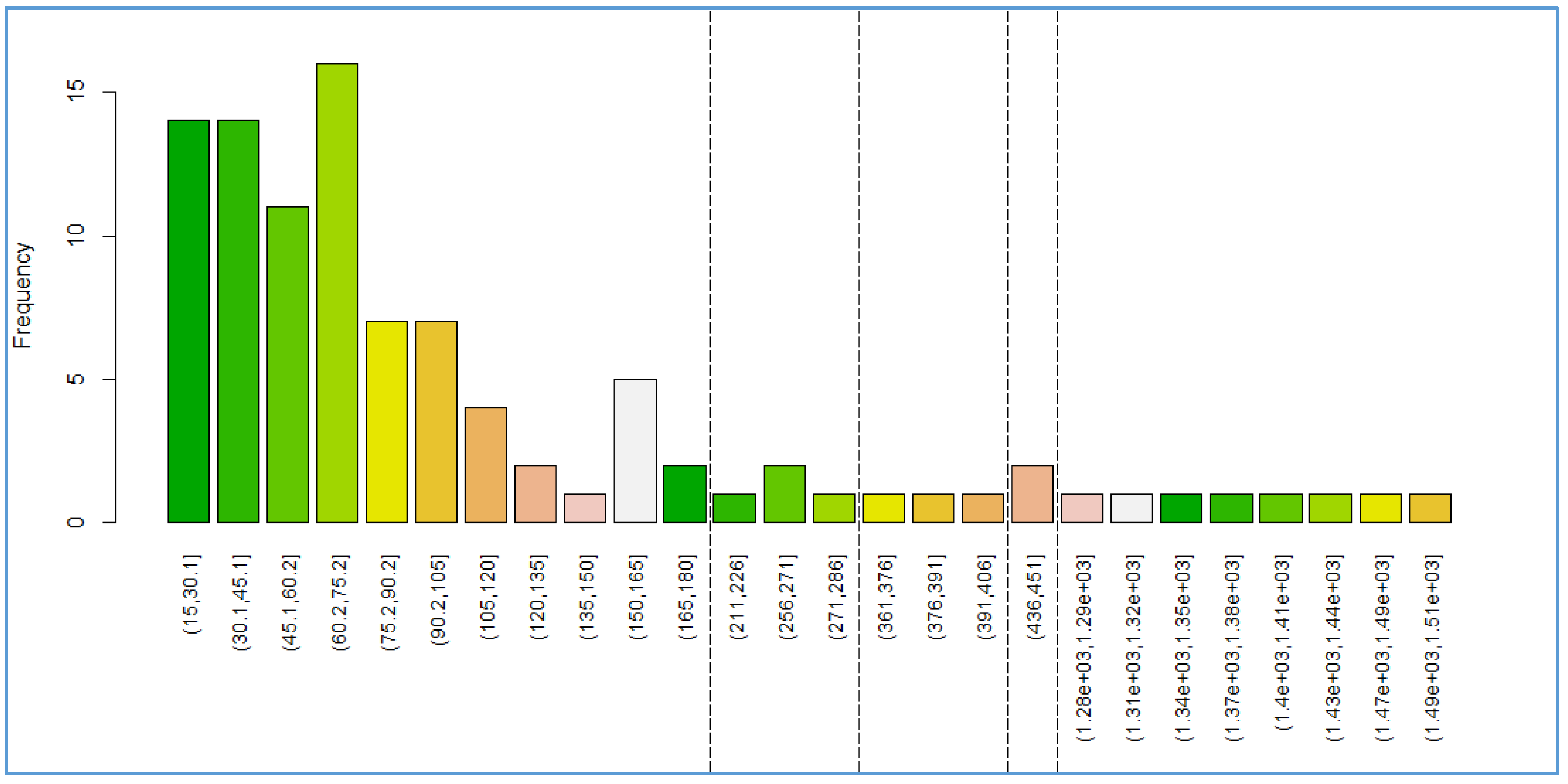
Figure 2 is a zoom-in of the remaining 3% of the pipes in
Figure 1. The vertical dotted lines indicate discontinuity in the ranges of ASPV*; for example, the first vertical line from the left to the right separates the ranges 165–180 and 211–226. As can be seen, the last value of the first range is lower than the first value of the second range, which indicates the presence of pipes of different classes. This type of discontinuity can be used as a criterion to define several scopes for the trunk network. For example, in the left plot in
Figure 3, the trunk network selection includes all of the pipes with ASPV* above the range 211–226, whereas the one to the right includes pipes with ASPV* values above 15.
Once the trunk network is selected, it is uncoupled from the distribution network, and this last one is treated as a social network graph. Of note is that social network graphs are specific versions of graphs, where there are no centroids, and all of the nodes have the same level of importance. The community detection algorithms based the social network theory aim at revealing network modules based on a modularity index proposed by [
17]. One of these algorithms corresponds to the so-called Louvain method. This is a multilevel algorithm, which works with a “bottom-up” approximation. Initially, each node is assigned to its own community. Iteratively, the algorithm builds up neighbor’s communities, with the aim of increasing the modularity index. In the next step and at a higher level, a new network of aggregated communities is formed. Then, the process is repeated until there is no more gain in the modularity index. The algorithm is classified as extremely fast and able to deal with networks of up to 10
9 edges in a reasonable time, with ordinary computing resources [
18]. It is important to note that, although the algorithm always finds a partition with maximized modularity, the result of the method is not only one partition, but a hierarchy of partitions, from which any particular partition may be selected. Let us note that the partition of maximum modularity can generate extremely small communities, whose implementation could be economically unfeasible. This is the reason why we propose a recursive merging process (see the pseudo-code below) to ensure that all of the sectors comply with a series of pre-established constraints.
In the next pseudo-code, we use the following notation:
Index m represents a pipe; INm represents the initial node of pipe m; FNm is the final node of pipe m; C stands for community; and L refers to the characteristic used as a criterion.
Pseudo-Code:
All of the pipes separating communities are selected and are input into the Set of Candidate Pipes (SCP):
Input: Communities with a maximized modularity index.
- 1.
Given m, if INm ∈ Ci and ENm ∈ Cj → m ∈ SCP.
From the SCP, a subset scpi from which their corresponding communities do not exceed a preset constraint for a given feature is extracted.
- 2.
From scpi ⊈ SCP, in which for every m, Li and Li < Lmax.
For every m, if Li + Lj < Lmax → i + j = {i, j}.
- 3.
Steps 1–2 are repeated until there are no more pipes entering into the scpi.
Output: Sectors satisfying a series of constraints.
It is also important to set a lower limit for the characteristic used to define the size of the sectors. Therefore, if at the end of the process there are some sectors with a value lower than the limit, they are declared as minisectors (no valves or CUs). This only applies in the case of minisectors that cannot be merged with larger sectors. In the case that a minisector shares at least one connection with a sector that has reached its maximum feature value, the maximum limit is slightly relaxed to allow their fusion. For example, if the characteristic that is used as a criterion is the sector pipe length (e.g., 30 km maximum constraint), the maximum final length that a given sector eventually will have will equal that maximum length (30 km) plus a value that is smaller than the minimum value of the sector pipe length (e.g., 4 km); in other words, a value between 30 km and 34 km may be accepted.
Finally, the trunk network is re-coupled with the distribution network, and the pipes connecting each sector with the trunk are included in a new set of candidate pipes. Each pipe in this set can be defined either as a boundary valve or as a sector entrance.
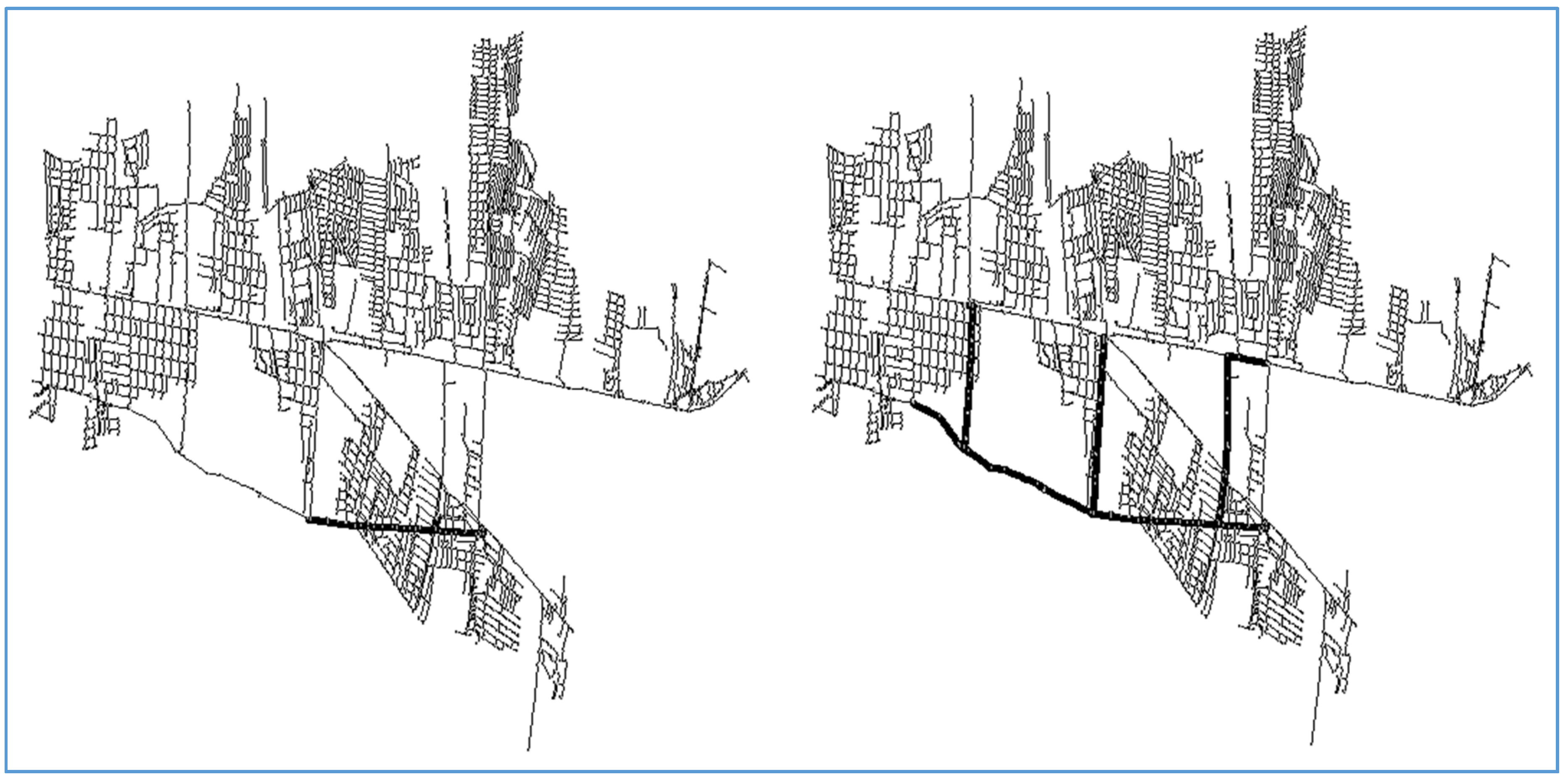
Figure 4 and
Figure 5 depict the output of the merging process over the partition with the greatest modularity index for the case study in this paper. In the first case, the maximum allowed elevation difference was set at 20 m, while for the second case, it was set at 40 m. Of note is that in the first partition (
Figure 4), there are many small sectors that in the second partition are merged into bigger sectors (
Figure 5).
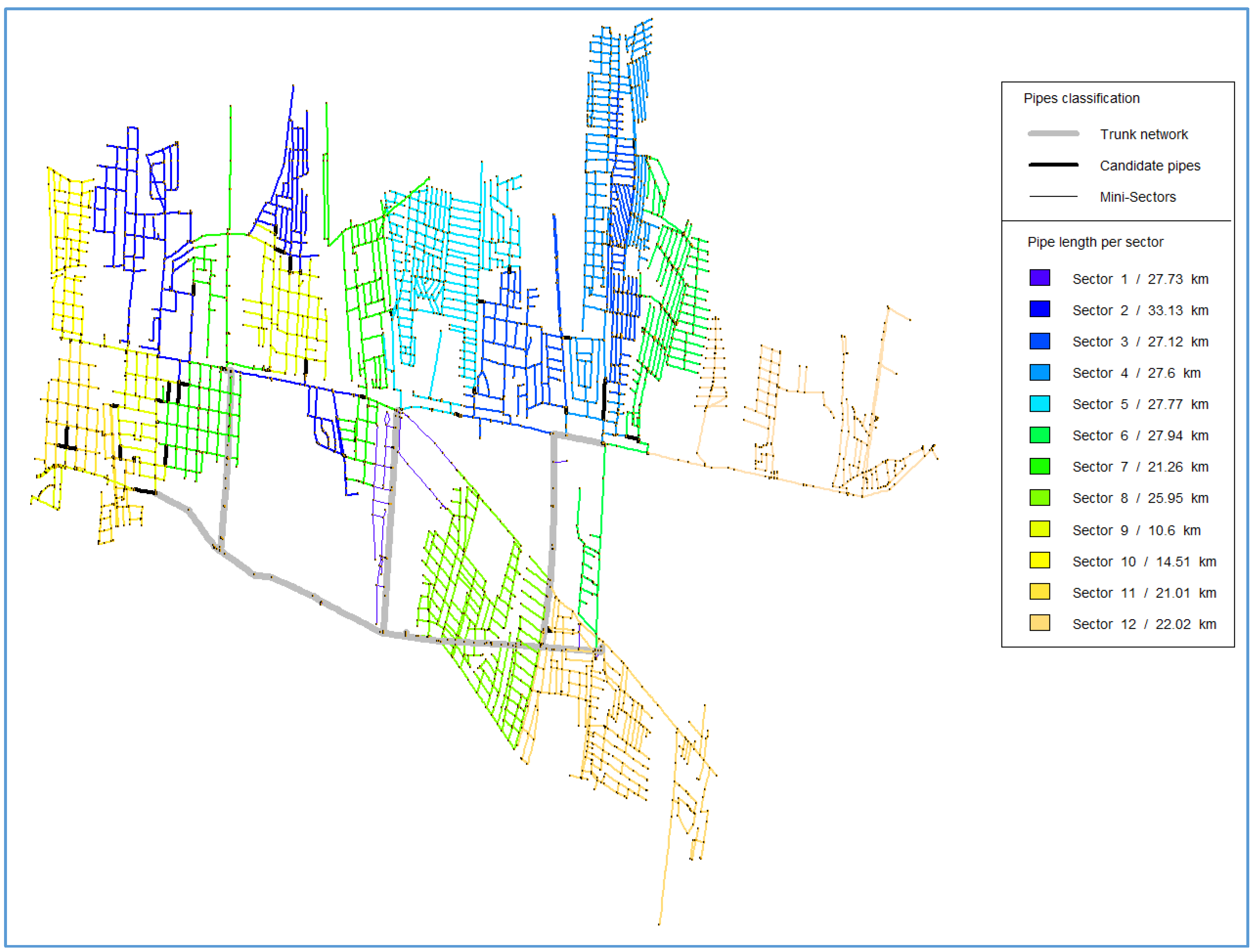
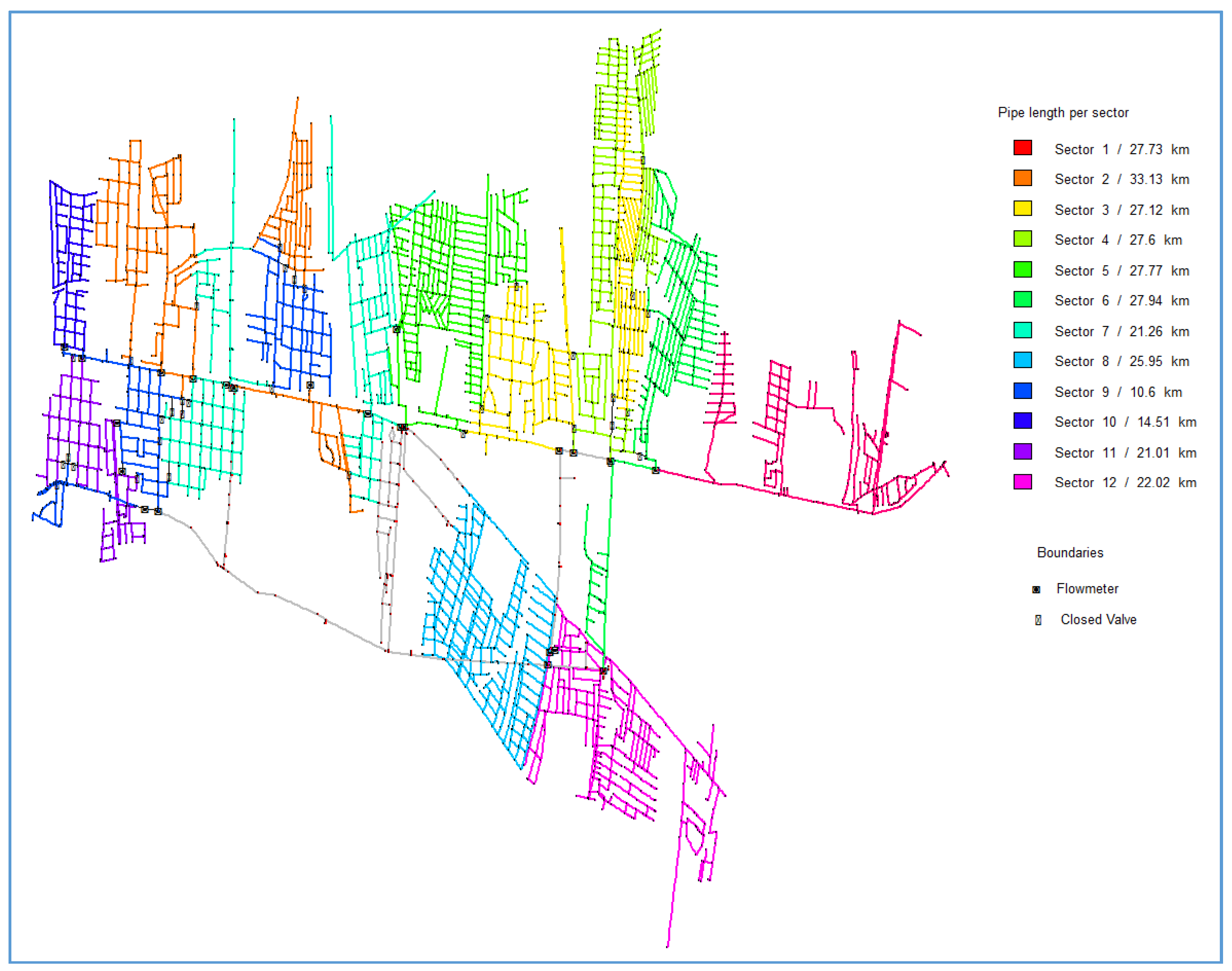
Finally,
Figure 6 depicts the layout after reincorporating the trunk network. The final configuration has 12 sectors with pipe lengths between 4 and 34 km.
2.2. Optimization of the Arrangement CUs/Boundary Valves
2.2.1. Short Run Economic Leakage Level
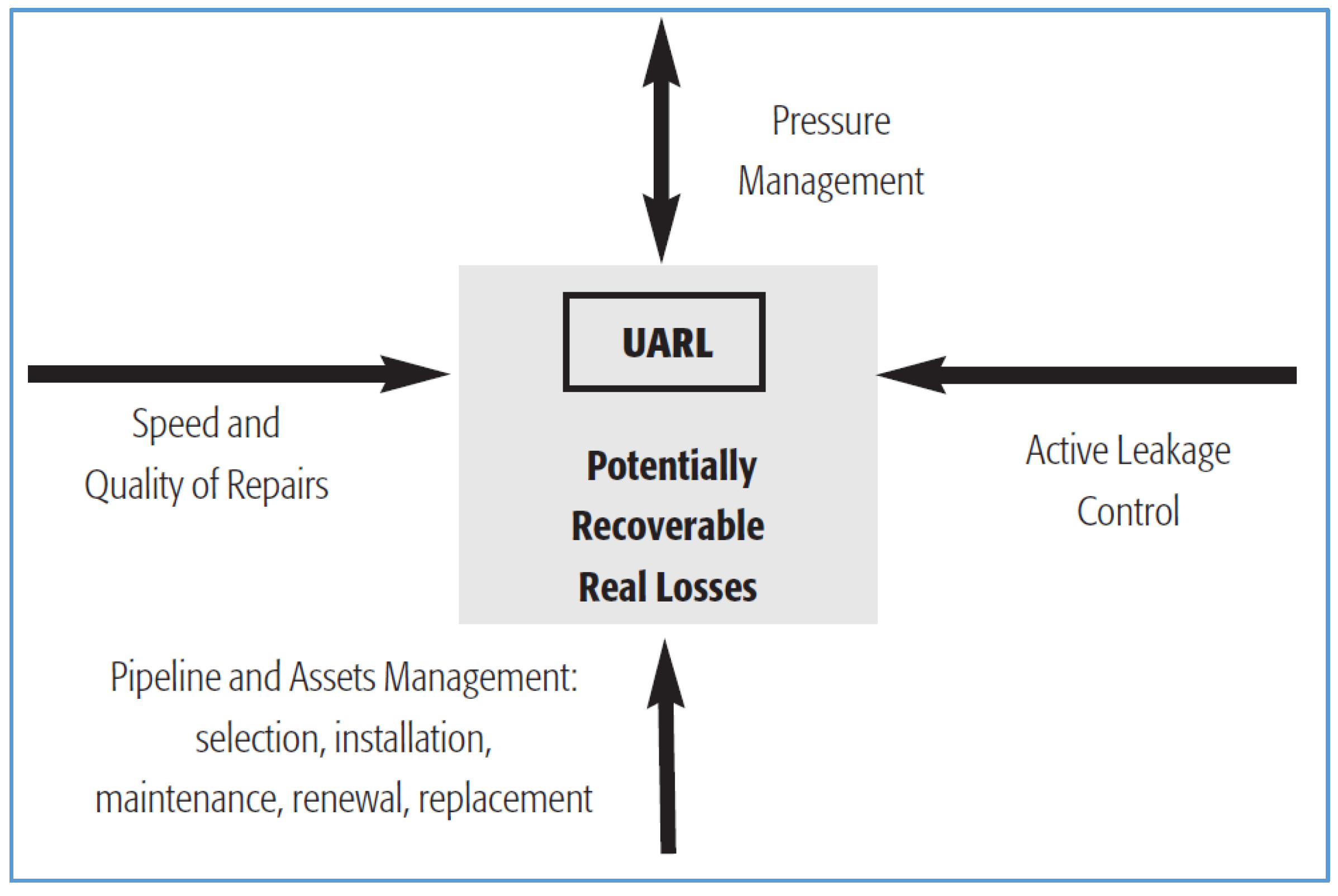
Figure 7 is broadly used to describe how real losses are structured in WSNs. It describes the way the management of real losses is conducted with four components: (1) speed and quality of repairs; (2) pressure management; (3) active leakage control; and (4) pipeline replacement. Between the Unavoidable Leakage Level (UARL) (background leakage) and the total leakage volume, there is an economic management level, which corresponds to the level where the cost of a new repair exceeds the payback.
More than a decade ago, Fantozzi and Lambert [
20] proposed a method to estimate the short run economical leakage level (
SRELL) based on a combination of BABE (Burst And Background Estimates)concepts, proposed by the United Kingdom National Leak Initiative [
16,
21] and the FAVAD (Fixed And Variable Area Discharge) theory [
22]. A very important result derived from this estimate is the
NRELL (Non-Reported Economical Leakage Level), which corresponds to the volume of unreported leakage that is feasible within a certain period of time.
According to the FAVAD theory (Equation (1)), the variation in the flow running through a crack in a pipe depends on the variation of the pressure in the pipe powered to
N1, an exponent that is related to the characteristic of the space (rigid pipe or flexible pipe) where the leak occurs.
here,
Q indicates leakage flow before and after some pressure variation
P.
The method to estimate the
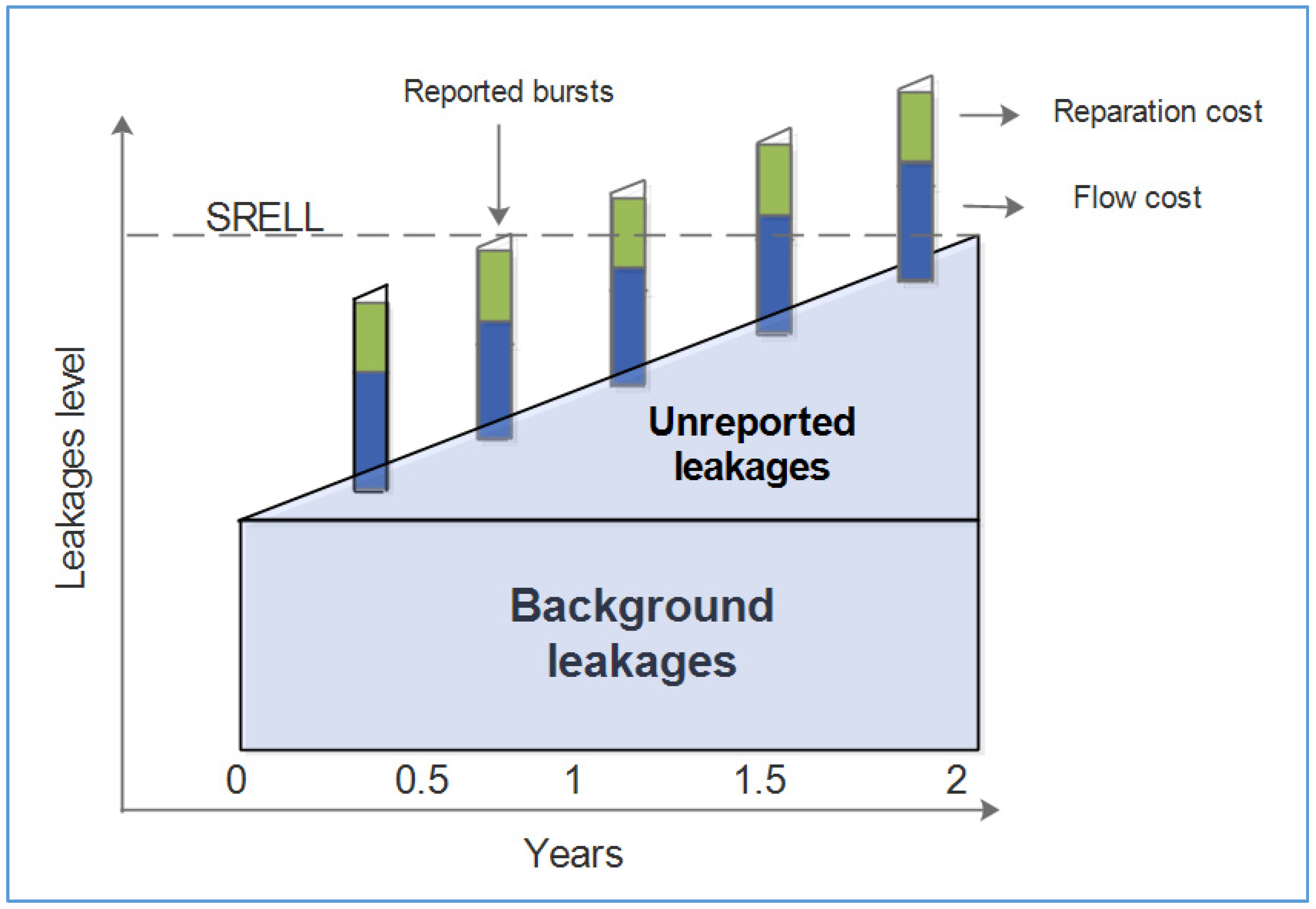
SRELL starts by making a division of the leakage flow according to the BABE concept, as shown in
Figure 8. In the same figure, it can be seen that, starting at time zero, background leakage remains constant over time; reported leaks (bursts) occur and are repaired (vertical bars); meanwhile, unreported leaks gradually increase until they reach a point where their cost equals the cost of inspecting the entire network. The slope of this increase is known as the Rate of Rise (
RR). The average of these three components corresponds to
SRELL, and it is represented by the dotted (horizontal) line in the same figure.
Of note is that reported leaks have a component-cost associated withthe flow that is lost through them and a component-cost associated withthe pipe repair. The longer the period of detection and repair, the higher the cost associated with the flow, while the component associated with the repair remains unchanged.
The method to assess the SRELL includes Equation (2) to calculate the Optimal Frequency of Inspection (OFI) of the entire WSN, based on three components: CI (Cost of Inspection) ($), CW (variable Cost of Water) ($/m3) and RR (Rate of Rise) (m3/day/year).
The
RR should be evaluated by comparing the minimum night flow just before repairing all reported and unreported leaks and at least one year later. The variation of minimum night flow expressed in m
3/day is then divided by the amount of years in which the evaluation was conducted, thus obtaining a value expressed in m
3/day/year:
From the result obtained by Equation (2), it is possible to calculate the
PI (annual Percentage of Inspection),
Additionally, from here, it is possible to calculate the budget that should be available every year for that purpose or
ABI (Annual Budget of Inspection):
By dividing the
ABI by the
CW, the
NRELL is obtained:
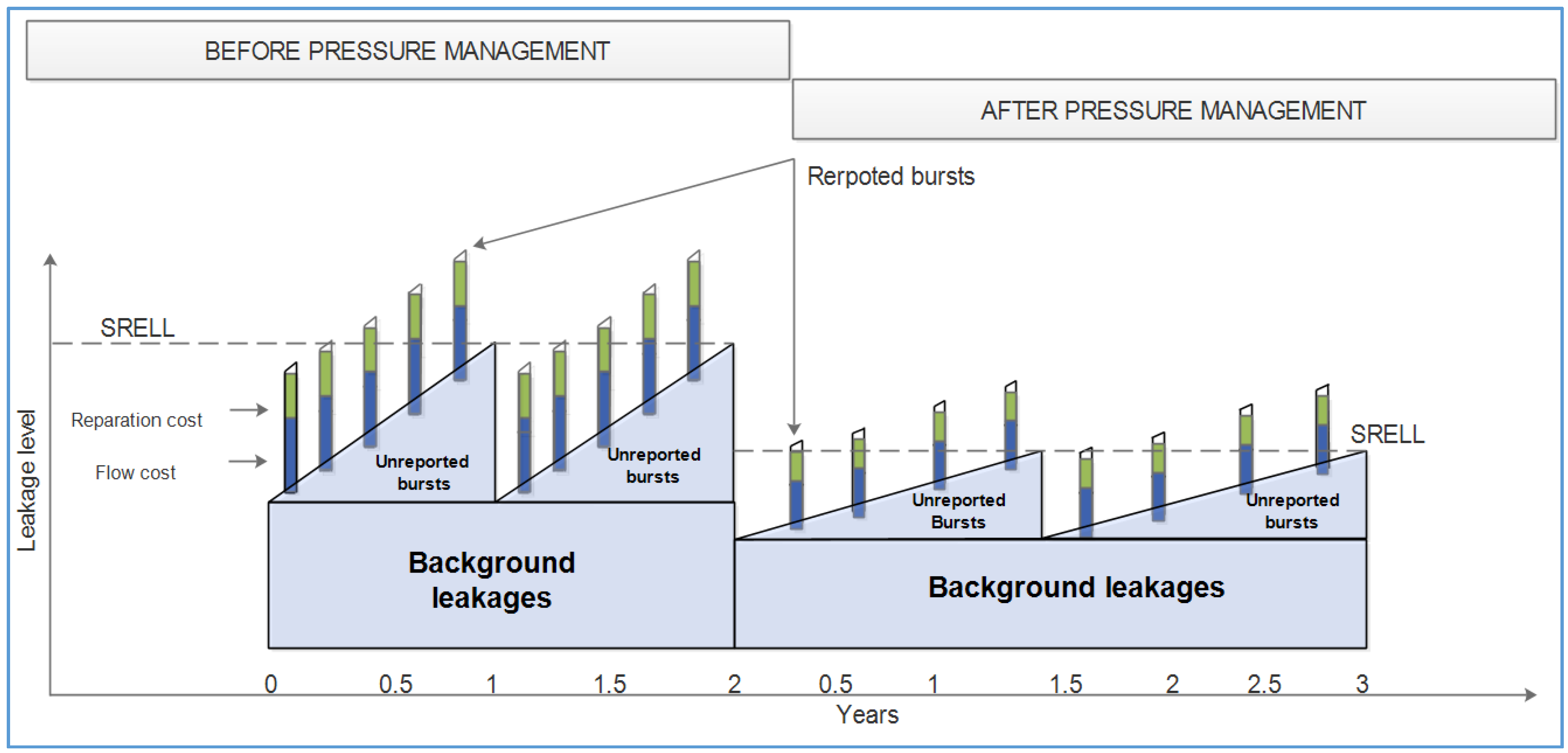
The previously presented calculation can be used to predict the benefits of pressure management in a WSN. Following the principle of the FAVAD theory, by reducing the pressure in a WSN, it is expected to reduce the background, reported and unreported leaks, as shown in
Figure 9. Furthermore, in the same figure, it can be seen that a pressure reduction translates into a decrease of the
RR, a reduction of the time required to perform a complete inspection (which implies a reduction of the
PI) and, therefore, a reduction of the
ABI. The consequence of all of this is a reduction of both the
SRELL and the
NRELL.
2.2.2. Effect of Pressure Reduction over Burst Frequency and Domestic Consumption
In 2006, Thornton and Lambert [
24] put in place the approach currently used to address the prediction of burst reduction. This approach is based on data (the relationship between pressure variation and burst reduction) from 112 WSNs in 10 different countries. The idea behind this approach is to multiply either the maximum, medium or minimum pressure variation by three constants (1.4, 2.8 or 0.7), respectively, in order to obtain a burst frequency reduction factor. With this factor, it is possible to estimate the reduction in burst frequency, as shown in Equation (6),
where
r′ represents the amount of bursts after reducing the pressure,
r is the initial frequency of bursts and
BRF stands for Burst frequency Reduction Factor.
Domestic consumption is also susceptible to pressure variations. This variation is represented by a slight modification of the FAVAD Equation (7). Now, the flow terms refer to domestic consumption (internal or external), and the exponent
N1 has been replaced by a new exponent
N3. For external domestic consumption, a value of
N3 around 0.5 is usually employed, while for internal consumption, a value 0.1 is suitable, unless the majority of the households count on a water deposit, in which Case 0 would be more appropriate.
here,
Q is the domestic consumption (internal and external) before and after pressure variation
P.
2.2.3. Leakage Management by Means of Sectorization
From all of the above, it can be concluded that a reduction in pressure translates into economic benefits due to a reduction of:
Background leakage;
Reported leaks;
Detectable unreported leaks;
Number (frequency) of bursts;
Domestic (internal and external) consumption.
Depending on the sectorization layout, the energy consumption may locally increase or decrease. If the increase in head loss generated by the sectorization is not excessive, the energy consumption is expected to decrease due to the reduction on leakage flow.
To reduce pressure in a WSN, the use of pressure-reducing valves is the option most broadly employed. In general terms, sectorization is not intended to reduce pressure, but to improve leakage management. However, when a WSN is sectorized, there is an unavoidable impact over pressure. This applies only in the case that boundary pipes are closed. If all sectors are delimited with flowmeters, no variations of pressure are expected. The idea herein proposed is to estimate the profit generated by sectorizing a WSN as a result of both reducing pressure and improving monitoring. To do so: (1) the FAVAD equation is used to calculate the reduction of leakage flow (background and reported leaks), domestic consumption and the NRELL; then, (2) the flow associated with reported leaks and NRELL is distributed among the sectors, based on technical criteria from the network operator; (3) depending on the pipe length and the number of entries in each sector, a percentage of leakage events’ detection (immediate detection and repair) is estimated; and (4) the value of reported leakage flow and NRELL are updated.
All of the benefits are summed in order to obtain the annual gross profit. From the result, three values are subtracted: a penalty cost associated with the nodes that fail to meet the requirements in terms of minimum pressure, a percentage of the total investment and an annual maintenance cost. Regarding the second cost, the gross profit is calculated on an annual basis; thus, the investment cost is multiplied by an amortization factor (Equation 8), in order to know the percentage of the investment that has to be covered every year. Finally, the maintenance cost is defined as a percentage of the latter.
here,
AF stands for amortization factor,
r is the discount rate in % and
T is the life span of the equipment (in this case, flowmeters and boundary valves).
To calculate the cost of energy, the hourly consumption (kWh) is multiplied by the price of energy ($/kWh) at the respective time. The daily value is converted to an annual basis and added to the gross profit; although, as explained below, it can also be added to the cost, depending on the final scheme of sectorization.
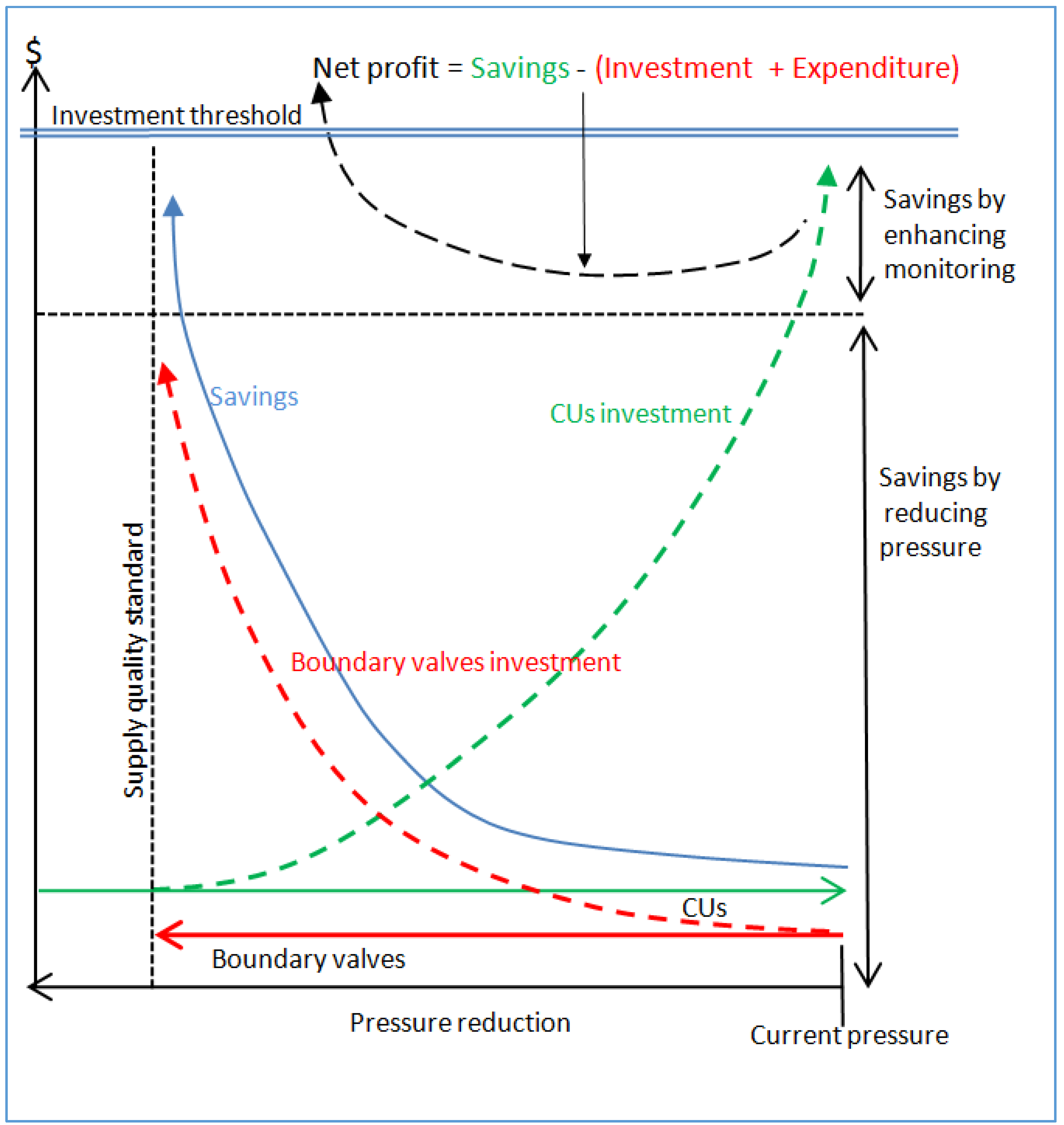
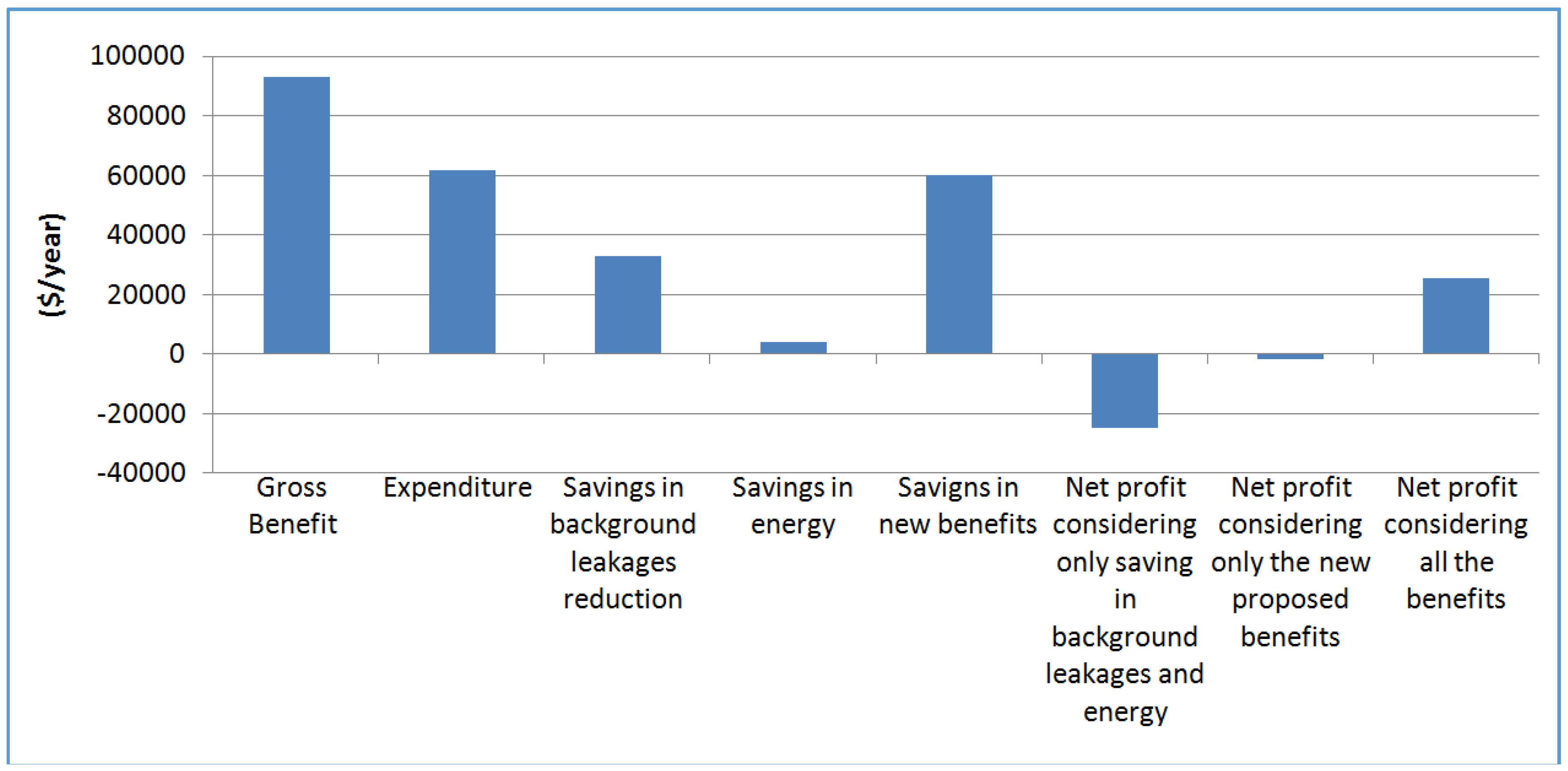
Figure 10 depicts how the benefits obtained by reducing physical losses by means of sectorization and the respective investment are related. The y axis represents the economic benefits and cost of investments; the two lines parallel to the x axis represent the total amount of candidate pipes that are set as CU or as boundary valves. It can be seen that the curves labeled as CU and boundary valves follow opposite directions, given the fact that if a pipe is not set as a CU, it is set as a boundary valve. The x axis represents the pressure reduction generated when some of the boundary valves are shutoff. Such a pressure reduction cannot exceed the supply quality standard. As the pressure is reduced, the benefits, in terms of leakage reduction, increase, as well as the cost of boundary valves. Since the establishment of sectors allows rapid detection/repairing of leakages (when they occur), the curve of savings goes beyond the benefits obtained through pressure reduction. Finally, the top line corresponds to the annual net profit (annual gross profit-annual expenditure).
2.2.4. Objective Function
In a WSN of hundreds of kilometers of pipe extension, the number of possible combinations CUs/boundary valves can be significantly large. The more CUs a given sector has, the lower is the negative impact over the pressure in its nodes, but the lower is the likelihood to detect leakage events in a short period of time.
Equation (9) shows the objective function to be maximized, followed by the constraints.
A: savings from the reduction of background leakage (volume) ($/year);
B: savings from the reduction of reported leaks (volume) ($/year);
C: savings from the reduction of the number of pipes to repair (reported bursts) ($/year);
D: savings from the reduction of the number of pipes to repair (unreported bursts) ($/year);
E: savings from the reduction of domestic consumption (volume) ($/year);
F: savings from the reduction of the external domestic consumption (volume) ($/year);
G: savings from the reduction of unreported leaks (volume) ($/year);
H: savings/expenses from decreasing/increasing energy consumption ($/year);
A′: amortized cost of valves and CUs ($/year);
B′: compensation cost for pressure deficit ($/year);
C′: maintenance cost of valves and CUs ($/year);
ΔIr and ΔIrreq: variation in the resilience index and maximum variation allowed;
Pmin and Pminreq: minimum pressure and minimum pressure required;
A + B and (A + B)max: budget for the purchase of boundary valves and CUs and the budget threshold.
Background leakages indicated by term A correspond to a leakage that is undetectable by the available technology and that can only be diminished by reducing the pressure. Reported leakages, indicated by B, are leakages that are visually detectable; C and D indicate repairing of pipe cracks for either leakages that are visually detectable or leakages that are not visually detectable, but that might be localized in a leakage detection campaign. E and F indicate the water consumption inside and outside the households(i.e., garden watering), respectively; the term G indicates leakages that can be detectable (localized) in a leakage detection campaign; H indicates the energy consumptionthrough pumping; A′ indicates the yearly cost (amortized cost) of investment for the purchase of boundary valves and CUs; B′ indicates the cost of compensation for the nodes that cannot meet the duty pressure, which is estimated by multiplying the total demand of the critical nodes by the cost of supplying one cubic meter of water by means of a cistern.
The resilience index used here corresponds to the index proposed by Todini [
25], which is calculated by subtracting from 1 the fraction that represents the current head loss over the total head loss required to ensure that all of the nodes meet a certain pressure threshold.
It is important to note the complexity of the objective function, especially if it is compared to theobjective functions used in previous research work. In fact, such an approach has two maindrawbacks. The first one is related to larger calculation times. Nevertheless, as previously explained, the reduction of pressure by means of sectorization brings very important benefits that should be taken into consideration in order to make the optimization more realistic. One way to solve the calculation time problem could be the grouping of some of the benefits (parameter) into one single parameter; however, this would require new research in order to know how they are interrelated, which at this moment is not really clear and, in fact, is one of the topics on which the authors are currently working. The second drawback is related to the information itself, since it is not easily obtained and, on the contrary, requires a big effort from the water authority.
2.2.5. Monte Carlo Simulations to Deal with Uncertainties in the Optimization Process
The ability to detect and locate new leakage events will depend on two characteristics of each sector: the sector pipe length and the number of CUs; it also depends on the technical capacity of the water operator. The probability of detecting and locating a new leakage event is inversely proportional to its size and the number of CUs. Due to the lack of a mathematical formulation to describe this probability, this information should be estimated by the technical staff of the water utility based on their experience.
Values in
Table 1 can be set as single values (fixed values) and then be used in a classical optimization model. In other words, a single leakage flow volume that is controlled due to the sectorization implementation is defined. However, the prediction of a percentage of detection has a high degree of uncertainty. To deal with this, we propose to represent such a percentage as a range of probabilities. This range can be defined by probability curves (or by an equation describing the probability density). In this regard, there is a broad range of distribution curves that can be used; however, in this work, we select a “triangular”distribution, based on the fact that only the minimum and maximum expected values and a trend are required for its construction. This type of curve, despite the lack of precision, has the advantage of being useful when data are missing (due to the high cost of collection). However, it is possible to estimate the relationship between them.
Leakage flows are expected to be differently distributed among the sectors (sectors located in older and/or with less maintenance areas are expected to have a higher frequency of leakage than those located in newer and/or better managed areas).The allocation of the expected leakage rate in each sector must be carried out by the technical staff of the water utility based on their experience.
Once the detection probability curve of each sector is established, the optimization process is initialized; however, differently from a classical optimization model, for each iteration that generates a feasible solution, an MCS is carried out. Accordingly, probabilistic values are randomly sampled from the predefined distribution curves. Then, the average of each sampling is calculated and included in the objective function. The solutions in which the simulation result meets the established constraints are marked as valid and used as feedback to generate new solutions, while the solutions outside the feasible region are discarded.
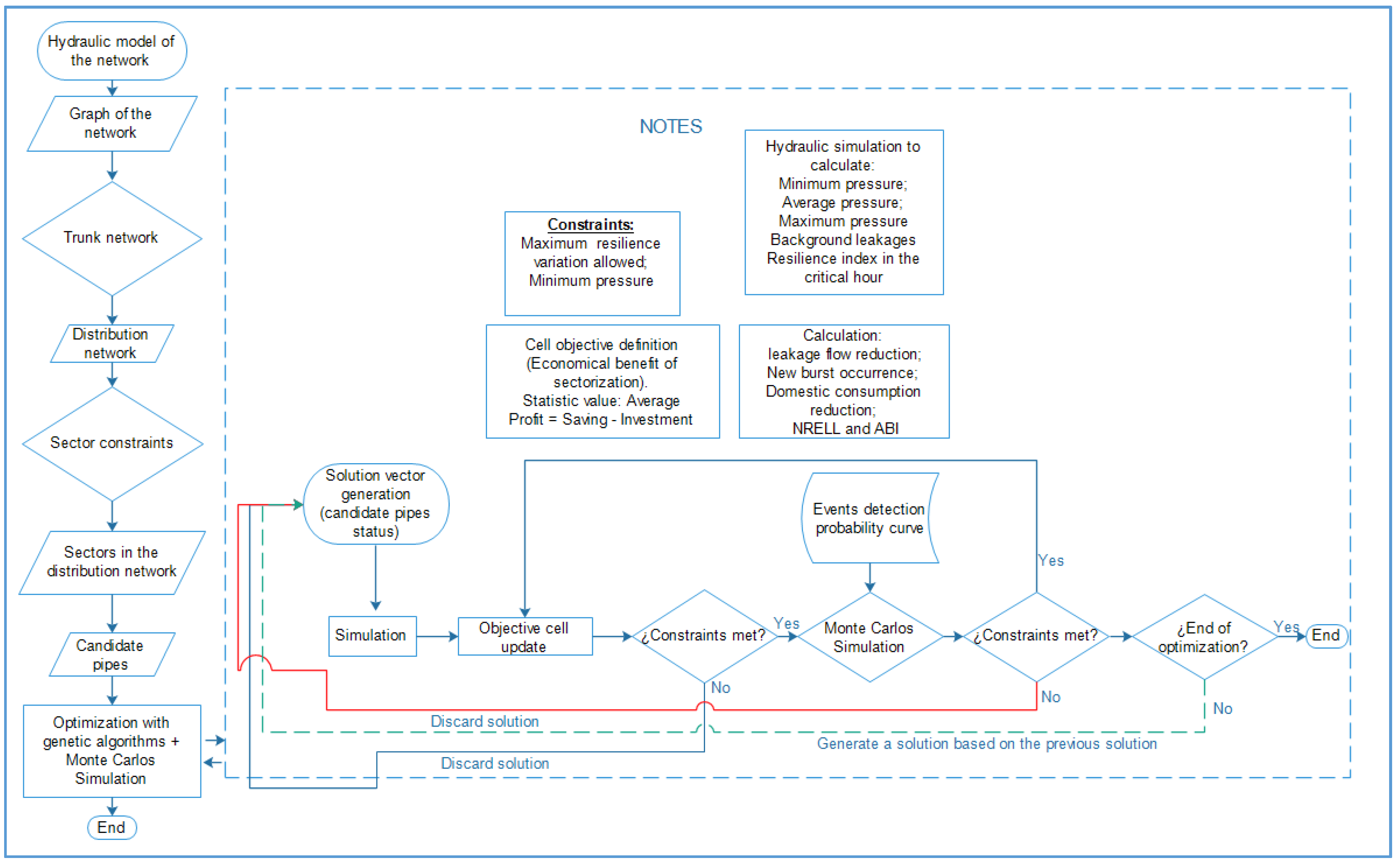
Figure 11 depicts the whole methodology. The first column (left) shows the sector definition algorithm; while the section to the right shows the process to optimize the arrangement entrances/boundary valves. In this part, for every iteration, a solution vector is generated by the GA and imputed in the simulation. Then, the constraints are reviewed. If the solution meets the constraints, an MCS is conducted; otherwise, the solution is discarded. It is important to note that the results of the MCS depend on the solution generated by the GA and on the event detection probability curve. Once the MCS is completed, the constraints are revised; if they are met, the objective cells are updated; otherwise, the results of the MCS are discarded.
The community detection process is carried out with the Igraph package [
26] implemented in R, and the optimization of CUs and boundary valves is conducted with the RiskOptimizer
® tool [
27].