Quantifying Spatial Changes in the Structure of Water Quality Constituents in a Large Prairie River within Two Frameworks of a Water Quality Model
Abstract
:1. Introduction
2. Methods
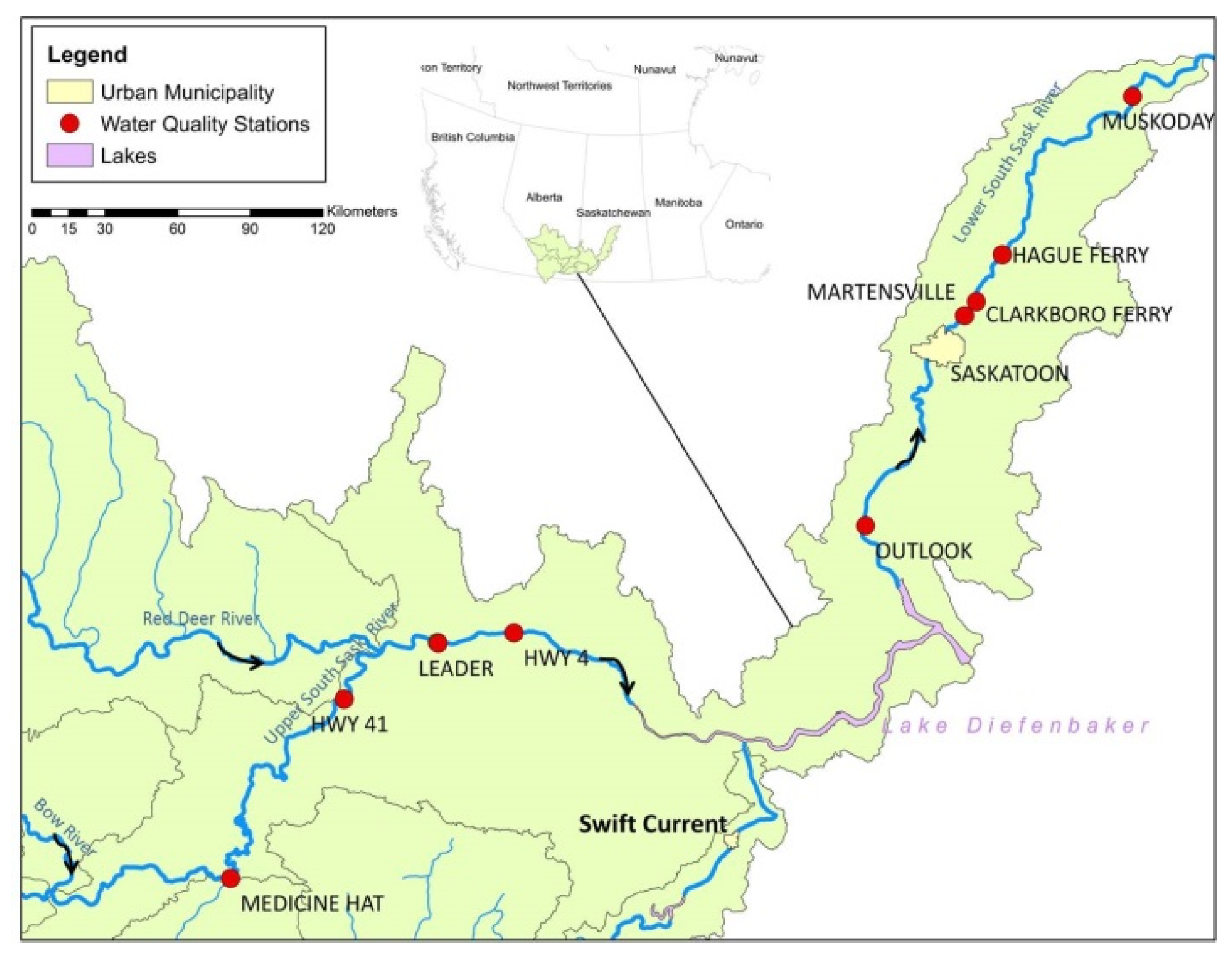
2.1. Site Description
- upper SSR (uSSR), originating at the confluence of Bow and Oldman rivers to the inlet of Lake Diefenbaker.
- lower SSR (lSSR), originating at the Gardiner Dam and extending to the confluence of the North and South Saskatchewan rivers at the Saskatchewan River Forks east of Prince Albert.
2.2. Model Description and Set-up
2.3. Parameter Sensitivity
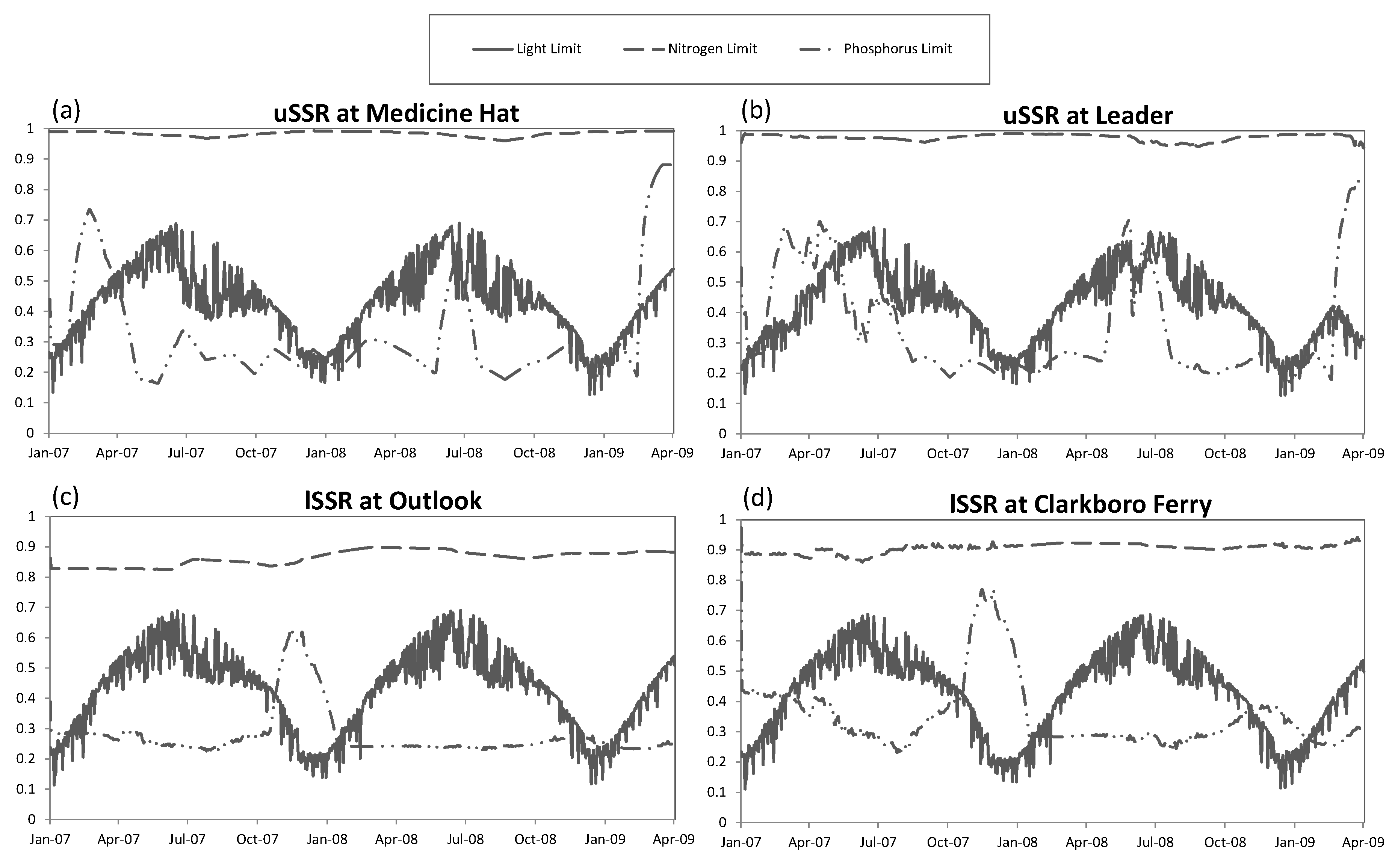
2.4. Nutrient and Light Limitations
- ɸL = light limitation factor
- = the average incident light intensity during daylight hours below the surface, (ly/day)
- = the saturating light intensity of phytoplankton, (ly/day)
- Ke = the light extinction coefficient, (m−1)
- D = depth of the water column or model segment, (m)
- f = fraction day that is daylight, (unitless)
- ɸN = nutrient limitation factor
- Km = the Michaelis or half-saturation constant, (mg/L)
- DIN = dissolved inorganic nitrogen (ammonium plus nitrate), (mg/L)
- DIP = dissolved inorganic phosphorus (orthophosphate), (mg/L)
2.5. Variable Interactions
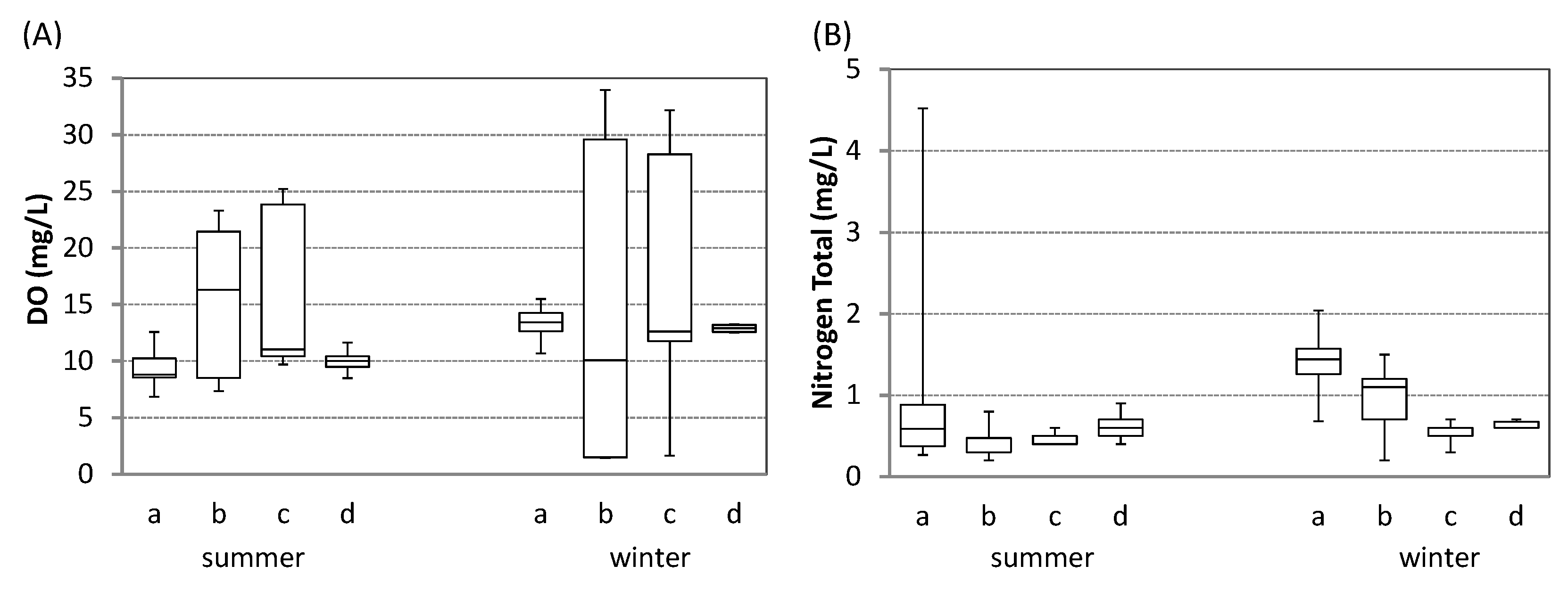
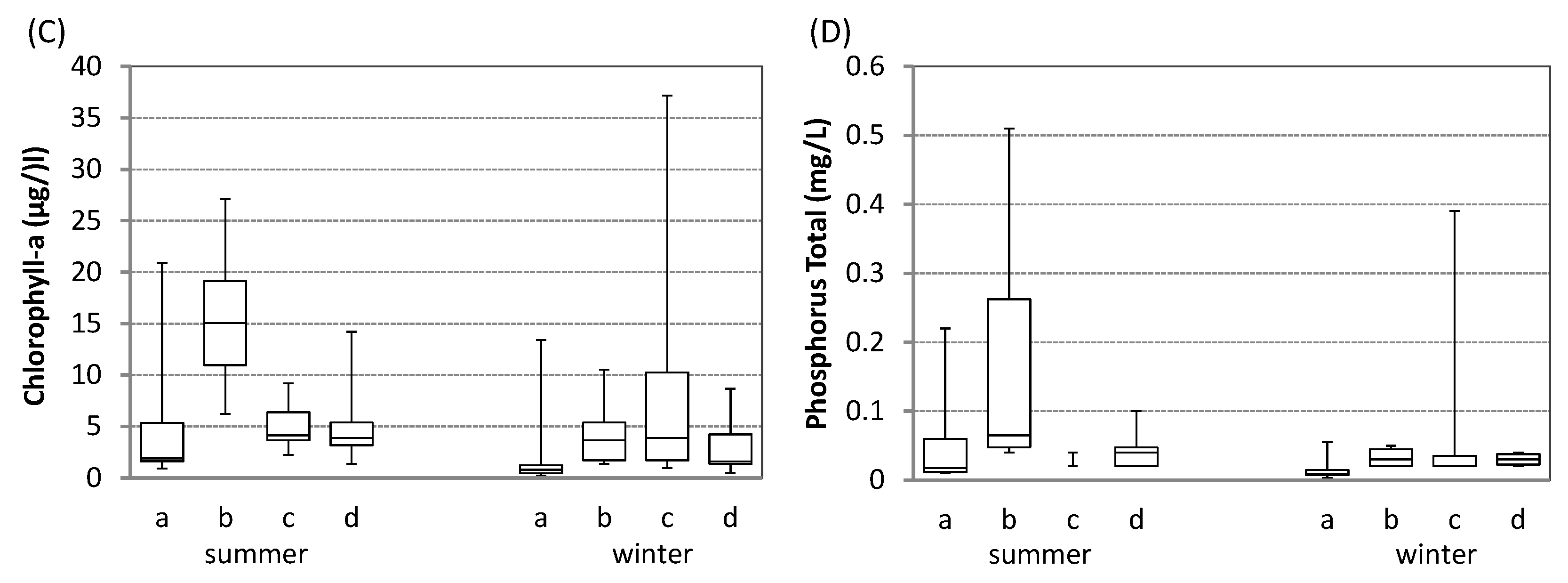
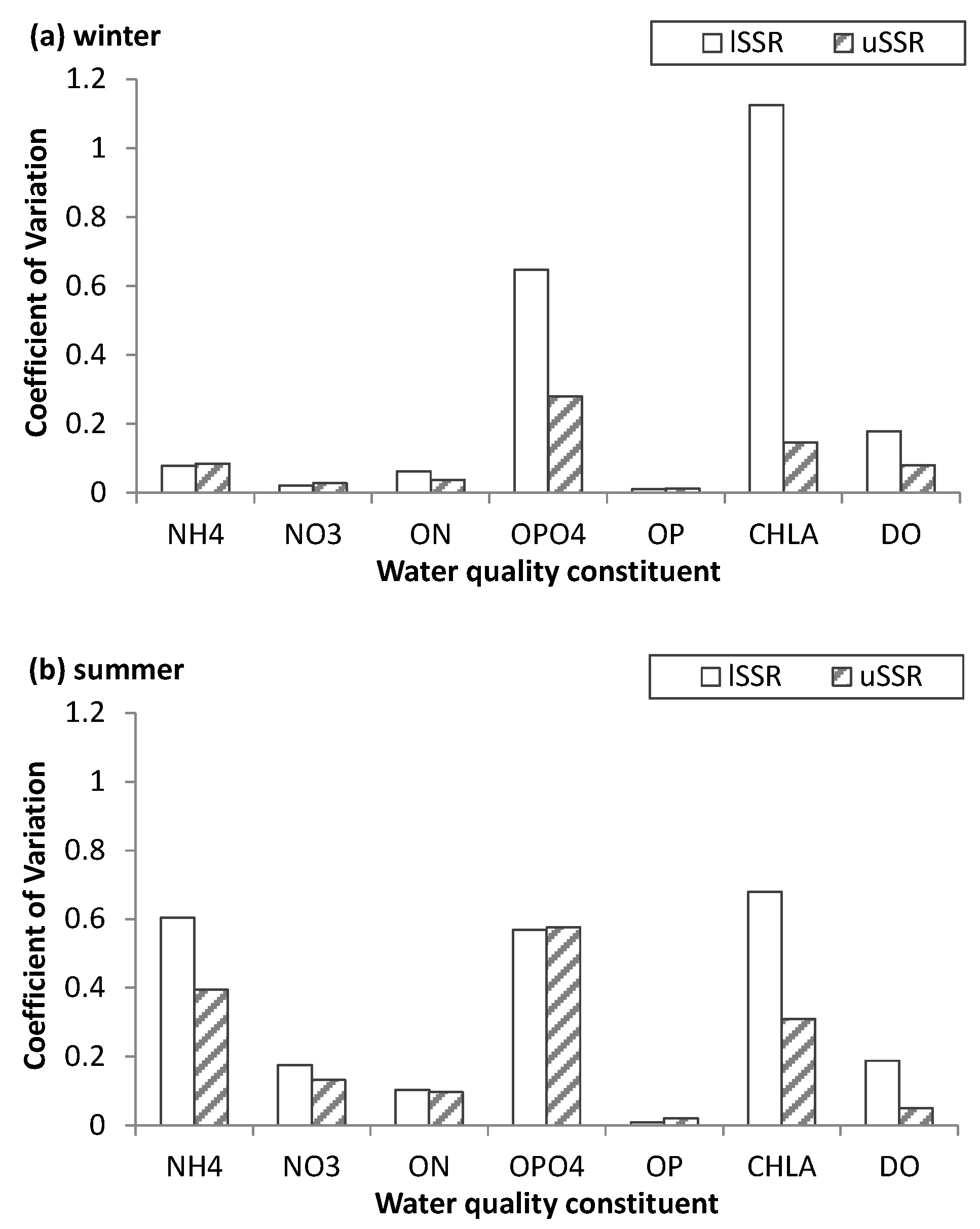
3. Results and Discussion
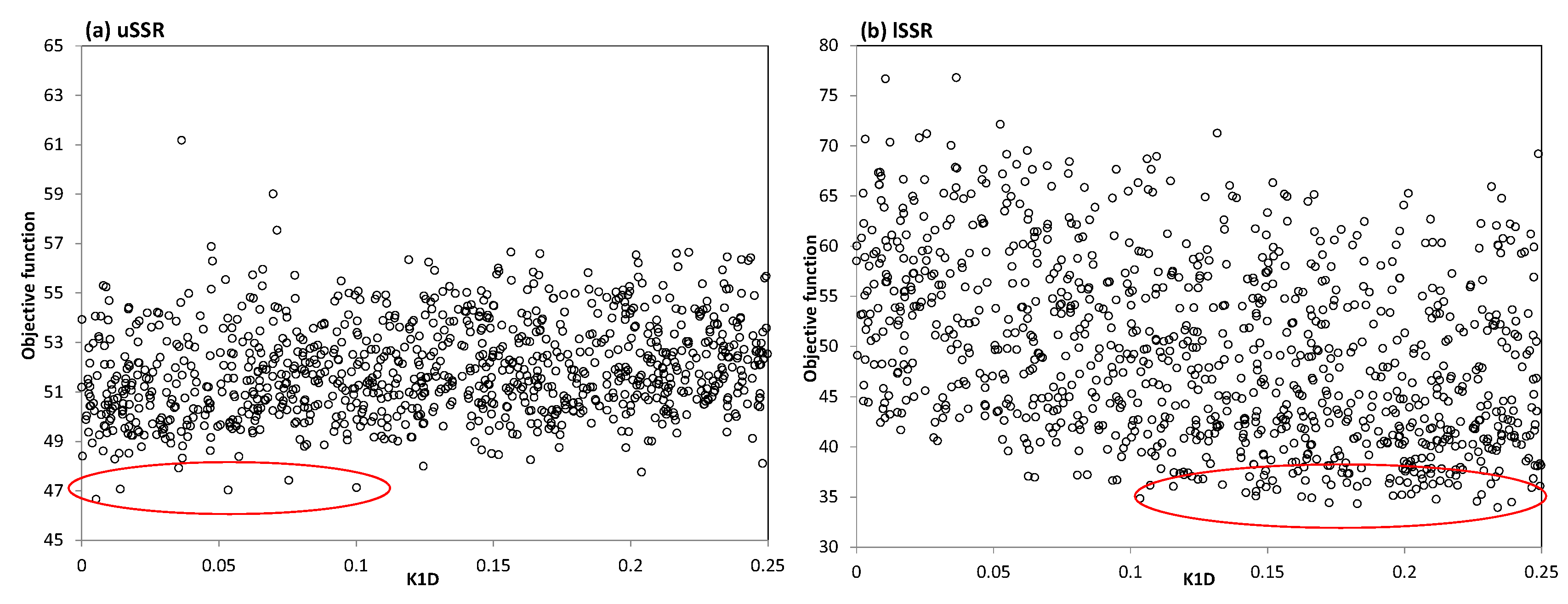
3.1. Global Sensitivity Analysis (GSA)
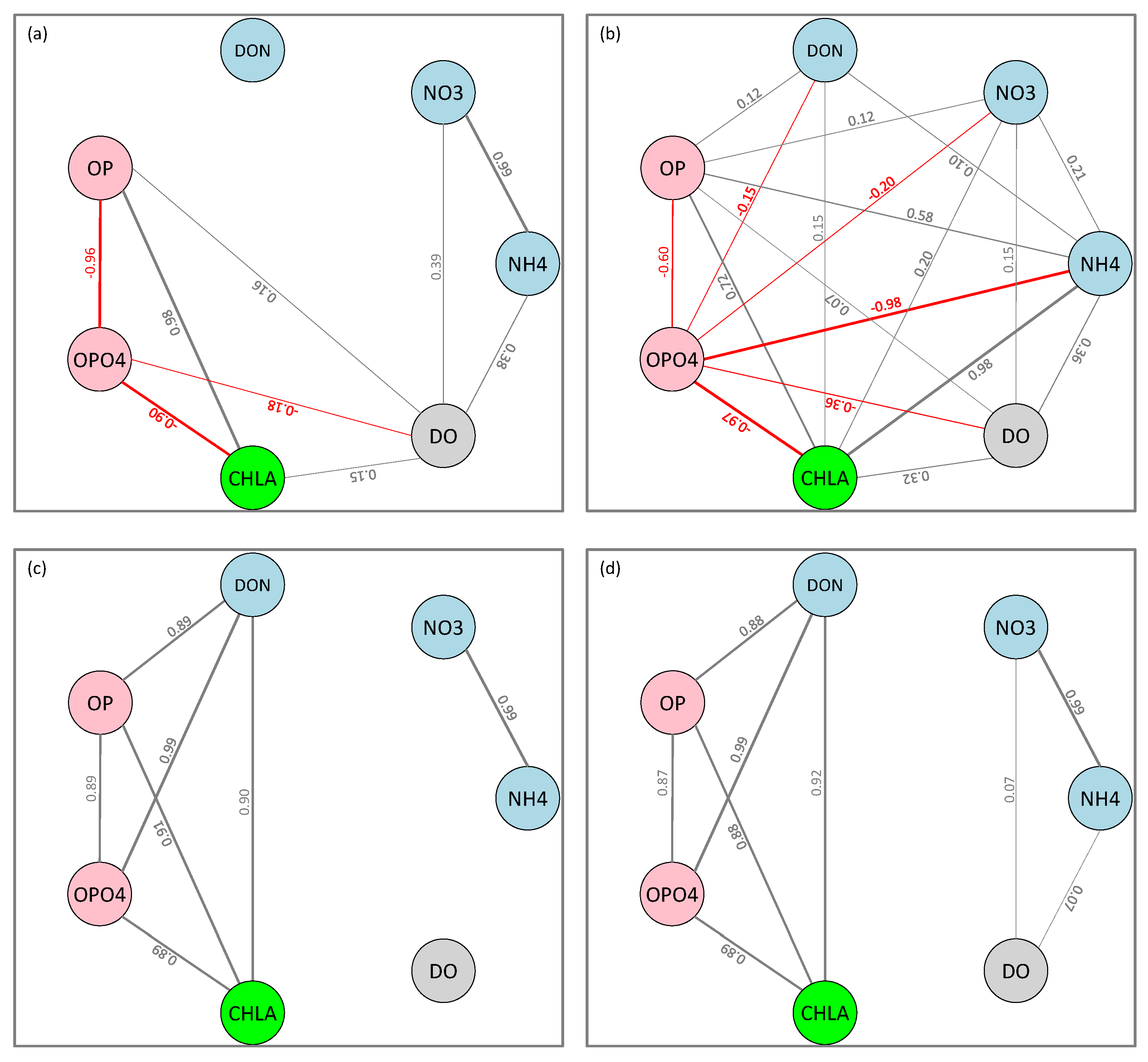
3.2. Interactions between State Variables
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hagy, J.D.; Boynton, W.R.; Keefe, C.W.; Wood, K.V. Chesapeake Bay, 1950–2001: Long-term change in relation to nutrient loading and river flow. Estuaries 2004, 27, 634–658. [Google Scholar] [CrossRef]
- Smith, V.; Tilman, G.; Nekola, J. Eutrophication: impacts of excess nutrient inputs on freshwater, marine, and terrestrial ecosystems. Environ. Pollut. 1999, 100, 179–196. [Google Scholar] [CrossRef]
- Ji, Z.-G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Prowse, T.D. River-ice ecology. I: Hydrologic, geomorphic, and water-quality aspects. J. Cold Region. Eng. 2001, 15, 1–16. [Google Scholar] [CrossRef]
- Martin, N.; McEacherm, P.; Yu, T.; Zhu, D. Model development for prediction and mitigation of dissolved oxygen sags in the Athabasca River, Canada. Sci. Total Environ. 2012, 443, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Wagener, T.; Kollat, J. Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox. Environ Model. Softw. 2007, 22, 1021–1033. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. What do we mean by sensitivity analysis? The need for comprehensive characterization of “Global” sensitivity in Earth and Environmental Systems Models. Water Resour. Res. 2015, 51, 3070–3092. [Google Scholar] [CrossRef]
- Sun, X.Y.; Newham, L.; Croke, B.; Norton, J. Three complementary methods for sensitivity analysis of a water quality model. Environ Model. Softw. 2012, 37, 19–29. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Lakshmi, G.; Chaubey, I. Application of a pseudo simulator to evaluate the sensitivity of parameters in complex watershed models. Environ Model. Softw. 2011, 26, 135–143. [Google Scholar] [CrossRef]
- Reusser, D.E.; Zehe, E. Inferring model structural deficits by analyzing temporal dynamics of model performance and parameter sensitivity. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Guse, B.; Reusser, D.E.; Fohrer, N. How to improve the representation of hydrological processes in SWAT for a lowland catchment—Temporal analysis of parameter sensitivity and model performance. Hydrol. Process 2014, 28, 2651–2670. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Reusser, D.; Fohrer, N. Process verification of a hydrological model using a temporal parameter sensitivity analysis. Hydrol. Earth Syst. Sci. 2015, 19, 4365–4376. [Google Scholar] [CrossRef]
- Lindenschmidt, K.-E.; Chun, K.P. Evaluating the impact of fluvial geomorphology on river ice cover formation based on a global sensitivity analysis of a river ice model. Can. J. Civil Eng. 2013, 40, 623–632. [Google Scholar] [CrossRef]
- Brown, L.C.; Barnwell, T.O. The Enhanced Stream Water Quality Models QUAL2E and QUAL2E-UNCAS; Environmental protection Agency, Environmental Research Laboratory: Athens, GA, USA, 1987.
- Chapra, S.C.; Pelletier, G.J. Qual2k: A Modeling Framework for Simulating River and Stream Water Quality: Documentation and Users Manual; Civil and Environmental Engineering Department, Tufts University: Medford, MA, USA, 2003. [Google Scholar]
- Ambrose, R.; Wool, T.A.; Connolly, J.; Schanz, R.W. WASP4, A Hydrodynamic and Water-Quality Model-Model Theory, User’s Manual, and Programmer’s Guide; No. PB-88-185095/XAB; EPA-600/3-87/039; Environmental protection Agency, Environmental Research Laboratory: Athens, GA, USA, 1988.
- Environmental Laboratory. CE-QUAL-RIV1: A Dynamic, One-Dimensional (Longitudinal) Water Quality Model for Streams: User’s Manual; Instruction Report EL-95-2; USACE Waterways Experiments Station: Vicksburg, MS, USA, 1995. [Google Scholar]
- Francos, A.; Elorza, F.J.; Bouraoui, F.; Galbiati, L. Sensitivity analysis of distributed environmental simulation models: Understanding the model behaviour in hydrological studies at the catchment scale. Reliab. Eng. Syst. Saf. 2003, 79, 205–218. [Google Scholar] [CrossRef]
- Van Griensven, A.; Francos, A.; Bauwens, W. Sensitivity analysis and auto-calibration of an integral dynamic model for river water quality. Water Sci. Technol. 2002, 45, 321–328. [Google Scholar]
- Drolc, A.; Končan, J.Z. Water quality modelling of the river Sava, Slovenia. Water Res. 1996, 30, 2587–2592. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Franceschini, S.; Tsai, C.W. Assessment of uncertainty sources in water quality modeling in the Niagara River. Adv. Water Resour. 2010, 33, 493–503. [Google Scholar] [CrossRef]
- Kaufman, G.B. Application of the Water Quality Analysis Simulation Program (WASP) to Evaluate Dissolved Nitrogen Concentrations in the Altamaha River Estuary, Georgia. Master’s Thesis, University of Florida, Gainesville, FL, USA, 2003. [Google Scholar]
- Lindenschmidt, K.-E. The effect of complexity on parameter sensitivity and model uncertainty in river water quality modelling. Ecol. Model. 2006, 190, 72–86. [Google Scholar] [CrossRef]
- Abirhire, O.; North, R.L.; Hunter, K.; Vandergucht, D.M.; Sereda, J.; Hudson, J.J. Environmental factors influencing phytoplankton communities in Lake Diefenbaker, Saskatchewan, Canada. J. Gt. Lakes Res. 2015, 41, 118–128. [Google Scholar] [CrossRef]
- North, R.L.; Johansson, J.; Vandergucht, D.M.; Doig, L.E.; Liber, K.; Lindenschmidt, K.-E.; Baulch, H.; Hudson, J.J. Evidence for internal phosphorus loading in a large prairie reservoir (Lake Diefenbaker, Saskatchewan). J. Gt. Lakes Res. 2015, 41, 91–99. [Google Scholar] [CrossRef]
- Morales-Marín, L.; Wheater, H.; Lindenschmidt, K.-E. Assessing the transport of total phosphorus from a prairie river basin using SPARROW. Hydrol. Process. 2015, 29, 4144–4160. [Google Scholar] [CrossRef]
- Donald, D.B.; Parker, B.R.; Davies, J.-M.; Leavitt, P.R. Nutrient sequestration in the Lake Winnipeg watershed. J. Gt. Lakes Res. 2015, 41, 630–642. [Google Scholar] [CrossRef]
- Dubourg, P.; North, R.L.; Hunter, K.; Vandergucht, D.M.; Abirhire, O.; Silsbe, G.M.; Guildford, S.J.; Hudson, J.J. Light and nutrient co-limitation of phytoplankton communities in a large reservoir: Lake 1 Diefenbaker, Saskatchewan, Canada. J. Gt. Lakes Res. 2015, 41, 129–143. [Google Scholar] [CrossRef]
- Hudson, J.; Vandergucht, D. Spatial and Temporal Patterns in Physical Properties and Dissolved Oxygen in Lake Diefenbaker, a Large Reservoir on the Canadian Prairies. J. Gt. Lakes Res. 2015, 41, 22–33. [Google Scholar] [CrossRef]
- Di Toro, D.; Fitzpatrick, J.; Thomann, R. Water Quality Analysis Simulation Program (WASP) and Model Verification Program (MVP) Documentation; U.S. EPA-600/3-81-044; US Environmental Protection Agency (EPA): Duluth, MI, USA, 1983.
- Connolly, J.P.; Winfield, R.P. A User’s Guide for WASTOX, A Framework for Modeling the Fate of Toxic Chemicals in Aquatic Environments. Part 1: Exposure Concentration; Environmental Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Washington, DC, USA, 1984.
- Akomeah, E.; Chun, K.P.; Lindenschmidt, K.-E. Dynamic water quality modelling and uncertainty analysis of phytoplankton and nutrient cycles for the upper South Saskatchewan River. Environ. Sci. Pollut. Res. 2015, 22, 18239–18251. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, C.W.L. Parameter sensitivity of a surface water quality model of the lower South Saskatchewan River—Comparison between ice-on and ice-off periods. ENMO 2016, submitted. [Google Scholar]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Spear, R.C. An approach to the preliminary analysis of environmental systems. J. Environ. Manag. 1981, 12, 7–18. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 1. Theory. Water Resour. Res. 2016, 52, 423–439. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 2. Application. Water Resour. Res. 2016, 52, 440–455. [Google Scholar] [CrossRef]
- Matott, L.S. Ostrich: An Optimization Software Tool, Documentation and User’s Guide; Version 1.6; University at Buffalo, Department of Civil, Structural, and Environmental Engineering: Buffalo, NY, USA, 2005. [Google Scholar]
- Wagener, T.; Wheater, H.S.; Gupta, H.V. Rainfall-Runoff Modelling in Gauged and Ungauged Catchments; Imperial College Press: London, UK, 2004. [Google Scholar]
- Chapra, S.C. Surface Water Quality Modeling; McGraw-Hill Companies: New York, NY, USA, 1997. [Google Scholar]
- Karrh, R. Nutrient Limitation. Available online: http://dnr.state.md.us/bay/monitoring/limit/index.html (accessed on 13 April 2016).
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- MacDonald, N. Trees and Networks in Biological Models; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Shammas, N.K. Interactions of Temperature, pH, and Biomass on the Nitrification Process. Water Pollut. Control Feder. 1986, 58, 52–59. [Google Scholar]
- Lindenschmidt, K.-E.; Poser, K.; Rode, M. Impact of morphological parameters on water quality variables of a regulated lowland river. Water Sci.Technol. 2005, 52, 187–194. [Google Scholar] [PubMed]
- Montoya, J.M.; Pimm, S.L.; Solé, R.V. Ecological networks and their fragility. Nature 2006, 442, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Ings, T.C.; Montoya, J.M.; Bascompte, J.; Blüthgen, N.; Brown, L.; Dormann, C.F.; Edwards, F.; Figueroa, D.; Jacob, U.; Jones, J.I.; et al. Review: Ecological networks—Beyond food webs. J. Anim.Ecol. 2009, 78, 253–269. [Google Scholar] [CrossRef] [PubMed]

| Parameter Description | Parameter (Unit) | Ranges | Initial Values | |
|---|---|---|---|---|
| uSSR | lSSR | |||
| Nitrification rate | K12C (1/day) | 0–3 | 0.1 | 2 |
| Denitrification rate | K20C (1/day) | 0–0.09 | 0.05 | 0.01 |
| Phytoplankton growth | K1C (1/day) | 0–3 | 0.6 | 0.5 |
| Carbon to Chlorophyll-a ratio | CCHL (mgC/mgChla) | 20–60 | 30 | 40 |
| Phytoplankton death rate | K1D (1/day) | 0–0.25 | 0 | 0.2 |
| 1/2 saturation for N-limitation | KMNG1 (mg N/L) | 0–0.05 | 0.02 | 0.03 |
| 1/2 saturation for P-limitation | KMPG1 (mg P/L) | 0–0.05 | 0 | 0.03 |
| Nitrogen to Carbon ratio | NCRB (mg N/mg C) | 0–0.43 | 0.15 | 0.1 |
| Phosphorus to Carbon ratio | PCRB (mg P/mg C) | 0–0.24 | 0 | 0.15 |
| TON mineralization rate | K71C (1/day) | 0–1.08 | 0.075 | 0.075 |
| TOP mineralization rate | K83C (1/day) | 0–0.22 | 0.02 | 0.22 |
| Fraction of phyto. death recycled to ON | fON | 0–1 | 0.5 | 0.8 |
| Fraction of phyto. death recycled to OP | fOP | 0–1 | 1 | 0.8 |
| Sediment Oxygen Demand | SOD (g/m2/day) | 0–0.5 | 0.5 | 0.5 |
| Reaeration in winter | K2w (1/day) | 0–0.5 | 1.4 * | 0.1 |
| Reaeration in summer | K2s (1/day) | 1–3 | 1.4 | 1.5 |
| Winter | NH4 | NO3 | ON | OPO4 | OP | CHLA | DO | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters/ Segments | a | b | c | d | a | b | c | d | a | b | c | D | a | b | c | d | a | b | c | d | a | b | c | d | a | b | c | d |
| K12C | ● | ● | ● | ● | ||||||||||||||||||||||||
| K20C | ||||||||||||||||||||||||||||
| K1C | ● | ● | ○ | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| CCHL | ○ | ● | ● | ● | ○ | ○ | ● | ○ | ||||||||||||||||||||
| K1D | ● | ○ | ○ | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||
| KMNG1 | ● | |||||||||||||||||||||||||||
| KMPG1 | ● | ● | ● | ○ | ● | ● | ● | ○ | ||||||||||||||||||||
| NCRB | ● | ● | ○ | ○ | ● | |||||||||||||||||||||||
| PCRB | ● | ● | ● | ● | ● | ○ | ● | |||||||||||||||||||||
| K71C | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||
| K83C | ● | ● | ● | ● | ● | |||||||||||||||||||||||
| fON | ● | ● | ● | |||||||||||||||||||||||||
| fOP | ● | ● | ● | |||||||||||||||||||||||||
| SOD | ● | ● | ● | ● | ||||||||||||||||||||||||
| K2w | ○ | ● | ○ | |||||||||||||||||||||||||
| K2s | ||||||||||||||||||||||||||||
| Summer | NH4 | NO3 | ON | OPO4 | OP | CHLA | DO | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters/ Segments | a | b | c | d | a | b | c | d | a | b | c | D | a | b | c | d | a | b | c | d | a | b | c | d | a | b | c | d |
| K12C | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||
| K20C | ||||||||||||||||||||||||||||
| K1C | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||||||||
| CCHL | ● | ● | ● | |||||||||||||||||||||||||
| K1D | ● | ○ | ○ | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||
| KMNG1 | ||||||||||||||||||||||||||||
| KMPG1 | ○ | ● | ● | ● | ● | |||||||||||||||||||||||
| NCRB | ○ | |||||||||||||||||||||||||||
| PCRB | ○ | ● | ● | ● | ● | ○ | ● | ● | ||||||||||||||||||||
| K71C | ● | ● | ● | ○ | ● | ● | ● | ● | ||||||||||||||||||||
| K83C | ● | ● | ● | ● | ||||||||||||||||||||||||
| fON | ● | |||||||||||||||||||||||||||
| fOP | ○ | ● | ● | ● | ● | |||||||||||||||||||||||
| SOD | ○ | ● | ● | ● | ● | |||||||||||||||||||||||
| K2w | ○ | |||||||||||||||||||||||||||
| K2s | ● | |||||||||||||||||||||||||||
| Parameters | Rank | P-Values from KS Test | Optimal Range | |||
|---|---|---|---|---|---|---|
| uSSR | lSSR | uSSR | lSSR | uSSR | lSSR | |
| K12C | 2 | 16 | 1.8×10–9 | 1 | 1–2 | 0–3 |
| K20C | 8 | 15 | 0.19 | 0.94 | ||
| K1C | 10 | 1 | 0.27 | 7.4 × 10–28 | 0.5–2.4 | 0–1.5 |
| CCHL | 6 | 9 | 0.05 | 0.58 | ||
| K1D | 4 | 3 | 2.4 × 10–6 | 1.4 × 10–10 | 0–0.12 | 0.1–0.25 |
| KMNG1 | 15 | 11 | 0.95 | 0.61 | ||
| KMPG1 | 7 | 5 | 0.13 | 2.7 × 10–4 | 0.005–0.018 | 0–0.05 |
| NCRB | 11 | 6 | 0.37 | 0.01 | ||
| PCRB | 5 | 4 | 4.0 × 10–4 | 5.0 × 10–6 | 0–0.08 | 0.125–0.24 |
| K71C | 3 | 8 | 1.6 × 10–6 | 0.33 | 0–0.18 | 0–1 |
| K83C | 12 | 13 | 0.57 | 0.71 | ||
| fON | 16 | 14 | 0.96 | 0.86 | ||
| fOP | 9 | 2 | 0.25 | 2.2 × 10–11 | 0.6 | 0–0.45 |
| SOD | 1 | 7 | 1.8 × 10–18 | 0.32 | 0–0.5 | 0–2.5 |
| K2w | 14 | 10 | 0.88 | 0.6 | ||
| K2s | 13 | 12 | 0.86 | 0.67 | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, N.; Chun, K.P.; Lindenschmidt, K.-E. Quantifying Spatial Changes in the Structure of Water Quality Constituents in a Large Prairie River within Two Frameworks of a Water Quality Model. Water 2016, 8, 158. https://doi.org/10.3390/w8040158
Hosseini N, Chun KP, Lindenschmidt K-E. Quantifying Spatial Changes in the Structure of Water Quality Constituents in a Large Prairie River within Two Frameworks of a Water Quality Model. Water. 2016; 8(4):158. https://doi.org/10.3390/w8040158
Chicago/Turabian StyleHosseini, Nasim, Kwok Pan Chun, and Karl-Erich Lindenschmidt. 2016. "Quantifying Spatial Changes in the Structure of Water Quality Constituents in a Large Prairie River within Two Frameworks of a Water Quality Model" Water 8, no. 4: 158. https://doi.org/10.3390/w8040158
APA StyleHosseini, N., Chun, K. P., & Lindenschmidt, K.-E. (2016). Quantifying Spatial Changes in the Structure of Water Quality Constituents in a Large Prairie River within Two Frameworks of a Water Quality Model. Water, 8(4), 158. https://doi.org/10.3390/w8040158







