Agent Based Modelling for Water Resource Allocation in the Transboundary Nile River
Abstract
:1. Introduction
Fair Resource Allocation
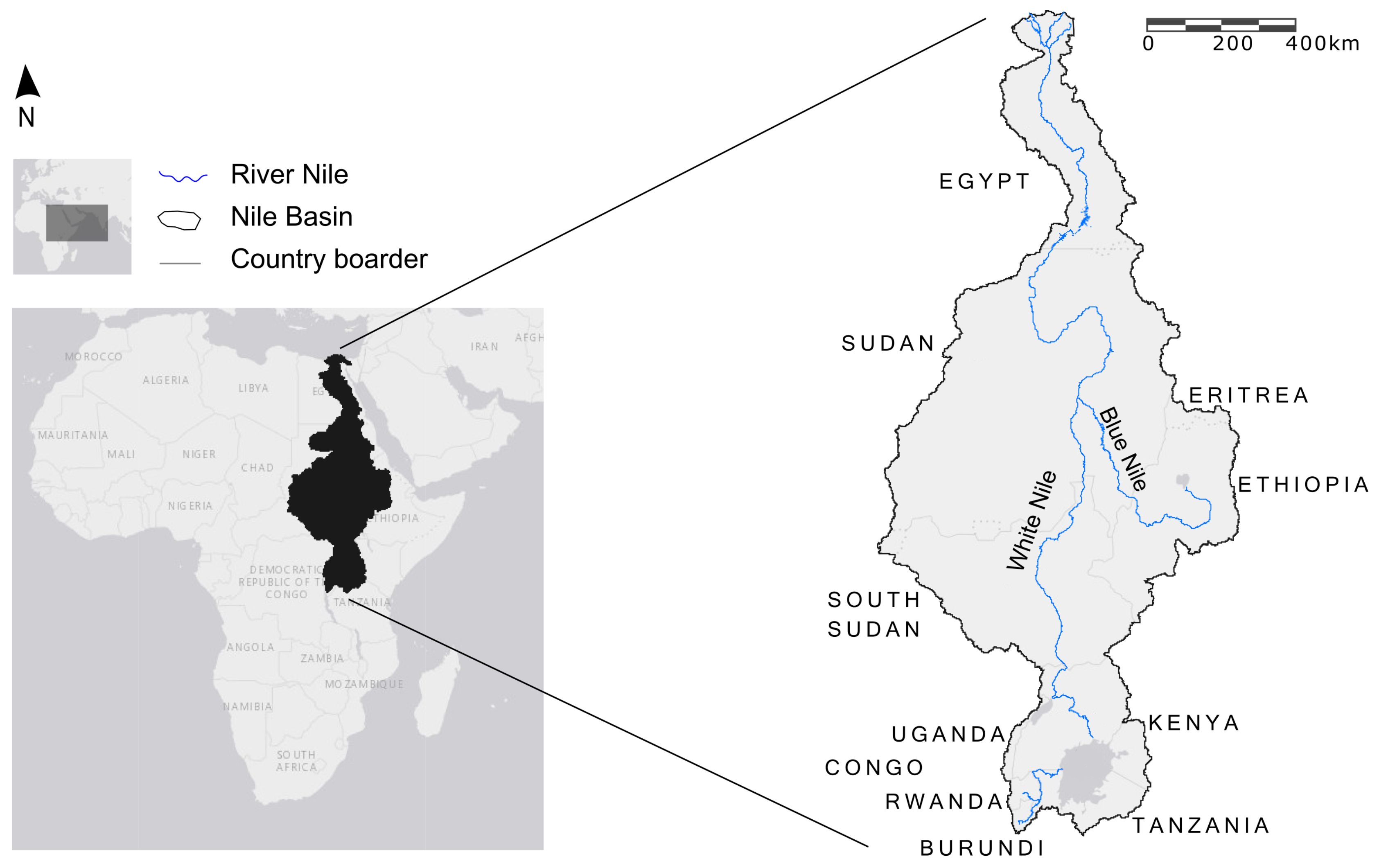
2. Problem Identification: Nile River Basin
3. Preliminaries and Definitions for Fair Resource Allocation
3.1. Preliminary and Definitions
Definition: (Central Planner Welfare Maximisation (CP))
Definition: (Contribution to Cooperation)
Definition: (Fairness)
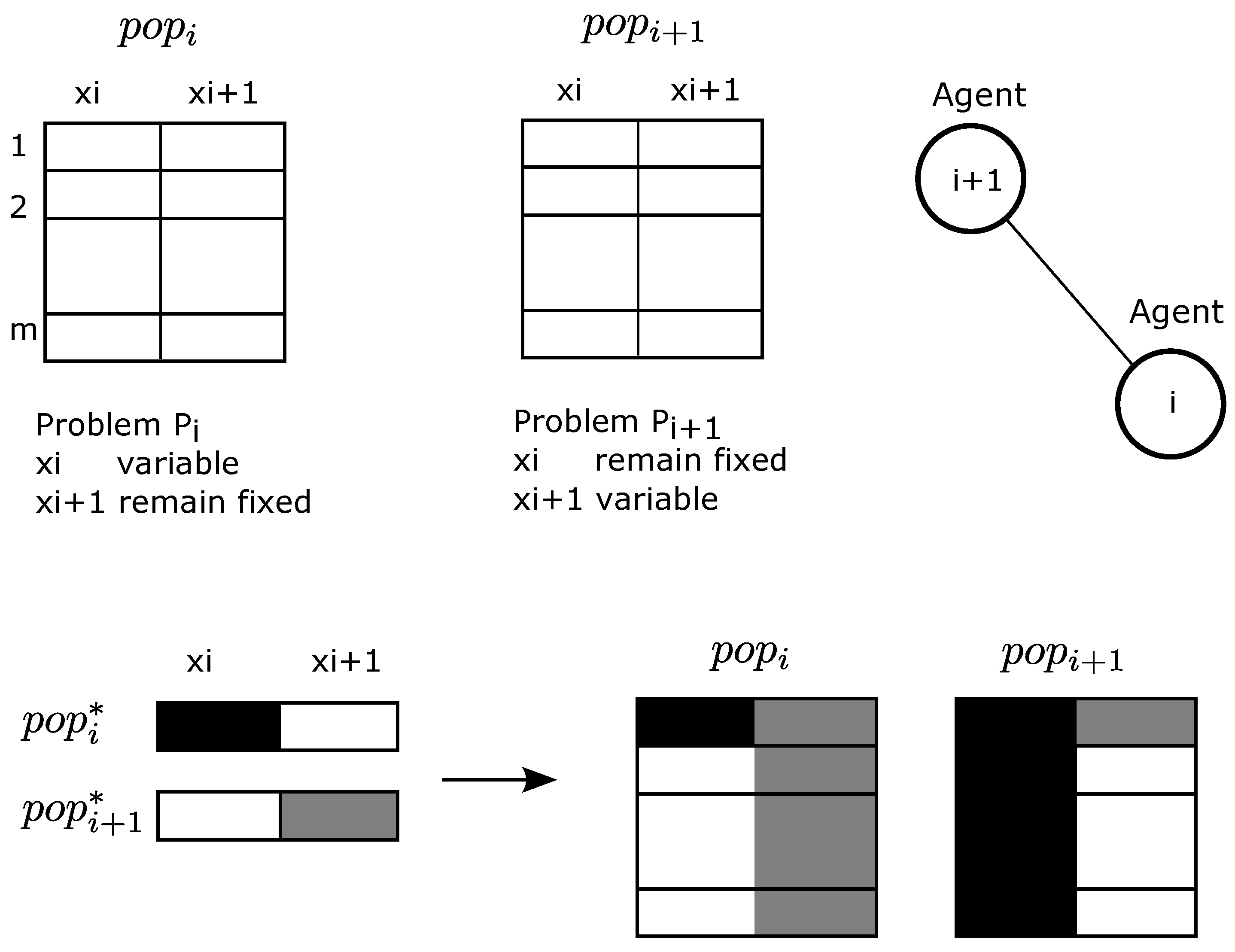
3.2. Parallel Search Algorithm

3.3. Resource Allocation Context
| 2: Illustrative procedure: Steps to redistribute utilities amongst self-interested agents |
| 1 Find ; |
| 2 for i = 1 n do |
| 3 Solve problem and using Algorithm 1; |
| 4 For each agent i, calculate , ; |
| 5 ; |
| 6 Distribute to each agent ; |
4. Nile River Basin Water Sharing Mechanism
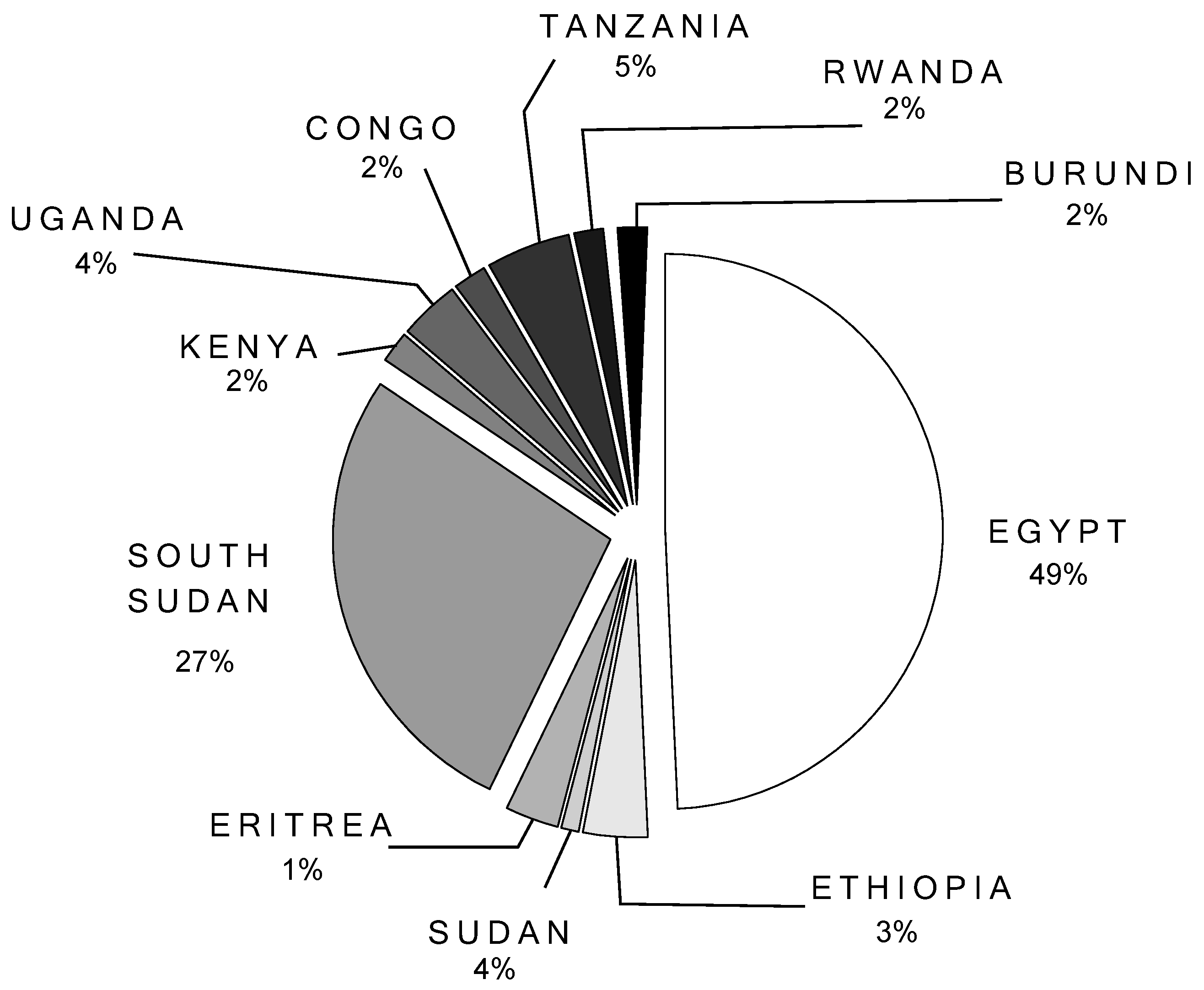
4.1. Water Availability
4.2. Population and Demand Values
5. Results and Discussion
5.1. Centralised Solution
5.2. Decentralised Solution
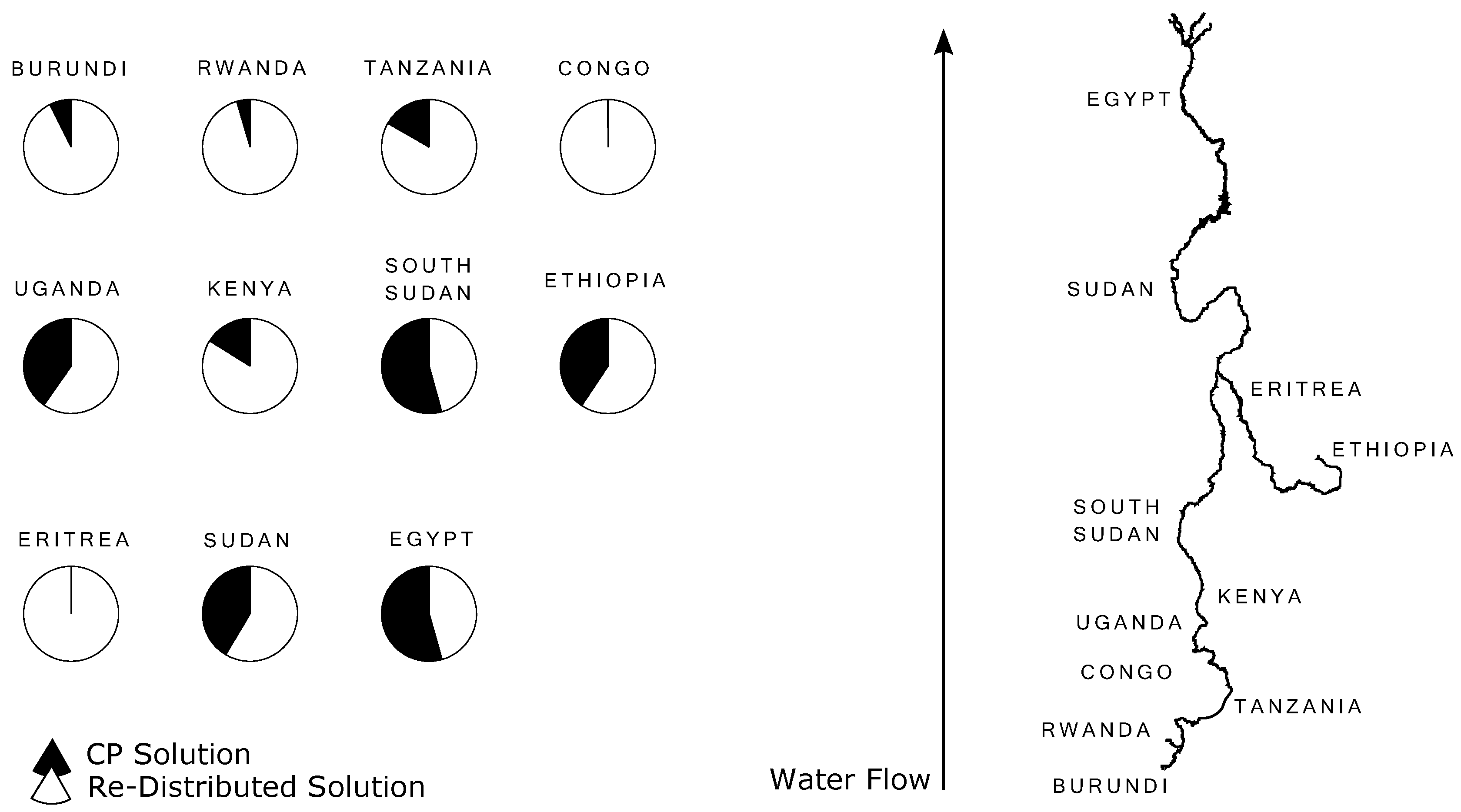
5.3. Re-Allocation Solution
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Speed, R.; Yuanyuan, L.; Zhiwei, Z.; Le Quesne, T.; Pegram, G. Basin Water Allocation Planning: Principles, Procedures and Approaches for Basin Allocation Planning; UNESCO: Paris, France, 2013. [Google Scholar]
- Erfani, T.; Binions, O.; Harou, J.J. Simulating water markets with transaction costs. Water Resour. Res. 2014, 50, 4726–4745. [Google Scholar] [CrossRef] [PubMed]
- Erfani, T.; Binions, O.; Harou, J. Protecting environmental flows through enhanced water licensing and water markets. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 2967–3003. [Google Scholar] [CrossRef]
- Harou, J.J.; Pulido-Velazquez, M.; Rosenberg, D.E.; Medellín-Azuara, J.; Lund, J.R.; Howitt, R.E. Hydro-economic models: Concepts, design, applications, and future prospects. J. Hydrol. 2009, 375, 627–643. [Google Scholar] [CrossRef]
- Britz, W.; Ferris, M.; Kuhn, A. Modeling water allocating institutions based on Multiple Optimization Problems with Equilibrium Constraints. Environ. Model. Softw. 2013, 46, 196–207. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K.W. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Barreteau, O.; Bousquet, F.; Millier, C.; Weber, J. Suitability of Multi-Agent Simulations to study irrigated system viability: Application to case studies in the Senegal River Valley. Agric. Syst. 2004, 80, 255–275. [Google Scholar] [CrossRef]
- Bousquet, F.; Barreteau, O.; d’Aquino, P.; Etienne, M.; Boissau, S.; Aubert, S.; Page, C.L.; Babin, D.; Castella, J.C.; Janssen, M.; et al. Multi-agent systems and role games: Collective learning processes for ecosystem management. In Complexity and Ecosystem Management: The Theory and Practice of Multi-Agent Systems; ACM Digital Library: New York, NY, USA, 2002; pp. 248–285. [Google Scholar]
- Yang, Y.C.E.; Cai, X.; Stipanović, D.M. A decentralized optimization algorithm for multiagent system–based watershed management. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Yang, Y.C.E.; Zhao, J.; Cai, X. Decentralized Optimization Method for Water Allocation Management in the Yellow River Basin. J. Water Resour. Plan. Manag. 2011, 138, 313–325. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, X.; Wang, Z. Comparing administered and market-based water allocation systems through a consistent agent-based modeling framework. J. Environ. Manag. 2013, 123, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Heusinger, A.V. Numerical Methods for the Solution of the Generalized Nash Equilibrium Problem. Ph.D. Thesis, Wuĺrzburg University, Würzburg Germany, 2009. [Google Scholar]
- Kolstad, C.D.; Mathiesen, L. Computing Cournot-Nash equilibria. Oper. Res. 1991, 39, 739–748. [Google Scholar] [CrossRef]
- Erfani, T.; Erfani, R. Fair Resource Allocation Using Multi-population Evolutionary Algorithm. In Applications of Evolutionary Computation; Springer: Berlin, Germany, 2015; pp. 214–224. [Google Scholar]
- Read, L.; Madani, K.; Inanloo, B. Optimality versus stability in water resource allocation. J. Environ. Manag. 2014, 133, 343–354. [Google Scholar] [CrossRef] [PubMed]
- El-Fadel, M.; El-Sayegh, Y.; El-Fadl, K.; Khorbotly, D. The Nile River Basin: A case study in surface water conflict resolution. J. Natl. Resour. Life Sci. Educ. 2003, 32, 107–117. [Google Scholar]
- Kameri-Mbote, P.G. Water, Conflict, and Cooperation: Lessons from the Nile River Basin; Woodrow Wilson International Center for Scholars: Washington, DC, USA, 2007. [Google Scholar]
- Mohamoda, D.Y. Nile Basin Cooperation: A Review of the Literature; Number 26; Nordic Africa Institute: Uppsala, Sweden, 2003. [Google Scholar]
- Hu, W.; Yang, J.; Huang, H. A study of water resources development and utilization and management cooperation across the Nile River Basin. Resour. Sci. 2011, 10, 003. [Google Scholar]
- Hamouda, M.A.; El-Din, M.M.N.; Moursy, F.I. Vulnerability assessment of water resources systems in the Eastern Nile Basin. Water Resour. Manag. 2009, 23, 2697–2725. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations Regional Office for Africa. FAO Statistical Yearbook 2014 Africa Food and Agriculture; FAO Uited Nation: Accra, Ghana, 2014. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Aquastat FAO; FAO Uited Nation: Accra, Ghana, 2015. [Google Scholar]
- Erfani, T.; Erfani, R. An evolutionary approach to solve a system of multiple interrelated agent problems. Appl. Soft Comput. 2015, 37, 40–47. [Google Scholar] [CrossRef]
- Mühlenbein, H.; Schomisch, M.; Born, J. The parallel genetic algorithm as function optimizer. Parallel Comput. 1991, 17, 619–632. [Google Scholar] [CrossRef]
- Potter, M.A.; De Jong, K.A. Cooperative coevolution: An architecture for evolving coadapted subcomponents. Evolut. Comput. 2000, 8, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Gonzalez, L.F.; Periaux, J.; Srinivas, K. Efficient hybrid-game strategies coupled to evolutionary algorithms for robust multidisciplinary design optimization in aerospace engineering. IEEE Trans. Evolut. Comput. 2011, 15, 133–150. [Google Scholar] [CrossRef]
- Cai, X.; McKinney, D.C.; Rosegrant, M.W. Sustainability analysis for irrigation water management in the Aral Sea region. Agric. Syst. 2003, 76, 1043–1066. [Google Scholar] [CrossRef]
- Gibbons, D.C. The Economic Value of Water; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Griffin, R.C. Water Resource Economics: The Analysis of Scarcity, Policies, and Projects; MIT Press Books: Cambridge, MA, USA, 2006; Volume 1. [Google Scholar]
- Erfani, T.; Huskova, I.; Harou, J.J. Tracking trade transactions in water resource systems: A node-arc optimization formulation. Water Resour. Res. 2013, 49, 3038–3043. [Google Scholar] [CrossRef]
- Understanding Nile Basin Hydrology: Mapping Actual Evapotranspiration Over The Nile Basin. In Technical Bulletin from the Nile Basin Initiative Secretariat; Nile Waters: Entebbe, Uganda, 2015.
- Sutcliffe, J.V.; Parks, Y.P. The Hydrology of the Nile; Number 5; International Association of Hydrological Sciences Wallingford: Oxfordshire, UK, 1999. [Google Scholar]
| Country | Internal | Actual | ||||
|---|---|---|---|---|---|---|
| Water | Water | Dependancy | Diverted Water | % of Total | Diverted | |
| Resources | Resources | Ratio | from Nile | Resources | for Use | |
| (IRWR) | (ARWR) | |||||
| Burundi | 10.06 | 12.54 | 19.75 | 40.9 | 2.3 | 1.77 |
| Rwanda | 9.5 | 13.3 | 28.57 | 17.1 | 1.58 | 1.07 |
| Tanzania | 84 | 96.27 | 12.75 | N/A | N/A | N/A |
| Uganda | 39 | 60.1 | 35.11 | 11.4 | 0.46 | 0.18 |
| Sudan | 4.0 | 37.8 | 96.13 | 1074 | 58 | 56 |
| S.Sudan | 26.0 | 49.5 | 65.8 | 1074 | 58 | 56 |
| Egypt | 1.8 | 58.3 | 96.91 | 990 | 94.7 | 103 |
| Ethiopia | 122 | 122 | 0 | 76 | 4.56 | 4.27 |
| Eritrea | 2.8 | 7.315 | 61.72 | 124.0 | N/A | N/A |
| Congo | 900 | 1283 | 29.85 | 6.7 | N/A | N/A |
| Kenya | 20.7 | 30.7 | 32.57 | 74.85 | 8.91 | 7.05 |
| Agent | Sectors | Population Within | % of Total | Water Usage | Water Demand | Source |
|---|---|---|---|---|---|---|
| the Basin (Million) | Population | (BCM) | with the Basin (BCM) | |||
| BU | Agriculture | 4.88 | 44.50% | 0.22 | 0.0979 | 1 |
| RW | Agriculture | 8.17 | 69.40% | 0.1 | 0.0694 | 1 |
| TA | Agriculture | 8.24 | 16.70% | 4.632 | 0.7749 | 1 |
| CO | Agriculture | 2.8 | 4.10% | 0.11 | 0.0046 | 1 |
| UG | Industry | 30.28 | 76.40% | 0.12 | 0.0917 | 1 |
| KE | Agriculture | 14.62 | 33.00% | 1.01 | 0.3329 | 1 |
| SS | Energy | 10 | 85.50% | 0.21 | 0.1818 | 1 |
| ET | Agriculture | 29.56 | 31.40% | 5.204 | 1.6347 | 2 |
| ER | Agriculture | 0.21 | 3.30% | 0.29 | 0.0096 | 2 |
| SU | Agriculture | 20 | 29.60% | 6.56 | 1.9445 | 1+2 |
| EG | Municipal | 51 | 62.20% | 5.3 | 3.2941 | 1+2 |
| Agent | BU | RW | TA | CO | UG | KE | SS | ET | ER | SU | EG |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 100 | 100 | 100 | 100 | 1860 | 100 | 13000 | 100 | 100 | 100 | 1300 |
| b | 511 | 721 | 65 | 10960 | 10139 | 150 | 35757 | 31 | 5200 | 26 | 197 |
| Agent | BU | RW | TA | CO | UG | KE | SS | ET | ER | SU | EG |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Water (bcm) | 0.1 | 0.04 | 0.54 | 0 | 0.08 | 0.17 | 0.16 | 1.24 | 0 | 1.72 | 2.85 |
| Benefit (mGBP) | 4.9 | 2.8 | 35 | 0 | 84.7 | 12.5 | 1159.5 | 76.3 | 0 | 95.1 | 2105.1 |
| Total benefit | |||||||||||
| Agent | Country | Contribution | Singleton | Group | Fairness | Final |
|---|---|---|---|---|---|---|
| Revenue | ||||||
| BU | Burundi | 76.94 | 4.89 | 3499 | 0.017 | 61.16 |
| RW | Rwanda | 75.94 | 2.802 | 3500 | 0.017 | 60.37 |
| TA | Tanzania | 219.94 | 35 | 3356 | 0.049 | 174.84 |
| CO | Congo | 86.94 | 0 | 3489 | 0.019 | 69.11 |
| UG | Uganda | 157.94 | 85.09 | 3418 | 0.035 | 125.55 |
| KE | Kenya | 81.94 | 13.01 | 3494 | 0.018 | 65.14 |
| SS | S.Sudan | 1226.94 | 1168 | 2349 | 0.273 | 975.35 |
| ET | Ethiopia | 139.94 | 76.37 | 3436 | 0.031 | 111.24 |
| ER | Eritrea | 45.94 | 0 | 3530 | 0.01 | 36.52 |
| SU | Sudan | 168.94 | 96.01 | 3407 | 0.038 | 134.3 |
| EG | Egypt | 2216.94 | 1947 | 1359 | 0.493 | 1762.35 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, N.; Erfani, R.; Mokhtar, H.; Erfani, T. Agent Based Modelling for Water Resource Allocation in the Transboundary Nile River. Water 2016, 8, 139. https://doi.org/10.3390/w8040139
Ding N, Erfani R, Mokhtar H, Erfani T. Agent Based Modelling for Water Resource Allocation in the Transboundary Nile River. Water. 2016; 8(4):139. https://doi.org/10.3390/w8040139
Chicago/Turabian StyleDing, Ning, Rasool Erfani, Hamid Mokhtar, and Tohid Erfani. 2016. "Agent Based Modelling for Water Resource Allocation in the Transboundary Nile River" Water 8, no. 4: 139. https://doi.org/10.3390/w8040139
APA StyleDing, N., Erfani, R., Mokhtar, H., & Erfani, T. (2016). Agent Based Modelling for Water Resource Allocation in the Transboundary Nile River. Water, 8(4), 139. https://doi.org/10.3390/w8040139





