Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments
Abstract
:1. Introduction
2. Materials: Rainfall Erosivity Database at European Scale (REDES) and 2015 Updates
3. Methods
3.1. Monthly R-factor Calculation
3.2. Calibration of Monthly R-factors Calculated from Different Temporal Resolution Rainfall Data
- -
- The R-factor was calculated at the highest available resolution (i.e., <30 min) for a number of stations (86 stations well distributed across Europe).
- -
- Data have been aggregated to coarser resolution(s) and the R-factor was calculated at the coarser resolution for the same stations.
- -
- A calibration function, derived from regression analysis, has been developed based on the R-factor results at the highest possible resolution and the coarser resolution(s).
4. Results and Discussion
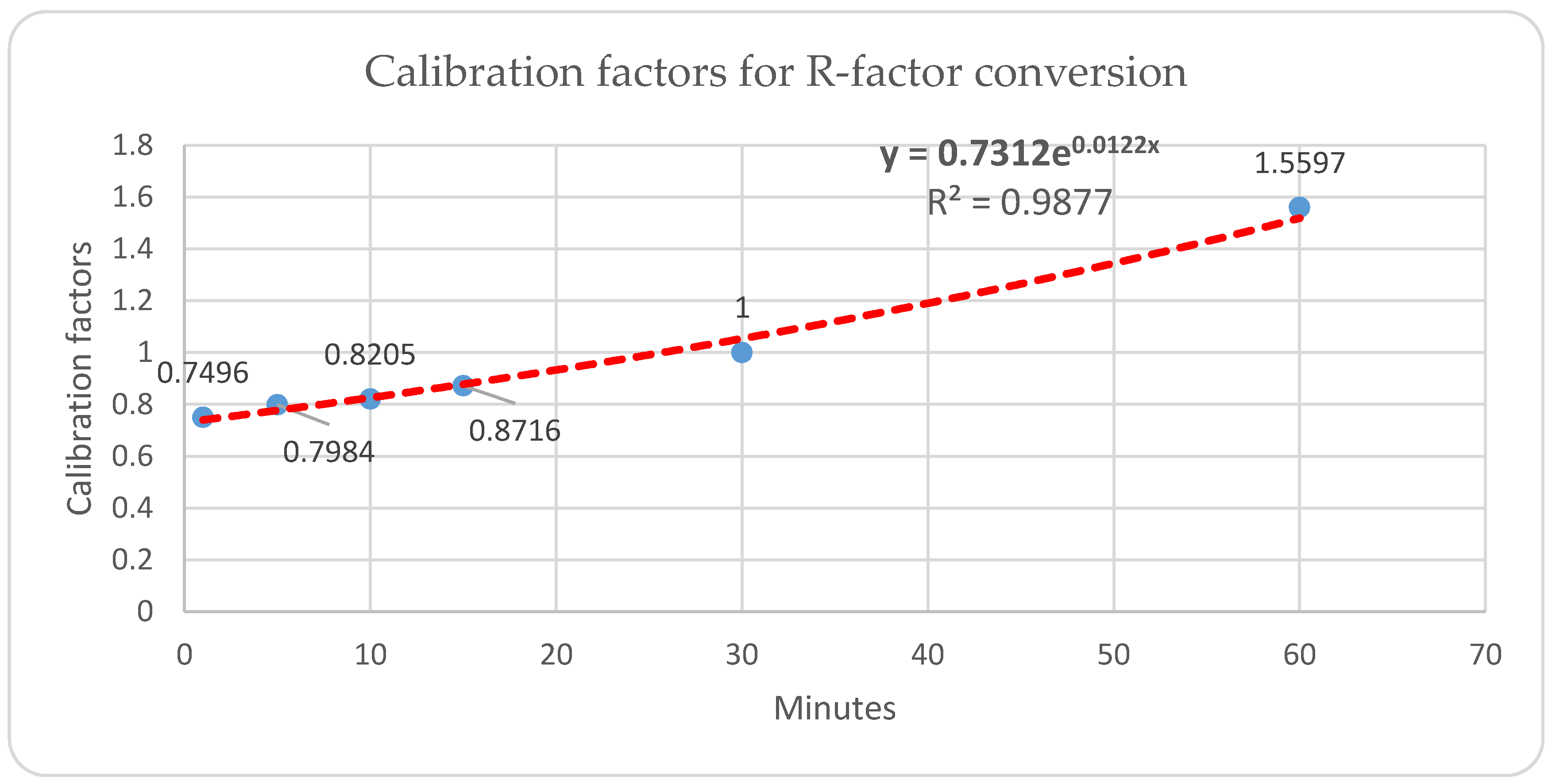
4.1. Regression Curve for Annual R-factor Value
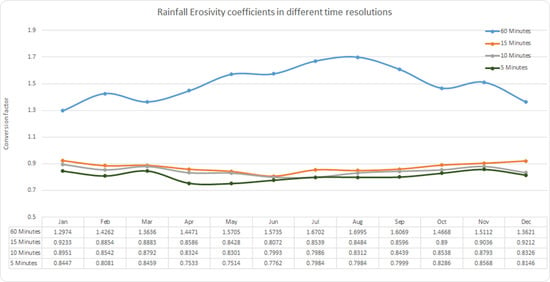
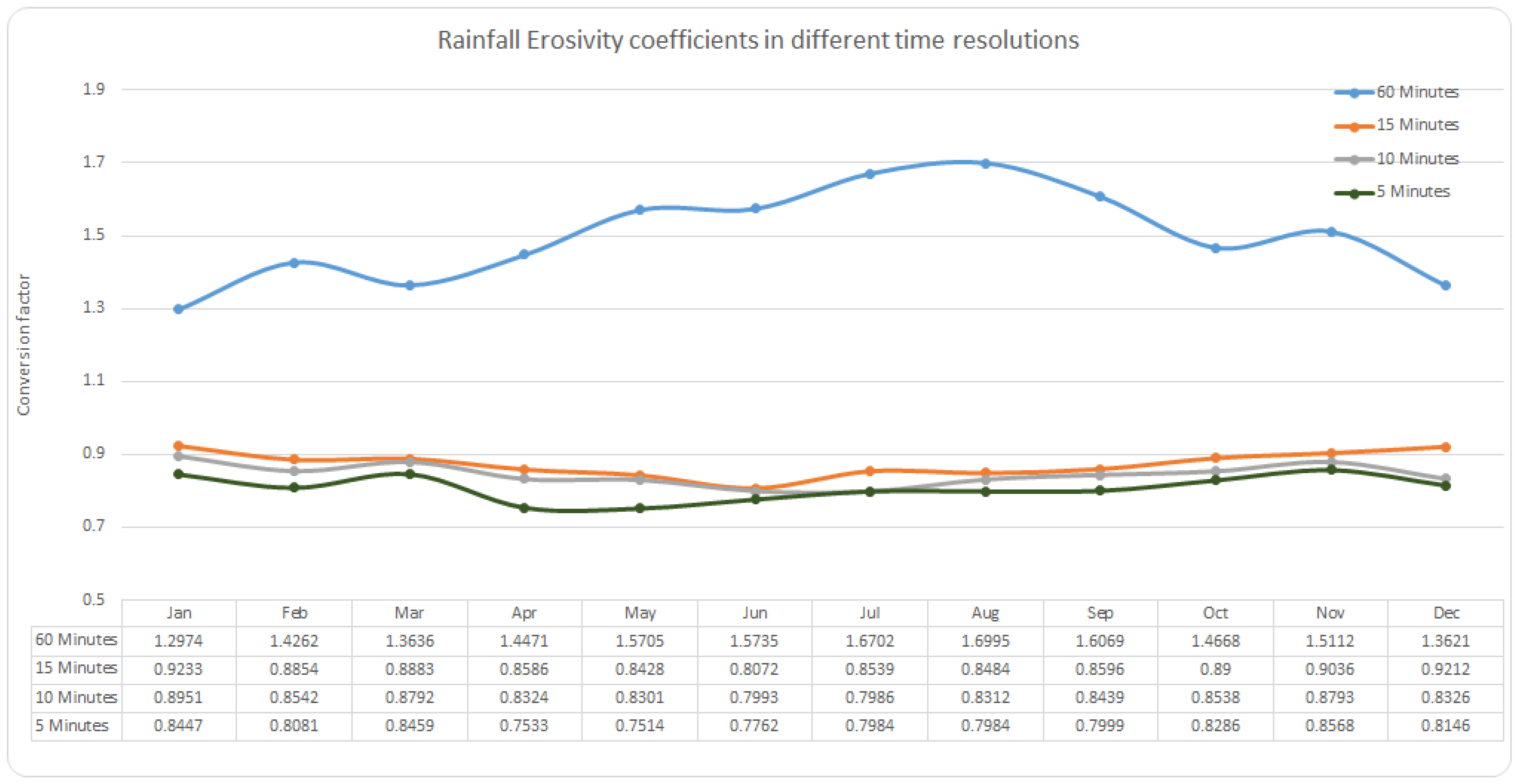
4.2. Monthly Calibration Factors for Different Temporal Resolution
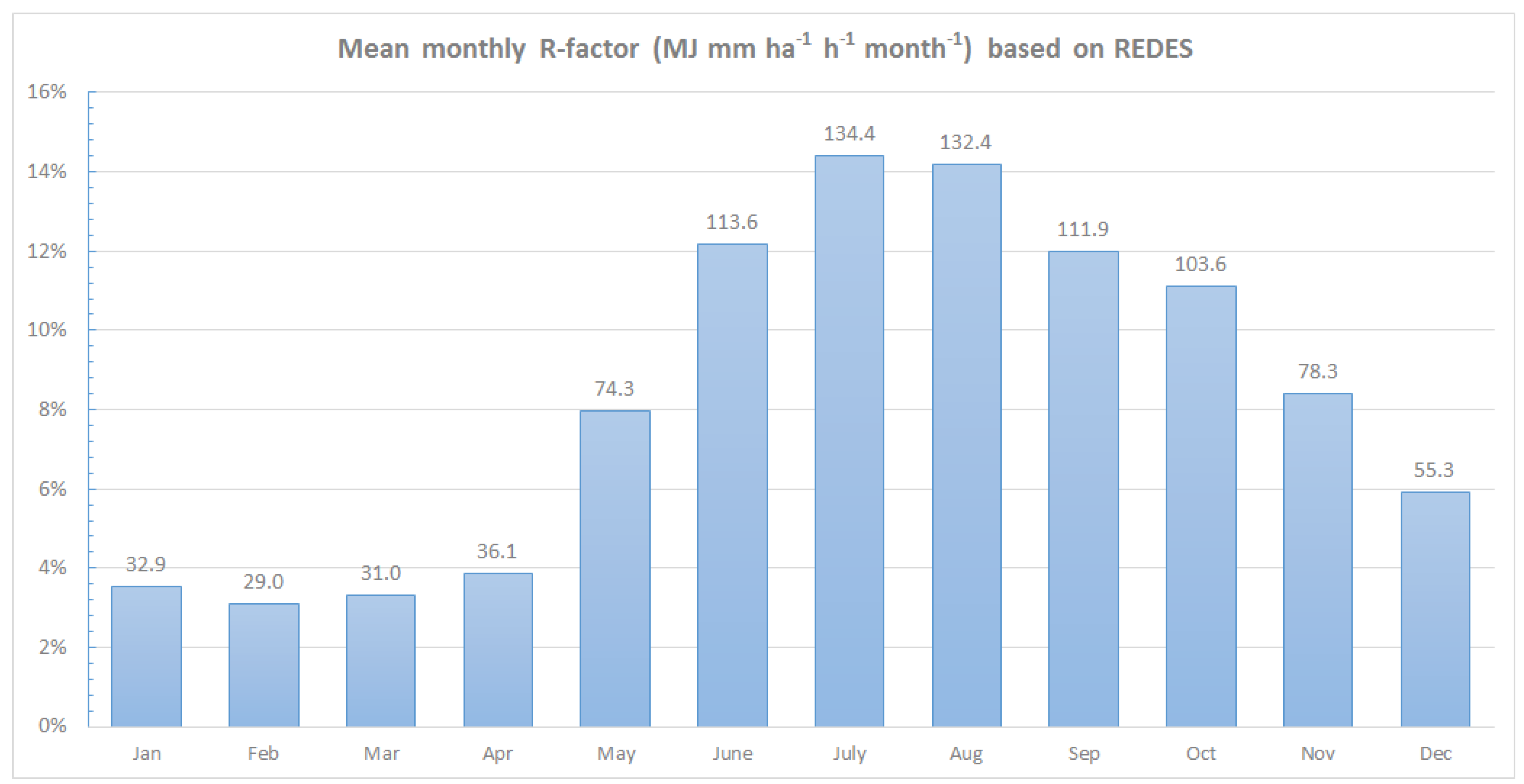
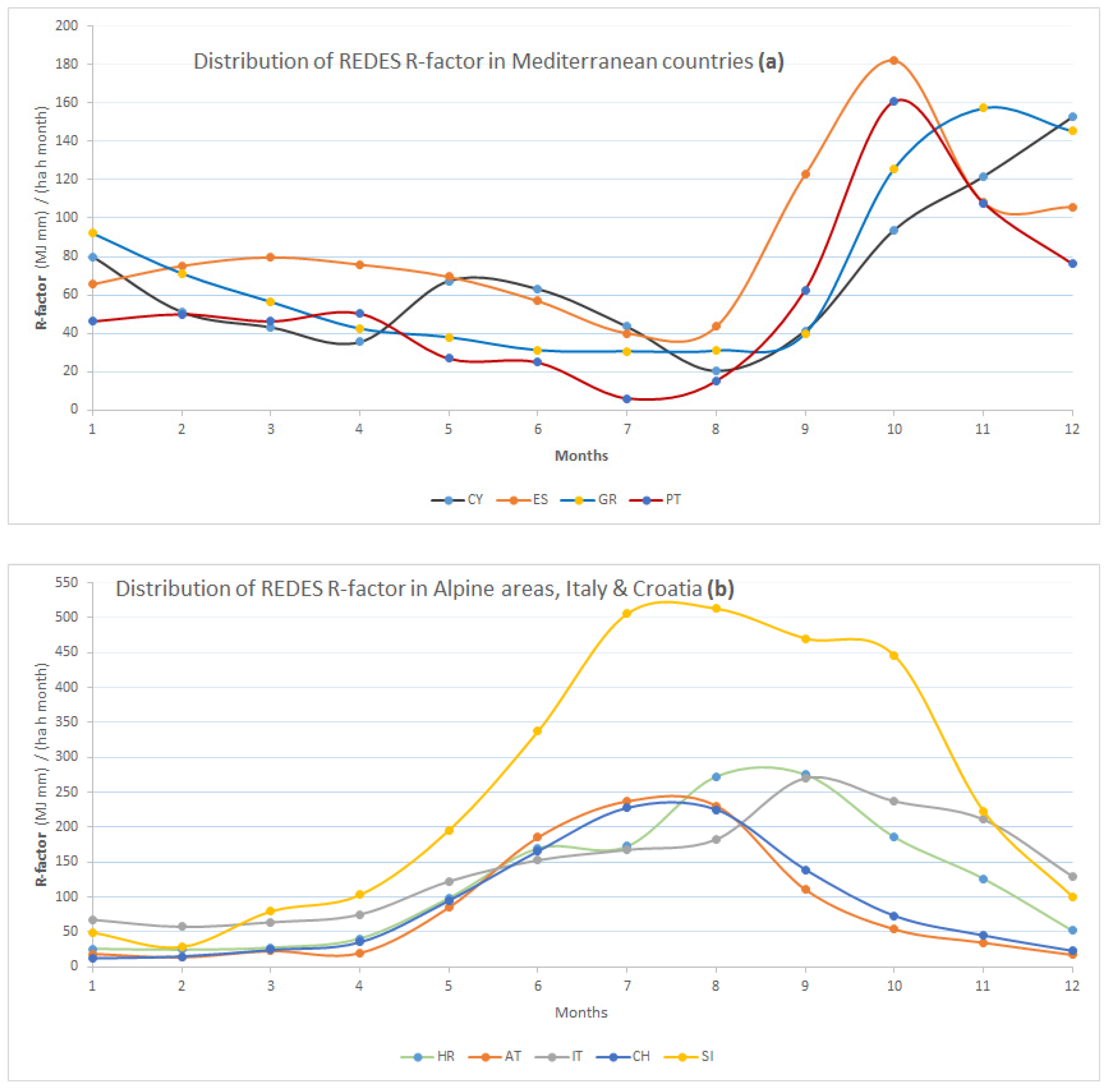
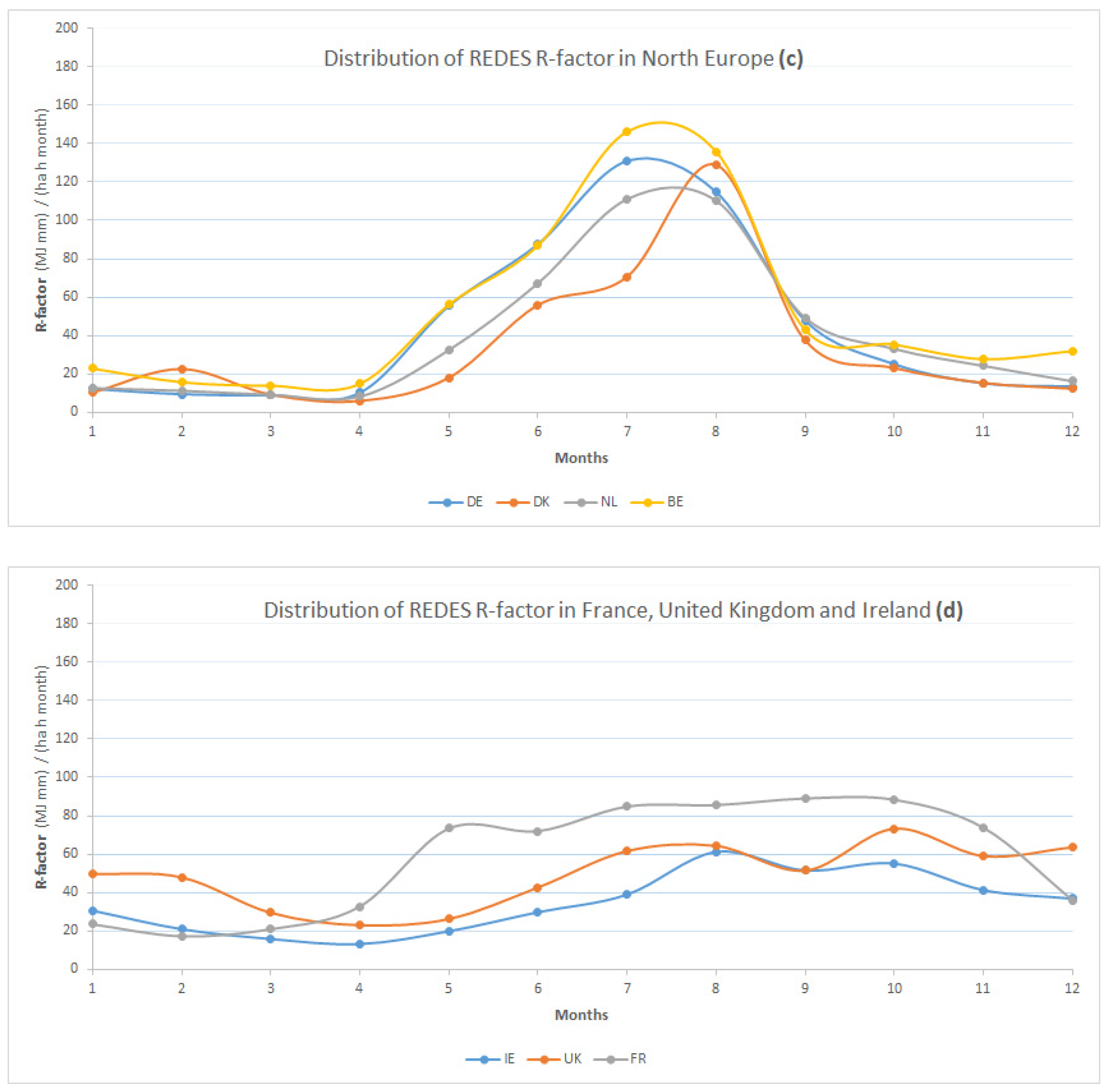
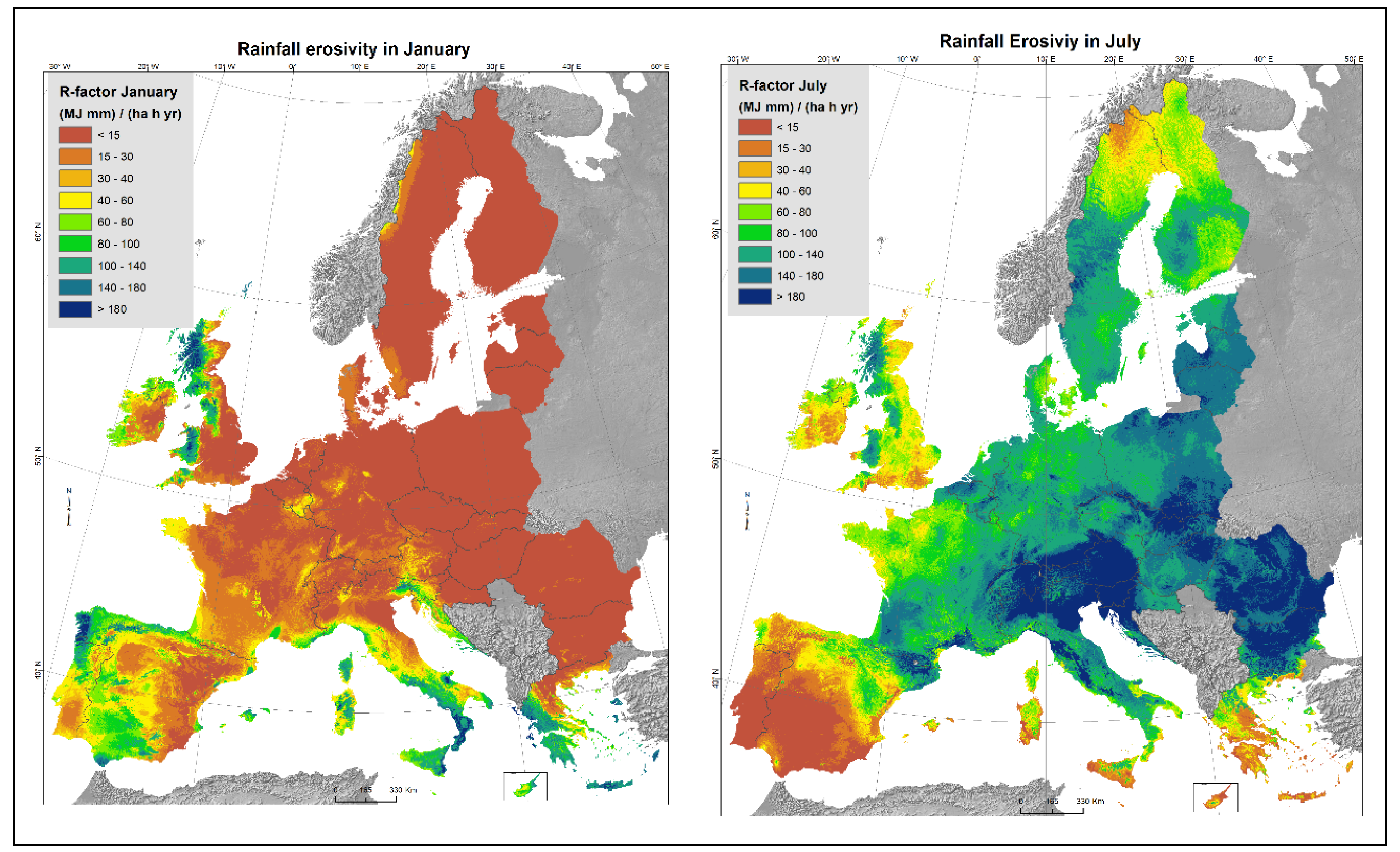
4.3. Seasonal and Monthly Rainfall Erosivity
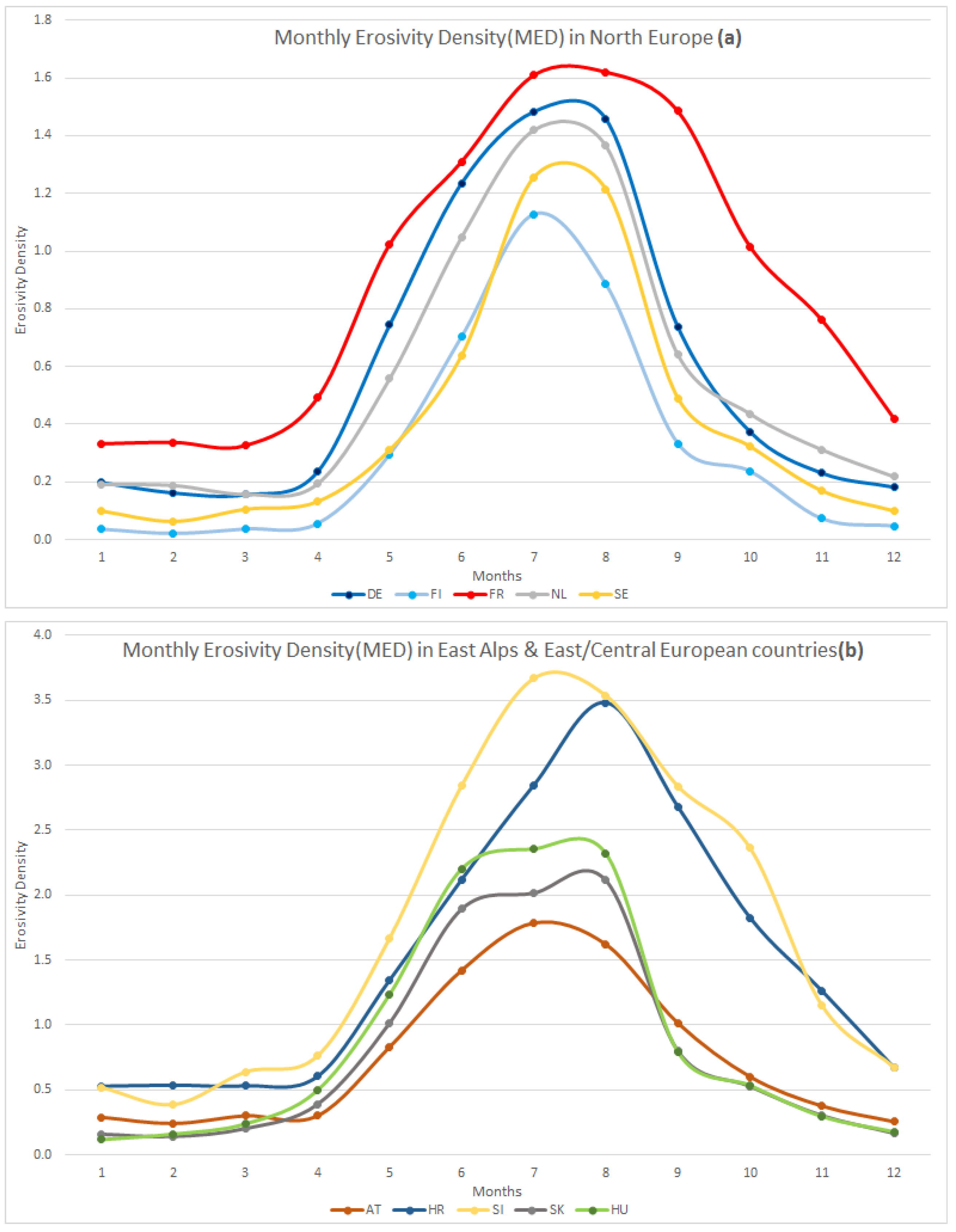
4.4. Monthly Rainfall Erosivity Density
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lal, R. Soil degradation by erosion. Land Degrad. Dev. 2001, 12, 519–539. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Van Liedekerke, M.; Alewell, C.; Hiederer, R.; Montanarella, L. Assessing soil erosion in Europe based on data collected through a European Network. Soil Sci. Plant Nutr. 2014, 60, 15–29. [Google Scholar] [CrossRef]
- Wang, G.; Gertner, G.; Singh, V.; Shinkareva, S.; Parysow, P.; Anderson, A. Spatial and temporal prediction and uncertainty of soil loss using the revised universal soil loss equation: A case study of the rainfall-runoff erosivity R factor. Ecol. Model. 2002, 153, 143–155. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.A.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agricultural Handbook 703; US Department of Agriculture: Washington, DC, USA, 1997; pp. 1–404.
- Wischmeier, W.; Smith, D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Agricultural Handbook No. 537; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- Istok, J.D.; McCool, D.K.; King, L.G.; Boersma, L. Effect of rainfall measurement interval on EI calculation. Trans. Am. Soc. Agric. Eng. 1986, 29, 730–734. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadic, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.C.; Foster, G.R. Storm erosivity using idealized intensity distributions. Trans. ASAE 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Begueria, S.; Klik, A.; Rymszewicz, A.; Michaelides, S.; Olsen, P.; Tadic, M.P.; et al. Reply to the comment on “Rainfall erosivity in Europe” by Auerswald et al. Sci.Total Environ. 2015, 532, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Diodato, N. Predicting RUSLE (Revised Universal Soil Loss Equation) monthly erosivity index from readily available rainfall data in Mediterranean area. Environmentalist 2006, 26, 63–70. [Google Scholar] [CrossRef]
- Meusburger, K.; Steel, A.; Panagos, P.; Montanarella, L.; Alewell, C. Spatial and temporal variability of rainfall erosivity factor for Switzerland. Hydrol. Earth Syst. Sci. 2012, 16, 167–177. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Hazbavi, Z. Trend analysis of the rainfall erosivity index at different time scales in Iran. Nat. Hazard. 2015, 77, 383–404. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena 2016, 137, 161–172. [Google Scholar] [CrossRef]
- Klik, A.; Konecny, F. Rainfall erosivity in northeastern Austria. Trans. ASABE 2013, 56, 719–725. [Google Scholar] [CrossRef]
- Weiss, L.L. Ratio of true to fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar]
- Yin, S.; Xie, Y.; Nearing, M.A.; Wang, C. Estimation of rainfall erosivity using 5- to 60-minute fixed-interval rainfall data from China. CATENA 2007, 70, 306–312. [Google Scholar] [CrossRef]
- Agnese, C.; Bagarello, V.; Corrao, C.; D’Agostino, L.; D’Asaro, F. Influence of the rainfall measurement interval on the erosivity determinations in the Mediterranean area. J. Hydrol. 2006, 329, 39–48. [Google Scholar] [CrossRef]
- Coumou, D.; Rahmstorf, S. A decade of weather extremes. Nat. Clim. Chang. 2012, 2, 491–496. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; van Vuuren, D. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Alfred-Wegener-Institut (AWI): Potsdam, Germany, 2014. [Google Scholar]
- Porto, P. Exploring the effect of different time resolutions to calculate the rainfall erosivity factor R in Calabria, southern Italy. Hydrol. Process. 2015, in press. [Google Scholar] [CrossRef]
- Williams, R.G.; Sheridan, J.M. Effect of measurement time and depth resolution on EI calculation. Trans. ASAE 1991, 34, 402–405. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L. Observed trends in extreme precipitation events in China during 1961–2001 and the associated changes in large-scale circulation. Geophys. Rese. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhai, P.M.; Pan, X.H. Change in extreme temperature and precipitation over northern China during the second half of the 20th century. Acta Geogr. Sin. 2003, 58, 1–10. [Google Scholar]
- Pauling, A.; Luterbacher, J.; Casty, C.; Wanner, H. Five hundred years of gridded high-resolution precipitation reconstructions over Europe and the connection to large-scale circulation. Clim. Dyn. 2006, 26, 387–405. [Google Scholar] [CrossRef]
- Wei, W.; Chen, L.; Fu, B.; Huang, Z.; Wu, D.; Gui, L. The effect of land uses and rainfall regimes on runoff and soil erosion in the semi-arid loess hilly area, China. J. hydrol. 2007, 335, 247–258. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Wagener, T.; Tallaksen, L.M.; Engeland, K. Evaluation of nine large-scale hydrological models with respect to the seasonal runoff climatology in Europe. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Marker, M.; Angeli, L.; Bottai, L.; Costantini, R.; Ferrari, R.; Innocenti, L.; Siciliano, G. Assessment of land degradation susceptibility by scenario analysis: A case study in Southern Tuscany, Italy. Geomorphology 2008, 93, 120–129. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Hoyos, N.; Waylen, P.R.; Jaramillo, A. Seasonal and spatial patterns of erosivity in a tropical watershed of the Colombian Andes. J. Hydrol. 2005, 314, 177–191. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, C.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the soil erosion cover-management factor at European scale. Land Use Policy 2015, 48, 38–50. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- González-Hidalgo, J.C.; Brunetti, M.; de Luis, M. A new tool for monthly precipitation analysis in Spain: MOPREDAS database (monthly precipitation trends December 1945–November 2005). Int. J. Climatol. 2011, 31, 715–731. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the increased frequency of Mediterranean drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef]
- Xoplaki, E.; Gonzalez-Rouco, J.F.; Luterbacher, J.U.; Wanner, H. Wet season Mediterranean precipitation variability: influence of large-scale dynamics and trends. Clim. Dyn. 2004, 23, 63–78. [Google Scholar] [CrossRef]
- Wibig, J. Precipitation in Europe in relation to circulation patterns at the 500 hPa level. Int. J. Climatol. 1999, 19, 253–269. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. Seasonal prediction of European spring precipitation from El Niño–Southern Oscillation and Local sea-surface temperatures. Int. J. Climatol. 2002, 22, 1–14. [Google Scholar] [CrossRef]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Frei, C.; Davies, H.C.; Gurtz, J.; Schär, C. Climate dynamics and extreme precipitation and flood events in Central Europe. Integr. Assess. 2000, 1, 281–300. [Google Scholar] [CrossRef]
- Peristeri, M.; Ulrich, W.; Smith, R.K. Genesis conditions for thunderstorm growth and the development of a squall line in the northern alpine foreland. Meteorol. Atmos. Phys. 2000, 72, 251–260. [Google Scholar] [CrossRef]
- Christian, H.J.; Blakeslee, R.J.; Boccippio, D.J.; Boeck, W.L.; Buechler, D.E.; Driscoll, K.T.; Goodman, S.J.; Hall, J.M.; Koshak, W.J.; March, D.M.; et al. Global frequency and distribution of lightning as observed from space by the Optical Transient Detector. J. Geophys. Res. Atmospheres 2003, 108. [Google Scholar] [CrossRef]
- Bartholy, J.; Pongrácz, R. Regional analysis of extreme temperature and precipitation indices for the Carpathian Basin from 1946 to 2001. Glob. Planet. Chang. 2007, 57, 83–95. [Google Scholar] [CrossRef]
- Spinoni, J.; Szalai, S.; Szentimrey, T.; Lakatos, M.; Bihari, Z.; Nagy, A.; Nemeth, A.; Kovacs, T.; Mihic, D.; Dacic, M.; et al. Climate of the Carpathian Region in the period 1961–2010: climatologies and trends of 10 variables. Int. J. Climatol. 2015, 35, 1322–1341. [Google Scholar] [CrossRef]
- Dumitrescu, A.; Birsan, M.V.; Manea, A. Spatio-temporal interpolation of sub-daily (6 h) precipitation over Romania for the period 1975–2010. Int. J. Climatol. 2015, 36, 1331–1343. [Google Scholar] [CrossRef]
- Linderson, M.L. Objective classification of atmospheric circulation over southern Scandinavia. Int. J. Climatol. 2001, 21, 155–169. [Google Scholar] [CrossRef]
- Klutke, G.A.; Kiessler, P.C.; Wortman, M.A. A critical look at the bathtub curve. IEEE Trans. Reliab. 2003, 52, 125–129. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 3—A nonparametric probabilistic forecast model. J. Hydrol. 2000, 239, 249–258. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining instance-based and model based learning. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; Morgan Kaufman: Burlington, MA, USA, 2013; pp. 236–243. [Google Scholar]
- Blanco, H.; Lal, R. Principles of Soil Conservation and Management; Springer Science & Business Media: Berlin, Heidelberg, Germany, 2008; pp. 513–534. [Google Scholar]
- O’Neal, M.R.; Nearing, M.A.; Vining, R.C.; Southworth, J.; Pfeifer, R.A. Climate change impacts on soil erosion in Midwest United States with changes in crop management. Catena 2005, 61, 165–184. [Google Scholar] [CrossRef]
- Orlowsky, B.; Seneviratne, S.I. Global changes in extreme events: Regional and seasonal dimension. Clim. Chang. 2012, 110, 669–696. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Bonilla, C.A.; Vidal, K.L. Rainfall erosivity in Central Chile. J. Hydrol. 2011, 410, 126–133. [Google Scholar] [CrossRef]
- Dabney, S.M.; Yoder, D.C.; Vieira, D.A.N. The application of the Revised Universal Soil Loss Equation, Version 2, to evaluate the impacts of alternative climate change scenarios on runoff and sediment yield. J. Soil Water Conserv. 2012, 67, 343–353. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G. Decadal modelling of rainfall-runoff erosivity in the Euro-Mediterranean region using extreme precipitation indices. Glob. Planet. Chang. 2012, 86, 79–91. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagos, P.; Borrelli, P.; Spinoni, J.; Ballabio, C.; Meusburger, K.; Beguería, S.; Klik, A.; Michaelides, S.; Petan, S.; Hrabalíková, M.; et al. Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments. Water 2016, 8, 119. https://doi.org/10.3390/w8040119
Panagos P, Borrelli P, Spinoni J, Ballabio C, Meusburger K, Beguería S, Klik A, Michaelides S, Petan S, Hrabalíková M, et al. Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments. Water. 2016; 8(4):119. https://doi.org/10.3390/w8040119
Chicago/Turabian StylePanagos, Panos, Pasquale Borrelli, Jonathan Spinoni, Cristiano Ballabio, Katrin Meusburger, Santiago Beguería, Andreas Klik, Silas Michaelides, Sašo Petan, Michaela Hrabalíková, and et al. 2016. "Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments" Water 8, no. 4: 119. https://doi.org/10.3390/w8040119
APA StylePanagos, P., Borrelli, P., Spinoni, J., Ballabio, C., Meusburger, K., Beguería, S., Klik, A., Michaelides, S., Petan, S., Hrabalíková, M., Olsen, P., Aalto, J., Lakatos, M., Rymszewicz, A., Dumitrescu, A., Perčec Tadić, M., Diodato, N., Kostalova, J., Rousseva, S., ... Alewell, C. (2016). Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments. Water, 8(4), 119. https://doi.org/10.3390/w8040119