1. Introduction
Flood disaster risk has become an increasingly important problem and a growing issue around the world. Since it continues to be at the top of the agenda for many cities, the development of sufficiently accurate and efficient flood modelling tools has become of utmost importance for many researchers and practitioners, and particularly for those dealing with mitigation of floods and flood-related disasters. Correspondingly, there is nowadays a range of modelling tools available for modelling floods, and hence, numerical modelling is at the heart of hydroinformatics [
1,
2].
Typically, one-dimensional (1D) hydrodynamic models have been used as a standard industry practice. More recently, however, model formulations have included two-dimensional (2D) representation of the floodplains. Since the physical process occurring on urban floodplains can be represented in different ways, the common assumption is that the predictive capability of different modelling approaches can also vary. These models describe free surface flow conditions by means of the shallow water equations (SWEs) [
3,
4]. A system of 2D SWEs is obtained by integrating the Navier Stokes equations over depth and replacing the bed stress by a velocity squared resistance term in the two orthogonal directions. Further simplification leads to 1D de Saint-Venant equations. The key assumptions used in de Saint-Venant equations are: uniform velocity distribution in the vertical direction, incompressible fluid, hydrostatic pressure distribution, and small bottom slope (e.g., [
5,
6,
7,
8,
9]). Since the 1D and 2D systems of equations contain nonlinear terms, analytical solutions are limited to simplified terms (see examples of analytical solutions in [
10,
11]) while numerical solutions are usually used [
5]. Numerical solutions of the SWEs equations are based on finite element (e.g., [
12]), finite volume (e.g., [
13]) or finite difference (e.g., [
14]) discretisations. Though finite volume method is becoming more popular within the research community, there are many popular commercial modelling packages that use finite difference methods (see [
15]).
Discretising SWE through time is possible in two ways: through explicit and implicit schemes (see a detailed description in [
5]). A main difference between these two schemes is a stability issue associated with using longer time steps. Explicit schemes are subject to time step limitations while implicit schemes are not, at least theoretically. For this, and some other reasons, commercial numerical modelling software such as MIKE11 [
16], MIKE21 [
17], TUFLOW classic 2D [
18], Flood Modeller pro 2D alternating direction implicit (ADI) solver [
19], InfoWorks RS [
20] and non-commercial software such as hydrologic engineering center’s river analysis system (HEC-RAS) [
21] solve the flow equations using implicit finite difference schemes. However, as described in [
22], discretising the full flow equations using implicit finite difference schemes is difficult to implement as it incurs complications in the application of boundary conditions in the case of supercritical and transcritical flows. They define the transcritical flow as phenomena with existence of supercritical and subcritical flows within the considered domain under unsteady conditions.
An option to address the boundary condition problem would be to ignore the convective acceleration terms (CATs) in the momentum equations of the flow equations. The basis for this assumption is that such terms are insignificant when compared to other terms that play role in urban floodplain flows, and therefore one boundary condition at each end (i.e., upstream and downstream) is provided and the same solution algorithm is used in both subcritical and supercritical flows. Furthermore, reduction of CATs reduces the complexity of equations and also the computational time (types of simplifications of SWEs are mentioned in [
10,
23]).
Some modelling packages make the assumption that the algorithm for subcritical flow does not change the structure but the non-linear CATs in the momentum equations are reduced to zero as Froude number approaches unity (e.g., the case of the MIKE11 hydrodynamic model). This gradual reduction of the CATs has also been implemented in [
24] to assess its effect on jump movement. In [
24], the authors implemented the reduction locally by multiplying the CAT with a reduction factor that is based on the Froude number of the flow.
However, some researchers argue that incorporating CATs for modelling urban floodplains is relevant. As mentioned in [
25], the flows generated in urban flood disasters are normally highly complex because the morphology of the urban surface is eminently artificial, with its highly irregular geometry, and it is often contrary to natural flow paths. Hence, frequently the urban flows are super-critical. In [
26,
27], it was also argued that in rapidly varied flow, the CATs become locally dominant. As a result, modelling flow conditions such as supercritical flow in steep channels and moving hydraulic jumps requires an appropriate implementation of the CATs (see also [
28]).
To better simulate supercritical flows in 1D, one approach was proposed in [
29] which partially reduced the CATs in the momentum equation. This was done by splitting the CAT and by reducing only part of it. In [
30], a modification was proposed in the scheme and its solution algorithm to solve the problem that the 4-point Preissmann scheme breaks down for transcritical flows. However, apart from indicating that it is physically incorrect, the authors have not undertaken further work to demonstrate the drawbacks of using modified governing flow equations by partially or completely removing CATs in simulating supercritical flows. Therefore, the present work provides a contribution in this direction and it attempts to compare the effects of reducing CATs in the 1D and 2D models in modelling supercritical and transcritical flow conditions. In our work, we used the following three methods for modelling 1D flows: MIKE11 flow model [
16], Kutija’s method (i.e., [
29]) and the Roe scheme [
31]; and two methods for modelling 2D flows: MIKE21 flow model [
17] and a non-inertia 2D model [
14]. These models were evaluated on hypothetical case studies which were conceived with the idea to represent urban floodplains. It is important to note that our intention in the present work is not to test these models in modelling different topographical features that may be found on urban floodplains (such examples can be found in our literature references) but rather to focus on how they perform in simulating supercritical and transcritical flows. Therefore, we prepared some typical cases which yield different flow conditions and carried out our model simulation work. Details of these models are further elaborated in the following sections.
3. Numerical Experiments and Discussion
3.1. 1D Experiments
Numerical experiments were conducted based on two unsteady flow tests for supercritical flow conditions—a channel with uniform cross-section, and a channel with contracted cross-section. Both tests were conducted for three channel bed slopes of = 0.01, = 0.02 and = 0.05.
Test 1 Prismatic Channel
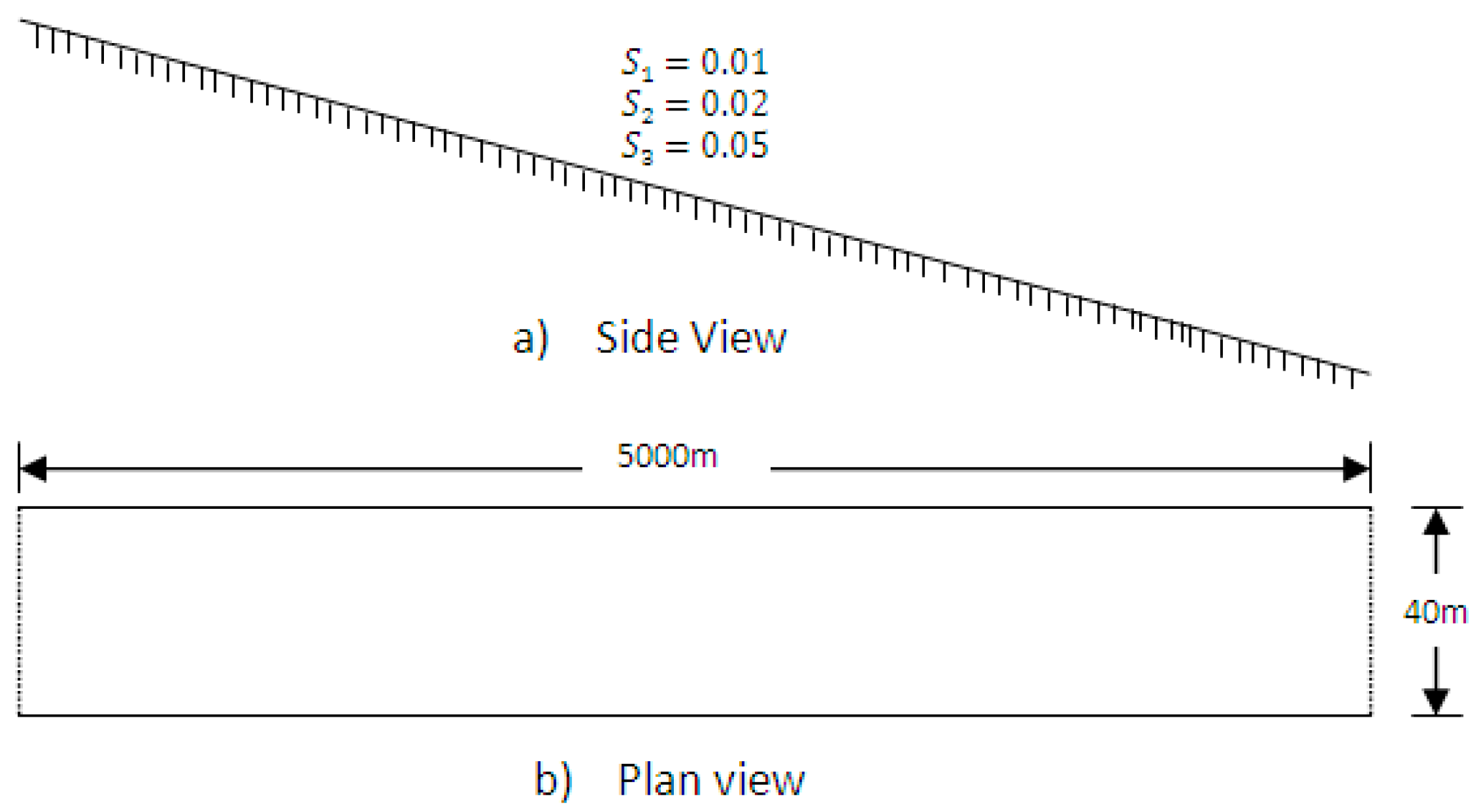
The hypothetical channel used for this test was a 5000-m long rectangular channel with a uniform cross-section with a width of 40 m throughout the length, as illustrated in
Figure 1. A Manning’s roughness coefficient of 0.035 was used for all sections of the channel. There are 101 channel cross-sections which were defined every 50 m. The time step used for the Roe method was a fixed time step of 5 s for the first two slopes and 2 s for the steepest slope. These were the maximum time steps that satisfied the Courant condition for the respective slopes. For the implicit methods, which do not require a strict Courant condition, an adaptive time step with a maximum of 20 s was used.
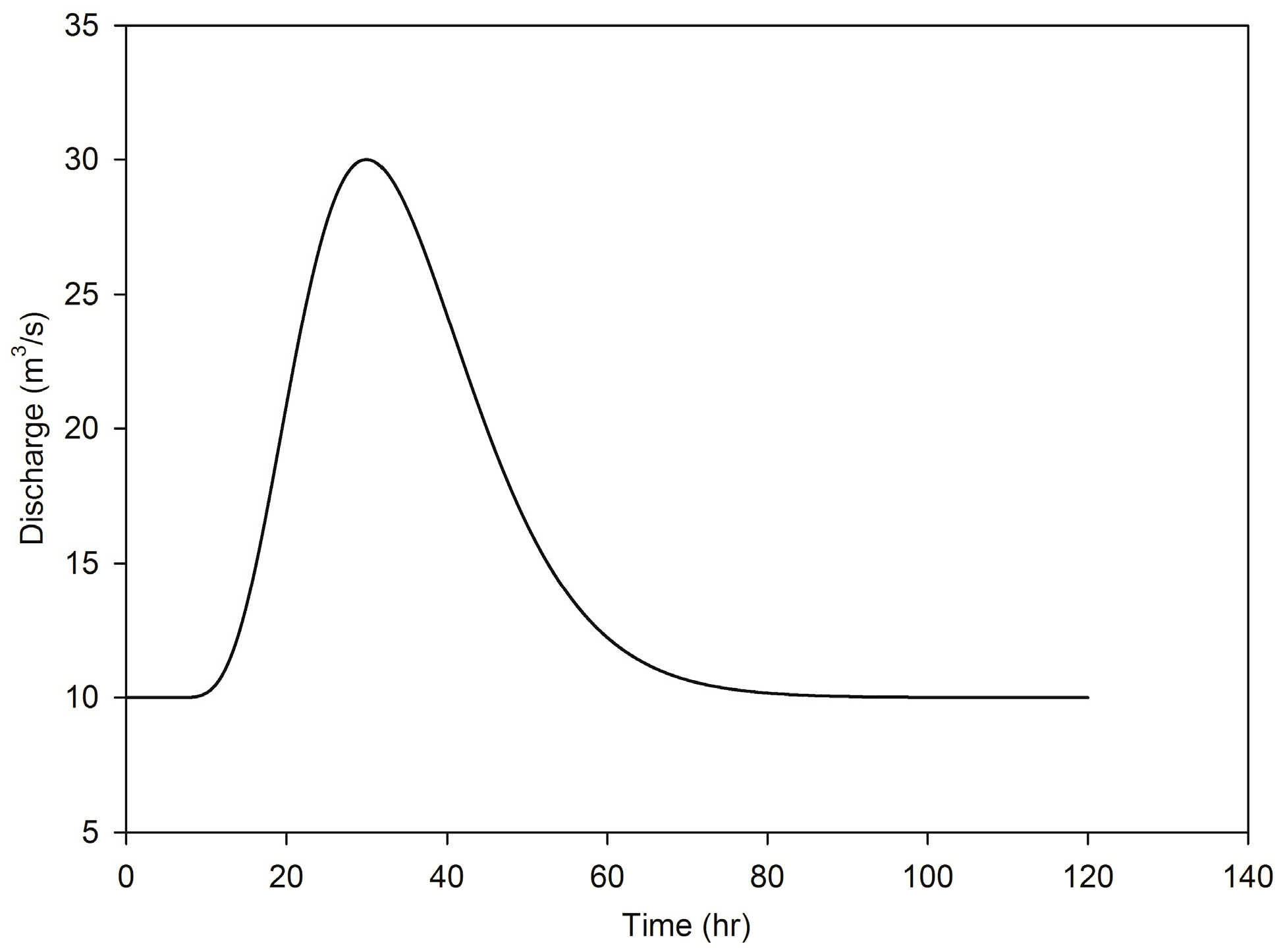
A discharge hydrograph shown in
Figure 2 was used as upstream boundary condition for all methods. The hydrograph has a peak of 30 m
3/s, base flow of 10 m
3/s and base period of 5 days. The downstream boundary condition used was a water depth based on uniform flow conditions, which was defined by the bottom slope and Manning’s
.
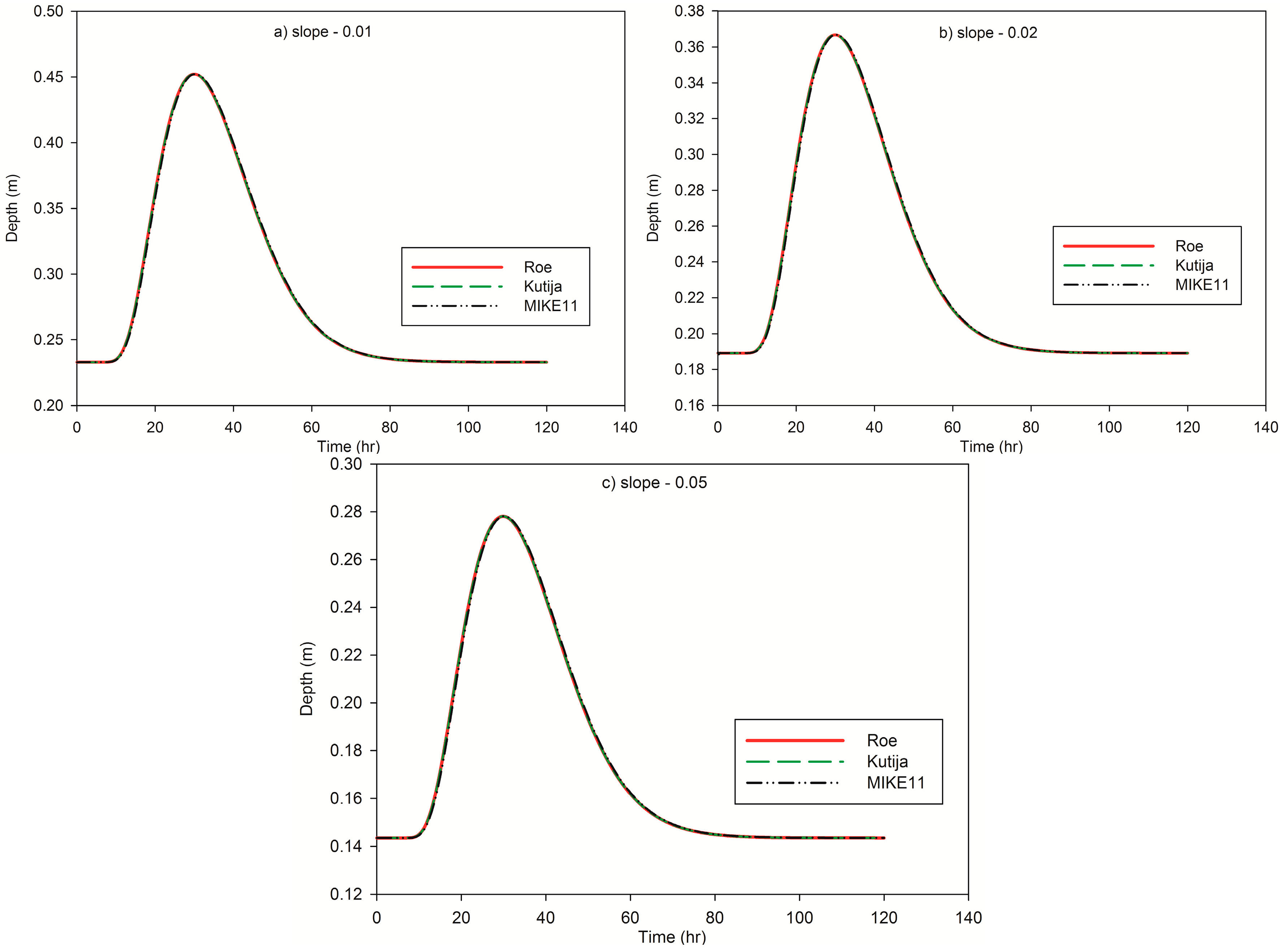
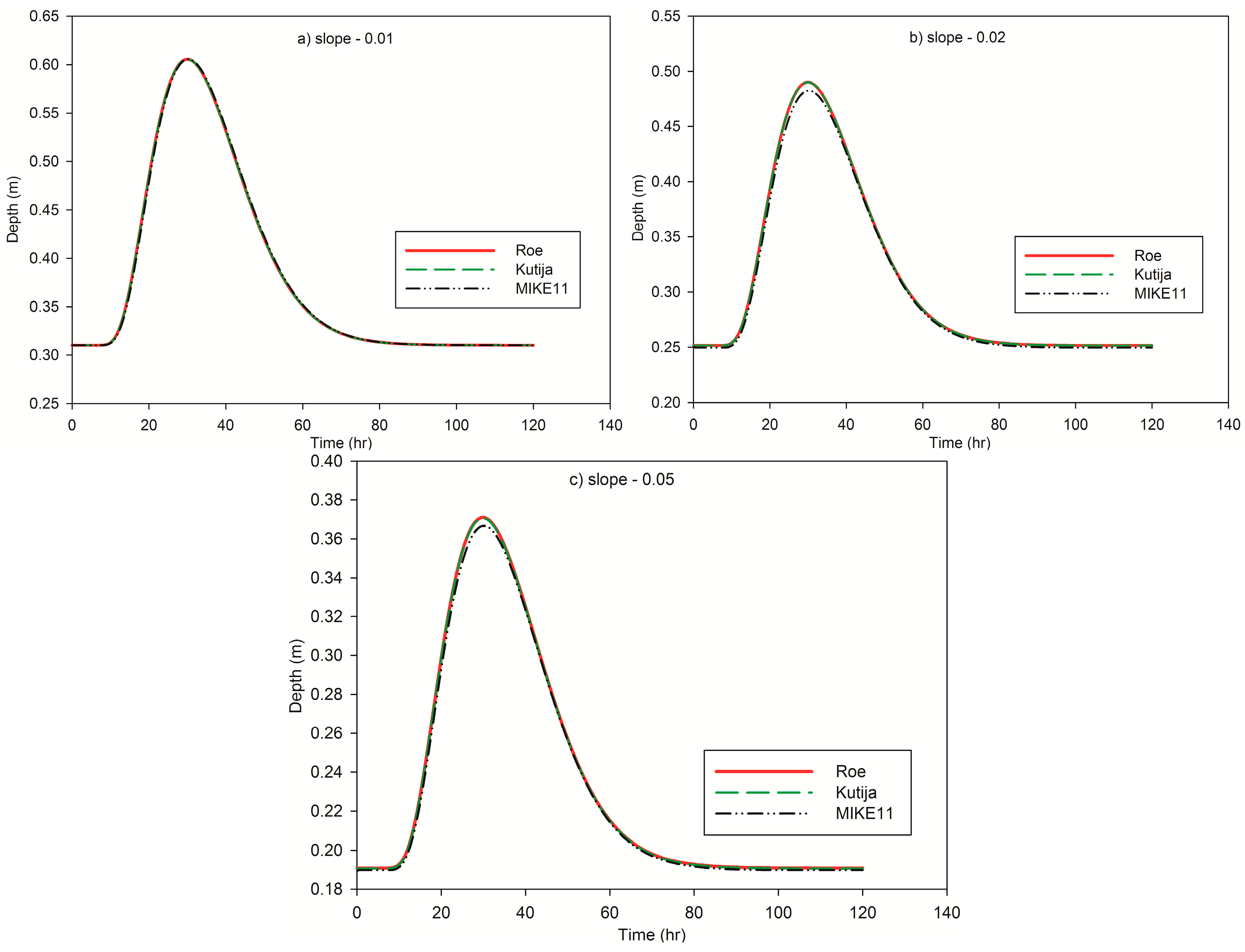
With more emphasis on flood depths, the depth outputs of the simulations are used as a means of comparison. The simulation results of the three methods at the centre of the channel (2500 m) are shown in
Figure 3 by graphical representation of water depths as a function of time. The first model run was for a channel of bed slope
. In that test, the Froude number varied from 0.71 to 0.79; hence a subcritical flow condition was observed. The second and third model runs were for slopes of
and
with Froude numbers of 0.97–1.08 and 1.47–1.63, respectively; hence supercritical flows. As shown in
Figure 3, at
= 2500 m, the water depths computed by the Kutija method and MIKE11 are the same as those of the Roe scheme for all slopes. Therefore, in this case, the SWEs with partially or totally reduced momentum equations computed the same result as the full SWEs in simulating supercritical flows. Moreover,
Figure 3 demonstrates that the time to peak depth is the same in all the three methods. This depicts that there was no phase error by the methods that reduced the convective acceleration term partially or completely in case of supercritical flows.
Considering the simulation time, the Kutija method and the Roe scheme take less than 4 min for the first two slopes. However, the explicit Roe scheme took twice the simulation time needed by the Kutija method for flows of high Froude number, in this case the third slope. MIKE11, on the other hand, registered the fastest computation time.
Test 2 Non-prismatic Channel (Contracted Cross-Section)
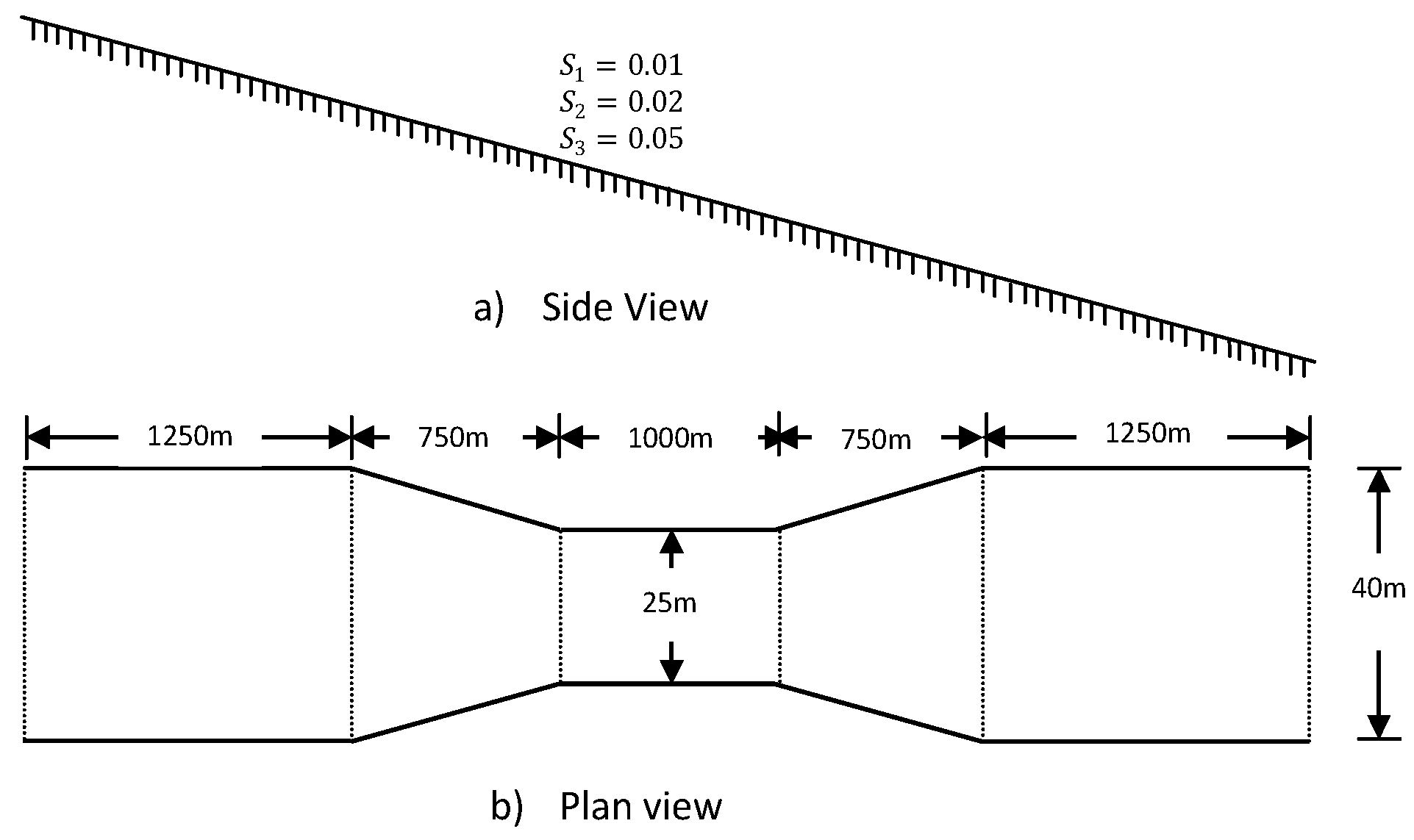
This case study was designed to test the capability of the methods in handling flows in contracted channel. The hypothetical channel used for this test was a 5000-m long rectangular channel with a contracted cross-section in which the widest sections had a width of 40 m and the narrowest were 25 m wide, as illustrated in
Figure 4. In a manner similar to the above channel, Manning’s
= 0.035 was used throughout the channel.
There were 101 computational points along the channel located at every 50 m. The time step used for the Roe method was a fixed time step of 2 s for all slopes, and for the rest of the methods an adaptive time step with a maximum of 20 s was used. The upstream boundary condition used in this test was the discharge hydrograph shown in
Figure 2. The downstream boundary condition used was a water depth based on uniform flow conditions, which is defined by the bottom slope and Manning’s
.
Figure 5 shows water depth simulation results for the three slopes at
= 2500 m. The first model run was for a channel of bed slope
in which the flow was subcritical (Froude number of 0.74 to 0.81). The second and third model runs were for slopes of
and
(Froude number of 1.01 to 1.12 and 1.54 to 1.70, respectively), which simulated supercritical flow conditions. The results show that the depth outputs from Kutija method and MIKE11 are very close to those of Roe scheme in all the three slopes (with only around 5 mm difference in the peak flood depth by MIKE11). Therefore, in this case as well, the SWEs with partially or completely reduced momentum equation give almost the same result as the full SWEs in simulating supercritical flows.
Figure 5 also demonstrates that the time to peak depth is the same in all the three methods, which indicates no phase error. Regarding computation time, this test case showed similar situation to Test 1—the explicit Roe scheme took almost double the time of the Kutija method while MIKE11 was the fastest.
3.2. 2D Experiments
For 2D experiments, we also conducted two steady flow tests for supercritical and transcritical flow conditions. However, in this case, both tests were conducted on channels with a uniform cross-section but one with a constant bed slope throughout the length and the other with variable bed slopes. To reproduce the different flow regimes, each test was conducted for three different Chézy channel bed resistance coefficients—, and . The non-inertia model was initialised with the dry bed; however, to guarantee stable model initialization, an initial condition of 8 cm water depth was used for the MIKE21 model set up. For both test cases, an upstream boundary condition of a steady 5 m3/s flow for a duration of one hour was used. As a downstream boundary condition, a normal depth boundary for subcritical flows and a critical depth boundary for critical and supercritical flows were used. In all experiments, a 1 m grid resolution and a time step of s were used.
Test 1 Prismatic channel with constant bed slope
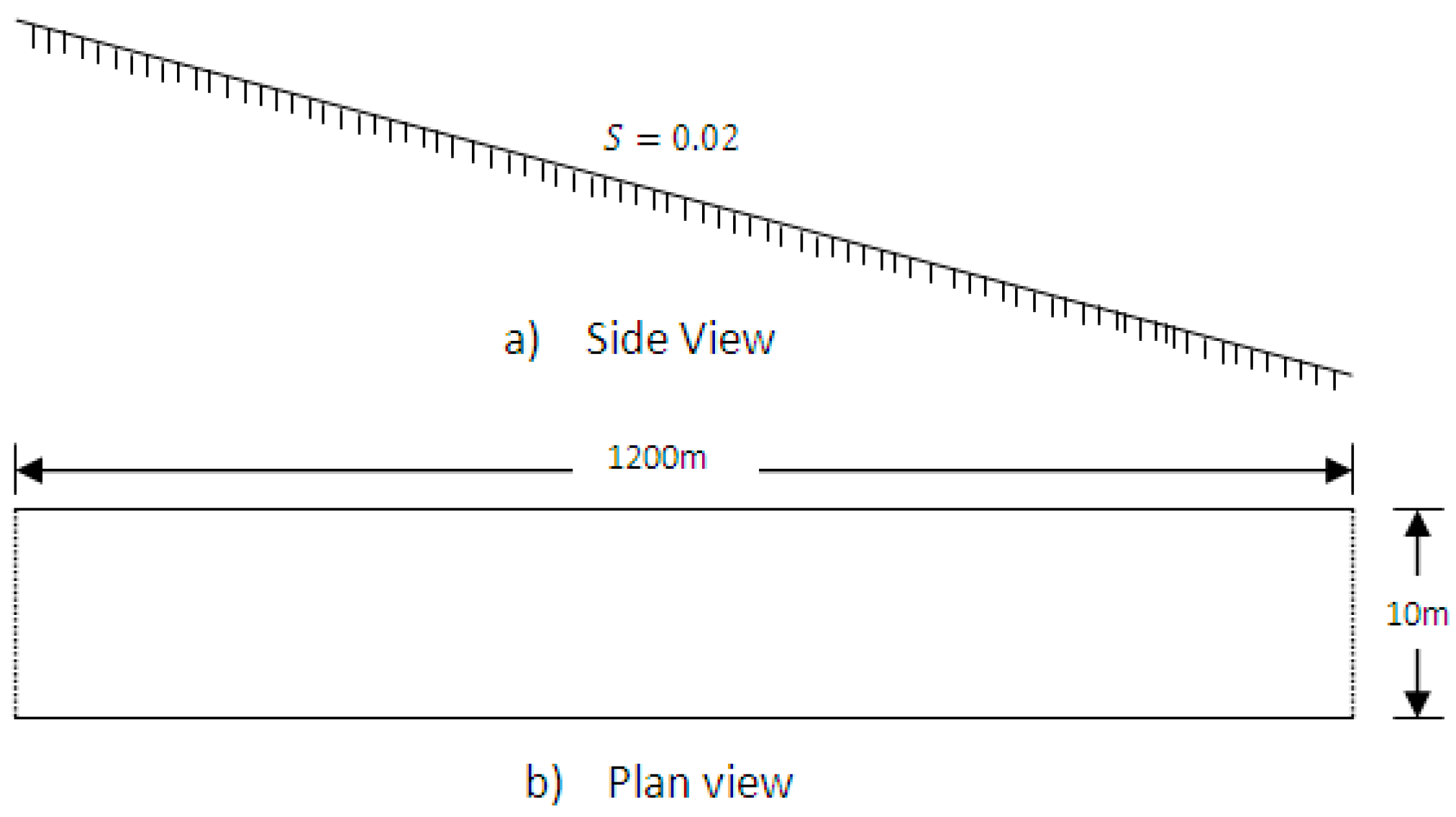
As shown in
Figure 6, a hypothetical prismatic channel 1200 m in length and 10 m in width was used for this test. The channel has a constant bed slope of
. The channel bed was made horizontal across the channel width. Therefore, the flow in that direction is insignificant.
Three simulations were carried out in this test (
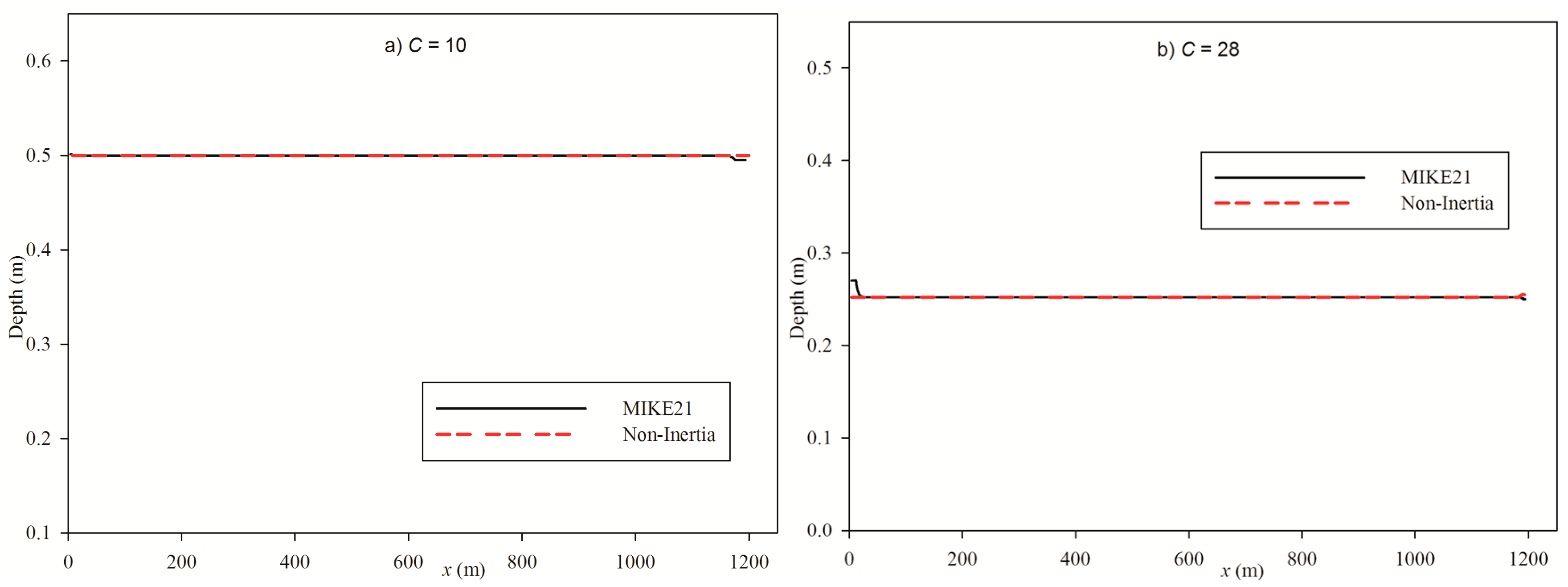
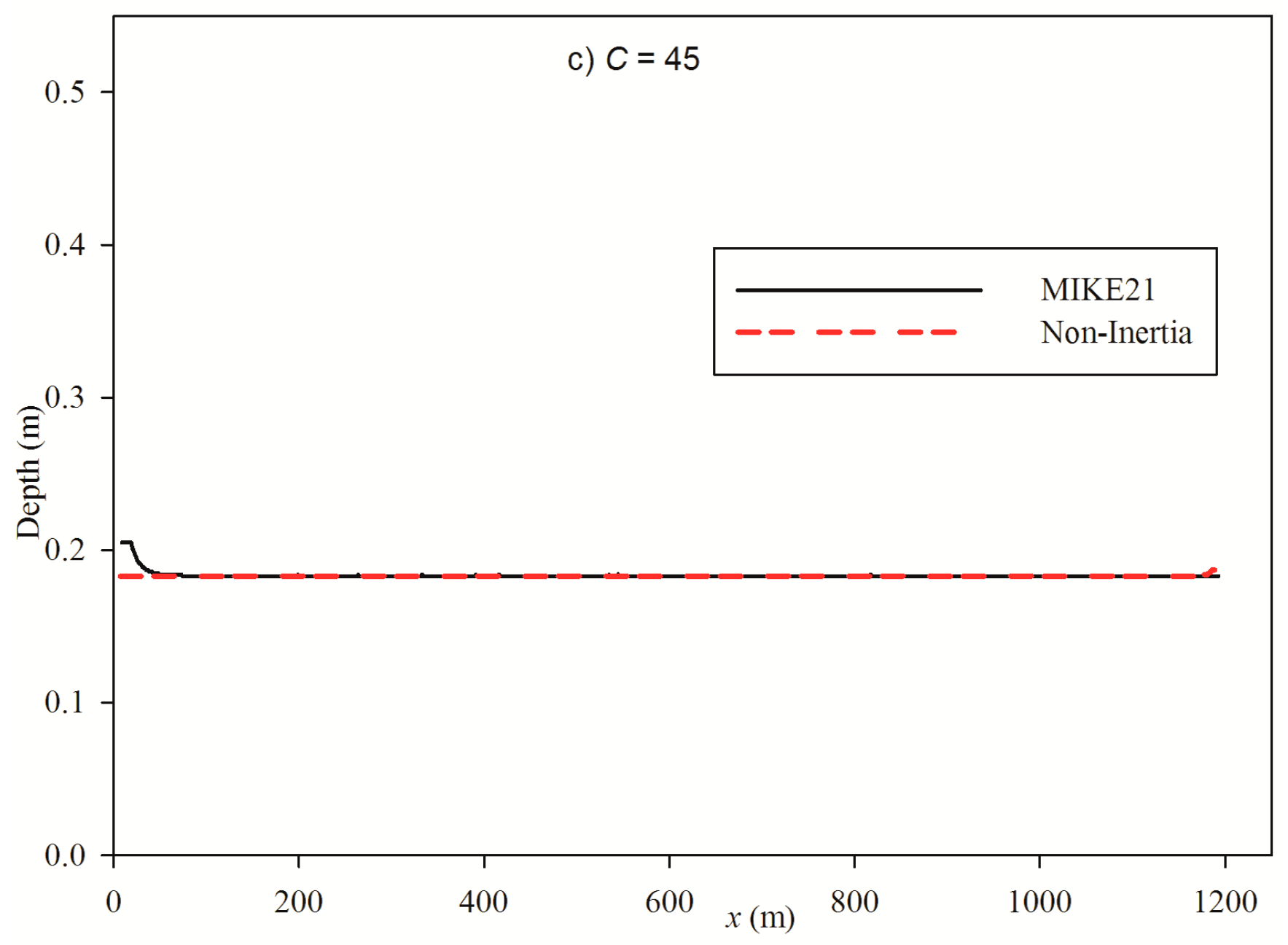
Table 1). The simulation with the lowest roughness coefficient of
was a subcritical flow. However, the other two flows showed Froude numbers greater than one, hence characterised as supercritical flow.
Simulation results of MIKE21 and non-inertia model setups show that even in supercritical flow conditions, the two models registered quite similar flow depths (
Figure 7b,c). The upstream and downstream depth results show disagreement and that is due to the boundary condition implementations of the two modelling software.
Test 2 Prismatic channel with variable bed gradient
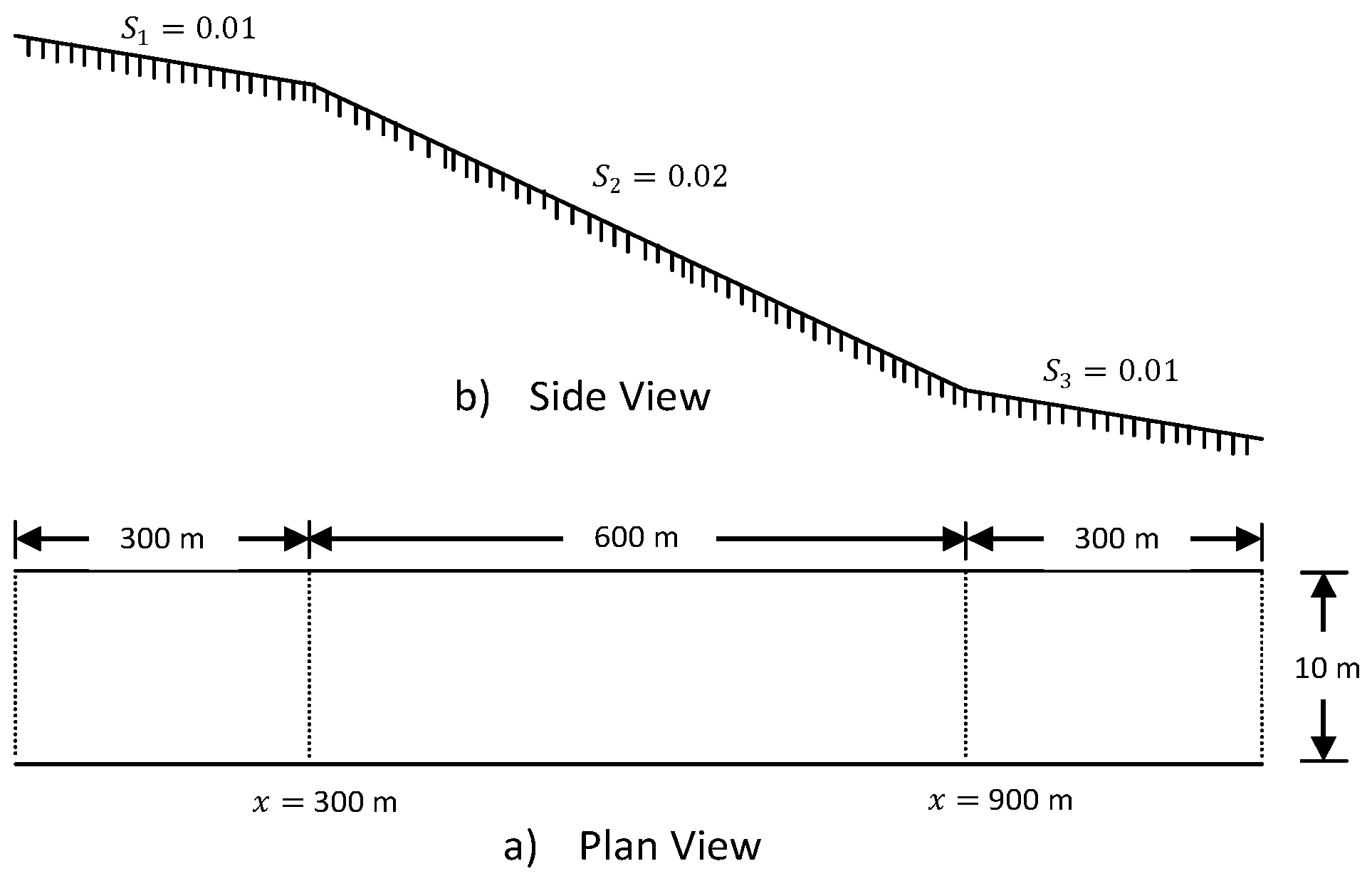
The second experiment was also conducted on a similar channel cross-section as the previous test. However, instead of having a uniform bed slope, the channel was divided in to three reaches of variable gradient (
Figure 8). The first and last 300-m reaches have bed slopes of
and
; whereas, the middle 600-m reach has a steeper bed slope of
. The experiment was designed to represent slope changes in streets of urban environment and also test how the numerical schemes handle flow regime changes. The channel bed was made horizontal across the channel width. Therefore, the flow in that direction is insignificant.
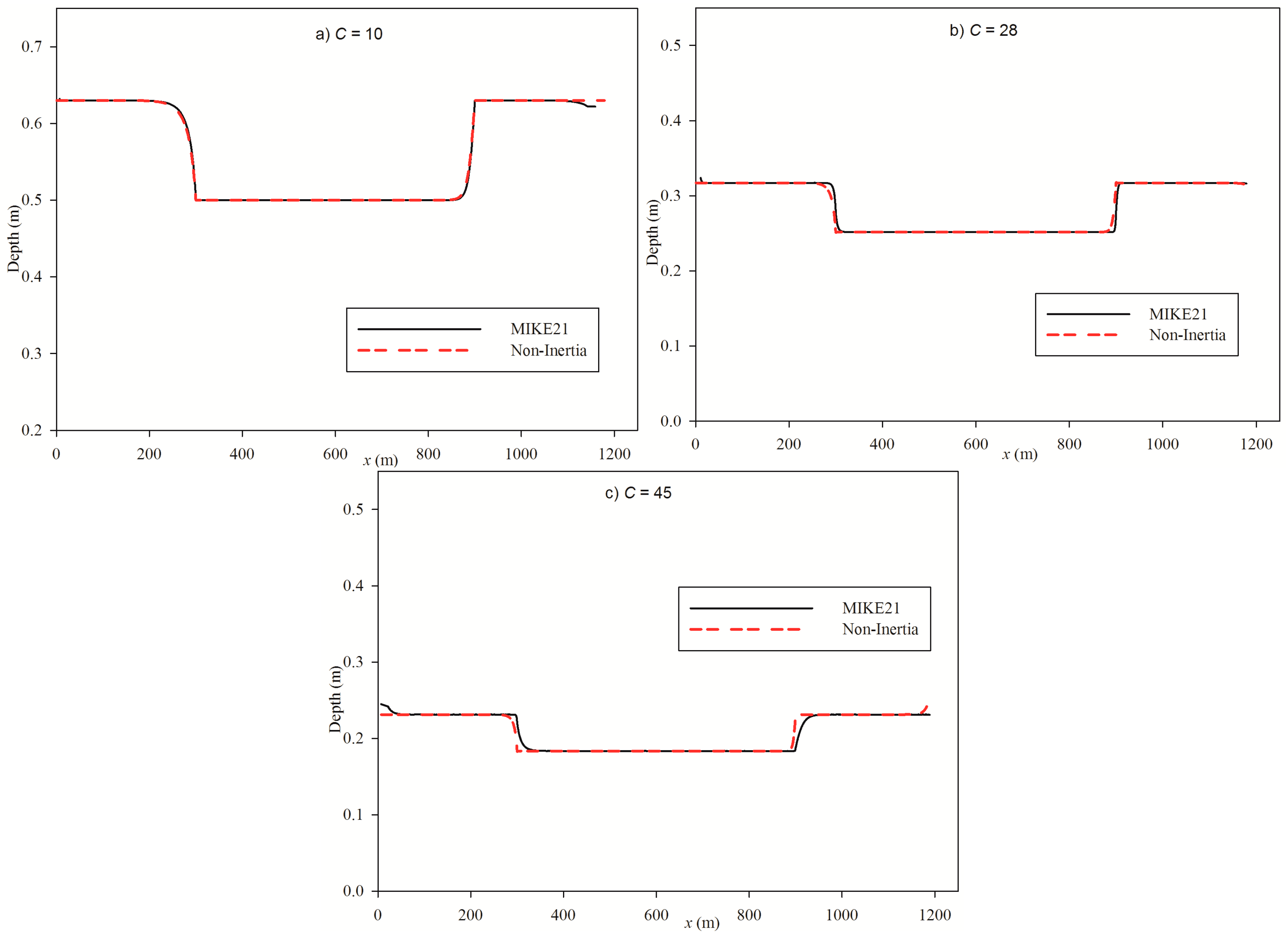
Once again, three simulations were conducted in this test (
Table 2). The first simulation with the lowest roughness coefficient showed a subcritical flow, while the last simulation with the highest roughness coefficient showed a supercritical flow condition in all the three reaches. However, the second simulation with
showed an interesting characteristic of mixed flows regimes—subcritical in the first and third reaches and supercritical in the steeper second reach.
In this test also, the model results in the three reaches showed very close flow depths not only in subcritical flow conditions, but also in mixed and pure supercritical flow conditions. In this case again, the discrepancies at the two ends were due to the implementation of boundary conditions by the modelling software.
In the hypothetical channel used in this test, the slope breaks at two points, marking critical and shock points (
m and
m respectively in
Figure 8). A closer look at these points in the depth outputs of
Figure 9 showed disagreement between the two types of modelling software. This disagreement increases as the roughness coefficient increases. For example, the difference between the two model outputs at the shock point was 0.05%, 12.40% and 19.00% for the respective roughness of
,
and
.
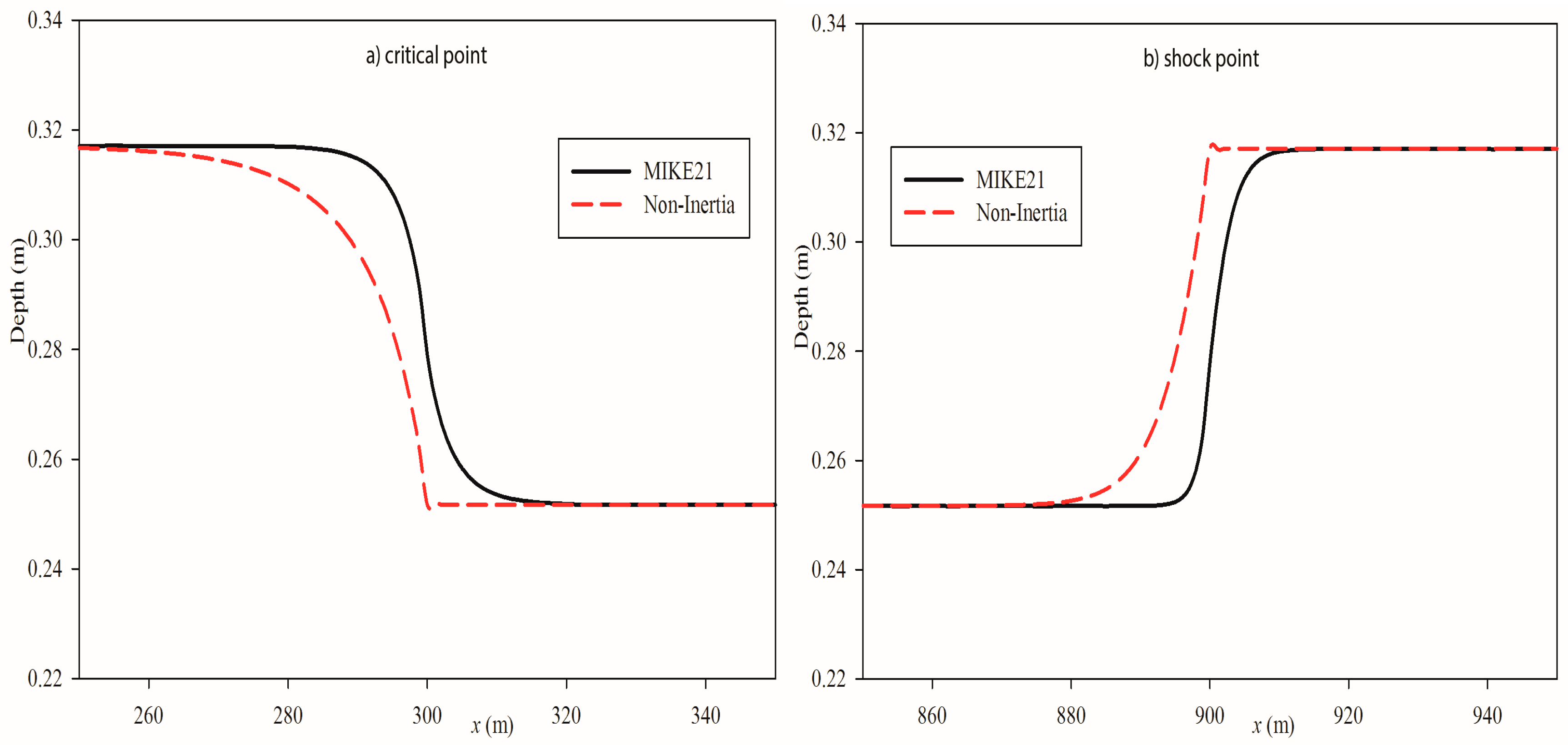
Figure 10 also shows zoomed profiles of the depths around critical and shock points for
(mixed-flow case). The critical points mark the transition from subcritical to supercritical and shock points from supercritical to subcritical. The figures demonstrate that the results of the two models were different around the two points. As mentioned above, the disagreements are close to these two points and the two types of modelling software showed similar results in the significant part of the reaches in all the three simulations. The same situation has also been experienced by [
33]. The authors in [
33] mentioned that even though flows in urban environments are characterized by flow transitions and numerical shocks, the effects are localized and did not appear to affect the overall wave propagation. As a result, in this case also, solving the 2D SWEs which completely ignore the CATs gives almost the same result as the full 2D SWEs (upwinded) in simulating pure supercritical and transcritical flows.
4. Conclusions
Flood disaster risk has been at the top of the agenda for many cities, and the development of sufficiently accurate and efficient flood modelling tools has become of the utmost importance for many researchers and practitioners, and particularly for those dealing with mitigation of floods and flood-related disasters. This comes with the necessity to address various drivers and scenarios such as urbanisation and land use change (e.g., [
34,
35]), population growth and climate change in rainfall patterns [
36]. The present work provides contribution in this direction as it attempts to compare the effects in reducing CATs in the 1D and 2D models in modelling supercritical and transcritical flow conditions. The following modelling methods were used in the present work: three 1D methods being MIKE11 flow model, Kutija’s method and Roe scheme; and two 2D methods: MIKE21 flow model and a non-inertia 2D model. All these models were evaluated with hypothetical case studies which were conceived with the idea to simulate different flow regimes and not to replicate a large variety of urban features. Therefore, the present paper did not aim to address issues in relation to modelling different topographical features that may be found on urban floodplains but rather it focuses on how they perform in simulating supercritical and transcritical flows.
In our case study work, the 1D model that partially reduces the convective acceleration term in the momentum equation of the SWEs gives results much closer to the results of the explicit Roe scheme, which solves the full SWEs. The results somehow go in line with the results obtained in [
29]. However, contrary to what the same author concluded, the MIKE11 model, which completely removes the CATs for supercritical flows, provided much closer results compared to the Roe scheme. For non-prismatic channels, care should be taken as MIKE11 underestimates outputs and this may become significant if the change in channel width is large. Apparently, considering the 1D test cases used in this paper, reducing the CATs does not imply a significant cost. Yet, this approximation may not hold in cases such as those of flows characterised by steep fronted wave.
In the 2D cases, the comparison of results showed that the differences are insignificant. This is particularly evident in the simulation of flows in channels with uniform bed gradient. The results suggest that modelling flat terrains does not gain many advantages from the presence of CATs while the computational time can be reduced significantly. However, in case of critical and shock points, the non-inertia model is likely to produce larger differences when compared to the model with the presence of CATs. This is to say that, if one is interested in designing hydraulic structures with breaks in bed gradient, then it may prove necessary to trace features such as hydraulic jumps with the use of the model that treats CATs and captures shocks more effectively. The same may also refer to the numerical modelling of dam breaks, tsunamis and reflected waves.
The overall conclusion from the present work is that modelling flows across floodplains (such as those evaluated in our experiments) does not always require full SWEs. One crucial point has then to be emphasised: success in applying non-inertia models will depend on the local characteristics, and the results obtained might be insignificantly different from the model which uses full SWEs, with the advantages of using one generic solution algorithm and a significant gain in computational time. The conclusions are based on the findings from the experiments carried out in the paper and to substantiate our findings, we will undertake further analysis in our future work.