Reservoir Routing on Double-Peak Design Flood
Abstract
:1. Introduction
2. Methods
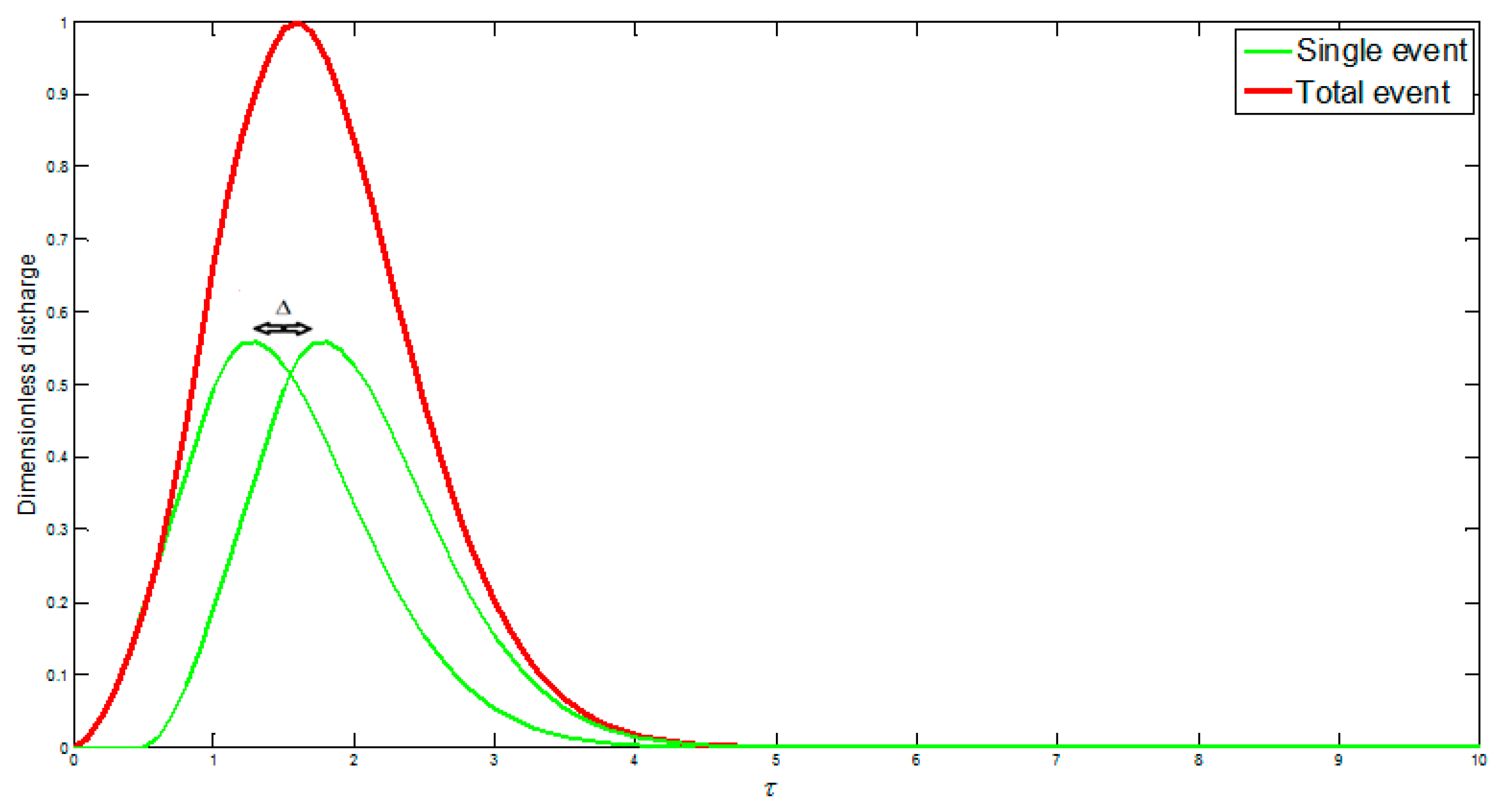
2.1. Dimensionless Double-Peak Flood
- (i)
- analytical definition of a double-peak design flood based on the fractal instantaneous unit hydrograph (FIUH) of a river network (i.e., [41]);
- (ii)
- numerical solution of the differential equation that describes the dimensionless water balance of the reservoir, aimed to estimate the reservoir RC as a function of the morphological characteristics of the valley, and the DC of the spillway;
- (iii)
- numerical determination of the “critical” temporal distance between two consecutive peaks of the design flood aimed to find the maximum water level.
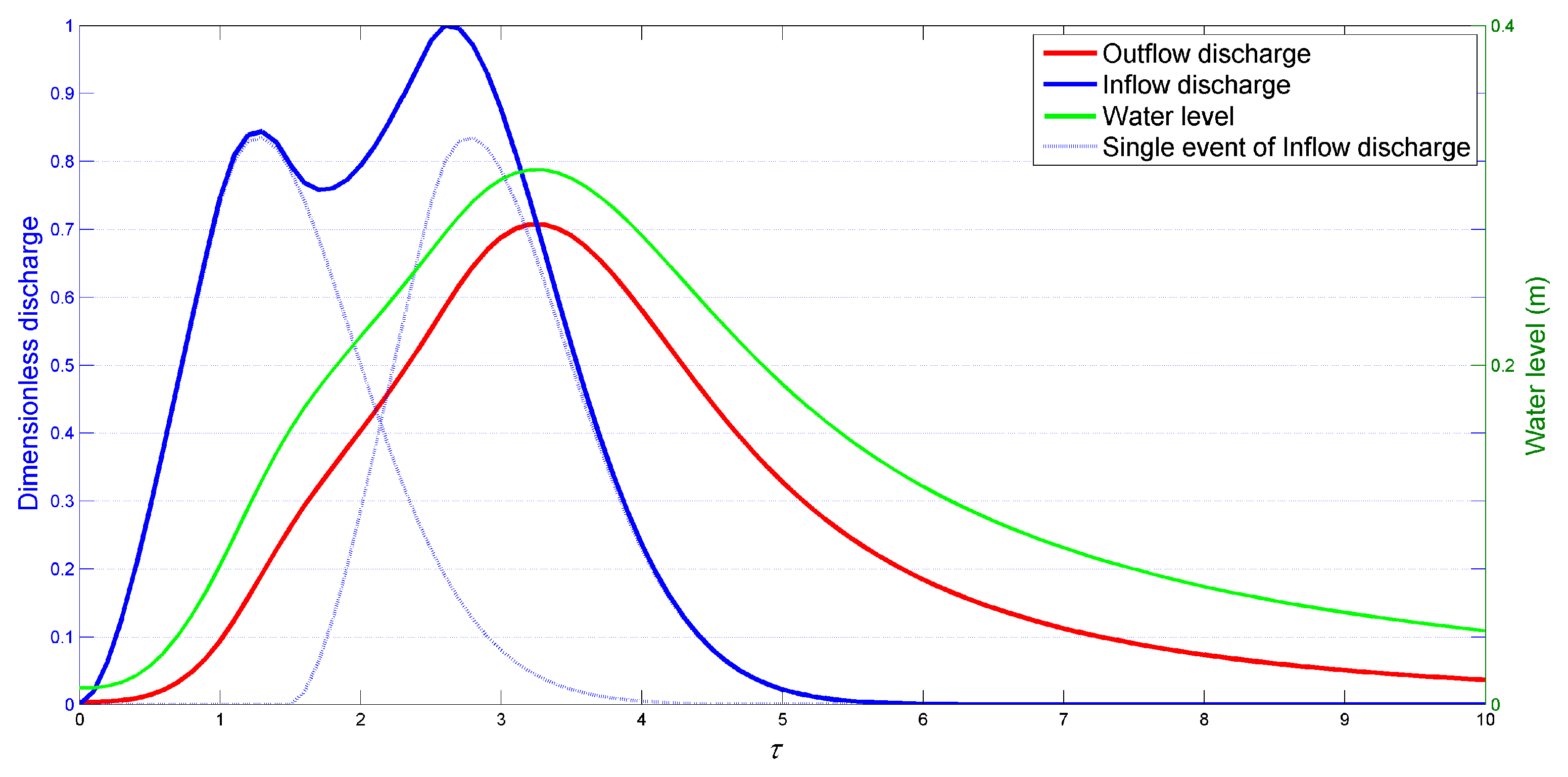
2.2. Dimensionless Reservoir Water Balance
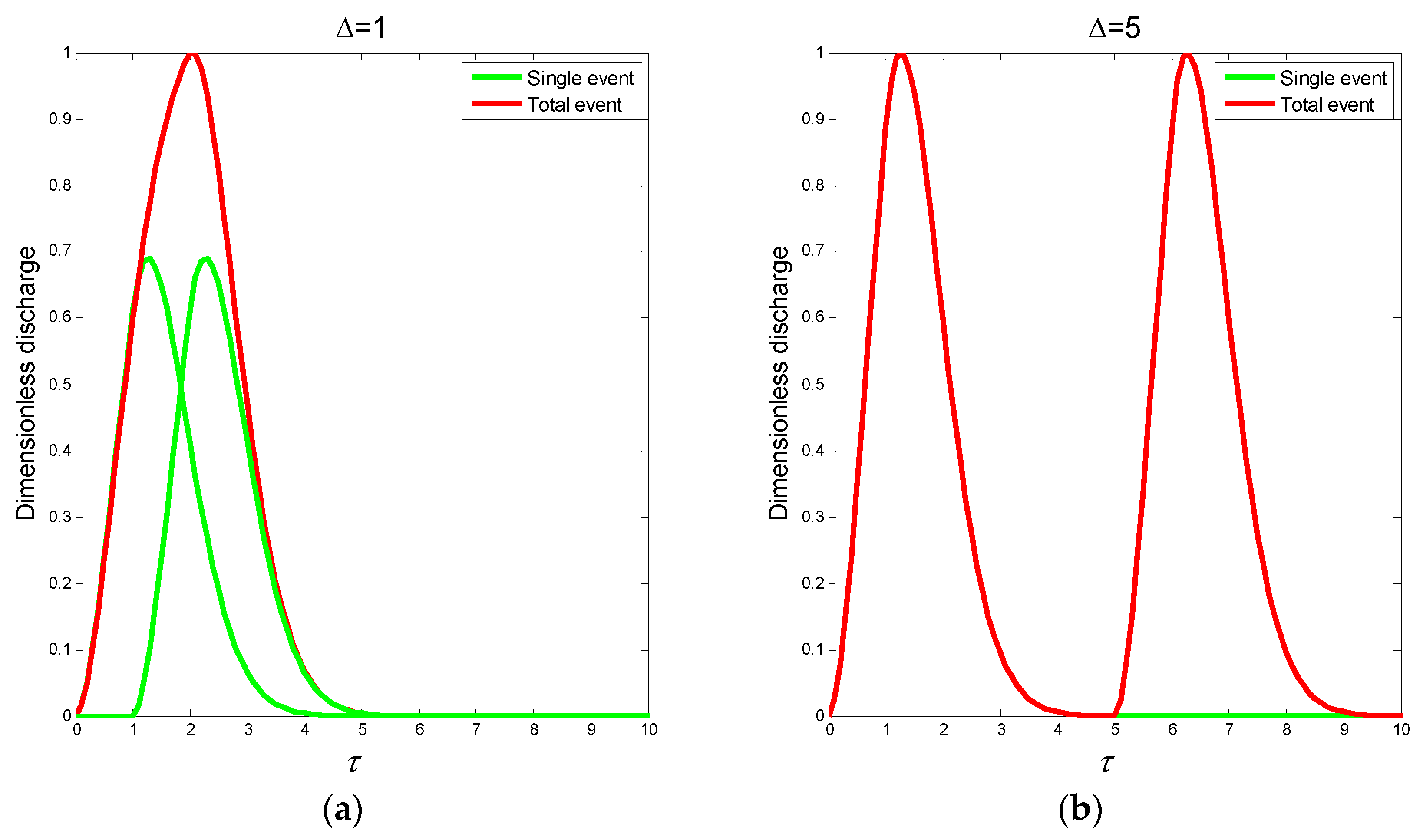
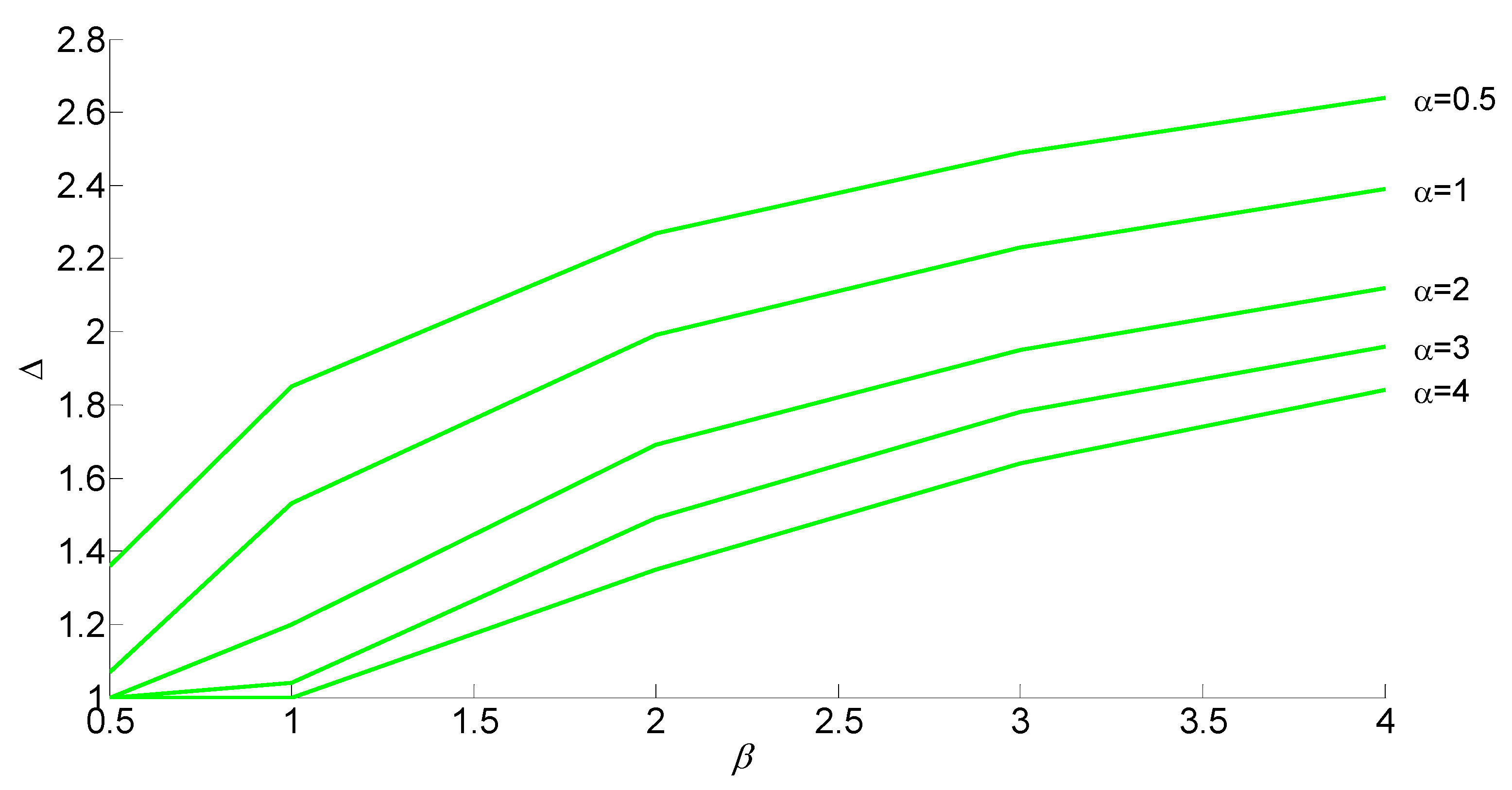
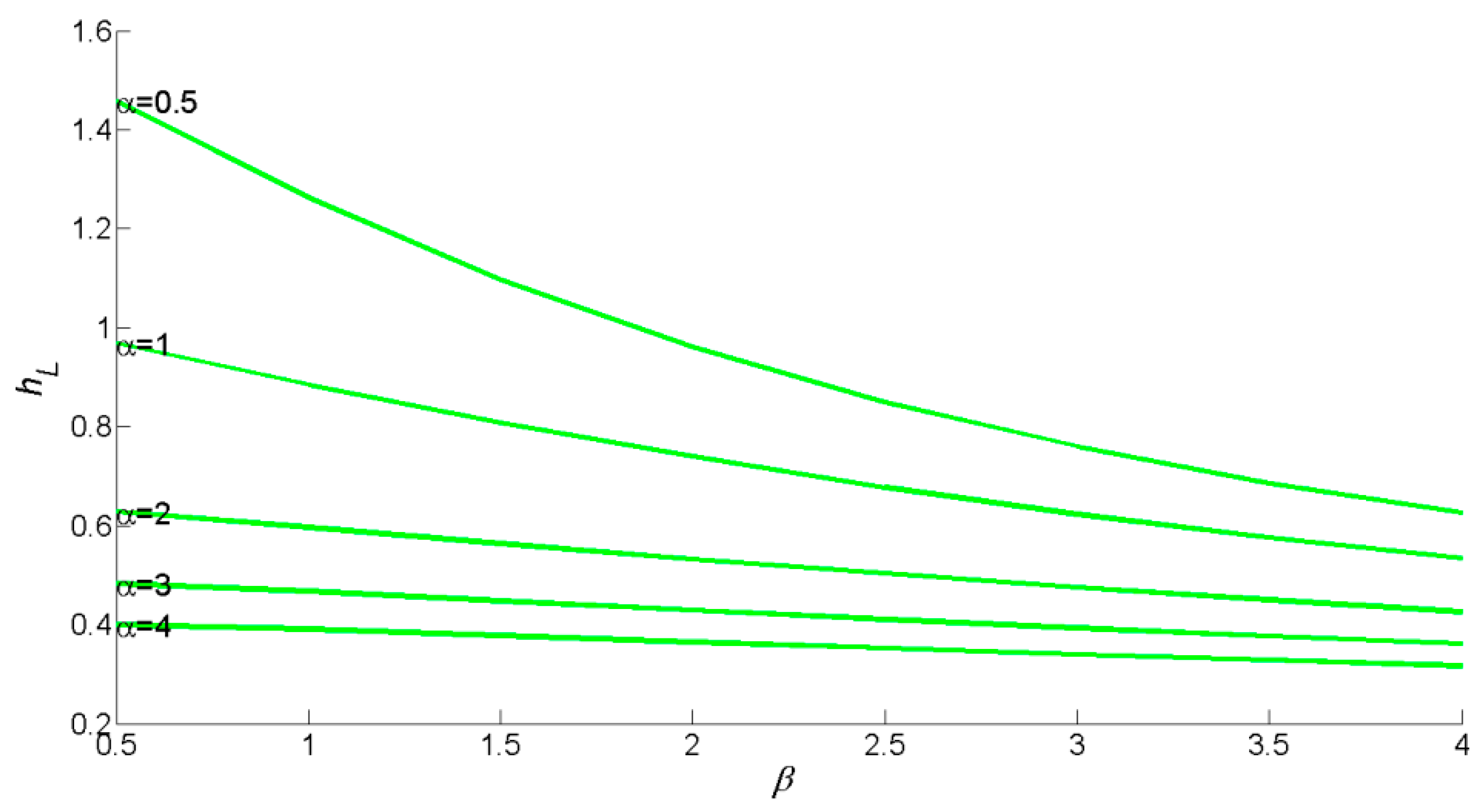
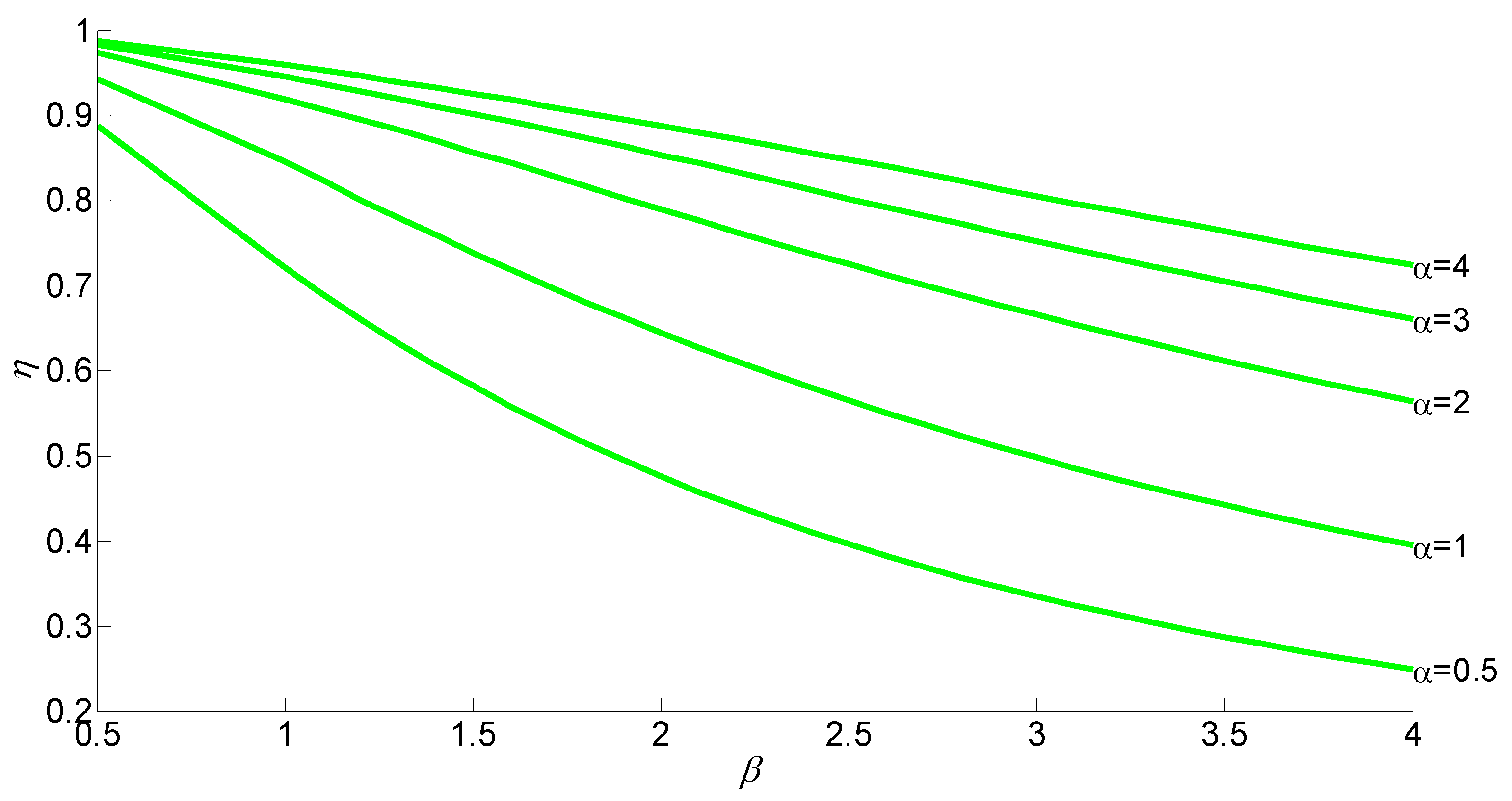
3. Evaluation of the Dimensionless Design Double-Peak Flood and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| RC | routing coefficient |
| SC | storage capacity |
| DC | discharge capacity |
| SFA | synthetic flood attenuation |
References
- Bagatur, T.; Onen, F. Computation of design coefficients in ogee-crested spillway structure using GEP and regression models. KSCE J. Civ. Eng. 2016, 20, 951–959. [Google Scholar] [CrossRef]
- Savage, B.; Johnson, M. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- U.S. Army Corp of Engineers (USACE). Hydraulic Design of Spillways; EM 1110-2-1603; Department of the Army: Washington, DC, USA, 1990. [Google Scholar]
- Gonzalez, C.A.; Chanson, H. Hydraulic Design of Stepped Spillways and Downstream Energy Dissipators for Embankment Dams. Dam Eng. 2007, 17, 223–244. [Google Scholar]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Flow Characteristics of Skimming Flows in Stepped Channels. J. Hydraul. Eng. 2004, 130, 860–869. [Google Scholar] [CrossRef]
- Johnson, M.; Savage, B. Physical and Numerical Comparison of Flow over Ogee Spillway in the Presence of Tailwater. J. Hydraul. Eng. 2006, 132, 1353–1357. [Google Scholar] [CrossRef]
- Graf, W.L. Downstream hydrologic and geomorphic effects of large dams on American rivers. Geomorphology 2006, 79, 336–360. [Google Scholar] [CrossRef]
- Cheng, C.T.; Chau, K.W. Flood control management system for reservoirs. Environ. Model. Softw. 2004, 19, 1141–1150. [Google Scholar] [CrossRef]
- Chang, L.C. Guiding rational reservoir flood operation using penalty-type genetic algorithm. J. Hydrol. 2008, 354, 65–74. [Google Scholar] [CrossRef]
- Magilligan, F.J.; Nislow, K.H. Changes in hydrologic regime by dams. Geomorphology 2005, 71, 61–78. [Google Scholar] [CrossRef]
- Collier, M.; Webb, R.H.; Schmidt, J.C. Dams and Rivers: Primer on the Downstream Effects of Dams; U.S. Geological Survey Circular; U.S. Geological Survey: Tucson, AZ, USA, 1996; Volume 1126, p. 94.
- Mediero, L.; Jiménez-Álvarez, A.; Garrote, L. Design flood hydrographs from the relationship between flood peak and volume. International Workshop. Hydrol. Earth Syst. Sci. 2010, 14, 2495–2505. [Google Scholar] [CrossRef]
- Klein, B.; Schumann, A.; Pahlow, M. Stochastic Generation of Hydrographs for the Flood Design of Dams. In Proceedings of the 3rd International Symposium on Integrated Water Resources Management, Ruhr-University Bochum, Bochum, Germany, 26–28 September 2006.
- Klein, B.; Pahlow, M.; Hundecha, Y.; Schumann, A. Probability Analysis of Hydrological Loads for the Design of Flood Control Systems Using Copulas. J. Hydrol. Eng. 2010, 15, 360–369. [Google Scholar] [CrossRef]
- Flores-Montoya, I.; Sordo-Ward, Á.; Mediero, L.; Garrote, L. Fully Stochastic Distributed Methodology for Multivariate Flood Frequency Analysis. Water 2016, 8, 225. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Micovic, Z.; Hartford, D.N.; Schaefer, M.G.; Barker, B.L. A non-traditional approach to the analysis of flood hazard for dams. Stoch. Environ. Res. Risk Assess. 2016, 30, 559–581. [Google Scholar] [CrossRef]
- Liu, D.; Xie, B.; Li, H. Design Flood Volume of the Three Gorges Dam Project. J. Hydrol. Eng. 2011, 16, 71–80. [Google Scholar] [CrossRef]
- Marone, V. Calcolo di massima dell’effetto di laminazione di un serbatoio sulle piene. L’energia Elettrica 1964, 41, 693–698. (In Italian) [Google Scholar]
- Marone, V. Calcolo di massima di un serbatoio di laminazione. L’Energia Elettrica 1971, 48, 561–567. (In Italian) [Google Scholar]
- Damiani, P.; Di Santo, A. Valutazione del volume di laminazione di un’onda di piena per il dimensionamento degli scarichi di superficie. Idrotecnica 1986, 4, 231–238. (In Italian) [Google Scholar]
- Scarrott, R.M.J.; Reed, D.W.; Bayliss, A.C. Indexing the attenuation effect attributable to reservoirs and lakes. In Statistical Procedures for Flood Frequency Estimation; Robson, A., Reed, D., Eds.; Flood Estimation Handbook; Centre for Ecology & Hydrology: Wallingford, UK, 1999; Volume 5, pp. 19–26. [Google Scholar]
- Piga, E.; Saba, A.; Salis, F.; Sechi, G.M. Distribuzione probabilistica delle portate massime annue laminate da un invaso con sfioratore superficiale. In Proceedings of the XXVII Convegno di Idraulica e Costruzioni Idrauliche, Genova, Italy, 12–15 September 2000; Volume 3, pp. 85–92. (In Italian)
- Miotto, F.; Laio, F.; Claps, P. Metodologie speditive per la valutazione dell’effetto di laminazione dei grandi invasi. In Proceedings of the XXX Convegno di Idraulica e Costruzioni Idrauliche, Roma, Italy, 10–15 September 2006. (In Italian)
- Pianese, D.; Rossi, F. Curve di possibilità di laminazione delle piene. Giornale Genio Civile 1986, 4–6, 131–148. (In Italian) [Google Scholar]
- Fiorentino, M.; Margiotta, M.R. La valutazione dei volumi di piena e il calcolo semplificato dell’effetto di laminazione di grandi invasi. In Proceedings of the XIV Corso di Aggiornamento Sulle Tecniche per la Difesa Dall’inquinamento, Cosenza, Italy, 28–30 June 1998. (In Italian)
- Fiorentino, M. La valutazione dei volumi di piena nelle reti di drenaggio urbano. Idrotecnica 1985, 3, 141–152. (In Italian) [Google Scholar]
- Montaldo, M.; Mancini, M.; Rosso, R. Flood hydrograph attenuation induced by a reservoir system: Analysis with a distributed rainfall-runoff model. Hydrol. Process. 2004, 18, 545–563. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Bacchi, B.; Grossi, G. Stima delle prestazioni di una vasca di laminazione: Confronto tra simulazioni continue e metodi analitico-probabilistici. In Proceedings of the XXXII Convegno Nazionale di Idraulica e Costruzioni Idrauliche, Palermo, Italy, 14–17 September 2010. (In Italian)
- Liu, P.; Guo, S.L.; Xiong, L.H.; Li, W.; Zhang, H.G. Deriving reservoir refill operating rules by using the proposed DPNS model. Water Resour. Manag. 2006, 20, 337–357. [Google Scholar] [CrossRef]
- Hsu, N.S.; Wei, C.C. A multipurpose reservoir real-time operation model for flood control during typhoon invasion. J. Hydrol. 2007, 336, 282–293. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsu, N.S. Optimal tree-based release rules for real-time flood control operations on a multipurpose multi reservoir system. J. Hydrol. 2009, 365, 213–224. [Google Scholar] [CrossRef]
- Mediero, L.; Garrote, L.; Martin-Carrasco, F. A probabilistic model to support reservoir operation decisions during flash floods. J. Hydrol. Sci. 2007, 52, 523–537. [Google Scholar] [CrossRef]
- Karbowski, A.; Malinowski, K.; Niewiadomska–Szynkiewicz, E. A hybrid analytic/rule-based approach to reservoir system management during flood. Decis. Support Syst. 2005, 38, 599–610. [Google Scholar] [CrossRef]
- Karaboga, D.; Bagis, A.; Haktanir, T. Controlling spillway gates of dams by using fuzzy logic controller with optimum rule number. Appl. Soft Comput. 2008, 8, 232–238. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evaluation of genetic algorithms for optimal reservoir system operation. J. Water Resour. Plan. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Akter, T.; Simonovic, S.P. Modeling uncertainties in short-term reservoir operation using fuzzy sets and a genetic algorithm. Hydrol. Sci. J. 2004, 49, 1081–1097. [Google Scholar] [CrossRef]
- Zahraie, B.; Kerachian, R.; Malekmohammadi, B. Reservoir operation optimization using adaptive varying chromosome length genetic algorithm. Water Int. 2008, 33, 380–391. [Google Scholar] [CrossRef]
- Negede, A.K.; Horlacher, H.B. Approaches for Dam Overtopping Probability Evaluation. In Proceedings of the 33rd IAHR Congress: Water Engineering for a Sustainable Environment, Vancouver, BC, Canada, 9–14 August 2009.
- Castorani, A.; Piccinni, A.F. The influence of a runoff hydrograph in reservoir routing. In Proceedings of the Fifth Congress Asian and Pacific Regional Division of the International Association for Hydraulic Research, Seoul, Korea, 18–20 August 1986.
- Fiorentino, M.; Oliveto, G.; Rossi, A. Alcuni aspetti del controllo energetico ed idrologico sulla geometria delle reti e delle sezioni fluviali. Parte Prima: Controllo idrologico. In Proceedings of the XXVIII Convegno di Idraulica e Costruzioni Idrauliche, Potenza, Italy, 16–19 September 2002. (In Italian)
- Veneziano, D.; Iacobellis, V. Self-Similarity and Multifractality of Topographic Surfaces at Basin and Sub-Basin Scales. J. Geophys. Res. 1999, 104, 12797–12813. [Google Scholar] [CrossRef]
- Claps, P.; Oliveto, G. Re-examining the determination of the fractal dimension of river networks. Water Resour. Res. 1996, 32, 3123–3135. [Google Scholar] [CrossRef]
- Fiorentino, M.; Rossi, F.; Villani, P. Effect of the basin geomorphoclimatic characteristics on the mean annual flood reduction curve. In Proceedings of the 18th Annual Conference on Modeling and Simulation, Pittsburgh, PA, USA, 23–24 April 1987; pp. 1777–1784.
- Iacobellis, V.; Fiorentino, M. Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 2000, 36, 469–482. [Google Scholar] [CrossRef]
- Fiorentino, M.; Gioia, A.; Iacobellis, V.; Manfreda, S. Regional analysis of runoff thresholds behavior in Southern Italy based on theoretically derived distributions. Adv. Geosci. 2011, 26, 139–144. [Google Scholar] [CrossRef]
- Gioia, A.; Iacobellis, V.; Manfreda, S.; Fiorentino, M. Influence of infiltration and soil storage capacity on the skewness of the annual maximum flood peaks in a theoretically derived distribution. Hydrol. Earth Syst. Sci. 2012, 16, 937–951. [Google Scholar] [CrossRef]
- Iacobellis, V.; Castorani, A.; Di Santo, A.R.; Gioia, A. Rationale for flood prediction in karst endorheic areas. J. Arid Environ. 2015, 112, 98–108. [Google Scholar] [CrossRef]
- Iacobellis, V.; Claps, P.; Fiorentino, M. Climatic control on the variability of flood distribution. Hydrol. Earth Syst. Sci. 2002, 6, 229–237. [Google Scholar] [CrossRef]
- Fac-Beneda, J. Fractal structure of the Kashubian hydrographic system. J. Hydrol. 2013, 488, 48–54. [Google Scholar] [CrossRef]
- De Bartolo, S.G.; Gaudio, R.; Gabriele, S. Multifractal analysis of river networks: Sandbox approach. Water Resour. Res. 2004, 40, 183–188. [Google Scholar] [CrossRef]
- Donadio, C.; Magdaleno, F.; Mazzarella, A.; Kondolf, G.M. Fractal Dimension of the Hydrographic Pattern of Three Large Rivers in the Mediterranean Morphoclimatic System: Geomorphologic Interpretation of Russian (USA), Ebro (Spain) and Volturno (Italy) Fluvial Geometry. Pure Appl. Geophys. 2015, 172, 1975–1984. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gioia, A. Reservoir Routing on Double-Peak Design Flood. Water 2016, 8, 553. https://doi.org/10.3390/w8120553
Gioia A. Reservoir Routing on Double-Peak Design Flood. Water. 2016; 8(12):553. https://doi.org/10.3390/w8120553
Chicago/Turabian StyleGioia, Andrea. 2016. "Reservoir Routing on Double-Peak Design Flood" Water 8, no. 12: 553. https://doi.org/10.3390/w8120553
APA StyleGioia, A. (2016). Reservoir Routing on Double-Peak Design Flood. Water, 8(12), 553. https://doi.org/10.3390/w8120553






