Abstract
Land surface characteristics, including soil type, terrain slope, and antecedent soil moisture, have significant impacts on surface runoff during heavy precipitation in highly urbanized areas. In this study, a Linear Spectral Mixture Analysis (LSMA) method is modified to extract high-precision impervious surface, vegetation, and soil fractions. In the modified LSMA method, the representative endmembers are first selected by combining a high-resolution image from Google Earth; the unmixing results of the LSMA are then post-processed to reduce errors of misclassification with Normalized Difference Built-up Index (NDBI) and Normalized Difference Vegetation Index (NDVI). The modified LSMA is applied to the Landsat 8 Operational Land Imager (OLI) image from 18 October 2015 of the main urban area of Guangzhou city. The experimental result indicates that the modified LSMA shows improved extraction performance compared with the conventional LSMA, as it can significantly reduce the bias and root-mean-square error (RMSE). The improved impervious surface, vegetation, and soil fractions are used to calculate the composite curve number (CN) for each pixel according to the Soil Conservation Service curve number (SCS-CN) model. The composite CN is then adjusted with regional data of the terrain slope and total 5-day antecedent precipitation. Finally, the surface runoff is simulated with the SCS-CN model by combining the adjusted CN and real precipitation data at 1 p.m., 4 May 2015.
1. Introduction
With the rapid process of urbanization, the portion of impervious area has significantly increased and the urban pervious surface including forest, green land, bare soil, and wetland has decreased, which may lead to a high risk of urban rainstorm waterlogging [1]. Therefore, it is very important to quantitatively model the relationship between rainfall-runoff and different land use conditions [2]. This has significant importance and has fundamental influence on urban planning, urban management, exploitation, and utilization of water resources [3].
The Soil Conservation Service curve number (SCS-CN) was developed by the United States Department of Agriculture Natural Resources Conservation Service (NRCS) [4]. Because of its simplicity and operability, the SCS-CN model, with only a few data requirements [5], has been widely applied for surface runoff estimation [6,7,8,9,10]. Currently, the SCS-CN model has been integrated into many widely used hydrological models to simulate surface runoff, including the Soil and Water Assessment Tool (SWAT) [11], the Long-term Hydrologic Impact Assessment (L-THIA) [12], the Hydrologic Modeling System (HEC-HMS) [13], the Erosion Productivity Impact Calculator (EPIC) [14], and the Agricultural Non-point Source Pollution Model (AGNPS) [15]. Rejani et al. [16] used the SCS-CN model to estimate the daily runoff in a semi-arid microwatershed of Warangal district in Southern India in combination with Geographic Information System (GIS) data. Suribabu and Bhaskar [17] evaluated the urban growth effects on surface runoff by combining the SCS-CN and Green-Ampt infiltration models, which revealed that land cover/use change showed more significant impact for longer duration storms than shorter duration storms of the same magnitude. Yao et al. [3] selected the SCS-CN method to simulate the surface runoff potentials within different urban functional zones in Beijing with the aid of GIS and remote sensing (RS) technology. Kowalik and Walega [18] claimed that the errors in CN affect the surface runoff calculation to a much greater extent than errors in the storm rainfall. These works showed that the runoff curve number (CN) in the SCS-CN model is greatly affected by land use, soil conservation measures, land use cover, terrain slope, and antecedent moisture conditions [19,20].
Therefore, based on local and regional data, the SCS-CN model was modified to improve surface runoff simulation [2,21,22,23,24]. Soulis et al. [25] investigated the SCS-CN applicability in partial area watersheds, and Soulis and Valiantzas [26,27] proposed an improved method for the CN estimation in watersheds with high spatial variability. Grunwald and Norton [28] showed that the simulation results for uncalibrated SCS-CN parameters underestimated the observed surface runoff using the Agricultural Non-Point Source Pollution Model (AGNPS), and the results for calibrated AGNPS were better than the uncalibrated results. Adjusting the antecedent moisture conditions in the SCS-CN model may be used to improve surface runoff simulation. However, the CN is highly dependent on the local and regional land characteristics. Thus, Ludlow [29] and Fan et al. [30] developed a method to calculate the composite CN by integrating a Linear Spectral Mixture Analysis (LSMA) method. The LSMA method was used to estimate the impervious surface, vegetation, and soil fractions. Some previous studies showed that the use of the area-weighted average composite CN values only may introduce significant errors in surface runoff estimates and underestimate surface runoff, especially for small size storms [27,31,32,33]. Grove et al. [33] also have documented that there was no significant difference in runoff computed using composite and distributed CNs for large storms. Zhang et al. [34] and Fan et al. [30] have applied the composite CN to estimate urban surface runoff with remote sensing imagery in Dongguan and Guangzhou cities. The Pearl River Delta is frequently struck by the heavy rainstorms, which may result in urban waterlogging. Therefore, the composite CN may be used in surface runoff estimates in this study. However, the composite CN method of Ludlow [29] and Fan et al. [30] was highly dependent on the accuracy of the impervious surface, vegetation, and soil fractions.
The conventional LSMA method can decompose the reflectance of a mixed pixel into different proportions, which was widely used to quantitatively extract the impervious surface, vegetation, and soil fractions from remote sensing images [35,36,37]. However, because of similar spectral responses among the land cover types, the conventional LSMA still has certain difficulty in the accurate extraction of the impervious surface, vegetation, and soil fractions. Therefore, some modified LSMA methods were proposed and applied in the extraction of impervious surface, vegetation, and soil fractions [38,39]. Ma et al. [40] proposed a two-step constrained nonlinear spectral mixture analysis (SMA) method for improving the estimation of soil and vegetation fractions. Li et al. [41] explored a segmentation-based and rule-based SMA method for estimating urban imperviousness in the Milwaukee River Watershed with a Landsat Thematic Mapper (TM) image. The results indicate that this method may achieve higher estimation accuracy than the traditional SMA method. The endmember class selection is an important step in implementing SMA. However, little attention was paid to the selection of an appropriate number or appropriate types of endmember classes [42]. Li and Wu [42] incorporated land use/land cover probability data into endmember class selections for temporal mixture analysis. In the urban areas, researchers are more concerned with impervious surface data. In general, the impervious surface fraction may be estimated by the addition of low-albedo and high-albedo fraction images resulting from the LSMA method [43,44]. However, low-albedo and high-albedo fractions may relate to the pervious surfaces, including tree, grass, and dry soil [45,46]. Therefore, Fan et al. [46] proposed a modified LSMA method by integrating the spectral indices, including the Normalized Difference Built-up Index (NDBI), the Normalized Difference Bare-soil Index (NDBaI), and albedo. These spectral indices were used to remove pervious pixels in the low-albedo and high-albedo fraction images by establishing thresholds for each index. The results indicated that the modified LSMA method could enhance the accuracy of urban impervious surface estimation. However, they only focused on improving the impervious surface fraction, not including the improvement of the soil and vegetation fractions. The impervious surface, vegetation, and soil fraction images are required to estimate surface runoff with the SCS-CN model modified by Fan et al. [30], which determines the precision of surface runoff simulation.
In this study, we proposed a modified LSMA method to extract the impervious surface, vegetation, and soil fractions in the main region of Guangzhou, China, by combining a high-resolution image from Google Earth, the NDBI, and the Normalized Difference Vegetation Index (NDVI). The high-precision impervious surface, vegetation, and soil fractions can be then integrated into the SCS-CN model of Fan et al. [30] to simulate surface runoff. The goal of this study is to improve the CN in simulating surface runoff, which includes: (1) modifying the conventional LSMA with a high-resolution image, the NDBI, and NDVI to extract the high-quality impervious surface, vegetation, and soil fractions of each pixel; (2) calculating the composite CN for each pixel based on the unmixing results of the modified LSMA; (3) adjusting the CN with the regional terrain slope and antecedent soil moisture; and (4) simulating the surface runoff in the main urban area of Guangzhou city during the precipitation of 1 p.m., 4 May 2015.
2. Study Area and Data
2.1. Study Area
Guangzhou, the core city of the Pearl River Delta, is located in the south central Guangdong province, and is the political, economic, and cultural center of the Guangdong province. The study area contains the Liwan, Yuexiu, Haizhu, Tianhe, and Huangpu districts (Figure 1). Situated in the coastal subtropical zones, it has a subtropical monsoon climate with plenty of rainfall. The annual average temperature is around 20–22 °C and the annual rainfall reaches 1720 mm. The precipitation period is between April and June. Hourly precipitation data were derived from 91 meteorological stations (Figure 1). The precipitation data of 1 p.m., 4 May 2015 and total 5-day antecedent precipitation data were used to simulate surface runoff in this study.
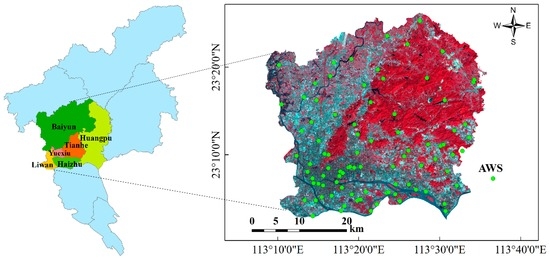
Figure 1.
Location of the main urban area of Guangzhou. AWS: automatic weather station.
2.2. Remote Sensing Image
In this study, the Landsat 8 Operational Land Imager (OLI) with cloud cover of 0% (Path 122/Row 44, acquired on 18 October 2015) is used for extracting the fraction maps of impervious surface, vegetation, and soil. The digital number of the OLI image was converted to surface reflectance through radiometric calibration and atmospheric correction, which was provided by the United States Geological Survey (USGS), Earth Resources Observation and Science (EROS) and Center Science Processing Architecture (ESPA) On Demand Interface [47]. The surface reflectance products are geometrically rectified to the Universal Transverse Mercator (UTM) projection system (zone 49 N), and the error for geometric correction is less than 0.5 pixels (15 m).
2.3. Soil Data
Because of the stable property of soils, the soil types are regarded as constant for the model calculation. Soil types of the study area are derived from the soil image of Guangdong Province with a spatial scale of 1:1,000,000. The soil type map is geometrically corrected to Landsat 8 OLI image with UTM projection, and the pixel size is set to 30 m. Figure 2 shows four soil types in the study area, which includes red soil, paddy soil, deposited soil, and aquic soil. Regarding Technical Release 55 (TR-55) [48], infiltration rates of soils have a wide spatial variance and are affected by subsurface permeability. Soils are classified into four hydrologic soil groups (A, B, C, and D) according to their minimum infiltration rate. Following the works of Fan et al. [30] and the United States Department of Agriculture (USDA) [48], red soil has moderately fine to moderately coarse textures and moderate infiltration rates and is classified into group B, deposited and aquic soils have moderately fine to fine textures and low infiltration rates and are classified into group C, and paddy soil has a clay pan or clay layer at or near the surface and very low infiltration rates and is classified into group D.
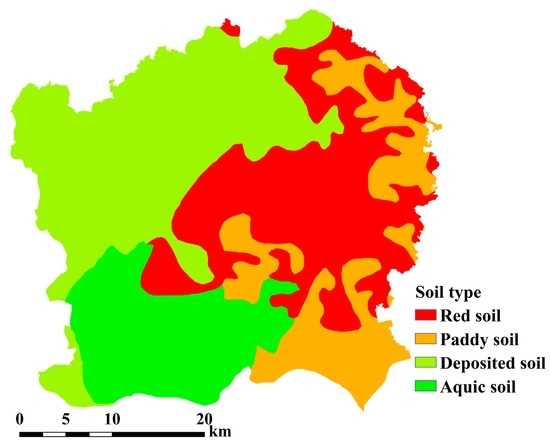
Figure 2.
Soil type map of the study area.
3. Methods
The overall workflow (Figure 3) is divided into three steps: (1) extracting the fraction maps of impervious surface, vegetation, and soil (Section 3.1); (2) calculating the composite curve number (CN) of the study area (Section 3.2); and (3) simulating the surface runoff with the SCS-CN model (Section 3.2).

Figure 3.
Flow chart for the surface runoff estimation in this study. LSMA: Linear Spectral Mixture Analysis; NDVI: Normalized Difference Vegetation Index; NDBI: Normalized Difference Built-up Index; CN: Curve Number; OLI: Operational Land Imager
3.1. Linear Spectral Mixture Analysis
3.1.1. Modified Linear Spectral Mixture Analysis
The conventional Linear Spectral Mixture Analysis (LSMA) method assumes that each mixed pixel of an image is a linear combination of all components [49], and its mathematical model can be expressed as:
where i = 1, 2, …, m, m is the number of spectral bands, k = 1, 2, …, n, n is the number of endmembers, Ri is the spectral reflectance of band i of a mixed pixel, fk is a proportion of endmember k within the mixed pixel, Rik is the known spectral reflectance of endmember k within a mixed pixel of band i, and is the error of band i. The water body of the Landsat 8 OLI image is first masked by the Modified Normalized Difference Water Index (MNDWI) [50]. Four endmembers are then selected, including soil, vegetation, high-albedo, and low-albedo endmembers. The proportion fk of four endmembers is solved by the least square method with the following constraint:
Endmember selection is a particularly important prerequisite task for the mixed spectral analysis and is critical to improving the fraction extraction accuracy. However, some endmembers may be artificially misclassified during the process of endmember selection, which may lead to large errors in the LSMA results. Thus, a two-step method is applied to improve the accuracy of endmember selection. First, the Maximum Noise Fraction (MNF) is carried out to help select endmembers. Based on the endmembers of MNF, the respective endmembers are then selected by combining a high-resolution image from Google Earth. Impervious surface fraction can be estimated by the summation of high-albedo and low-albedo fractions. However, some low-albedo pixels that belong to the pervious surface may be misclassified as impervious surface, which directly results in large errors in the LSMA results. In this study, the NDBI [51] and the NDVI are used to differentiate impervious surface, vegetation, and soil fractions by setting an appropriate threshold value based on the above LSMA results. The detailed post-processing of the low-albedo fraction image is shown in Figure 2. In general, a pixel with NDBI value greater than 0 is classified as impervious surface. However, compared with a high-resolution image from Google Earth, we have found that most pixels belonging to impervious surface have an NDBI value greater than −0.15. Thus, pixels with an NDBI value greater than −0.15 are classified as impervious surface. For the low-albedo fraction image, if the NDBI value of a pixel is greater than −0.15, that pixel is classified as low-albedo impervious surface; otherwise, pixels in the low-albedo fraction image are kept and classified as low-albedo pervious surface. Sobrino et al. [52] has pointed out that a pixel with an NDVI value less than 0.2 belongs to bare soil. In this study, we set pixels with NDVI values less than 0.2 as soil, and greater than 0.2 as vegetation in the low-albedo pervious surface fraction image. For the low-albedo pervious surface fraction image, pixels with an NDVI value less than 0.2 are classified as low-albedo soil fraction, while the other pixels are classified as low-albedo vegetation fraction. Finally, the impervious surface fraction is equal to the summation of high-albedo and low-albedo impervious surface fractions. The vegetation fraction can be estimated by the addition of original vegetation and low-albedo vegetation fractions. The soil fraction can be calculated by the summation of original soil and low-albedo soil fractions.
3.1.2. Accuracy Assessment
To verify the accuracy of the impervious surface, vegetation, and soil maps, we conducted fieldwork in 170 randomly selected sizes of 480 m × 480 m (Figure 4). For each sample area, the impervious surface, vegetation and soil are digitized on the geometrically-corrected high-resolution image from Google Earth using ArcGIS. After digitization, the proportions of impervious surface, vegetation, and soil areas are estimated by dividing the areas of impervious surface, vegetation, and soil by the sampling area (480 m × 480 m = 230,400 m2). The digitized proportions are considered as “ground” reference for validating results of the conventional and modified LSMA methods. Two assessment metrics are used in this study, including root mean square error (RMSE), and bias error (Bias):
where is the estimated impervious surface, vegetation, and soil fractions of sample i from Landsat, is the digitized proportion from the high-resolution image, and N is the number of samples.
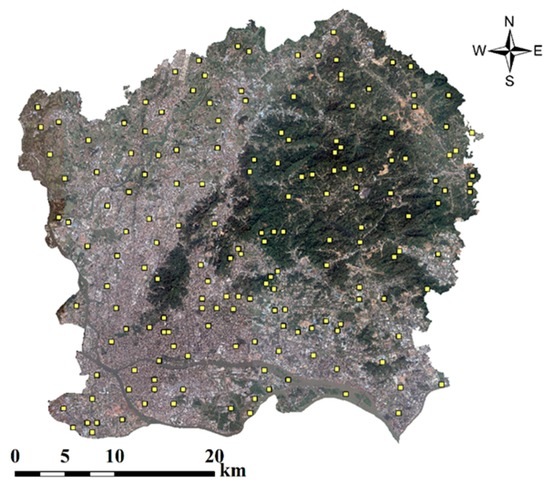
Figure 4.
Spatial distribution of the sample areas.
3.2. Surface Runoff Simulation
In this study, the surface runoff is simulated with the SCS-CN (Soil Conservation Service curve number) model, which is based on the water balance equation. The SCS-CN model hypothesizes that the ratio of the actual retention in the watershed to the potential maximum retention S is equal to the ratio of the actual direct surface runoff Q to the maximum potential surface runoff (or total precipitation P) [24,53]. The mathematical formula of the SCS-CN method is expressed as:
where Q is the direct runoff (mm), P is the total precipitation (mm), S is the potential maximum retention (mm), λS is the initial abstraction (mm), and λ is the initial abstraction coefficient (dimensionless) with a default value of 0.2 in this study. The potential maximum retention S is related to the soil and land use/land cover (LULC) conditions and can be estimated by CN:
where the CN value is the main parameter of the SCS-CN model and is used to describe the relationship between precipitation and runoff. In this study, CN is estimated jointly by the fractions of impervious surface, vegetation, and soil [30]:
where CNc is the composite CN value; fimp, fveg, and fsoil are the fraction of impervious surface, vegetation, and soil extracted by the modified LSMA, respectively; CNimp, CNveg, and CNsoil are the initial CN values of impervious surface, vegetation, and soil, respectively.
The CN value is influenced by the antecedent soil moisture condition (referred to as S). The antecedent moisture condition (AMC) is a function of the antecedent precipitation and the characteristics of the watershed. The AMCs are grouped into three categories based on the total 5-day antecedent precipitation (P5) and the dormant/growing season, representing dry, normal, and wet conditions (AMC I, AMC II, and AMC III). The composite CN value in Equation (7) is calculated under the AMC II condition. The CN values for the AMC I and AMC III conditions are adjusted using the following conversion formulas, respectively [5,54]:
where CNII is the composite curve number calculated with Equation (3), and CNI and CNIII are the adjusted curve numbers for the AMC I and AMC III condition, respectively.
Furthermore, CN is affected by the basin slope, especially for a slope value greater than 5%. Thus, the composite CN values are adjusted with the basin average slope [14,55]. Following the formula of Sharpley and Williams [14], if the average slope is greater than 5%, the composite CN value under AMC II condition is adjusted:
where CNIIα is the adjusted CN for AMC II; CNII and CNIII are the composite CN values for AMC II and AMC III condition, respectively; and α (%) is the basin average slope.
4. Results and Discussion
4.1. Extraction Results of the Modified LSMA
The NDBI and NDVI images are shown in Figure 5. Figure 5 shows that high values of the NDBI are largely found in Liwan, Yuexiu, Haizhu, Tianhe, west Baiyu, and south Huangpu while lower values are found in southwest Baiyu and north Huangpu. However, the NDVI exhibits the opposite behavior. This indicates that a pixel with a high NDBI value may have a low NDVI value, with the exception of the water body.
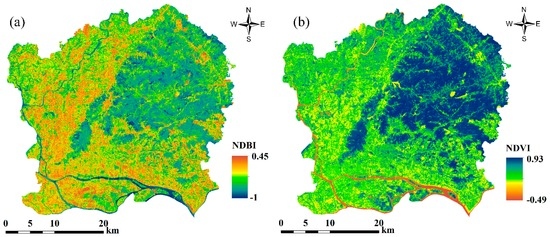
Figure 5.
(a) Normalized Difference Built-up Index (NDBI); and (b) Normalized Difference Vegetation Index (NDVI) maps.
The modified and conventional LSMA methods are applied to the Landsat 8 OLI image from 18 October 2015 to extract the impervious surface, vegetation, and soil fractions. Impervious surface, vegetation, and soil maps generated by the conventional and modified LSMA are shown in Figure 6. Apparently, the modified LSMA shows better extraction performance than the conventional LSMA. For the conventional LSMA, most pixels in the forest region still have an impervious surface fraction (referring to Figure 6a), which leads to a low vegetation fraction (referring to Figure 6b). The above result is not reasonable. In general, pixels in the forest region have a high vegetation fraction, along with a low impervious surface fraction or an impervious surface fraction of 0%. The errors of the conventional LSMA may be introduced by the endmember selection. Inaccurate endmember selection may make the reflectance of vegetation endmember higher than that of the high-albedo endmember, as shown in Figure 7a. This may mistakenly treat the vegetation fraction as the impervious surface fraction in the solving process of the LSMA. Therefore, a modified LSMA method is proposed in this study. Endmember selection of the modified LSMA combines a high-resolution image, which may accurately differentiate the vegetation and high-albedo endmembers (Figure 7b). However, the reflectance difference between low-albedo and vegetation endmembers may likely narrow, leading to difficulty in differentiating the vegetation and low-albedo endmembers. Based on the above results, the NDBI and the NDVI are used to differentiate impervious surface, vegetation, and soil fractions by setting an appropriate threshold value in the modified LSMA. The set threshold values are presented in Section 3.1.1. As shown in Figure 6d,e, many pixels in the forest region have a vegetation fraction of 100%, with an impervious surface fraction of 0% in the modified LSMA. Figure 6 shows that impervious surface regions are largely found in Liwan, Yuexiu, Haizhu, Tianhe, southwest Baiyu, and south Huangpu while vegetation is found in northeast Baiyu, central and north Huangpu. Regions with a high fraction of soil are mainly located in the northeast part of the study area.

Figure 6.
Extracted results of the conventional (a–c); and modified LSMA (d–f) methods: (a,d) impervious surface; (b,e) vegetation; and (c,f) soil fractions.
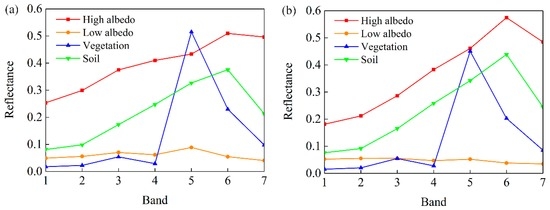
Figure 7.
Spectral curves of endmember selection of the conventional (a); and modified (b) LSMA methods.
The accuracy assessment results are shown in Figure 8. In Figure 8, the results of the modified LSMA show good consistency with the “ground” reference. The RMSE of the impervious surface and vegetation fractions in the conventional LSMA are 0.329 and 0.280, respectively, whereas the RMSE of the impervious surface and vegetation fractions in the modified LSMA reach 0.123 and 0.144, respectively. The modified LSMA improved the impervious surface and vegetation accuracy by 62.6% and 48.6%, respectively. For the soil fraction, the modified LSMA has almost the same bias and RMSE as the conventional LSMA, but the former has a larger determination coefficient (R2). This indicates that the modified LSMA can enhance the accuracy of soil mapping. On the whole, the modified LSMA does make a significant contribution to the improvement of impervious surface, vegetation, and soil mapping accuracy.

Figure 8.
Scatter plots of accuracy assessment results: (a) impervious surface; (b) vegetation; and (c) soil. RMSE: root-mean-square error.
4.2. Calculation of the Composite CN
According to the hydrologic soil group and soil infiltration rate, the CN values of paddy and red soils were set to 94 and 86, respectively, and the CN values of deposited and aquic soil were set to 91. The CN map of soil types is then obtained and shown in Figure 9.
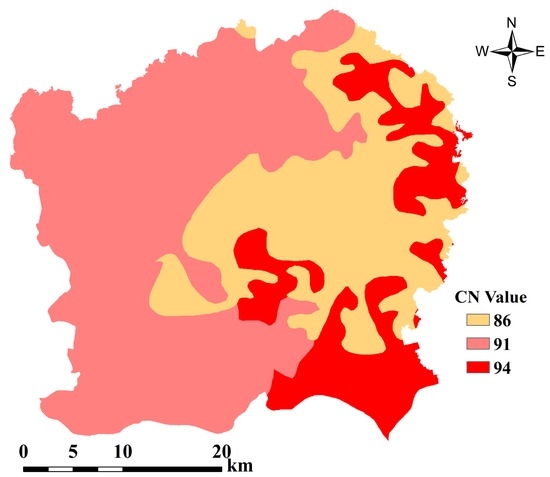
Figure 9.
CN map of soil types in this study.
Water body was first masked before implementing the LSMA process. Then, the CN value of water was provided individually and set to 100 in this study followed the work of Quan et al. [56]. Referring to the previous works [30,48], the CN values of the impervious surface for different hydrologic soil groups are set combining the impervious surface range, shown in Figure 10.
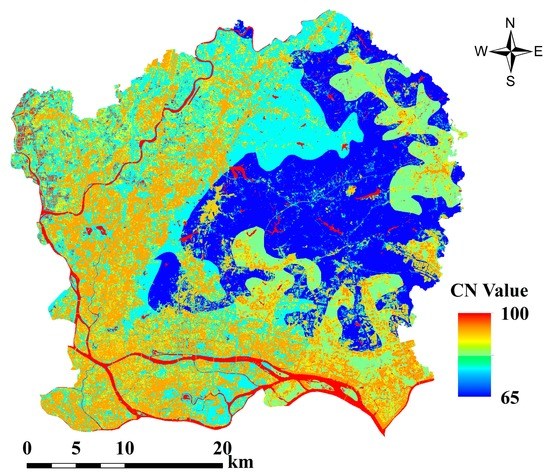
Figure 10.
CN map of the impervious surface in this study.
To estimate the vegetation CN values, the NDVI is used in combination with the vegetation fraction. Following the proposed method of Fan et al. [30], four vegetation types are first classified according to the NDVI values: (1) forest for NDVI values larger than 0.65; (2) grass and bush for NDVI values between 0.57 and 0.65; (3) farmland for NDVI values between 0.4 and 0.57; and (4) other type for NDVI values less than 0.4. Each vegetation type is further classified into three groups, good, moderate, and poor vegetation covers, according to the vegetation fraction. The details can be found in the work of Fan et al. [30]. The vegetation CN values for different hydrologic soil groups are shown in Figure 11.
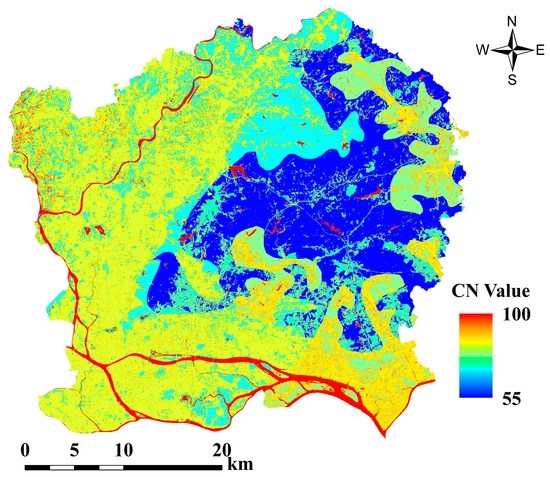
Figure 11.
CN map of vegetation in this study.
Combining the fractions of impervious surface, vegetation, and soil (Figure 6d–f) and the corresponding CN maps (Figure 9, Figure 10 and Figure 11), the composite CN map was calculated with Equation (7). The final composite CN map under the AMC II condition is shown in Figure 12. Figure 12 shows that large composite CN values tend to gather in Liwan, Yuexiu, Haizhu, Tianhe, west Baiyu, and south Huangpu, which shows a similar spatial pattern as impervious surface or NDBI maps. Low composite CN values can be found in the forest region. This indicates that pixels with a high impervious surface fraction and a low vegetation fraction may have a large composite CN value. This may also be explained by Equation (7).

Figure 12.
Composite CN map under the AMC II condition.
Figure 13 shows the slope (%) map of the study area and the slope-adjusted CN map for the AMC II condition. The slope of many pixels in this study area is greater than 5%, especially for the forest region with slopes greater than 50%. Figure 12 and Figure 13 show that the slope value can augment the composite CN values. The higher the slope value is, the faster the CN values increase. High CN values with high slope values may make more surface runoff and little infiltration under the same conditions.
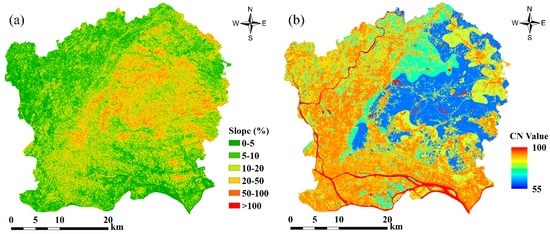
Figure 13.
Slope map (a) and its adjusted CN map (b) under the AMC II condition.
4.3. Runoff Calculation
In addition to the above parameters, CN is also significantly affected by the antecedent soil moisture condition. In this study, the total 5-day antecedent precipitation (P5) is typically used to identify the soil moisture condition that shifts the soil from one AMC condition to another. The amount of antecedent precipitation varies from the dormant season to the growing season. Here, the antecedent soil moisture condition was categorized according to P5 in the growing season as follows: AMC I (if P5 < 35.56 mm), AMC II (if 35.56 mm ≤ P5 ≤ 53.34 mm), and AMC III (if P5 > 53.34 mm) [53].
Figure 14a shows the total 5-day antecedent precipitation map, which is generated by the Kriging method in ArcGIS. The highest P5 is found to be 105.5 mm, while the lowest P5 is only 0.51 mm. Most of the study area has antecedent precipitation greater than 20 mm. Three centers of heavy precipitation of greater than 81 mm are formed and distributed in Liwan, southwest Huangpu, and west Baiyun. Figure 14b shows the adjusted CN map for different AMC conditions. By comparing with Figure 13b, we find that the CN values, adjusted based on the antecedent soil moisture condition are significantly increased under the AMC III condition. The CN values in centers of heavy precipitation are greater than 90, at times approaching 100. However, the CN values decrease under the AMC I condition. This indicates that soil moisture is an important parameter for setting CN. The accurate estimate of the soil moisture is crucial to improve the accuracy of CN estimation.
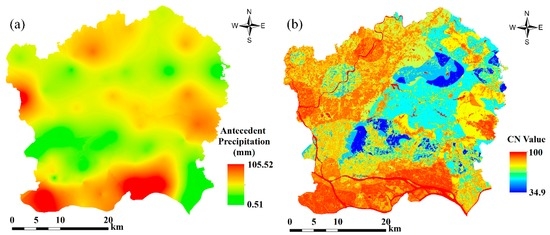
Figure 14.
Map of the total 5-day antecedent precipitation (a) and its adjusted CN map (b).
In this study, the precipitation data from 91 meteorological stations were interpolated by the Kriging method in ArcGIS to obtain the spatial pattern of precipitation, as shown in Figure 15. The highest precipitation is 87.79 mm and the lowest precipitation is 0 mm. The heavy precipitation is mainly distributed in Tianhe.
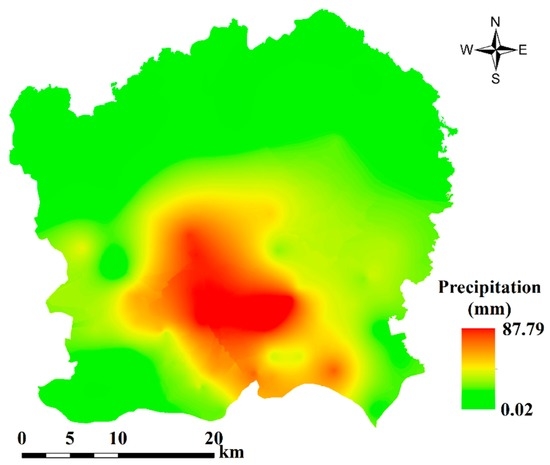
Figure 15.
Precipitation map generated by the Kriging method at 1 p.m., 4 May 2015.
Combining the CN and precipitation maps, surface runoff was simulated using the SCS-CN method. The simulation results are illustrated in Figure 16. As shown in Figure 16, the highest surface runoff approaches 82.83 mm, while the lowest surface runoff is only 0 mm. Most of the study areas have a runoff of 0 mm. High runoff is mainly distributed in the Tianhe, Haizhu, and Huangpu districts. Compared with Figure 15, the center of the surface runoff is inconsistent with that of heavy precipitation. This means that the areas of heavy precipitation do not have large runoff volume. Compared with Figure 14b, we find that the runoff volume is large in the areas that possess a large CN value. This indicates that large CN values may have high surface runoff under the same condition of precipitation and surface drainage. This can be explained by the fact that soil with large CN values has a low infiltration rate. The cumulative infiltration increases with decreasing CN value. It is inferred from Figure 6, Figure 14b and Figure 15 that large CN values and large amounts of precipitation lead to large surface runoff. This implies that when the CN values reach 100, the intensity of precipitation is greater and more surface runoff is produced. In that case, the area may likely be threatened by waterlogging. In other words, heavy precipitation may not directly lead to flooding or waterlogging if the composite CN value is small enough. This is because a small composite CN value may lead to a large amount of the cumulative infiltration. Due to the lack of real runoff observations, no efforts have been made to verify the simulated runoff.
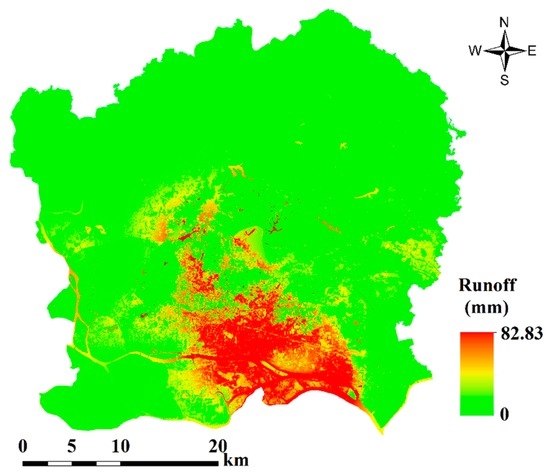
Figure 16.
Spatial distribution of simulated surface runoff at 1 p.m., 4 May 2015.
5. Conclusions
This study presented a method for extracting the impervious surface, vegetation, and soil fractions. The modified method was built based on the conventional LSMA combining a high-resolution image, the NDBI, and the NDVI. The modified LSMA method was performed on the Landsat 8 OLI image from 18 October 2015 in the main urban area of Guangzhou city. Compared with the conventional LSMA, the modified LSMA performs better, as it significantly reduces the bias and RMSE for the impervious surface and vegetation fractions. The biases of the impervious surface and vegetation fractions decrease from 0.253 and 0.196 to 0.008 and 0.067, respectively. Combining the improved impervious surface, vegetation, and soil fractions and the corresponding initial CN, the composite CN was calculated, which shows a strong positive relationship with the impervious surface fraction. In addition to the impact of the land surface characteristics, the changes in antecedent soil moisture and terrain slope contributing to CN may have a vital effect as well. Therefore, the composite CN was adjusted with the regional terrain slope and total 5-day antecedent precipitation in this study. The adjusted CN values are significantly enhanced for the AMC III condition while decreased for the AMC I condition. Based on the CN and the actual interpolated precipitation calculated from the Kriging method, surface runoff is simulated by using the SCS-CN model. However, the main scope of this study was to present a novel method for the estimation of CN spatial distribution using GIS and remote sensing and for the estimation the spatial distribution of surface runoff, and thus the SCS-CN model performance was not evaluated. In the future, more hydrological data and precipitation data could be integrated into the SCS-CN model to test the validity of the model and study the impact of precipitation on surface runoff.
Acknowledgments
We sincerely thank the reviewers for their helpful comments and suggestions about our manuscript. We thank the Guangdong Meteorological Observation Data Center for providing the hourly precipitation data from the meteorological stations in the study area. We thank Editage (www.editage.cn) for English language editing. This research is jointly supported by the Creative Talents Fund of Guangzhou Institute of Geography, the Water Conservancy Science and Technology Innovation Project of Guangdong Province (2015-13), the Natural Science Foundation of Guangdong Province (2014A030313747), the Science and Technology Planning Project of Guangdong Province (2016A020210059, 2016A020222006) and the Scientific Platform and Innovation Capability Construction Program of GDAS (2016GDASPT-0103).
Author Contributions
Jianhui Xu and Kaiwen Zhong conceived and designed the experiments; Jianhui Xu and Yi Zhao performed the experiments; Huihua Ruan and Xulong Liu processed the data and analyzed the experimental results; Jianhui Xu and Yi Zhao wrote the manuscript; Xulong Liu and Huihua Ruan reviewed the manuscript and made helpful suggestions; Jianhui Xu and Kaiwen Zhong revised the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brabec, E.; Schulte, S.; Richards, P.L. Impervious surfaces and water quality: A review of current literature and its implications for watershed planning. J. Plan. Lit. 2002, 16, 499–514. [Google Scholar] [CrossRef]
- Gao, G.Y.; Fu, B.J.; Lu, Y.H.; Liu, Y.; Wang, S.; Zhou, J.M. Coupling the modified SCS-CN and rusle models to simulate hydrological effects of restoring vegetation in the loess plateau of China. Hydrol. Earth Syst. Sci. 2012, 16, 2347–2364. [Google Scholar] [CrossRef]
- Yao, L.; Wei, W.; Yu, Y.; Xiao, J.; Chen, L. Research on potential runoff risk of urban functional zones in beijing city based on GIS and RS. Acta Geogr. Sin. 2015, 70, 308–318. (In Chinese) [Google Scholar]
- National Engineering Handbook. 2009. Available online: http://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=22526.wba (accessed on 26 January 2009).
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Geetha, K.; Mishra, S.K.; Eldho, T.I.; Rastogi, A.K.; Pandey, R.P. SCS-CN-based continuous simulation model for hydrologic forecasting. Water Resour. Manag. 2007, 22, 165–190. [Google Scholar] [CrossRef]
- Anubha, T.; Singh, A.K.; Vaishya, R.C. SCS CN runoff estimation for vindhyachal region using remote sensing and GIS. Int. J. Adv. Remote Sens. GIS 2015, 4, 1214–1223. [Google Scholar]
- Xiao, B.; Wang, Q.-H.; Fan, J.; Han, F.-P.; Dai, Q.-H. Application of the SCS-CN model to runoff estimation in a small watershed with high spatial heterogeneity. Pedosphere 2011, 21, 738–749. [Google Scholar] [CrossRef]
- Choi, J.; Engel, B.A.; Chung, H.W. Daily streamflow modelling and assessment based on the curve-number technique. Hydrol. Process. 2002, 16, 3131–3150. [Google Scholar] [CrossRef]
- Soulis, K.X.; Dercas, N. Development of a gis-based spatially distributed continuous hydrological model and its first application. Water Int. 2009, 32, 177–192. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation: Version 2009; Texas Water Resources Institute Technical Report 406; Texas A & M University System: College Station, TX, USA, 2009. [Google Scholar]
- Harbor, J.M. A practical method for estimating the impact of land-use change on surface runoff, groundwater recharge and wetland hydrology. J. Am. Plan. Assoc. 2007, 60, 95–108. [Google Scholar] [CrossRef]
- United States Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS, User’s Manual; Version 4.0; United States Army Corps of Engineers: Washington, DC, USA, 2013.
- Sharpley, A.N.; Williams, J.R. Epic-Erosion/Productivity Impact Calculator: 1. Model Documentation; Technical Bulletin 1768; U.S. Department of Agriculture: Washington, DC, USA, 1990; p. 235.
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. Agnps: A nonpoint-source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Rejani, R.; Rao, K.V.; Osman, M.; Chary, G.R.; Pushpanjali; Reddy, K.S.; Rao, C.S. Spatial and temporal estimation of runoff in a semi-arid microwatershed of Southern India. Environ. Monit. Assess. 2015, 187. [Google Scholar] [CrossRef] [PubMed]
- Suribabu, C.R.; Bhaskar, J. Evaluation of urban growth effects on surface runoff using SCS-CN method and green-ampt infiltration model. Earth Sci. Inf. 2014, 8, 609–626. [Google Scholar] [CrossRef]
- Kowalik, T.; Walega, A. Estimation of cn parameter for small agricultural watersheds using asymptotic functions. Water 2015, 7, 939–955. [Google Scholar] [CrossRef]
- Fu, S.; Wang, H.; Wang, X.; Yuan, A.; Lu, B. The runoff curve number of SCS-CN method in Beijing. Geogr. Res. 2013, 32, 797–807. (In Chinese) [Google Scholar]
- Lal, M.; Mishra, S.K.; Pandey, A. Physical verification of the effect of land features and antecedent moisture on runoff curve number. Catena 2015, 133, 318–327. [Google Scholar] [CrossRef]
- Ajmal, M.; Moon, G.-W.; Ahn, J.-H.; Kim, T.-W. Investigation of SCS-CN and its inspired modified models for runoff estimation in South Korean watersheds. J. Hydro-Environ. Res. 2015, 9, 592–603. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Ahn, J.; Kim, T. Runoff estimation using the nrcs slope-adjusted curve number in mountainous watersheds. J. Irrig. Drain. Eng. ASCE 2016, 142, 04016002. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Lim, K.; Engel, B. Regional calibration of SCS-CN l-thia model: Application for ungauged basins. Water 2014, 6, 1339–1359. [Google Scholar] [CrossRef]
- Deshmukh, D.S.; Chaube, U.C.; Hailu, A.E.; Gudeta, D.A.; Kassa, M.T. Estimation and comparision of curve numbers based on dynamic land use land cover change, observed rainfall-runoff data and land slope. J. Hydrol. 2013, 492, 89–101. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D.; Dercas, N.; Londra, P.A. Analysis of the runoff generation mechanism for the investigation of the SCS-CN method applicability to a partial area experimental watershed. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 373–400. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN parameter spatial distribution using rainfall-runoff data in heterogeneous watersheds. Water Resour. Manag. 2012, 27, 1737–1749. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Grunwald, S.; Norton, L.D. Calibration and validation of a non-point source pollution model. Agric. Water Manag. 2000, 45, 17–39. [Google Scholar] [CrossRef]
- Ludlow, C.D. Flood Modeling in a Data-Poor Region: A Satellite Data-Supported Model for Accra, Ghana; George Washington University: Washington, DC, USA, 2009. [Google Scholar]
- Fan, F.; Deng, Y.; Hu, X.; Weng, Q. Estimating composite curve number using an improved SCS-CN method with remotely sensed variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef]
- Paudel, M.; Nelson, E.J.; Scharffenberg, W. Comparison of lumped and quasi-distributed clark runoff models using the SCS curve number equation. J. Hydrol. Eng. 2009, 14, 1098–1106. [Google Scholar] [CrossRef]
- Bhaduri, B.L.; Minner, M.; Tatalovich, S.; Harbor, J. Long-term hydrologic impact of urbanization: A tale of two models. J. Water Resour. Plan. Manag. 2001, 127, 13–19. [Google Scholar] [CrossRef]
- Grove, M.; Harbor, J.; Engel, B.A. Composite vs. Distributed curve numbers: Effects on estimates of storm runoff depths. J. Am. Water Resour. Assoc. 1998, 34, 1015–1023. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Zhou, J. Assessing the long-term impact of urbanization on run-off using a remote-sensing-supported hydrological model. Int. J. Remote Sens. 2015, 36, 5336–5352. [Google Scholar] [CrossRef]
- Zhang, Y.; Harris, A.; Balzter, H. Characterizing fractional vegetation cover and land surface temperature based on sub-pixel fractional impervious surfaces from landsat TM/ETM+. Int. J. Remote Sens. 2015, 36, 4213–4232. [Google Scholar] [CrossRef]
- Yang, J.; Li, P. Impervious surface extraction in urban areas from high spatial resolution imagery using linear spectral unmixing. Remote Sens. Appl. Soc. Environ. 2015, 1, 61–71. [Google Scholar] [CrossRef]
- Mayes, M.T.; Mustard, J.F.; Melillo, J.M. Forest cover change in miombo woodlands: Modeling land cover of african dry tropical forests with linear spectral mixture analysis. Remote Sens. Environ. 2015, 165, 203–215. [Google Scholar] [CrossRef]
- Thouvenin, P.; Dobigeon, N.; Tourneret, J. Hyperspectral unmixing with spectral variability using a perturbed linear mixing model. IEEE Trans. Signal Process. 2016, 64, 525–538. [Google Scholar]
- Yang, J.; He, Y. Automated mapping of impervious surfaces in urban and suburban areas: Linear spectral unmixing of high spatial resolution imagery. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 53–64. [Google Scholar] [CrossRef]
- Ma, L.; Chen, J.; Zhou, Y.; Chen, X. Two-step constrained nonlinear spectral mixture analysis method for mitigating the collinearity effect. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2873–2886. [Google Scholar] [CrossRef]
- Li, M.; Zang, S.; Wu, C.; Deng, Y. Segmentation-based and rule-based spectral mixture analysis for estimating urban imperviousness. Adv. Space Res. 2015, 55, 1307–1315. [Google Scholar] [CrossRef]
- Li, W.; Wu, C. Incorporating land use land cover probability information into endmember class selections for temporal mixture analysis. ISPRS J. Photogramm. Remote Sens. 2015, 101, 163–173. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Wu, C. Normalized spectral mixture analysis for monitoring urban composition using ETM+ imagery. Remote Sens. Environ. 2004, 93, 480–492. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sens. Environ. 2006, 102, 146–160. [Google Scholar] [CrossRef]
- Fan, F.; Fan, W.; Weng, Q. Improving urban impervious surface mapping by linear spectral mixture analysis and using spectral indices. Can. J. Remote Sens. 2015, 41, 577–586. [Google Scholar] [CrossRef]
- United States Geological Survey Homepage. Available online: https://espa.cr.usgs.gov/ (accessed on 18 October 2015).
- United States Department of Agriculture (USDA). Urban Hydrology for Small Watersheds (TR-55 Rev.); Technical Release 55; USDA: Washington, DC, USA, 1986.
- Adams, J.L.; Sabol, D.E.; Kapos, V.; Filho, R.A.; Roberts, D.A.; Smith, M.O.; Gillespie, A.R. Classification of multispectral images based on fractions of endmembers: Application to land-cover change in the Brazilian Amazon. Remote Sens. Environ. 1995, 52, 137–154. [Google Scholar] [CrossRef]
- Xu, H. A study on information extraction of water body with the modified normalized difference water index (mndwi). J. Remote Sens. 2005, 9, 589–595. (In Chinese) [Google Scholar]
- Zha, Y.; Gao, J.P.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2010, 24, 583–594. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenezmunoz, J.C.; Paolini, L. Land surface temperature retrieval from landsat TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- United States Department of Agriculture, Soil Conservation Service (USDA-SCS). Estimation of Direct Runoff from Storm Rainfall. In National Engineering Handbook; USDA-SCS: Washington, DC, USA, 2004. [Google Scholar]
- Hawkins, R.H.; Hjelmfelt, A.T.; Zevenbergen, A.W. Runoff probability, storm depth, and curve numbers. J. Irrig. Drain. Eng. ASCE 1985, 111, 330–340. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the soil conservation service curve number method for steep slopes in the loess plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Quan, R.-S.; Liu, M.; Lu, M.; Zhang, L.-J.; Wang, J.-J.; Xu, S.-Y. Waterlogging risk assessment based on land use/cover change: A case study in pudong new area, Shanghai. Environ. Earth Sci. 2010, 61, 1113–1121. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).