1. Introduction
Beijing, the capital of China, is suffering from a serious lack of water resources because of its rapid development and dense population [
1]. Beijing is located in the north of the North China Plain and covers an area of 16,410.54 km
2, of which 2208.56 km
2 is arable land. As the most affluent and populous city in China, Beijing has 21.52 million residents, and the city’s GDP reached 2133.1 billion Yuan, accounting for 3.35% of the GDP of the entire country in 2014 [
2]. According to the Beijing Water Authority, the per capita water resources in Beijing were 94 m
3 in 2014 [
3], which is far below the internationally recognized minimum standard of 1000 m
3 per year [
4].
Water is one of the most important resources and is necessary to maintain the sustainable development of the earth’s ecological environment. Sustainability indicators for any system are essential for decision makers, especially when the earth is facing environmental and social problems [
5]. Several indicators have been used in the last few years to present a quantifiable and rational basis by which to measure the efficiency of production processes and to address the sustainable use of ecological assets across the globe, for instance, the ecological footprint, the carbon footprint, and the water footprint [
6]. Among these indicators, the water footprint (
WF) was originally proposed by Hoekstra (2003) to measure the quantity of water resources required for all the products and services consumed within a certain period of time [
7]. According to the types of water use, the water footprint can be divided into blue water (fresh surface or groundwater), green water (the precipitation on land that does not run off or recharge the groundwater but is stored in the soil or temporarily stays on the top of the soil or vegetation), and grey water (the volume of fresh water that is required to assimilate the load of pollutants based on natural background concentrations and existing ambient water quality standards) [
8]. Currently, there are two main
WF assessment methods: the Water Footprint Network (WFN) method and the ISO 14046 method, which was developed by the Life Cycle Assessment (LCA) community [
9]. Hoekstra believed that the LCA used in the water-scarcity weighted water footprint has some limitations [
10]. In contrast, Pfister stressed that the WFN aims to account for the water productivity of global fresh water as a limited resource, while ISO 14046 is concerned with the environment impact [
11]. Despite the two communities being somewhat in conflict in the past few years, the two approaches can have the same application [
12]. The calculation of the water footprint using the WFN method has been widely used in previous studies at the basin [
13], regional [
14], national [
15], and global scales [
16]. For Beijing, Zhang reported the
WF of the agriculture in Beijing as 0.667 km
3/year in 2002, using an interregional input–output framework [
17], and we have also evaluated the gross
WF of different sectors in Beijing using an input–output approach [
18]. Because this paper aims to account for the water consumed in production processes, we applied the WFN method to quantify the
WF.
Agriculture is the largest water use sector in the world, and agricultural production consumes a large proportion of the water resources [
19]. The agricultural water consumption of China in 2012 was 3899.443 × 10
9 m
3, accounting for 63.66% of the total water consumption [
20]. With the increasing pressure of agricultural water resources, an urgent response is currently needed, and a better understanding of the influence of anthropogenic factors on the environment should be employed. Structural decomposition analysis (SDA) [
21], the Logarithmic-Mean Divisia Index (LMDI) [
22,
23], and stochastic impact by regression on population, affluence, and technology (STIRPAT) [
24] are methods that are commonly used to analyze the driving force of changes in the
WF. Dietz and Rosa reformulated the IPAT into STIRPAT, which is used to analyze the impact of non-proportional variables on the environment [
25,
26]. As a stochastic model, the STIRPAT model allows a hypothesis test. In addition, it permits falsifiable tests of the environmental Kuznets curve and modernization theory [
27]. This model has simple, systematic, powerful features. It simply includes key anthropogenic driving forces and clarifies the mathematical relationship between the driving forces and their impacts. In addition, it applies to a wide variety of effects [
25]. Compared with other decomposition methods, the STIRPAT model is more flexible and easier to operate, while the SDA model needs an input–output table. Moreover, the STIRPAT model can examine more detailed factors than the LMDI, so it can provide more detailed and reliable information [
28].
Recently, the STIRPAT model has been extended and applied in several other applications for empirical analyses and policy recommendations [
29]. Liddle used the STIRPAT model to study changes in the age structure, urbanization, and climate in developed countries [
30], Martínez-Zarzoso analyzed the impact of urbanization on CO
2 emissions using the STIRPAT model [
31], and Ignatius used the STIRPAT model to examine the impacts of anthropogenic factors on the environment in Nigeria [
32]. Our study differs in several ways from previous studies. In particular, the STIRPAT model was widely used to examine the driving factors of CO
2 emissions in previous studies, but few works have undertaken a decomposition analysis of the
WF [
24]. In addition, we make use of this method at the regional scale, which is more targeted. Most importantly, in previous studies, the main drivers of the agricultural
WF were the population, GDP, urbanization level, plantation structure, and diet structure. However, these studies ignored the impact of two major transformations that are occurring in Beijing: the constantly increasing standard of living and improvements in cultivation technology. In 2012, the Engel coefficient of Beijing was 31.3%, compared with 55.3% in 1980. In this process, technology develops rapidly. For example, the area of mechanical cultivation as a proportion of the total area of cultivated land has risen from 61% in 2004 to 82.9% in 2012 [
33].
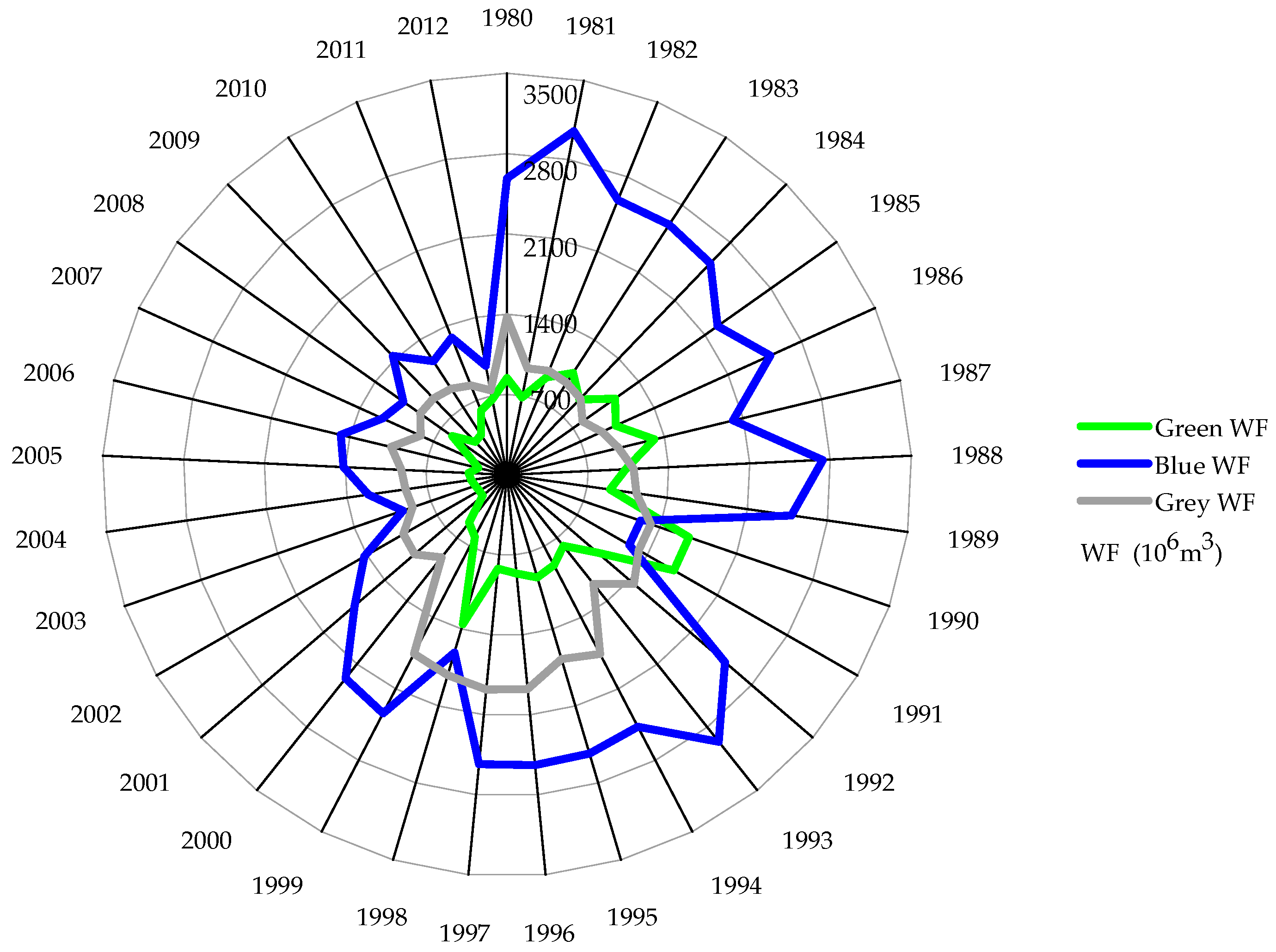
In view of these significant changes, this study aims to quantify the influence of anthropogenic factors on the agricultural WF within Beijing by applying the STIRPAT model. First, we calculated the agricultural WF within Beijing from 1980 to 2012. Second, we used a correlation analysis to select the main influencing factors. Finally, we employed an extended STIRPAT model that incorporated ridge regression to decompose and determine the influencing factors. The results of this study provide new insights in the analysis of the anthropogenic driving factors of the agricultural WF within Beijing.
4. Discussion
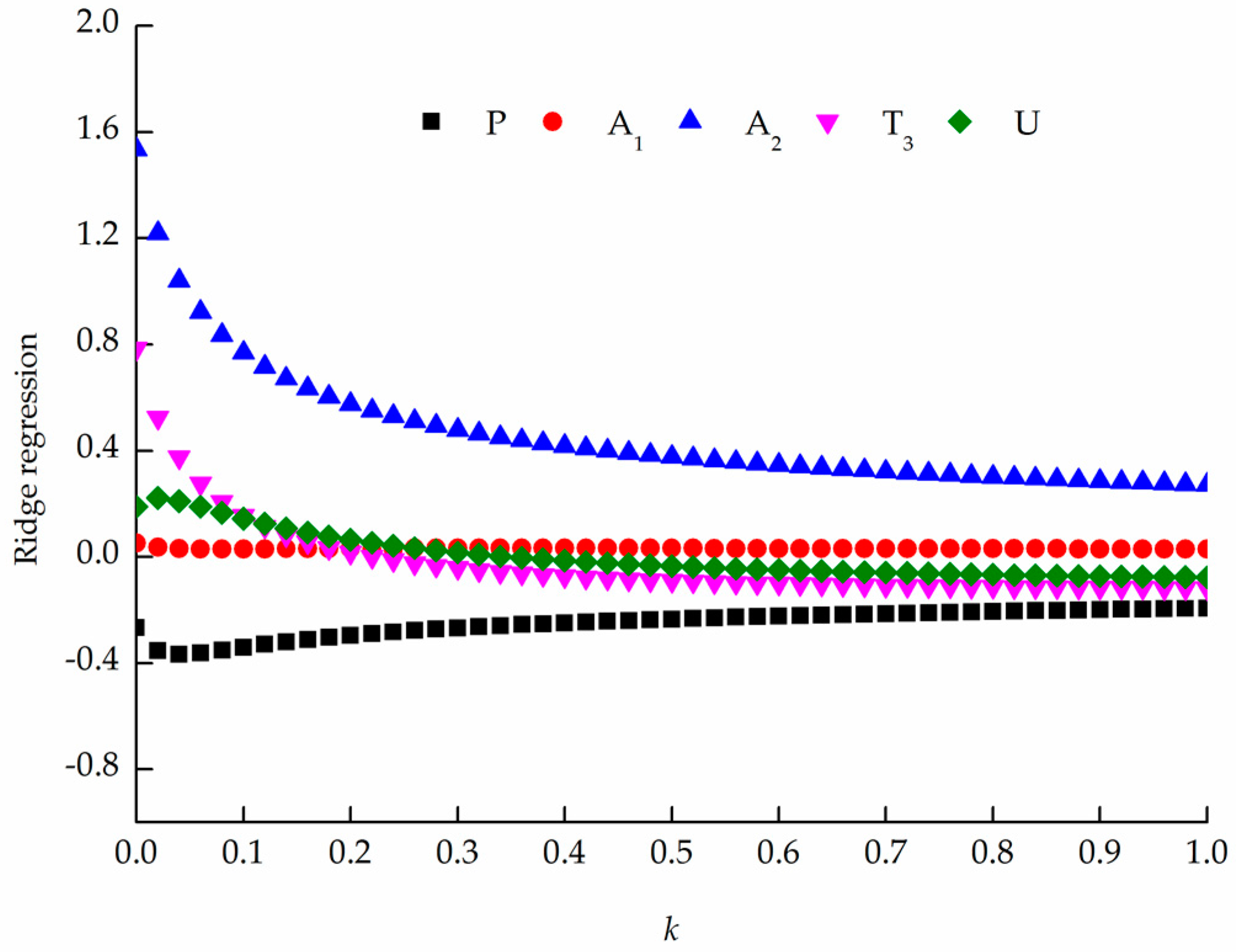
Based on the calculation of the agricultural WF within Beijing from 1980 to 2012, this paper analyzed the influence of anthropogenic factors on the water footprint using the STIRPAT model. From the results of the ridge regression estimation, we know that the model simulation results are significant. Based on their coefficients, population, urbanization, GDP, the Engel coefficient, and total rural power all have different influences on the agricultural WF within Beijing.
In the middle of 1970s, the United Nations Food and Agriculture Organization (FAO) adopted the Engel coefficient as one of the important criteria to evaluate the living standards in a country or region. The Engel coefficient of Beijing has decreased from 55.3% in 1980 to 31.3% in 2012. According to the life criterion of the FAO, during the past three decades, the living standard of Beijing citizens has changed from “adequate food and clothing” to “richness” and is approaching “the most rich.” The Engel coefficient has the largest influence and the most positive driving force for the increase in the
WF. With China's reform and opening up in 1978, social productive forces rapidly developed. In Beijing, as the capital of China, the people’s living standard has greatly changed. Residents are no longer satisfied with the provision of enough food and clothing but also tend to pursue a quality lifestyle characterized by a balanced diet structure, nutritious food, and even luxury products [
43]. According to the principle of the Environmental Kuznets Curve (EKC) [
44], there is an inverted U-shaped relationship between environmental pressure and economic growth [
28]. In this paper, the relationship between the Engel coefficient and the agricultural
WF within Beijing has no environmental Kuznets curve during the study period, which is similar to China. This means that economic development and water conservation have not yet achieved synergy. Urbanization also increases the
WF. The urbanization of Beijing has risen from 57.629% in 1980 to 86.198% in 2012 [
33]. Due to its steady growth during the past 30 years, urbanization still plays a significant role in the agricultural
WF within Beijing.
Population, as the largest inhibited factor of the agricultural
WF within Beijing, has risen from 9.043 million to 20.693 million from 1980 to 2012. This is in contrast to the situation in China. For the whole country, population is a positive driving force for increases in the agricultural
WF [
22]. The rapid population growth in China has led to increased demand for crops, which has directly led to an increase in the
WF. However, for Beijing, the political center of China, the sown area of crops has decreased with the increase in population. The sown area of crops has strongly decreased from 6570 km
2 to 2830 km
2 [
33]. This causes a reduction in the agricultural
WF within Beijing.
Total rural power, as a measure of technical development, is a very important index that reflects the development of agricultural mechanization in an area. Total rural power plays an inhibitory role in the agricultural
WF within Beijing. From 1980 to 2012, total rural power has grown more than sixfold. Similar to the results of other studies, other scholars found that, in China, technology has contributed to a decline in energy intensity [
45]. On the one hand, planting technology in Beijing has significantly improved. With the development of water-saving irrigation technology, Beijing has used sprinkler irrigation, micro irrigation, mechanical film, and mechanized furrow sowing instead of the traditional irrigation. For instance, the Tongzhou district applied the integrated management of water and fertilizer in 2005, which significantly improved the water use efficiency under protected cultivation. In addition, Beijing has actively promoted the mechanization of agriculture. In 1980, Beijing only had 2755 motorized sprayers, but there were 29,505 units in 2012. These technologies have effectively solved the problems of agricultural water shortage, poor water storage capacity, and the low efficiency of irrigation water, which have a significant impact on the reduction in the use of agricultural water within Beijing [
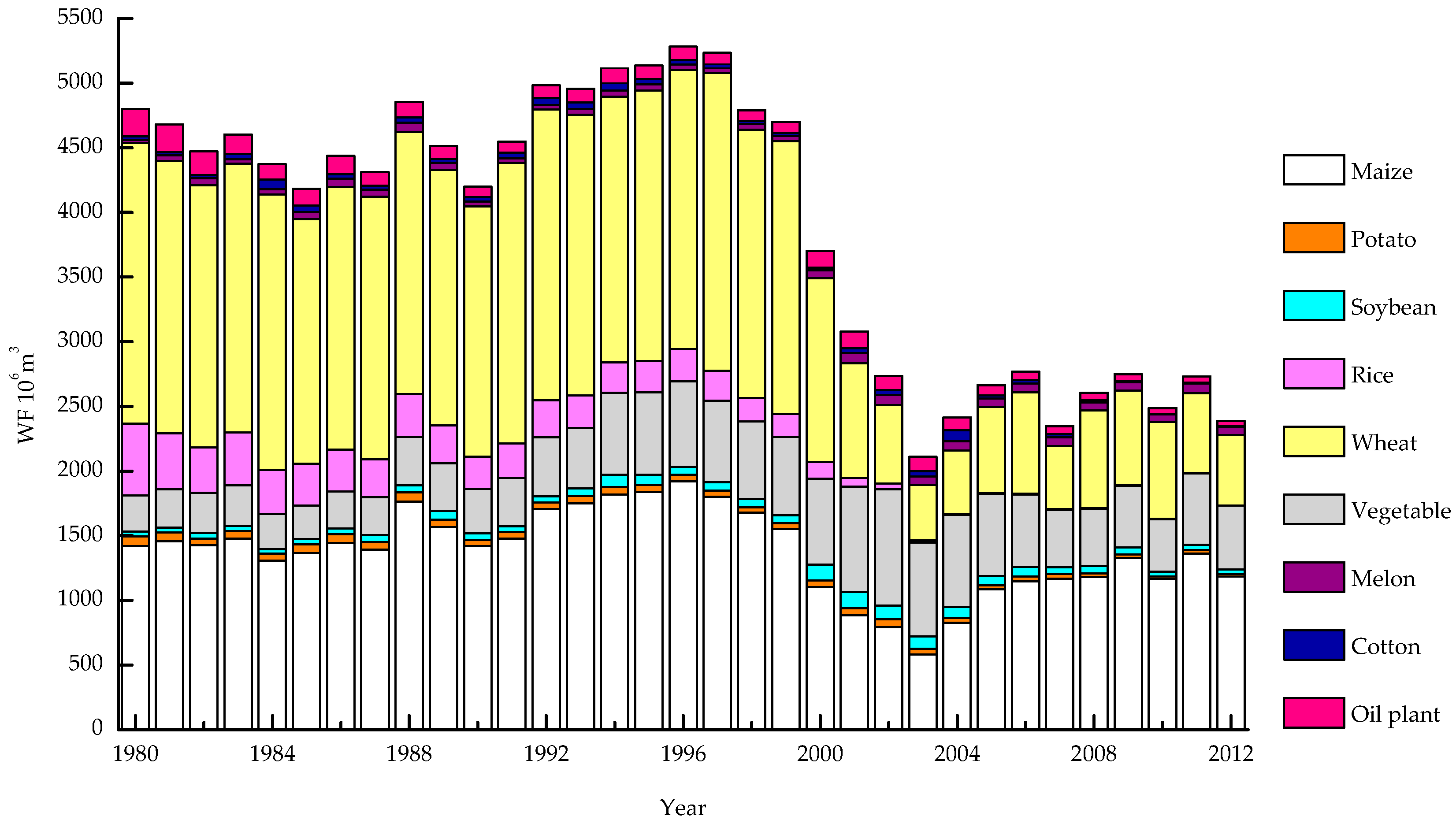
46]. On the other hand, Beijing has an adjusted plantation structure. Rain-fed maize has largely replaced wheat planting in Beijing, which is also reflected in
Figure 1, which will drastically reduce the blue
WF.
GDP also has an inhibitory influence on the agricultural
WF with Beijing during the study period, with an elastic coefficient of −0.078. The per capita GDP in Beijing has increased from $1,009 to $13,857, a 13-fold increase [
33]. Since China joined the WTO in 2001, Beijing has actively adjusted the direction of development and made an effort to establish a resource-saving industrial structure and an export-oriented trade structure; as a result, Beijing has imported large quantities of agricultural products from other regions [
47]. Trade in agricultural products not only plays a positive role in ensuring the healthy development of the social economy of Beijing but also inhibits the agricultural
WF within Beijing.
5. Conclusions and Policy Implications
The quantitative analysis of the impact of anthropogenic factors on the water footprint is a hot spot in terms of research on water sustainability. In this paper, the extended STIRPAT model and the ridge regression method are employed to examine the factors that influence the agricultural WF within Beijing from 1980 to 2012.
The utilization of water resources in Beijing is unsustainable, and the prominent contradiction between supply and demand has become a social and economic development bottleneck [
48]. In this paper, we calculated the agricultural
WF within Beijing from the production point of view. The optimization and adjustment of agricultural planting structures and the improvement of agricultural water saving technology are the keys to relieving the shortage of water resources in Beijing.
First, Beijing should increase the use of water-saving technology to decrease the agricultural WF. From Equation (16), we know that technology reduces the use of water in agriculture in Beijing. Water-saving technology can use limited water resources in the most effective way. Compared with flood irrigation, water-saving well irrigation, deep plowing, soil moisture maintenance, the selection of drought-resistant varieties, and other agronomic water-saving techniques should be widely promoted. In addition, the government can build a number of modern and efficient agricultural parks and modern agricultural enterprises in order to promote the industrialization of high-tech agriculture.
Second, water regulation and environmental management in Beijing should place greater emphasis on the plantation structure. Beijing is seriously lacking in water. In addition to considering market-oriented changes, Beijing must also give full consideration to the limits of local resources and the carrying capacity, especially the water supply capacity, when adjusting to the plantation structure. According to the calculation of the agricultural
WF, the
WF of wheat and rice are very large. Therefore, the crops with small
WF, such as maize, vegetables, and melons, should be given priority for cultivation, and the planting of wheat and rice should be discouraged. Beijing can import crops with large
WF from water-rich regions to ease the pressure of water resources, which will be cheaper than water transfer projects [
49].