Hydraulic Simulations
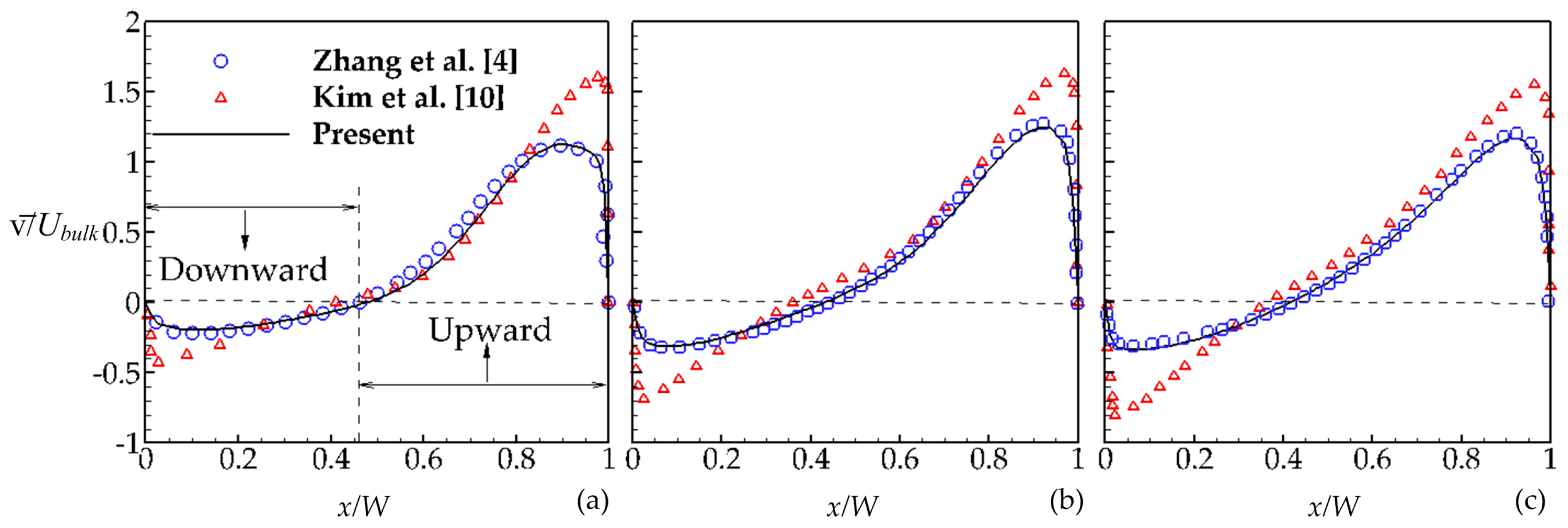
Span-wise averaged vertical velocity profiles obtained from RANS simulation are compared with the RANS results reported in the literature [
4,
10] at different vertical locations in the third chamber in
Figure 2. The present numerical results are in good agreement with the results of [
4]. However, some discrepancy is observed near the solid walls between the present results and [
10]. The negative vertical velocity near the inlet of the chamber indicates that the flow in this region is in a downward direction, which indicates that the downward flow in this region is a part of the large circulating zone that develops in the third chamber to the left of the jet zone. This implies that in RANS solution there is one circulation zone and this outcome is different than the LES simulation results, which capture a second recirculation zone, as will be discussed later. The absence of a second recirculation region near the inlet of the third chamber shows that RANS simulation could not capture the dynamically important eddies, whereas in the LES results two counter-rotating recirculation regions have been observed in the vicinity of the inlet. In the RANS solution the flow direction changes from vertically negative to positive at
along the chamber width, as shown in
Figure 2a. This implies that a large recirculation region is occupying the region to the left of the jet region in the chamber. We note that the upward flow in the chamber occurs in both the recirculation and jet regions, which are separated by the separation layer. The key question that will be addressed in what follows is: How much of the upward flow is in the jet region and how much of it is in the recirculation region? This separation is important in defining the hydraulic efficiency of the chamber.
Figure 2 also shows that the position of the peak velocity of the water jet shifts towards the wall horizontally as the flow develops in an upward direction.
The Reynolds number of the flow considered in this study is in transition range. The k-ε turbulence model selected in this application is more suitable for high Reynolds number flows, which may be used in the numerical simulation of full-scale contact tanks due to its lower computational power requirements in comparison to LES. The use of an improved low Reynolds number turbulence model would have been better, as was used in [
9] to capture the hydrodynamics in water disinfection tanks for relatively low turbulence levels. In this study one purpose is the comparison of numerical results that were reported in the literature. Thus we have used the k-ε model to be consistent with those cases.
A series of LES runs were conducted in order to capture the dynamically varying large eddies in the tank and to achieve a validated time-averaged flow field. Flow parameters evaluated in the LES are in terms of mean flow and its turbulent fluctuating components since the flow field in the contact tank is characterized by time-varying turbulence effects. This is due to the action of the energetic coherent eddies, especially in the vicinity of the corner of the baffles at the inlet that creates the turbulent wakes to enter into the chamber. In the validation process of the LES results, some discrepancy has been observed between the previously reported LES results [
6,
10] and the results obtained in this study. This discrepancy was also evident in between these studies as well [
6,
10]. A comprehensive data analysis needs to be carried out to resolve this issue and to determine when the turbulent flow in the tank reaches mean flow spatially and temporally and over what period these time averages are to be computed for proper comparison of the results. Since the hydraulic efficiency analysis will be based on the time-averaged flow field in the later stages of this study, this characterization is important for that purpose as well.
The LES run was performed for 400 s. To analyze the mean flow chamber-by-chamber, four sampling lines are placed within the contact tank at the same coordinates of the velocity profiles, as reported in [
6,
10]. The location of these lines can be seen in
Figure 3 for each chamber. Mean velocity magnitudes and pressure are recorded for 100 points on each line and written to output files at
t = 5 s time intervals during the simulation duration of 400 s. The Euclidean norm can be used to evaluate the variation of a mean quantity
between two successive time levels,
n − 1 and
n. In this equation the subscript
i refers to the points sampled on the line and
may represent either the velocity or the pressure;
m is the chamber number:
The variation of
for velocity and pressure with time at each sampling line is shown in
Figure 4. It can be seen in this figure that the difference between two successive time levels is high at the initial stages of the simulation and this difference starts to decrease as the flow reaches the mean flow condition as a function of time. This occurs after approximately
t = 300 s, which corresponds to approximately 300,000 time steps since time step size is variable during a simulation based on the Courant stability condition. Note that the LES mean results in [
10] were obtained using Δ
t = 0.005 s and at 10,000 time steps, which corresponds to
t = 50 s. The output data is scattered in the early stages of the simulation at
t = 50 s, which collapses to a narrow band as the simulation time increases. The results shown in
Figure 4 indicate that the flow in the contact tank reaches almost mean flow spatially after
t ≈ 300 s in this simulation. It would be useful to compare the duration to a characteristic time scale. Theoretical mean residence time can be used as a characteristic time scale for the contact tank system studied, which is defined as the ratio of the volume of the tank to the flow rate. The theoretical mean residence time is calculated as τ = 109.2 s for the present contact tank. Finally, a numerical simulation needs to be performed during about 3τ in order to obtain a time-averaged flow field.
The time variations of instantaneous vertical velocities on the six points in
Figure 4 are recorded at each time step of the simulation and plotted in
Figure 5. These are normalized values using the bulk velocity at the inlet. Locations of the points were selected such that the large eddies would be dominant and peak values of the mean velocity profiles given in the literature could be captured (
Figure 3). One can observe from this figure that the intensity of turbulence is higher in the jet region compared to those in the wake region due to the high velocity magnitudes and momentum in vertical direction in the jet. As can be seen from
Figure 4a, it takes longer for the mean flow properties to establish in the wake region due to the time it takes for the wake effects to develop behind the baffle, whereas the flow reaches the mean flow values in a shorter period in the jet region. Thus the wake region requires more time to stabilize than the jet region, which should not be ignored when characterizing the mean flow conditions in the chamber. Thus, we can conclude that the stability characteristics of the wake region determine the time required to achieve mean flow conditions in the chambers and not the stability of the jet region. The direction of the vertical velocity at Point 4 is downward in the initial stages of the flow development since the momentum of recirculating flow in the large recirculation region that is separated from the jet flow forces the flow particles in the wake near the wall to move in the downward direction temporarily. Then, with the effect of dynamically important eddies near the entrance, the flow particles in the vicinity of the baffle move in the upward direction, which is evidence of formation of a counter-rotating second recirculation zone near the chamber inlet, with a maximum positive value at
t ≈ 24 s. It takes about 300 s to develop a mean-flow in the wake region, as can be seen in
Figure 4a and
Figure 5a.
Different averaging procedures can be used to identify the possibility of oscillations in instantaneous velocity at Point 4. Similar oscillations are not observed in the jet region since this region stabilizes very fast. This is another reason why the mean flow conditions should be based not on the evaluation of the mean flow stabilization in the jet region but on the stabilization of the wake region. The stabilization of the recirculation zone and the determination of recirculation zone volumes will be described in the following sections. The time variations of calculated time-averaged values are plotted in
Figure 5b in order to see the effect of different averaging procedures used to obtain mean flow field in the wake region. The time-averaged value of dimensionless vertical velocity at Point 4 was reported as 0.4 in [
6]. The same time-averaged value can be obtained by using different averaging methods and periods, namely continuous and moving averaging, as can be seen in
Figure 5b. This observation shows that when the continuous averaging is performed from
t = 20 s to
t = 41.4 s, the computed mean velocity is the same as the value that was obtained by using a moving average for 20 s at the same instant of time. Thus, in the present LES results, the capture of the same peak value as 0.4 is possible [
6] if the same averaging period is used. However, this comparison cannot be validated since the time period used in the averaging process was not given in [
6]. As can be seen in
Figure 5b, this peak value decreases with time as the recirculation zone behind the baffle inlet develops. Thus, to show the effect of longer simulations on the averaging process, the time-averaged flow profile is compared with the results at previous instants of time and also with the previously reported numerical results [
6,
10] in
Figure 6.
As can be seen in
Figure 6, there is a significant difference between the previously published LES results that appeared in the literature. This may be due to the use of different averaging periods and the starting time of this averaging process. The magnitudes of the velocity profile obtained in this study at
t = 40 s is consistent with the results of [
6], showing that the LES gives a higher vertical velocity at the initial stages of the simulation. However, the peak value of the velocity profile starts to decrease as can be seen in
Figure 5b and
Figure 6. This detailed analysis of different time-averaging data for the same flow conditions may show that the LES results reported in [
6] were probably obtained before the flow field in the chamber reaches the mean flow conditions with respect to wake parameters. It should be noted that the peak value of the jet flow is also shifting towards the wall with time as the flow develops, which is consistent with the results of [
10]. This may explain some of the differences that are reported in the literature. Probably all results are correct for the time averaging periods that are used. We were not able to confirm this since the time averaging periods used were not reported in earlier studies. However, we conclude that a minimum of 300 s simulation time is necessary for the stabilization of the flow in the wake region and the mean flow analysis in the chamber should be based on this period. The pressure parameter is not a sensitive indicator of mean flow in the chamber (
Figure 4b). Thus, pressure cannot be used to characterize the mean flow in the chamber.
It should be mentioned here that the effects of wall roughness are not considered in this study in order to be consistent with the previously reported numerical results. However, the effects of wall roughness must be considered at the implementation of wall functions in order to compare the numerical results with the experimental results, which are available for the hydrodynamics of contact tanks [
9,
24,
25,
26,
27,
28].
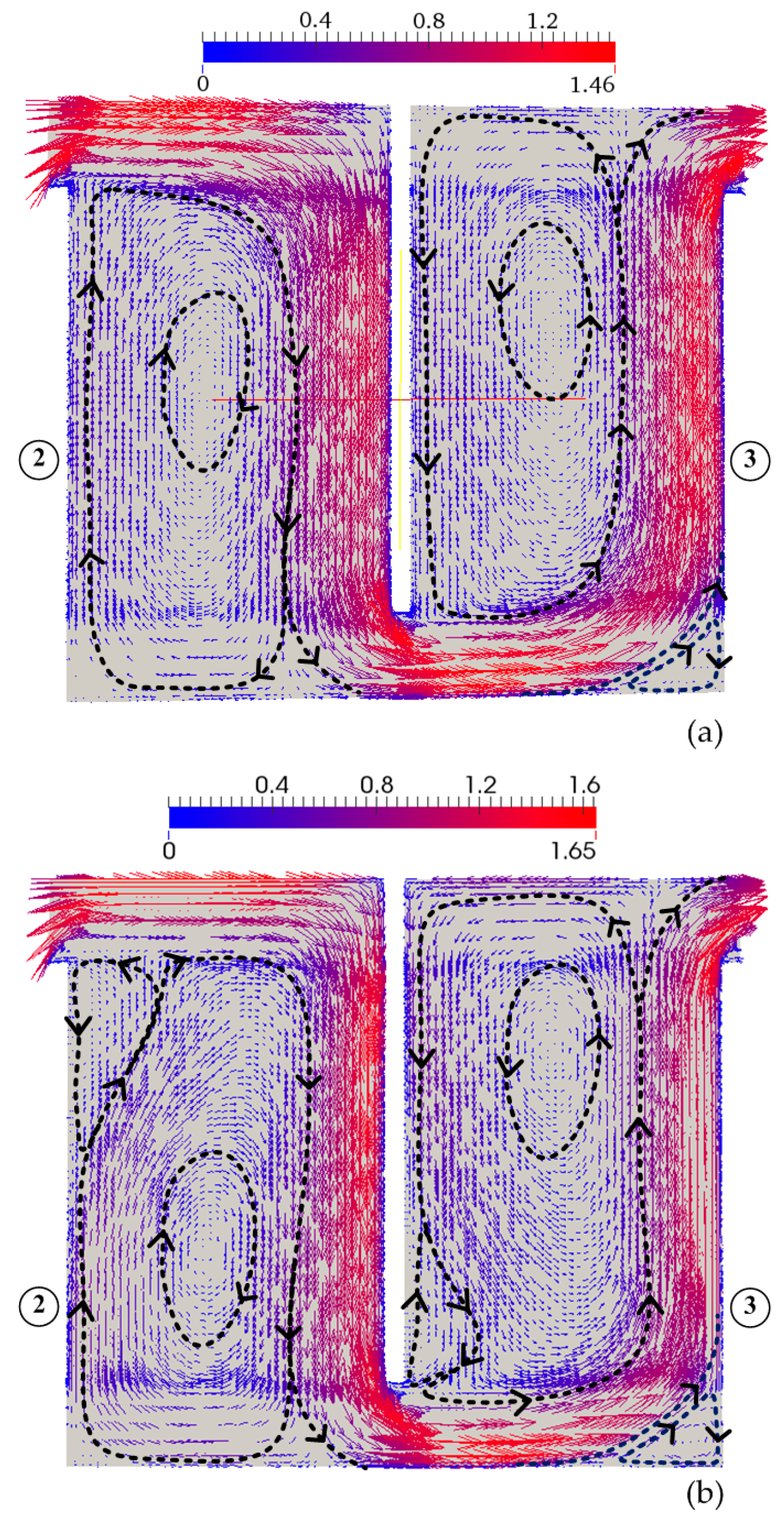
Velocity vectors along with the flow patterns represented by the dashed lines are shown for both steady state flow field in RANS and time-averaged flow field in LES in
Figure 7. Steady state flow field in RANS (
Figure 7a) depicts a large recirculation region and jet region in Chamber 2, whereas two recirculation zones and a jet region are encountered in Chamber 3, showing that the flow characteristics are not identical in adjacent chambers. Short-circuiting effects in Chamber 3 are greater than in Chamber 2 since the thickness of the jet region in Chamber 3 is smaller due to the presence of a short recirculation zone at the right-bottom corner of Chamber 3 and a relatively larger recirculation zone. Flow velocity in the jet region will increase as the thickness of the jet gets smaller to pass the same flow rate through a smaller fluid volume, which is responsible for the short-circuiting effects. The vertical location of the center of the recirculation region in Chamber 2 is below the center of recirculation zone in Chamber 3, which will be also shown later by the definition of the Lamb vector in order to locate the vortex core line accurately.
In LES results, another recirculation zone is encountered in the vicinity of the inlet of the chamber due to energetically important eddies near the sharp edge of the baffle, which could only be simulated in LES as shown in
Figure 7b, even though the same grid resolution was used in RANS. This comparison of flow patterns in RANS and LES shows that RANS could not capture the unsteady entrance effects due to the energetic eddies since only time-averaged field of turbulence effects are simulated in RANS. The thickness of the flow jet reduces in LES due to the presence of the wake region at the entrance of the chamber, which produces a greater maximum dimensionless flow velocity of 1.65 in the jet flow, which is 13% higher than the maximum flow velocity obtained in RANS.
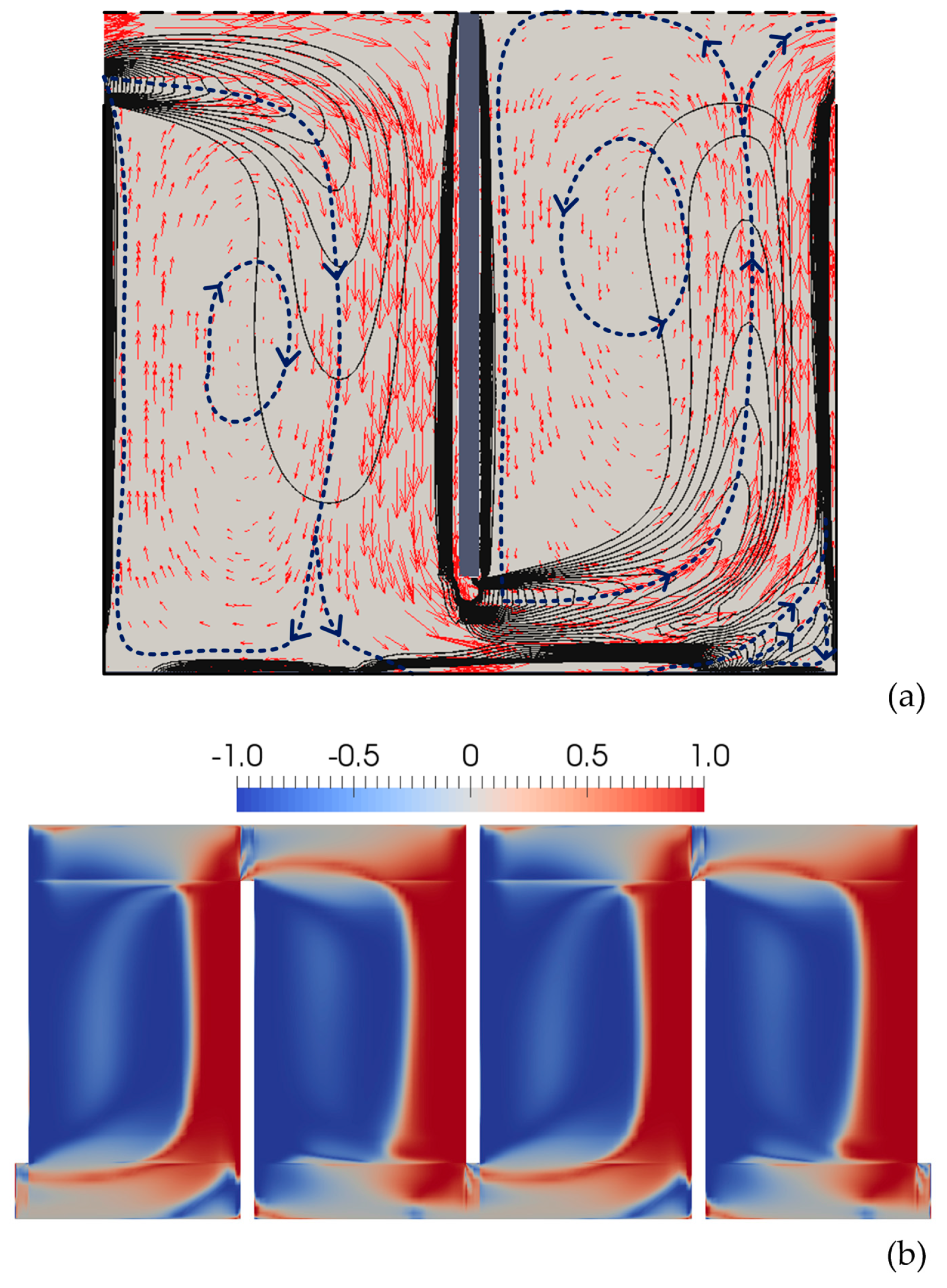
Based on the LES studies conducted in the present study, the general structure of the time-averaged flow field in the tank has been identified as shown in
Figure 8 schematically. Large (2
2 and 2
3) and small (4
3) recirculating regions are evolving in the chambers, separated from each other by water jets (3
2 and 3
3). Here the capital number shows the zone number and the subscript shows the chamber number. The separation layer between the jet region and recirculation region develops at the inlet of the chamber and impinges on the right baffle at approximately the same elevation as the inlet, which can also be seen in
Figure 7b. Similar behavior has been observed in the adjacent flow pattern between the jet region and recirculation region in Chamber 2, in which the flow tends to separate from the mean flow when it approaches the outlet opening. This observation shows that the baffle opening has a positive effect on the efficiency of the chamber at reducing the areas of the recirculation regions. The flow field in the downward and upward directions in Chambers 2 and 3 can theoretically be separated by a layer that splits the region into recirculation and jet flow regions. The separation layer could be identified based on the flow characteristics. Different definitions are available in the literature to distinguish rotational (recirculation zones) from the mean flow (jet region), as mentioned earlier.
In addition to primary recirculation regions, a secondary recirculation region has been observed at the upper and lower parts of the inlet of Chambers 2 and 3, respectively. It should be noted that the small recirculation regions (12 and 13) correspond to the energetically dynamic eddies in the vicinity of the sharp corner of the baffles, which could be captured by LES only. In this study, gradient of vorticity and flexion product concepts will be employed to identify the separation layer.
Three recirculation regions are encountered in Chamber 3, whereas only two recirculation zones appear in Chamber 2 since the free-slip boundary condition (less resistance) at the top of the computational domain does not allow the evolution of a recirculation zone at the upper right corner of Chamber 2. A recirculation zone cannot be observed at the bottom left corner of Chamber 2 due to low flow velocities near the corner. This observation confirms that the flow characteristics in each chamber are distinct, and thus the hydraulic efficiency of each chamber is not identical.