Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America
Abstract
:1. Introduction
2. Methods
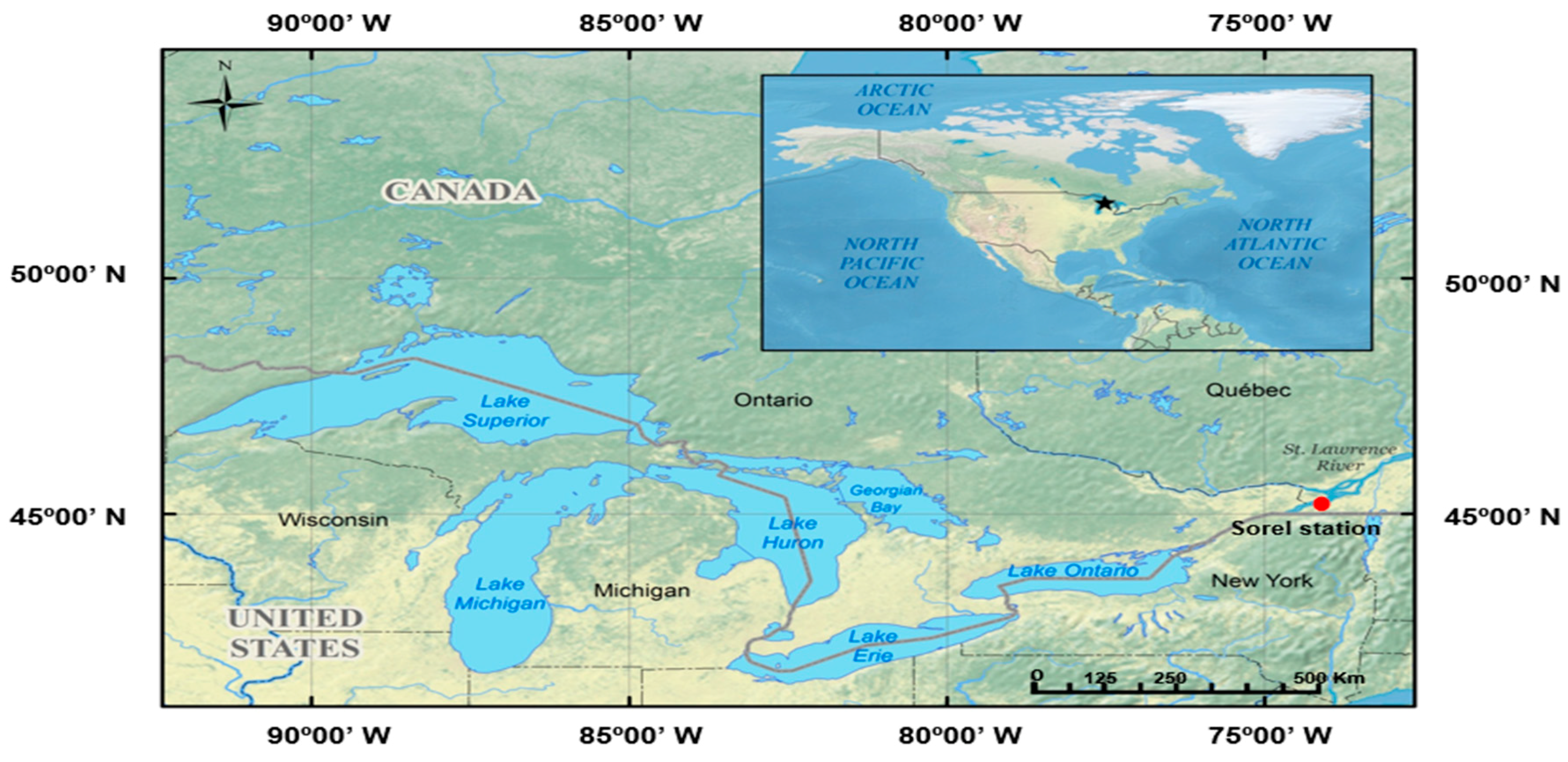
2.1. Study Sites and Source of Hydrological Data
2.2. Statistical Analysis
3. Results
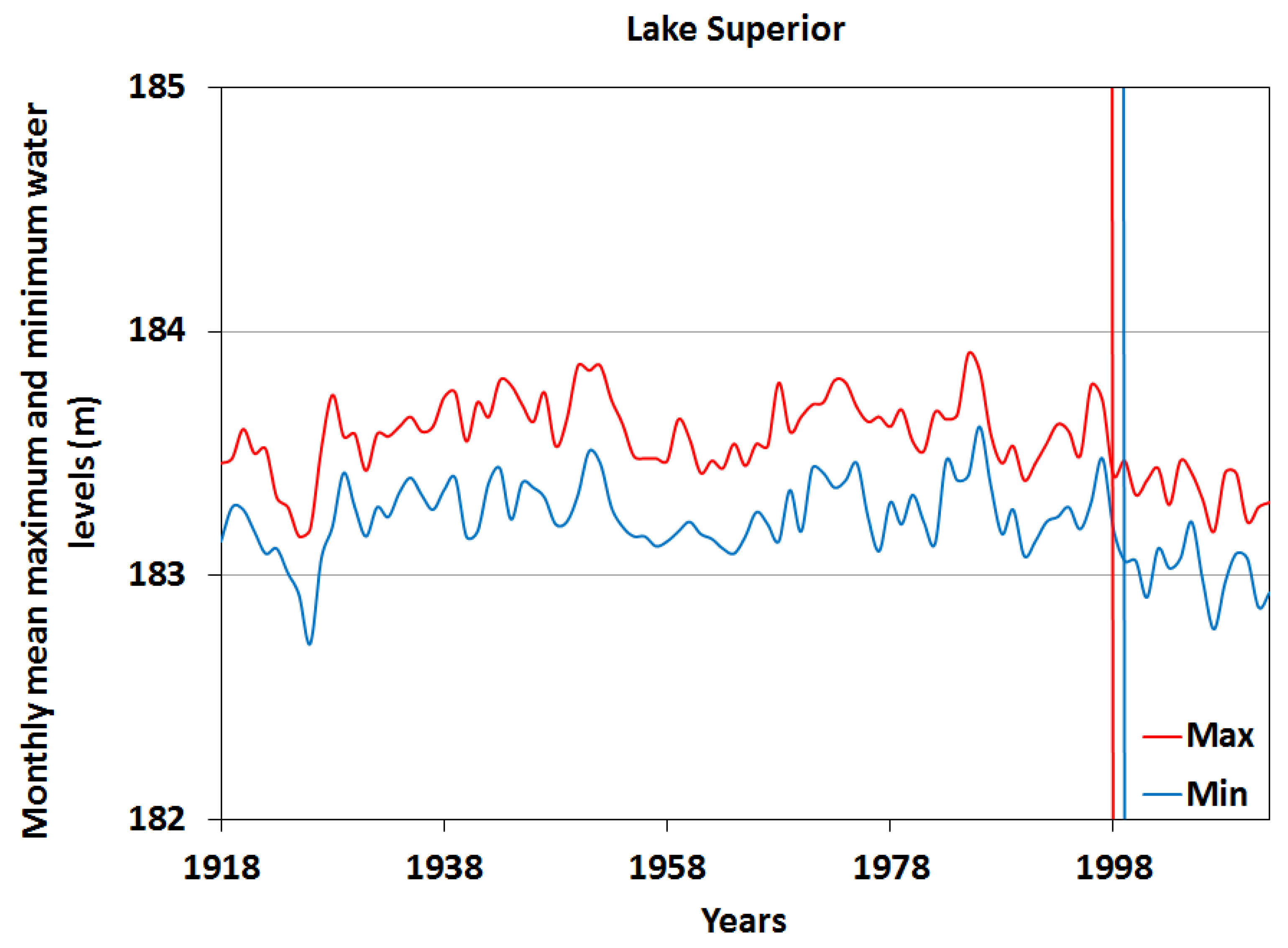
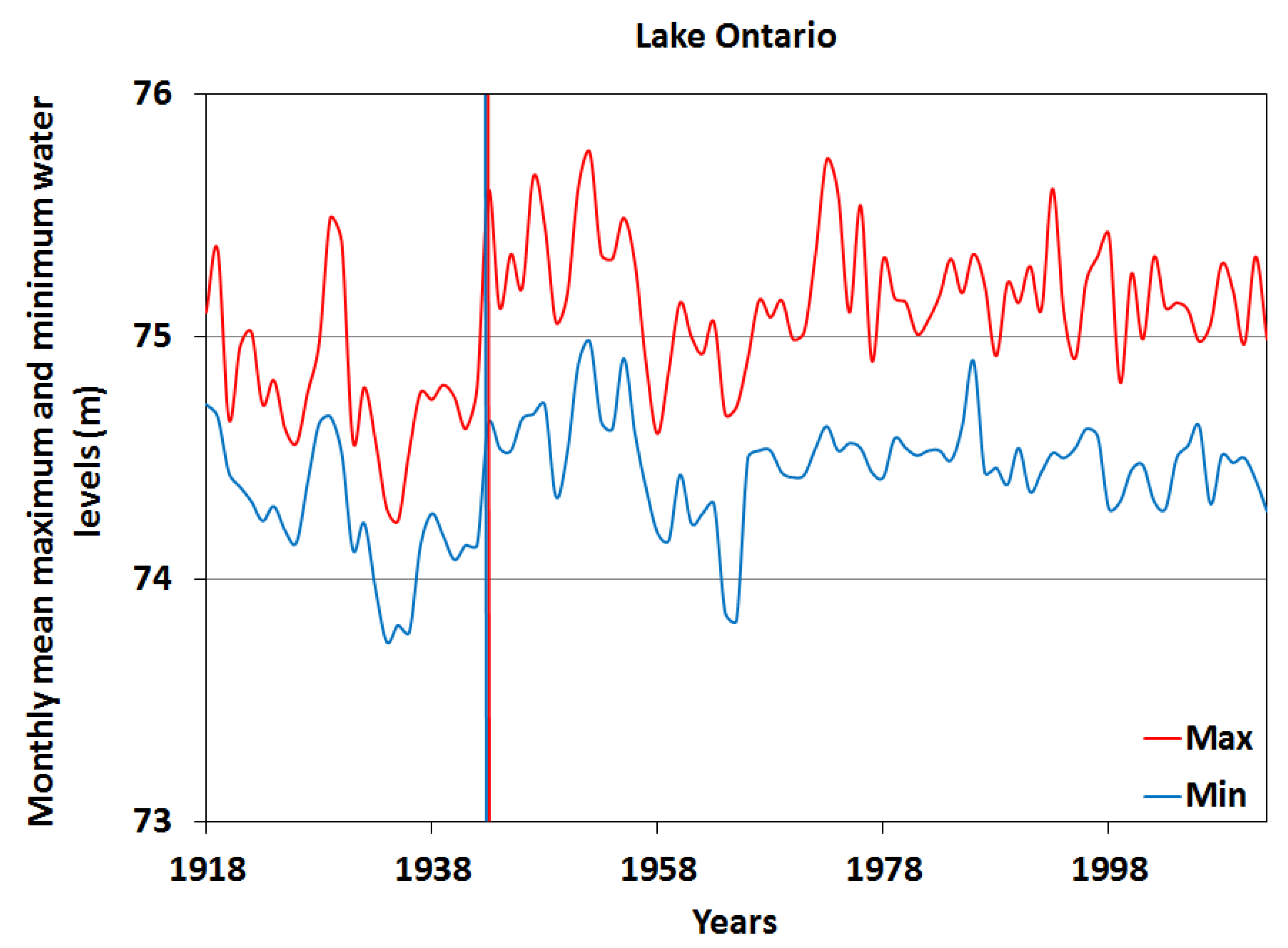
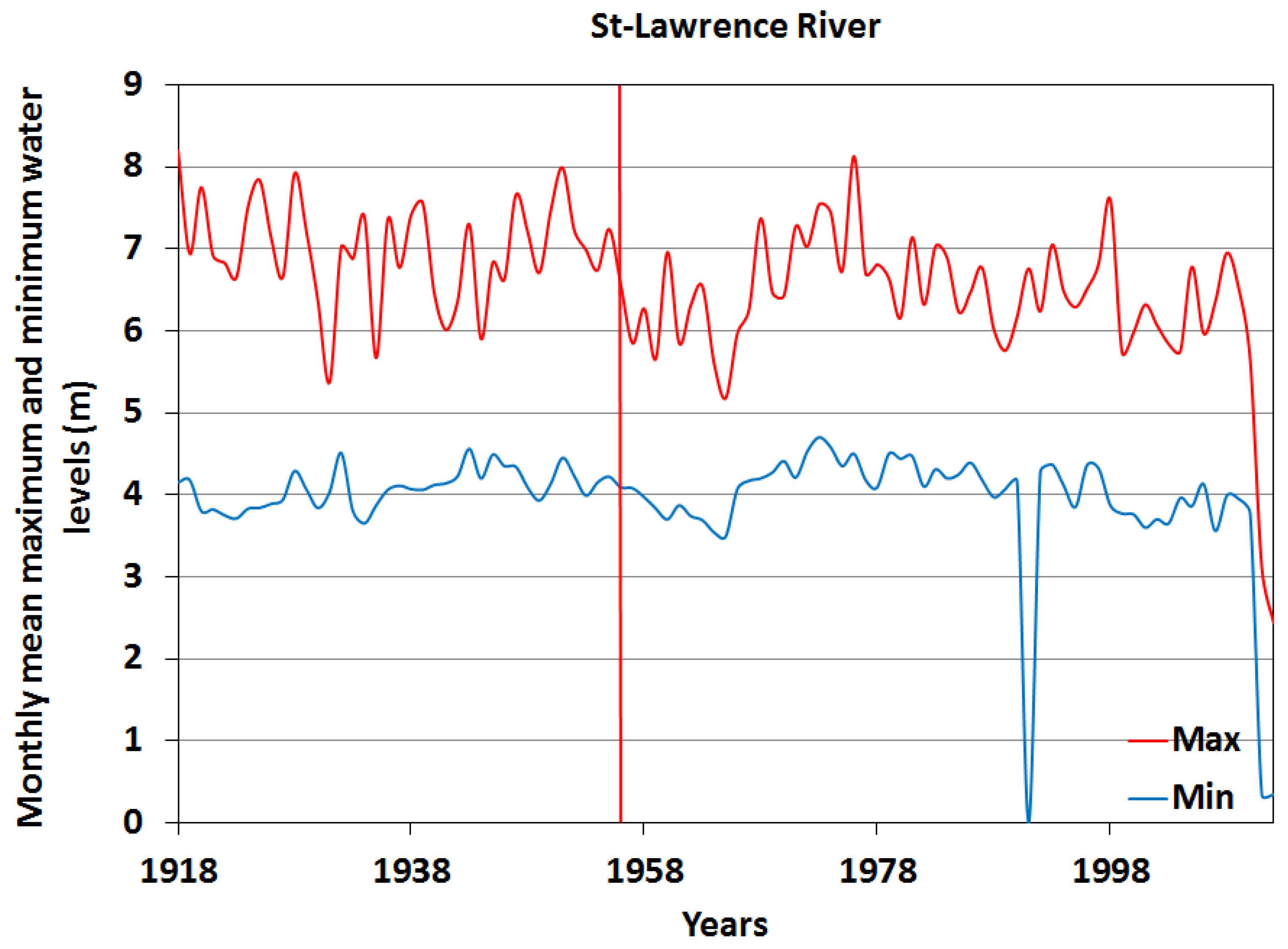
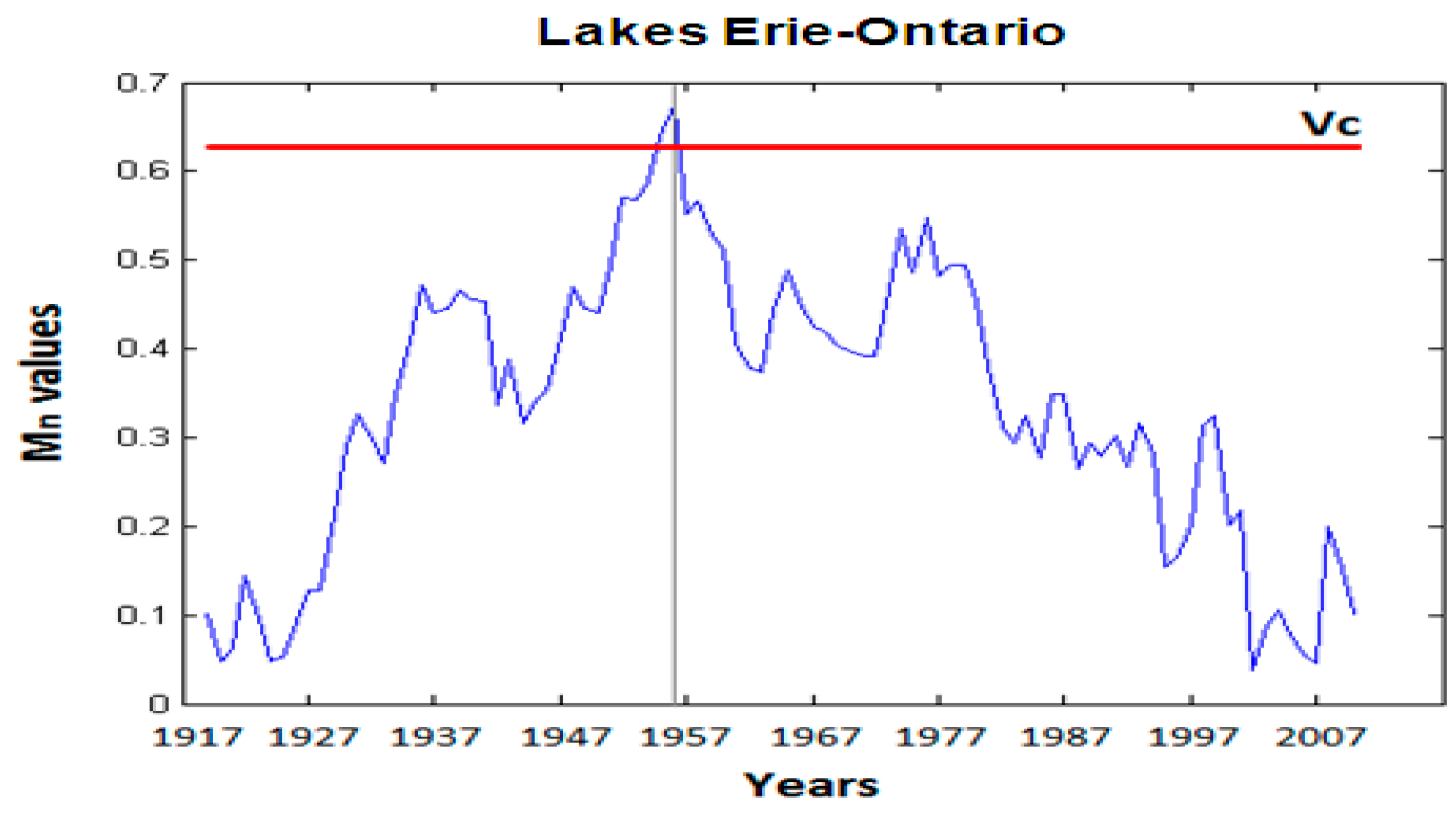
3.1. Analysis of Water Level Stationarity
3.2. Analysis of Dependence Using the Copula Method
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Clites, A.H.; Quinn, F.H. The history of Lake Superior regulation: Implications for the future. J. Gt. Lakes Res. 2003, 29, 157–171. [Google Scholar] [CrossRef]
- Lee, D.H.; Quinn, F.H.; Sparks, D.; Rassam, J.C. Modification of great lakes regulation plans for simulation of maximum Lake Ontario outflows. J. Gt. Lakes Res. 1994, 20, 569–582. [Google Scholar] [CrossRef]
- Quinn, F.H. Lake Superior regulation effects. Water Resour. Bull. 1978, 14, 1129–1142. [Google Scholar] [CrossRef]
- Quinn, F.H. Anthropogenic changes to Great Lakes water levels. Gt. Lakes Update 1999, 136, 1–4. [Google Scholar]
- Assani, A.A.; Landry, R.; Stacey, B.; Frenette, J.J. Analysis of the interannual variability of annual daily extreme water levels in the St. Lawrence River and Lake Ontario from 1918 to 2010. Hydrol. Process. 2014, 28, 4011–4022. [Google Scholar] [CrossRef]
- Assani, A.A.; Landry, R.; Azouaoui, O.; Massicotte, P.; Gratton, D. Comparison of the characteristics (frequency and timing) of drought and wetness indices of annual mean water levels in the five North American Great Lakes. Water Resour. Manag. 2016, 30, 359–373. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Webster, K.E.; Assel, R.A.; Bowser, C.J.; Dillon, P.J.; Eaton, J.G.; Evans, H.E.; Fee, E.J.; Hall, R.I.; Mortsch, L.R.; et al. Potential effects of climate changes on aquatic systems Laurentian Great Lakes and Precambrian Shield Region. Hydrol. Process. 1997, 11, 825–871. [Google Scholar] [CrossRef]
- Assani, A.A.; Gravel, E.; Buffin-Bélanger, T.; Roy, A.G. Impacts of dams on the annual minimum discharges according to artificialized hydrologic regimes in Quebec (Canada). J. Water Sci. 2005, 16, 103–127. (In French) [Google Scholar]
- Assani, A.A.; Stichelbout, E.; Roy, A.G.; Petit, F. Comparison of impacts of dams on the annual maximum flow characteristics in three regulated hydrologic regimes in Quebec (Canada). Hydrol. Process. 2006, 20, 3485–3501. [Google Scholar] [CrossRef]
- Government of Canada. Fisheries and Oceans. Historical Monthly and Yearly Mean Water Level 1918–2013. Available online: http://tides.gc.ca/C&A/historical-eng.html (accessed on 26 November 2013).
- Assel, R.A.; Quinn, F.H.; Sellinger, C.E. Hydroclimatic factors of the recent record drop in Laurentian great lakes water levels. Bull. Am. Meteorol. Soc. 2004, 85, 1143–1151. [Google Scholar] [CrossRef]
- Gronewold, A.A.; Fortin, V.; Logfren, B.; Clites, A.; Stow, C.A.; Quinn, F. Coasts, water levels, and climate change: A Great Lakes perspective. Clim. Chang. 2013, 120, 697–711. [Google Scholar] [CrossRef]
- McBean, E.; Motiee, H. Assessment of impact of climate change on water resources: A long term analysis of the Great Lakes of North America. Hydrol. Earth Syst. Sci. 2008, 12, 239–255. [Google Scholar] [CrossRef]
- Lombard, F. Rank tests for changepoint problems. Biometrika 1987, 74, 615–624. [Google Scholar] [CrossRef]
- Quessy, J.-F.; Favre, A.-C.; Saïd, M.; Champagne, M. Statistical inference in Lombard’s smooth-change model. Environmetrics 2011, 22, 882–893. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Ntelekos, A.A. Analyses of seasonal and annual maximum daily discharge records for Central Europe. J. Hydrol. 2011, 399, 299–312. [Google Scholar] [CrossRef]
- Assani, A.A.; Landry, R.; Daigle, J.; Chalifour, A. Reservoirs effects on the interannual variability of winter and spring streamflow in the St. Maurice River Watershed (Quebec, Canada). Water Resour. Manag. 2011, 25, 3661–3675. [Google Scholar] [CrossRef]
- Mazouz, R.; Assani, A.A.; Quessy, J.-F. Comparison of the interannual variability of spring heavy floods characteristics of tributaries of the St. Lawrence in Quebec (Canada). Adv. Water Resour. 2012, 35, 110–120. [Google Scholar] [CrossRef]
- Quessy, J.-F.; Saïd, M.; Favre, A.-C. Multivariate Kendall’s tau for change-point detection in copulas. Can. J. Stat. 2012, 40, 1–18. [Google Scholar] [CrossRef]
- Guerfi, N.; Assani, A.A.; Mesfioui, M.; Kinnard, C. Comparison of the temporal variability of winter daily extreme temperatures and precipitations in southern Quebec (Canada) using the Lombard and copula methods. Int. J. Climatol. 2015, 35, 4237–4246. [Google Scholar] [CrossRef]
- Austin, J.; Colman, S. Lake Superior summer water temperature are increasing more rapidly than regional air temperature: A positive ice-albedo feedback. Geophys. Res. Lett. 2007, 34, L06604. [Google Scholar] [CrossRef]
- Van Cleave, K.; Lenters, J.D.; Wang, J.; Verhamme, E.M. A regime shift in Lake Superior ice cover, evaporation, and water temperature following the warm El Nino winter of 1997–1998. Limnol. Oceanogr. 2014, 59, 1889–1898. [Google Scholar] [CrossRef]




| Minimum | Maximum | |||||
|---|---|---|---|---|---|---|
| Sn | T1 | T2 | Sn | T1 | T2 | |
| Lake Superior | 0.0493 | 1998 | 1999 | 0.0627 | 1997 | 1998 |
| Lakes Michigan-Huron | 0.0204 | - | - | 0.0167 | - | - |
| Lake Erie | 0.2974 | 1966 | 1968 | 0.2300 | 1967 | 1970 |
| Lake Ontario | 0.1236 | 1942 | 1943 | 0.0417 | 1942 | 1943 |
| St. Lawrence River | 0.0123 | - | - | 0.1042 | 1955 | 1956 |
| Lake | Minimum | Maximum | |||||
|---|---|---|---|---|---|---|---|
| Periods | Sn | T1 | T2 | Sn | T1 | T2 | |
| Superior | 1918–1997 | 0.0201 | - | - | 0.0201 | - | - |
| 1998–2012 | 0.0097 | - | - | 0.0286 | - | - | |
| Erie | 1918–1965 | 0.0341 | - | - | 0.0276 | - | - |
| 1969–2012 | 0.2262 | 1997 | 1999 | 0.1716 | 1998 | 1999 | |
| Ontario | 1918–1941 | - | - | - | 0.0389 | - | - |
| 1944–2012 | - | - | - | 0.0045 | - | - | |
| St. Lawrence | 1918–1954 | - | - | - | 0.0063 | - | - |
| 1957–2012 | - | - | - | 0.0104 | - | - | |
| Minimum | Maximum | |||||
|---|---|---|---|---|---|---|
| Sn | T1 | T2 | Sn | T1 | T2 | |
| Lake Superior | 0.0416 | 1996 | 1997 | 0.0245 | - | - |
| Lakes Michigan-Huron | 0.0233 | - | - | 0.0003 | - | - |
| Lake Erie | 0.0138 | - | - | 0.0286 | - | - |
| Lake Ontario | 0.2416 | 1965 | 1966 | 0.1962 | 1958 | 1959 |
| St-Lawrence River | 0.0161 | - | 0.0129 | - | - | |
| Minimums | Maximums | |||||||
|---|---|---|---|---|---|---|---|---|
| Mn | Vc | p-Values | T | Mn | Vc | p-Values | T | |
| Superior-Michigan | 0.6702 | 0.8763 | 0.1880 | - | 0.7651 | 0.8080 | 0.0730 | - |
| Michigan-Erie | 0.5418 | 0.5339 | 0.0430 | 1970 | 0.5209 | 0.5419 | 0.0670 | - |
| Erie-Ontario | 0.9593 | 0.6690 | 0.0000 | 1958 | 0.6753 | 0.6278 | 0.0280 | 1956 |
| Ontario-St.Lawrence | 0.4620 | 0.8912 | 0.291 | - | 0.7641 | 0.7950 | 0.065 | - |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Assani, A.A. Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America. Water 2016, 8, 485. https://doi.org/10.3390/w8110485
Assani AA. Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America. Water. 2016; 8(11):485. https://doi.org/10.3390/w8110485
Chicago/Turabian StyleAssani, Ali Arkamose. 2016. "Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America" Water 8, no. 11: 485. https://doi.org/10.3390/w8110485
APA StyleAssani, A. A. (2016). Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America. Water, 8(11), 485. https://doi.org/10.3390/w8110485






