Risk Analysis of Reservoir Flood Routing Calculation Based on Inflow Forecast Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
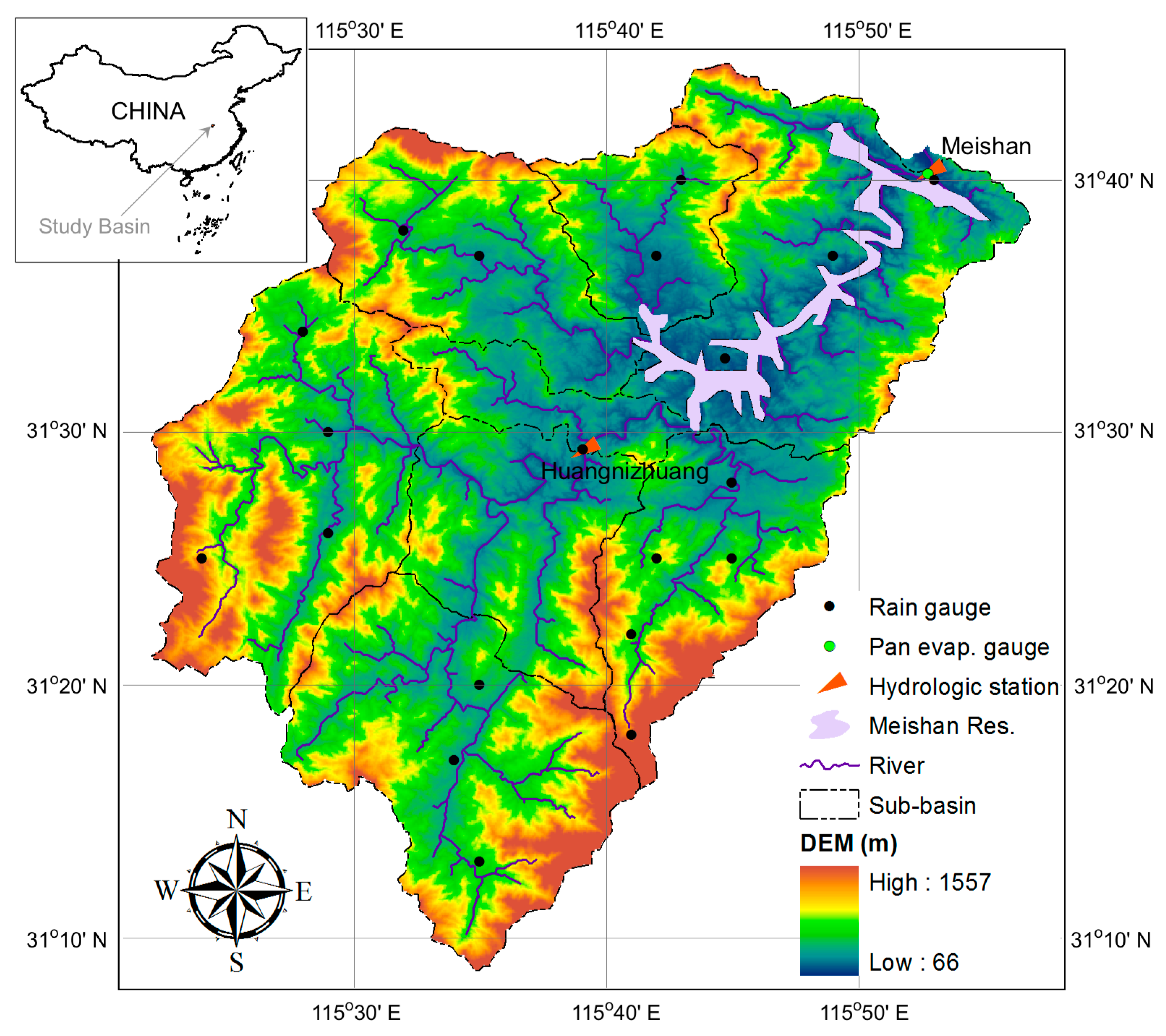
2.1. Study Basin and Forcing Data
2.2. The Xinanjiang Model
- when WU + P ≥ EP,EU = EP, EL = 0, ED = 0;
- when WU + P < EP and WL ≥ C·WLM,EU = WU + P, EL = (EP − EU)·WL/WLM, ED = 0;
- when WU + P < EP and C·(EP − EU) ≤ WL < C·WLM,EU = WU + P, EL = C·(EP − EU), ED = 0;
- when WU + P < EP and WL < C·(EP − EU),EU = WU + P, EL = WL, ED = C·(EP − EU) − EL;
2.3. The HUP Model
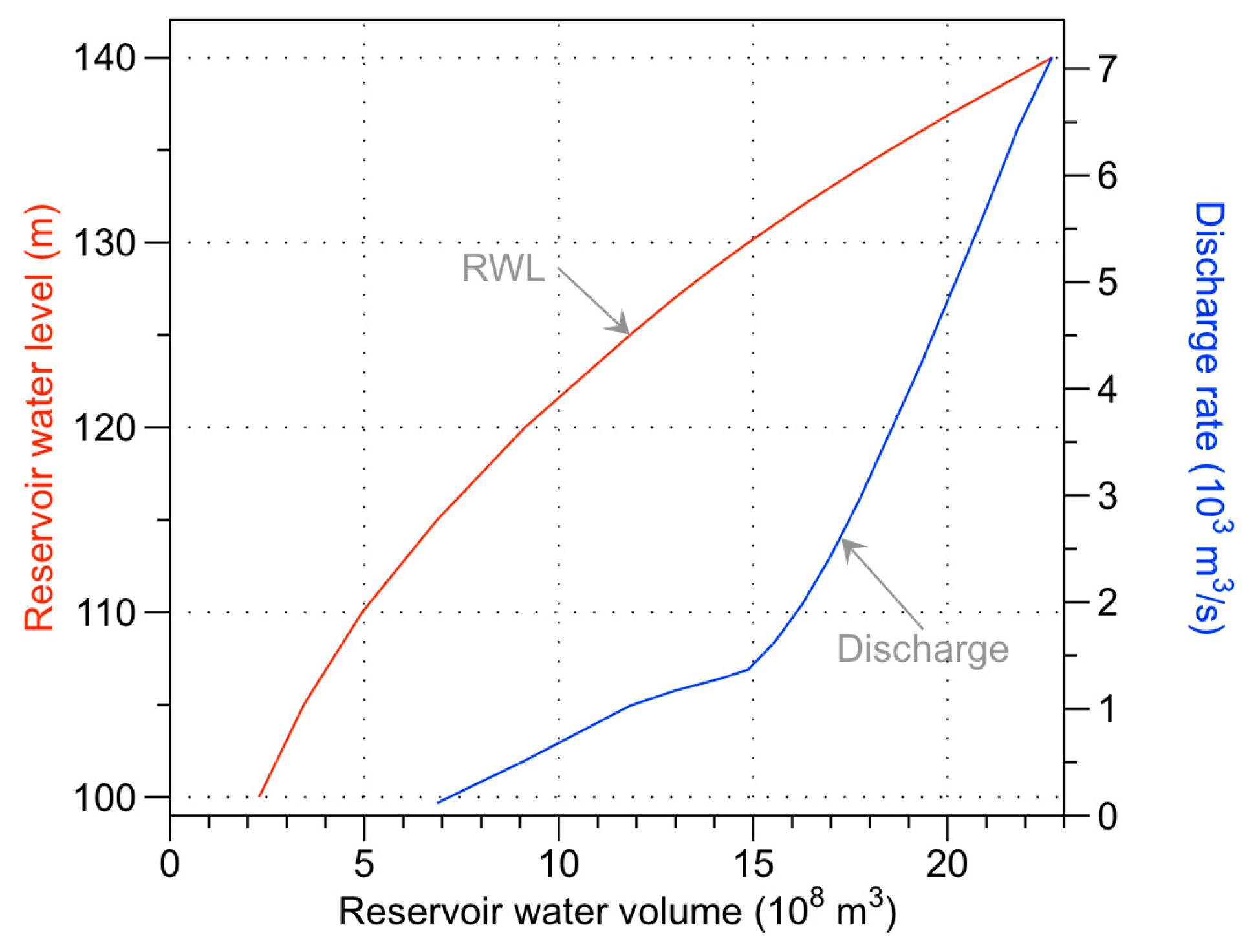
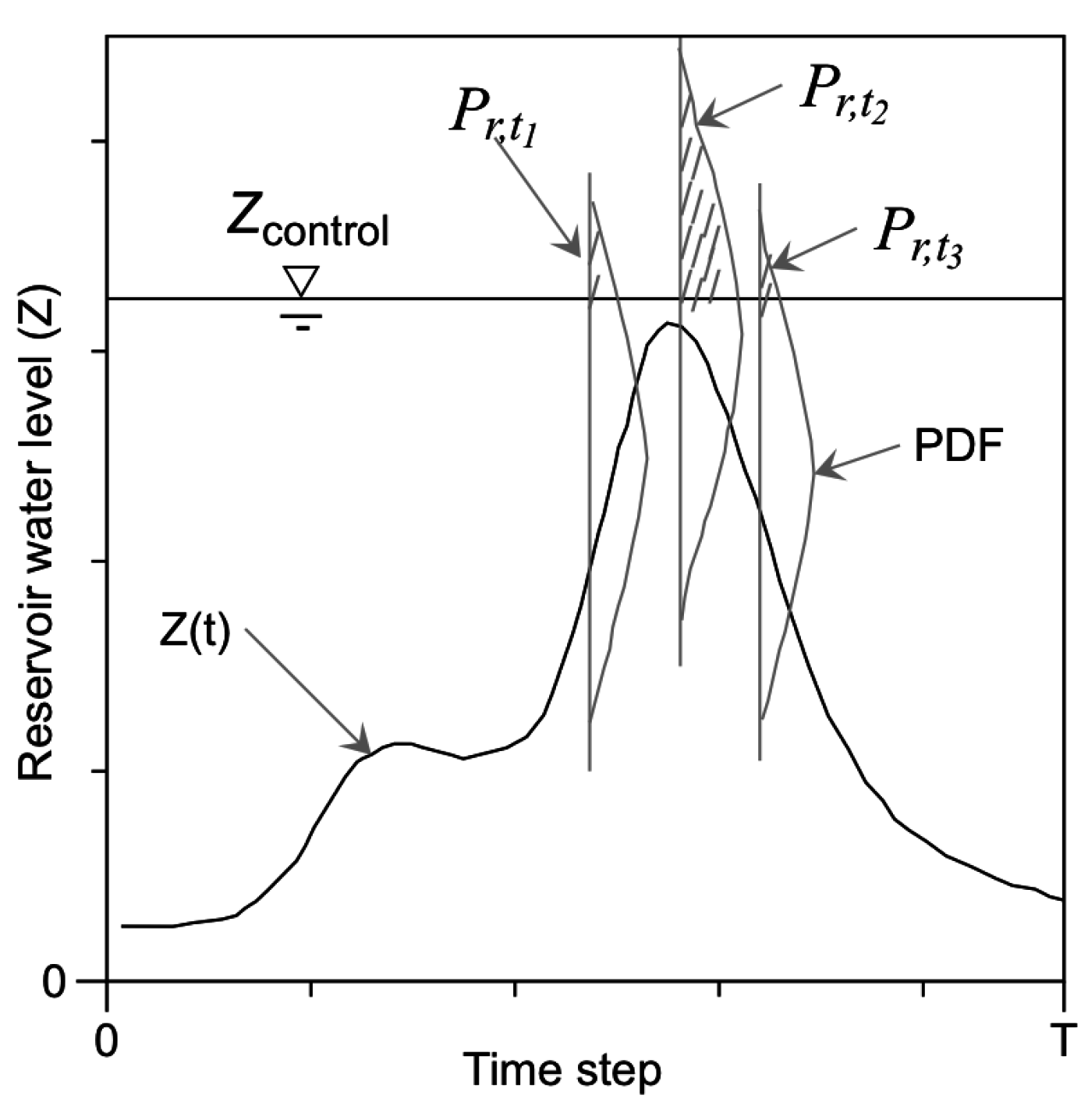
2.4. Risk Rate in Reservoir Flood Routing Calculation
3. Results and Discussion
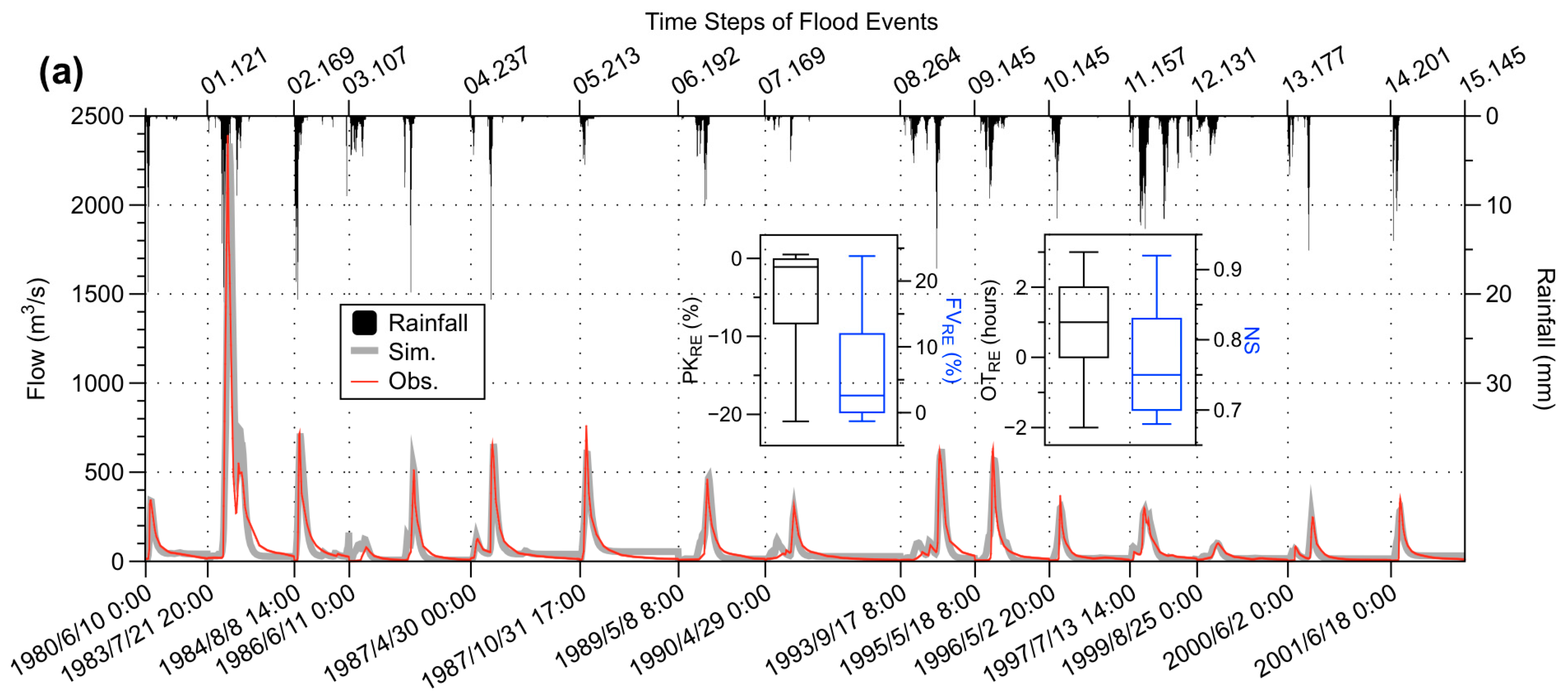
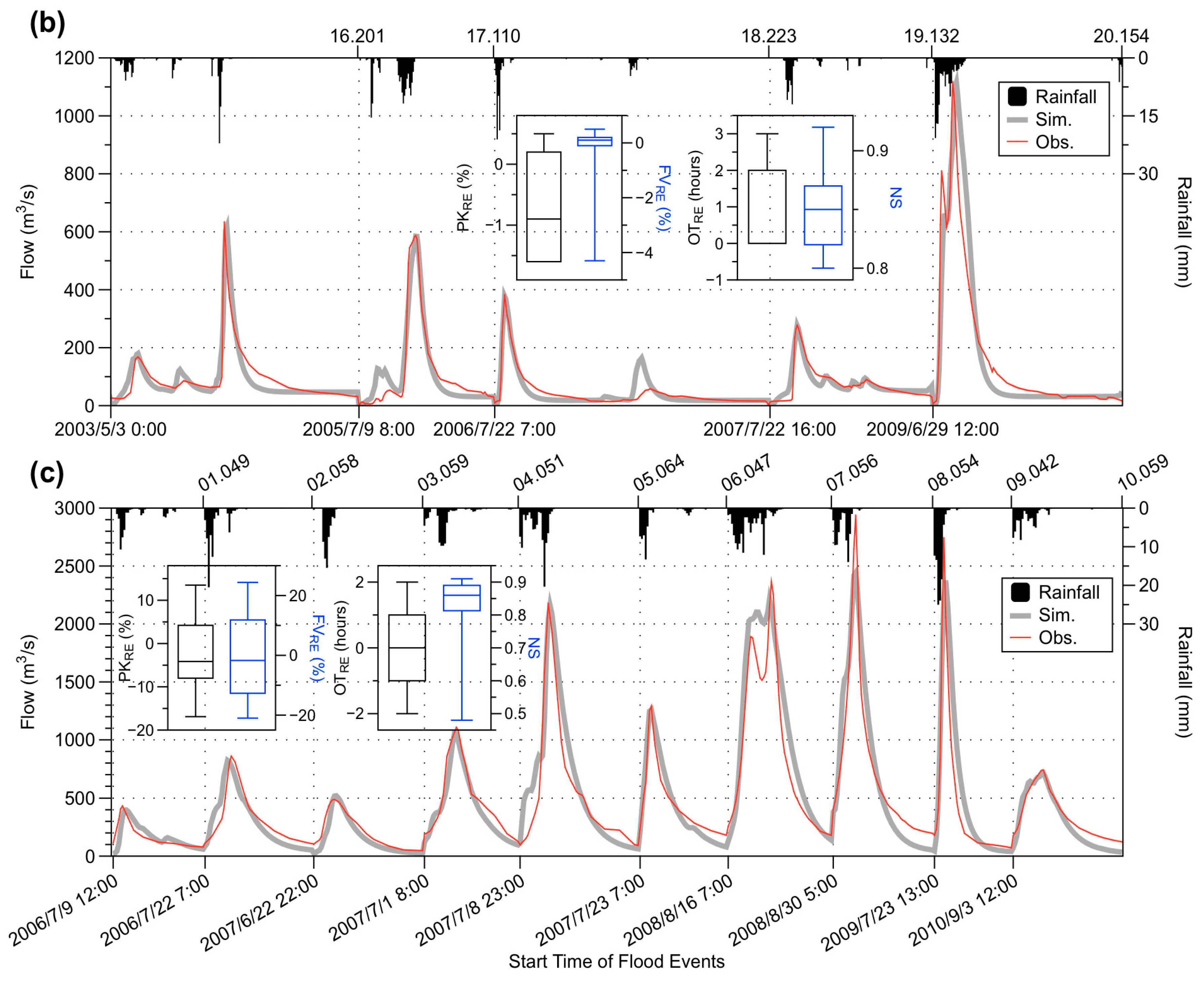
3.1. Calibration and Validation of Xinanjiang Model
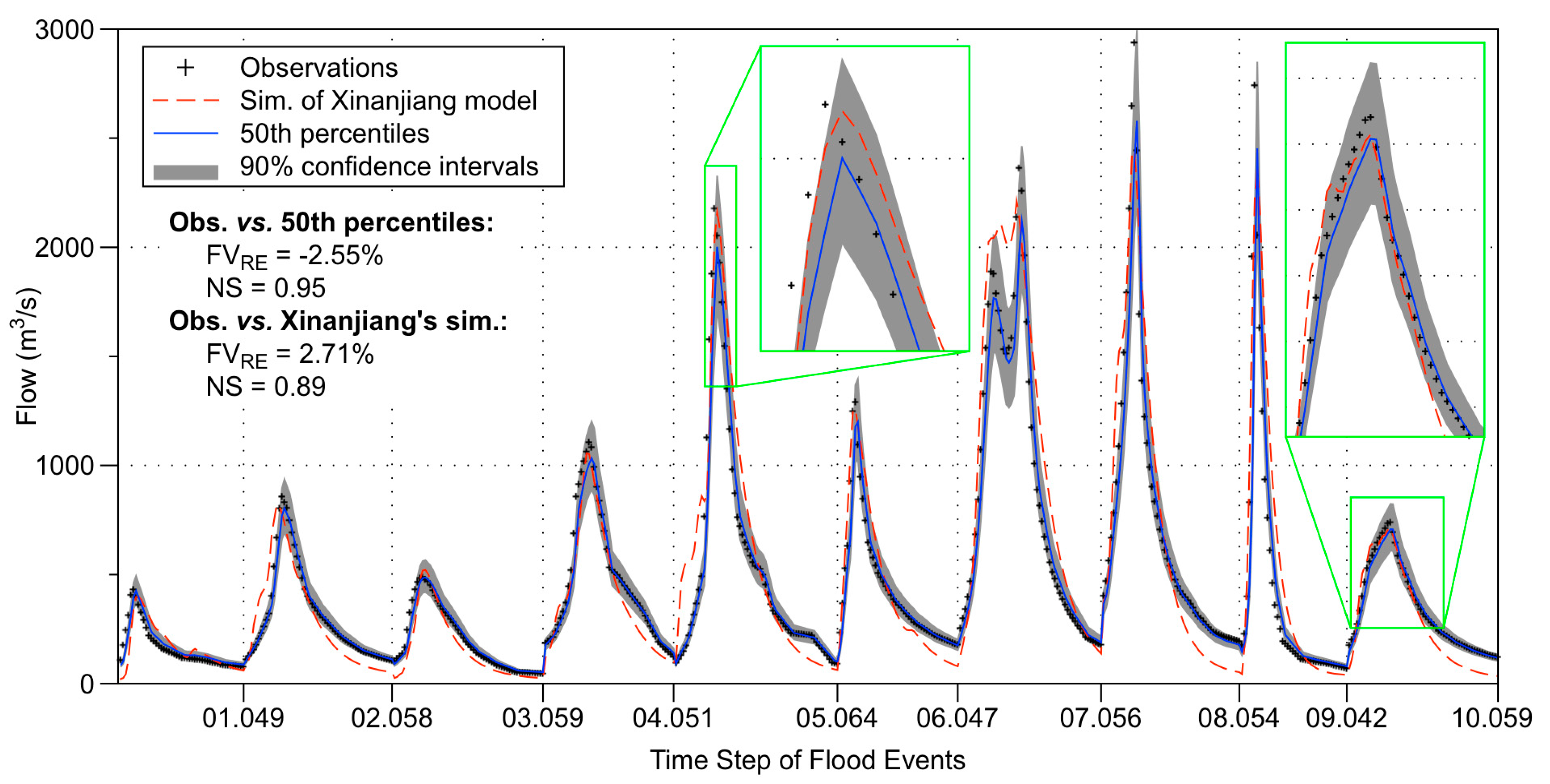
3.2. Inflow Forecast Uncertainty Analysis
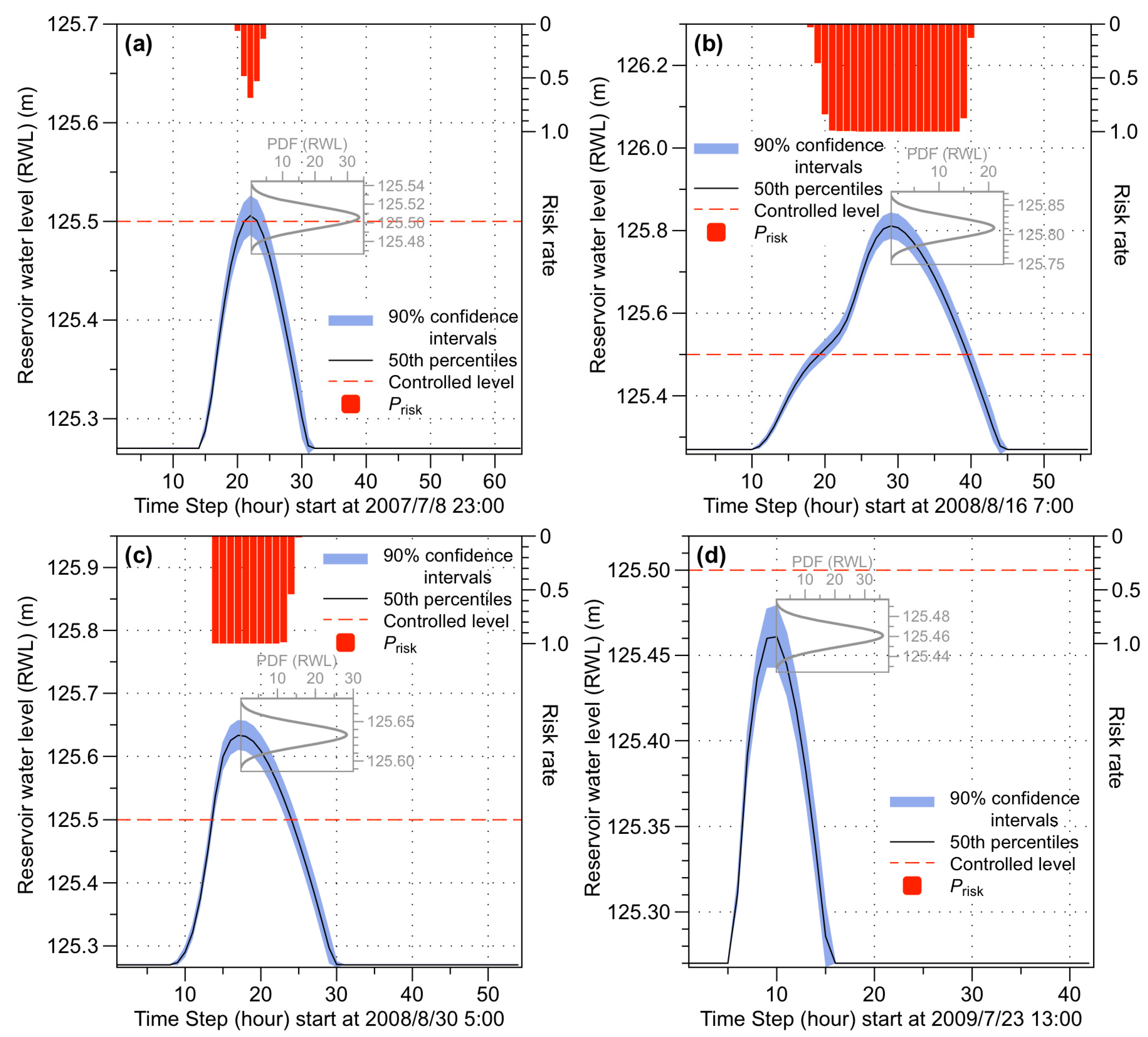
3.3. Risk Rate Calculation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mendoza, P.A.; McPhee, J.; Vargas, X. Uncertainty in flood forecasting: A distributed modeling approach in a sparse data catchment. Water Resour. Res. 2012, 48, W09532. [Google Scholar] [CrossRef]
- Beven, K.; Jim, H. Applied Uncertainty Analysis for Flood Risk Management; World Scientific: London, UK, 2014. [Google Scholar]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43, W01403. [Google Scholar] [CrossRef]
- Li, B.; Yu, Z.; Liang, Z.; Song, K.; Li, H.; Wang, Y.; Zhang, W.; Acharya, K. Effects of climate variations and human activities on runoff in the Zoige alpine wetland in the eastern edge of the Tibetan Plateau. J. Hydrol. Eng. 2014, 19, 1026–1035. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, S.; Zhang, H.; Liu, D.; Yang, G. Comparative study of three updating procedures for real-time flood forecasting. Water Resour. Manag. 2016, 30, 2111–2126. [Google Scholar] [CrossRef]
- Li, B.; Liang, Z.; He, Y.; Hu, L.; Zhao, W.; Acharya, K. Comparison of parameter uncertainty analysis techniques for a TOPMODEL application. Stoch. Environ. Res. Risk Assess. 2016. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A Markov Chain Monte Carlo Scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Kuczera, G.; Kavetski, D.; Franks, S.; Thyer, M. Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters. J. Hydrol. 2006, 331, 161–177. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]
- DeChant, C.M.; Moradkhani, H. On the assessment of reliability in probabilistic hydrometeorological event forecasting. Water Resour. Res. 2015, 51, 3867–3883. [Google Scholar] [CrossRef]
- Todini, E. History and perspectives of hydrological catchment modelling. Hydrol. Res. 2011, 42, 73–85. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Labadie, J.W. Chance-constrained optimal control for multireservoir system optimization and risk analysis. Stoch. Environ. Res. Risk Assess. 2001, 15, 185–204. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Peng, Y.; Zeng, R.; Zhou, H.; Cai, X. An analytical framework for flood water conservation considering forecast uncertainty and acceptable risk. Water Resour. Res. 2015, 51, 4702–4726. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, F.; Wu, J.X.; Fan, Z.W.; Wang, Y.Y. Application of minimum reward risk model in reservoir generation scheduling. Water Resour. Manag. 2016, 30, 1345–1355. [Google Scholar] [CrossRef]
- Jonkman, S.N.; van Gelder, P.H.A.J.M.; Vrijling, J.K. An overview of quantitative risk measures for loss of life and economic damage. J. Hazard. Mater. 2003, 99, 1–30. [Google Scholar] [CrossRef]
- Zhao, R.J. Flood Forecasting Method for Humid Regions of China; East China College of Hydraulic Engineering: Nanjing, China, 1977. [Google Scholar]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Wang, J.; Liang, Z.; Jiang, X.; Li, B.; Chen, L. Bayesian theory based self-adapting real-time correction model for flood forecasting. Water 2016, 8, 75. [Google Scholar] [CrossRef]
- Huaihe River Water Resources Commission. Handbook for Flood Control and Drought Relief of the Huaihe River Basin; Huaihe River Water Resources Commission: Bengbu, China, 2014. [Google Scholar]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F. One-dimensional statistical dynamic representation of subgrid spatial variability of precipitation in the two-layer variable infiltration capacity model. J. Geophys. Res. 1996, 101, 21403–21422. [Google Scholar] [CrossRef]
- Todini, E. The ARNO rainfall-runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, J.; Li, B.; Yu, Z. A statistically based runoff-yield model coupling infiltration excess and saturation excess mechanisms. Hydrol. Process. 2012, 26, 2856–2865. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Herr, H.D. Hydrologic uncertainty processor for probabilistic river stage forecasting: Precipitation-dependent model. J. Hydrol. 2001, 249, 46–68. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Kelly, K.S. Hydrologic uncertainty processor for probabilistic river stage forecasting. Water Resour. Res. 2000, 36, 3265–3277. [Google Scholar] [CrossRef]
| Evapotranspiration | Runoff Production | Runoff Separation | Runoff Concentration |
|---|---|---|---|
| KC = 0.998 | WM = 120 mm | SM = 10 mm | CI = 0.98 |
| WUM = 20 mm | B = 0.4 | EX = 1.2 | CG = 0.85 |
| WLM = 60 mm | IM = 0.1 | KG = 0.45 | CS = 0.01 |
| C = 0.2 | KI = 0.25 | L 1 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liang, Z.; Zhang, J.; Chen, X.; Jiang, X.; Wang, J.; Hu, Y. Risk Analysis of Reservoir Flood Routing Calculation Based on Inflow Forecast Uncertainty. Water 2016, 8, 486. https://doi.org/10.3390/w8110486
Li B, Liang Z, Zhang J, Chen X, Jiang X, Wang J, Hu Y. Risk Analysis of Reservoir Flood Routing Calculation Based on Inflow Forecast Uncertainty. Water. 2016; 8(11):486. https://doi.org/10.3390/w8110486
Chicago/Turabian StyleLi, Binquan, Zhongmin Liang, Jianyun Zhang, Xueqing Chen, Xiaolei Jiang, Jun Wang, and Yiming Hu. 2016. "Risk Analysis of Reservoir Flood Routing Calculation Based on Inflow Forecast Uncertainty" Water 8, no. 11: 486. https://doi.org/10.3390/w8110486
APA StyleLi, B., Liang, Z., Zhang, J., Chen, X., Jiang, X., Wang, J., & Hu, Y. (2016). Risk Analysis of Reservoir Flood Routing Calculation Based on Inflow Forecast Uncertainty. Water, 8(11), 486. https://doi.org/10.3390/w8110486







