Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants
Abstract
:1. Introduction
2. Materials and Methods
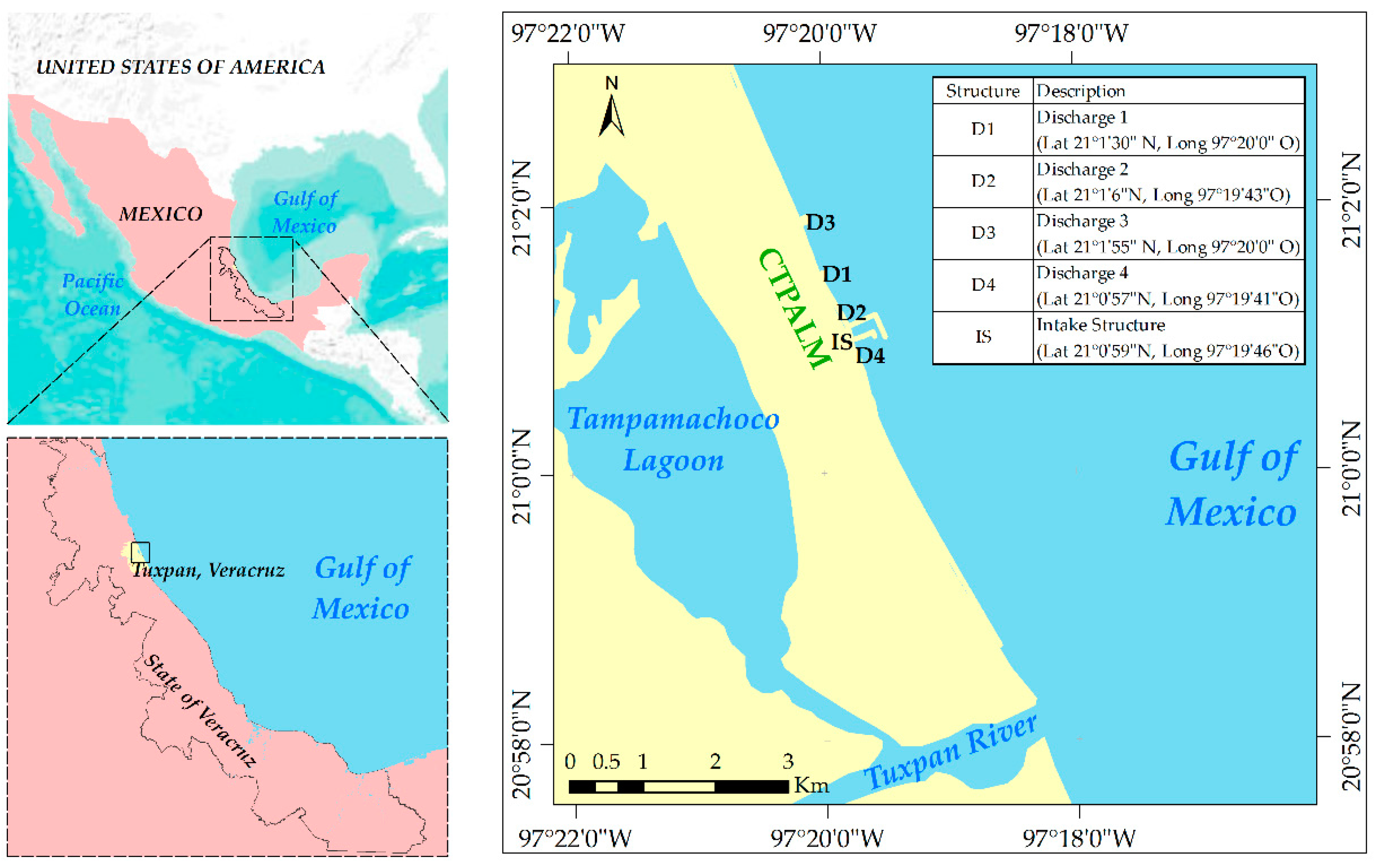
2.1. Case Study
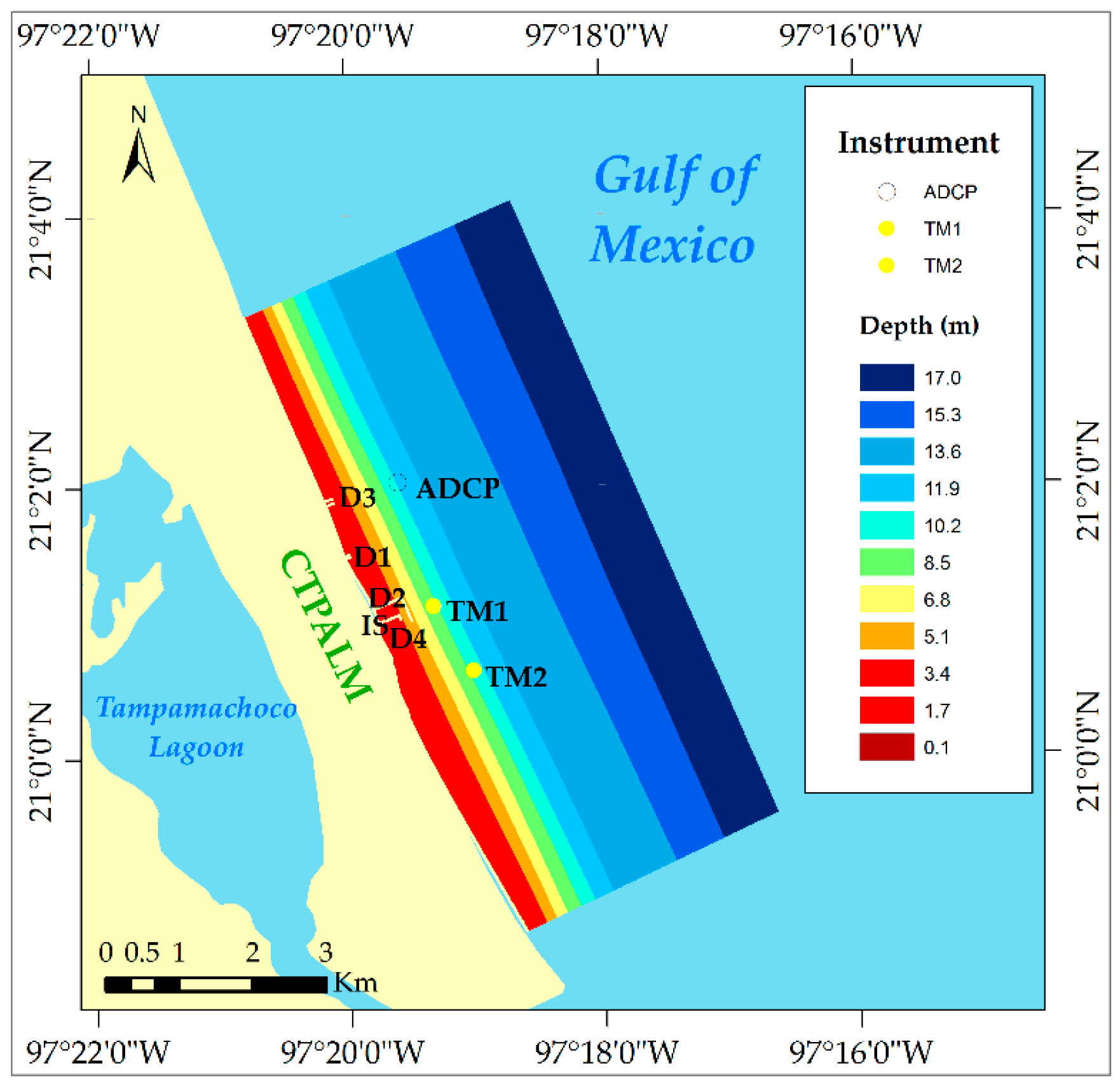
2.2. Field Measurements
2.3. Numerical Model
2.4. Implementation of the Numerical Model
3. Results and Discussion
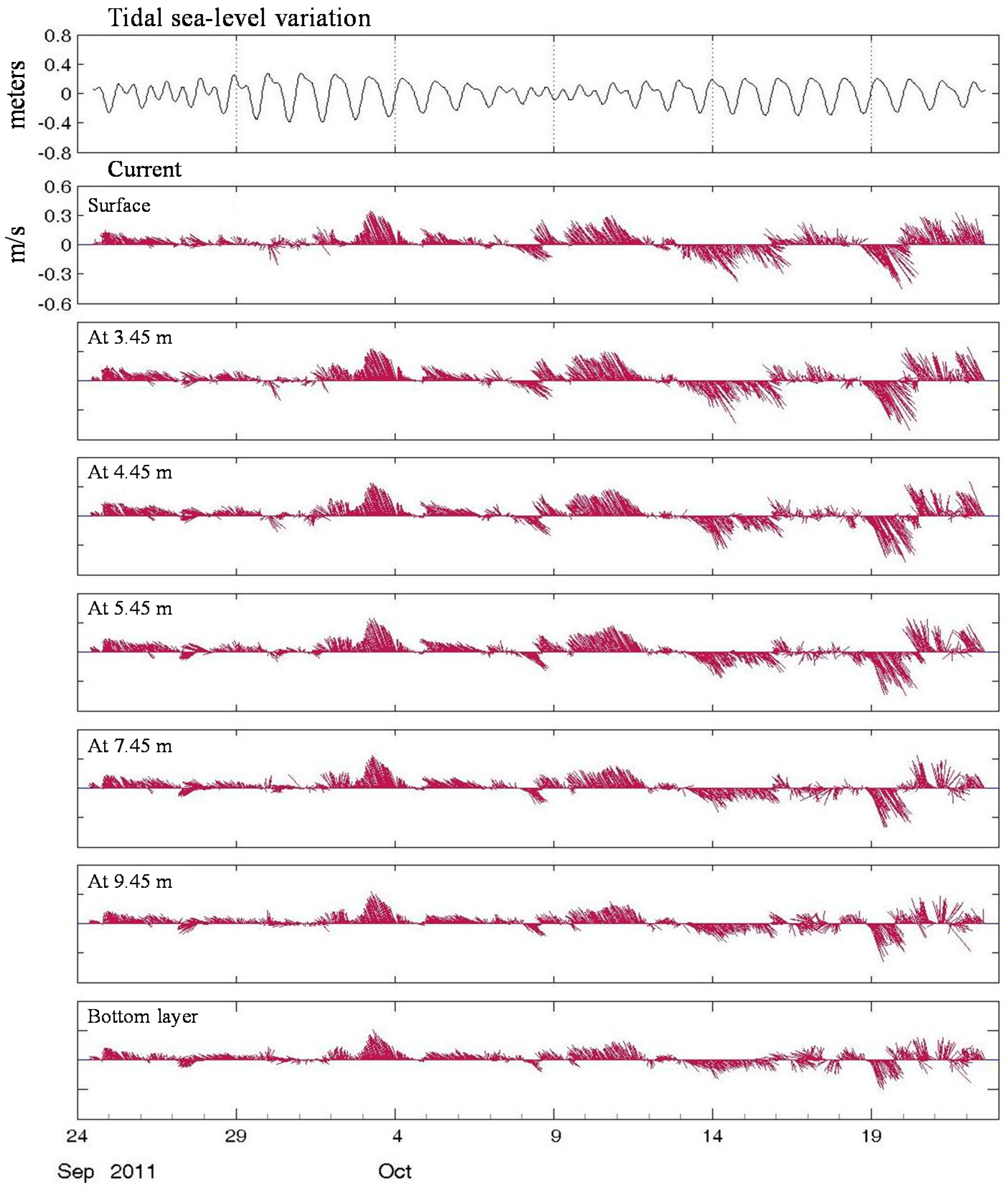
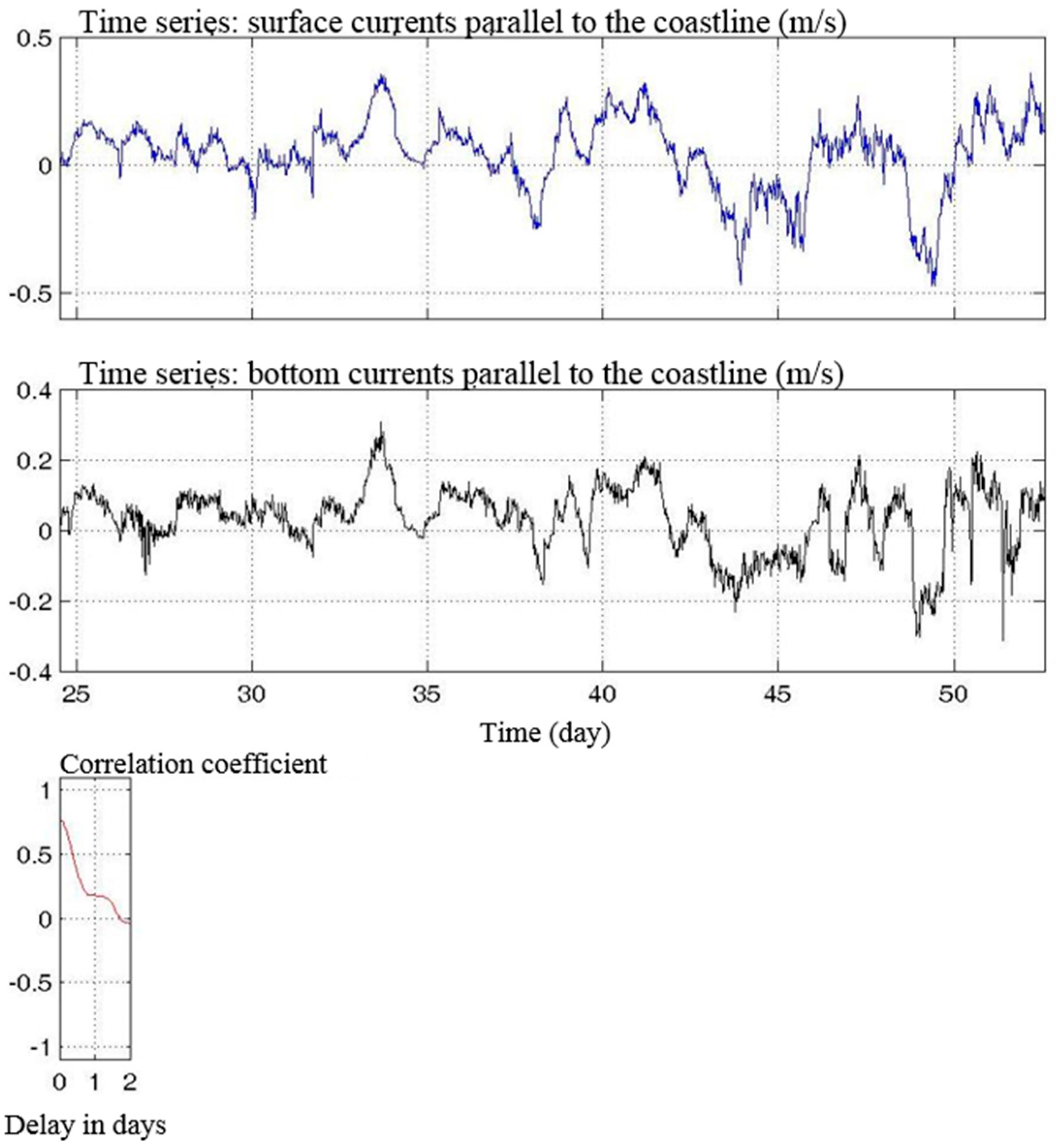
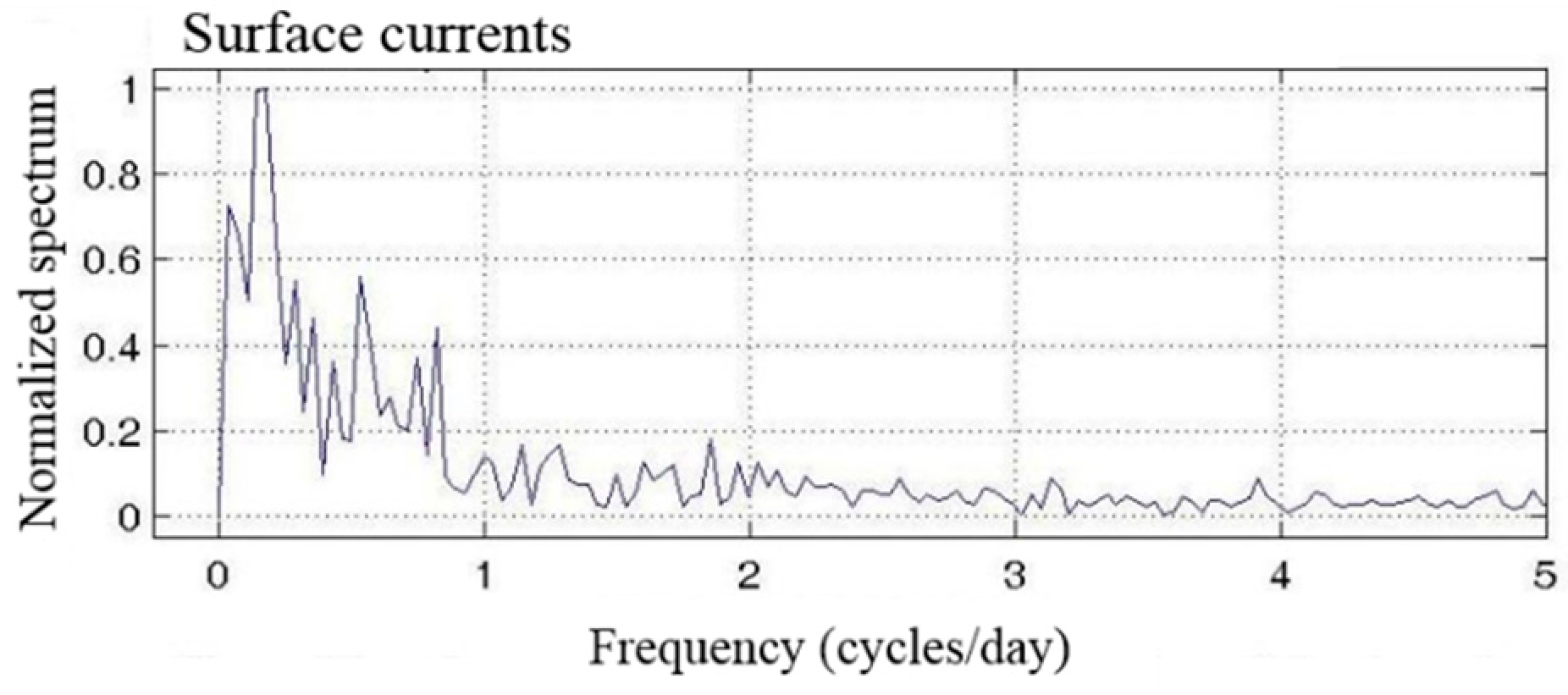
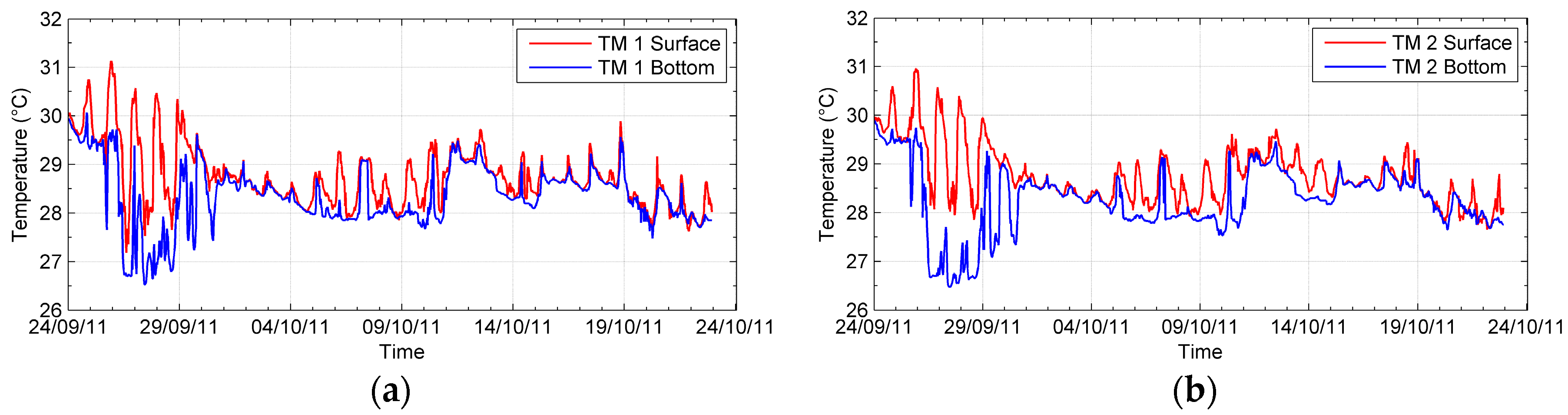
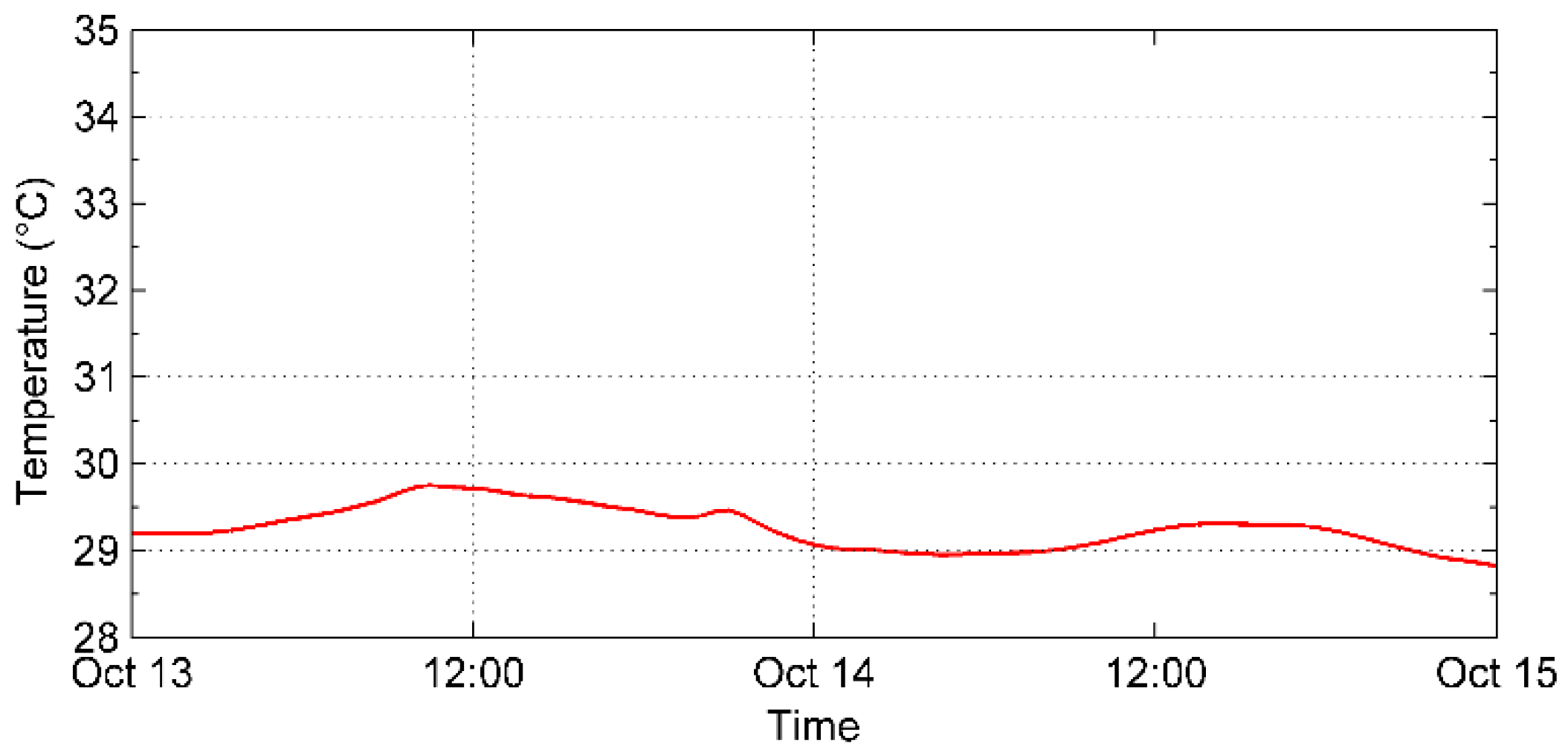
3.1. Results of the Field Measurements
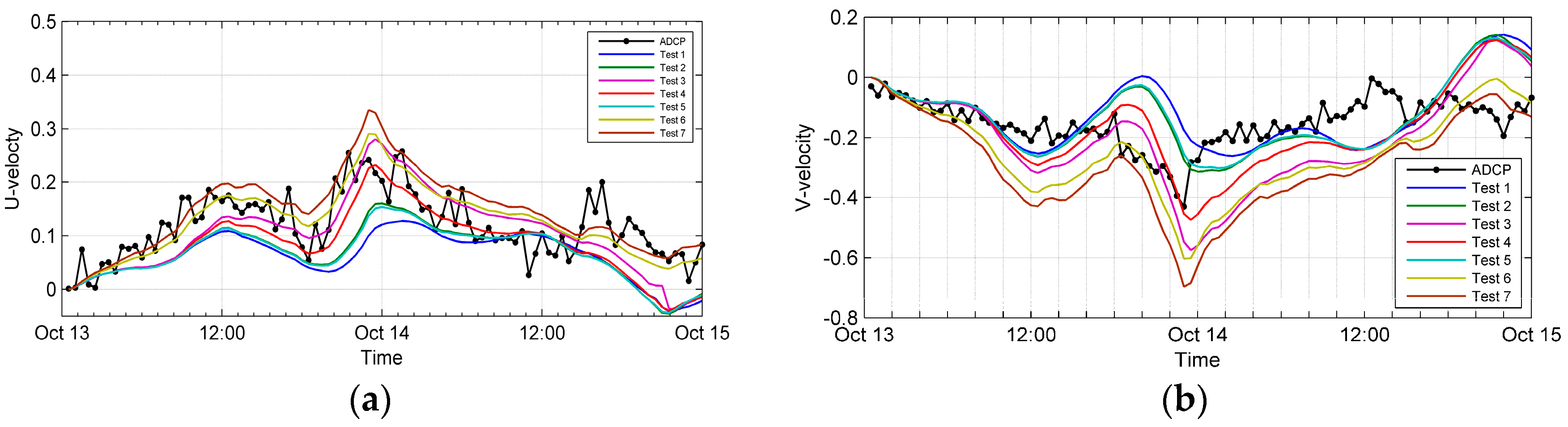
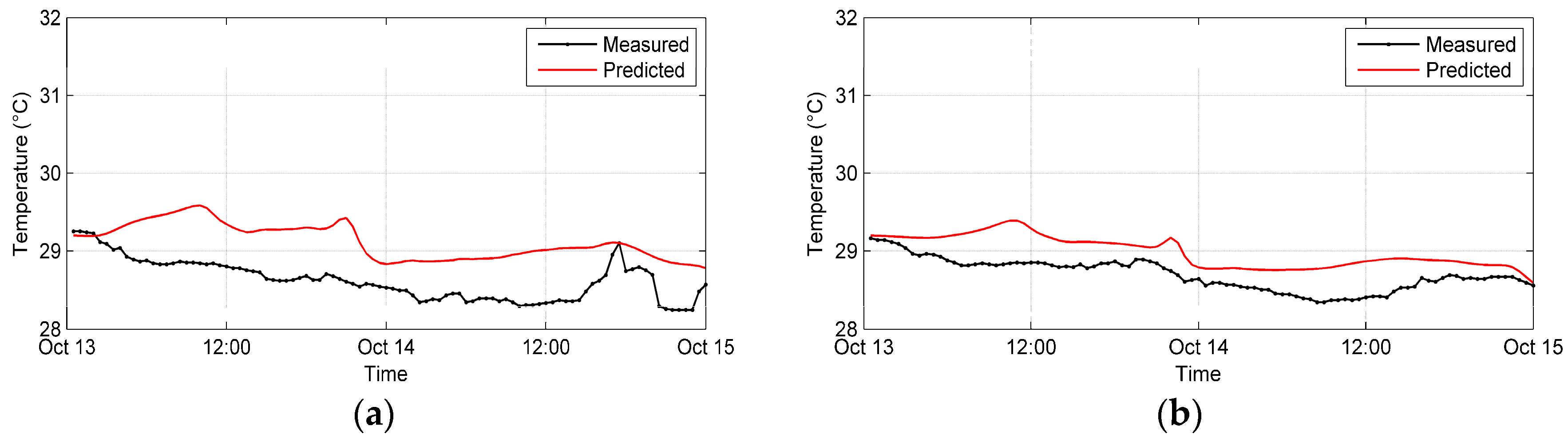
3.2. Calibration and Validation of the Numerical Simulations
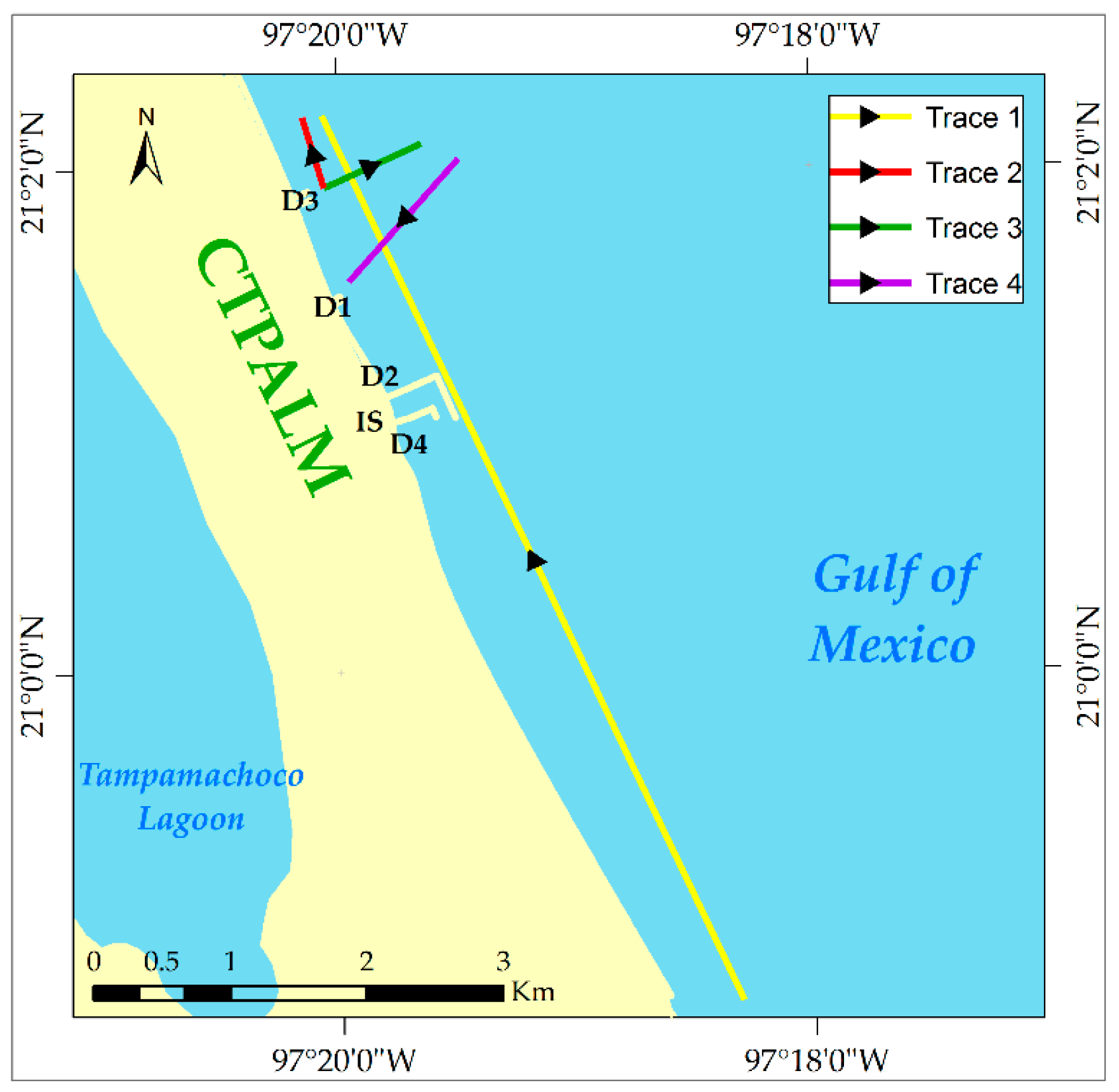
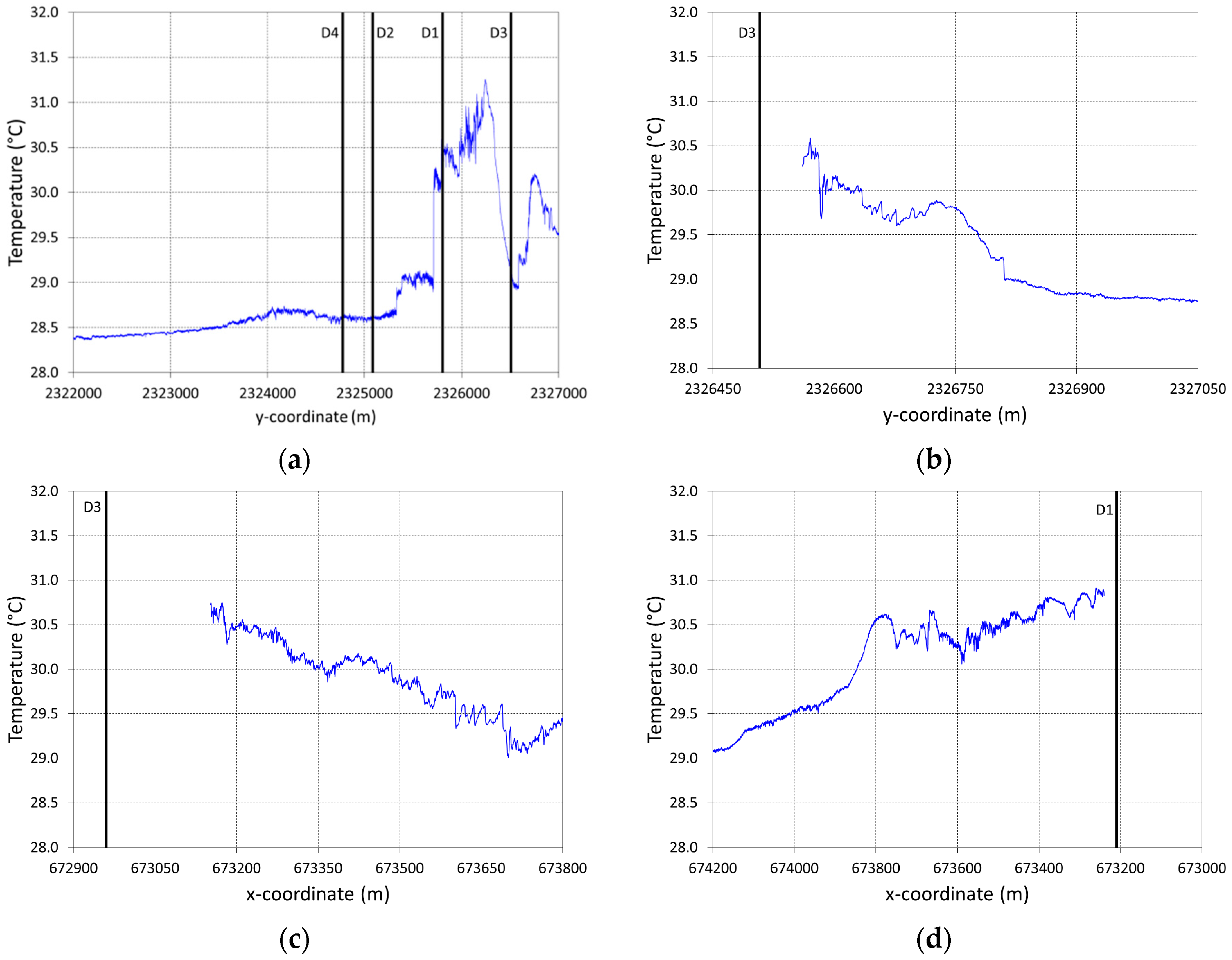
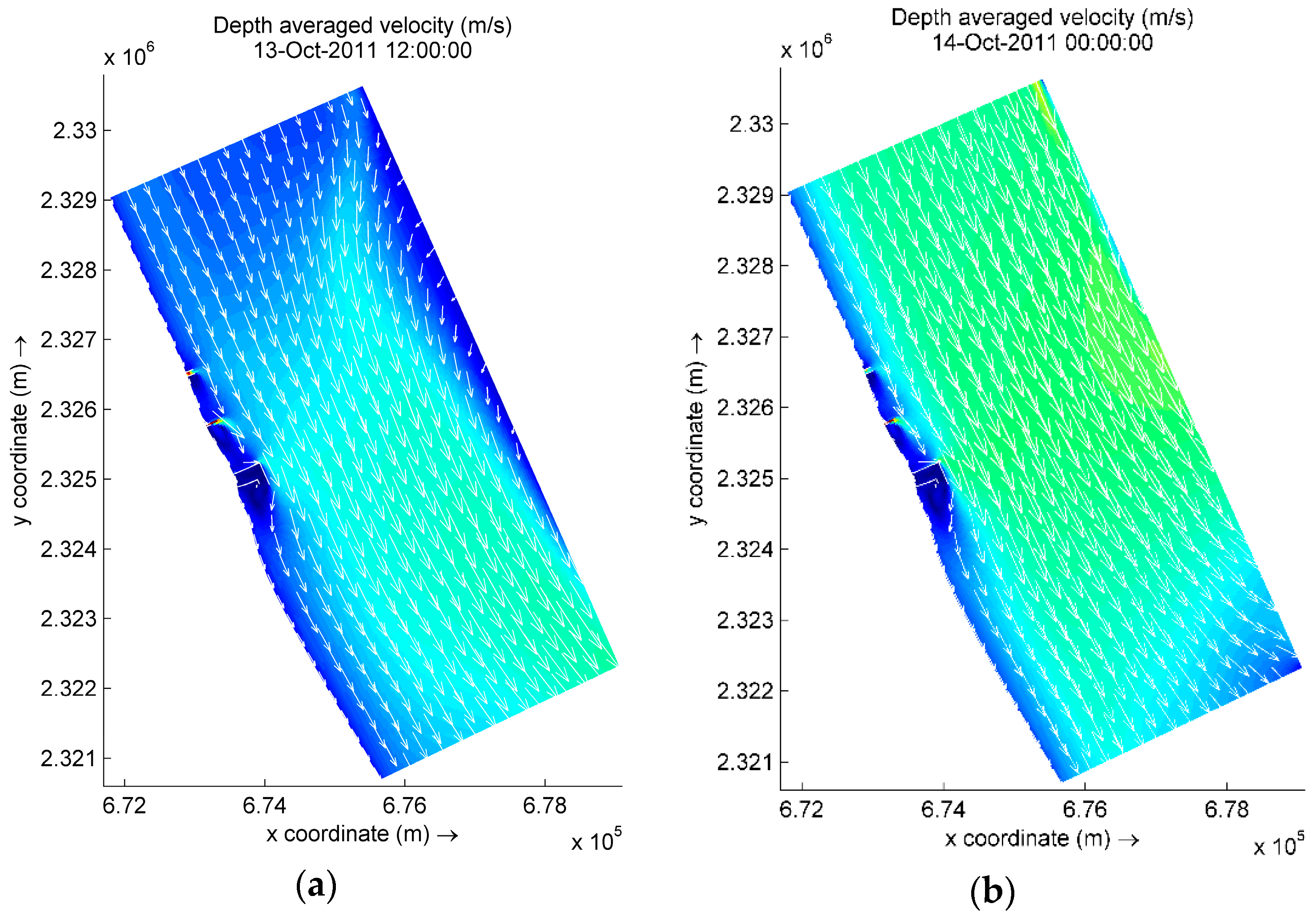
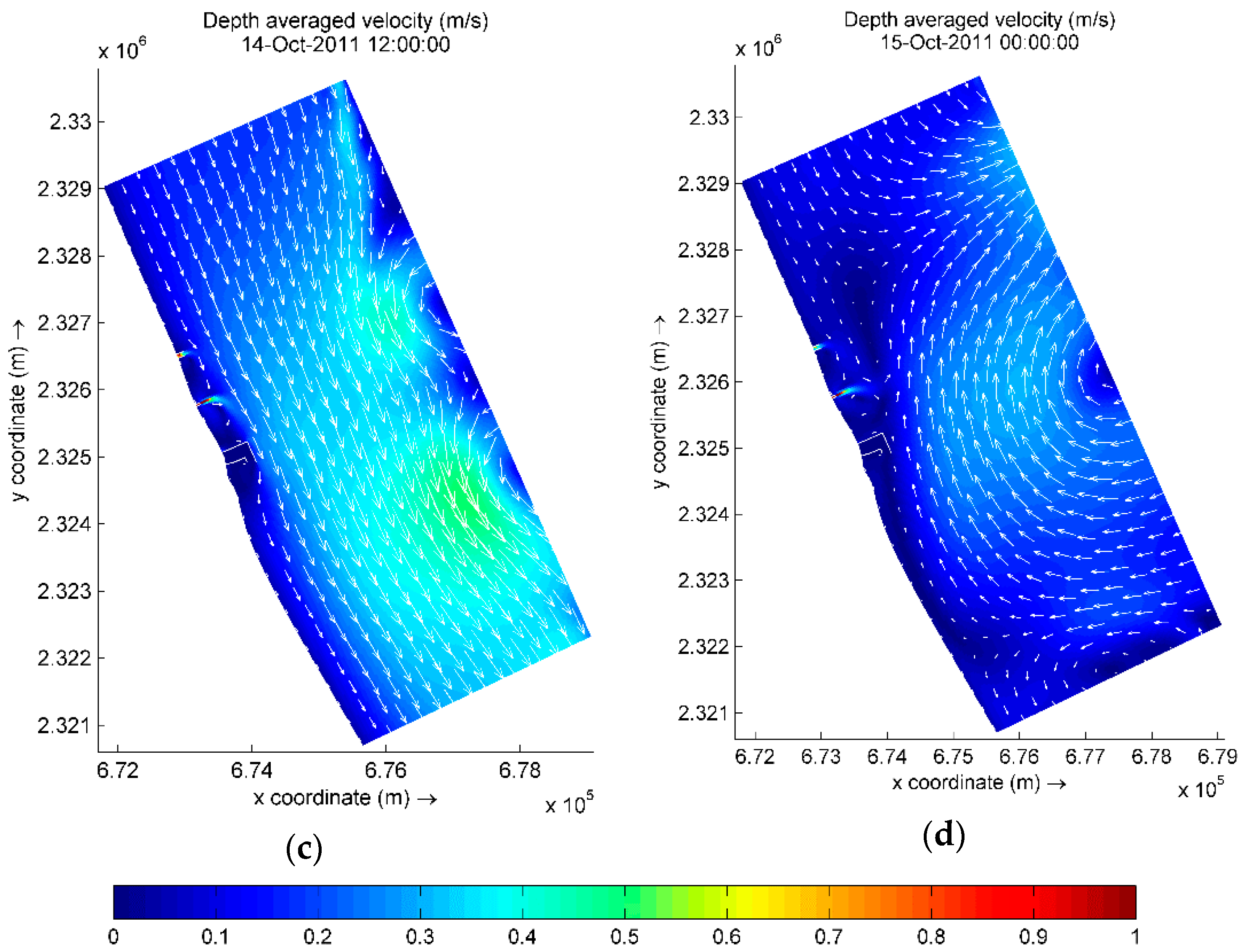
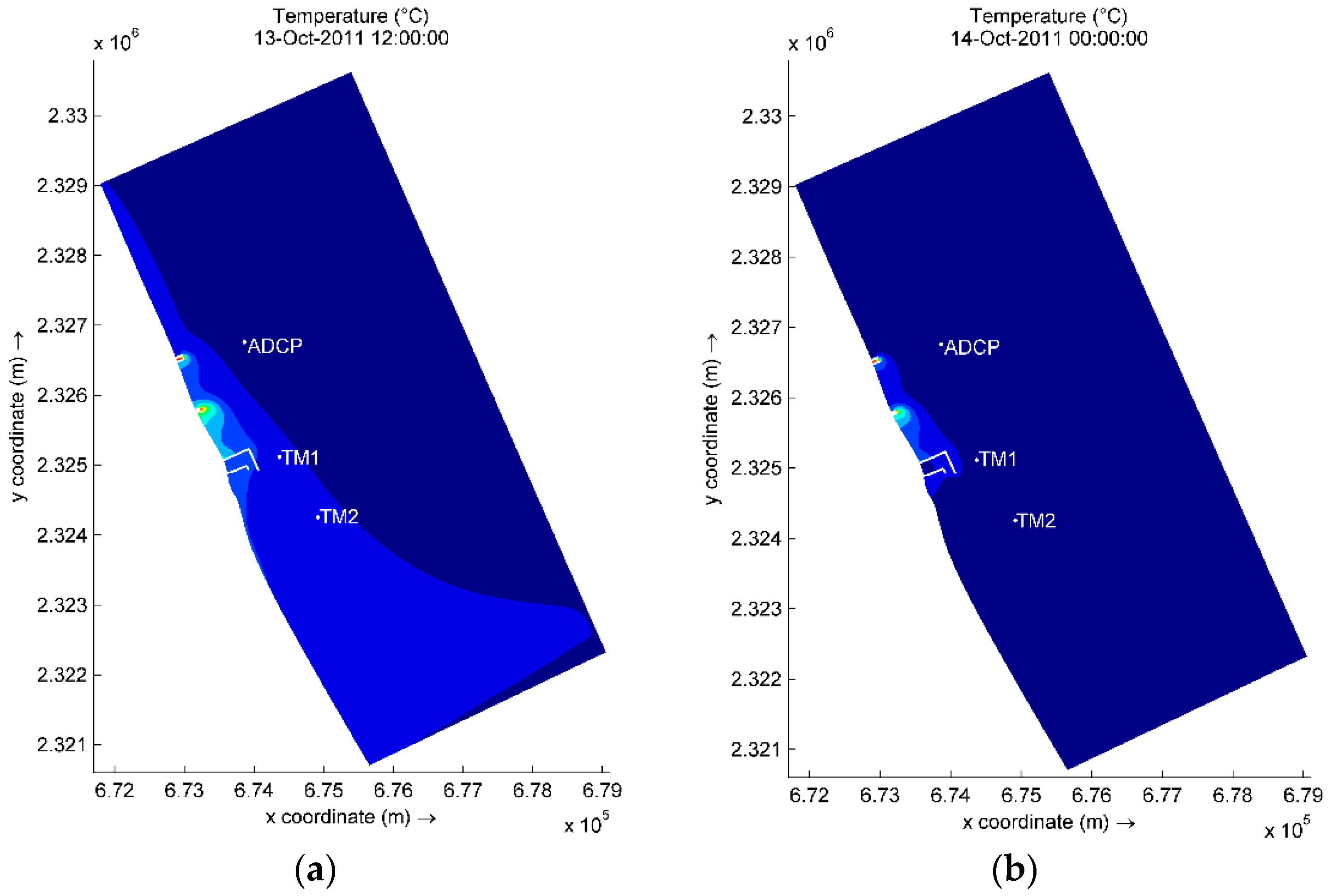
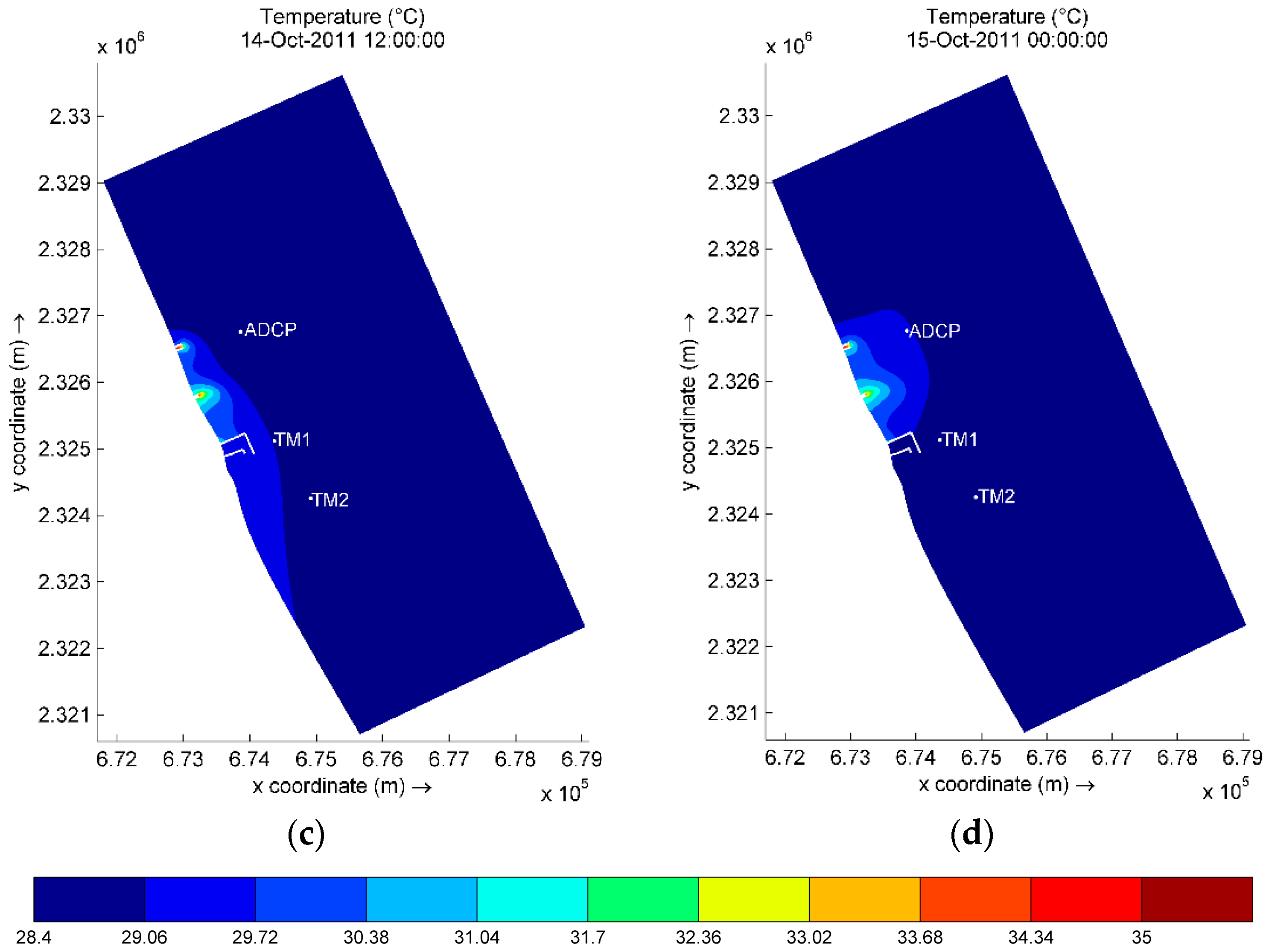
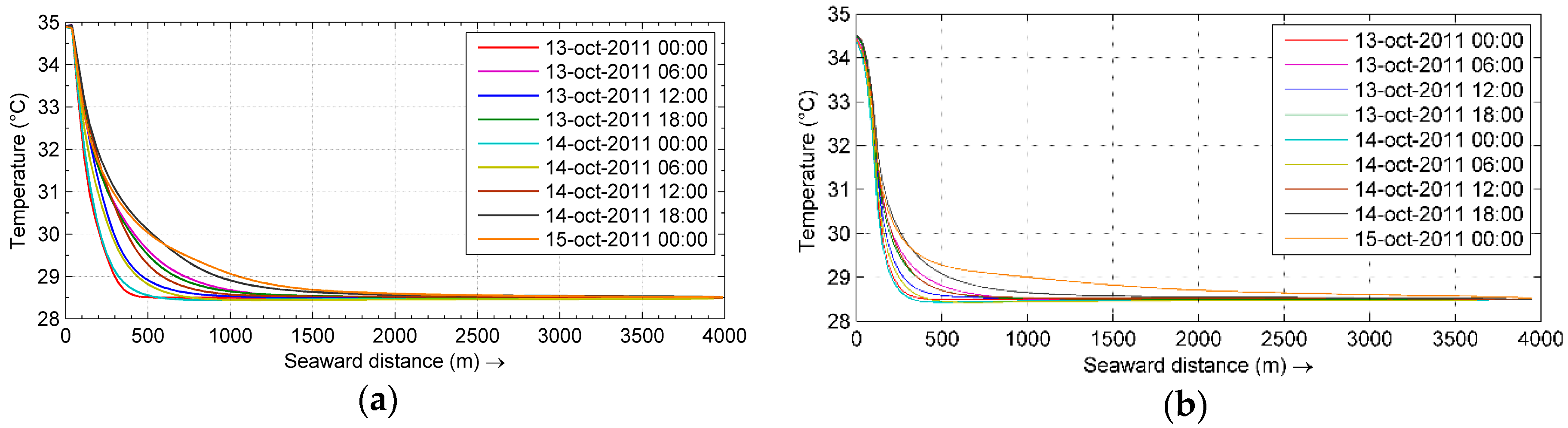
3.3. Thermal Plume Dispersion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADCP | Acoustic Doppler Profiler |
| CFE | Federal Electricity Commission of Mexico |
| CONAGUA | National Water Commission of Mexico |
| CTD | Refers to the instrument to measure Conductivity, Temperature, and Depth |
| CTPALM | Presidente Adolfo López Mateos Power Plant |
| GM | Gulf of Mexico |
| GPS | Global Positioning System |
| RMSE | root-mean-square error |
References
- Botello, A.V.; Rendón, J. Evaluación del Impacto ambiental de la central Nucleoeléctrica Laguna Verde a 15 años de operación. In Golfo de México. Contaminación e Impacto Ambiental: Diagnóstico y Tendencias, 2nd ed.; Botello, A.V., Rendón, J., Bouchot, G.G., Hernández, C.A., Eds.; EPOMEX: Campeche, Mexcio, 2005. [Google Scholar]
- Silva, H.A.; Botello, A.V. Evaluación del Impacto ambiental de la central Nucleoeléctrica Laguna Verde. In Golfo de México. Contaminación e Impacto Ambiental: Diagnóstico y Tendencias; EPOMEX: Campeche, Mexcio, 1996. [Google Scholar]
- Maupin, M.A.; Kenny, J.F.; Hutson, S.S.; Lovelace, J.K.; Barber, N.L.; Linsey, K.S. Estimated Use of Water in the United States in 2010; Circular 1405; U.S. Geological Survey: Reston, VA, USA, 2014; p. 56.
- Ramírez-León, H.; Couder-Castaneda, C.; Herrera-Díaz, I.E.; Barrios-Pina, H.A. Modelación numérica de la descarga térmica de la Central Nucleoeléctrica Laguna Verde. Revista Internacional Métodos Numéricos Cálculo Diseño Ingeniería 2013, 29, 114–121. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, Z.; Xu, M.; Jing, Q. Variation of Water Temperature in the Southwestern Daya Bay before and after the Operation of Daya Bay Nuclear Power Plant; Annual Research Reports; Marine Biology Research Station at Daya Bay: Beijing, China, 1998; pp. 102–112. [Google Scholar]
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2002, 15, 353–369. [Google Scholar] [CrossRef]
- Ahn, Y.-H.; Shanmugam, P.; Lee, J.-H.; Kang, Y.Q. Application of satellite infrared data for mapping of thermal plume contamination in coastal ecosystem of Korea. Mar. Environ. Res. 2006, 61, 186–201. [Google Scholar] [CrossRef] [PubMed]
- Buvaneshwari, S.; Ravichandran, V.; Mudgal, B.V. Thermal pollution of cooling water discharge into a closed creek system. Indian J. Mar. Sci. 2014, 43, 1–7. [Google Scholar]
- Salgueiro, D.V.; de Pablo, H.; Neves, R.; Mateus, M. Modelling the thermal effluent of a near coast power plant (Sines, Portugal). J. Integr. Coast. Zone Manag. 2015, 15, 533–544. [Google Scholar] [CrossRef]
- Secretaría de Energía. 2014 Balance Nacional de Energía; Subsecretaría de Planeación y Transición Energética, Dirección General de Planeación e Información Energéticas: Ciudad de México, Mexico, 2013. [Google Scholar]
- Barrios-Piña, H.A.; Ramírez-León, H.; Rodríguez-Cuevas, C.; Torres-Bejarano, F. Estudio Hidrodinámico y de dispersión de plumas térmicas en zonas costeras. In Proceedings of the XXV Congreso Latinoamericano de Hidraúlica, Santiago, Chile, 25–29 August 2014.
- Leendertse, J.J.; Alexander, R.C.; Liu, S.K. A Three-Dimensional Model for Estuaries and Coastal Seas: Volume I, Principles of Computations; Report R-1417-OWRR; Rand Corporation: Santa Monica, CA, USA, 1973. [Google Scholar]
- Leendertse, J.J.; Liu, S.K. A Three-Dimensional Model for Estuaries and Coastal Seas: Volume II: Aspects of Computation; Report R-1764-OWRT; Rand Corporation: Santa Monica, CA, USA, 1975. [Google Scholar]
- Leendertse, J.J.; Liu, S.K.; Nelson, A.B. A Three-Dimensional Model for Estuaries and Coastal Seas: Volume III, The Interim Program; Report R-1884-OWRT; Rand Corporation: Santa Monica, CA, USA, 1975. [Google Scholar]
- Leendertse, J.J.; Liu, S.K. A Three-Dimensional Model for Estuaries and Coastal Seas: Volume IV, Turbulent energy computation; Report R-2187-OWRT; Rand Corporation: Santa Monica, CA, USA, 1977. [Google Scholar]
- Stelling, G.S. On the Construction of Computational Methods for Shallow Water Flow Problems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, December 1983; p. 35. [Google Scholar]
- Stelling, G.S.; Leendertse, J.J. Approximation of Convective Processes by Cyclic AOI methods. In Proceeding of the 2nd Conference on Estuarine and Coastal Modeling, Tampa, FL, USA, 13–15 November 1991; Spaulding, M.L., Bedford, K., Blumberg, A., Eds.; American Society of Civil Engineers: New York, NY, USA, 1992; pp. 771–782. [Google Scholar]
- Stelling, G.S.; Duinmeijer, S.P.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Methods Fluids 2003, 43, 1329–1354. [Google Scholar] [CrossRef]
- Uittenbogaard, R.E.; van Vossen, B. Subgrid-scale model for Quasi-2D turbulence in shallow water. In Shallow Flows; Uijttewaal, W.S.J., Jirka, G.H., Eds.; Taylor & Francis: London, UK, 2004; pp. 575–582. [Google Scholar]
- Deltares. Delft3D-Flow User Manual, 3.15 ed.; Deltares: Delft, The Netherlands, 2011. [Google Scholar]
- Morelissen, R.; van der Kaaij, T.; Bleninger, T. Dynamic coupling of near field and far field models for simulating effluent discharges. Water Sci. Technol. 2013, 67, 2210–2220. [Google Scholar] [CrossRef] [PubMed]
- De Graaff, R.; Lindfors, A.; de Goede, E.; Rasmus, K.; Morelissen, R. Modelling of a Thermal Discharge in an Ice-covered Estuary in Finland. In Proceedings of the OTC Arctic Technology Conference, Copenhagen, Denmark, 23–25 March 2015.
- Duy Vinh, V.; Ouillon, S.; Van Thao, N.; Ngoc Tien, N. Numerical Simulations of Suspended Sediment Dynamics Due to Seasonal Forcing in the Mekong Coastal Area. Water 2016, 8, 255. [Google Scholar] [CrossRef]

| Parameter | Value | Time Variation |
|---|---|---|
| Initial velocities | 0 m/s | |
| Initial temperature | 29.2 from thermistors | |
| Temperature at open boundaries | 29.2 from thermistors | Fluctuation, according to the thermistors’ signal |
| Discharge 1 | 50.058 m3/s | Constant |
| Temperature of Discharge 1 | 34.89 °C | Constant |
| Discharge 2 | 4.432 m3/s | Constant |
| Temperature of Discharge 2 | 33.58 °C | Constant |
| Discharge 3 | 30.087 m3/s | Constant |
| Temperature of Discharge 3 | 34.55 °C | Constant |
| Discharge 4 | 1.43 m3/s | Constant |
| Temperature of Discharge 4 | 32.57 °C | Constant |
| Suction flow rate at intake | 90 m3/s | Constant |
| Test | Cd | Wind Speed Limits (in m/s) | n |
|---|---|---|---|
| 1 | 0.010 0.007 0.015 | <2.5 >2.5, <5.0 >5 | 0.025 |
| 2 | 0.010 0.030 | <2.5 >5.0 | 0.025 |
| 3 | 0.010 0.020 0.030 | >2.5 >2.5, <5.0 >5 | 0.020 |
| 4 | 0.010 0.020 0.030 | <2.5 >2.5, <5.0 >5 | 0.025 |
| 5 | 0.010 | >0 | 0.025 |
| 6 | 0.030 | >0 | 0.025 |
| 7 | 0.040 0.010 | <2.0 >2.0 >5 | 0.025 |
| Coeff | Calibration Test | Range | Perfect Match | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| RMSE | 0.110 | 0.096 | 0.120 | 0.087 | 0.099 | 0.132 | 0.168 | (0,∞) | 0 |
| m | 0.380 | 0.360 | 0.480 | 0.360 | 0.360 | 0.550 | 0.710 | (0,1) | 0 |
| Coeff | Thermistor | Range | Perfect Match | |
|---|---|---|---|---|
| TM 1 | TM 2 | |||
| RMSE | 0.28 | 0.10 | (0,∞) | 0 |
| m | 0.02 | 0.01 | (0,1) | 0 |
| Isotherm (in °C) | Temperature Difference with Respect to 34.89 °C (in °C) | % of Heat Dissipated | Influence Area (in m2) | |||
|---|---|---|---|---|---|---|
| 13 Oct. at 12:00 | 14 Oct. at 00:00 | 14 Oct. at 12:00 | 15 Oct. at 00:00 | |||
| 34.34 | 0.55 | 9 | 1695 | 402.8 | 1710 | 604.78 |
| 33.68 | 1.21 | 19 | 4748 | 2856 | 4800 | 3787 |
| 33.02 | 1.87 | 30 | 8635 | 5371 | 8733 | 7291 |
| 32.36 | 2.53 | 41 | 15,704 | 8562 | 15,390 | 13,037 |
| 31.7 | 3.19 | 51 | 33,607 | 14,699 | 31,130 | 27,652 |
| 31.04 | 3.85 | 62 | 74,079 | 30,605 | 67,214 | 69,611 |
| 30.38 | 4.51 | 72 | 235,028 | 66,346 | 158,387 | 193,222 |
| 29.72 | 5.17 | 83 | 856,495 | 220,195 | 534,342 | 674,638 |
| 29.06 | 5.83 | 94 | 12,010,000 | 823,879 | 2,420,704 | 1,843,919 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durán-Colmenares, A.; Barrios-Piña, H.; Ramírez-León, H. Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants. Water 2016, 8, 482. https://doi.org/10.3390/w8110482
Durán-Colmenares A, Barrios-Piña H, Ramírez-León H. Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants. Water. 2016; 8(11):482. https://doi.org/10.3390/w8110482
Chicago/Turabian StyleDurán-Colmenares, Azucena, Hector Barrios-Piña, and Hermilo Ramírez-León. 2016. "Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants" Water 8, no. 11: 482. https://doi.org/10.3390/w8110482
APA StyleDurán-Colmenares, A., Barrios-Piña, H., & Ramírez-León, H. (2016). Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants. Water, 8(11), 482. https://doi.org/10.3390/w8110482





