Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil and Water Assessment Tool (SWAT) Model
2.3. Glacier and Snow Melt Algorithm
2.3.1. Snow Melt Algorithm
2.3.2. Glacier Melt Algorithm
2.4. Data Availability
2.5. Model Setup
2.6. Model Calibration and Uncertainty Analysis
2.7. Model Assessment
3. Results
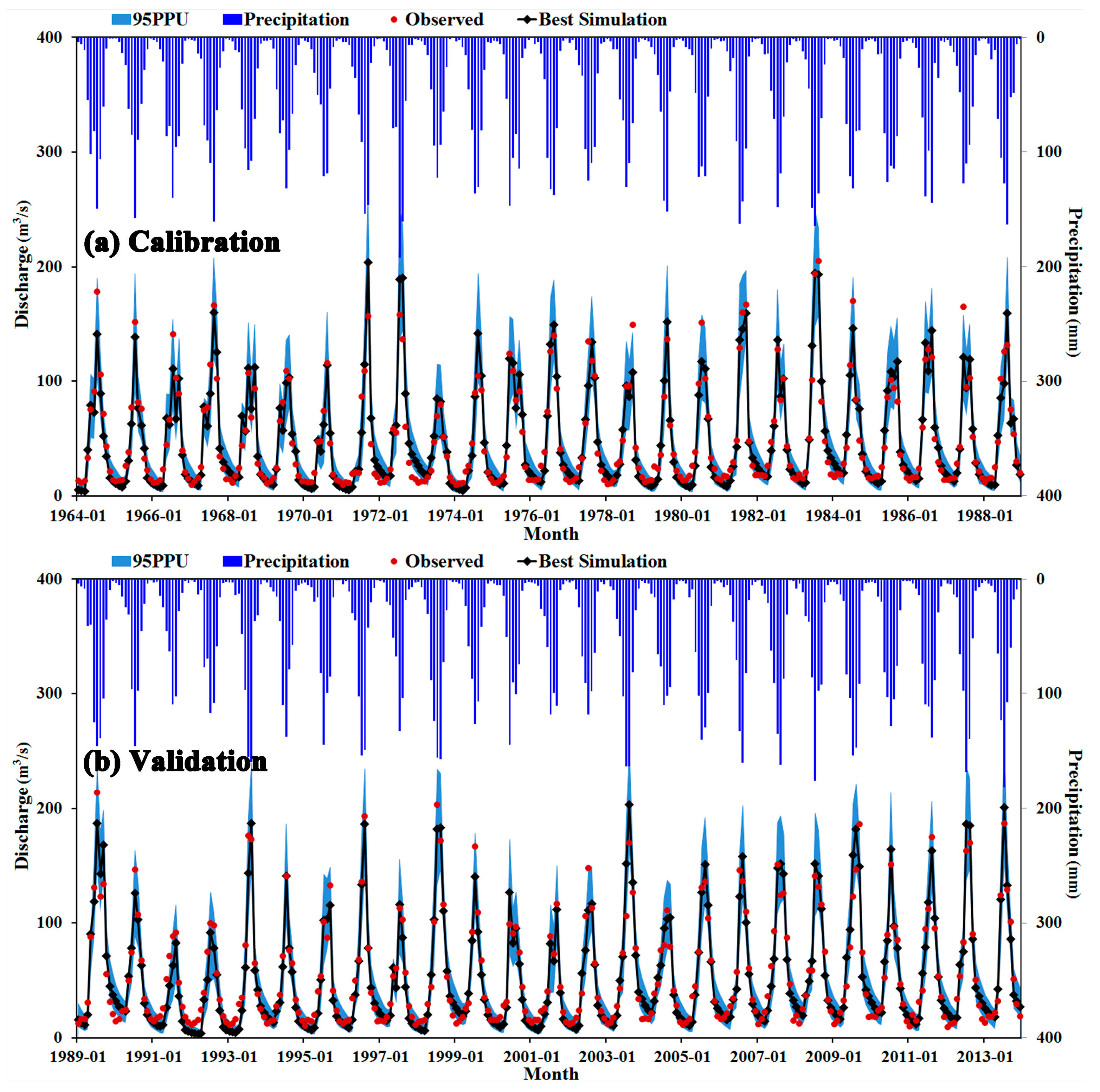
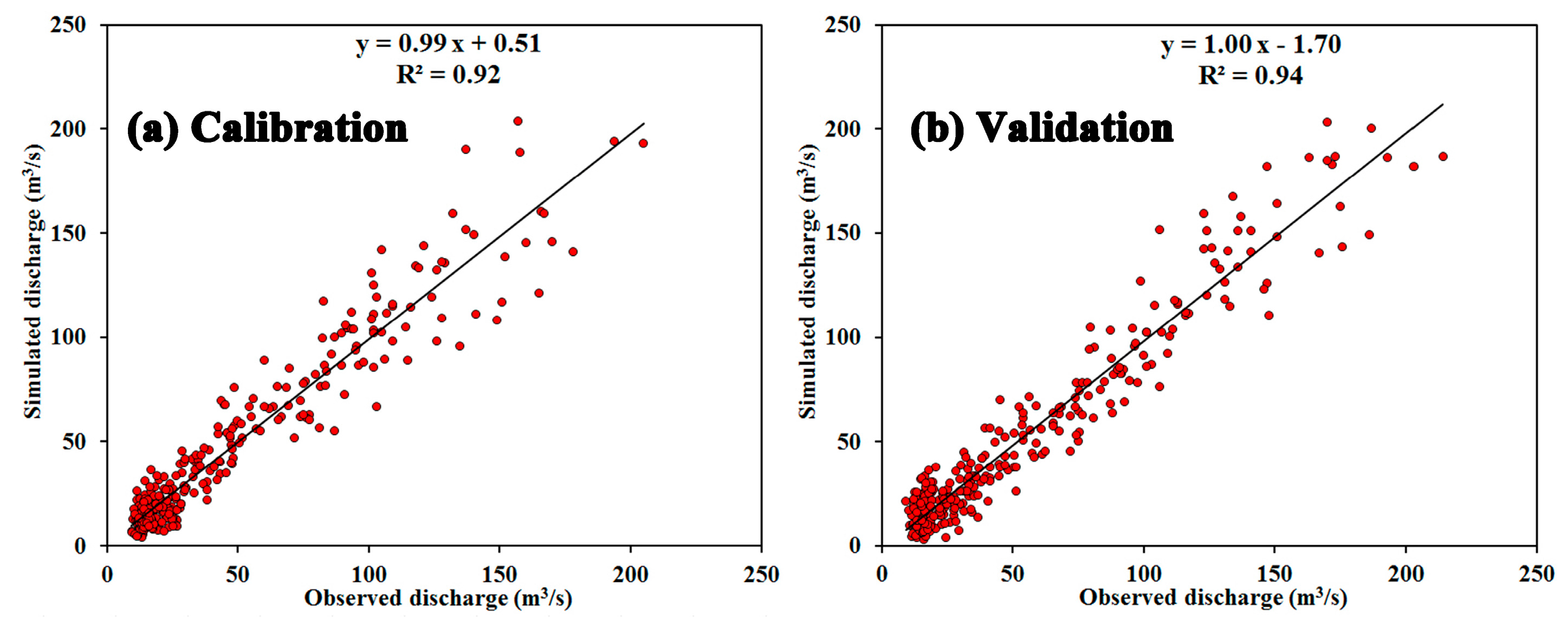
3.1. Model Performance
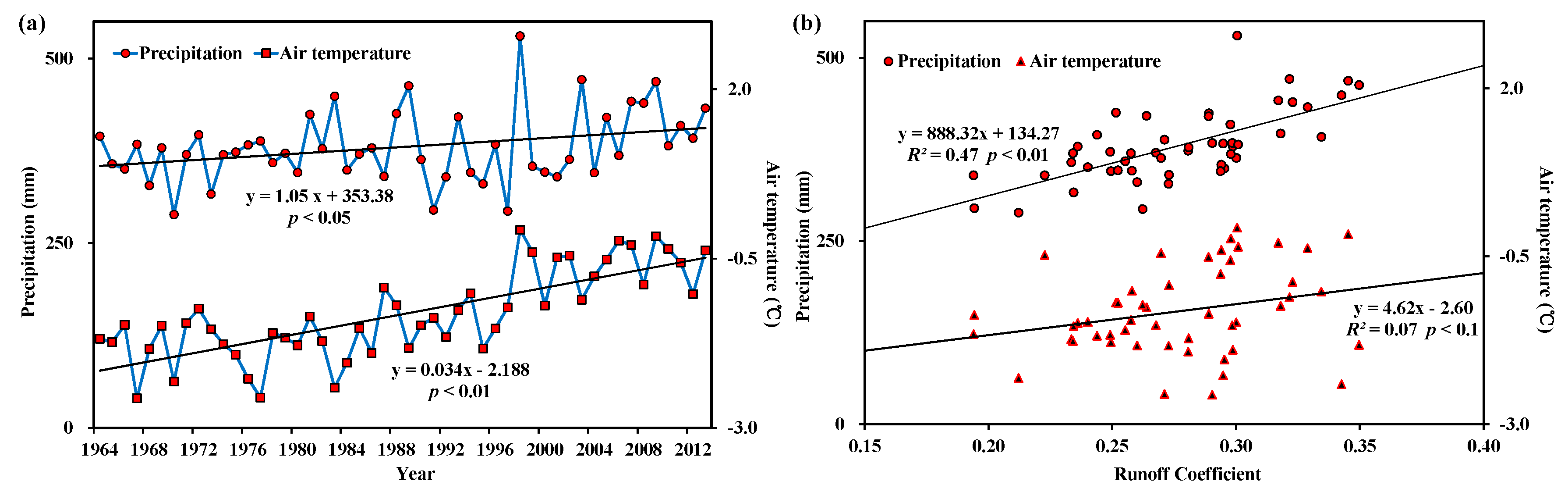
3.2. A Changing Trend in Water Balance Components at the Watershed Scale
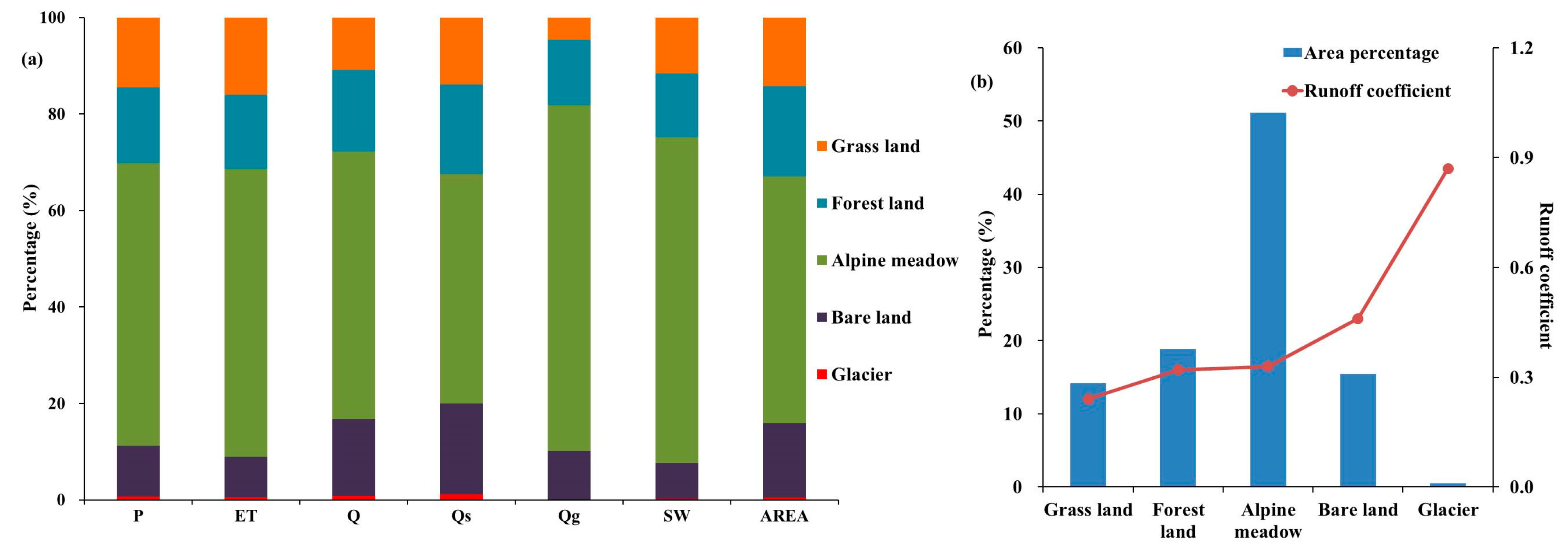
3.3. Quantification of Water Balance Components at the Landscape Scale
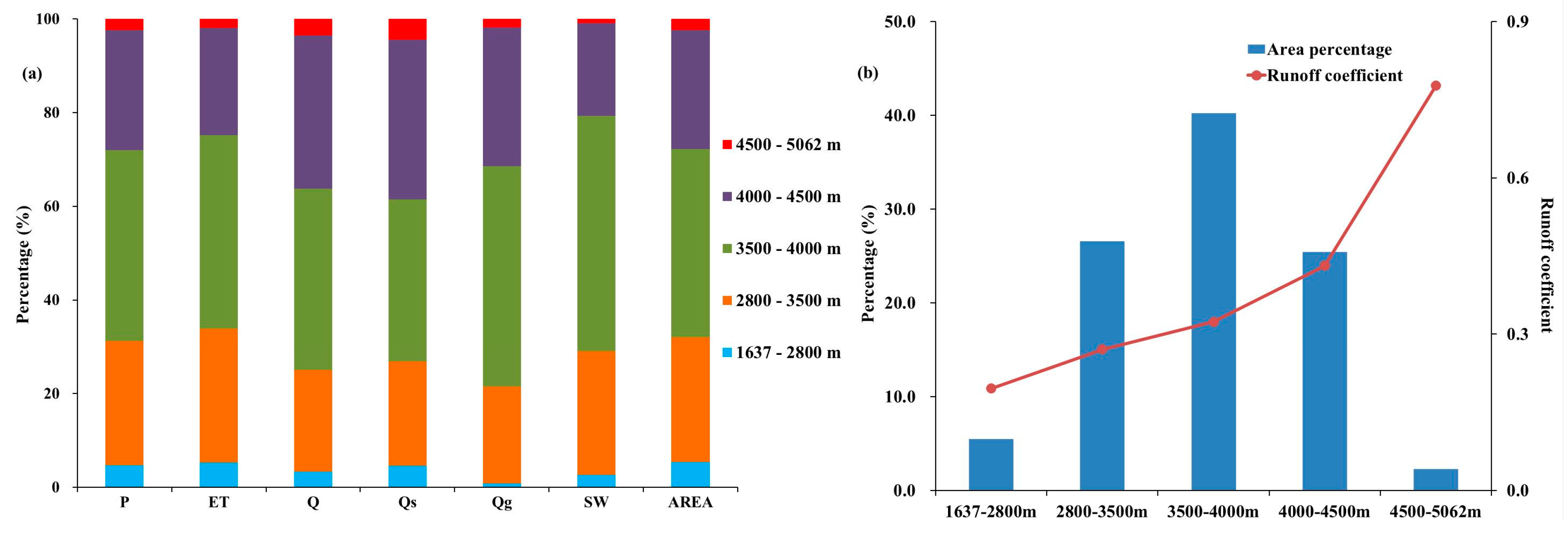
3.4. Quantification of Water Balance Components and Changing Trends across Elevation Zones
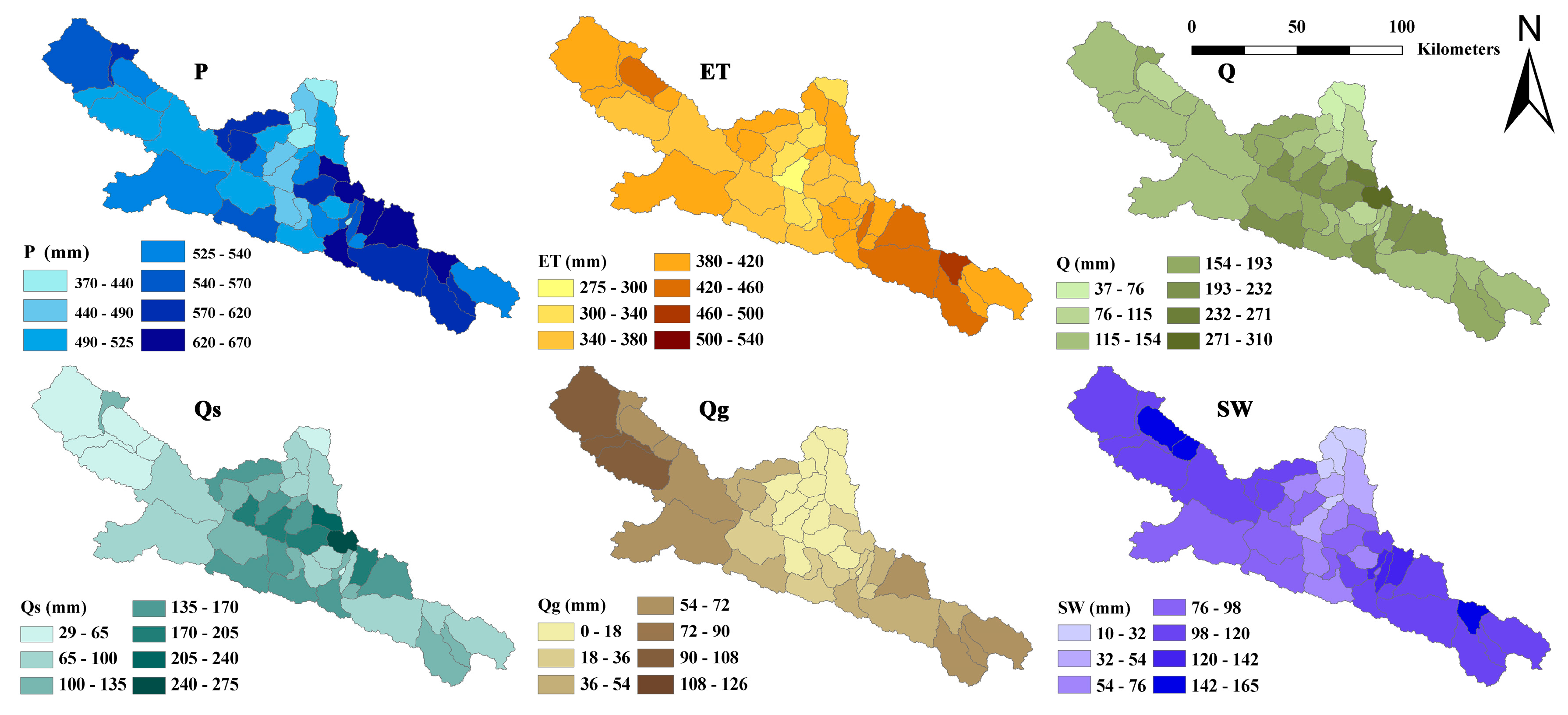
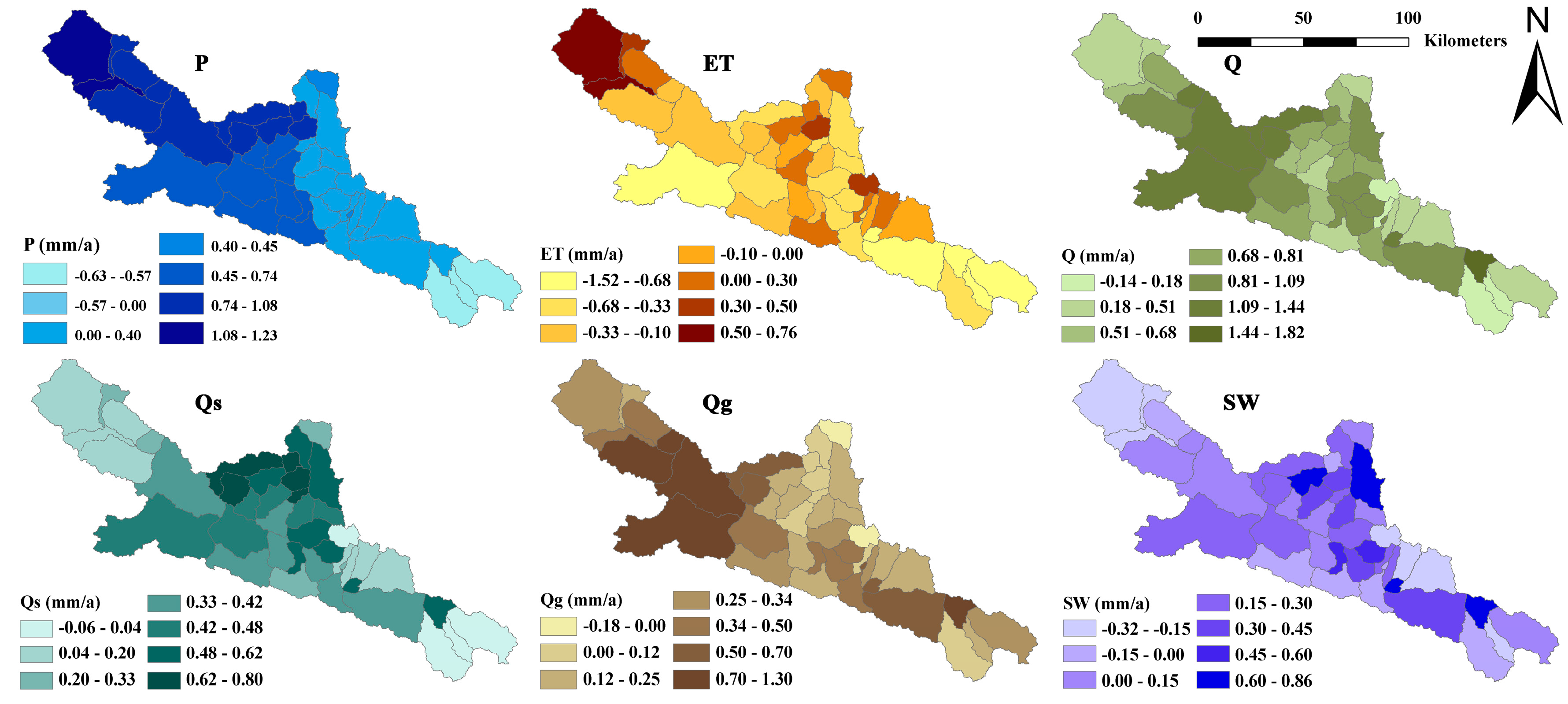
3.5. Quantification of Water Balance Components and the Change Trends at the Sub-Watershed Scale
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eder, G.; Fuchs, M.; Nachtnebel, H.P.; Loibl, W. Semi-distributed modeling of the monthly water balance in an alpine catchment. Hydrol. Process. 2005, 19, 2339–2360. [Google Scholar] [CrossRef]
- Wang, W.; Peng, S.; Yang, T.; Shao, Q.; Xu, J.; Xing, W. Spatial and temporal characteristics of reference evapotranspiration trends in the Haihe River Basin, China. J. Hydrol. Eng. 2011, 16, 239–252. [Google Scholar] [CrossRef]
- Gunkel, A.; Shadeed, S.; Hartmann, A.; Wagener, T.; Lange, J. Model signatures and aridity indices enhance the accuracy of water balance estimation in a data-scarce Eastern Mediterranean catchment. J. Hydrol. Reg. Stud. 2015, 4, 487–501. [Google Scholar] [CrossRef]
- Wang, N.L.; Wu, H.B.; Wu, Y.W.; Chen, A.A. Variations of the glacier mass balance and lake water storage in the Tarim Basin, northwest China, over the period of 2003–2009 estimated by the ICESatGLAS data. Environ. Earth Sci. 2015, 74, 1997–2008. [Google Scholar] [CrossRef]
- Fujieda, M.; Kudoh, T.; Cicco, V.; Calvarcho, J.L. Hydrological processes at two subtropical forest catchments: The Serra do Mar, São Paulo, Brazil. J. Hydrol. 1997, 196, 26–46. [Google Scholar] [CrossRef]
- Fiseha, B.M.; Setegn, S.G.; Melesse, A.M.; Volpi, E.; Fiori, A. Hydrological analysis of the Upper Tiber River Basin, Central Italy: A watershed modeling approach. Hydrol. Process. 2013, 27, 2339–2351. [Google Scholar] [CrossRef]
- Ngongondo, C.; Xu, C.Y.; Tallaksen, L.M.; Alemaw, B. Observed and simulated changes in the water balance components over Malawi, during 1971–2000. Quatern. Int. 2015, 369, 7–16. [Google Scholar] [CrossRef]
- Ning, J.C.; Gao, Z.Q.; Lu, Q.S. Runoff simulation using a modified SWAT model with spatially continuous HRUs. Environ. Earth Sci. 2015, 74, 5895–5905. [Google Scholar] [CrossRef]
- Lu, Z.X.; Zou, S.B.; Xiao, H.L.; Zheng, C.M.; Yin, Z.L.; Wang, W.H. Comprehensive hydrologic calibration of SWAT and water balance analysis in mountainous watersheds in northwest China. Phys. Chem. Earth 2015, 79–82, 76–85. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Allen, P.M. Continental scale simulation of the hydrologic balance. J. Am. Water Resour. Assoc. 1999, 35, 1037–1051. [Google Scholar] [CrossRef]
- Jiang, R.; Li, Y.; Wang, Q.; Kuramochi, K.; Hayakawa, A.; Woli, K.P.; Hatano, R. Modeling the water balance processes for understanding the components of river discharge in a Non-conservative Watershed. Tran. ASABE 2011, 54, 2171–2180. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Xu, C.C.; Maeyer, P.D. Contribution of meteorological input in calibrating a distributed hydrologic model in a watershed in the Tianshan Mountains, China. Environ. Earth Sci. 2015, 74, 2413–2424. [Google Scholar] [CrossRef]
- Kling, H.; Nachtnebel, H.P. A spatio-temporal comparison of water balance modeling in an Alpine catchment. Hydrol. Process. 2009, 23, 997–1009. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Zhang, S.F.; Xia, J.; Hua, D. Temporal and spatial variation of the main water balance components in the three rivers source region, China from 1960 to 2000. Environ. Earth Sci. 2013, 68, 973–983. [Google Scholar] [CrossRef]
- Gregory, J.M.; David, M.W. Temporal and spatial variability of the global water balance. Clim. Chang. 2013, 120, 375–387. [Google Scholar]
- Herrmann, F.; Keller, L.; Kunkel, R.; Vereechen, H.; Wendland, F. Determination of spatially differentiated water balance components including groundwater recharge on the Federal State level—A case study using the mGROWA model in North Rhine-Westphalia (Germany). J. Hydrol. Reg. Stud. 2015, 4, 294–312. [Google Scholar] [CrossRef]
- White, E.D.; Easton, Z.M.; Fuka, D.R.; Collick, A.S.; Adgo, E.; McCartney, M.; Awulachew, S.B.; Selassie, Y.G.; Steenhuis, T.S. Development and application of a physically based landscape water balance in the SWAT model. Hydrol. Process. 2011, 25, 915–925. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Assessing climate change impact on water balance components of a river basin using SWAT model. Hydrol. Process. 2015, 29, 4767–4785. [Google Scholar] [CrossRef]
- Jian, S.Q.; Zhao, C.Y.; Fang, S.M.; Yu, K. Effects of different vegetation restoration on soil water storage and water balance in the Chinese Loess Plateau. Agric. For. Meteorol. 2015, 206, 85–96. [Google Scholar] [CrossRef]
- Thompson, S.E.; Harman, C.J.; Troch, P.A.; Brooks, P.D.; Sivapalan, M. Spatial scale dependence of ecohydrologically mediated water balance partitioning: A systhesis framework for catchment ecohydrology. Water Resour. Res. 2011, 47, 143–158. [Google Scholar] [CrossRef]
- Knowles, J.F.; Harpold, A.A.; Cowie, R.; Zeliff, M.; Barnard, H.R.; Burns, S.P.; Blanken, P.D.; Morse, J.F.; Williams, M.W. The relative contributions of alpine and subalpine ecosystems to the water balance of a mountainous, headwater catchment. Hydrol. Process. 2015, 29, 4794–4808. [Google Scholar] [CrossRef]
- Qin, J.; Ding, Y.J.; Wu, J.K.; Gao, M.J.; Yi, S.H.; Zhao, C.C.; Ye, B.S.; Li, M.; Wang, S.X. Understanding the impact of mountain landscapes on water balance in the upper Heihe River watershed in northwestern China. J. Arid Land 2013, 5, 366–383. [Google Scholar] [CrossRef]
- Guo, J.; Su, X.L.; Singh, V.P.; Jin, J.M. Impacts of climate and land use/cover change on streamflow using SWAT and a separation method for the Xiying River Basin in Northwestern China. Water 2016, 8, 192. [Google Scholar] [CrossRef]
- Li, Z.L.; Wang, Y.H.; Zhao, W.; Xu, Z.X.; Li, Z.J. Frequency analysis of high flow extremes in the Yingluoxia watershed in Northwest China. Water 2016, 8, 215. [Google Scholar] [CrossRef]
- Zang, C.F.; Liu, J.G. Trend analysis for the flows of green and blue water in the Heihe River basin, northwestern China. J. Hydrol. 2013, 502, 27–36. [Google Scholar] [CrossRef]
- Yin, Z.L.; Xiao, H.L.; Zou, S.B.; Zhu, R.; Lu, Z.X.; Lan, Y.C.; Shen, Y.P. Simulation of hydrological processes of mountainous watersheds in inland river basin: Taking the Heihe mainstream river as an example. J. Arid Land 2014, 6, 16–26. [Google Scholar] [CrossRef]
- Yang, D.W.; Gao, B.; Jiao, Y.; Lei, H.M.; Zhang, Y.L.; Yang, H.B.; Cong, Z.T. A distributed scheme developed for eco-hydrological modeling in the upper Heihe River. Sci. China Earth Sci. 2015, 58, 36–45. [Google Scholar] [CrossRef]
- Deng, X.Z.; Shi, Q.L.; Zhang, Q.; Shi, C.C.; Yin, F. Impacts of land use and land cover changes on surface energy and water balance in the Heihe River Basin of China, 2000–2010. Phys. Chem. Earth 2015, 79–82, 2–10. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.Y.; Wang, Z.; Zhang, Q. Streamflow variation due to glacier melting and climate change in upstream Heihe River Basin, Northwest China. Phys. Chem. Earth 2015, 79–82, 11–19. [Google Scholar] [CrossRef]
- Wang, J.F.; Gao, Y.C.; Wang, S. Land use/cover change impacts on water table change over 25 years in a desert-oasis transition zone of the Heihe River Basin, China. Water 2016, 8, 11. [Google Scholar] [CrossRef]
- Cheng, G.D.; Li, X.; Zhao, W.Z.; Xu, Z.M.; Feng, Q.; Xiao, S.C.; Xiao, H.L. Integrated study of the water-ecosystem-economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation: Version 2005; USDA-ARS Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2005. [Google Scholar]
- Hock, R. Temperature index melt modeling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Rahman, K.; Maringanti, C.; Beniston, M.; Windmer, F.; Abbaspour, K.; Lehmann, A. Streamflow modeling in a highly managed mountainous glacier watershed using SWAT: The upper Rhone River watershed case in Switzerland. Water Resour. Manag. 2013, 27, 323–339. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Arya, L.M.; Shouse, P.J.; Mohanty, B.P. Estimating particle-size distribution from limited soil texture data. Soil Sci. Soc. Am. J. 2001, 65, 1038–1044. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP, SWAT Calibration and Uncertainty Programs; Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2011. [Google Scholar]
- Moriasi, D.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.; Harmel, R.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Shi, Y.F.; Shen, Y.P.; Hu, R.J. Preliminary study on signal, impact and foreground of climatic shift from warm-dry to warm-humid in Northwest China. J. Glaciol. Geocryol. 2002, 24, 219–226. [Google Scholar]
- Wang, J.; Meng, J. Characteristics and tendencies of annual runoff variations in the Heihe River Basin during the past 60 years. Sci. Geogr. Sin. 2008, 28, 83–88. [Google Scholar]
- Wang, N.L.; Zhang, S.B.; He, J.Q.; Pu, J.C.; Wu, X.B.; Jiang, X. Tracing the major source area of the mountainous runoff generation of the Heihe River in northwest China using stable isotope technique. Chin. Sci. Bull. 2009, 54, 2751–2757. [Google Scholar] [CrossRef]
- Li, Z.H.; Deng, X.Z.; Wu, F.; Hasan, S.S. Scenario analysis for water resources in response to land use change in the middle and upper reaches of the Heihe River Basin. Sustainability 2015, 7, 3086–3108. [Google Scholar] [CrossRef]
- Nian, Y.Y.; Li, X.; Zhou, J.; Hu, X.L. Impact of land use change on water resource allocation in the middle reaches of the Heihe River Basin in northwestern China. J. Arid Land 2014, 6, 273–286. [Google Scholar] [CrossRef]
- Ji, X.B.; Kang, E.S.; Chen, R.S.; Zhao, W.Z.; Xiao, S.C.; Jin, B.W. Analysis of water resources supply and demand and security of water resources development in irrigation regions of the middle reaches of the Heihe River Basin, Northwest China. Agric. Sci. China 2006, 5, 130–140. [Google Scholar] [CrossRef]
- Du, C.; Sun, F.; Yu, J.; Liu, X.; Chen, Y. New interpretation of the role of water balance in an extended Budyko hypothesis in arid regions. Hydrol. Earth Syst. Sci. 2016, 20, 393–409. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, J.; Koeneman, P.H.; Zarate, E.; Hoekstra, A.Y. Assessing water footprint at river basin level: A case study for the Heihe River Basin in northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 2771–2781. [Google Scholar] [CrossRef]
- Zang, C.; Liu, J.; Jiang, L.; Gerten, D. Impacts of human activities and climate variability on green and blue water flows in the Heihe River Basin in Northwest China. Hydrol. Earth Syst. Sci. Disscuss. 2013, 10, 9477–9504. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.Y.; Su, H.B.; Yan, H.M.; Ma, E.J. Scenario-based impact assessment of land use/cover and climate changes on watershed hydrology in Heihe River Basin of Northwest China. Adv. Meteorol. 2015, 2015, 410198. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.T.; Yu, W.J.; Ge, Y.C. Modeling land-use and land-cover change and hydrological responses under consistent climate change scenarios in the Heihe River Basin, China. Water Resour. Manag. 2015, 29, 4701–4717. [Google Scholar] [CrossRef]
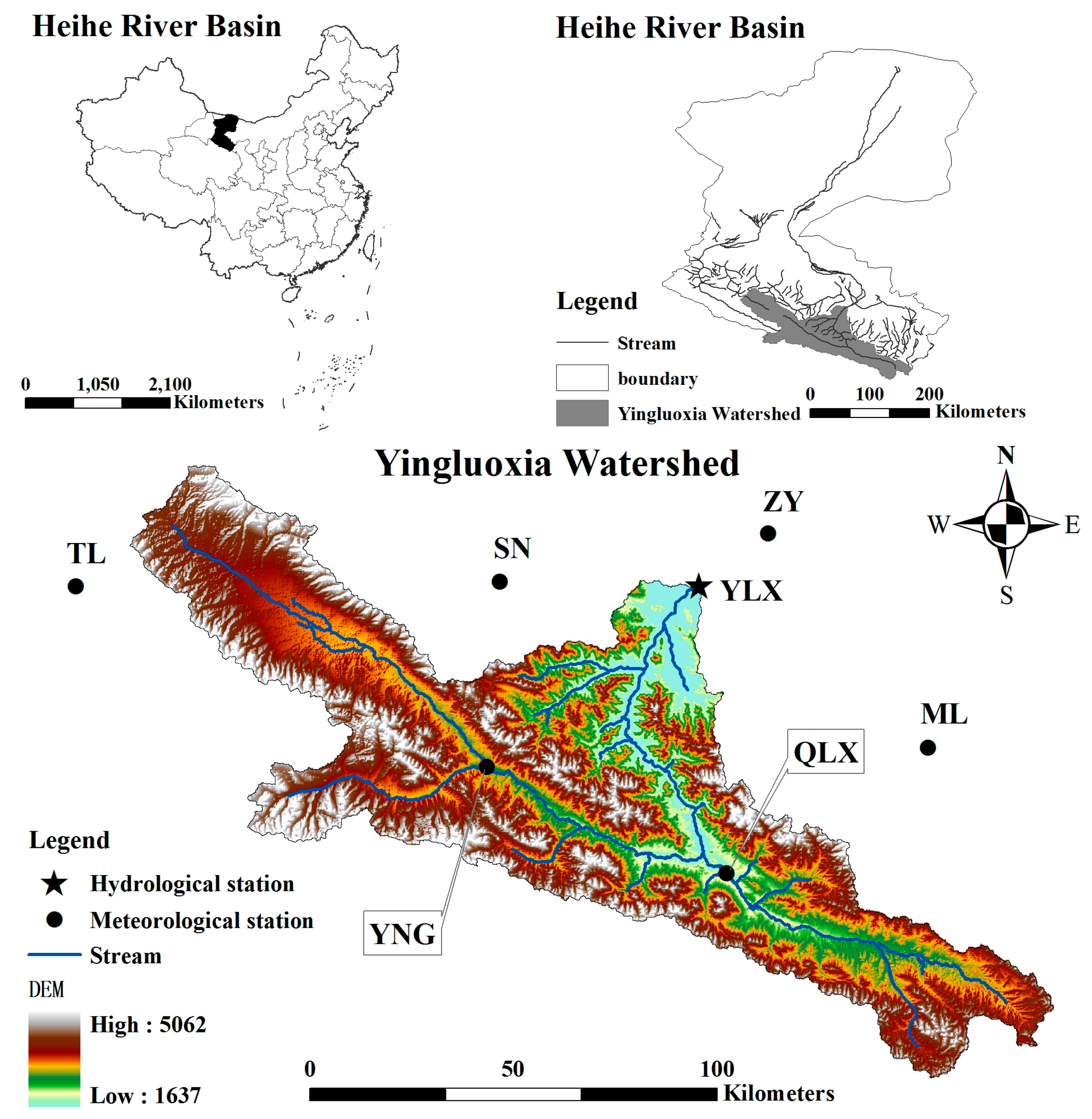
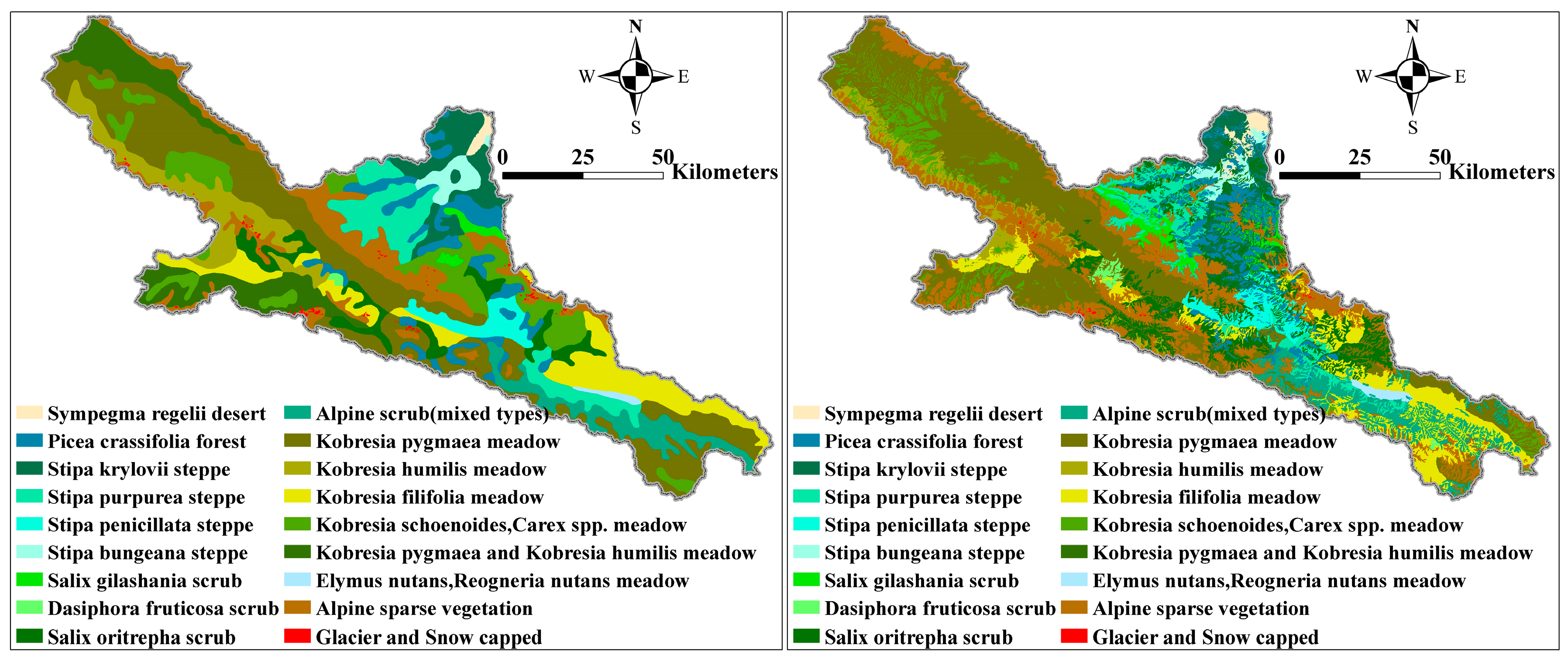
| Station | Longitude/° | Latitude/° | Elevation/m | Period | Average Air Temperature/°C | Average Precipitation/mm |
|---|---|---|---|---|---|---|
| Meteorological stations | ||||||
| Zhangye (ZY) | E 100.38 | N 38.93 | 1483 | 1961–2013 | 7.3 | 131.9 |
| Minle (ML) | E 100.82 | N 38.45 | 2271 | 1961–2013 | 3.4 | 337.1 |
| Sunan (SN) | E 99.62 | N 38.83 | 2312 | 1961–2013 | 3.8 | 250.9 |
| Qilianxian (QLX) | E 100.25 | N 38.18 | 2787 | 1961–2013 | 1.1 | 410.6 |
| Yeniugou (YNG) | E 99.58 | N 38.42 | 3180 | 1961–2013 | −2.6 | 420.9 |
| Tuole (TL) | E 98.42 | N 38.82 | 3360 | 1961–2013 | −2.5 | 299.9 |
| Hydrological stations | ||||||
| Yingluoxia (YLX) | E 100.18 | N 38.82 | 1637 | 1961–2013 | - | - |
| Parameter 1 | Description | Parameter Range | Fitted Value |
|---|---|---|---|
| r_CN2.mgt | Initial SCS runoff curve number for moisture condition II | −0.4–0.2 | −0.28 |
| v_ALPHA_BF.gw | Base flow alpha factor (days) | 0.0–0.5 | 0.45 |
| v_GW_DELAY.gw | Groundwater delay time (days) | 90.0–180.0 | 174.0 |
| v_GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur (mm) | 0.0–2.0 | 0.62 |
| v_GW_REVAP.gw | Groundwater ‘rewap’ coefficient | 0.0–0.2 | 0.037 |
| v_ESCO.hru | Soil evaporation compensation factor | 0.5–0.9 | 0.80 |
| v_CH_N2.rte | Manning’s ‘n’ value for the main channel | 0.0–0.3 | 0.026 |
| v_CH_K2.rte | Effective hydraulic conductivity in main channel alluvium (mm/h) | 5.0–40.0 | 35.0 |
| v_ALPHA_BNK.rte | Base flow alpha factor for bank storage | 0.0–1.0 | 0.61 |
| r_SOL_AWC.sol | Available water capacity of the soil layer (mm H2O/mm soil) | −0.2–0.4 | −0.10 |
| r_SOL_K.sol | Saturated hydraulic conductivity (mm/h) | −0.8–0.8 | −0.54 |
| r_SOL_BD.sol | Moist bulk density (mg/m3) | −0.5–0.6 | 0.44 |
| v_SFTMP.bsn | Snowfall temperature (°C) | −2.0–1.0 | 0.21 |
| v_SMFMN.bsn | Melt factor on December 21 (mm H2O/°C-day) | 0–10.0 | 3.5 |
| v_SMFMX.bsn | Melt factor on 21 June (mm H2O/°C-day) | 0–10.0 | 7.5 |
| v_TLPAS.sub | Temperature lapse rate (°C/km) | −8.0–−4.0 | −5.5 |
| Period | NSE | R2 | PBIAS (%) |
|---|---|---|---|
| Calibration (1964–1988) | 0.91 | 0.92 | −4.5 |
| Validation (1989–2013) | 0.92 | 0.94 | −6.8 |
| The whole period (1964–2013) | 0.92 | 0.93 | −5.3 |
| Elevation Zone/m | Precipitation | ET | Runoff | Surface Runoff | Groundwater Flow | Soil Water Content |
|---|---|---|---|---|---|---|
| 1637–2800 | 5.0 | −2.0 | 7.1 ** | 5.3 ** | 1.8 ** | 3.8 ** |
| 2800–3500 | 4.3 | −3.4 | 7.9 ** | 3.4 ** | 4.5 ** | 2.4 * |
| 3500–4000 | 5.8 | −3.4 | 8.8 ** | 3.1 * | 5.7 ** | 0.8 |
| 4000–4500 | 7.4 | −1.2 | 8.1 ** | 3.6 | 4.5 ** | 0.0 |
| 4500–5062 | 7.8 | 0.5 | 6.9 * | 4.6 | 2.3 ** | −0.8 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change. Water 2016, 8, 472. https://doi.org/10.3390/w8100472
Yin Z, Feng Q, Zou S, Yang L. Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change. Water. 2016; 8(10):472. https://doi.org/10.3390/w8100472
Chicago/Turabian StyleYin, Zhenliang, Qi Feng, Songbing Zou, and Linshan Yang. 2016. "Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change" Water 8, no. 10: 472. https://doi.org/10.3390/w8100472
APA StyleYin, Z., Feng, Q., Zou, S., & Yang, L. (2016). Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change. Water, 8(10), 472. https://doi.org/10.3390/w8100472









