Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments
Abstract
:1. Introduction
2. Methodology
- Step 1: Search for feasible sites in which to implement SuDS, according to a set of geometric and hydrologic criteria to be met for the location of these practices.
- Step 2: Generate a prioritization map to highlight flood-prone areas that required retrofitting, based on the infiltration capability of the subcatchments forming the whole catchment area.
- Step 3: Parameterize PPS for the stormwater simulation of new catchment configurations derived from their inclusion, in order to assess the capability of these systems to mitigate floods.
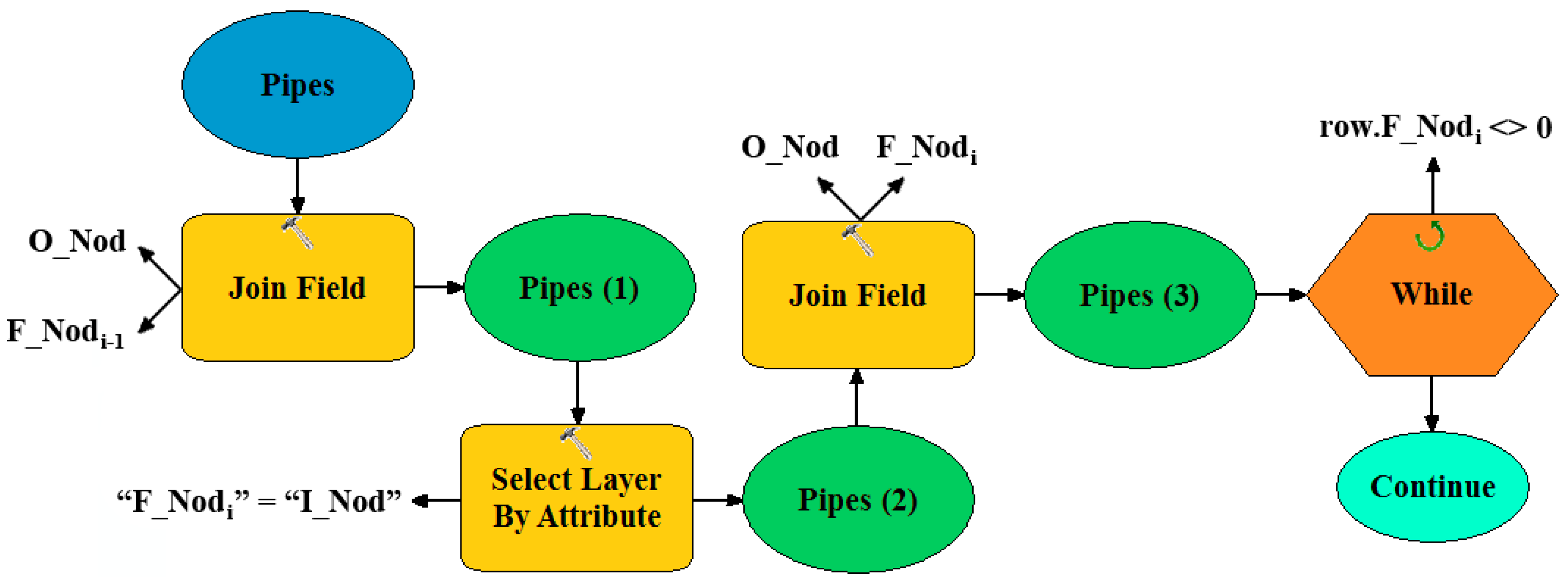
2.1. Search for Feasible Locations for the Implementation of Sustainable Drainage Systems (SuDS)
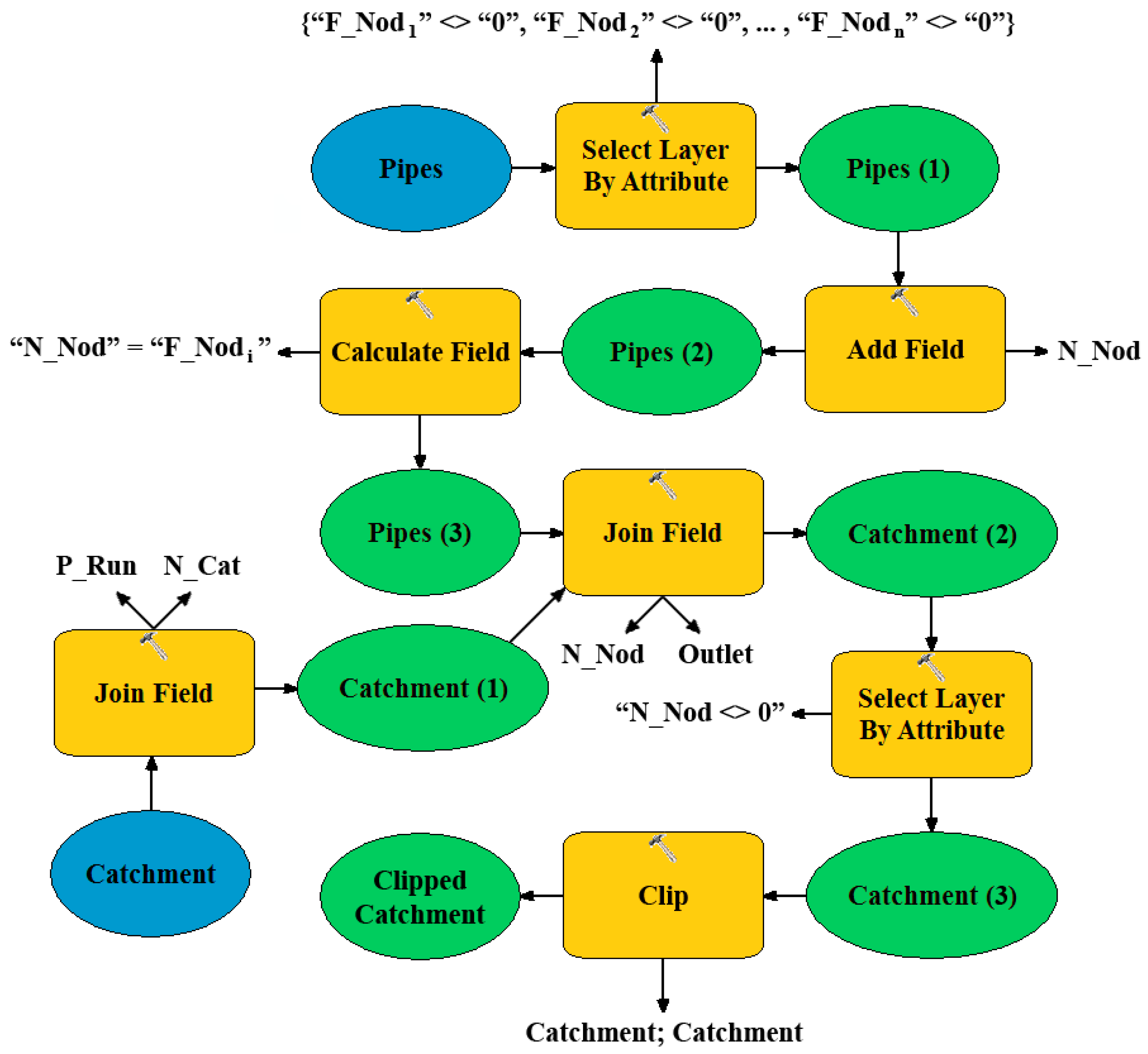
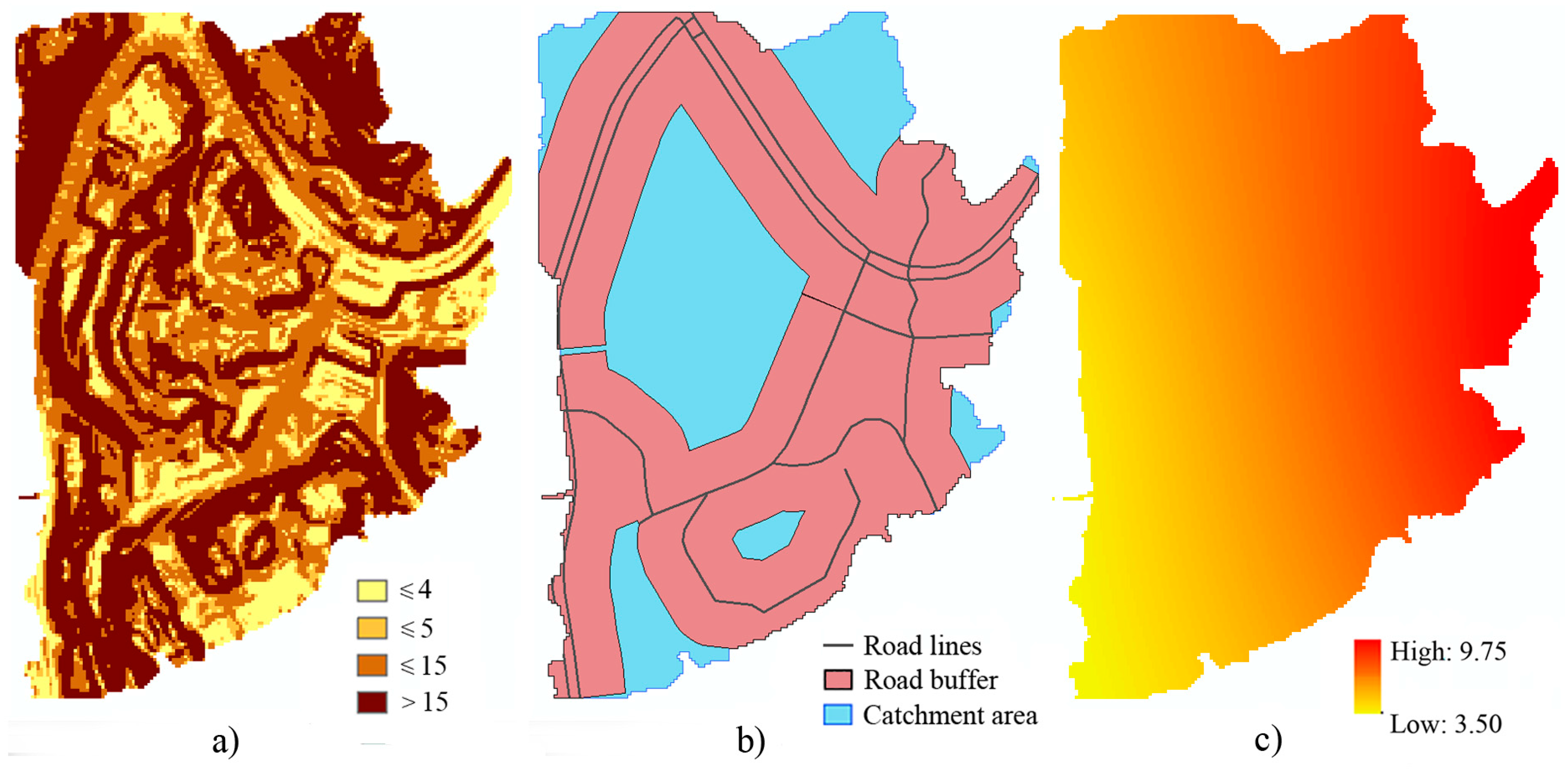
2.2. Prioritization of Flood-Sensitive Areas
2.3. Hydrological Simulation of Permeable Pavement Systems (PPS)
3. Results and Discussion: A Case Study in Espoo, Finland
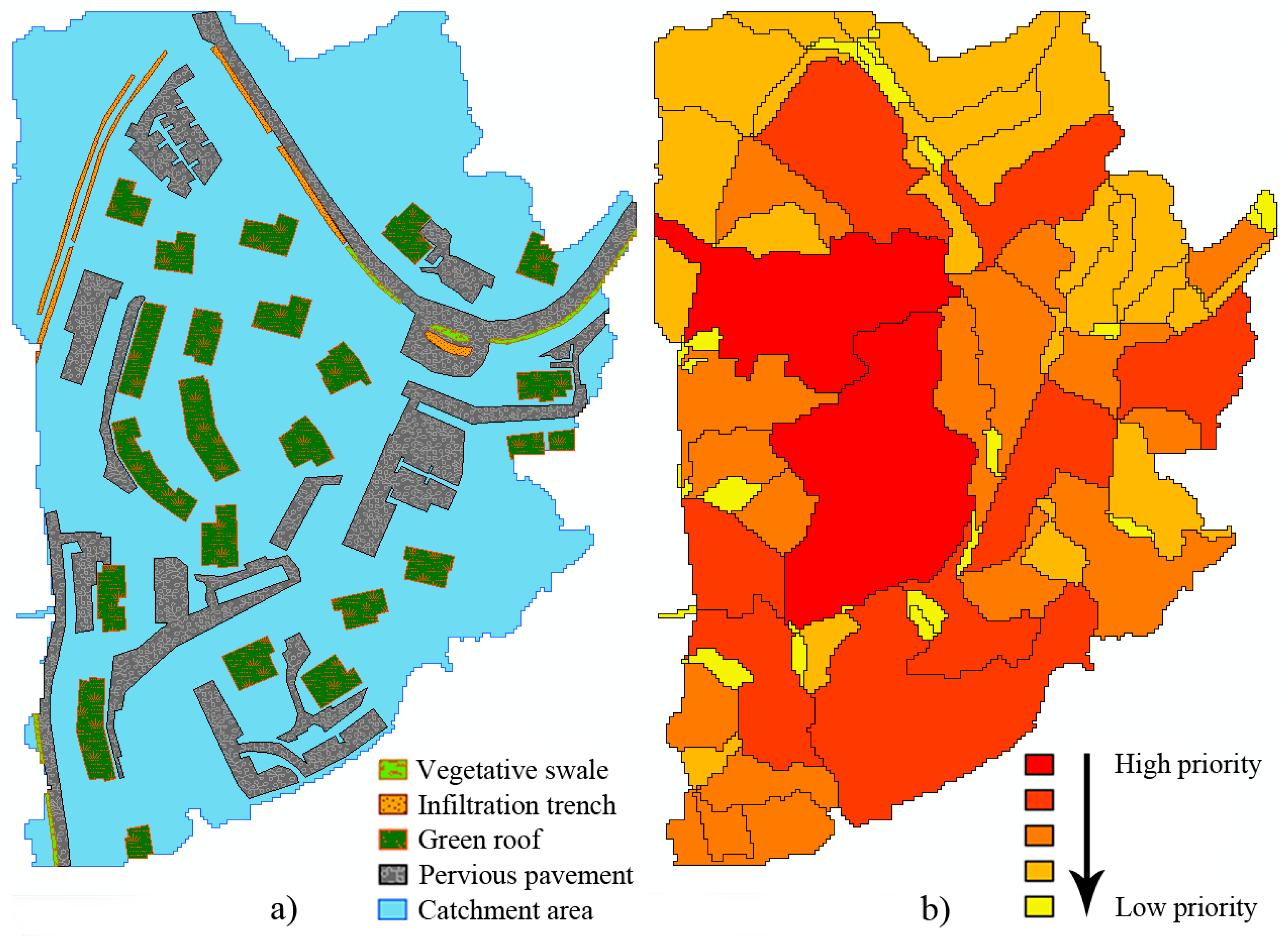
3.1. Search for Feasible Locations for the Implementation of Sustainable Drainage Systems (SuDS)
3.2. Prioritization of Flood-Sensitive Areas
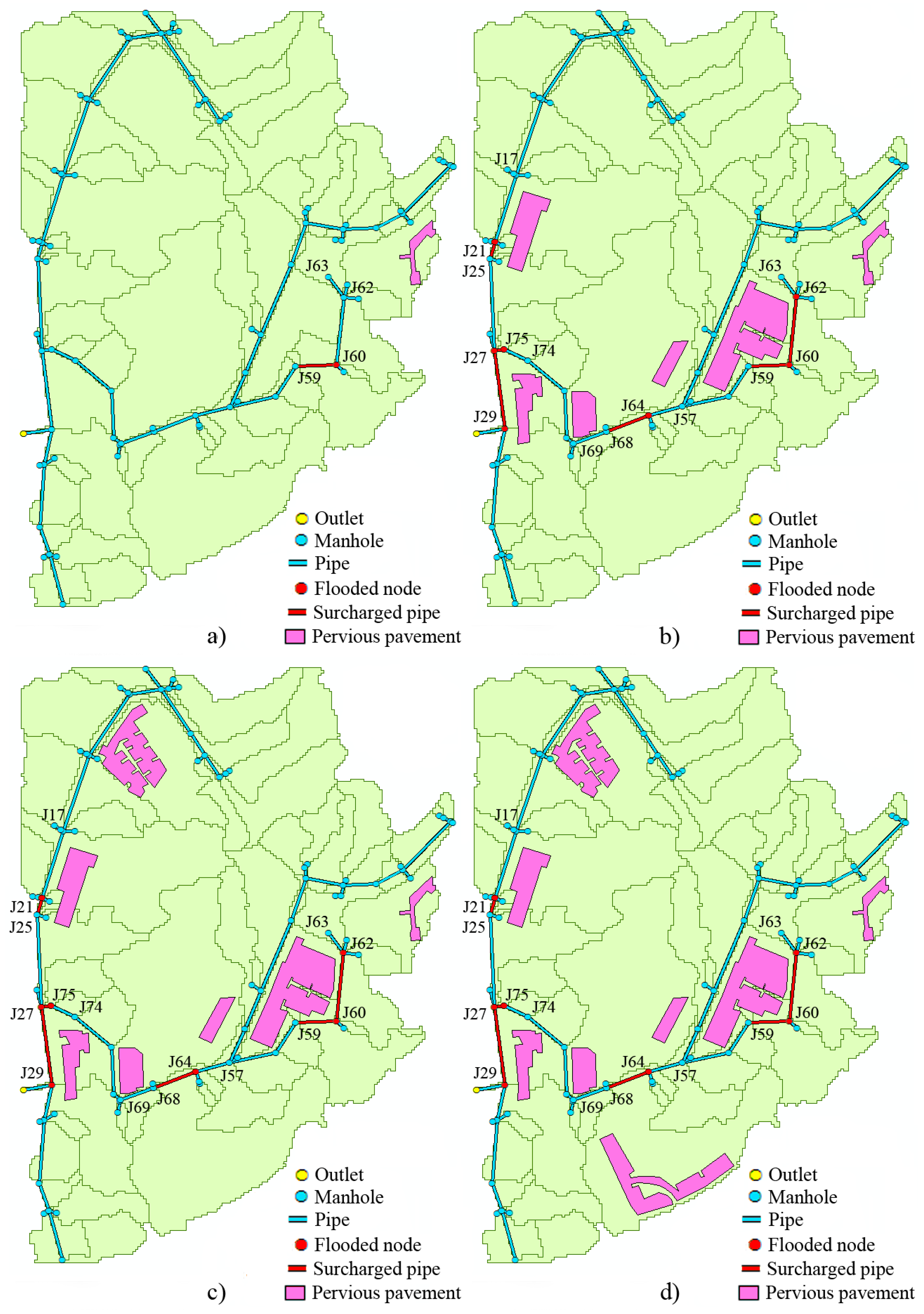
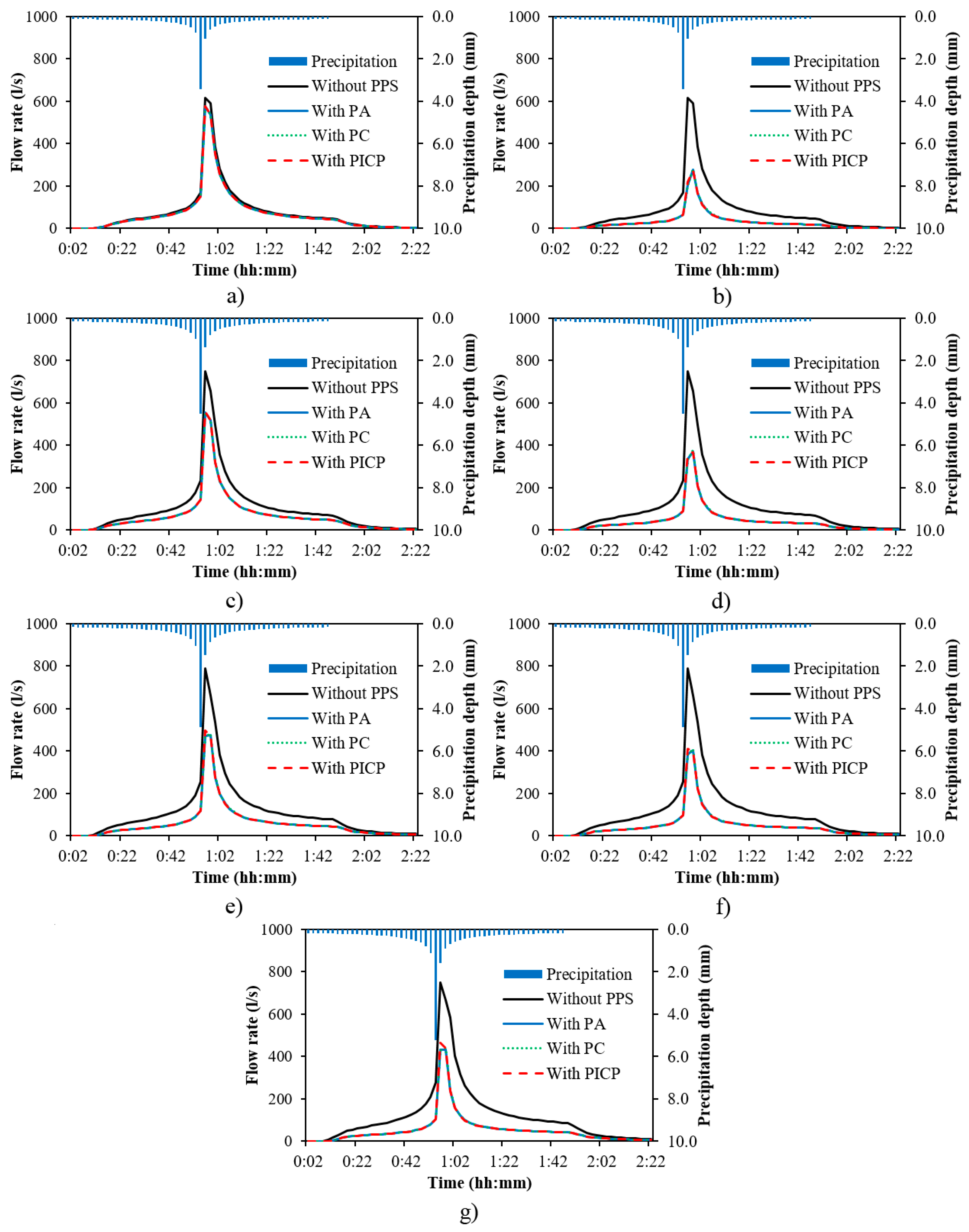
3.3. Hydrological Simulation of Permeable Pavement Systems (PPS)
4. Conclusions
- The percentage of feasible area available in the study catchment for the location of SuDS indicated that PPS were the easiest systems to implement in urban areas due to their multifunctionality.
- The magnitude of lateral inflows in the study catchment was mainly given by the area of its subcatchments, which was the only factor that proved to have a statistically significant correlation to peak runoff rates.
- The inclusion of PPS was found to reduce runoff volumes and delay hydrograph peaks produced by severe storms beyond the standard return periods (2, 5 and 10 years under stationarity) used to design urban drainage systems.
- Although the parameters that characterized their layers were different, the differences between the hydrological impacts of the three main PPS cross-sections (PA, PC and PICP) at the scale of the study catchment were negligible.
- PPS had a statistically significant hydrological impact on the response of the study catchment and reduced discharge by 50% in comparison with situations exclusively based on conventional drainage systems.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Franczyk, J.; Chang, H. The effects of climate change and urbanization on the runoff of the rock creek basin in the Portland Metropolitan Area, Oregon, USA. Hydrol. Process. 2009, 23, 805–815. [Google Scholar] [CrossRef]
- Charlesworth, S.M. A review of the adaptation and mitigation of global climate change using sustainable drainage in cities. J. Water Clim. Chang. 2010, 1, 165–180. [Google Scholar] [CrossRef]
- Pratt, C.J.; Wilson, S.; Cooper, P. Source Control Using Constructed Pervious Pavements. Hydraulic, Structural and Water Quality Performance Issues; CIRIA: London, UK, 2002. [Google Scholar]
- Rodriguez-Hernandez, J. Estudio, Análisis y Diseño de Secciones Permeables de Firmes Para Vías Urbanas con un Comportamiento Adecuado Frente a la Colmatación y con la Capacidad Portante Necesaria para Soportar Tráficos Ligeros. Ph.D. Thesis, Universidad de Cantabria, Santander, Spain, 2008. [Google Scholar]
- Hollinrake, P.G. Permeable Pavements; Report SR 264; HR Wallingford: Wallingford, UK, 1991; pp. 1–58. [Google Scholar]
- Jato-Espino, D.; Charlesworth, S.M.; Bayon, J.R.; Warwick, F. Rainfall-runoff simulations to assess the potential of SuDS for mitigating flooding in highly urbanized catchments. Int. J. Environ. Res. Public Health 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Perez-Pedini, C.; Limbrunner, J.F.; Vogel, R.M. Optimal location of infiltration-based best management practices for storm water management. J. Water Resour. Plan. Manag. 2005, 131, 441–448. [Google Scholar] [CrossRef]
- Cooper, D.; Calvert, J. Draft Strategic Flood Risk Assessment; Ipswich Borough Council: Ipswich, UK, 2007; p. 77.
- Kodz, M.; Caroline Mills, C. Sustainable Drainage Systems for Local Development Framework; Halcrow Group Limited: London, UK, 2011; p. 44. [Google Scholar]
- Doncaster, S.; Stovin, V.; Brian Morrow, B. Lower Irwell Valley, Salford integrated urban drainage pilot project. Integr. Urban Drain. Pilot. 2008, TRE344, 3–30. [Google Scholar]
- Dearden, R.A.; Price, S.J. A proposed decision-making framework for a national infiltration SuDS map. Manag. Environ. Qual. Int. J. 2012, 23, 478–485. [Google Scholar] [CrossRef]
- Becker, M.; Geretshauser, G.; Spengler, B.; Sieker, H. A stormwater management information system for the catchment area of the River Emscher. Water Pract. Technol. 2006, 1, 1–8. [Google Scholar] [CrossRef]
- Sieker, H.; Bandermann, S.; Becker, M.; Raasch, U. Urban stormwater management demonstration projects in the Emscher Region. In First SWITCH Scientific Meeting; The SWITCH Consortium: Birmingham, UK, 2006; pp. 1–8. [Google Scholar]
- Moore, S.L.; Stovin, V.R.; Wall, M.; Ashley, R.M. A GIS-based methodology for selecting stormwater disconnection opportunities. Water Sci. Technol. 2012, 66, 275–283. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, L.; Riverson, J., Jr.; Alvi, K.; Zhen, J.X.; Paul, S.; Rafi, T. SUSTAIN—A Framework for Placement of Best Management Practices in Urban Watersheds to Protect Water Quality; EPA/600/R-09/095; U.S. Environmental Protection Agency: Washington, DC, USA, 2009; pp. 1–202.
- Charlesworth, S.M.; Warwick, F.; Lashford, C. Decision-making and sustainable drainage: Design and scale. Sustainability 2016, 8, 782. [Google Scholar] [CrossRef]
- Viavattene, C.; Scholes, L.; Revitt, D.M.; Ellis, J.B. A GIS based decision support system for the implementation of stormwater best management practices. In Proceedings of the 11th International Conference on Urban Drainage, Scotland, UK, 31 August–5 September 2008; Volume 11, pp. 1–9.
- Ellis, J.B.; Viavattene, C.; Chlebek, J.; Hetherington, D. Integrated modelling for urban surface water exceedance flows. Proc. Inst. Civ. Eng. Struct. Build. 2012, 165, 543–552. [Google Scholar] [CrossRef]
- Environmental Systems Research Institute (ESRI). ArcGIS for Desktop; ESRI: Redlands, CA, USA, 2013. [Google Scholar]
- United States Environmental Protection Agency (U.S. EPA). SWMM 5.1.010; U.S. EPA: Washington, DC, USA, 2015.
- Temprano, J.; Arango, Ó.; Cagiao, J.; Suárez, J.; Tejero, I. Stormwater quality calibration by SWMM: A case study in Northern Spain. Water SA 2006, 32, 55–63. [Google Scholar] [CrossRef]
- Beling, F.A.; Garcia, J.I.B.; Paiva, E.M.C.D.; Bastos, G.A.P.; Paiva, J.B.D. Analysis of the SWMM model parameters for runoff evaluation in Periurban Basins from Southern Brazil. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011; pp. 1–8.
- Guan, M.; Sillanpää, N.; Koivusalo, H. Modelling and assessment of hydrological changes in a developing urban catchment. Hydrol. Process. 2015, 29, 2880–2894. [Google Scholar] [CrossRef]
- Rossman, L. Storm Water Management Model User’s Manual—Version 5.0; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2010.
- Woods-Ballard, B.; Wilson, S.; Udale-Clarke, H.; Illman, S.; Scott, T.; Ashley, R.; Kellagher, R. The SuDS Manual; CIRIA: London, UK, 2015; p. 937. [Google Scholar]
- Clar, M.L.; Barfield, B.J.; O’Connor, T.P. Section 5: BMP Types and Selection. In Stormwater Best Management Practice Design Guide; EPA/600/R-04/121; United States Environmental Protection Agency (U.S. EPA): Washington, DC, USA, 2004; pp. 71–88. [Google Scholar]
- Muthukrishnan, S.; Selvakumar, A. Chapter 3: Structural BMP Design Practices. In The Use of Best Management Practices (BMPs) in Urban Watersheds; EPA/600/R-04/184; United States Environmental Protection Agency (U.S. EPA): Washington, DC, USA, 2004; pp. 78–170. [Google Scholar]
- Beaupre, D.; Jencks, R.; Minick, S.; Mundy, J.; Navarret, A. Appendix A: BMP Fact Sheets. In San Francisco Stormwater Design Guidelines; San Francisco Public Utilities Commission: San Francisco, CA, USA, 2010; pp. 24–31. [Google Scholar]
- Sample, D.J. Best management practice fact sheet 1: Rooftop disconnection. Va. Coop. Ext. 2013, 426–120, 2–3. [Google Scholar]
- Bratieres, K.; Fletcher, T.D.; Deletic, A.; Zinger, Y. Nutrient and sediment removal by stormwater biofilters: A large-scale design optimisation study. Water Res. 2008, 42, 3930–3940. [Google Scholar] [CrossRef] [PubMed]
- ArcGIS for Desktop. ModelBuilder—Creating Tools Tutorial. Available online: http://desktop.arcgis.com/es/arcmap/10.3/analyze/modelbuilder/what-is-modelbuilder.htm (accessed on 23 March 2016).
- Cronshey, R.; McCuen, R.H.; Miller, N.; Rawls, R.; Robbins, S.; Woodward, D. Urban Hydrology for Small Watersheds; TR-55; U.S. Department of Agriculture (USDA): Washington, DC, USA, 1986; pp. 13–21.
- Childs, C. Interpolating Surfaces in ArcGIS Spatial Analyst; ArcUser: Redlands, CA, USA, 2004. [Google Scholar]
- Hirsch, R.M.; Helsel, D.R.; Cohn, T.A.; Gilroy, E.J. Statistical analysis of hydrologic data. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; pp. 1–55. [Google Scholar]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Microsoft Office. MS Excel 2013; Microsoft Corporation: Redmond, WA, USA, 2013. [Google Scholar]
- Smith, D.R. Permeable Interlocking Concrete Pavements, 3rd ed.; Interlocking Concrete Pavement Institute: Burlington, ON, Canada, 2006. [Google Scholar]
- National Asphalt Pavement Association (NAPA). Porous Asphalt Pavements for Stormwater Management. Design, Construction and Maintenance Guide; National Asphalt Pavement Association: Lanham, MD, USA, 2008. [Google Scholar]
- Interlocking Concrete Pavement Institute (ICPI). A Comparison Guide to Porous Asphalt and Pervious Concrete; Interlocking Concrete Pavement Institute: Chantilly, VA, USA, 2009. [Google Scholar]
- ACI Committee 522. Specification for Pervious Concrete Pavement; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Federal Highway Administration (FHWA). Permeable Interlocking Concrete Pavement; HIF-15-007; Federal Highway Administration: Washington, DC, USA, 2015; pp. 3–4.
- Zhang, S.; Guo, Y. SWMM simulation of the storm water volume control performance of permeable pavement systems. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Tennessee Department of Environment and Conservation (TDEC). Permeable Pavement. In Tennessee Permanent Stormwater Management and Design Guidance Manual; University of Tennessee: Knoxville, TN, USA, 2014; pp. 187–214. [Google Scholar]
- McCuen, R.H.; Johnson, P.; Ragan, R. Highway Hydrology: Hydraulic Design Series, 2nd ed.; Federal Highway Administration: Washington, DC, USA, 1996. [Google Scholar]
- Jato-Espino, D.; Rodriguez-Hernandez, J.; Andrés-Valeri, V.C.; Ballester-Muñoz, F. A Fuzzy Stochastic Multi-Criteria Model for the Selection of Urban Pervious Pavements. Expert Syst. Appl. 2014, 41, 6807–6817. [Google Scholar] [CrossRef]
- Bannerman, R.; Horwatich, J.; Selbig, B. Technical Note for Conducting Pavement Surface Infiltration Rate, Pollutant Load and Runoff Volume Reduction Modeling in Accordance with WDNR Conservation Practice Standard 1008, Permeable Pavement; United States Geological Survey (USGS): Reston, VA, USA, 2014.
- Vergura, S.; Acciani, G.; Amoruso, V.; Patrono, G.E.; Vacca, F. Descriptive and inferential statistics for supervising and monitoring the operation of PV plants. IEEE Trans. Ind. Electron. 2009, 56, 4456–4464. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers; Cosmo Publications: New Delhi, India, 1925. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality. Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B.; Chen, H.J. A comparative study of various tests for normality. J. Am. Stat. Assoc. 1968, 63, 1343–1372. [Google Scholar] [CrossRef]
- Fisher, R.A. The correlation between relatives on the supposition of mendelian inheritance. Trans. R. Soc. Edinb. 1919, 52, 399–433. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Gosset, W.S. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar]
- Mann, H.B.; Whitney, D.R. On a test of whether one or more random variables is stochastically larger than in the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Sillanpää, N.; Koivusalo, H. Impacts of urban development on runoff event characteristics and unit hydrographs across warm and cold seasons in high latitudes. J. Hydrol. 2015, 521, 328–340. [Google Scholar] [CrossRef]
- espoo.fi. Map Service. Available online: http://kartat.espoo.fi/IMS/en/Map (accessed on 20 May 2016).
- NLS. National Land Survey of Finland—File Service of Open Data. Available online: https://tiedostopalvelu.maanmittauslaitos.fi/tp/kartta?lang=en (accessed on 20 May 2016).
- Fan, Y.; Li, H.; Miguez-Macho, G. Global patterns of groundwater table depth. Science 2013, 339, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Jato-Espino, D.; Sillanpää, N.; Charlesworth, S.M.; Andrés-Doménech, I. Optimization of the hydrological modelling of urban catchments for assessing their response to extreme rainfall events caused by climate change. Environ. Model. Softw. 2016. under review. [Google Scholar]
- Moss, R.; Babiker, M.; Brinkman, S.; Calvo, E.; Carter, T.; Edmonds, J.; Elgizouli, I.; Emori, S.; Erda, L.; Hibbard, K.; et al. III. “Representative Concentration Pathways”. In Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies; Technical Summary; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2008; pp. 9–19. [Google Scholar]
- Jato-Espino, D.; Castillo-Lopez, E.; Charleswoth, S.M.; Warwick, F. Site selection for sustainable drainage in flood-sensitive highly urbanised catchments using hydrologic and geometric variables. In Proceedings of the 6th International Conference on Sustainable Techniques and Strategies in Urban Water Management (NOVATECH), Lyon, France, 25–28 June 2007; pp. 1–4.

| SuDS | Area (ha) | Hydrologic Soil Group | Building Buffer (m) | Road Buffer (m) | Stream Buffer (m) | Slope (%) | Water Table Depth (m) |
|---|---|---|---|---|---|---|---|
| Bio-retention cell | <0.4 | A–D | - | <30 | >30 | <5 | >0.6 |
| Green roof | - | - | - | - | - | - | - |
| Infiltration trench | <2.0 | A–B | - | - | >30 | <15 | >1.2 |
| Permeable pavement | <1.2 | A–B | - | - | - | <5 | >0.6 |
| Rain barrel | - | - | <9 1 | - | - | - | - |
| Rain garden | <0.4 | A–D | - | - | >30 | <5 | >0.6 |
| Rooftop disconnection | <0.1 2 | - | <1.5 3 | - | - | - | - |
| Vegetative swale | <2.0 | A–D | - | - | - | <4 | >0.6 |
| Layer | Parameter | Value | ||
|---|---|---|---|---|
| PA | PC | PICP | ||
| Surface | Roughness | 0.011 | 0.011 | 0.030 |
| Slope | - | - | - | |
| Pavement | Thickness (mm) | 100 | 130 | 80 |
| Void ratio | 0.20 | 0.25 | 0.10 | |
| Impervious surface fraction | 0.00 | 0.00 | 0.90 | |
| Permeability (mm/h) | 620 | 373 | 815 | |
| Soil/Bedding layer | Thickness (mm) | 30 | - | 50 |
| Porosity | 0.40 | - | 0.40 | |
| Conductivity (mm/h) | 2540 | - | 1270 | |
| Storage/Base | Thickness (mm) | 300 | 300 | 300 |
| Void ratio | 0.40 | 0.40 | 0.40 | |
| Seepage rate (mm/h) | 3600 | 2400 | 3175 | |
| Event | Duration (h) | Depth (mm) | RSSE | R2 | E |
|---|---|---|---|---|---|
| CAL 1 | 5:52 | 5.0 | 81.944 | 0.91 | 0.85 |
| CAL 2 | 11:26 | 37.4 | 212.81 | 0.93 | 0.86 |
| CAL 3 | 6:58 | 12.2 | 92.67 | 0.96 | 0.93 |
| VAL 1 | 6:36 | 5.2 | 42.46 | 0.97 | 0.97 |
| VAL 2 | 4:48 | 9.0 | 68.26 | 0.95 | 0.92 |
| VAL 3 | 6:48 | 23.4 | 115.64 | 0.97 | 0.96 |
| Return Period (Year) | Stationary | RCP4.5 | RCP8.5 |
|---|---|---|---|
| 2 | 31 | 39 | 50 |
| 5 | 40 | 51 | 69 |
| 10 | 46 | 60 | 84 |
| 25 | 55 | 73 | 106 |
| 50 | 63 | 85 | 124 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jato-Espino, D.; Sillanpää, N.; Charlesworth, S.M.; Andrés-Doménech, I. Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments. Water 2016, 8, 451. https://doi.org/10.3390/w8100451
Jato-Espino D, Sillanpää N, Charlesworth SM, Andrés-Doménech I. Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments. Water. 2016; 8(10):451. https://doi.org/10.3390/w8100451
Chicago/Turabian StyleJato-Espino, Daniel, Nora Sillanpää, Susanne M. Charlesworth, and Ignacio Andrés-Doménech. 2016. "Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments" Water 8, no. 10: 451. https://doi.org/10.3390/w8100451
APA StyleJato-Espino, D., Sillanpää, N., Charlesworth, S. M., & Andrés-Doménech, I. (2016). Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments. Water, 8(10), 451. https://doi.org/10.3390/w8100451








