Evaluation of Radiation Components in a Global Freshwater Model with Station-Based Observations
Abstract
:1. Introduction
2. Data and Methods
2.1. Experimental Setup
2.1.1. ERA-Interim
2.1.2. WATCH Forcing Data Methodology Applied to ERA-Interim Reanalysis
2.1.3. Princeton Global Meteorological Forcing Dataset
2.2. WaterGAP Global Hydrology Model (WGHM)
2.3. Radiation Validation Data
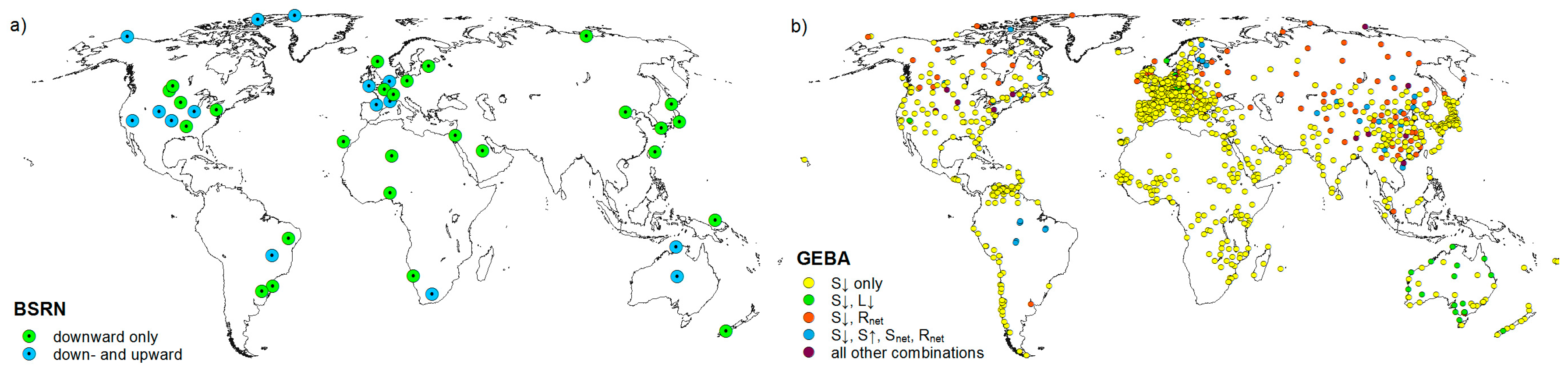
2.3.1. Baseline Surface Radiation Network (BSRN)
2.3.2. Global Energy Balance Archive (GEBA)
2.3.3. Calculation of Net Radiation and Its Components
2.4. Efficiency Metrics
2.4.1. Kling–Gupta Efficiency
2.4.2. Mean Absolute Error
2.4.3. Sum of Ranks
3. Results and Discussion
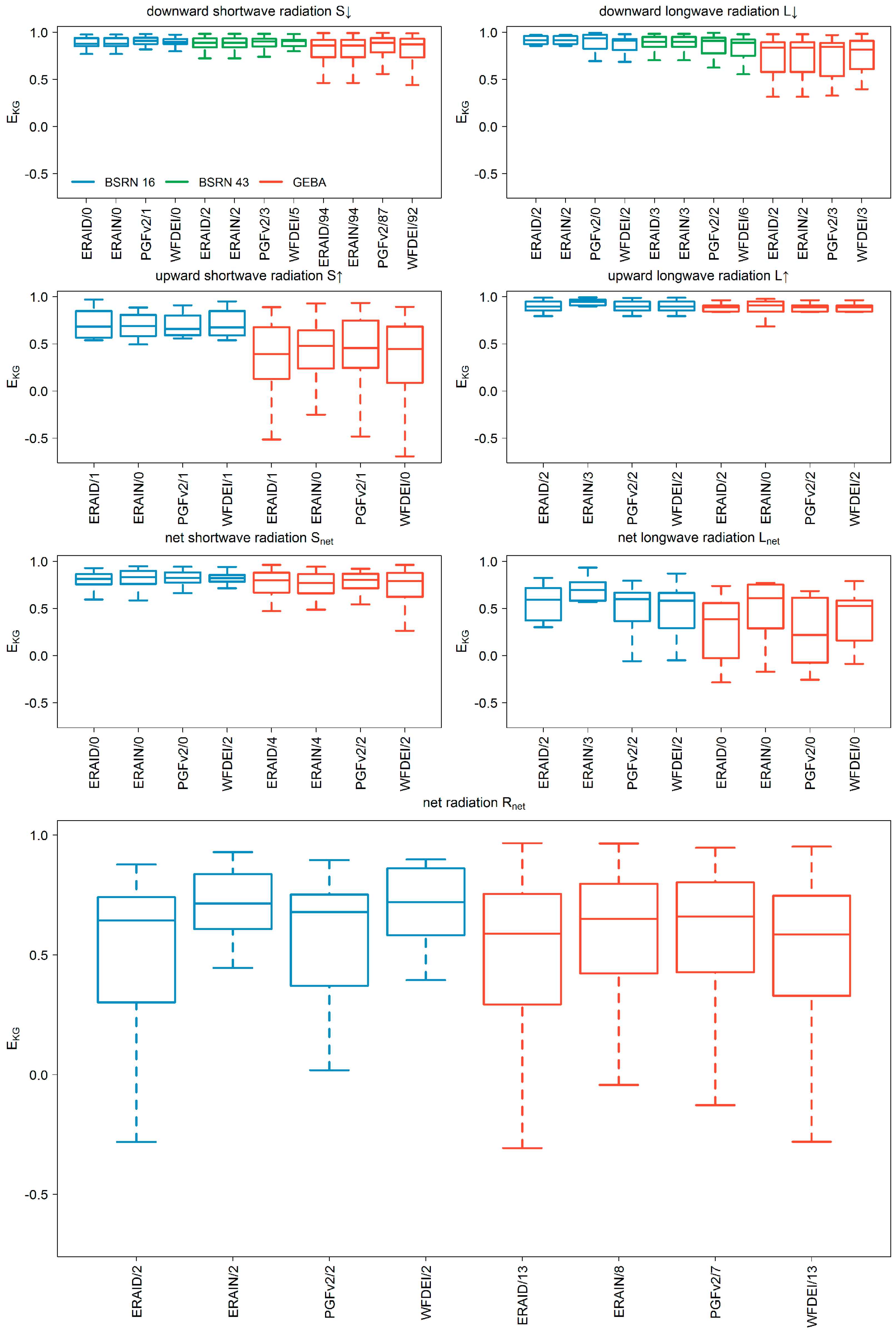
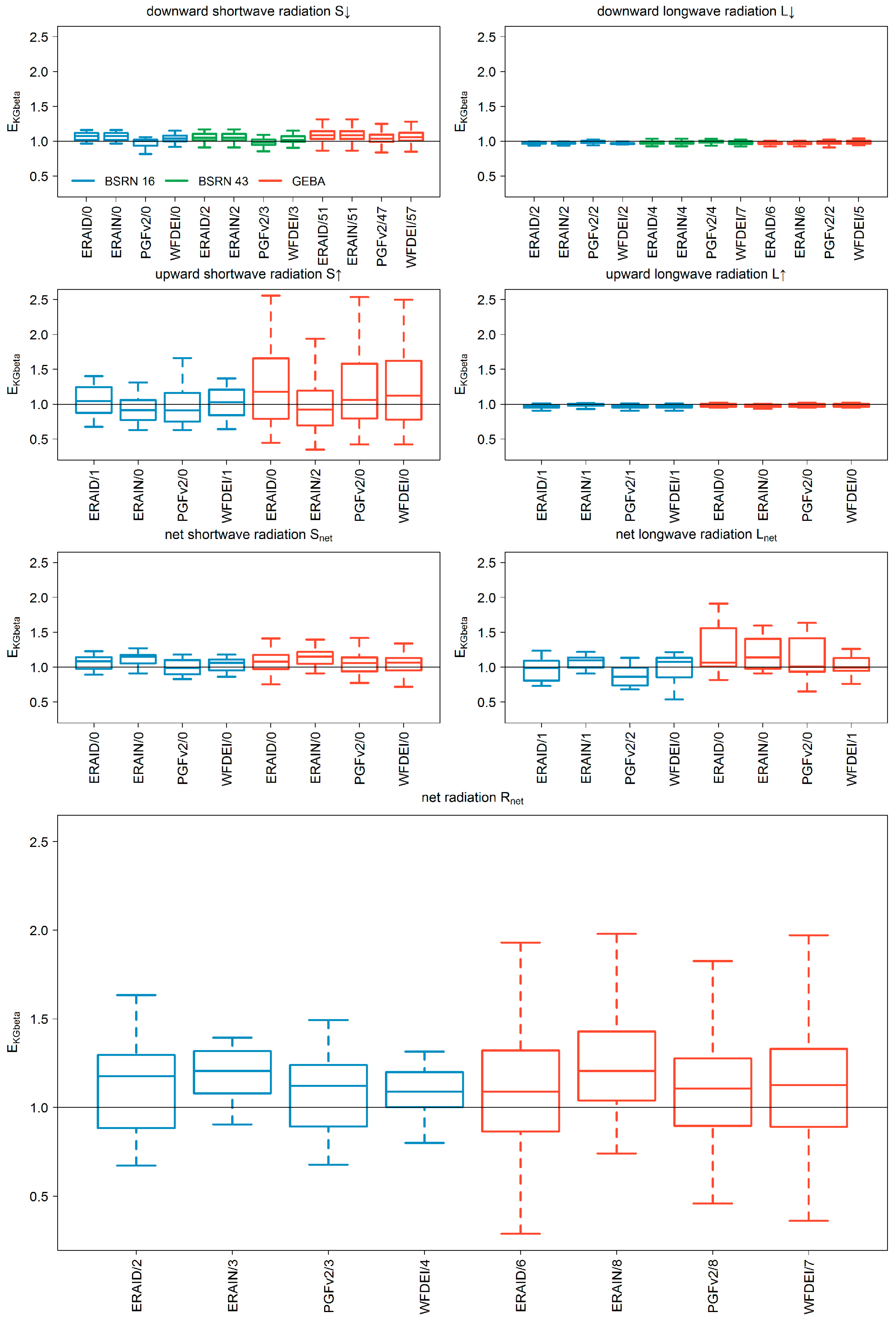
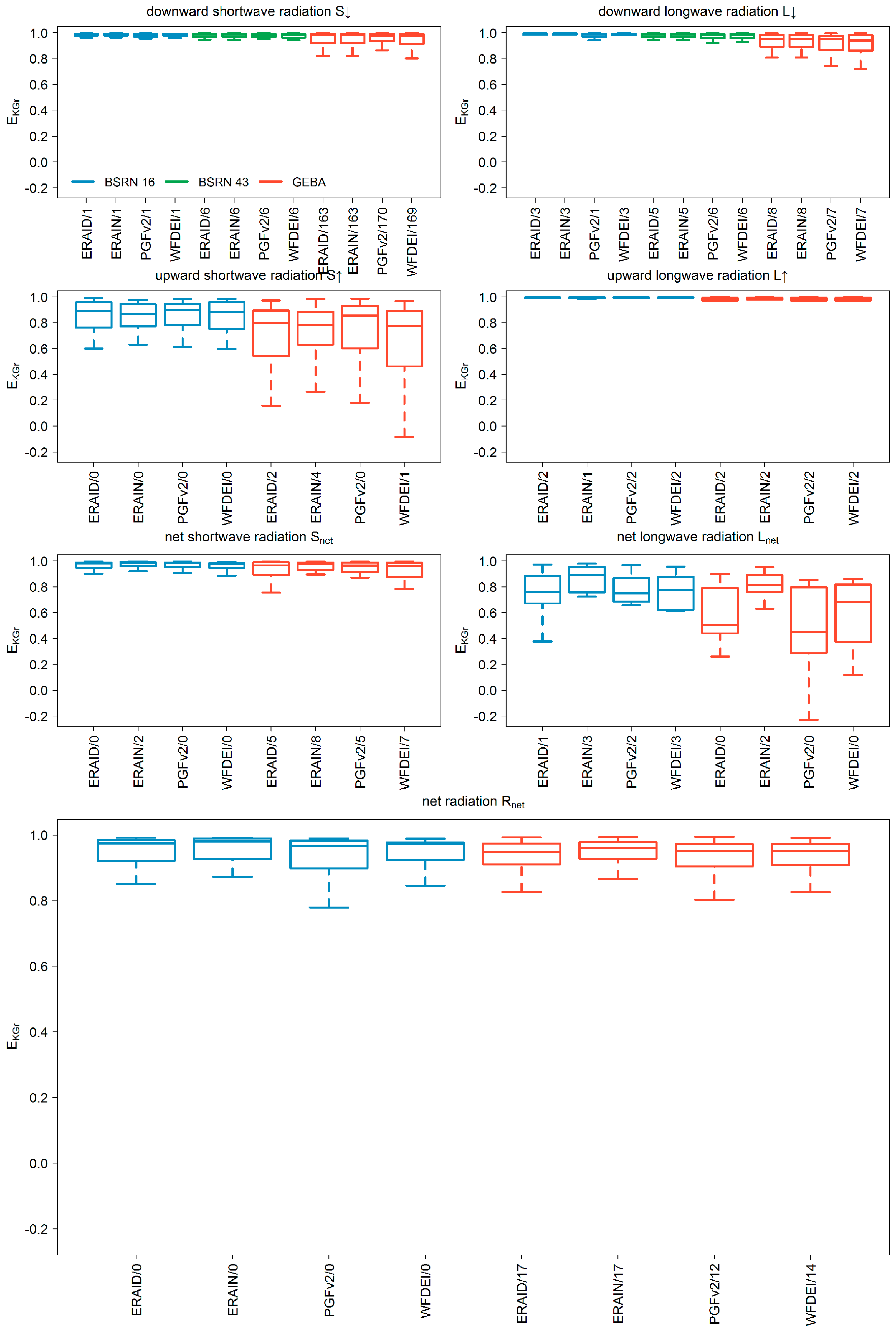
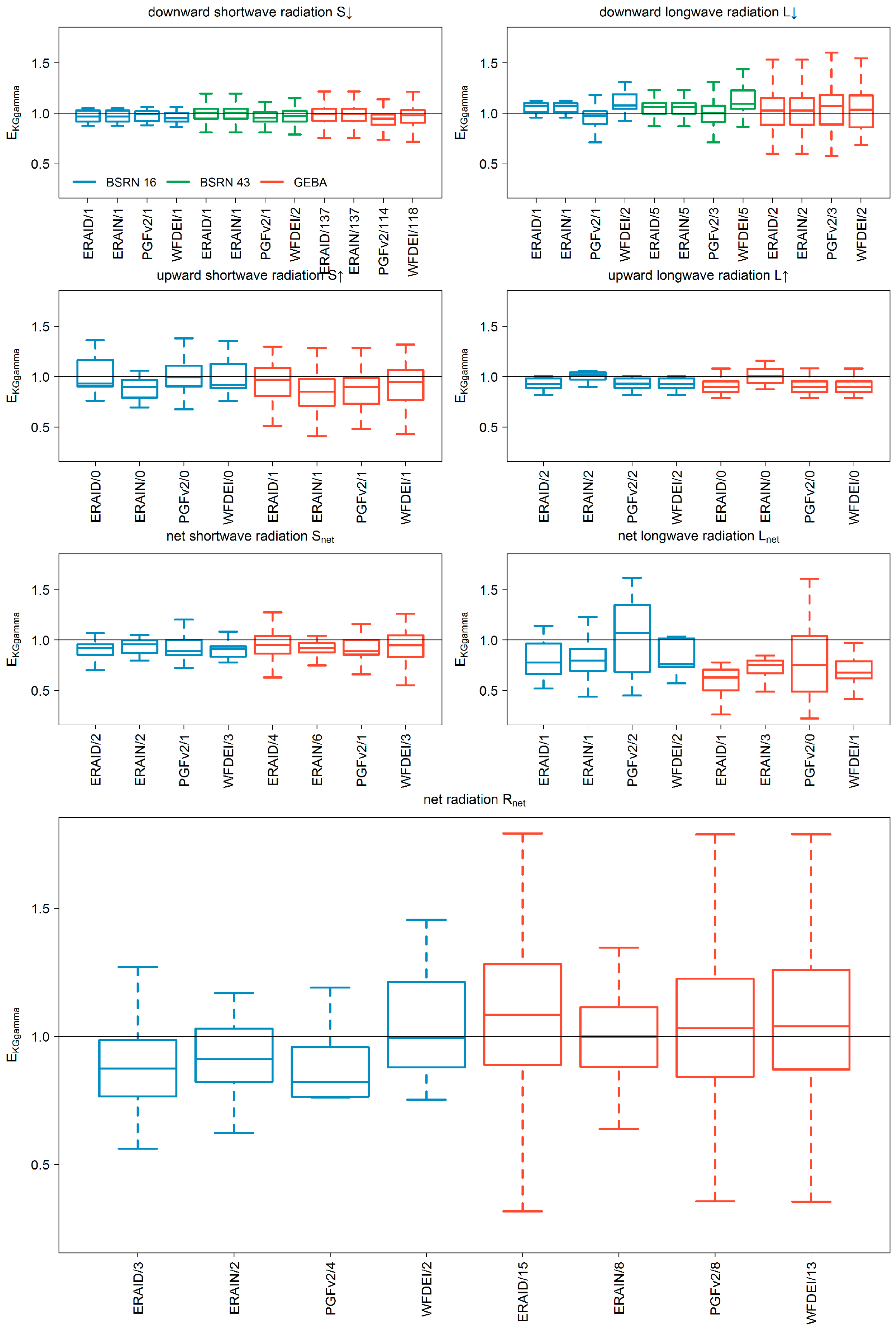
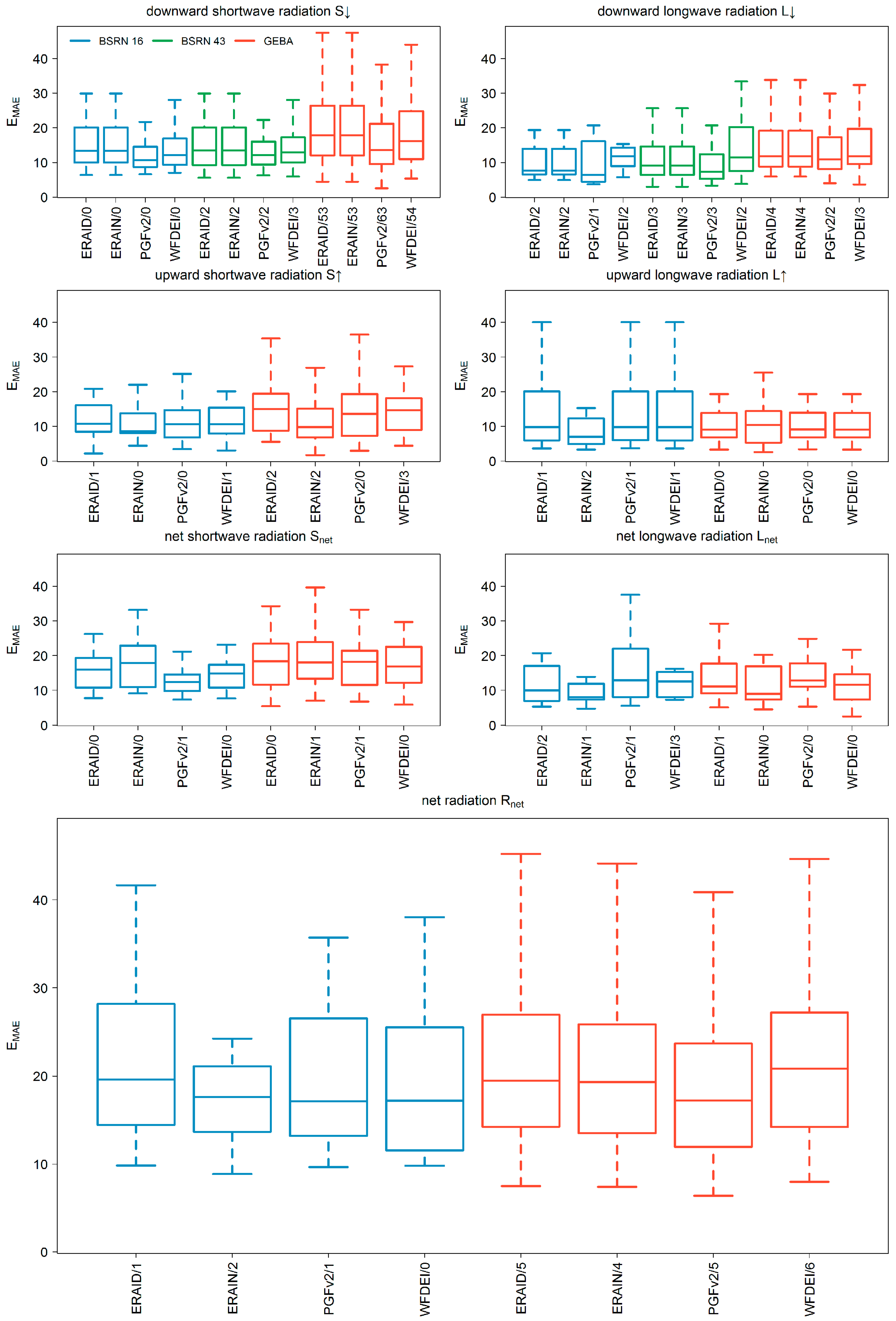
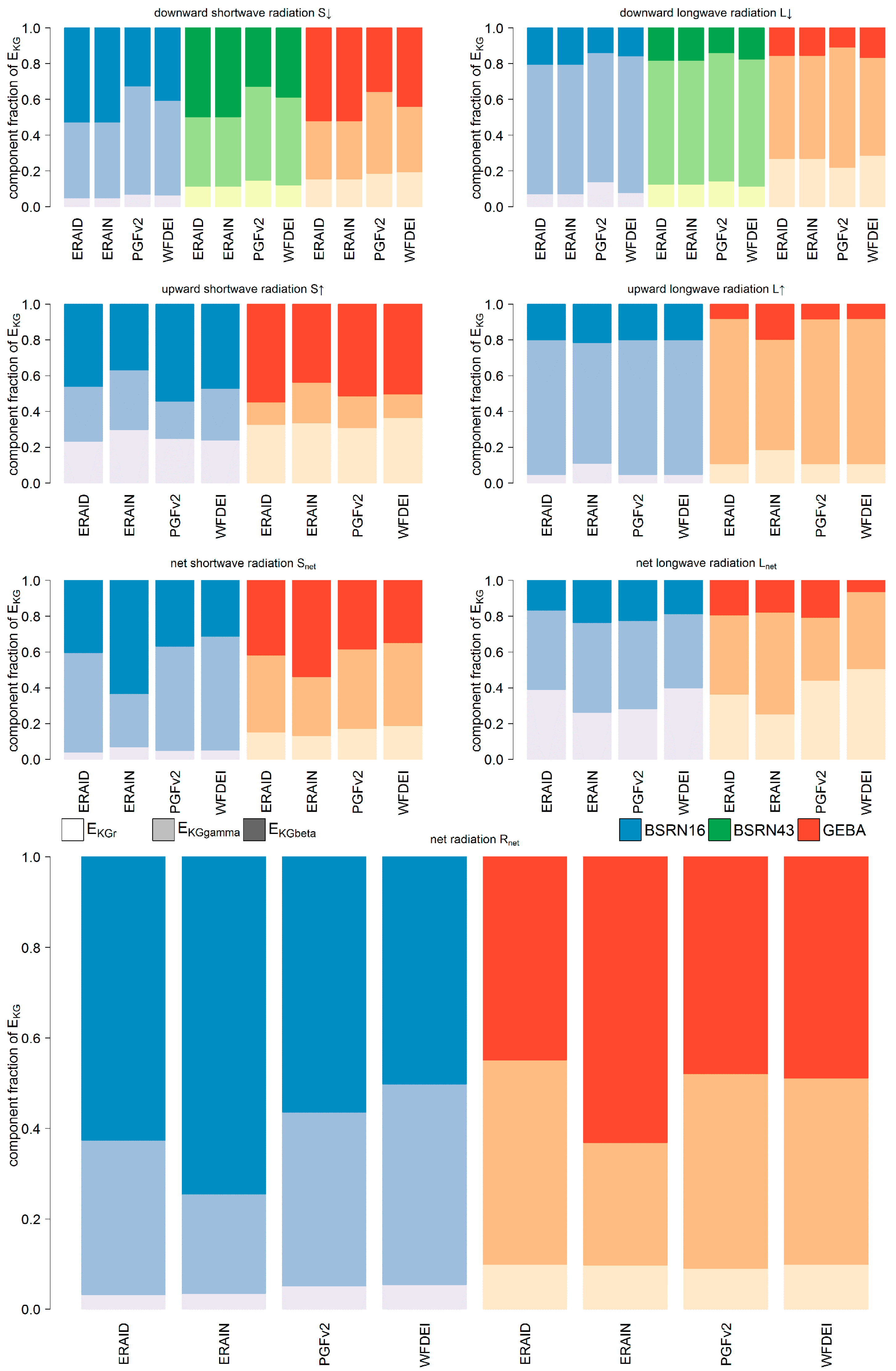
3.1. Comparison to Station Measurements
3.2. Intercomparison of Global-Scale Net Radiation and Its Components
3.3. Discussion of Optimal Radiation Input
4. Conclusions
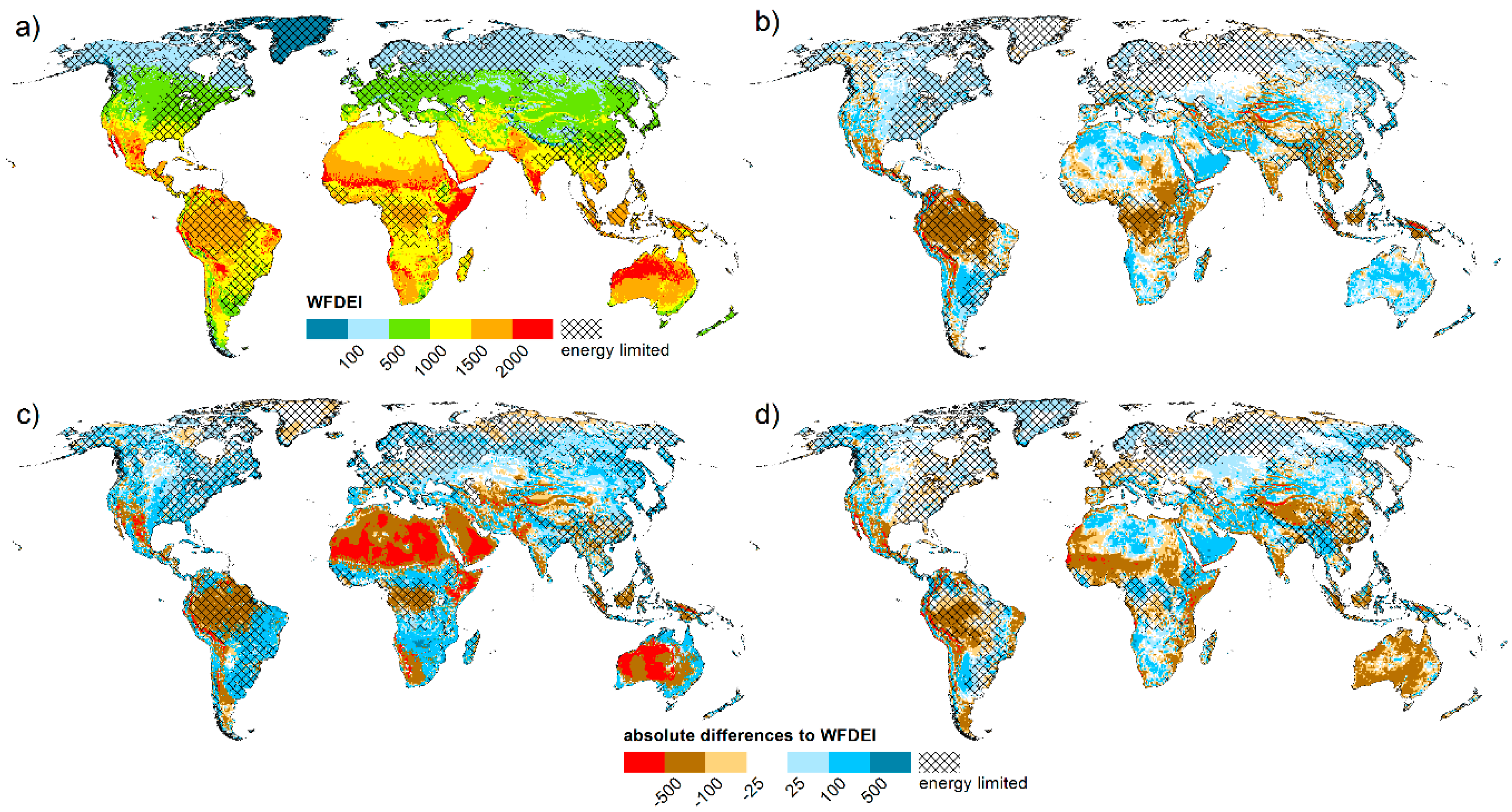
- For global land averages, Rnet differs only slightly among the model variants (~2 Wm−2). However, regionally large differences of Rnet, S↑ and Lnet were found, especially in comparison with ERA-Interim reanalysis (Figure 8).
- Rnet values of WaterGAP as forced by WFDEI is within ±5 Wm−2 agreement to the ERA-Interim reanalysis for 19.1% of the global land area, with similar numbers for energy-limited and water-limited regions.
- In 62.0% of energy-limited regions (relates to 28.8% of the global land area), Rnet of the full radiation dataset from ERA-Interim is higher by more than 5 Wm−2 and has, therefore, the highest potential to increase the simulated evapotranspiration as compared to the other forcings.
- The downward radiation components of ERA-Interim show less or similar agreement to station observations compared to those from meteorological forcings (Table 3). The interpolation and correction approach of Weedon et al. [8] improves both downward radiation components (Table 3). However, for all model variants, a systematical overestimation of S↓ and Rnet was found when comparing to observation data.
- The performance of S↑ radiation of ERA-Interim lies between the meteorological forcings WFDEI and PGFv2. For BSRN stations, the model variant where ERA-Interim downward components are used has a higher performance than the variant where also ERA-Interim upward components are used, whereas the opposite is true for GEBA stations. ERA-Interim values for L↑ are superior compared to those of WaterGAP except for the absolute error measure derived at the GEBA stations (Table 3).
- Best results for Rnet are found for current standard forcing (WFDEI, BSRN) or alternative forcing (PGFv2, GEBA) (Table 3), but median absolute errors are around 20 Wm−2 (comparable to the study of Troy and Wood [16]) and are mainly due to a higher mean value independent on the model variant (Figure 3 and Figure 4).
- Global values for PET vary only by 25 mm·year−1 and the highest values are achieved with WFDEI forcing. However, in energy limited regions, where a change in PET directly influences AET, WFDEI has the second lowest value while ERAIN is 60 mm·year−1 higher.
- The relatively small number of some radiation measurements (e.g., 16 stations with upward flux measurements for BSRN) limits the overall assessment and hinders a robust assessment of the performance of the model variants, especially when separating into energy-limited/water-limited areas.
- In contrast to the downward components, which show a reasonable representativeness of station measurements at the grid cell level [26], upward measurements have a small footprint and thus a high uncertainty in terms of representativeness for the grid cell.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schär, C.; Loeb, N.; Dutton, E.G.; König-Langlo, G. The global energy balance from a surface perspective. Clim. Dyn. 2013, 40, 3107–3134. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Hakuba, M.Z.; Schär, C.; Seneviratne, S.I.; Kato, S.; Rutan, D.; Ammann, C.; Wood, E.F.; König-Langlo, G.; et al. The energy balance over land and oceans: An assessment based on direct observations and CMIP5 climate models. Clim. Dyn. 2015, 44, 3393–3429. [Google Scholar] [CrossRef]
- Wild, M.; Liepert, B. The Earth radiation balance as driver of the global hydrological cycle. Environ. Res. Lett. 2010, 5. [Google Scholar] [CrossRef]
- Sood, A.; Smakhtin, V. Global hydrological models: A review. Hydrol. Sci. J. 2014, 60, 549–565. [Google Scholar] [CrossRef]
- Bierkens, M.F.P. Global hydrology 2015: State, trends, and directions. Water Resour. Res. 2015, 51, 4923–4947. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Adam, L.; Eisner, S.; Fink, G.; Flörke, M.; Kim, H.; Oki, T.; Portmann, F.T.; Reinecke, R.; Riedel, C.; et al. Variations of global and continental water balance components as impacted by climate forcing uncertainty and human water use. Hydrol. Earth Syst. Sci. 2016, 20, 2877–2898. [Google Scholar] [CrossRef]
- Nasonova, O.N.; Gusev, Y.M.; Kovalev, Y.E. Impact of uncertainties in meteorological forcing data and land surface parameters on global estimates of terrestrial water balance components. Hydrol. Process. 2011, 25, 1074–1090. [Google Scholar] [CrossRef]
- Biemans, H.; Hutjes, R.W.A.; Kabat, P.; Strengers, B.J.; Gerten, D.; Rost, S. Effects of precipitation uncertainty on discharge calculations for main river basins. J. Hydrometeorol. 2009, 10, 1011–1025. [Google Scholar] [CrossRef]
- Döll, P.; Douville, H.; Güntner, A.; Müller Schmied, H.; Wada, Y. Modelling freshwater resources at the global scale: Challenges and prospects. Surv. Geophys. 2016, 37, 195–221. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Gilgen, H.; Morcrette, J.-J. The distribution of solar energy at the Earth’s sufrace as calculated in the ECMWF re-analysis. Geophys. Res. Lett. 1998, 25, 4373–4376. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Gilgen, H.; Morcrette, J.-J.; Slingo, A. Evaluation of downward longwave radiation in General Circulation Models. J. Clim. 2001, 14, 3227–3239. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F. Comparison and evaluation of gridded radiation products across northern Eurasia. Environ. Res. Lett. 2009, 4. [Google Scholar] [CrossRef]
- Jin, Y.; Randerson, J.T.; Goulden, M.L. Continental-scale net radiation and evapotranspiration estimated using MODIS satellite observations. Remote Sens. Environ. 2011, 115, 2302–2319. [Google Scholar] [CrossRef]
- Posselt, R.; Mueller, R.W.; Stöckli, R.; Trentmann, J. Remote sensing of solar surface radiation for climate monitoring—The CM-SAF retrieval in international comparison. Remote Sens. Environ. 2012, 118, 186–198. [Google Scholar] [CrossRef]
- Gómez, I.; Caselles, V.; Estrela, M. Seasonal Characterization of Solar Radiation Estimates Obtained from a MSG-SEVIRI-Derived Dataset and a RAMS-Based Operational Forecasting System over the Western Mediterranean Coast. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Inamdar, A.; Guillevic, P. Net surface shortwave radiation from GOES imagery—Product evaluation using ground-based measurements from SURFRAD. Remote Sens. 2015, 7, 10788–10814. [Google Scholar] [CrossRef]
- Boilley, A.; Wald, L. Comparison between meteorological re-analyses from ERA-Interim and MERRA and measurements of daily solar irradiation at surface. Renew. Energy 2015, 75, 135–143. [Google Scholar] [CrossRef] [Green Version]
- König-Langlo, G.; Sieger, R.; Schmithüsen, H.; Bücker, A.; Richter, F.; Dutton, E.G. Baseline Surface Radiation Network (BSRN) Update of the Technical Plan for BSRN Data Management; WCRP Report 24/2013; World Meteorological Organization (WMO): Geneva, Switzerland, 2013. [Google Scholar]
- Gilgen, H.; Ohmura, A. The Global Energy Balance Archive. Bull. Am. Meteorol. Soc. 1999, 80, 831–850. [Google Scholar] [CrossRef]
- Heinemann, G.; Kerschgens, M. Simulation of surface energy fluxes using high-resolution non-hydrostatic simulations and comparisons with measurements for the LITFASS-2003 experiment. Bound.-Layer Meteorol. 2006, 121, 195–220. [Google Scholar] [CrossRef]
- Horlacher, V.; Osborne, S.; Price, J.D. Comparison of two closely located meteorological measurement sites and consequences for their areal representativity. Bound.-Layer Meteorol. 2012, 142, 469–493. [Google Scholar] [CrossRef]
- Hakuba, M.Z.; Folini, D.; Sanchez-Lorenzo, A.; Wild, M. Spatial representativeness of ground-based solar radiation measurements-Extension to the full Meteosat disk. J. Geophys. Res. Atmos. 2014, 119, 11760–11771. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Shuttleworth, W.J.; Blyth, E.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. Creation of the WATCH Forcing Data and its use to assess global and regional reference crop evaporation over land during the twentieth century. J. Hydrometeorol. 2011, 12, 823–848. [Google Scholar] [CrossRef]
- ECMWF IFS Documentation—Cy40r1 Part IV: Physical Processes; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2014.
- Uppala, S.M.M.; KÅllberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) IPCC Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013.
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Alcamo, J.; Döll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rösch, T.; Siebert, S. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 2003, 48, 317–337. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K. Global-scale modeling of groundwater recharge. Hydrol. Earth Syst. Sci. 2008, 12, 863–885. [Google Scholar] [CrossRef]
- Döll, P.; Müller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Haddeland, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertrand, N.; Best, M.; Folwell, S.; Gerten, D.; et al. Multimodel estimate of the global terrestrial water balance: Setup and first results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef]
- Schewe, J.; Heinke, J.; Gerten, D.; Haddeland, I.; Arnell, N.W.; Clark, D.B.; Dankers, R.; Eisner, S.; Fekete, B.M.; Colón-González, F.J.; et al. Multimodel assessment of water scarcity under climate change. Proc. Natl. Acad. Sci. USA 2014, 111, 3245–3250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagemann, S.; Chen, C.; Clark, D.B.; Folwell, S.; Gosling, S.N.; Haddeland, I.; Hanasaki, N.; Heinke, J.; Ludwig, F.; Voss, F.; et al. Climate change impact on available water resources obtained using multiple global climate and hydrology models. Earth Syst. Dyn. 2013, 4, 129–144. [Google Scholar] [CrossRef]
- Döll, P.; Müller Schmied, H. How is the impact of climate change on river flow regimes related to the impact on mean annual runoff? A global-scale analysis. Environ. Res. Lett. 2012, 7. [Google Scholar] [CrossRef]
- Portmann, F.T.; Döll, P.; Eisner, S.; Flörke, M. Impact of climate change on renewable groundwater resources: Assessing the benefits of avoided greenhouse gas emissions using selected CMIP5 climate projections. Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef]
- Alcamo, J.; Leemans, R.; Kreileman, E. Global Change Scenarios of the 21st Century—Results from the IMAGE 2.1 Model; Pergamon: Oxford, UK, 1998. [Google Scholar]
- Wilber, A.C.; Kratz, D.P.; Gupta, S.K. Surface Emissivity Maps for Use in Satellite Retrievals of Longwave Radiation; NASA/TP-1999-209362; Langley Research Center: Hampton, VA, USA, 1999; 35p. [Google Scholar]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Möller, M.I. Vergleich von Modellierten Globalskaligen Rasterdaten der Strahlung Mit Stationsbasierten Messwerten: Methodenentwicklung und Analyse. Master’s Thesis, Goethe-University Frankfurt, Frankfurt, Germany, 16 July 2015. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Raschke, E.; Kinne, S.; Stackhouse, P.W. GEWEX Radiative Flux Assessment (RFA) Volume 1: Assessment. A Project of the World Climate Research Programme Global Energy and Water Cycle Experiment (GEWEX) Radiation Panel; WCRP Report 19/2012; World Meteorological Organization (WMO): Geneva, Switzerland, 2012. [Google Scholar]
- Russak, V.; Niklus, I. Longwave radiation at the earth’s surface in Estonia. Proc. Estonian Acad. Sci. 2015, 64, 480. [Google Scholar] [CrossRef]
- Hori, M.; Aoki, T.; Tanikawa, T.; Motoyoshi, H.; Hachikubo, A.; Sugiura, K.; Yasunari, T.J.; Eide, H.; Storvold, R.; Nakajima, Y.; et al. In-situ measured spectral directional emissivity of snow and ice in the 8–14 μm atmospheric window. Remote Sens. Environ. 2006, 100, 486–502. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. Assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
| Name | S↓ | S↑ | L↓ | L↑ | P, T |
|---|---|---|---|---|---|
| WFDEI | WFDEI | WaterGAP | WFDEI | WaterGAP | WFDEI |
| ERAID | ERA-Interim | WaterGAP | ERA-Interim | WaterGAP | WFDEI |
| ERAIN | ERA-Interim | ERA-Interim | ERA-Interim | ERA-Interim | WFDEI |
| PGFv2 | PGFv2 | WaterGAP | PGFv2 | WaterGAP | PGFv2 |
| Variable | # Stations | # Stations (Calculated) | # Months | # Months (Calculated) |
|---|---|---|---|---|
| BSRN | ||||
| S↓ | 43 | 5099 | ||
| S↑ | 16 | 2317 | ||
| Snet | 16 | 2289 | ||
| L↓ | 43 | 4872 | ||
| L↑ | 16 | 2210 | ||
| Lnet | 16 | 2205 | ||
| Rnet | 16 | 2171 | ||
| GEBA | ||||
| S↓ | 1061 | 171,169 | ||
| S↑ | 43 | 3067 | ||
| Snet | 40 | 2791 | ||
| L↓ | 42 | 2933 | ||
| L↑ | 14 | 839 | ||
| Lnet | 13 | 692 | ||
| Rnet | 142 | 11,525 | ||
| BSRN | GEBA | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | |
| S↓ | 2.8 | 2.8 | 2.6 | 1.8 | 2.8 | 2.8 | 2.3 | 2.1 | 2.8 | 2.8 | 2.0 | 2.4 | 2.9 | 2.9 | 2.0 | 2.3 |
| S↑ | 2.2 | 2.5 | 3.0 | 2.3 | 2.3 | 2.7 | 3.0 | 2.0 | 3.0 | 2.3 | 1.9 | 2.9 | 3.0 | 2.0 | 2.0 | 3.0 |
| Sn | 3.0 | 2.3 | 2.5 | 2.2 | 3.0 | 3.2 | 1.3 | 2.5 | 2.3 | 2.6 | 2.6 | 2.5 | 2.4 | 2.6 | 2.6 | 2.4 |
| L↓ | 2.4 | 2.4 | 2.4 | 2.9 | 2.4 | 2.4 | 1.8 | 3.4 | 2.5 | 2.5 | 2.6 | 2.5 | 2.6 | 2.6 | 2.2 | 2.6 |
| L↑ | 2.6 | 2.0 | 2.8 | 2.6 | 2.6 | 2.0 | 2.8 | 2.6 | 2.5 | 2.1 | 2.8 | 2.5 | 2.1 | 2.5 | 3.4 | 2.1 |
| Ln | 2.8 | 1.5 | 3.2 | 2.5 | 2.2 | 1.7 | 3.5 | 2.7 | 3.0 | 1.5 | 3.0 | 2.5 | 2.8 | 2.1 | 3.0 | 2.1 |
| Rn | 3.2 | 2.2 | 2.7 | 2.0 | 3.0 | 2.8 | 2.2 | 2.0 | 2.8 | 2.4 | 2.2 | 2.6 | 2.5 | 2.5 | 2.3 | 2.7 |
| ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S↓ | 2.1 | 2.1 | 2.6 | 3.2 | 2.2 | 2.2 | 2.6 | 2.9 | 2.6 | 2.6 | 2.5 | 2.3 |
| S↑ | 2.4 | 2.6 | 2.4 | 2.7 | 2.5 | 2.8 | 2.2 | 2.5 | 2.6 | 2.6 | 2.7 | 2.1 |
| Sn | 2.2 | 2.1 | 2.2 | 3.5 | 2.3 | 1.8 | 2.9 | 2.9 | 2.3 | 3.1 | 2.6 | 1.9 |
| L↓ | 1.8 | 1.8 | 3.1 | 3.2 | 2.4 | 2.4 | 3.1 | 2.0 | 2.7 | 2.7 | 2.5 | 2.2 |
| L↑ | 2.5 | 2.2 | 2.9 | 2.5 | 2.5 | 3.2 | 1.8 | 2.5 | 2.3 | 2.9 | 2.4 | 2.3 |
| Ln | 2.8 | 1.4 | 2.6 | 3.2 | 2.7 | 2.8 | 2.0 | 2.6 | 2.6 | 2.8 | 2.1 | 2.6 |
| Rn | 2.4 | 1.6 | 3.1 | 2.9 | 1.9 | 2.5 | 2.4 | 3.2 | 2.3 | 3.2 | 2.0 | 2.4 |
| ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | ERD | ERN | PGF | WFD | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S↓ | 2.3 | 2.3 | 2.2 | 3.2 | 2.1 | 2.1 | 3.0 | 2.9 | 2.6 | 2.6 | 2.4 | 2.4 |
| S↑ | 2.7 | 2.3 | 1.8 | 3.2 | 2.0 | 3.0 | 2.9 | 2.1 | 2.8 | 2.1 | 2.5 | 2.6 |
| Sn | 2.4 | 2.1 | 2.0 | 3.4 | 2.6 | 2.3 | 2.4 | 2.8 | 2.7 | 2.7 | 2.4 | 2.2 |
| L↓ | 2.1 | 2.1 | 2.8 | 3.0 | 2.4 | 2.4 | 2.9 | 2.2 | 2.6 | 2.6 | 2.4 | 2.5 |
| L↑ | 2.4 | 2.2 | 3.0 | 2.4 | 2.7 | 2.6 | 2.0 | 2.7 | 2.4 | 3.1 | 2.1 | 2.4 |
| Ln | 2.6 | 1.2 | 3.4 | 2.8 | 2.2 | 2.4 | 2.6 | 2.8 | 1.8 | 3.1 | 2.2 | 2.8 |
| Rn | 2.7 | 1.8 | 2.7 | 2.9 | 2.5 | 2.4 | 2.7 | 2.4 | 2.3 | 3.0 | 2.5 | 2.3 |
| Region | ERD | ERN | PGF | WFD |
|---|---|---|---|---|
| Global | 1113 | 1092 | 1103 | 1116 |
| Energy-limited | 864 | 933 | 894 | 872 |
| Water-limited | 1336 | 1235 | 1292 | 1336 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller Schmied, H.; Müller, R.; Sanchez-Lorenzo, A.; Ahrens, B.; Wild, M. Evaluation of Radiation Components in a Global Freshwater Model with Station-Based Observations. Water 2016, 8, 450. https://doi.org/10.3390/w8100450
Müller Schmied H, Müller R, Sanchez-Lorenzo A, Ahrens B, Wild M. Evaluation of Radiation Components in a Global Freshwater Model with Station-Based Observations. Water. 2016; 8(10):450. https://doi.org/10.3390/w8100450
Chicago/Turabian StyleMüller Schmied, Hannes, Richard Müller, Arturo Sanchez-Lorenzo, Bodo Ahrens, and Martin Wild. 2016. "Evaluation of Radiation Components in a Global Freshwater Model with Station-Based Observations" Water 8, no. 10: 450. https://doi.org/10.3390/w8100450
APA StyleMüller Schmied, H., Müller, R., Sanchez-Lorenzo, A., Ahrens, B., & Wild, M. (2016). Evaluation of Radiation Components in a Global Freshwater Model with Station-Based Observations. Water, 8(10), 450. https://doi.org/10.3390/w8100450








