1. Introduction
Droughts are a climatic phenomenon that may impact large and small regions alike for long or short time periods and influence almost all aspects of society [
1]. Historically, droughts have had negative effects on domestic and agricultural water supply needs [
2] and consequently altered the behavior of ecosystems [
3,
4]. Plans, designs, and operational applications for water resources systems, therefore, require accurate estimation of different drought characteristics, like duration (
), average severity (
), average areal extent (
), and re-occurrence rate under various scenarios.
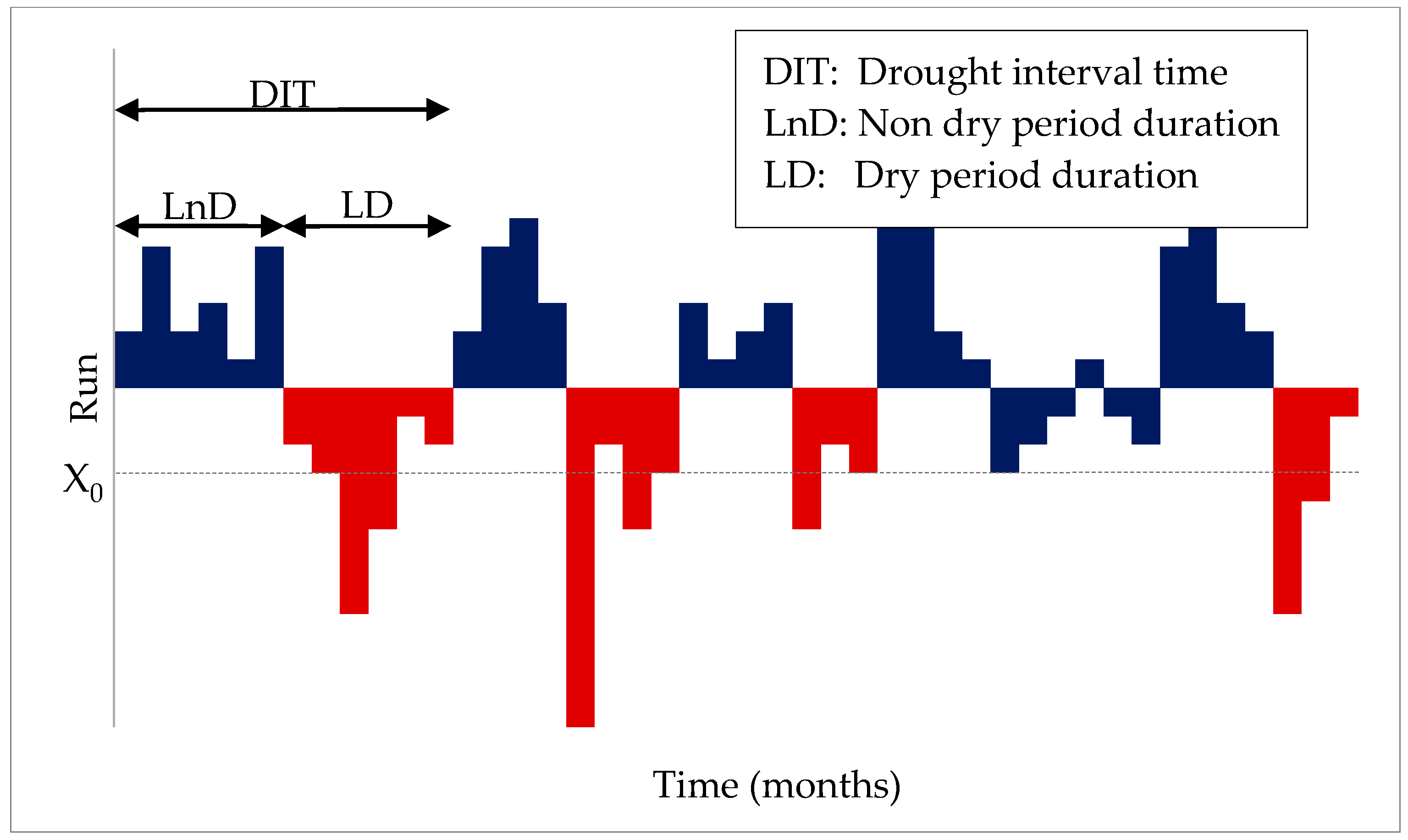
Drought characteristics have been analyzed using various methods that have evolved over time. Earlier studies investigated the analytical or stochastic nature of past droughts using runs theory. Based on this theory, observed time series of drought-related variables are divided into wet and dry periods (positive and negative runs, respectively; see
Figure 1) depending on a given threshold or critical level [
5,
6]. Later studies focused more on probabilistic drought estimation using ground station-based datasets [
7,
8,
9]. The scarcity of ground stations and short recording lengths motivated the following studies to use synthetic datasets to analyze the frequencies of drought events [
10,
11]. Since the spatial–temporal relationships among drought characteristics are complex, recent studies have diversified their efforts by analyzing the return periods of droughts using various
or
scenarios [
12,
13,
14].
The copula approach [
15] provides an ideal test bed in which to analyze multivariate probabilistic problems without making explicit assumptions about the marginal or joint distributions of the variables involved in the estimation problem. Perhaps this ability has motivated studies to implement a multivariate probabilistic approach via copula functions to solve many different problems in hydrologic science and water resources-related applications [
16,
17,
18,
19].
Given that drought return periods can be immediately formulated in a probabilistic framework, copula-related methods have the necessary utility required to investigate different drought characteristics. Shiau [
13] used bivariate copula functions to investigate bivariate drought analysis, including joint probabilities and return periods. Song and Singh [
20] expanded this drought frequency analysis from bivariate to trivariate via a new method that constructs trivariate copulas to describe the joint distribution function of the temporal characteristics of meteorological drought events. Recently, Xu et al. [
14] used a trivariate drought identification method within the copula approach to calculate the joint probability and return period of different drought spatial–temporal characteristic pairs. Overall, these studies demonstrated the advantages of the copula approach on bivariate and trivariate modeling of drought characteristics.
Certain characteristics of drought may precede others. For example, droughts with longer durations may tend to have higher maximum severity, or it may take longer to dissipate severe droughts than droughts with moderate severity. Such dependencies between drought characteristics can be immediately studied in a conditional copula framework, particularly when the occurrence of certain characteristics signals the occurrence of other characteristic functions in multivariate problems. Even though joint copula functions have been implemented in many studies, the implementation of conditional copulas remained limited in the literature [
14,
21]; hence there is still more room for more conditional copula-based applications to fully comprehend the utility of these functions.
Drought characteristics could be profoundly linked both in time and space. Accordingly, knowledge (i.e., observations) of some drought characteristics in time or space may help us predict others. This temporal and/or spatial dependency between different drought characteristics may immediately be exploited using copula functions, particularly using conditional probabilities. Even though spatial–temporal dependencies of drought characteristics have been investigated before using copula functions [
22,
23,
24], such investigations have not been carried out in a conditional framework before.
The main objective of this study is to implement a copula-based methodology to analyze the joint and conditional dependency among various spatial–temporal characteristics of droughts, including , , and . The analysis utilizes univariate cumulative distribution functions (CDF) of drought characteristics obtained over Ankara, Turkey to establish joint and conditional relations between them, using bivariate and trivariate copula functions to calculate expected return periods of droughts with different characteristics scenarios.
3. Results and Discussion
The drought characteristics
,
, and
were calculated for each drought period separately (
Table 3). Accordingly, higher
values indicate more severe drought conditions and values closer to 0 indicate near to normal conditions. For example, the drought event starting in July 1985 and ending in January 1986 (
Table 3) has an
of seven months,
of 1.05, and
of 0.74. Here
is calculated as the absolute value of the average of seven SPI values:
; and
is calculated as the fraction of total months under drought condition (i.e., the regional average SPI time series show the drought duration is seven months, while the six separate SPI time series over each station show 31 months are under drought conditions out of a total of six stations × seven months = 42 months, implying
). Overall results show that drought conditions influenced the study area during 39% of the total study period (summation of all
/650 months), while these drought events, on average, have
of 0.94, last for 6.92 months, and impact 73% of the area covered by the stations (
Table 3).
Droughts tend to start during drier months (July–September) and end during wetter winter months (November–February). This result is expected as SPI-6 considers six-monthly accumulated precipitation values (Equation (28)): SPI-6 values for July–September are calculated using relatively drier months and values for November–February are calculated using relatively wetter months, where the summer and the winter months are climatologically dry and wet, respectively. This systematic pattern is consistent with the drought definition of many water resources managers who are interested in the lack of water. Removal of this strong SPI-6 seasonality may result in reduced SPI-6 sensitivity to actual water deficit (i.e., anomalies obtained during drier months may not necessarily mean the same “water deficit” during wetter months), hence SPI-6 seasonality is retained in this study.
Strong linear dependence is found between
and
(correlations are statistically significant at 95% confidence level), while the relationships between other drought characteristics are much weaker (
Table 4). This implies that predictability studies involving
and
may contain high predictive skill, while particularly
prediction using
or
relations may not yield accurate results. Here, drought characteristics
and
have boundaries (0 and 1.0, respectively); however, there are not many values close to these boundary values, hence the use of correlation statistics may not be problematic assuming these drought characteristics are approximately normal.
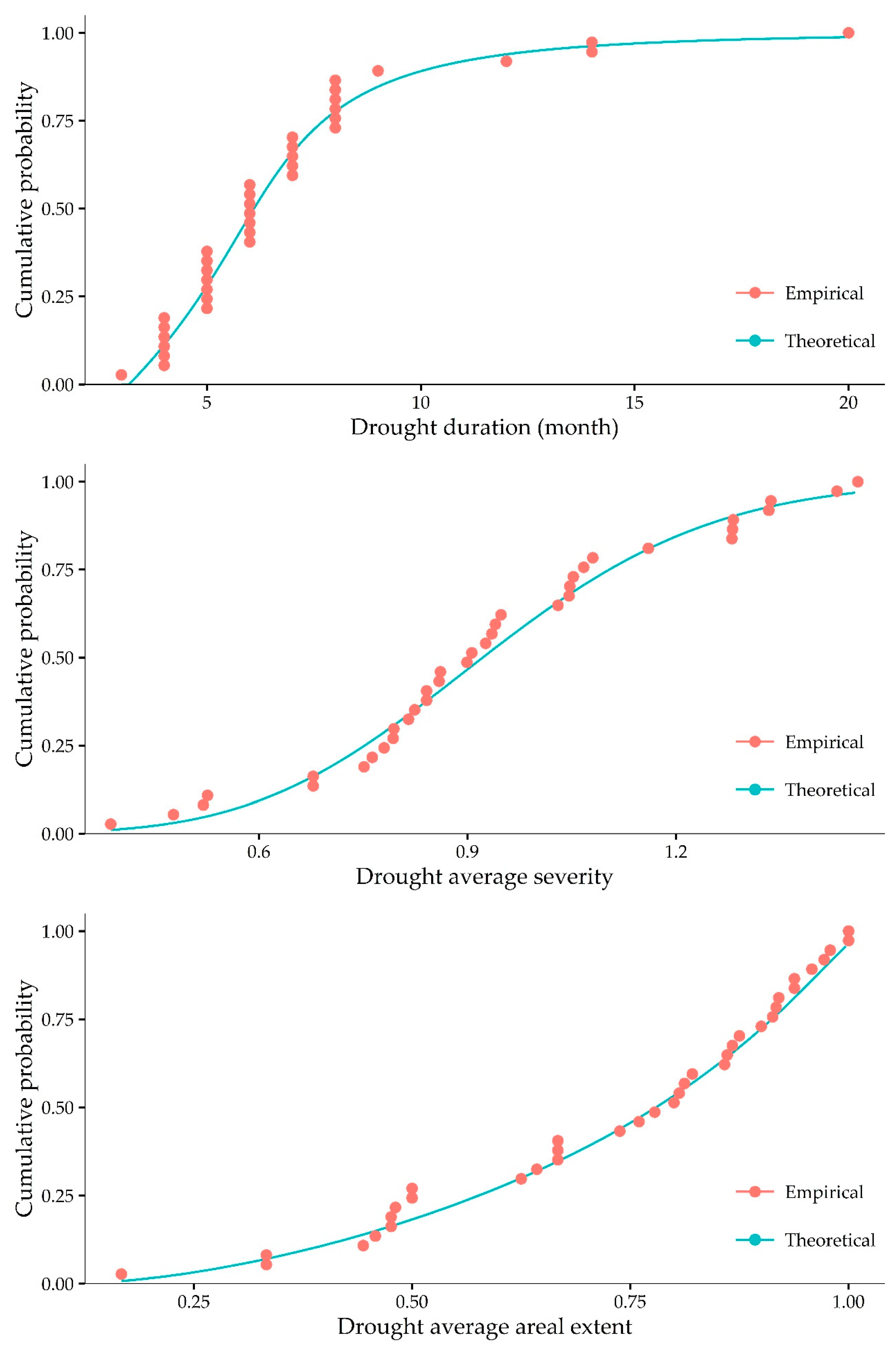
The univariate CDFs of drought characteristics are necessary to fit the copula functions [
], so the best fitting copula function can be used for further analysis. Here, the best-fitting copula is obtained after performing validation efforts utilizing
as the truth. For the purpose of fitting copulas, univariate empirical CDF values are used while the theoretical univariate CDF values are used in the synthetic simulations described below (
Figure 3). Among copula functions, by definition, the nature of the AMH requires Kendall’s tau between variables to be bounded between −0.18 and 0.33 [
27]. Since the
–
pair does not satisfy this requirement (
Table 4), an AMH function could not be fitted to this pair. Leave-one-out type validation of copula parameters show that the elliptical copula family results in better performance in bivariate and trivariate joint CDF estimation analysis than other copula families, while normal copula seems to have the best overall performance (
Table 5).
Analysis of drought period counts show a drought event is expected on average every 18 months (i.e.,
). Univariate drought
calculations using the univariate CDF of variables (
Figure 3) show on average drought events with
are expected every 4.15 years,
every 3.06 years, and
every 2.53 years (
Table 6). However, in many cases these univariate
estimates may not be sufficient for various drought investigations requiring bivariate or trivariate
information. These multivariate drought
values are calculated using the best fitting copula functions for the bivariate and the trivariate cases. As an example,
is calculated for the bivariate case as 7.13 years for the drought event with
and
; as 3.41 years for a drought event with
and
; and for the trivariate case
is calculated as 6.65 years for a drought event with
,
, and
.
The examples given above could be reproduced for infinitely many drought characteristic pairs or triplets. However, plots showing their multivariate variations often are necessary to understand the exact nature of their multivariate relations. However, to generate such plots the lengths of the available 37 drought events are not sufficient. Instead, the drought characteristics are fitted to different distributions and the best fitting distributions are later used to generate synthetic drought characteristic datasets that are used to generate multivariate
plots (
Figure 4 and
Figure 5). Parameters result in the smallest Kolmogorov–Smirnov statistics (
Table 7) are used to generate the relevant synthetic datasets. Results show log-logistic, normal, and logistic distributions result in the best fit (i.e., lowest errors) for the drought characteristics of
,
, and
, respectively (
Table 7). Hence, these distributions are used to create synthetic
,
, and
data.
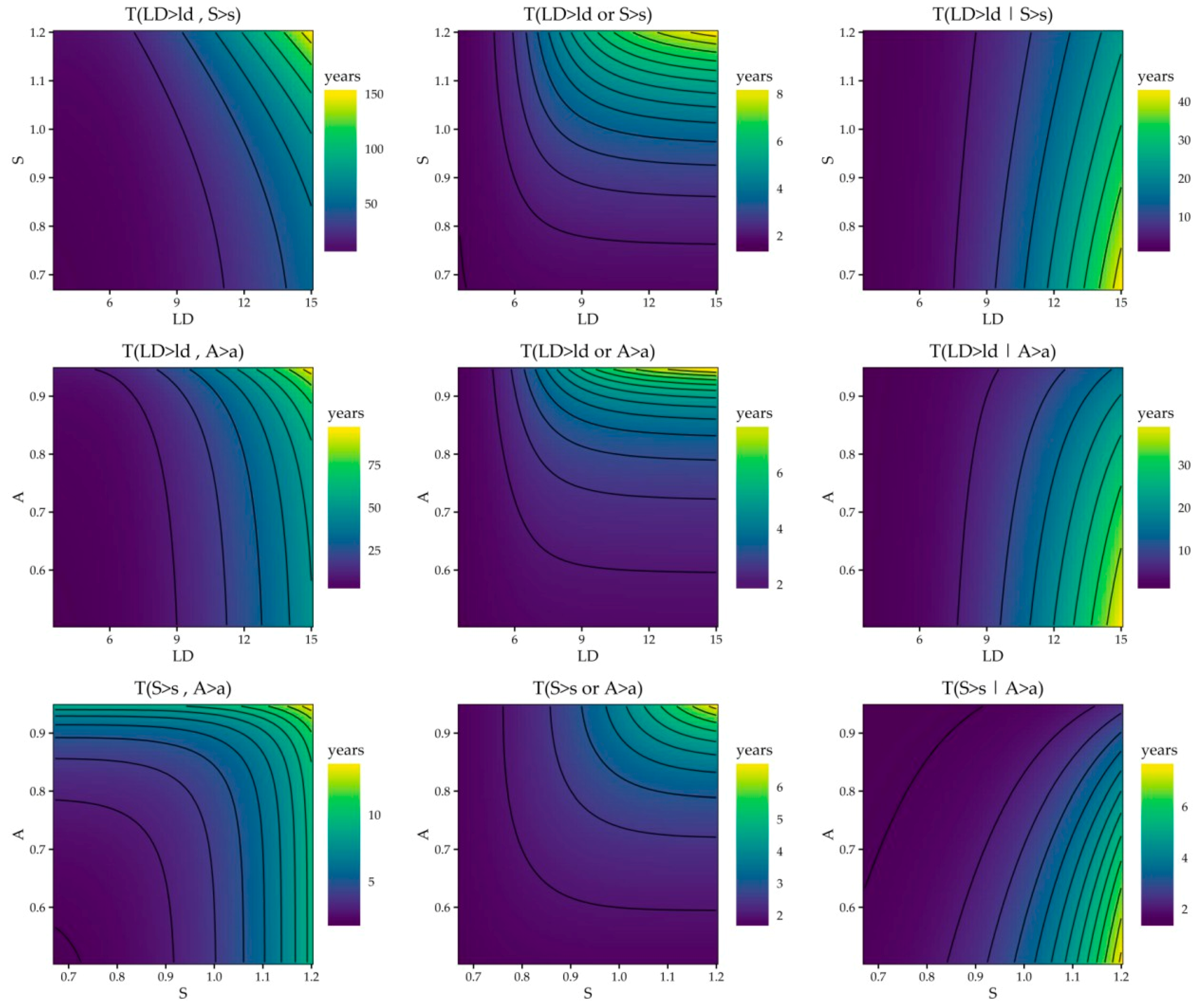
Three drought characteristics (
,
, and
) are considered in this study, hence three bivariate drought characteristic pairs (
,
, and
) are analyzed. Additionally, three bivariate drought operators (“and”, “or”, “conditional”) that are suited for various drought applications are also considered. Accordingly, a total of nine bivariate
maps were obtained for visual presentation efforts (
Figure 4). In
Figure 4, the left, middle, and right columns show “and”, “or”, and “conditional” scenarios, respectively; the top, middle, and bottom rows show the
,
, and
–S pairs, respectively.
The “and” scenario shows that the bivariate
has a higher sensitivity to
than
or
: When
is included in the bivariate
maps (left middle and top panels),
values are more impacted by
than
or
, particularly for higher values of
, while the sensitivity difference between
pairs is marginal. If a line is drawn from the lower left corner to the upper right corner of the
bivariate
figure (lower-left panel of
Figure 4), then the area to the left of this line shows the region where
is more sensitive to changes in
than
while the area on the right side of the line shows the region where
is more sensitive to changes in
than
. These results suggest that the overall sensitivity of
to these drought characteristics can be compared via
>
–
. On average, bivariate
values are much higher, particularly for higher values of
(
). Similar to the “and” case, the “or” case also show pareto front type plots but the pareto front direction is reversed (i.e., the middle column): on average almost one in 2.33 years a mild drought event with “
or
” or “
” is observed. As expected, the average
value for the “or” case is much lower than for the “and” case as the probability of an “or” case is higher than an “and” case. In the case of “conditional” drought
plots, the
values are most sensitive to the unconditioned value rather than the given observation (i.e., the lines are vertical), while this sensitivity decreases as the drought impact increases (higher
,
, or
). On average, the dynamic range of
values for conditional case are more similar to the “or” case, particularly for less severe drought events (e.g., for the bivariate case they range between 1.5 and 42 years). These conditional
values could be particularly useful if certain observations could be obtained. For example, if
, then
values range between 1.86 and 9.95 years for
(
Figure 4, top right panel).
Figure 5 shows that the trivariate
values are conditioned on both
and
. Given that it would be harder to digest 3D plots, trivariate cases are plotted for four separate
values (0.65, 0.75, 0.85, and 0.95). Similar to conditional bivariate plots, conditional trivariate plots also show that
values are sensitive to the unconditioned variables (i.e., the plots are perpendicular to the unconditioned variable). Additionally, the conditional trivariate contour plots show that when additional observations are available compared to the bivariate case, then
values decrease (i.e., if
, it is more likely that drought events with longer duration will happen). For example, the bivariate conditional plot for
shows
values ranging between 1.95 and 42.04, while the trivariate conditional plot for
shows
values ranging between 2.05 and 13.69. The conditional
values have much higher sensitivity to
when
than when
(
Figure 5); for greater
values, the return periods are much smaller for conditional
compared to smaller
values.
4. Conclusions
Droughts have many different spatial–temporal characteristics; hence, a better way to describe them is to use joint probability-based functions, rather than building drought-related analyses on univariate datasets as joint distribution of these drought characteristics often do not follow a particular known distribution. The current study offers a methodology to analyze the spatial–temporal multivariate aspect of droughts via copula functions in a probabilistic approach.
The results show that, among the drought characteristics, and are found to have significant linear dependence, implying their predictions using each other may yield reasonable forecasts, while the same may not be true for other relationships including . On the other hand, bivariate is more sensitive to variability in than or , implying that predictions of bivariate could be more accurate with the presence of than or . Nevertheless, observations of or narrow the variability window of trivariate predictions, particularly for higher values of or ; implying that or observations have utility in predictions of even though such predictions are more sensitive to variability in .
The flexibility of calculation for different multivariate drought scenarios clearly illustrates the power of the introduced methodology. Additionally, certain drought characteristics may precede others, hence such observed drought characteristics may prove very valuable when making inferences about non-observed drought characteristics, while such relations can be easily studied using the multivariate conditional copula methodology presented in this study. In particular, trivariate drought analysis scenarios could prove very helpful in estimating a particular drought characteristic given availability of other drought characteristic info.
Drought characteristics often have dataset-specific distributions. Even though elliptical family-based copula functions yielded better performance in this study, other studies found that different copula families perform better [
13,
20]. This implies that the optimality of the copula functions could be dataset- and case-specific; hence inter-comparisons of copula functions could be necessary before estimation of return periods in other studies. However, this result should be confirmed via independent studies before it can be generalized for copula function-related drought analyses.
In this study, ground station-based datasets are utilized in all of the analyses. While they provide the longest datasets over the most locations, these station-based datasets are spatially limited, often contain gaps in their time series, and may have user-dependent data quality. On the other hand, remote sensing-based datasets prove very powerful alternatives to station-based datasets as these spatially and temporally consistent datasets are available everywhere, including remote locations where installation of stations is not economically feasible. Therefore, remotely sensed datasets could be recommended as alternative reanalysis products to be used as such model datasets may provide consistent and sufficiently long time series for drought analysis.