The study of propagation, diffusion, and dispersion phenomena by analytical methods is possible only for few cases. Therefore, several researchers have proposed new approaches to better represent these phenomena. For several decades, a great number of numerical methods were initiated but found real use only in recent years with the rapid evolution of computing. Thus, numerical modeling has become an indispensable tool for a wide range of applications. Among these methods, Transmission Line Matrix (TLM) method is being increasingly used since seventies [
11], and its application field continues to expand [
19,
20,
21].
2.2.1. Transmission Line Matrix Method
TLM is a spatiotemporal numerical technique, explicit and stable, based on electrical networks [
19,
20,
21,
22]. It is introduced by Professors Peter Johns and Raymond Beurle [
23] at the electrical engineering department of Nottingham University (UK). This technique uses Huygens’ principle and is based on Maxwell’s equations [
11,
22,
24,
25]. It operates on a mesh structure where each element is represented by a transmission line that acts as an analogy between the physical quantity and an electrical equivalent (voltage or current) [
20,
24,
25,
26].
In TLM, each transmission line is excited with a pulse which will be monitored throughout the network. The injected pulse propagates along the line until it reaches a discontinuity (node) where it disperses [
27]. Each reflected pulse moves back along the line and becomes incident on the adjacent node after a time step Δt(s), and so on [
19,
21] (
Figure 1). At each iteration
k (Equation (11)), the TLM routine calculates the incoming pulses to determine the evolution of the physical quantity at a given point, then the reflected pulses in preparation for the next iteration [
26,
28] TLM can be one-dimensional, two-dimensional, or three-dimensional [
11,
28].
TLM has been compared with various other numerical methods such as the Finite Difference method (FDTD) [
22,
26,
29]. These comparisons define the power of this method to the studied case.
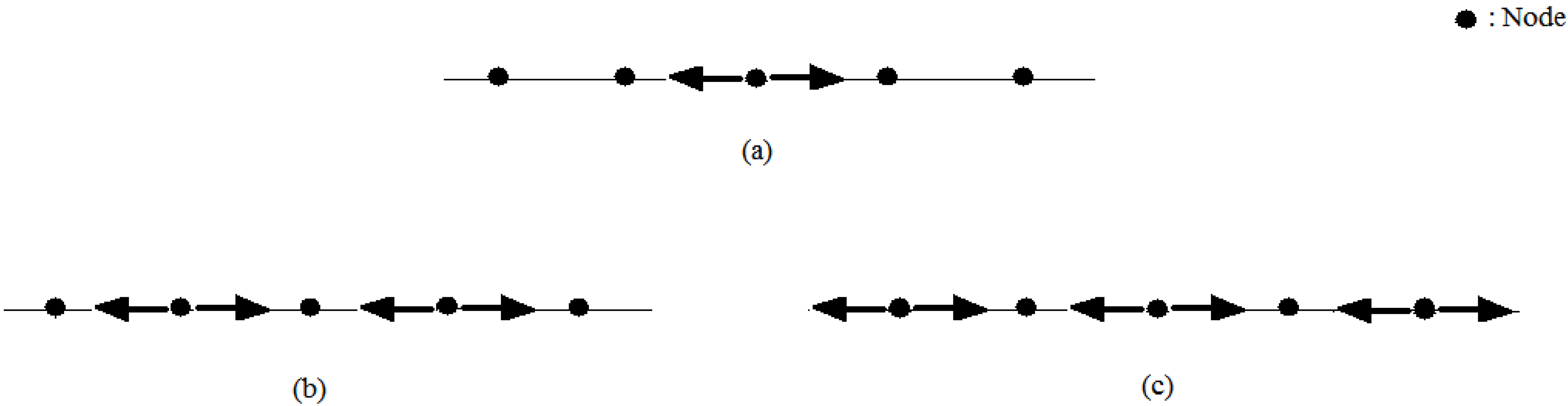
Figure 1.
Dispersion of an injected pulse. (a) pulse reflection; (b) the first iteration result; and (c) the second iteration result.
Figure 1.
Dispersion of an injected pulse. (a) pulse reflection; (b) the first iteration result; and (c) the second iteration result.
2.2.2. TLM Model for Pollutant Dispersion Phenomenon
Early TLM models for dispersion of a physical quantity, proposed the study of both phenomena (advection and diffusion) separately [
30,
31]. They were based on the concept that transfers the physical content of each node to the node adjacent downstream along the flow direction. According to the results obtained by de Cogan and Henini [
11,
31], this approach is poor. An alternative method is proposed [
11,
32] where the TLM model of dispersion is identical to the TLM model for diffusion with an added current generator
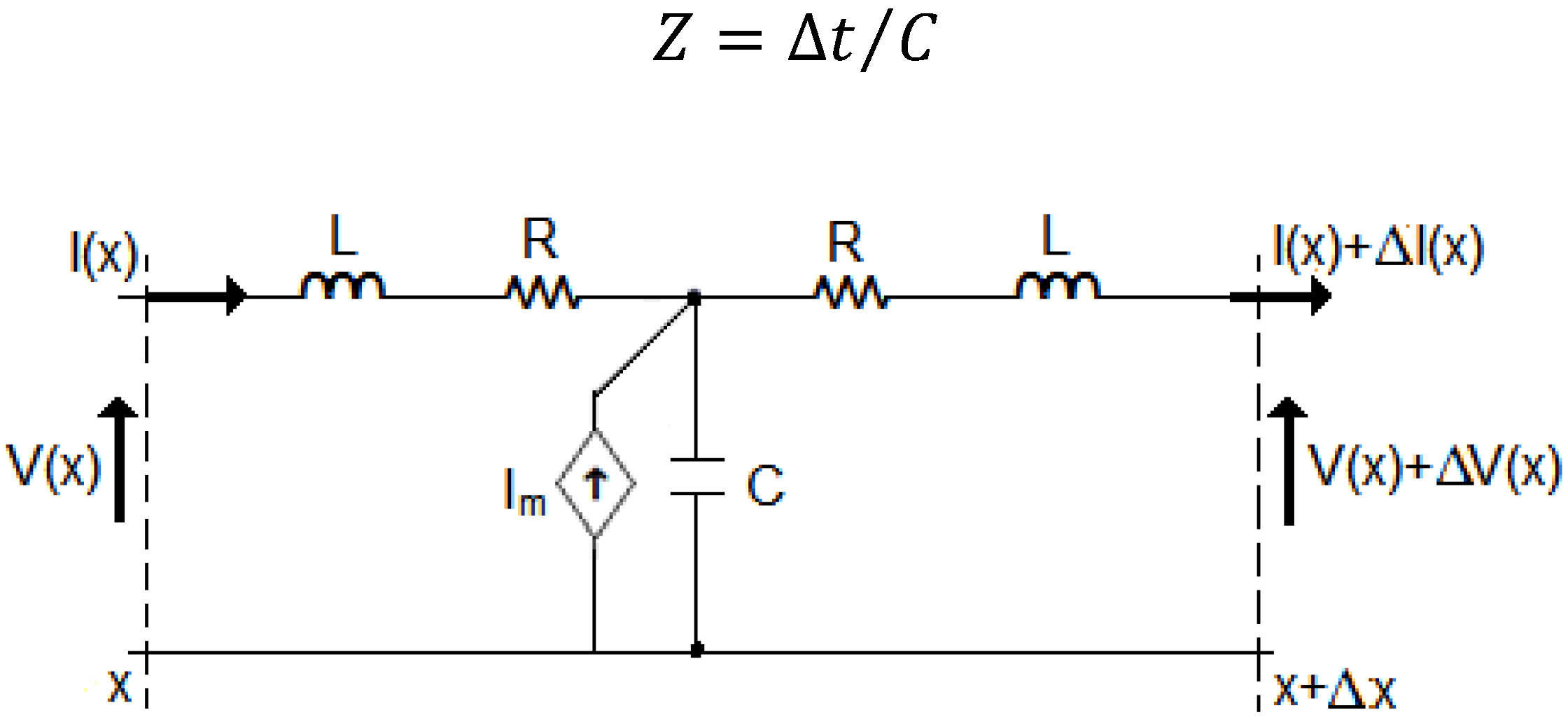
Im(A) at each node. Hence, a TLM model of a pollutant dispersion phenomenon is a perfectly insulated transmission line (conductance
G(Ω) null) of length Δ
x(m), that is electrically represented by two resistors
R(Ω), two inductors
L(H), and a capacitor
C(F) (
Figure 2). The TLM node is given on
Figure 3, where
I(x),
V(x), and
Z are, respectively, the intensity of current (A), the voltage (Volt), and the characteristic impedance (Ω) of the line. The latter is defined by the relation from Equation (12).
Figure 2.
Electrical representation of TLM dispersion model.
Figure 2.
Electrical representation of TLM dispersion model.
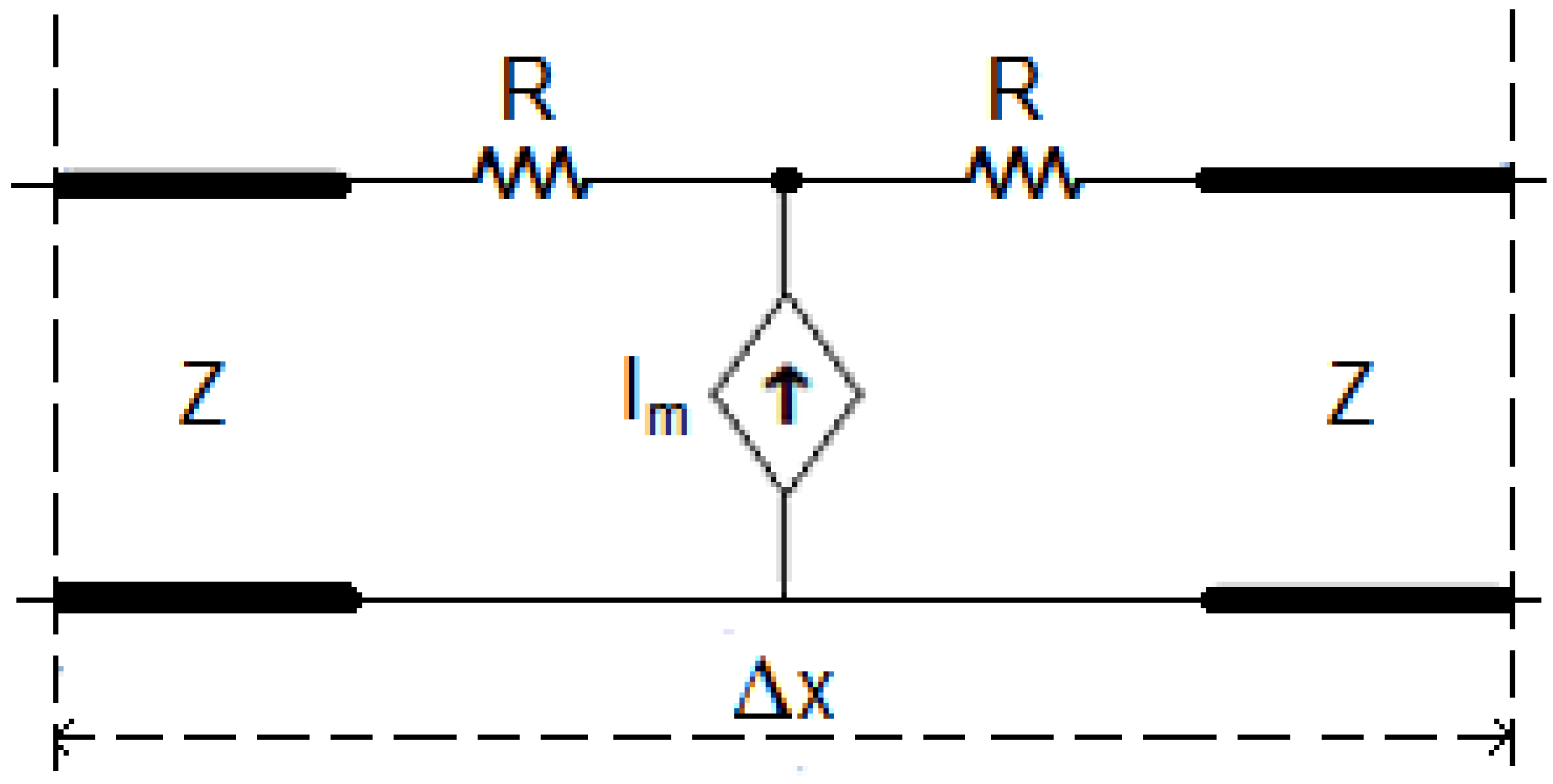
Figure 3.
TLM dispersion node.
Figure 3.
TLM dispersion node.
Rd,
Cd, and
Ld are, respectively, distributed resistance, capacitance, and inductance over the entire length Δ
x of the transmission line and are given by the following relationships:
The variation of the voltage on a piece of transmission line is equal to the sum of the voltage variation due to the inductance and the voltage drop across the resistor as shown in Equation (16):
The current intensity variation flowing through this piece of transmission line is equal to the current flowing through the capacitor to which we add a current generator
Im at the node (
n) as indicated by Equation (17):
where,
: Transconductance (Ω).
If ∆
x→0, Equation (17) becomes:
If we neglect the influence of the inductance by taking a small enough time step, the combination of Equation (16) and Equation (19) gives:
This equation is similar to Equation 3 and, therefore, we can model a phenomenon of pollutant dispersion by an electrical equivalent.
The addition of a current generator produces an additional voltage
at node (
n). Hence, the total pulse at iteration
k,
becomes:
and are, respectively, the incident pulses on left and right of node (n) at iteration k. and are the pulses at nodes adjacent (n+1) and (n–1) at iteration k–1.
Pulses reflected on left and right of node (
n) at iteration
k:
and
are given by Equation (23) and Equation (24):
The reflected pulses become incident on adjacent nodes at next iteration.
and
are incident pulses on left and right of node (
n) at iteration
k+1 and are given by Equation (25) and Equation (26):
and are respectively reflected pulses on right of node (n–1) and left of node (n+1).
Equations (21) to (26) form the TLM algorithm used to solve a wide variety of dispersion problems, such as chromatographic processes, heat exchanges, heat flow and diffusion of electric species in semiconductors [
32,
33]. Analogy between Equation (3) and Equation (20) gives:
According to the Courant-Friedrichs-Lewy stability criterion [
11,
34], TLM Dispersion models are stable if:
, where
s is the convection number (Equation (31)) and
r is the diffusion number (Equation (32)).
2.2.4. TLM parameters Optimization
The TLM dispersion model is applied on experimental data of Atkinson and Davis [
12] and uses the input data of
Table 2. The injected total tension is equivalent to initial concentration at dumping point (Equation (29)). The tracer is poured into an elementary volume of the river
∆v = ∆x∆y∆z, where
∆y and
∆z are, respectively, the width (m) and depth (m) of the river at the dumping point. This dilution leads to an initial concentration of the tracer of 1110 μg/L at dumping point.
Table 2.
TLM input data.
| Input Data | Parameter/Unit | Value |
|---|
| Experiment duration | t (s) | 35,000 |
| Time step | ∆t (s) | 10 |
| Test distance | ℓ (m) | 14,000 |
| Distance step | ∆x (m) | 25 |
| Characteristic impedance | Z (Ω) | 10 |
| Injected total tension | V(1) (Volt) | 1110 |
The TLM parameters Rd, gm, and initial total tension V0 have been optimized to keep the modeling simple. In TLM technique, the time step ∆t must be less than the time constant (RC) leading to a choice of Rd > 0.8. The conductance is the resistance inverse, so gm < 1.25. The initial total tension at each node must be inferior to the injected total tension (first node), so V0 (n ≠ 1) < 1110.
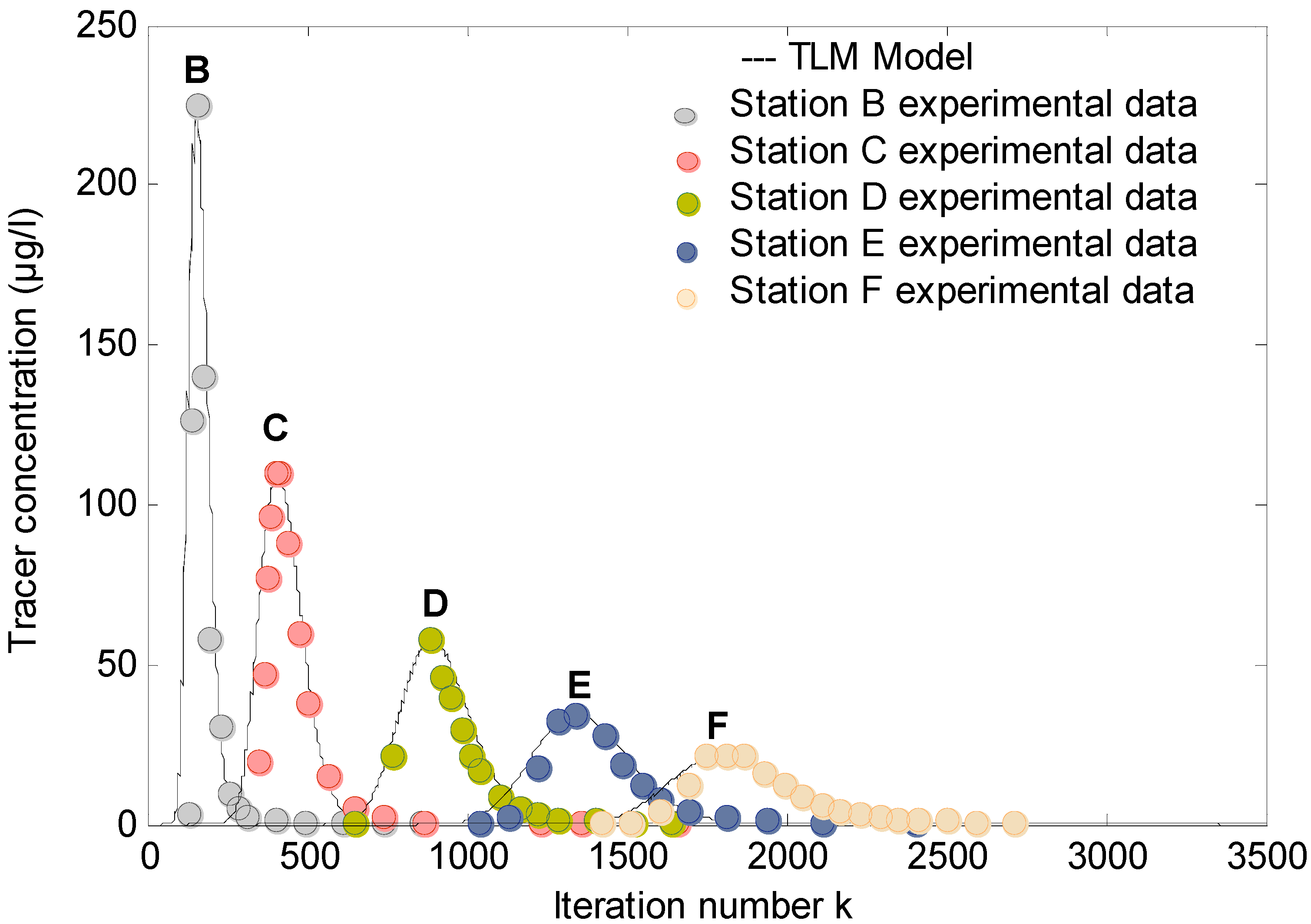
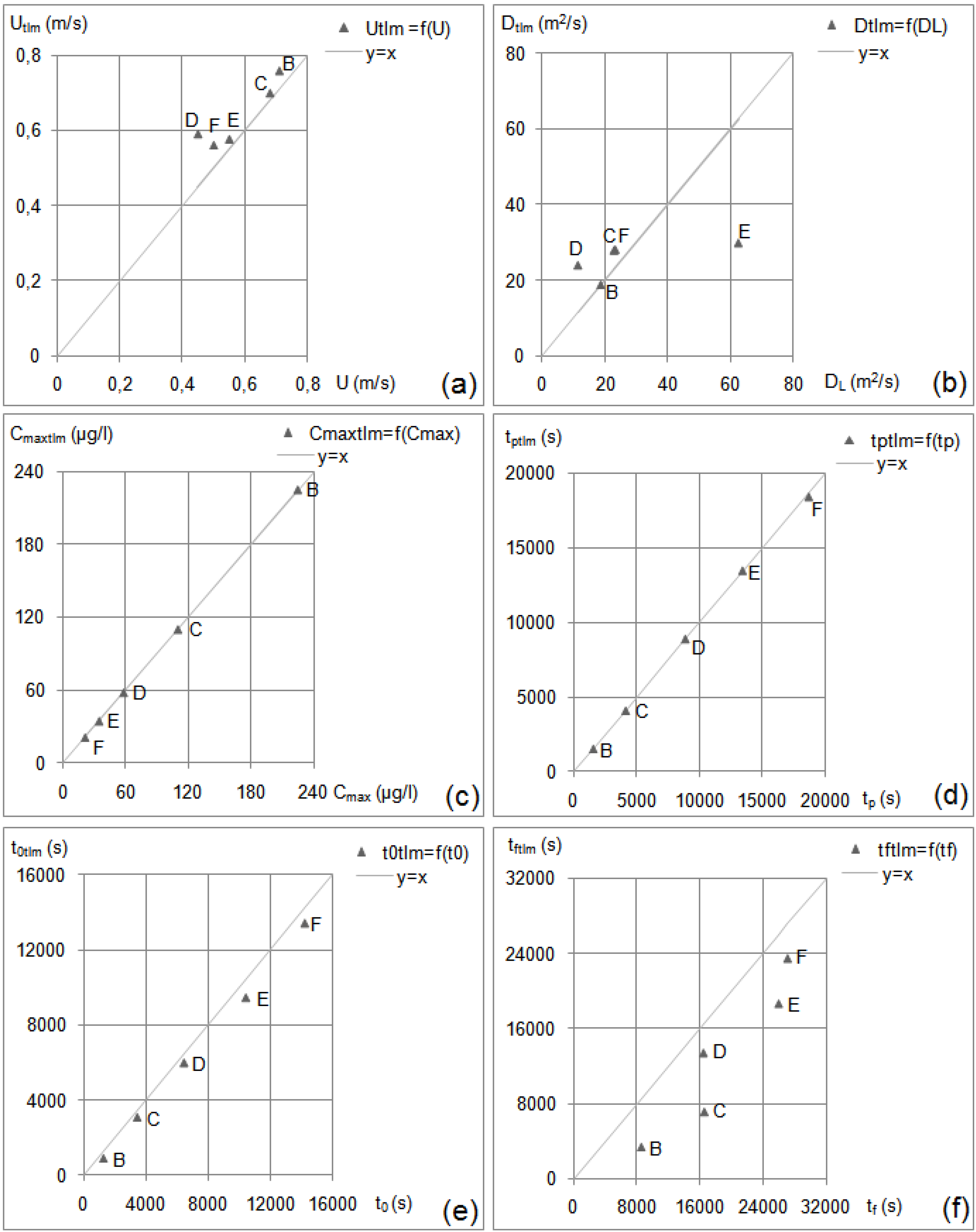
The TLM model, with the input data of
Table 2 and the above TLM parameters, is run. The obtained TLM results
V =
f(
k) are compared to the experimental data of Atkinson and Davis
C =
f(
t),
i.e., the TLM characteristic parameters (
k0, Vmax, kp, kf) are compared to the electrical equivalents of experimental characteristic parameters (
t0, Cmax, tp, tf) (
Table 1). The electrical equivalents (
k'0, V'max, k'p, k'f) are deduced from Equation (11) and Equation (29). The optimized TLM parameters (
Rd,
gm, and
V0) correspond to the minimal values
(∆k0, ∆Vmax, ∆kp, ∆kf).
This optimization is acceptable if we can validate, statistically, and interpret, physically, the differences between the experimental parameters and the physical equivalents of TLM parameters which are calculated using Equation (27), Equation (28), and Equation (29).